Положительный угол. Отрицательный угол. Полный оборот в градусах.
- Альфашкола
- Статьи
- Положительное и отрицательное направление угла
Когда два луча выходят из одной точки и при этом не совпадают, они образуют угол.
Углы обычно измеряются в градусах обозначается как \(°\). Углы имеют положительное направление:
и отрицательное напрвление:
Полный оборот, это когда угол проходит \(360°\). Поэтому один градус это \(\frac{1}{360}\) окружности:
Углы больше 360 градусов
Мы обсуждали, что когда объект совершает один полный оборот вокруг точки, он охватывает \(360°\), однако, когда объект делает более одного оборота, он делает угол больше \(360°\) градусов.
Чтобы узнать количество оборотов, сделанных при вращении, мы подсчитываем, сколько раз к нему можно добавить \(360\), чтобы получить число, равное или меньшее заданного угла. Аналогично, мы находим число, которое можно умножить на \(360\) чтобы получить число меньше, но ближе к заданному углу.
Пример 1.
1. Найдите количество оборотов и угол:
- \(380°\)
- \(770°\)
- \(1000°\)
Решение
- \(380°\) \(= (1 × 360°) + 20°\) один оборот и \(20°\)
- \(770° = (2 × 360°) + 50°\) два оборота и \(50°\)
- \(1000° = (2 × 360°) + 280°\) два оборота \(280°\)
Положительные и отрицательные углы
Пример 2. Найти соответствующий положительный угол:
- -35°
- -60°
- -180°
- — 670°
Решение:
Мы будем добавляем 360 к углу, чтобы получить соответствующий положительный угол.
- -\(35°= 360 + (-35) = 360 — 35 = 325°\)
- \( -60°= 360 + (-60) = 360 — 60 = 300°\)
- \( -180°= 360 + (-180) = 360 — 180 = 180°\)
- \(-670°= 360 + (-670) = -310\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Жанна Игоревна Стефанович
Репетитор по математике
Стаж (лет)
Образование:
Гродненский государственный университет им.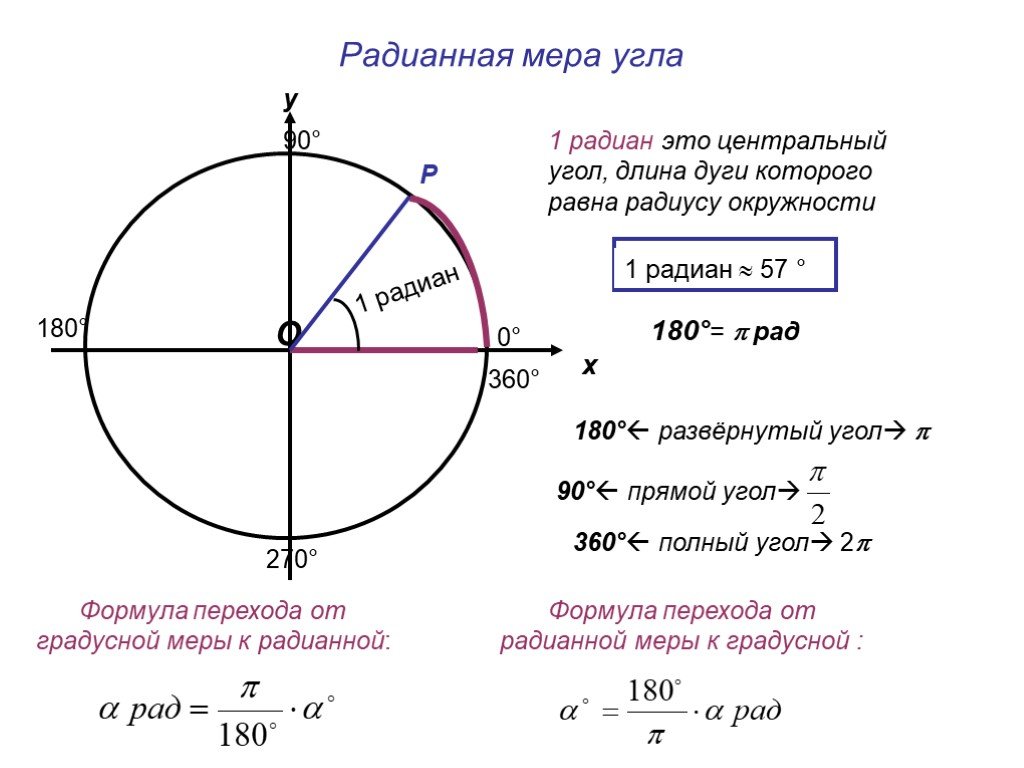 Янки Купалы
Янки Купалы
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Елена Сергеевна Журова
Репетитор по математике
Стаж (лет)
Образование:
Белорусский государственный педагогический университет им. М. Танка
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Адель Василевич Халиков
Репетитор по математике
Стаж (лет)
Образование:
Казанский федеральный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Репетитор по олимпиадной математике
- Репетитор по алгебре
- Подготовка к ЕГЭ по математике (профильный уровень)
- Репетитор для подготовки к ЕГЭ по физике
- Репетитор по грамматике русского языка
- Репетитор по английскому для взрослых
- ВПР по математике
- Репетитор по географии для подготовки к ЕГЭ
- Репетитор по информатике для подготовки к ОГЭ
- Подготовка к ОГЭ по литературе
Похожие статьи
- Теорема Виета
- Задачи на оптимальный выбор
- Интегралы от тригонометрических функций
- Задачи на движение по воде
- Летнее меню: рацион школьника летом
- Обучение старшеклассников: как найти общий язык с учениками, если разница в возрасте небольшая?
- 7 продуктов для памяти
- Как сделать первый шаг и пригласить объект симпатии на свидание
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
Репетитор ЕГЭ, ОГЭ (ГИА) подготовка к сдаче экзамена по физике и математике за 500 руб.
 в месяц
в месяцЧем больше ваш ребенок знает,
тем большей властью обладает.
Древняя мудрость
Репетитор ЕГЭ, Репетитор ОГЭ (ГИА) — с каким трепетом произносит эти слова любой родитель, желающий чтобы его чадо успешно сдало этот ненавистный ЕГЭ или ОГЭ(ГИА) и поступило в желаемый ВУЗ.
Да, проблема есть …
Единый государственный экзамен (ЕГЭ), Основной государственный экзамен (ОГЭ) или как его называли раньше ГИА, серьезное испытание в жизни любого учащегося. От его результата зависит, удастся ли ему получить желаемое образование и профессию, о которой он мечтает.
Хватает ли одной школьной подготовки для успешной сдачи ЕГЭ или ОГЭ?
Ответ очевиден – нет!
Школьная подготовка к ЕГЭ (ОГЭ) сейчас стала значительно лучше. Однако, для получения высокого результата по ЕГЭ (ОГЭ) одной школьной подготовкой, несомненно, не обойтись. Дополнительные занятия просто необходимы, причем индивидуально, а не в группе.
Дополнительные занятия просто необходимы, причем индивидуально, а не в группе.
Здесь две проблемы:
- найти хорошего репетитора – в сельской местности да и в небольших городах это далеко не всегда можно сделать
- хороший репетитор стоит дорого – от 1500 руб/час
А если нужно заниматься по двум предметам? Такую финансовую нагрузку позволить себе может далеко не каждая семья.
Выход из данной, казалось бы, безнадежной ситуации есть – поступить в «Твою Школу», где можно изучать физику и математику всего за 500 руб/месяц!!!
Даже если ученик круглый отличник и ему не нужны репетиторы, все равно необходимо ликвидировать «белые пятна», которые наверняка у него есть …
Если математика и физика для него — это инструмент для осуществления своей мечты о профессии, то этим инструментом необходимо владеть профессионально. Всякие хитрости здесь не помогут, если он «плавает» по этим предметам…
Самая большая неприятность «белых пятен» — их не видно «изнутри». Трудно понять, где и какие пробелы имеются в знаниях.
Трудно понять, где и какие пробелы имеются в знаниях.
Школьники искренне считают, что они в общем все знают. «Белые пятна» просто не проявляются, пока дело не доходит до практики. И лучший вариант, если это будет практика учебная, а не «боевая»…
«Белые пятна» — самая большая проблема для современного школьного образования. Поэтому мы и создали «Твою Школу», которая устраняет «подводные камни» на пути учащихся.
И еще…
В «Твоей Школе» идет настоящий учебный процесс. Репетиторство в наше время — уже устаревшее явление. Оно было актуально во времена вступительных экзаменов в ВУЗы. Особенно прискорбно, что за последние годы появилось большое число лже-репетиторов, не имеющих высшего образования. Возможно некоторые из них и знают предмет, но не знакомы с методикой преподавания и школьной психологией. А знать самому это еще не значит уметь научить других – это совсем не одно и то же. Репетировать ЕГЭ и ОГЭ — бессмысленное занятие по нашему мнению.
«Твоя Школа» — это уникальная возможность гарантированно подготовиться на высоком уровне к сдаче экзамена на желаемый балл.
Готовиться к ЕГЭ и ОГЭ вместе с «Твоей Школой»: удобно в любое время и в любом месте.
И так…
Если Ты решил, что нужно повысить квалификацию — у Тебя есть возможность приступить к этому немедленно! «Твоя Школа» ждет Тебя и желает успеха!
Поступить в «Твою школу» очень просто: нажми на кнопку «Оформить заявку» и заполни регистрационную форму. Наш сотрудник обязательно свяжется с Тобой и ответит на все твои вопросы.
Первое занятие в «Твоей Школе» — БЕСПЛАТНО!!!
Добро пожаловать в «ТВОЮ ШКОЛУ»
Сколько градусов в окружности?
МАТЕМАТИКА — Геометрия
Задумывались ли вы когда-нибудь…
- Сколько градусов в окружности?
- Какая связь между радиусом и диаметром круга?
- Как называется расстояние вокруг края круга?
Теги:
См. все теги
все теги
- 2πr,
- Вавилоняне,
- форма,
- πr2,
- Математика,
- Геометрия,
- Круг,
- Степень,
- Площадь,
- Треугольник,
- Пирог,
- Хулахуп,
- Самолет,
- Точка,
- Расстояние,
- Радиус,
- Диаметр,
- Окружность,
- Район,
- Периметр,
- Пи,
- Экспонента,
- Земля,
- Вс,
- Орбита,
- Календарь
Сегодняшнее чудо дня было вдохновлено Анной Грейс из Зимнего Интервилля. Анна Грейс Уондерс , “ Почему круг имеет бесконечные линии симметрии? «Спасибо, что ДУМАЕТЕ вместе с нами, Анна Грейс!
Анна Грейс Уондерс , “ Почему круг имеет бесконечные линии симметрии? «Спасибо, что ДУМАЕТЕ вместе с нами, Анна Грейс!
Любишь геометрию? Мы делаем! Мы хотели сделать Чудо дня об особой форме, но не могли решить, какую фигуру использовать. Однако чем больше мы думали об этом, тем больше мы возвращались к той же форме. Что это было? Круг, конечно!
Что вам больше всего нравится в кругах? Нам нравятся их идеально круглые формы. У них нет тех заостренных концов, которые вы найдете на квадратах и треугольниках.
Некоторые из наших любимых вещей имеют форму кругов. Например, наш любимый десерт — пирог — имеет форму круга. Как и наша любимая игрушка: хула-хуп. Какие еще предметы в форме круга вы видите или используете каждый день?
Учителя геометрии определяют окружность как набор точек на плоскости, находящихся на одинаковом расстоянии от центральной точки. Это означает, что круги плоские. Когда вы изучаете круги, вы узнаете, что у каждого круга есть радиус, диаметр, длина окружности и площадь.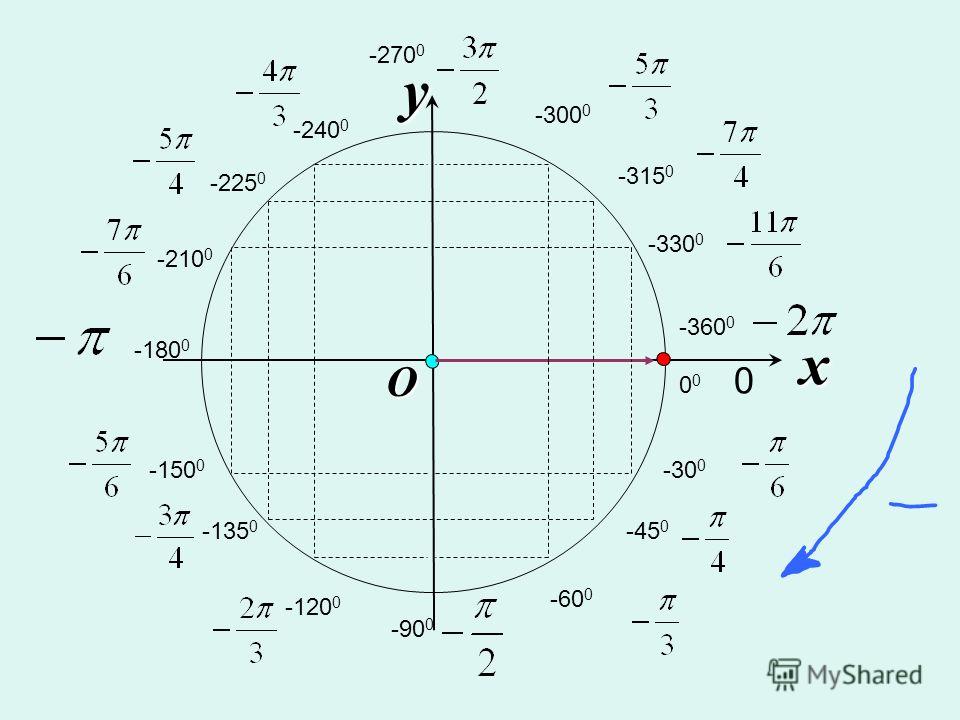
Радиус круга — это расстояние от его центра до края. Диаметр круга — это расстояние поперек круга в его самом широком месте. Диаметр круга всегда ровно в два раза больше его радиуса.
Периметр круга — расстояние вокруг его края — называется его окружностью. Чтобы вычислить длину окружности, нужно знать ее радиус.
Формула длины окружности: 2πr, где r — радиус окружности, а π — число пи (приблизительно 3,141592). Поскольку диаметр круга в два раза больше радиуса, вы также можете представить формулу длины окружности как πd, где d — диаметр круга.
Площадь круга измеряется количеством квадратных единиц внутри круга. Еще раз, вам нужно знать радиус. Формула площади круга: πr 2 . 2 в формуле — это показатель степени, что означает, что вы умножаете радиус сам на себя. Таким образом, вместо формулы площади круга можно было бы написать πrr.
Одна замечательная вещь о кругах, которую знают все учителя геометрии, заключается в том, что если вы знаете один из этих фактов — радиус, диаметр, длину окружности или площадь — вы можете вычислить все остальные значения! Например, если вы знаете радиус круга, вы можете вычислить его диаметр, длину окружности и площадь.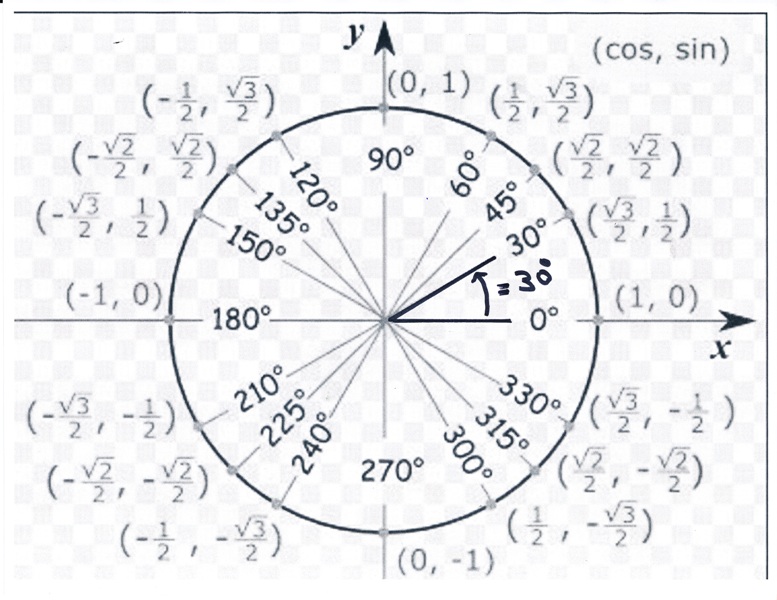
Еще один интересный аспект кругов заключается в том, что каждый круг можно разделить на 360 единиц, называемых градусами. Итак, если вы совершите полный круг, вы повернетесь на 360 градусов. Если вы просто повернетесь наполовину — полукругом — вы повернетесь на 180 градусов.
Так почему же 360 градусов вместо чего-то попроще, например, 100 градусов? Математики считают, что виноваты древние вавилоняне. Около 2400 г. до н.э. они заметили круговое движение Земли вокруг Солнца. Они также подсчитали, что для завершения этой круговой орбиты потребовалось около 360 дней.
Поэтому круговой путь решили разделить на 360 градусов. Таким образом, они могли легко отслеживать прохождение каждого дня по круговому календарю. Так что если вы запутались в геометрии с количеством градусов в окружности, виноваты вавилоняне!
Интересно, что дальше?
Завтрашнее чудо дня — это глоток свежего воздуха!
Попробуйте
Готовы повеселиться с геометрией? Обязательно проверьте следующие задания с другом или членом семьи:
- Если вы хотите узнать больше о градусах и углах, посмотрите это увлекательное онлайн-занятие «Углы».
 Сможете ли вы правильно угадать все углы, которые вам нужны, чтобы брызгать водой из шланга на различные предметы?
Сможете ли вы правильно угадать все углы, которые вам нужны, чтобы брызгать водой из шланга на различные предметы? - После того, как вы попрактикуетесь с углами, попробуйте онлайн-задание «Угадай случайный угол». Нажмите кнопку, чтобы сгенерировать случайный угол, введите свое предположение, а затем посмотрите, насколько близко вы были к метке!
- Вам трудно представить себе, как определяется число Пи? Зайдите в Интернет, чтобы посмотреть визуальное представление о том, как катящийся круг иллюстрирует число Пи. Попробуйте повторить то, что видите, с помощью круга и линейки дома.
Wonder Sources
- http://www.coolmath.com/reference/circles-geometry.html
- http://mathforum.org/library/drmath/view/59075.html
Получили?
Проверьте свои знанияWonder Contributors
Благодарим:
Braeden
за ответы на вопросы по сегодняшней теме Wonder!
Продолжайте удивляться вместе с нами!
Что вас интересует?
Wonder Words
- радиус
- диаметр
- окружность
- район
- геометрия
- самолет
- периметр
- формула
- заостренный
- аспект
- расстояние
- показатель степени
- решил
- запутался
- интересно
- рассчитано
- измерение
- математиков
Примите участие в конкурсе Wonder Word
Оцените это чудо
Поделись этим чудом
×ПОЛУЧАЙТЕ СВОЕ ЧУДО ЕЖЕДНЕВНО
Подпишитесь на Wonderopolis и получайте Чудо дня® по электронной почте или SMS
Присоединяйтесь к Buzz
Не пропустите наши специальные предложения, подарки и рекламные акции.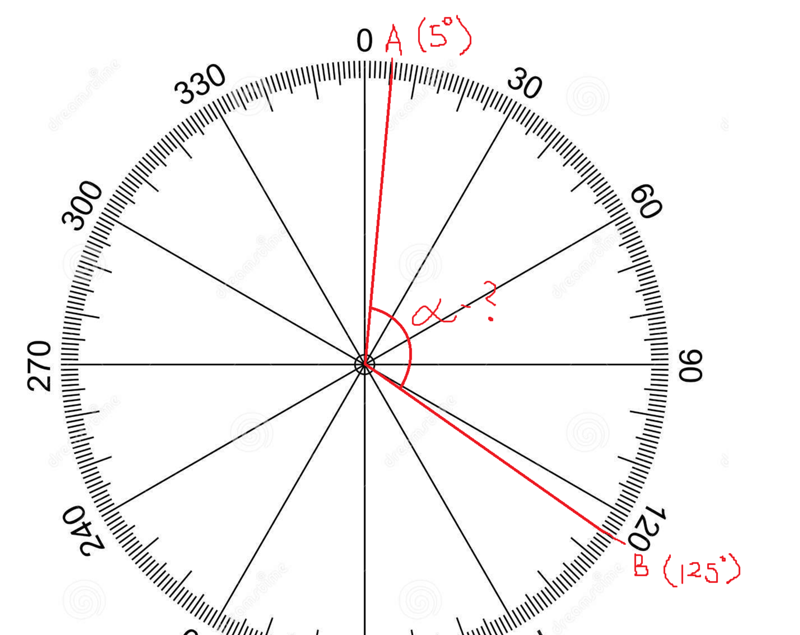 Узнай первым!
Узнай первым!
Поделитесь со всем миром
Расскажите всем о Вандополисе и его чудесах.
Поделиться Wonderopolis
Wonderopolis Widget
Хотите делиться информацией о Wonderopolis® каждый день? Хотите добавить немного чуда на свой сайт? Помогите распространить чудо семейного обучения вместе.
Добавить виджет
Ты понял!
Продолжить
Не совсем!
Попробуйте еще раз
5.2: Углы — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 13859
- Дэвид Липпман и Мелони Расмуссен
- Магазин OpenTextBookStore
Поскольку многие приложения, связанные с кругами, также включают в себя вращение круга, естественно ввести меру поворота или угла между двумя лучами (прямыми сегментами), исходящими из центра круга.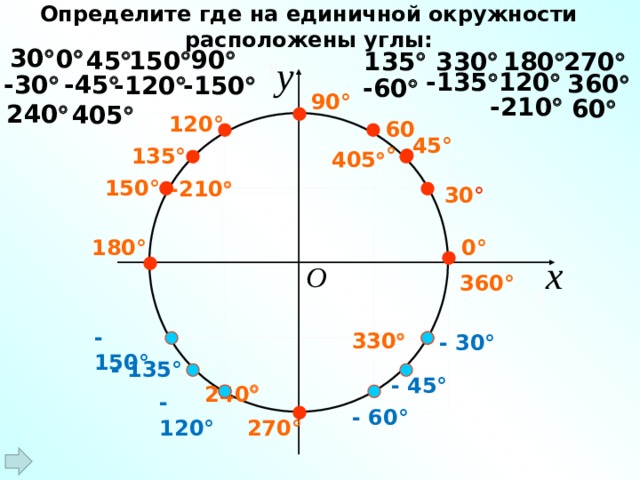 Измерение угла, с которым вы, скорее всего, знакомы, — это градусы, поэтому мы начнем с него.
Измерение угла, с которым вы, скорее всего, знакомы, — это градусы, поэтому мы начнем с него.
Определение: мера угла
мера угла — это мера между двумя пересекающимися линиями, отрезками линий или лучами, начинающаяся с начальной стороны и заканчивающаяся на конечной стороне . Это мера вращения, а не линейная мера.
Измерение углов
Определение: градусы
градус является измерением угла. Один полный оборот вокруг окружности равен 360 градусам, поэтому один градус равен 1/360 окружности.
9{\circ}\).Определение: стандартное положение
При измерении углов на окружности, если не указано иное, мы измеряем углы в стандартном положении : начиная с положительной горизонтальной оси и с вращением против часовой стрелки.
Пример \(\PageIndex{1}\)
Задайте градусную меру угла, изображенного на окружности.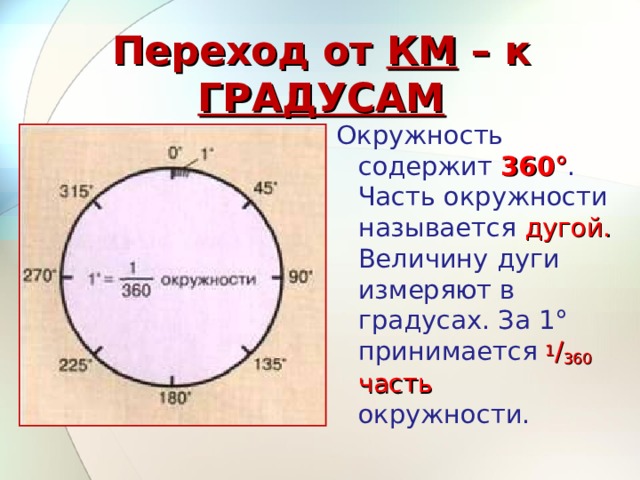 \circ\), каждый четверть оборота равен 360/4 = \(9{\circ}\).
\circ\), каждый четверть оборота равен 360/4 = \(9{\circ}\).
Переход на греческий язык
При представлении углов с помощью переменных традиционно используются греческие буквы. Вот список часто встречающихся греческих букв.
| \(\тета\) | \(varphi\) или \(\phi\) | \(\альфа\) | \(\бета\) | \(\гамма\) |
| тета | фи | альфа | бета | гамма |
Работа с углами в градусах
Обратите внимание, что, поскольку в одном обороте 360 градусов, угол больше 360 градусов будет означать более 1 полного оборота. Показанное на окружности результирующее направление, в котором конечные точки сторон этого угла будут такими же, как и для другого угла от 0 до 360 градусов.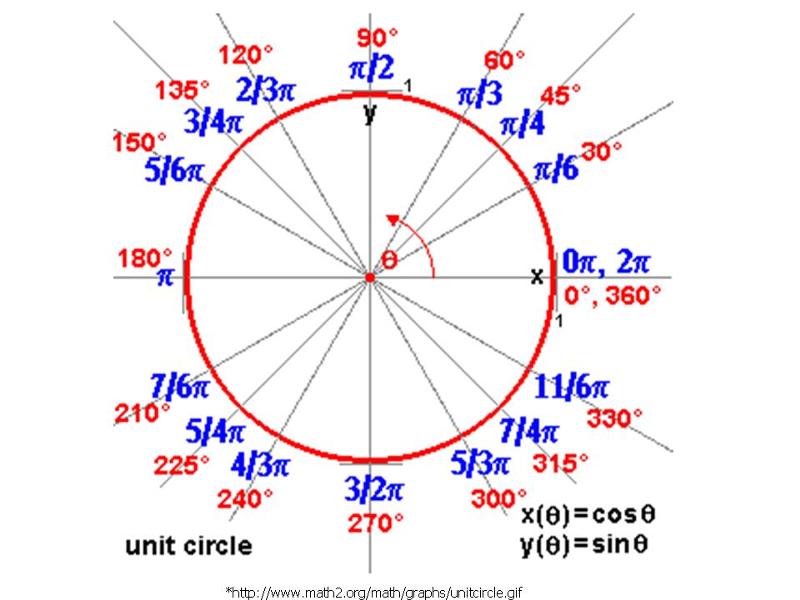 Эти углы будут называться котерминалов 9.{\circ}\номер\]
Эти углы будут называться котерминалов 9.{\circ}\номер\]
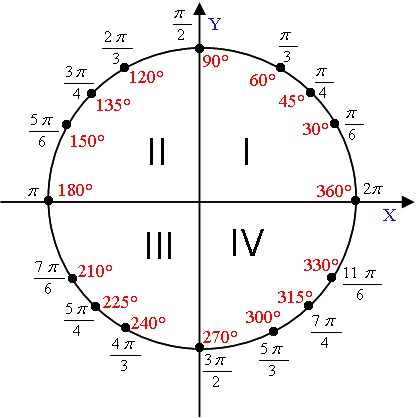
Может быть полезно ознакомиться с часто встречающимися углами за один оборот окружности. Обычно встречаются углы, кратные 30, 45, 60 и 90 градусам. Эти значения показаны справа. Запоминание этих углов и понимание их свойств будет очень полезно, поскольку мы изучаем свойства, связанные с углами
.Углы в радианах
Хотя измерение углов в градусах может быть привычным делом, это часто усложняет дело, поскольку единицы измерения могут мешать вычислениям. По этой причине обычно используется другая мера углов. Эта мера основана на расстоянии вокруг окружности.
Определение: длина дуги
Длина дуги — это длина дуги, \(s\), вдоль окружности радиуса \(r\), стянутой (вытянутой) углом \(\theta\).
Это часть окружности между начальной и конечной сторонами угла.
Длина дуги, огибающей весь круг, называется окружностью круга.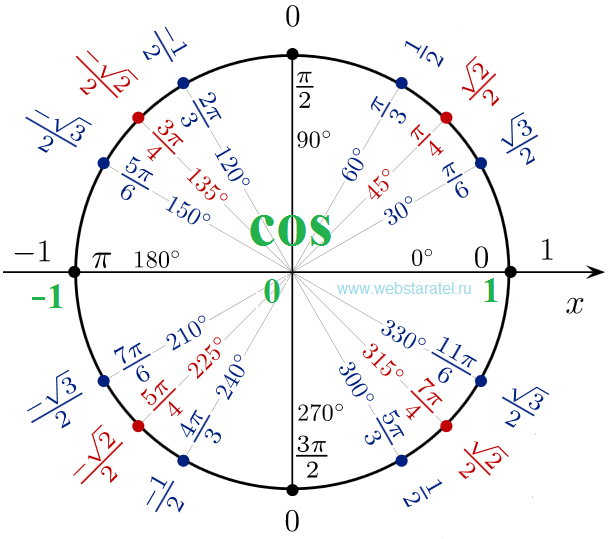 {th}\) полной окружности, поэтому для меньшего круга длина дуги = \(\dfrac{1}{8 } (4\pi )=\dfrac{1}{2} \pi\), а для большего круга длина дуги или длина дуги = \(\dfrac{1}{8} (6\pi )= \dfrac{3}{4} \pi\).
{th}\) полной окружности, поэтому для меньшего круга длина дуги = \(\dfrac{1}{8 } (4\pi )=\dfrac{1}{2} \pi\), а для большего круга длина дуги или длина дуги = \(\dfrac{1}{8} (6\pi )= \dfrac{3}{4} \pi\).
Обратите внимание, что произойдет, если мы найдем отношение длины дуги к радиусу окружности:
Меньший круг: \(\dfrac{\dfrac{1}{2} \pi }{2} =\dfrac{1}{4} \pi\)
Большой круг: \(\dfrac{\dfrac{3}{4} \pi }{3} =\dfrac{1}{4} \pi\)
Отношение одинаковое независимо от радиуса круга – оно зависит только от угла. Это свойство позволяет нам определить меру угла на основе длины дуги.
радиан
радиан мера угла – это отношение длины дуги окружности, образуемой углом, к радиусу окружности.
Другими словами, если s — длина дуги окружности, а \(r\) — радиус окружности, то
радиан мера\(=\dfrac{s}{r}\)
Если радиус окружности равен 1, то мера радиана соответствует длине дуги.
Поскольку мера радиана представляет собой отношение двух длин, это безразмерная мера 9\ circ \) = \ (\ dfrac {\ pi} {2} \) радиан
Пример \(\PageIndex{5}\)
Найдите в радианах меру одной трети полного оборота.
Решение
Для любого круга длина дуги вдоль такого поворота будет равна одной трети окружности, \(C=\dfrac{1}{3} (2\pi r)=\dfrac{2\pi г{3}\). Радианная мера будет равна длине дуги, деленной на радиус:
\[\text{Радианная мера} = \dfrac{2\pi r}{3r} =\dfrac{2\pi }{3}\]
преобразование между радианами и градусами 9{\circ}\номер\]
Точно так же, как мы перечислили все общие углы в градусах на окружности, мы должны также перечислить соответствующие значения в радианах для обычных мер окружности, соответствующих градусам, кратным 30, 45, 60 и 90 градусам. Как и в случае с измерениями градусов, было бы целесообразно запомнить их.
Мы можем работать с радианами угла так же, как мы работаем с градусами.
Пример \(\PageIndex{8}\)
Найдите угол \(\beta\), котерминальный углу \(\dfrac{19\pi }{4}\), где \(0\le \beta <2\pi\).
Решение
Работая в градусах, мы нашли котерминальные углы, прибавив или вычитая 360 градусов, то есть полный оборот. Точно так же в радианах мы можем найти котерминальные углы, добавляя или вычитая полные обороты \(2\pi\) радиан.
Точно так же в радианах мы можем найти котерминальные углы, добавляя или вычитая полные обороты \(2\pi\) радиан.
\[\dfrac{19\pi }{4} -2\pi =\dfrac{19\pi }{4} -\dfrac{8\pi }{4} =\dfrac{11\pi }{4 }\nonumber\]
Угол\(\dfrac{11\pi }{4}\) котерминальный, но не меньше \(2\pi\), поэтому вычитаем еще один поворот.
\[\dfrac{11\pi }{4} -2\pi =\dfrac{11\pi }{4} -\dfrac{8\pi }{4} =\dfrac{3\pi }{4 }\nonumber\]
Угол \(\dfrac{3\pi }{4}\) является котерминальным углу \(\dfrac{19\pi }{4}\).
Упражнение \(\PageIndex{4}\)
Найдите угол \(\phi\), котерминальный углу \(-\dfrac{17\pi }{6}\), где \(0\le \phi < 2\пи\).
- Ответить
\[-\dfrac{17\pi }{6} +2\pi +2\pi =-\dfrac{17\pi }{6} +\dfrac{12\pi }{6} +\dfrac{12 \pi }{6} =\dfrac{7\pi }{6}\номер\]
Длина дуги и площадь сектора
Напомним, что мера угла в радианах определялась как отношение длины дуги окружности к радиусу окружности, \(\theta =\dfrac{s}{r}\). Из этого соотношения мы можем найти длину дуги вдоль окружности с заданным углом.
Из этого соотношения мы можем найти длину дуги вдоль окружности с заданным углом.
длина дуги на окружности
Длина дуги \(s\) вдоль окружности радиуса \(r\), опирающейся на угол \(\theta\) в радианах, равна
\[s=r\theta \]
Пример \(\PageIndex{9}\)
Меркурий вращается вокруг Солнца на расстоянии примерно 36 миллионов миль. За один земной день он совершает 0,0114 оборота вокруг Солнца. Если бы орбита была идеально круговой, какое расстояние в космосе преодолел бы Меркурий за один земной день?
Решение
Для начала нам нужно преобразовать десятичное значение вращения в радианы.
Поскольку один оборот = \(2\pi\) радиан,
0,0114 оборот = \(2\pi (0,0114)=0,0716\) радиан. 9{2}\]
Пример \(\PageIndex{10}\)
Автоматический разбрызгиватель для газонов распыляет воду на расстояние 20 футов при повороте на 30 градусов. Чему равна площадь сектора травяных поливов?
Решение
Во-первых, нам нужно преобразовать угловую меру в радианы. Поскольку 30 градусов — это один из наших общих углов, в идеале вы уже должны знать эквивалентную меру в радианах, но если нет, мы можем преобразовать:
Поскольку 30 градусов — это один из наших общих углов, в идеале вы уже должны знать эквивалентную меру в радианах, но если нет, мы можем преобразовать:
30 градусов = \(30 \cdot \dfrac{\pi }{180} =\dfrac{ \pi }{6}\) радиан. 9{2}\)
Упражнение \(\PageIndex{6}\)
При центральном круговом орошении большая ирригационная труба на колесах вращается вокруг центральной точки, как показано здесь (http://commons.wikimedia.org/wiki/Fi… _otech_002.JPG CC-BY-SA). Фермер имеет центральную поворотную систему с радиусом действия 400 метров. Если ограничения по воде позволяют ей поливать только 150 тысяч квадратных метров в день, какой угол она должна покрывать системой?
- Ответить
- 9{\circ}\)
Линейная и угловая скорость
Когда ваша машина едет по дороге, имеет смысл описать ее скорость в милях в час или метрах в секунду. Это меры скорости вдоль линии, также называемые линейной скоростью.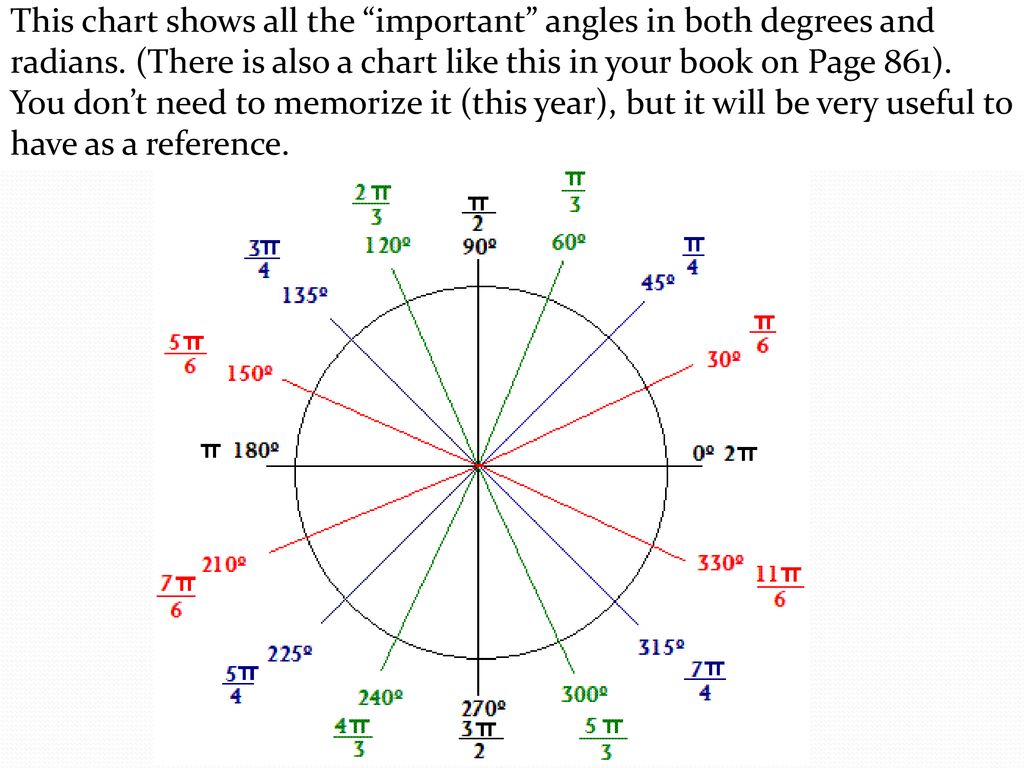 Когда точка на окружности вращается, мы бы описали ее угловую скорость или скорость вращения в радианах в секунду, оборотах в минуту или градусах в час.
Когда точка на окружности вращается, мы бы описали ее угловую скорость или скорость вращения в радианах в секунду, оборотах в минуту или градусах в час.
Определение: угловая и линейная скорость
Когда точка движется по окружности радиуса \(r\), ее угловая скорость, \(\omega\), может быть найдена как угловой поворот \(\theta\) в единицу времени, \(t \).
\[\omega =\dfrac{\theta}{t}\]
линейная скорость , \(v\), точки может быть найдена как пройденное расстояние, длина дуги \(s\), в единицу времени \(t\).
\[v=\dfrac{s}{t}\]
Пример \(\PageIndex{11}\)
Водяное колесо совершает 1 оборот каждые 5 секунд. Найдите угловую скорость в радианах в секунду. (http://en.Wikipedia.org/wiki/File:R%…m%C3%BChle.svg CC-BY)
Решение
Колесо совершает 1 оборот = \(2\pi\) радиан за 5 секунд, поэтому угловая скорость будет \(\omega =\dfrac{2\pi }{5} \примерно 1,257\ ) радиан в секунду.
Объединив приведенные выше определения с уравнением длины дуги \(s=r\theta\), мы можем найти взаимосвязь между угловой и линейной скоростями. Уравнение угловой скорости может быть решено относительно \(\theta\), что дает \(\theta =\omega t\). Подстановка этого в уравнение длины дуги дает \(s=r\theta =r\omega t\).
Подставляя это в уравнение линейной скорости, получаем
\(v=\dfrac{s}{t} =\dfrac{r\omega t}{t} =r\omega\)
связь между линейной и угловой скоростью
Когда угловая скорость измеряется в радианах в единицу времени, линейная скорость и угловая скорость связаны уравнением
\[v=r\omega\]
Пример \(\PageIndex{12}\)
Велосипед имеет колеса диаметром 28 дюймов. Тахометр определяет, что колеса вращаются со скоростью 180 об/мин (оборотов в минуту). Найдите скорость, с которой велосипед движется по дороге.
Решение
Здесь у нас есть угловая скорость, и нам нужно найти соответствующую линейную скорость, поскольку линейная скорость внешней стороны шин — это скорость, с которой велосипед движется по дороге.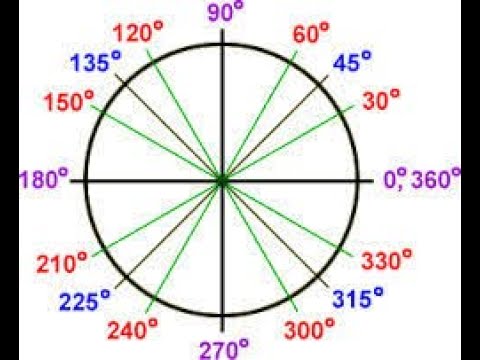
Начнем с преобразования оборотов в минуту в радианы в минуту. Для выполнения этого преобразования может быть полезно использовать единицы измерения
\[180\dfrac{\text{вращения}}{\text{минуты}} \cdot \dfrac{2\pi \text{радианы}}{\text {вращение}} = 360\pi \dfrac{\text{радианы}}{\text{минуты}}\nonnumber\]
Используя приведенную выше формулу вместе с радиусом колес, мы можем найти линейную скорость
\[v=(14 \text{дюймов})\left(360\pi \dfrac{\text{радиан}} {\text{минуты}} \right)=5040\pi \dfrac{\text{дюймы}}{\text{минуты}}\nonumber\]
Вам может быть интересно, куда делись «радианы» в этом последнем уравнении. . Помните, что радианы — это безразмерная мера, поэтому их не обязательно включать.
Наконец, мы можем преобразовать эту линейную скорость в более привычное измерение, например мили в час.
\[5040\pi \dfrac{\text{дюймы}}{\text{минуты}} \cdot \dfrac{1 \text{футы}}{12 \text{дюймы}} \cdot \dfrac{1 \ text{мили}}{5280 \text{футов}} \cdot \dfrac{60 \text{минут}}{1 \text{час}} =14,99\text{ миль в час (миль/ч)}\nonumber\]
Упражнение \(\PageIndex{7}\)
Спутник вращается вокруг Земли со скоростью 27 934 км/мин на высоте 242 км над землей.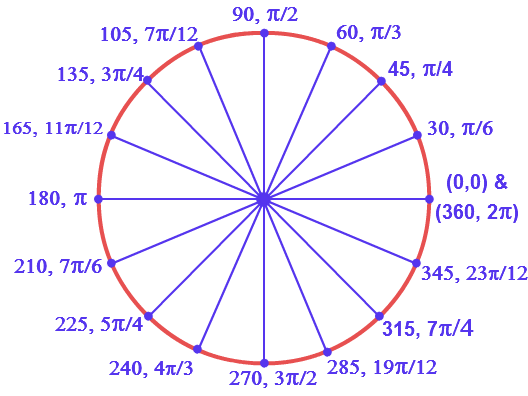

 Сможете ли вы правильно угадать все углы, которые вам нужны, чтобы брызгать водой из шланга на различные предметы?
Сможете ли вы правильно угадать все углы, которые вам нужны, чтобы брызгать водой из шланга на различные предметы?