конвертировать из угловых секунд в радиан
КОНВЕРТЕР УГОЛ
Альтернативное название: Конвертировать arcsec в rad
Вы можете использовать этот преобразователь для преобразования угол в угловых секунд (arcsec) в эквивалент угол в радиан (rad).
Формула, используемая в этом конвертере угол, указана ниже. Для вашего удобства также существует таблица преобразования угловых секунд (arcsec) в радиан (rad).
угловых секунд для преобразования:
Поделиться этим результатом
360 угловых секунд совпадает с:
0.001745 радиан
Если вы хотите преобразовать этот угол наоборот, попробуйте этот конвертер: радиан в угловых секунд конвертер
Угловых Секунд также могут быть преобразованы в другие единицы измерения:
Радиан
Градус
Градиан
Угловая Минута
Формула преобразования угловых секунд в радиан
Мы знаем, что 1 радиан совпадает с 206265 угловая секунда. . Это позволяет нам настроить следующую формулу:
. Это позволяет нам настроить следующую формулу:
угол(rad) = угол(arcsec) ÷ 206265
206265 – это константа преобразования, которую необходимо запомнить для выполнения этого преобразования..
Пример использования формулы угловых секунд в радиан
Если вы знаете формулу угловых секунд (arcsec) в радиан (rad), вы можете рассчитать angle следующим образом.
В примере 360 arcsec преобразуется в тот же угол в радиан.
0.001745 rad = 360 arcsec ÷ 206265
Таблица преобразования угловых секунд в радиан
Эта таблица преобразования основана на формуле, использованной выше.
Вы можете создать таблицу конвертации для любого диапазона чисел, введя начальный и конечный диапазон чисел ниже.
Начальная стоимость конверсии
Конечная стоимость конверсии
| Угловая Секунда | Радиан |
|---|---|
| 1 arcsec | 0.000004848 rad |
| 2 arcsec | 0.000009696 rad |
| 3 arcsec | 0.00001454 rad |
| 4 arcsec | 0.00001939 rad |
| 5 arcsec | 0.00002424 rad |
| 6 arcsec | 0.00002909 rad |
| 7 arcsec | 0.00003394 rad |
| 8 arcsec | 0.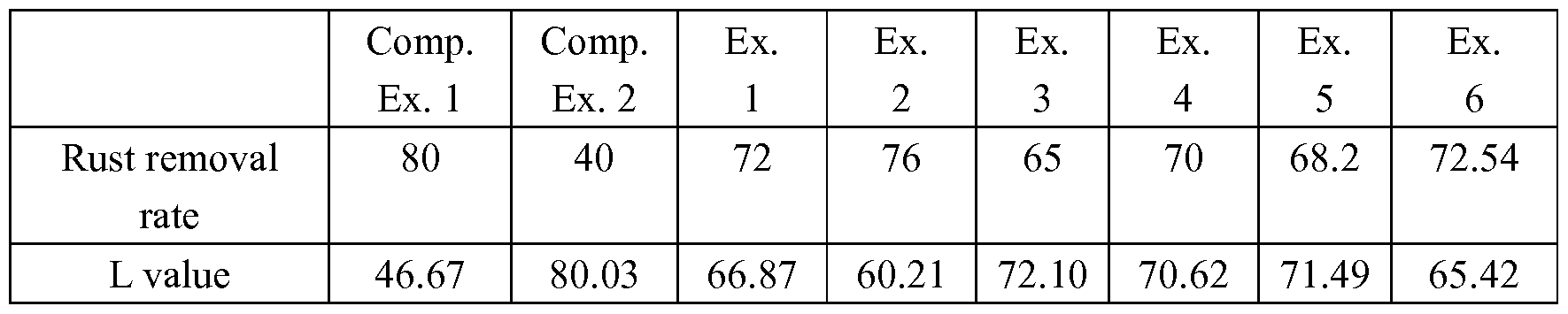 00003879 rad 00003879 rad |
| 9 arcsec | 0.00004363 rad |
| 10 arcsec | 0.00004848 rad |
| 11 arcsec | 0.00005333 rad |
| 12 arcsec | 0.00005818 rad |
| 13 arcsec | 0.00006303 rad |
| 14 arcsec | 0.00006787 rad |
| 15 arcsec | 0.00007272 rad |
| 16 arcsec | 0.00007757 rad |
| 17 arcsec | 0. 00008242 rad 00008242 rad |
| 18 arcsec | 0.00008727 rad |
| 19 arcsec | 0.00009211 rad |
| 20 arcsec | 0.00009696 rad |
| 21 arcsec | 0.0001018 rad |
| 22 arcsec | 0.0001067 rad |
| 23 arcsec | 0.0001115 rad |
| 24 arcsec | 0.0001164 rad |
| 25 arcsec | 0.0001212 rad |
| 26 arcsec | 0. 0001261 rad 0001261 rad |
| 27 arcsec | 0.0001309 rad |
| 28 arcsec | 0.0001357 rad |
| 29 arcsec | 0.0001406 rad |
| 30 arcsec | 0.0001454 rad |
| 31 arcsec | 0.0001503 rad |
| 32 arcsec | 0.0001551 rad |
| 33 arcsec | 0.00016 rad |
| 34 arcsec | 0.0001648 rad |
| 35 arcsec | 0. 0001697 rad 0001697 rad |
| 36 arcsec | 0.0001745 rad |
| 37 arcsec | 0.0001794 rad |
| 38 arcsec | 0.0001842 rad |
| 39 arcsec | 0.0001891 rad |
| 40 arcsec | 0.0001939 rad |
| 41 arcsec | 0.0001988 rad |
| 42 arcsec | 0.0002036 rad |
| 43 arcsec | 0.0002085 rad |
| 44 arcsec | 0. 0002133 rad 0002133 rad |
| 45 arcsec | 0.0002182 rad |
| 46 arcsec | 0.000223 rad |
| 47 arcsec | 0.0002279 rad |
| 48 arcsec | 0.0002327 rad |
| 49 arcsec | 0.0002376 rad |
| 50 arcsec | 0.0002424 rad |
Нажмите на любую ячейку таблицы преобразования, чтобы скопировать значение.
Если хотите, вы также можете просмотреть все другие связанные единицы измерения в этой категории, нажав здесь. Таблица обновлена, но начальный и конечный диапазон преобразования остаются прежними.
Если вам нужен более продвинутый контроль над таблицей, смотрите здесь: расширенная таблица конвертации
Погода в Павлодаре сегодня, прогноз погоды Павлодар на сегодня, Павлодар, Павлодарская область, Казахстан
GISMETEO: Погода в Павлодаре сегодня, прогноз погоды Павлодар на сегодня, Павлодар, Павлодарская область, КазахстанПерейти на мобильную версию
Сейчас
9:10
−2 28
По ощущению −4 25
Пт, 10 мар
Сегодня
−719
+134
Сб, 11 мар
Завтра
−327
+134
000
300
600
900
1200
1500
1800
2100
−228
−523
−719
−523
032
+134
032
−130
Скорость ветра, м/cкм/ч
2-5 7-18
4-8 14-29
4-9 14-32
3-8 11-29
3-7 11-25
Осадки, мм
Распечатать. ..
..
Снег
Пт, 10 мар, сегодня
Сб, 11
000
300
600
900
1200
1500
1800
2100
Выпадающий снег, см
Высота снежного покрова, см
8,3
8,3
8,3
8,3
8
7,2
7
6,9
/Ветер, м/скм/ч
Пт, 10 мар, сегодня
Сб, 11
000
300
600
900
1200
1500
1800
2100
Порывы
—
—
—
Давление, мм рт. ст.гПа
Пт, 10 мар, сегодня
Сб, 11
000
300
600
900
1200
1500
1800
2100
7651020
7651020
7651020
7621016
7611014
7601013
7591012
7571009
Влажность, %
Пт, 10 мар, сегодня
Сб, 11
000
300
600
900
1200
1500
1800
2100
80
86
86
71
57
60
64
65
Солнце и Луна
Пт, 10 мар, сегодня
Сб, 11
Долгота дня: 11 ч 27 мин
Восход — 7:19
Заход — 18:46
Сегодня день на 4 минуты длиннее, чем вчера
Луна стареющая, 93%
Восход — 20:49 (9 марта)
Заход — 8:21
Полнолуние — 6 апреля, через 27 дней
Ультрафиолетовый индекс, баллы
Пт, 10 мар, сегодня
Сб, 11
000
300
600
900
1200
1500
1800
2100
Геомагнитная активность, Кп-индекс
Пт, 10 мар, сегодня
Сб, 11
000
300
600
900
1200
1500
1800
2100
Осадки
Температура
Ветер
Облачность
Павлодарское
Алгабас
Сынтас
Жетекши
Мойылды
Айнаколь
Ленинский
Кенжеколь
Коктас
Павлодар
Жолкудук
Карабай
Коряковка
Байдала
Ребровка
Шанды
Кеменгер
Долгое
Мичурино
Умит апа
Караколь
Кеменгер
Подстёпка
Заозёрный
Измерение углов
Измерение угловКонцепция угла
Понятие угла — одно из важнейших понятий геометрии. Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов.
Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов.Существуют две широко используемые единицы измерения углов. Более привычной единицей измерения являются градусы. Окружность разделена на 360 равных градусов, так что прямой угол равен 90°. Пока мы будем рассматривать только углы от 0° до 360°, но позже, в разделе о тригонометрических функциях, мы рассмотрим углы больше 360° и отрицательные углы.
Градусов можно разделить на минуты и секунды, но это деление уже не так универсально, как раньше. Части степени теперь часто упоминаются в десятичном виде. Например, семь с половиной градусов теперь обычно записывают как 7,5°. Каждый градус делится на 60 равных частей, называемых 9.0004 минуты.
 Деление градусов на минуты и угловые секунды аналогично делению часы в минуты и секунды времени.
Деление градусов на минуты и угловые секунды аналогично делению часы в минуты и секунды времени. Обычно, когда для анализа рисуется один угол на плоскости xy , мы рисуем его с вершиной в начале координат (0,0), одна сторона угла вдоль x -ось, а другая сторона над осью x .
Другой распространенной единицей измерения углов является радиан. Для этого измерения рассмотрим единичную окружность (окружность радиуса 1), центр которой является вершиной рассматриваемого угла. Тогда угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко конвертировать между измерением в градусах и измерением в радианах. Длина окружности всего круга 2 π , отсюда следует, что 360° равняется 2 π радиан. Следовательно,
и
Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах. Убедитесь, что вы знаете, какой режим использует ваш калькулятор.
Убедитесь, что вы знаете, какой режим использует ваш калькулятор.
Краткая заметка об истории радианов
Хотя слово «радиан» было придумано Томасом Мьюиром и/или Джеймсом Томпсоном примерно в 1870 году, математики давно измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своей Элементы Алгебры прямо говорят, что углы измеряются длиной дуги, отсеченной в единичной окружности. Это было необходимо, чтобы дать его знаменитую формулу с комплексными числами, которая связывает функции знака и косинуса с показательной функцией.где θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. мой Краткий курс комплексных чисел.
Радианы и длина дуги
Альтернативное определение радианов иногда дается как отношение. Вместо единичной окружности с центром в вершине угла θ возьмите любую окружность с центром в вершине угла. Тогда радианной мерой угла является отношение длины стягиваемой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус окружности равен 2, то мера радиана равна 1,5. Причина, по которой это определение работает, заключается в том, что длина стягиваемой дуги пропорциональна радиусу окружности. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше, с использованием единичного круга. Однако это альтернативное определение более полезно, так как его можно использовать для связи длин дуг с углами. Длина дуги равна радиусу r , умноженному на угол θ , где угол измеряется в радианах.
Вместо единичной окружности с центром в вершине угла θ возьмите любую окружность с центром в вершине угла. Тогда радианной мерой угла является отношение длины стягиваемой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус окружности равен 2, то мера радиана равна 1,5. Причина, по которой это определение работает, заключается в том, что длина стягиваемой дуги пропорциональна радиусу окружности. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше, с использованием единичного круга. Однако это альтернативное определение более полезно, так как его можно использовать для связи длин дуг с углами. Длина дуги равна радиусу r , умноженному на угол θ , где угол измеряется в радианах.Например, дуга θ = 0,3 радиана в окружности радиусом r = 4 имеет длину 0,3 умножить на 4, то есть 1,2.
Радианы и площадь сектора
Сектором окружности называется та часть окружности, которая ограничена двумя радиусами и дугой окружности, соединяющей их концы. Площадь этого сектора легко вычислить из радиуса r окружности и угла θ между радиусами, если он измеряется в радианах. Так как площадь всего круга равна
Площадь этого сектора легко вычислить из радиуса r окружности и угла θ между радиусами, если он измеряется в радианах. Так как площадь всего круга равна Углы общие
Ниже приведена таблица общих углов как в градусах, так и в радианах. Обратите внимание, что измерение в радианах дается как π . Его можно, конечно, представить в десятичном виде, но радианы часто появляются с коэффициентом π . .| Уголок | градусов | радиан |
|---|---|---|
| 90° | № /2 | |
| 60° | № /3 | |
| 45° | № /4 | |
| 30° | № /6 |
Упражнения
Эдвин С. Кроули написал книгу «Тысяча упражнений в плоской и сферической тригонометрии», Университет Пенсильвании, Филадельфия, 1914 г. Задачи этого краткого курса взяты из этого текста (но не все 1000 из них!) Он дал свои задачи с точностью до пяти знаков, поэтому учащимся пришлось поработать некоторое время, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синусов-косинусов, тангенсов, логарифмов, логарифмических синусоидальных и логарифмических таблиц. Теперь мы можем использовать калькуляторы! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.
Кроули написал книгу «Тысяча упражнений в плоской и сферической тригонометрии», Университет Пенсильвании, Филадельфия, 1914 г. Задачи этого краткого курса взяты из этого текста (но не все 1000 из них!) Он дал свои задачи с точностью до пяти знаков, поэтому учащимся пришлось поработать некоторое время, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синусов-косинусов, тангенсов, логарифмов, логарифмических синусоидальных и логарифмических таблиц. Теперь мы можем использовать калькуляторы! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.Кроули использовал не десятичную запись для долей градуса, а минуты и секунды.
Каждый набор упражнений включает, во-первых, формулировки упражнений, во-вторых, несколько советов по решению упражнений и, в-третьих, ответы на упражнения.
1. Выразите следующие углы в радианах.
(а). 12 градусов 28 минут, то есть 12° 28′.
(б). 36° 12′.
2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.
3. Учитывая угол a и радиус r, найти длину стягивающей дуги.
(а). a = 0° 17′ 48″, r = 6,2935.
(б). a = 121° 6′ 18″, r = 0,2163.
4. Зная длину дуги l и радиус r, найти угол, опирающийся на центр.
(а). l = 0,16296, r = 12,587.
(б). l = 1,3672, r = 1,2978.
5. Зная длину дуги l и угол a , на который она опирается в центре, найти радиус.
(а). a = 0° 44′ 30″, l = 0,032592.
(б). a = 60° 21′ 6″, l = 0,4572.
6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус равен 3200 футов.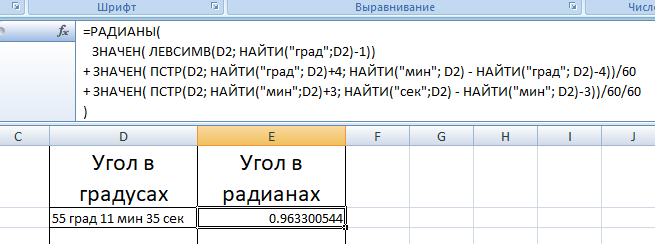
7. Железнодорожная кривая образует дугу окружности 9 градусов 36,7 минут, радиус от центральной линии пути составляет 2100 футов. Если ширина колеи 5 футов, найдите разницу в длине двух рельсов с точностью до полдюйма.
9. На сколько человек изменит широту, пройдя на север одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?
10. Вычислите длину одной угловой минуты в футах по большому кругу Земли. Какова длина одной угловой секунды?
14. На окружности радиусом 5,782 метра длина дуги составляет 1,742 метра. На какой угол он сужается в центре?
23. Известный воздушный шар диаметром 50 футов вытягивается из глаза под углом 8 1/2 минут. Как далеко это?
Подсказки
 Так, например, 12 ° 28 ‘это 12 + 28/60, что равно 12,467°. Далее умножить на π и разделите на 180, чтобы получить угол в радианах.
Так, например, 12 ° 28 ‘это 12 + 28/60, что равно 12,467°. Далее умножить на π и разделите на 180, чтобы получить угол в радианах.2. И наоборот, чтобы преобразовать радианы в градусы, разделите π и умножьте на 180. Таким образом, 0,47623, деленное на π и умноженное на 180, дает 27,286°. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27° 17,16′. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 примерно равно 10, поэтому угол можно также записать как 27° 17′ 10″.
3. Чтобы найти длину дуги, сначала переведите угол в радианы. Для 3(a) 0°17’48» составляет 0,0051778 радиан. Затем умножьте на радиус, чтобы найти длину дуги.
4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Это можно преобразовать в градусы, чтобы получить ответы Кроули.
Это можно преобразовать в градусы, чтобы получить ответы Кроули.
5. Как упоминалось выше, радиан умножить на радиус = длине дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градусов в радианы. Итак, чтобы найти радиус r, сначала преобразуйте угол a в радианы, а затем разделите его на длину l дуги.
6. Длина дуги равна произведению радиуса на угол в радианах.
7. Помогает нарисовать фигуру. Радиус внешней направляющей равен 2102,5, а радиус внутренней направляющей равен 209.7.5.
9. У вас есть окружность радиусом 3956 миль и дуга этой окружности длиной 1 миля. Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрите, сможете ли вы узнать, каким Эратосфен считал радиус Земли еще в третьем веке до нашей эры.)
10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус равен 3956. Какова длина дуги?
Преобразовать в радианы. Радиус равен 3956. Какова длина дуги?
14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус. Радианы легко перевести в градусы.
23. Представьте, что диаметр воздушного шара является частью дуги окружности, в центре которой вы находитесь. (Это не совсем часть дуги, но довольно близко.) Эта дуга имеет длину 50 футов. Вы знаете угол, так каков радиус этого круга?
Ответы
1. (а). 0,2176. (б). 0,6318.2. (а). 27° 17′ 10 дюймов (б). 14,56 ° = 14 °33,6′ = 14°33’36».
3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.
4. (а). 0,16296/12,587 = 0,012947 радиан = 0° 44′ 30″.
(б). 1,3672/1,2978 = 1,0535
радианы = 60,360° = 60° 21,6′ = 60° 21′ 35″.
5. (а). л/год = 0,032592/0,01294 = 2,518.
(б). л/год = 0,4572/1,0533 = 0,4340.
л/год = 0,4572/1,0533 = 0,4340.
6. ra = (3200′) (0,20604) = 659,31′ = 659′ 4 дюйма.
7. Угол a = 0,16776 радиан. Разница в длинах есть 2102.5 a – 1997.5 a , что равно 5 a. Таким образом, ответ равен 0,84 фута, что с точностью до дюйма равно 10 дюймам.
9. Угол = 1/3956 = 0,0002528 радиан = 0,01448° = 0,8690′ = 52,14″.
10. Одна минута = 0,0002909 радиан. 1,15075 мили = 6076 футов. Поэтому одна секунда будет соответствовать 101,3 фута.
14. a = л/об = 1,742/5,782 = 0,3013 радиан = 17,26° = 17°16′.
23. Угол a равен 8,5′, что составляет 0,00247 радиана. Значит радиус равен r = л/год = 50/0,00247 = 20222′ = 3,83 мили, почти четыре мили.
О разрядах точности.
Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах. Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 исходная точка равна 12°28′, что имеет точность около четырех знаков, поэтому ответ 0,2176 также должен быть дан с точностью только до четырех знаков. (Обратите внимание, что начальные нули не учитываются при подсчете цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.
Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 исходная точка равна 12°28′, что имеет точность около четырех знаков, поэтому ответ 0,2176 также должен быть дан с точностью только до четырех знаков. (Обратите внимание, что начальные нули не учитываются при подсчете цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.Другой пример см. в задаче 3(а). Данные равны 0°17’48» и 6,2935 с точностью до 4 и 5 цифр соответственно. Поэтому ответ должен быть дан только с точностью до 4 цифр, поскольку ответ не может быть более точным, чем наименее точные данные. Таким образом, ответ, который может дать калькулятор, а именно 0,032586547, следует округлить до четырех цифр (не считая ведущих нулей) до 0,03259.
Хотя окончательные ответы должны быть выражены с соответствующим количеством цифр точности, вы все равно должны сохранить все цифры для промежуточных вычислений.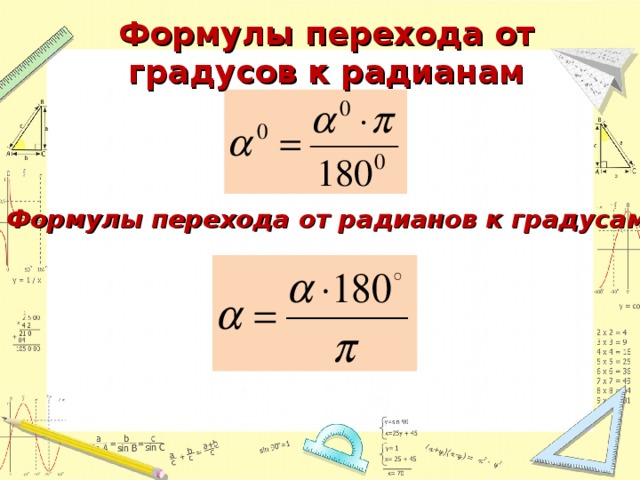
Градусы Минуты Секунды/Радианы/Градусы Конвертер Программа TI-84
Отсюда вы можете бесплатно загрузить программу на свой компьютер, а затем на свой калькулятор. (не волнуйтесь, мы проведем вас через это). Или вы можете использовать метод 2 и ввести код в калькулятор вручную. После этого продолжайте прокручивать эту страницу, чтобы узнать, что делает программа и как ее использовать.
Градусы Минуты Секунды/радианы/градусы Код конвертера
Метод 1 (скачать)
1. Чтобы загрузить программу, нажмите на ссылку ниже.
Загрузить программу
2. Нажмите <здесь> , чтобы получить руководство по установке программы на калькулятор после загрузки файла.
3. Продолжайте прокручивать, чтобы узнать, как работает программа и как ее использовать (необязательно).
4. В настоящее время программа хранится в оперативной памяти вашего калькулятора. Нажмите < здесь >, чтобы просмотреть руководство о том, как сохранить программу навсегда.
Нажмите < здесь >, чтобы просмотреть руководство о том, как сохранить программу навсегда.
Способ 2 (Тип)
1. Посмотрите, как запустить программу на калькуляторе <здесь> (необязательно).
2. Начните вводить код, показанный на изображении ниже.
НЕ вводите по отдельности двоеточие или имя « PROGRAM:EXAMPLE », двоеточия появятся автоматически, когда вы начнете новую строку, нажав [ввод]. « ПРОГРАММА: ПРИМЕР » уже будет вверху.
Не можете найти символ или функцию, которую видите в коде? См. , как ввести любую функцию/знак/символ на вашем TI-84 Plus>> .
*ВНИМАНИЕ*: Если вы очистите память калькулятора, программа будет потеряна. Чтобы узнать, как сохранить свою работу навсегда, нажмите <здесь> .
Как пользоваться программой
Для начала откройте программу.
