Задачи на параллелограмм 8 класс онлайн-подготовка на Ростелеком Лицей
Повторение определения, свойств и признака параллелограмма
Сегодня мы основное внимание уделим задачам на параллелограмм. Для этого нам необходимо владеть определением параллелограмма, его свойствами и признаками. Повторим эти факты, обобщим и структурируем их.
Определение. Параллелограмм – четырехугольник, у которого каждые две противоположные стороны параллельны (см. Рис. 1).
Рис. 1. Параллелограмм
Основные свойства параллелограмма:
Теорема. Первый признак параллелограмма. Если в четырехугольнике две противоположные стороны равны и параллельны (см. Рис. 2), то этот четырехугольник – параллелограмм. параллелограмм.
Рис. 2. Первый признак параллелограмма
Рис. 3. Второй признак параллелограмма
Теорема. Второй признак параллелограмма.
Если в четырехугольнике каждые две противоположные стороны равны (см. Рис. 3), то этот четырехугольник – параллелограмм. параллелограмм.
Теорема. Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам (см. Рис. 4), то этот четырехугольник – параллелограмм. параллелограмм.
Рис. 4. Третий признак параллелограмма
Задачи на параллелограммы
Теперь рассмотрим решение задач с использованием определения, свойств и признаков параллелограмма.
Пример 1. В параллелограмме проведены биссектрисы и , которые пересекаются в точке . Найти .
Решение. Изобразим Рис. 5.
Рис. 5
Обозначим для удобства: . Следовательно, поскольку и биссектрисы.
По теореме о сумме внутренних углов треугольника .
Вспомним свойство параллелограмма о сумме углов, прилежащих к одной стороне: . Тогда:
.
Ответ.
.
Пример 2. Прямая , проведенная через середину стороны параллельно стороне треугольника пересекает третью его сторону в середине. Доказать, что – это середина .
Доказательство. Изобразим Рис. 6 с дополнительными построениями: проведем .
Рис. 6
Рассмотрим четырехугольник :
параллелограмм по определению. Тогда по свойству равенства противоположных сторон , но по условию еще известно, что , следовательно, .
Рассмотрим треугольники и :
по второму признаку равенства треугольников (по стороне и прилежащим углам).
Из равенства указанных треугольников следует равенство их соответствующих сторон, т.е., например, что . Это означает, что точка является серединой стороны . Что и требовалось доказать.
Доказано.
3. Теорема Фалеса
Теорема Фалеса. Если параллельные прямые, которые пересекают стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.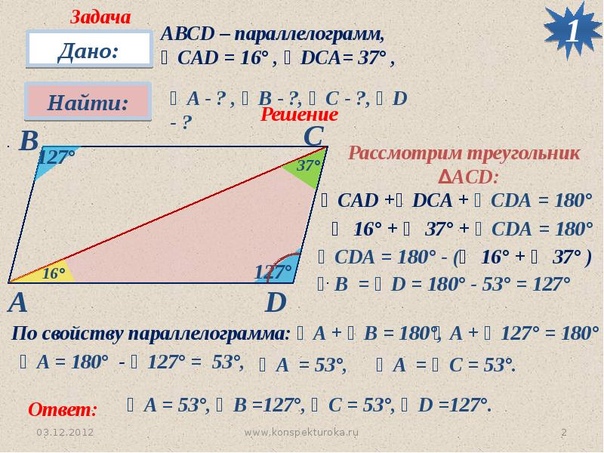
Доказательство. Изобразим Рис. 7.
Рис. 7. Теорема Фалеса
Рассмотрим . В нем точка – середина стороны , а прямая . Из предыдущего примера следует, что точка делит сторону на две равные части, т.е. . Равенство двух отрезков, ближайших к вершине угла доказано. Аналогично доказывается попарное равенство всех остальных отрезков на второй стороне угла, если проводить прямые параллельные первой стороне угла через начало первого отрезка в любой рассматриваемой паре.
Доказано.
4. Пример задачи на применение теоремы Фалеса
Рассмотрим пример на доказанную теорему.
Пример 3. Дан отрезок , разделить его на три равные части.
Решение. Изобразим указанный отрезок на Рис. 8 и сделаем дополнительные построения: отложим три равных отрезка любой длины вдоль одной прямой, не совпадающей с указанным в условии отрезком.
Рис. 8. Применение теоремы Фалеса
Соединим прямой точки и , а затем проведем прямые, параллельные прямой , через точки и : .
Полученные при пересечении отрезка точки и будут делить отрезок на три равных части по теореме Фалеса. Необходимое построение выполнено и задача решена.
Ответ: построено.
Методы, которые мы рассмотрели сегодня на примерах, демонстрирующих свойства и признаки параллелограмма, помогут нам в дальнейшем при работе с параллелограммами в более сложных случаях. А на следующем уроке мы познакомимся с таким видом четырехугольников, как трапеция, и обсудим ее свойства.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Narod.ru (Источник).
- Фестиваль педагогических наук «Открытый урок» (Источник).
Домашнее задание
- № 50 (г, д, е, ж, з, и), 51 (б, в, г, ж), 52 (б, в, е, ж). Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- В параллелограмме см, см, биссектрисы углов и пересекают сторону в точках и . Найдите длину отрезка .
- Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен . Найдите периметр параллелограмма, если его высоты равны 4 см и 6 см.
- ∗ Через середину диагонали параллелограмма проведена прямая, которая пересекает стороны и в точках и соответственно. Докажите, что четырехугольник параллелограмм.
Задачи категории В8. Параллелограмм, вычисление длин и углов
Задача 1. Сумма двух углов параллелограмма равна . Найдите один из оставшихся углов. Ответ дайте в градусах.
Решение: + показать
Задача 2. Один угол параллелограмма больше другого на .
Найдите больший угол. Ответ дайте в градусах.
Решение: + показать
Задача 3. Найдите больший угол параллелограмма, если два его угла относятся как Ответ дайте в градусах.
Решение: + показать
Задача 4. Диагональ параллелограмма образует с двумя его сторонами углы и Найдите больший угол параллелограмма. Ответ дайте в градусах.
Решение: + показать
Задача 5. Периметр параллелограмма равен Меньшая сторона равна Найдите большую сторону параллелограмма.
Решение: + показать
Задача 6. Две стороны параллелограмма относятся как а периметр его равен Найдите большую сторону параллелограмма.
Решение: + показать
Задача 7. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна Найдите его большую сторону.
Решение: + показать
Задача 8.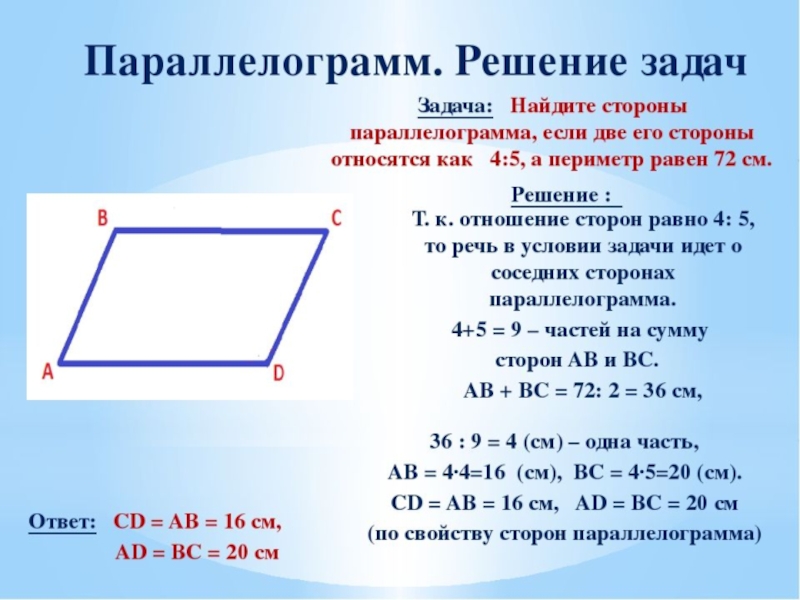
Решение: + показать
Задача 9. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен
Решение: + показать
Задача 10. В параллелограмме высота, опущенная на сторону из точки равна . Найдите синус угла .
Решение: + показать
Задача 11. В параллелограмме Найдите высоту, опущенную на сторону
Решение: + показать
Задача 12. В параллелограмме Найдите большую высоту параллелограмма.
Решение: + показать
Задача 13. Площадь параллелограмма равна две его стороны равны и Найдите большую высоту этого параллелограмма.
Решение: + показать
Задача 14. В параллелограмме .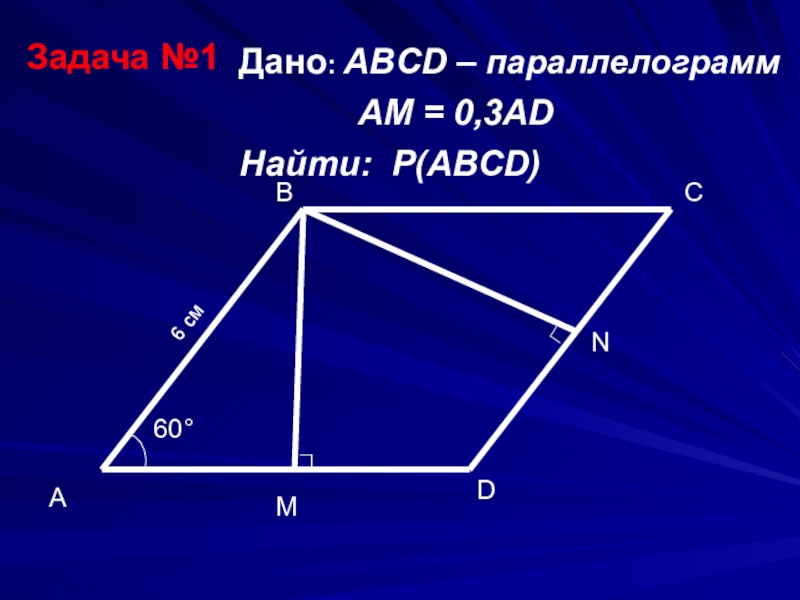
Найдите .
Решение: + показать
Задача 15. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Решение: + показать
Задача 16. Площадь параллелограмма равна Точка — середина стороны . Найдите площадь трапеции .
Решение: + показать
Задача 17. Площадь параллелограмма равна Найдите площадь параллелограмма вершинами которого являются середины сторон данного параллелограмма.
Решение: + показать
Задача 18. Найдите диагональ параллелограмма , если стороны квадратных клеток равны 1.
Решение: + показать
Задача 19. Диагонали четырехугольника равны и Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Решение: + показать
Вы можете пройти тест по теме «Параллелограмм.
Вычисление углов и длин».
Параллелограммы — Математика для старших классов
Все ресурсы по математике для старших классов
8 диагностических тестов 613 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по математике для средней школы » Геометрия » Плоская геометрия » Четырехугольники » Параллелограммы
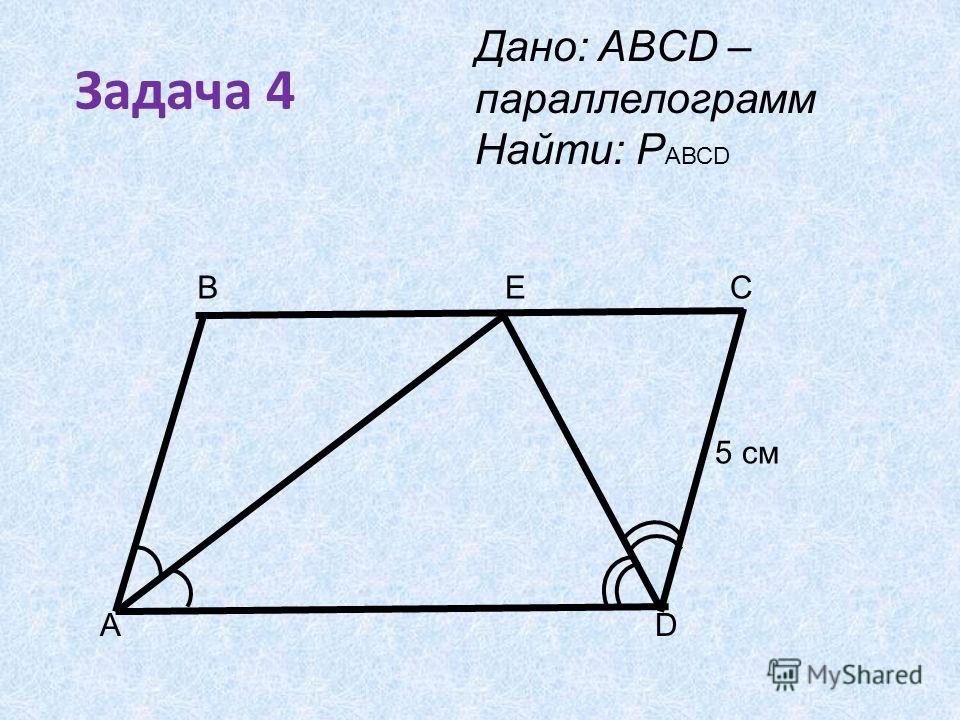
Ниже показан параллелограмм с размерами в см.
Чему равен периметр параллелограмма в см?
Возможные ответы:
Правильный ответ:
Объяснение:
Треугольник в левой части рисунка имеет угол a и . Поскольку сумма всех углов треугольника должна быть равна , мы можем найти угловую меру третьего угла:
Наш третий угол равен , и у нас есть треугольник.
Треугольник имеет стороны, которые находятся в соответствующем отношении . В этом случае сторона, противоположная нашему углу, равна , поэтому
Теперь мы также знаем, что
Теперь мы знаем длины всех недостающих сторон. Правая и левая стороны параллелограмма будут равны . Нижний и верхний будут каждый . Объединим их, чтобы найти периметр:
Сообщить об ошибке
Найдите периметр следующего параллелограмма:
9000 4 Возможные ответы:Правильный ответ:
Объяснение:
Формула периметра трапеции:
,
, где – длина основания, а – длина ребра.
Противоположные стороны параллелограмма имеют одинаковую длину. Следовательно, оба ребра и оба основания равны.
Подставив наши значения, мы получим:
Сообщить об ошибке
Найдите периметр следующего параллелограмма:
Возможные ответы:
Правильный ответ:
Объяснение:
Формула для периметра параллелограмма:
где это длина большей стороны и это длина более короткой стороны.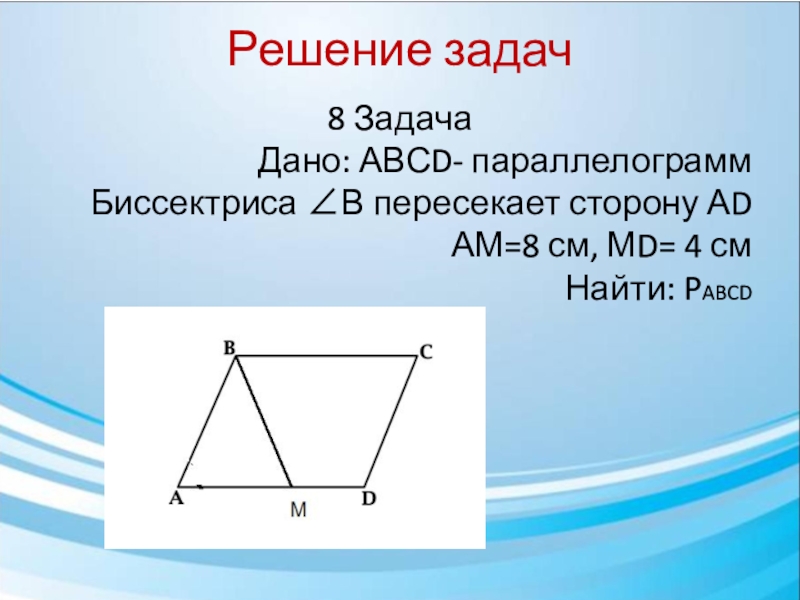
Подставив наши значения, мы получим:
Сообщить об ошибке
Найдите периметр следующего параллелограмма:
Возможные ответы:
Правильный ответ:
Объяснение:
Формула периметра параллелограмма:
.
Подставив наши значения, мы получим:
Сообщить об ошибке
ABCD — параллелограмм. BD = 5. Все углы треугольника ABD равны. Чему равен периметр параллелограмма?
Возможные ответы:
Правильный ответ:
Пояснение:
Если в треугольнике ABD все углы равны, а прямая BD делит параллелограмм, то и в треугольнике BDC должны быть равны все углы.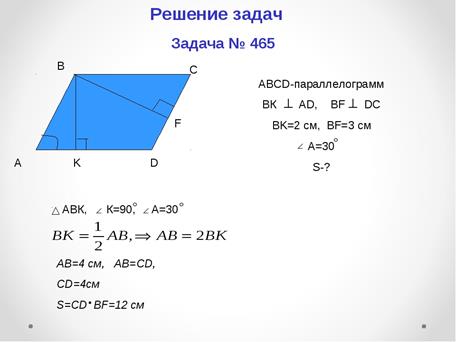
Теперь у нас есть два равносторонних треугольника, поэтому все стороны треугольников будут равны.
Следовательно, все стороны равны 5.
5+5+5+5 = 20
Сообщить об ошибке
Каково значение ?
Возможные ответы:
Правильный ответ:
Объяснение:
Противоположные углы равны, а соседние углы должны суммироваться до 180.
Следовательно, мы можем настроить уравнение для решения для z:
(z — 15) + 2Z = 180
3Z — 15 = 180
3z = 195
z = 65
Теперь найдите x:
2 z = x = 130°
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить этот вопрос, вы должны знать формулу площади параллелограмма.
В этом уравнении длина основания и длина высоты. Мы можем указать длину стороны как для основания, так и для высоты, как указано в вопросе.
Сообщить об ошибке
Какова площадь параллелограмма с основанием и высотой ?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить этот вопрос, вы должны знать формулу площади параллелограмма.
Формула
Таким образом, мы можем подставить длину стороны как для основания, так и для высоты, чтобы получить
Выполните умножение, чтобы получить ответ .
Сообщить об ошибке
Найдите площадь следующего параллелограмма:
Возможные ответы:
Невозможно определить по данной информации.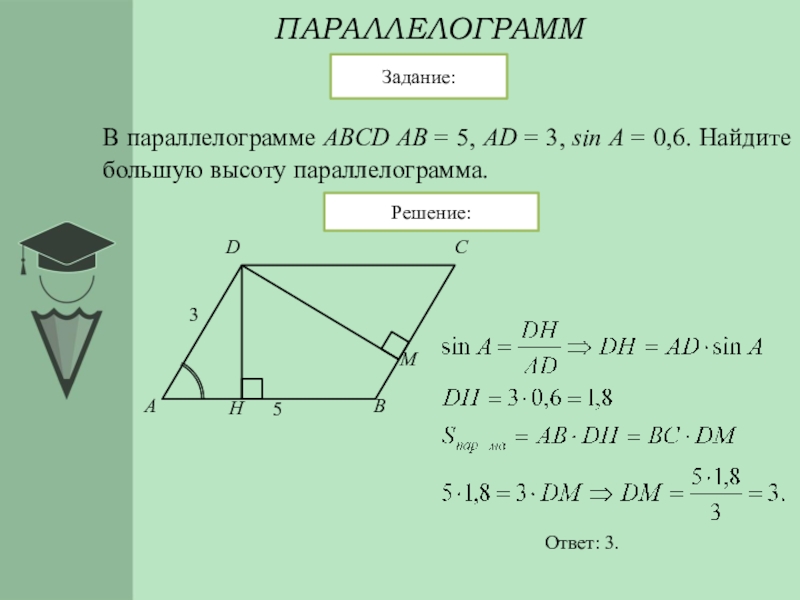
Правильный ответ:
Объяснение:
Формула площади параллелограмма:
,
где — длина основания, а — длина высоты.
Чтобы найти высоту параллелограмма, воспользуйтесь формулой для треугольника:
, где – сторона, противоположная .
Левая сторона параллелограмма образует следующий треугольник:
, где длина высоты.
Подставив наши значения, мы получим:
Сообщить об ошибке
Найдите площадь следующего параллелограмма:
Возможные ответы:
Правильный ответ:
Пояснение:
Используйте теорему Пифагора для определения длины диагонали:
Площадь параллелограмма в два раза больше площади прямоугольного треугольника:
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах
Все ресурсы по математике для старших классов
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
Свойства параллелограмма
Свойства параллелограмма перечислены ниже.
Мы будем использовать параллелограмм ABCD, чтобы показать эти свойства.
Свойство №1
Противоположные стороны параллелограмма равны.
Длина AB равна длине DC.
Длина BC равна длине AD.
Вот как доказать, что противоположные стороны параллелограмма равны.
Свойство №2
Противоположные углы параллелограмма равны.
Угол A равен углу C
Угол B равен углу D
Как доказать, что противоположные углы параллелограмма равны
Для данного параллелограмма ABCD нужно доказать, что ∠A ≅ ∠C; ∠В ≅ ∠D
1. Даны
ABCD — параллелограмм
2. Смежные углы — дополнительные углы в параллелограмме ( свойство #4 )
900 04 ∠A + ∠B = 180 градусов∠B + ∠C = 180 градусов
3. Свойство переходности в свойствах равенства
∠A + ∠B = ∠B + ∠C
4. Свойство вычитания в свойствах равенства
∠A + ∠B — ∠В = ∠В — ∠В + ∠С
5.
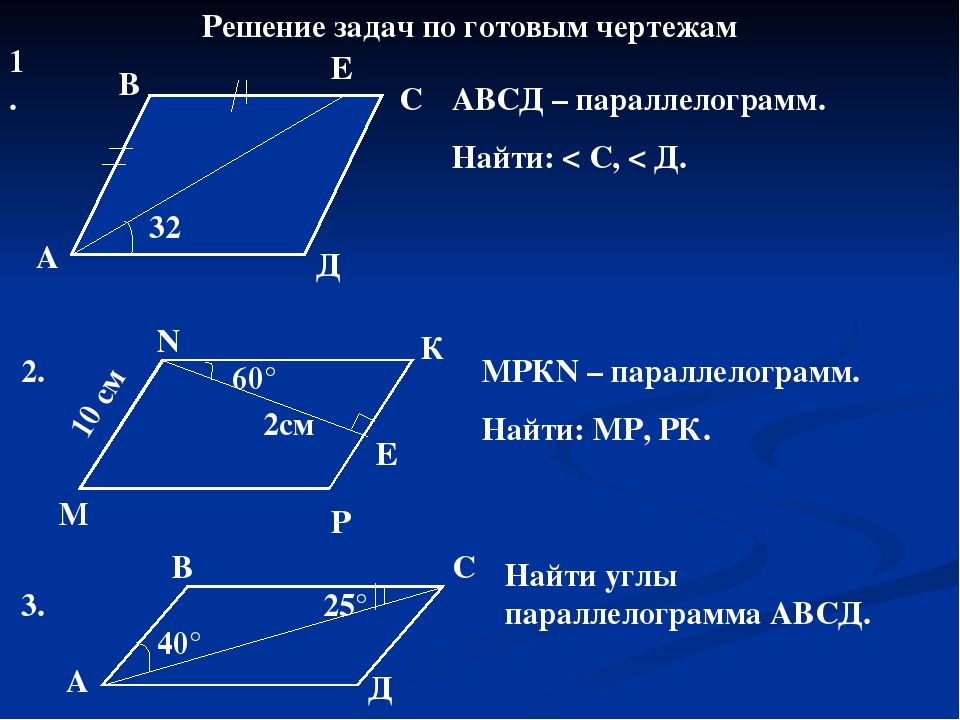∠A = ∠C
Используя аналогичные рассуждения, можно показать, что ∠B ≅ ∠D
Свойство #3
Диагональ s параллелограмма делят друг друга пополам.
Диагональ AC (красная линия) пересекает и делит пополам диагональ BD (зеленая линия) в точке E.
Как доказать, что диагонали параллелограмма делят друг друга пополам
Для данного параллелограмма ABCD нам нужно доказать, что отрезок AC и отрезок BD делят друг друга пополам в E.
1. Дано
ABCD — параллелограмм
2. Определение параллелограмма
Отрезок AB || отрезок DC
3. Параллельные прямые, разделенные секущей, образуют конгруэнтные внутренние углы
∠1 ≅ ∠4; ∠2 ≅ ∠3
4. Противоположные стороны параллелограмма равны
Отрезок AB ≅ отрезок DC
5. Треугольник ABE равен треугольнику CDE по ASA (угол -боковой угол)
6. Отрезок AE ≅ отрезок CE и отрезок BE ≅ отрезок DE по CPCTC (соответствующие части конгруэнтных треугольников конгруэнтны)
7.
Определение биссектрисы
Отрезок AC и отрезок BD делят друг друга пополам в точке E.
Свойство №4
Смежные углы являются дополнительными или в сумме составляют 180 градусов.
Угол A + угол B = 180 градусов
Угол B + угол C = 180 градусов
Угол C + угол D = 180 градусов
Угол D + угол A = 180 градусов
Свойство №5
Каждая диагональ параллелограмма превращает параллелограмм в 2 конгруэнтных треугольника.
Треугольник ABC равен или идентичен треугольнику ADC.
Треугольник BCD равен или идентичен треугольнику BAD.
Использование свойств параллелограмма для решения математических задач
Пример #1 : Используйте приведенный ниже параллелограмм, чтобы найти длину отрезка BC и отрезка AD.
Поскольку противоположные стороны параллелограмма равны, длина отрезка BC равна длине отрезка AD.
4x — 10 = 3x + 5.
Вычесть 3x с каждой стороны
4x — 3x — 10 = 3x — 3x + 5
Упростить каждую сторону
x — 10 = 5 900 05
Добавьте 10 с обеих сторон уравнение.
x — 10 + 10 = 5 + 10
Упрощение
x = 15
BC = AD = 4x — 10 = 4 x 15 — 10 = 60 — 10 = 50
Пример #2 : Используйте приведенный ниже параллелограмм, чтобы найти длину отрезка AC и отрезка BD.
Поскольку диагонали параллелограмма делят друг друга пополам, получаем следующие результаты:
- Длина отрезка AI равна длине отрезка CI
- Длина отрезка BI равна длине отрезок DI
Это приводит к системе линейных уравнений для решения
2y — 4 = 4x
y = x + 4
Подставить x + 4 вместо y в 2y — 4 = 4x
2(x + 4) — 4 = 4x
Распределить
2x + 8 — 4 = 4x
Упростить
90 004 2x + 4 = 4x4 = 2x
x = 4/2 = 2
y = x + 4 = 2 + 4 = 6 9 0005
АС = AI + CI = 2y — 4 + 4x = 2×6 — 4 + 4×2 = 12 — 4 + 8 = 16
BD = BI + DI = x + 4 + y = 2 + 4 + 6 = 12
Посмотрите также урок о параллелограмме, чтобы узнать кое-что интересное о параллелограмме, например:
- Что такое параллелограмм?
- Типы параллелограмма, такие как ромб и прямоугольник
- Периметр параллелограмма
- Площадь параллелограмма
Треугольник 45-45-90
01, 23 мая 07:00
Что такое треугольник 45-45-90? Определение, доказательство, площадь и простые примеры из реальной жизни.
