График 2 корня из х: График y = f(x) = sqrt(x-2) (квадратный корень из (х минус 2)) постройте график функции и изобразите его. Исследуйте данную функцию. [Есть ОТВЕТ!]

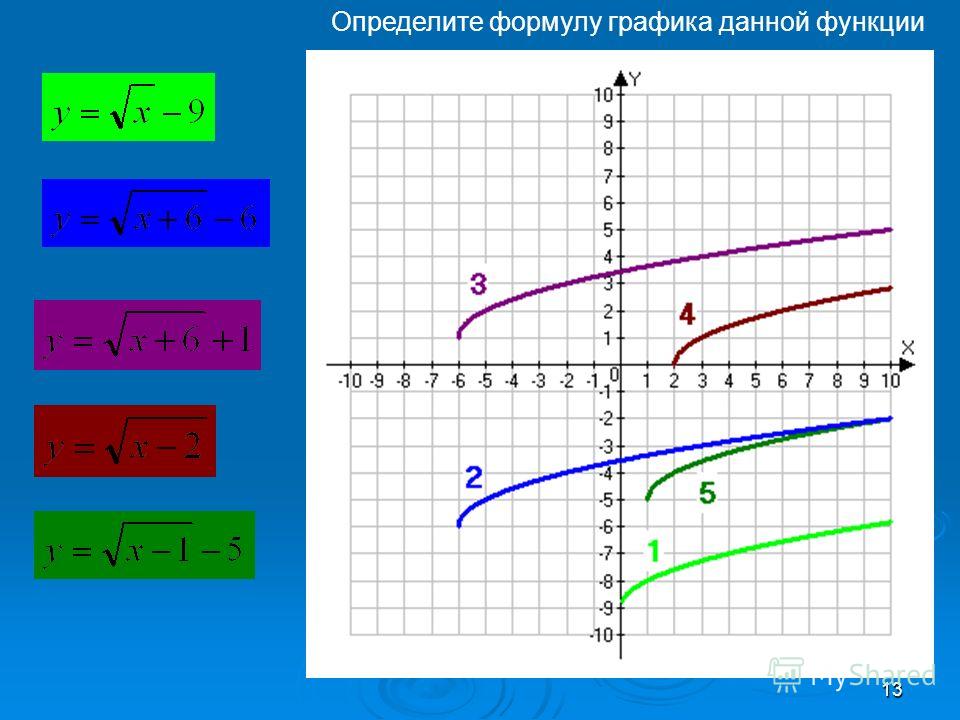
8 класс. Алгебра. Рациональные числа. Понятие квадратного корня. График функции квадратного корня. — Функция квадратного корня. Свойства функции корня.

Комментарии преподавателя

В реальной жизни встречаются процессы, которые можно описать различными математическими моделями в виде функций y = f(x). Если задать конкретное значение независимой переменной x(аргумента), то можно вычислить соответствующее значение зависимой переменной y (ординаты). На этом занятии мы рассмотрим функцию y=√x.

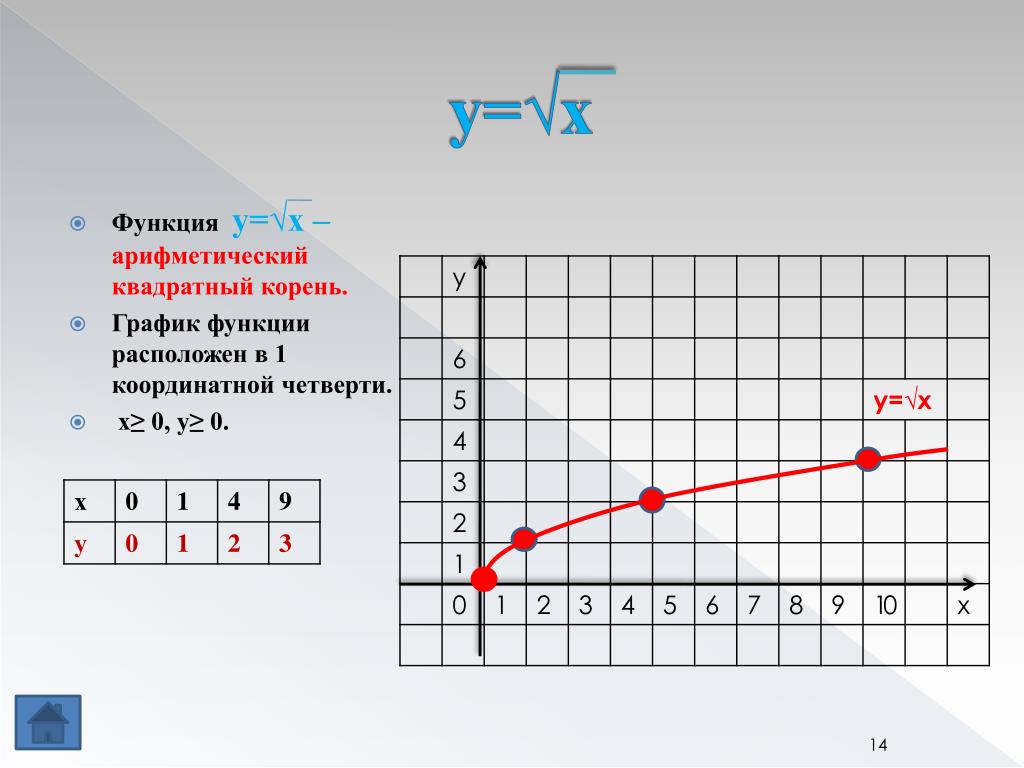
Для построения графика этой функции y = √x дадим независимой переменной x несколько конкретных значений (неотрицательных, т.к. при x < 0 квадратный корень √x не имеет смысла) и вычислим соответствующие значения переменной y.

При х равном нулю значение y равно нулю: x = 0, y = √0 = 0.

При х равном единице значение y равно единице: x=1,y = √1 = 1.

А если 

х взять равным четырем, то значение переменной y будет равняться двум:

x = 4, y = √4 = 2. Найдем y еще для двух значений х: x = 6.25,y = √6.25 = 2.5;

x = 9, y = √9 = 3. Из этих значений переменных х и y составим таблицу:

x	0	1	4	6.25	9
y	0	1	2	2. 5	3

И построим график нашей функции y = √x, отметив точки (0;0), (1;1), (4;2), (6.25;2.5), (9;3) на координатной плоскости:

На гра­фи­ке на­гляд­но виден смысл вы­чис­ле­ния квад­рат­но­го корня. На­при­мер, если рас­смот­реть ор­ди­на­ту 16, то ей будет со­от­вет­ство­вать абс­цис­са 4, т. к. . Ана­ло­гич­но, ор­ди­на­те 9 на гра­фи­ке со­от­вет­ству­ет точка с абс­цис­сой 3, по­сколь­ку , ор­ди­на­те 11 со­от­вет­ству­ет абс­цис­са , т. к.  (квад­рат­ный ко­рень из 11 не из­вле­ка­ет­ся в целых чис­лах).

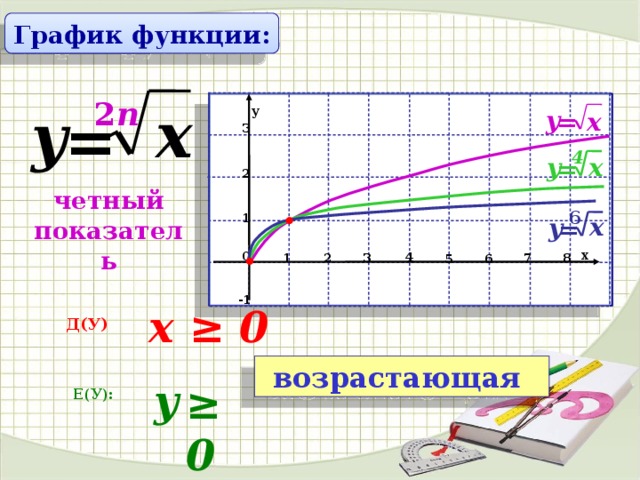
Те­перь рассмотрим гра­фик функ­ции  (рис. 2).

Рис. 2.

На гра­фи­ке для на­гляд­но­сти изоб­ра­же­ны несколь­ко точек, ор­ди­на­ты ко­то­рых вы­чис­ля­ют­ся с по­мо­щью из­вле­че­ния квад­рат­но­го корня: , , .

 

Рассмотрим свойства этой функции:

1. Область её определения – луч от нуля до плюс бесконечности [0;+∞).
2. y = 0 при x = 0; и y > 0 при x > 0.
3. Функция возрастает на луче от нуля до плюс бесконечности [0;+∞).

Напомним, что функцию y=f(x) называют возрастающей на промежутке Х, если на этом промежутке большему значению аргумента соответствует большее значение функции. А если на промежутке Х большему значению аргумента соответствует меньшее значение функции, то функцию y=f(x) называют убывающей на промежутке Х.

     4.  Наименьшее значение функции равно нулю yнаим = 0 (достигается при x = 0), наибольшее значение функции yнаиб не существует.

      5. Функция является непрерывной (так как её график есть сплошная непрерывная линия).

Точно такими же свойствами обладает и функция y = x2 при неотрицательных значениях переменной х: x ≥ 0. Только график функции y = √x обращен выпуклостью вверх, а y=x2,где x ≥ 0 обращен выпуклостью вниз.

Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка.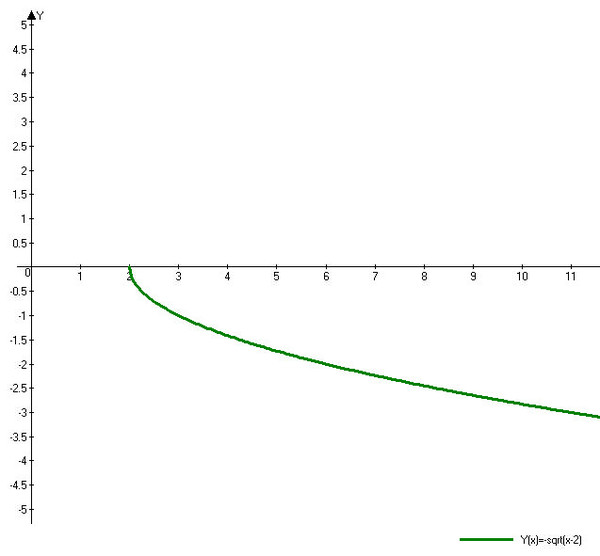 Аналогично, функция выпукла вверх, если соответствующая часть графика лежит выше проведенного отрезка.

6.    Множество всех значений функции y называют областью значений функции. Для функцииy=√x областью значений является луч от нуля до плюс бесконечности [0;+∞).

Источник конспекта: http://znaika.ru/catalog/8-klass/algebra/Funktsiya-y=√x,-ee-svoystva-i-grafik.

Источник видео: http://www.youtube.com/watch?v=jNajabpBlf8

Корни квадратного уравнения

Корни квадратного уравнения

БАН:: Дайана Браун

У него есть теперь стало довольно стандартным упражнением, с доступной технологией, чтобы построить графики для рассмотрения уравнения

 

и для наложение нескольких графиков

 

для различные значения a, b или c, поскольку два других остаются постоянными.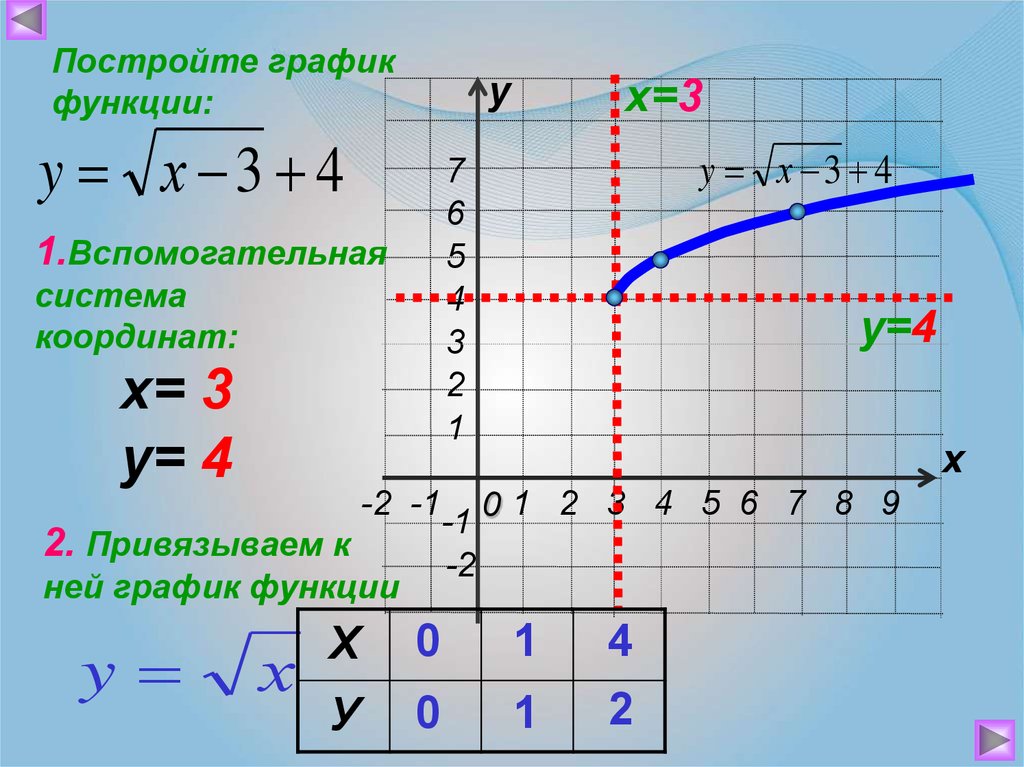 От них графики Я собираюсь исследовать корни

Сначала давайте установим a и c равными 1 и пусть b = -4, -3, -2, -1, 0, 1, 2, 3, 4. См. график ниже:

 

Уведомление на графике выше парабола всегда проходит через одну и ту же точку на ось y (точка (0, 1) с этим уравнением). При b < -2 парабола будет пересекают ось x в двух точках с положительными значениями x (т.е. уравнение будет иметь два действительных корня, оба положительные). Для b = -2 парабола касательной к оси x, поэтому исходное уравнение имеет одно действительное и положительное корень в точке касания. При -2 < b < 2 парабола не пересекают ось x - исходное уравнение не имеет действительных корней. Аналогично для b = 2 парабола касается оси x (один действительный отрицательный корень), а для b > 2, парабола дважды пересекает ось x, показывая два отрицательных действительных числа.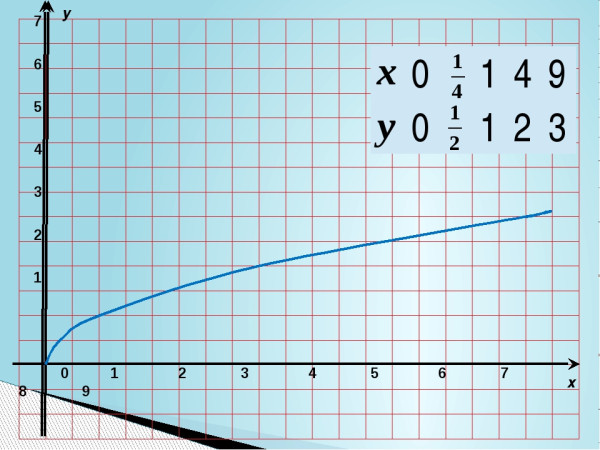 корни для каждого б.

 

Запомните корни (иногда их также называют «нули») квадратное уравнение, f (x) = 0, являются значениями x , для которых уравнение удовлетворен. Выведем формулу для найти решение квадратного уравнения:

Рассмотрим уравнение корни x можно найти, заполнив квадрат,

 

 

 

 

Solving for x then gives

 

 

Note that this is the quadratic formula and эта формула используется найти корни квадратного уравнения.

Теперь давайте посмотрим на геометрическое место вершин множества парабол, изображенных сверху:

 

УРАВНЕНИЕ	ВЕРТЕКС
у = х — 4х + 1	(2, -3)
у = х — 3х + 1	(1,5, -1,25)
у = х — 2х + 1	(1, 0)
у = х — х + 1	(0,5, 0,75)
у = х + 1	(0, 1)
у = х + х + 1	(-0,5, 0,75)
у = х + 2х + 1	(-1, 0)
у = х + 3х + 1	(-1,5, -1,25)
у = х + 4х + 1	(-2, -3)

 

 

См.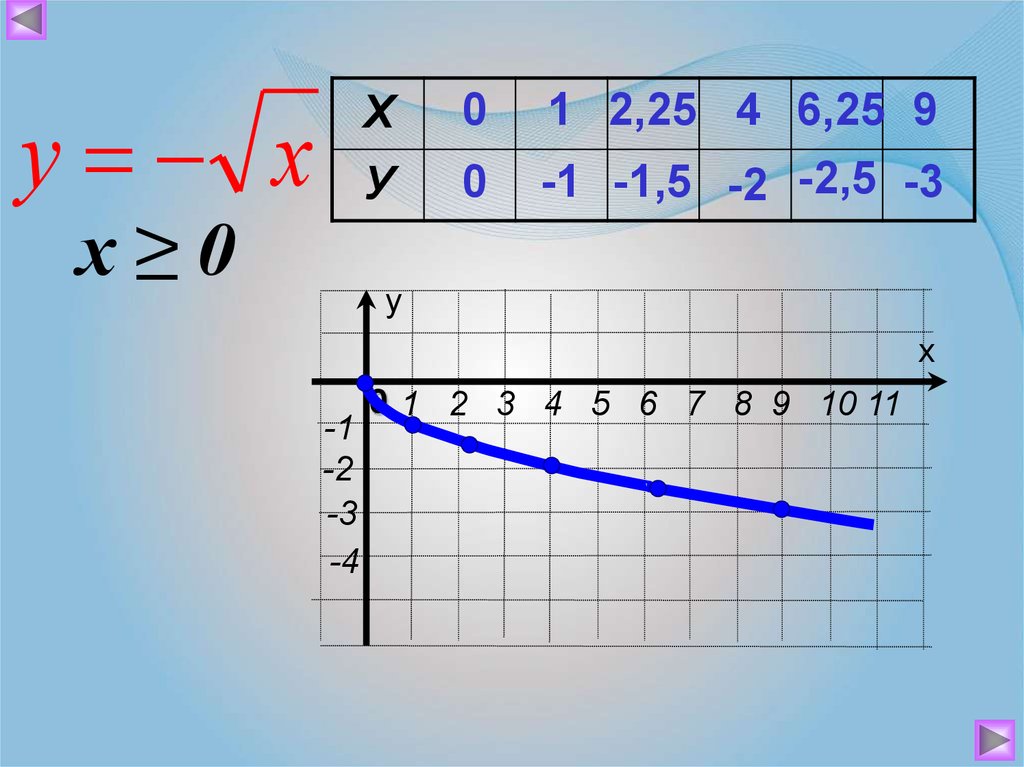 график геометрического места вершин парабол: 9Уведомление что геометрическое место является параболой. Мы можем увидеть что вершина приведенной выше параболы находится в (0, 1) и что каждая точка симметричны друг другу относительно прямой x=0. Также точки пересечения x находятся в точках (1, 0) и (-1, 0). Если мы установим y = корням уравнения, мы получить:

 

y= (x 1) (х + 1)

 

у = х — 1

 

и, так как парабола раскрывается вниз, следовательно, должно быть отрицательным, так что давайте посмотрим что происходит, когда мы рисуем уравнение y = -x + 1 на вышеуказанном графике:

Как вы можете видеть в вышеупомянутом граф, геометрическое место вершин множества парабол, построенных по y = x + bx+1, в начале разведки парабола:

.

Возврат на домашнюю страницу

 

математика — Как определить корни уравнения, построив его действительную и мнимую части

спросил 1 год, 11 месяцев назад

Изменено 1 год, 11 месяцев назад

Просмотрено 301 раз 92 — 0,5)я

, как показано на скриншоте Mathematica, тогда у нас есть действительная часть, которая пересекает ноль, и мнимая часть, которая также пересекает ноль, но с другим x. Итак, мой вопрос: можно ли определить корни такого уравнения, просто взглянув на действительную и мнимую части графика?

Примечание: частично меня смущает то, что если я использую FindRoot в Mathematica, я получаю либо 0,877659 — 0,142424i, либо -0,877659 + 0,142424i. Так что может быть какое-то фундаментальное свойство в математике, о котором я не знаю, которое мешает идентифицировать корни сложной функции путем разделения действительных и мнимых частей…

• математика
• wolfram-mathematica
• решение уравнений

3

у нас есть действительная часть, которая пересекает ноль, и мнимая часть, которая также пересекает ноль, но с другим x.

Это графики действительной и мнимой частей, построенные для действительных значений x . Если они оба пересекли горизонтальную ось в одних и тех же точках, это означало бы, что уравнение имеет 92 — 0,5) — комплексная функция комплексной переменной, которая отображает комплексную переменную x = a + i b в комплексное значение f(x) = Re(f(x)) + i Im(f(x )) .

Каждый из Re(f(x)) и Im(f(x)) является действительной функцией комплексной переменной.