| Формулы для объема, площади боковой поверхности и площади полной поверхности пирамиды |
| Произвольная |
Четырехугольной пирамидой называется многогранник, в основании которого лежит квадрат, а все боковые грани являются одинаковыми равнобедренными треугольниками.
У данного многогранника есть множество различных свойств:
- Его боковые ребра и прилегающие к ним двугранные углы равны между собой;
- Площади боковых граней одинаковы;
- В основании правильной четырехугольной пирамиды лежит квадрат;
- Высота, опущенная из вершины пирамиды, пересекается с точкой пересечения диагоналей основания.

Все эти свойства помогают легко находить . Однако довольно часто помимо нее требуется рассчитать объем многогранника. Для этого применяется формула объема четырехугольной пирамиды:
То есть объем пирамиды равен одной третьей произведения высоты пирамиды на площадь основания. Так как равна произведению его равных сторон, то мы сразу вписываем в выражение объема формулу площади квадрата.
Рассмотрим пример расчета объема четырехугольной пирамиды.
Пусть дана четырехугольная пирамида, в основании которой лежит квадрат со стороной a = 6 см. Боковая грань пирамиды равна b = 8 см. Найдите объем пирамиды.
Чтобы найти объем заданного многогранника, нам потребуется длина его высоты. Поэтому мы найдем ее, применив теорему Пифагора. Для начала рассчитаем длину диагонали. В синем треугольнике она будет гипотенузой. Стоит также помнить, что диагонали квадрата равны между собой и в точке пересечения делятся пополам:
Теперь из красного треугольника найдем необходимую нам высоту h
. Она будет равна:
Она будет равна:
Подставим необходимые значения и найдем высоту пирамиды:
Теперь, зная высоту, можем подставлять все значения в формулу объема пирамиды и рассчитывать необходимую величину:
Вот таким образом, зная несколько простых формул, мы смогли рассчитать объем правильной четырехугольной пирамиды. Не забывайте, что данная величина измеряется в кубических единицах.
Здесь собраны основные сведения о пирамидах и связанных с ней формулах и понятиях. Все они изучаются с репетитором по математике при подготовке к ЕГЭ.
Рассмотрим плоскость , многоугольник , лежащий в ней и точку S, не лежащую в ней. Соединим S со всеми вершинами многоугольника. Полученный при этом многогранник называется пирамидой. Отрезки называются боковыми ребрами. Многоугольник называется основанием, а точка S — вершиной пирамиды. В зависимости от числа n пирамида называется треугольной (n=3), четырехугольной (n=4), птяиугольной (n=5) и так далее. Альтернативное название треугольной пирамиды – тетраэдр .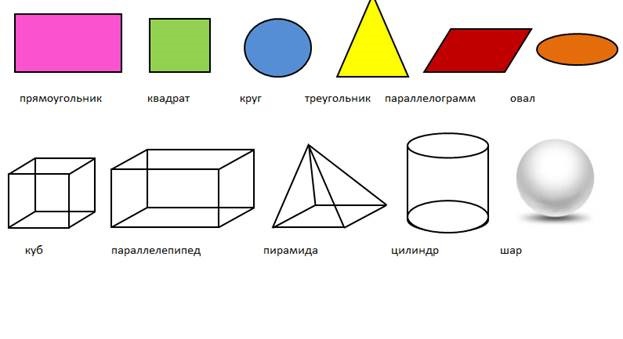 Высотой пирамиды называется перпендикуляр, опущенный из ее вершины к плоскости основания.
Высотой пирамиды называется перпендикуляр, опущенный из ее вершины к плоскости основания.
Пирамида называется правильной, если правильный многоугольник, а основание высоты пирамиды (основание перпендикуляра) является его центром.
Комментарий репетитора :
Не путайте понятие «правильная пирамида» и «правильный тетраэдр». У правильной пирамиды боковые ребра совсем не обязательно равны ребрам основания, а в правильном тетраэдре все 6 ребер ребра равные. Это его определение. Легко доказать, что из равенства следует совпадение центра P многоугольника с основанием высоты, поэтому правильный тетраэдр является правильной пирамидой.
Что такое апофема?
Апофемой пирамиды называется высота ее боковой грани. Если пирамида правильная, то все ее апофемы равны. Обратное неверно.
Репетитор по математике о своей терминологии: работа с пирамидами на 80% строится через два вида треугольников:
1) Содержащий апофему SK и высоту SP
2) Содержащий боковое ребро SA и его проекцию PA
Чтобы упростить ссылки на эти треугольники репетитору по математике удобнее называть первый из них апофемным , а второй реберным . К сожалению, этой терминологии вы не встретите ни в одном из учебников, и преподавателю приходится вводить ее в одностороннем порядке.
К сожалению, этой терминологии вы не встретите ни в одном из учебников, и преподавателю приходится вводить ее в одностороннем порядке.
Формула объема пирамиды :
1) , где – площадь основания пирамиды, а -высота пирамиды
2) , где – радиус вписанного шара, а – площадь полной поверхности пирамиды.
3) , где MN – расстояние любыми двумя скрещивающимися ребрами, а – площадь параллелограмма, образованного серединами четырех оставшихся ребер.
Свойство основания высоты пирамиды:
Точка P (смотри рисунок) совпадает с центром вписанной окружности в основание пирамиды, если выполняется одно из следующих условий:
1) Все апофемы равны
2) Все боковые грани одинаково наклонены к основанию
3) Все апофемы одинаково наклонены к высоте пирамиды
4) Высота пирамиды одинаково наклонена ко всем боковым граням
Комментарий репетитора по математике : обратите внимание, что все пункты объединяет одно общее свойство: так или иначе везде участвуют боковые грани (апофемы — это их элементы).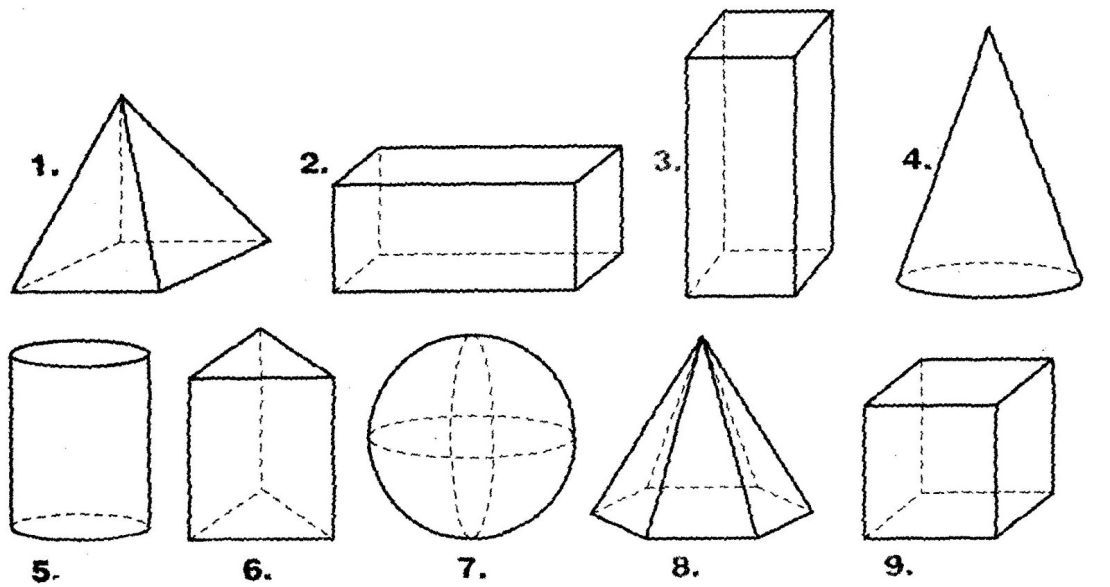
Точка P совпадает с центром описанной около основания пирамиды окружностью, если верно одно их трех условий:
1) Все боковые ребра равны
2) Все боковые ребра одинаково наклонены к основанию
3) Все боковые ребра одинаково наклонены к высоте
Когда человек слышит слово «пирамида», то сразу вспоминает величественные египетские сооружения. Тем не менее древние каменные гиганты являются лишь одним из представителей класса пирамид. В данной статье рассмотрим с геометрической точки зрения свойства правильной четырехугольной пирамиды.
Что такое пирамида в общем случае?
В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник.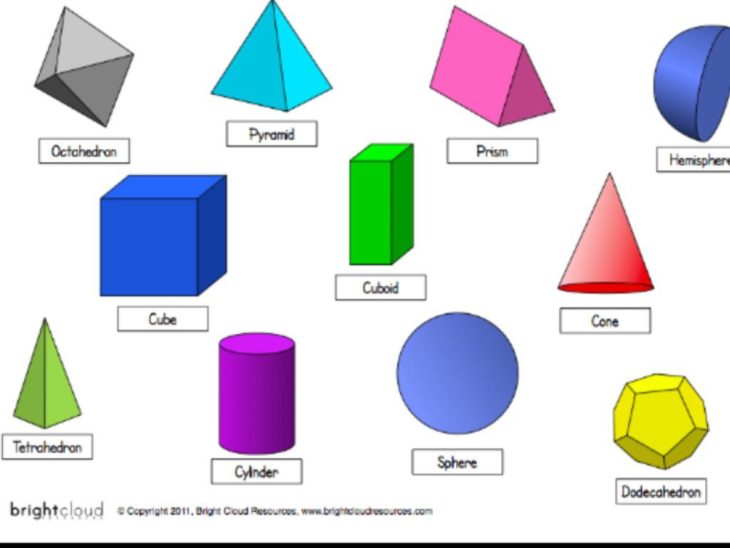
Мы видим что первая фигура имеет треугольное основание, вторая — четырехугольное. Две последние представлены пяти- и шестиугольным основанием. Однако боковая поверхность всех пирамид образована треугольниками. Их число точно равно количеству сторон или вершин многоугольника в основании.
Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:
- в основании должен находиться правильный многоугольник;
- боковая поверхность фигуры должна состоять из равных равнобедренных треугольников.
Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.
Сначала покажем на рисунке, как выглядит эта фигура.
Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).
Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90 o .
Египетские пирамиды в Гизе являются правильными четырехугольными.
Четыре основных линейных параметра
Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.
Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:
b = √(a 2 / 2 + h 2)
Теперь приведем формулу для длины a b апофемы (высота треугольника, опущенная на сторону основания):
a b = √(a 2 / 4 + h 2)
Очевидно, что боковое ребро b всегда больше апофемы a b .
Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например a b и h.
Площадь и объем фигуры
Это еще два важных свойства правильной четырехугольной пирамиды. Основание фигуры имеет следующую площадь:
Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему a b пирамиды так:
Если a b является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.
Общая площадь поверхности рассматриваемой фигуры складывается из площадей S o и S b:
S = S o + S b = a 2 + 2 × a × a b = a (a + 2 × a b)
Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.
Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:
То есть V равен третьей части произведения высоты фигуры на площадь ее основания.
Свойства правильной усеченной четырехугольной пирамиды
Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.
Удобнее всего изучать характеристики усеченной пирамиды, если ее основания параллельны друг другу. В этом случае нижнее и верхнее основания будут подобными многоугольниками. Поскольку в четырехугольной правильной пирамиде основание — это квадрат, то образованное при срезе сечение тоже будет представлять квадрат, но уже меньшего размера.
Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.
Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:
V = 1/3 × h × (S o1 + S o2 + √(S o1 × S o2))
Здесь h — расстояние между основаниями фигуры, S o1 , S o2 — площади нижнего и верхнего оснований.
Условия формирования у младших школьников геометрических понятий
%PDF-1.5 % 1 0 obj > /Metadata 4 0 R >> endobj 5 0 obj /Title >> endobj 2 0 obj > endobj 3 0 obj > endobj 4 0 obj > stream
 32 841.92]
/Contents [91 0 R 92 0 R 93 0 R]
/Group >
/Tabs /S
/StructParents 0
/Annots [94 0 R]
>>
endobj
7 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 95 0 R
/Group >
/Tabs /S
/StructParents 1
>>
endobj
8 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 96 0 R
/Group >
/Tabs /S
/StructParents 2
>>
endobj
9 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 97 0 R
/Group >
/Tabs /S
/StructParents 3
>>
endobj
10 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 98 0 R
/Group >
/Tabs /S
/StructParents 4
>>
endobj
11 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 100 0 R
/Group >
/Tabs /S
/StructParents 5
>>
endobj
12 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
32 841.92]
/Contents [91 0 R 92 0 R 93 0 R]
/Group >
/Tabs /S
/StructParents 0
/Annots [94 0 R]
>>
endobj
7 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 95 0 R
/Group >
/Tabs /S
/StructParents 1
>>
endobj
8 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 96 0 R
/Group >
/Tabs /S
/StructParents 2
>>
endobj
9 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 97 0 R
/Group >
/Tabs /S
/StructParents 3
>>
endobj
10 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 98 0 R
/Group >
/Tabs /S
/StructParents 4
>>
endobj
11 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 100 0 R
/Group >
/Tabs /S
/StructParents 5
>>
endobj
12 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 32 841.92]
/Contents 104 0 R
/Group >
/Tabs /S
/StructParents 6
>>
endobj
13 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 108 0 R
/Group >
/Tabs /S
/StructParents 7
>>
endobj
14 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 109 0 R
/Group >
/Tabs /S
/StructParents 8
>>
endobj
15 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 111 0 R
/Group >
/Tabs /S
/StructParents 9
>>
endobj
16 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 114 0 R
/Group >
/Tabs /S
/StructParents 10
>>
endobj
17 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 116 0 R
/Group >
/Tabs /S
/StructParents 11
>>
endobj
18 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
32 841.92]
/Contents 104 0 R
/Group >
/Tabs /S
/StructParents 6
>>
endobj
13 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 108 0 R
/Group >
/Tabs /S
/StructParents 7
>>
endobj
14 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 109 0 R
/Group >
/Tabs /S
/StructParents 8
>>
endobj
15 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 111 0 R
/Group >
/Tabs /S
/StructParents 9
>>
endobj
16 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 114 0 R
/Group >
/Tabs /S
/StructParents 10
>>
endobj
17 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 116 0 R
/Group >
/Tabs /S
/StructParents 11
>>
endobj
18 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 32 841.92]
/Contents 118 0 R
/Group >
/Tabs /S
/StructParents 12
>>
endobj
19 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 119 0 R
/Group >
/Tabs /S
/StructParents 13
>>
endobj
20 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 122 0 R
/Group >
/Tabs /S
/StructParents 14
>>
endobj
21 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 123 0 R
/Group >
/Tabs /S
/StructParents 15
>>
endobj
22 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 124 0 R
/Group >
/Tabs /S
/StructParents 16
>>
endobj
23 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 125 0 R
/Group >
/Tabs /S
/StructParents 17
>>
endobj
24 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
32 841.92]
/Contents 118 0 R
/Group >
/Tabs /S
/StructParents 12
>>
endobj
19 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 119 0 R
/Group >
/Tabs /S
/StructParents 13
>>
endobj
20 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 122 0 R
/Group >
/Tabs /S
/StructParents 14
>>
endobj
21 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 123 0 R
/Group >
/Tabs /S
/StructParents 15
>>
endobj
22 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 124 0 R
/Group >
/Tabs /S
/StructParents 16
>>
endobj
23 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 125 0 R
/Group >
/Tabs /S
/StructParents 17
>>
endobj
24 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 32 841.92]
/Contents 126 0 R
/Group >
/Tabs /S
/StructParents 18
>>
endobj
25 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 127 0 R
/Group >
/Tabs /S
/StructParents 19
>>
endobj
26 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 128 0 R
/Group >
/Tabs /S
/StructParents 20
>>
endobj
27 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 129 0 R
/Group >
/Tabs /S
/StructParents 21
>>
endobj
28 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 130 0 R
/Group >
/Tabs /S
/StructParents 22
>>
endobj
29 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 131 0 R
/Group >
/Tabs /S
/StructParents 23
>>
endobj
30 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
32 841.92]
/Contents 126 0 R
/Group >
/Tabs /S
/StructParents 18
>>
endobj
25 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 127 0 R
/Group >
/Tabs /S
/StructParents 19
>>
endobj
26 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 128 0 R
/Group >
/Tabs /S
/StructParents 20
>>
endobj
27 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 129 0 R
/Group >
/Tabs /S
/StructParents 21
>>
endobj
28 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 130 0 R
/Group >
/Tabs /S
/StructParents 22
>>
endobj
29 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 131 0 R
/Group >
/Tabs /S
/StructParents 23
>>
endobj
30 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 32 841.92]
/Contents 132 0 R
/Group >
/Tabs /S
/StructParents 24
>>
endobj
31 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 133 0 R
/Group >
/Tabs /S
/StructParents 25
>>
endobj
32 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 134 0 R
/Group >
/Tabs /S
/StructParents 26
>>
endobj
33 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 135 0 R
/Group >
/Tabs /S
/StructParents 27
>>
endobj
34 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 136 0 R
/Group >
/Tabs /S
/StructParents 28
>>
endobj
35 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 137 0 R
/Group >
/Tabs /S
/StructParents 29
>>
endobj
36 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
32 841.92]
/Contents 132 0 R
/Group >
/Tabs /S
/StructParents 24
>>
endobj
31 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 133 0 R
/Group >
/Tabs /S
/StructParents 25
>>
endobj
32 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 134 0 R
/Group >
/Tabs /S
/StructParents 26
>>
endobj
33 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 135 0 R
/Group >
/Tabs /S
/StructParents 27
>>
endobj
34 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 136 0 R
/Group >
/Tabs /S
/StructParents 28
>>
endobj
35 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 137 0 R
/Group >
/Tabs /S
/StructParents 29
>>
endobj
36 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 32 841.92]
/Contents 138 0 R
/Group >
/Tabs /S
/StructParents 30
>>
endobj
37 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 139 0 R
/Group >
/Tabs /S
/StructParents 31
>>
endobj
38 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 144 0 R
/Group >
/Tabs /S
/StructParents 32
>>
endobj
39 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 147 0 R
/Group >
/Tabs /S
/StructParents 33
>>
endobj
40 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 149 0 R
/Group >
/Tabs /S
/StructParents 34
>>
endobj
41 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 153 0 R
/Group >
/Tabs /S
/StructParents 35
>>
endobj
42 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
32 841.92]
/Contents 138 0 R
/Group >
/Tabs /S
/StructParents 30
>>
endobj
37 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 139 0 R
/Group >
/Tabs /S
/StructParents 31
>>
endobj
38 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 144 0 R
/Group >
/Tabs /S
/StructParents 32
>>
endobj
39 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 147 0 R
/Group >
/Tabs /S
/StructParents 33
>>
endobj
40 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 149 0 R
/Group >
/Tabs /S
/StructParents 34
>>
endobj
41 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 153 0 R
/Group >
/Tabs /S
/StructParents 35
>>
endobj
42 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 32 841.92]
/Contents 155 0 R
/Group >
/Tabs /S
/StructParents 36
>>
endobj
43 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 156 0 R
/Group >
/Tabs /S
/StructParents 37
>>
endobj
44 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 157 0 R
/Group >
/Tabs /S
/StructParents 38
>>
endobj
45 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 159 0 R
/Group >
/Tabs /S
/StructParents 39
>>
endobj
46 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 160 0 R
/Group >
/Tabs /S
/StructParents 40
>>
endobj
47 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 161 0 R
/Group >
/Tabs /S
/StructParents 41
>>
endobj
48 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
32 841.92]
/Contents 155 0 R
/Group >
/Tabs /S
/StructParents 36
>>
endobj
43 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 156 0 R
/Group >
/Tabs /S
/StructParents 37
>>
endobj
44 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 157 0 R
/Group >
/Tabs /S
/StructParents 38
>>
endobj
45 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 159 0 R
/Group >
/Tabs /S
/StructParents 39
>>
endobj
46 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 160 0 R
/Group >
/Tabs /S
/StructParents 40
>>
endobj
47 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 161 0 R
/Group >
/Tabs /S
/StructParents 41
>>
endobj
48 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 32 841.92]
/Contents 162 0 R
/Group >
/Tabs /S
/StructParents 42
>>
endobj
49 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 163 0 R
/Group >
/Tabs /S
/StructParents 43
>>
endobj
50 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 164 0 R
/Group >
/Tabs /S
/StructParents 44
>>
endobj
51 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 165 0 R
/Group >
/Tabs /S
/StructParents 45
>>
endobj
52 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 167 0 R
/Group >
/Tabs /S
/StructParents 46
>>
endobj
53 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 168 0 R
/Group >
/Tabs /S
/StructParents 47
>>
endobj
54 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
32 841.92]
/Contents 162 0 R
/Group >
/Tabs /S
/StructParents 42
>>
endobj
49 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 163 0 R
/Group >
/Tabs /S
/StructParents 43
>>
endobj
50 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 164 0 R
/Group >
/Tabs /S
/StructParents 44
>>
endobj
51 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 165 0 R
/Group >
/Tabs /S
/StructParents 45
>>
endobj
52 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 167 0 R
/Group >
/Tabs /S
/StructParents 46
>>
endobj
53 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 168 0 R
/Group >
/Tabs /S
/StructParents 47
>>
endobj
54 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 32 841.92]
/Contents 169 0 R
/Group >
/Tabs /S
/StructParents 48
>>
endobj
55 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 170 0 R
/Group >
/Tabs /S
/StructParents 49
>>
endobj
56 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 172 0 R
/Group >
/Tabs /S
/StructParents 50
>>
endobj
57 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 174 0 R
/Group >
/Tabs /S
/StructParents 51
>>
endobj
58 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 176 0 R
/Group >
/Tabs /S
/StructParents 52
>>
endobj
59 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 177 0 R
/Group >
/Tabs /S
/StructParents 53
>>
endobj
60 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
32 841.92]
/Contents 169 0 R
/Group >
/Tabs /S
/StructParents 48
>>
endobj
55 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 170 0 R
/Group >
/Tabs /S
/StructParents 49
>>
endobj
56 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 172 0 R
/Group >
/Tabs /S
/StructParents 50
>>
endobj
57 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 174 0 R
/Group >
/Tabs /S
/StructParents 51
>>
endobj
58 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 176 0 R
/Group >
/Tabs /S
/StructParents 52
>>
endobj
59 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 177 0 R
/Group >
/Tabs /S
/StructParents 53
>>
endobj
60 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 32 841.92]
/Contents 179 0 R
/Group >
/Tabs /S
/StructParents 54
>>
endobj
61 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 181 0 R
/Group >
/Tabs /S
/StructParents 55
>>
endobj
62 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 183 0 R
/Group >
/Tabs /S
/StructParents 56
>>
endobj
63 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 184 0 R
/Group >
/Tabs /S
/StructParents 57
>>
endobj
64 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 185 0 R
/Group >
/Tabs /S
/StructParents 58
>>
endobj
65 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 186 0 R
/Group >
/Tabs /S
/StructParents 59
>>
endobj
66 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
32 841.92]
/Contents 179 0 R
/Group >
/Tabs /S
/StructParents 54
>>
endobj
61 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 181 0 R
/Group >
/Tabs /S
/StructParents 55
>>
endobj
62 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 183 0 R
/Group >
/Tabs /S
/StructParents 56
>>
endobj
63 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 184 0 R
/Group >
/Tabs /S
/StructParents 57
>>
endobj
64 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 185 0 R
/Group >
/Tabs /S
/StructParents 58
>>
endobj
65 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 186 0 R
/Group >
/Tabs /S
/StructParents 59
>>
endobj
66 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 32 841.92]
/Contents 187 0 R
/Group >
/Tabs /S
/StructParents 60
>>
endobj
67 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 188 0 R
/Group >
/Tabs /S
/StructParents 61
>>
endobj
68 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 189 0 R
/Group >
/Tabs /S
/StructParents 62
>>
endobj
69 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 190 0 R
/Group >
/Tabs /S
/StructParents 63
>>
endobj
70 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 191 0 R
/Group >
/Tabs /S
/StructParents 64
>>
endobj
71 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 192 0 R
/Group >
/Tabs /S
/StructParents 65
>>
endobj
72 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
32 841.92]
/Contents 187 0 R
/Group >
/Tabs /S
/StructParents 60
>>
endobj
67 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 188 0 R
/Group >
/Tabs /S
/StructParents 61
>>
endobj
68 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 189 0 R
/Group >
/Tabs /S
/StructParents 62
>>
endobj
69 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 190 0 R
/Group >
/Tabs /S
/StructParents 63
>>
endobj
70 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 191 0 R
/Group >
/Tabs /S
/StructParents 64
>>
endobj
71 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 192 0 R
/Group >
/Tabs /S
/StructParents 65
>>
endobj
72 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 32 841.92]
/Contents 193 0 R
/Group >
/Tabs /S
/StructParents 66
>>
endobj
73 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 196 0 R
/Group >
/Tabs /S
/StructParents 67
>>
endobj
74 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 199 0 R
/Group >
/Tabs /S
/StructParents 68
>>
endobj
75 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 202 0 R
/Group >
/Tabs /S
/StructParents 69
>>
endobj
76 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 205 0 R
/Group >
/Tabs /S
/StructParents 70
>>
endobj
77 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 207 0 R
/Group >
/Tabs /S
/StructParents 71
>>
endobj
78 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
32 841.92]
/Contents 193 0 R
/Group >
/Tabs /S
/StructParents 66
>>
endobj
73 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 196 0 R
/Group >
/Tabs /S
/StructParents 67
>>
endobj
74 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 199 0 R
/Group >
/Tabs /S
/StructParents 68
>>
endobj
75 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 202 0 R
/Group >
/Tabs /S
/StructParents 69
>>
endobj
76 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 205 0 R
/Group >
/Tabs /S
/StructParents 70
>>
endobj
77 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.32 841.92]
/Contents 207 0 R
/Group >
/Tabs /S
/StructParents 71
>>
endobj
78 0 obj
>
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 3$, где r – радиус сферы. Теперь мы собираемся вывести эти формулы с помощью интегрирования.
3$, где r – радиус сферы. Теперь мы собираемся вывести эти формулы с помощью интегрирования.Объем квадратной пирамиды Вывод
Предположим, мы хотим найти объем квадратной пирамиды с основанием $b$ и высотой $h$. Диаграмма ниже иллюстрирует эти размеры:
Теперь предположим, что мы разрезаем пирамиду на горизонтальные прямоугольные плиты и складываем объемы каждой плиты. Чтобы найти определенный объем пирамиды, мы должны просуммировать объемы бесконечного множества плит на интервале $[0, h]$. Давайте сначала найдем ширину одной из этих плит, назовем их $s$: 92 ч$. Теперь мы получим это с интегрированием.
Предположим, что у нас есть линия $f(x) = \frac{r}{h}x$, которая определяет линию с подъемом $r$ и ходом $h$. Вращение области площади, созданной этой линией, ограниченной осью $x$, вокруг оси $x$ приведет к образованию конуса с радиусом $r$ и высотой $h$, как показано на следующей диаграмме:
Итак, мы можем составить интеграл для нахождения объема любого конуса. Для конуса длины $h$ и радиуса $r$ вычислим интеграл: 92 ч \end{align}
Для конуса длины $h$ и радиуса $r$ вычислим интеграл: 92 ч \end{align}
Вот что мы хотели получить!
Если не указано иное, содержимое этой страницы находится под лицензией Creative Commons Attribution-ShareAlike 3.0 License
Volume Formula — JavaTpoint
следующий → ← предыдущая В геометрии трехмерные фигуры — это твердые объекты, имеющие три измерения. Размеры содержат длину, ширину и высоту объекта. Некоторые примеры трехмерных форм: куб, конус, цилиндр, пирамида, сфера, и т. д. Мы находим объем этих форм, чтобы мы могли измерить, сколько места объект занимает для хранения жидкости, газа и т. д. Существуют разные формулы объема для разных форм. Используя эти формулы, мы можем найти объем фигур. В этом разделе мы изучим формулу объема всех трехмерных фигур. Том Объем пространства, занимаемый объектом, называется объемом этого объекта, где объект является трехмерным объектом. Том обозначается буквой V . Измеряем объем в кубических единицах или единицах 3 . В следующей таблице мы суммировали все формулы объема с цифрой для лучшего понимания.
|



 Находим объем для измерения вместимости предмета или емкости. Мы можем легко найти объем любой трехмерной формы, используя формулу. Если трехмерная форма сложная, мы используем интегральное исчисление, чтобы найти объем.
Находим объем для измерения вместимости предмета или емкости. Мы можем легко найти объем любой трехмерной формы, используя формулу. Если трехмерная форма сложная, мы используем интегральное исчисление, чтобы найти объем.