Три уравнения с тремя неизвестными
64. Три уравнения с тремя неизвестными. Пусть теперь требуется решить совместно 3 уравнения с тремя неизвестными:
3x + 2y – 5z = 8
x + 3y – 2z = 9
4x + 5y – 6z = 26.
Вспоминая все предыдущее, мы уже заранее вправе думать, что здесь произвольные значения ни одному из неизвестных давать нельзя и что здесь найдем единственное решение (по одному числу для каждого неизвестного).
При этом для нас уже намечен путь, как этого достигнуть. В предыдущем п. мы научились из двух уравнений с тремя неизвестными определять два неизвестных через третье. Выберем из наших трех уравнений те два, которые кажутся нам наиболее простыми, напр., 1-е и 2-ое:
3x + 2y – 5z = 8
x + 3y – 2z = 9
и из них определим x и y через z
Подставим теперь полученные выражения для x – a и для y – a в третье уравнение, — получим:
(4(6 + 11z)) / 7 + (5(19 + z)) / 7 – 6z = 26
т. е. получили одно уравнение с одним неизвестным z, которое умеем решить.
4(6 + 11z) + 5(19 + z) – 42z = 182.
Раскроем скобки
24 + 44z + 95 + 5z – 42z = 182.
Перенесем известные члены вправо и сделаем приведение подобных членов:
7z = 63, откуда z = 9.
Теперь из формул (1) и (2) получим:
x = (6 + 11 · 9) / 7 = 15 и y = (19 + 9) / 7 = 4.
Еще пример:
2x + 3y = 11
5y + 2z = 3
4z + 3x = 66
Определим из первых двух уравнений 2 неизвестных через третье: мы именно видим, что можно из первого уравнения определить x через y и из второго определить z через y:
x = (11 – 3y) / 2 и z = (3 – 5y) / 2.
Подставим полученные выражения в третье уравнение на место z и x:
(4(3 – 5y)) / 2 + (3(11 – 3y)) / 2 = 66.
Отсюда получим:
4(3 – 5y) + 3(11 – 3y) = 132
или
12 – 20y + 33 – 9y = 132
или
–29y = 87,
откуда
y = –3.
Тогда
x = (11 – 3 · (–3)) / 2 = 10
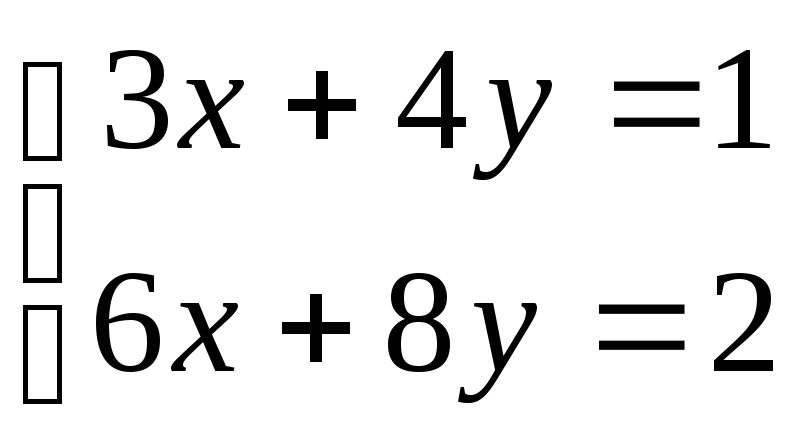
В этих двух примерах мы держались следующего плана; выбираем из данных трех уравнений какие-либо два, более удобных, и из них определяем два неизвестных через третье, – полученные выражения мы подставляем на место этих неизвестных в третье уравнение.
Возможны и иные планы. Поясним их на следующих примерах:
1. 3x – 4y + 3z = 19
4x – 6y + z = 22
7x – 18y = 33.
Мы видим, что в третье уравнение входят только 2 неизвестных, x и y. Поэтому постараемся получить из первых двух уравнений с тремя неизвестными новое уравнение с двумя неизвестными, а именно: также с x и y, — тогда мы будем иметь два уравнения с двумя неизвестными, которые умеем решать. Для этой цели исключим способом уравнивания коэффициентов из первых двух уравнений неизвестное z, для чего 1-ое уравнение оставим без изменения, а обе части второго умножим на –3. Получим:
3x – 4y + 3z = 19
–12x + 18y – 3z = –66.
Сложив по частям эти уравнения, получим:
–9x + 14y = –47
или
9x – 14y = 47.
Присоединим сюда еще третье из данных уравнений и решим их совместно способом уравнивания коэффициентов:
Подставляя это значение x – a в уравнение
9x – 14y = 47,
получим
54 – 14y = 47,
откуда
14y = 7 и y = ½
Подставляя полученные для x и для y значения в простейшее из данных уравнений, а именно в уравнение
4x – 6y + z = 22,
получим
24 – 3 + z = 22,
откуда
z = 1.
2. 3x + 5y – 9z = 29
5x + 2y – 6z = 17
4x – 10y + 3z = 17
Наметим следующий план: выберем сначала 2 из этих трех уравнений и из них способом уравнивания коэффициентов получим одно уравнение с двумя неизвестными; затем выберем вторую пару уравнений из данных и из них тем же способом получим второе уравнение с теми же двумя неизвестными. Применяясь к данным уравнениям, удобно будет выполнить этот план в следующем порядке: 1) возьмем 1-ое и 2-ое уравнение и из них, исключив способом уравнивания коэффициентов y, получим одно уравнение с x и z; 2) возьмем 1-ое и 3-е уравнения и из них также исключим y и получим второе уравнение с неизвестными x и z; 3) решим полученные 2 уравнения с неизвестными x и z также способом уравнения коэффициентов.
4) Подставим полученное для x значение в уравнение
2x – 3z = 15.
Получим:
–6 – 3z = 15 или 3z = –21 и z = –7.
Подставим полученные для x и z значения в уравнение
5x + 2y – 6z = 17.
Получим:
–15 + 2y + 42 = 17
или
2y = –10 и y = –5.
3. 4x – 2y + z = 4
5x + 3y – z = 11
3x + 7y – 2z = 7
Составим следующий план: 1) из первого уравнения определим z через x и y; 2) полученное выражение подставим на место z во 2-ое и в 3-е уравнения, – получим два уравнения с двумя неизвестными, а именно — с x и y; 3) решим полученные два уравнения.
1) z = 4 – 3x + 2y,
2) 5x + 3y – (4 – 3x + 2y) = 11
3x + 7y – 2(4 – 3x + 2y) = 7
Упростим каждое из этих уравнений:
1-ое: 5x + 3y – 4 + 3x – 2y = 11 или 8x + y = 15.
2-ое: 3x + 7y – 8 + 6x – 4y = 7 или 9x + 3y = 15 или 3x + y = 5.
3) Вычтем по частям из 1-го уравнения второе:
8x + y = 15
3x + y = 5
–————
5x = 10, откуда x = 2.
4) Подставим полученное для x значение в уравнение
3x + y = 5.
Получим
6 + y = 5,
откуда
y = –1.
Подставим эти значения x – a и y – a в выражение для z:
z = 4 – 3x + 2y.
Тогда
z = 4 – 6 – 2 = –4.
Глава А5. Система трех уравнений с тремя неизвестными
Рассмотрим систему уравнений
, , (1)
с неизвестными x, y, z (коэффициенты , , …, и свободные члены , , предположим данными). Введем обозначения
, , , .
Определитель , составленный из коэффициентов при неизвестных системы (1), называется определителем данной системы.
Полезно заметить, что определители
,
,
получаются из определителя
при помощи замены соответственно его первого,
второго и, наконец, третьего столбца столбцом
свободных членов данной системы.
, , .
Предположим теперь, что определитель системы равен нулю: . Если в случае хотя бы один из определителей , , отличен от нуля, то система (1) совсем не имеет решений.
В случае, когда и одновременно , , , система (1) также может совсем не иметь решений; но если система (1) при этих условиях имеет хотя бы одно решение, то она имеет бесконечно много различных решений. Однородной системой трех уравнений первой степени с тремя неизвестными называется система вида
, , (2)
то есть система уравнений, свободные
члены которых равны нулю. Очевидно, что такая
система всегда имеет решение: x=0,
y=0, z=0; оно называется нулевым. Если
,
то это решение является единственным. Если же
,
то однородная система (2) имеет бесконечно много
ненулевых решений.
| В задачах 1236-1243 требуется установить что системы уравнения имеют единственное решение,и найти его. | ||
| 1236 | ||
| 1237 | ||
| 1238 | ||
| 1239 | ||
| 1240 | ||
| 1241 | ||
| 1242 | ||
| 1243 | ||
| 1244 | Найти все решения системы | |
| 1245 | Найти все решения системы | |
| 1246 | Найти все решения системы | |
| 1247 | Определить, при
каких значениях a и b система уравнений 1). Имеет единственное решение, 2). Не
имеет решений, 3). Имеет бесконечно много решений. | |
| 1248 | Доказать, что если система уравнений совместна, то . | |
| 1249 | Найти все решения системы . | |
| 1250 | Найти все решения системы . | |
| 1251 | Определить, при каком значении а система однородных уравнений имеет нулевое решение. |
одновременных уравнений. Три уравнения с тремя неизвестными.
Содержание | Дом
Одновременные уравнения: Раздел 3
вернуться к разделу 2
Назад к Разделу 1
Пример 6.
Решите эту систему из трех уравнений с тремя неизвестными:
| 1) | х | + | г | − | я | = | 4 |
| 2) | х | − | 2 у | + | 3 з | = | −6 |
| 3) | 2 х | + | 3 г | + | я | = | 7 |
Стратегия состоит в том, чтобы свести это к двум уравнениям с двумя неизвестными.
Сделайте это, исключив одно из неизвестных из двух пар уравнений: либо из уравнений 1) и 2), либо 1) и 3), либо 2) и 3).
Например, удалим z . Сначала мы исключим его из уравнений 1) и 3), просто добавив их. Получаем:
4) 3 x + 4 y = 11
Далее мы исключим z из уравнений 1) и 2). Мы умножим уравнение 1) на 3. Мы назовем полученное уравнение 1′ («1 простое число»), чтобы показать, что мы получили его из уравнения 1):
| 1′) | 3 х | + | 3 г | − | 3 з | = | 12 |
| 2) | х | − | 2 у | + | 3 з | = | −6 |
| ____________________________________________________________________________________ | |||||||
| 5) | 4 х | + | г | = | 6 | ||
Теперь решим уравнения 4) и 5) для x и y .
Удалим y . Умножим уравнение 5) на −4 и добавим к уравнению 4):
| 5′) | −16 х | − | 4 у | = | −24 |
| 4) | 3 х | + | 4 у | = | 11 |
| __________________________________________________________________________________________ | |||||
| −13 х | = | −13 | |||
x = 1,
Чтобы найти y , подставим x = 1 в уравнении 4):
| 3 + 4 у | = | 11 |
| 4 г | = | 11 −3 |
| 4 г | = | 8 |
| г | = | 2. |
Наконец, чтобы найти z , подставьте эти значения x и y в одно из исходных уравнений; скажем уравнение 1):
| 1 + 2 − я | = | 4 |
| − z | = | 4 − 3 = 1 |
| z | = | −1. |
Задача 8. Решите эту систему уравнений.
| 1) | х | + | г | + | я | = | 6 |
| 2) | х | − | г | + | я | = | 2 |
| 3) | х | + | 2 у | − | я | = | 2 |
Исключить y , например, из уравнений 1) и 2, а затем из уравнений 2) и 3).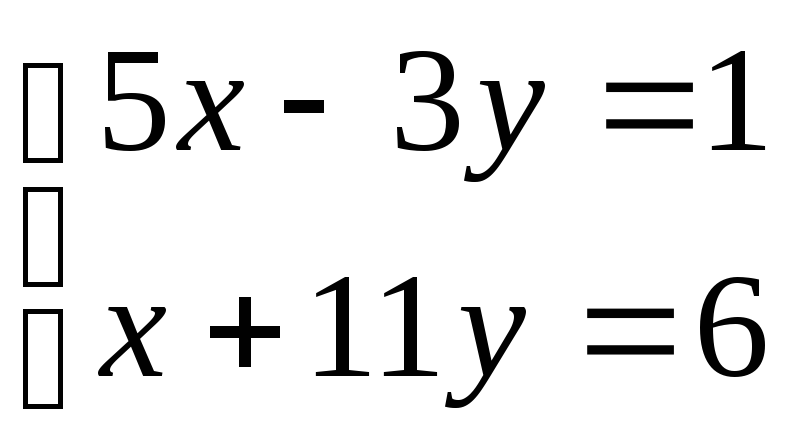
Добавить уравнения 1) и 2):
4) 2 x + 2 z = 8
Затем умножьте уравнение 2) на 2 и прибавьте к 3):
| 2′) | 2 х | − | 2 у | + | 2 с | = | 4 |
| 3) | х | + | 2 у | − | я | = | 2 |
| ____________________________________________________________________________________ | |||||||
| 5) | 3 х | + | z ; | = | 6 | ||
Решить 5) с 4).
Умножьте 5 на −2:
| 5′) | −6 х | − | 2 с | = | −12 |
| 4) | 2 х | + | 2 с | = | 8 |
| __________________________________________________________________________________________ | |||||
| −4 х | = | −4 | |||
| х | = | 1. | |||
Чтобы найти z , подставьте x = 1 в уравнение 5):
| 3 + z | = | 6 |
| z | = | 3. |
Наконец, чтобы найти y , подставьте эти значения x и z в одно из исходных уравнений; скажем уравнение 1):
| 1 + y + 3 | = | 6 |
| г | = | 2. |
Всегда проверяйте решение, подставляя числа в каждое из трех уравнений.
Задача 9. Решите эту систему уравнений.
| 1) | х | + | г | − | я | = | 1 |
| 2) | 8 х | + | 3 г | − | 6 с | = | 1 |
| 3) | −4 х | − | г | + | 3 з | = | 1 |
Вот решение: x = 2, y = 3, z = 4,
вернуться к разделу 2
Назад к Разделу 1
Следующий урок: текстовые задачи, ведущие к уравнениям на одновременные уравнения
Содержание | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Системы уравнений с тремя переменными | безграничная алгебра |
Решение систем уравнений с тремя переменными
Система уравнений с тремя переменными состоит из двух или более уравнений, каждое из которых содержит от одной до трех переменных.
Цели обучения
Решите систему уравнений с тремя переменными графически, используя подстановку или исключение уравнения, каждое из которых может содержать одну или несколько из трех переменных, обычно x , y и z . Введение переменной z означает, что графические функции теперь представляют собой плоскости, а не линии.
Повторяйте, пока не останется одно уравнение, а затем, используя это уравнение, вернитесь назад, чтобы решить предыдущие уравнения.Ключевые термины
- система уравнений с тремя переменными : Набор из одного или нескольких уравнений, каждое из которых может содержать одну или более из трех переменных, обычно x, y и z.
- система уравнений : Набор уравнений с несколькими переменными, которые можно решить, используя определенный набор значений.
Системы уравнений с тремя переменными
В математике одновременные уравнения представляют собой набор уравнений, содержащих несколько переменных.
Этот набор часто называют системой уравнений . Решением системы уравнений является конкретная спецификация значений всех переменных, которая одновременно удовлетворяет всем уравнениям. Графически решение находится там, где функции пересекаются.
В системе уравнений с тремя переменными у вас может быть одно или несколько уравнений, каждое из которых может содержать одну или несколько из трех переменных, обычно x , y и z . Введение переменной z означает, что отображаемые на графике функции теперь представляют собой плоскости, а не линии.
Простой пример
Это набор линейных уравнений, также известный как линейная система уравнений, с тремя переменными:
{3x+2y−z=6−2x+2y+z=3x+y+z=4\left\{\ begin{matrix} 3x+2y-z=6\\ -2x+2y+z=3\\ x+y+z=4\\ \end{matrix}\right.⎩
⎨
⎧3x+2y−z=6−2x+2y+z=3x+y+z=4
Решение этой системы уравнений:
{x=1y=2z=1 \left\{\begin{matrix} x=1\\ y=2\\ z=1\\ \end{matrix}\right.
⎩
⎨
⎧x=1y=2z=1
Подставьте эти значения к каждому из уравнений, чтобы убедиться, что решение удовлетворяет всем трем уравнениям.
Решение систем уравнений с тремя переменными
Графический метод
Графический метод решения системы уравнений с тремя переменными заключается в построении плоскостей, которые образуются при построении графика каждого уравнения системы, и последующем нахождении точки пересечения всех трех плоскостей. Единственная точка, в которой пересекаются все три плоскости, является единственным решением системы.
Система линейных уравнений: На этом изображении показана система из трех уравнений с тремя переменными. Точка пересечения (белая точка) является единственным решением этой системы.
Метод замены
Метод подстановки для решения системы уравнений с тремя переменными включает в себя определение уравнения, которое можно легко записать с одной переменной в качестве предмета (путем решения уравнения для этой переменной).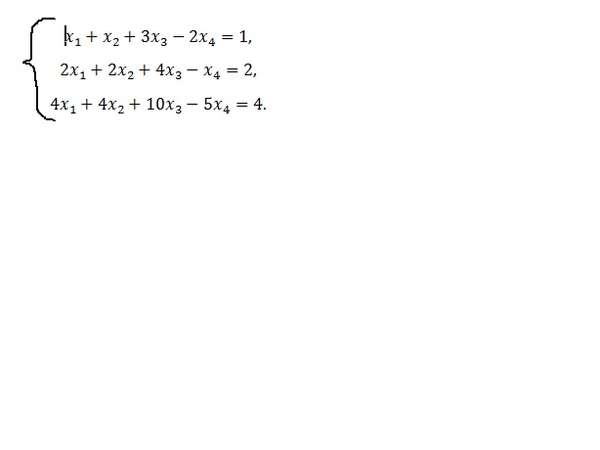
Затем подставьте это выражение там, где эта переменная появляется в двух других уравнениях, тем самым получив меньшую систему с меньшим количеством переменных. После того, как эта меньшая система будет решена, будь то дальнейшее применение метода подстановки или других методов, подставьте решения, найденные для переменных, обратно в первое выражение в правой части.
Например, рассмотрим следующую систему уравнений:
{3x+2y−z=6−2x+2y+z=3x+y+z=4\left\{\begin{matrix} 3x+2y-z= 6\\ -2x+2y+z=3\\ x+y+z=4\\ \end{matrix}\right.⎩
⎨
⎧3x+2y−z=6−2x+2y+ z=3x+y+z=4
Поскольку коэффициент при z уже равен 1 в первом уравнении, найдите z , чтобы получить:
z=3x+2y−6z=3x+2y-6z =3x+2y−6
Подставим это выражение вместо z в два других уравнения:
{−2x+2y+(3x+2y−6)=3x+y+(3x+2y−6)=4\left \{\begin{matrix} -2x+2y+(3x+2y-6)=3\\ x+y+(3x+2y-6)=4\\ \end{matrix}\right.
{−2x+2y+( 3x+2y−6)=3x+y+(3x+2y−6)=4
Эта новая система упрощается до:
{x+4y=94x+3y=10\left\{\begin{matrix} x+4y=9\\ 4x+3y=10\\ \end{matrix}\right .{x+4y=94x+3y=10
Теперь, решив x в первом уравнении, получим:
x=9−4yx=9-4yx=9−4y
.
Подставьте это выражение для x в последнее уравнение системы и решите для y :
4(9−4y)+3y=1036−16y+3y=1013y=26y=2\displaystyle \begin{выравнивание} 4(9-4г)+3г &=10 \\36-16л+3г&=10 \\13г&=26 \\у&=2 \end{выравнивание}4(9−4y)+3y36−16y+3y13yy=10=10=26=2
Теперь, когда у вас есть значение y , повторите уравнение. Подставьте
y=2y=2y=2
в уравнение
x=9−4yx=9-4yx=9−4y
, чтобы получить
x=1x=1x=1
.
Снова подставьте
(1,2)(1,2)(1,2)
в первое уравнение с подстановкой и найдите z :
z=3x+2y−6z=(3 ⋅1)+(2⋅2)−6z=1\begin {выравнивание}z&=3x+2y-6 \\z&=(3 \cdot 1)+(2 \cdot 2) -6 \\г&=1 \end{align}zzz=3x+2y−6=(3⋅1)+(2⋅2)−6=1
Следовательно, решение системы уравнений:
(1,2,1)(1,2,1)(1,2,1)
.
Метод исключения
Исключение с помощью разумного умножения — еще один широко используемый метод решения одновременных линейных уравнений. Он использует общие принципы, согласно которым каждая часть уравнения по-прежнему равна другой, когда обе части умножаются (или делятся) на одну и ту же величину или когда одна и та же величина добавляется (или вычитается) из обеих частей.
По мере того, как уравнения упрощаются за счет исключения некоторых переменных, переменная в конечном итоге появляется в полностью решаемой форме, и это значение затем можно «обратно подставить» в ранее полученные уравнения, подставив это значение вместо переменной. Как правило, каждая «обратная замена» может позволить решить другую переменную в системе.
Рассмотрим следующую систему:
{x+y+z=2x−y+3z=42x+2y+z=3\left\{\begin{matrix} x+y+z=2\\ x -y+3z=4\\ 2x+2y+z=3\\ \end{matrix}\right.⎩
⎨
⎧x+y+z=2x−y+3z=42x+2y+z=3
Используя метод исключения, начните с вычитания первого уравнения из второго и упрощения:
x− y+3z−(x+y+z)=4−2−2y+2z=2\displaystyle \begin{выравнивание} x-y+3z-(x+y+z)&=4-2 \\-2y+2z&=2 \end{align}x−y+3z−(x+y+z)−2y+2z=4−2=2
Теперь у нас есть следующая система уравнений:
{x+y+z =2−2y+2z=22x+2y+z=3\left\{\begin{matrix} x+y+z=2\\ -2y+2z=2\\ 2x+2y+z=3\\ \ конец{матрица}\справа.
⎩
⎨
⎧x+y+z=2−2y+2z=22x+2y+z=3
Теперь вычтите два раза первое уравнение из третьего уравнения, чтобы получить
2x+2y+z−2 (x+y+z)=3−2(2)2x+2y+z−2x−2y−2z=−1z=1\begin {align}2x+2y+z-2(x+y+z)& =3-2(2) \\2x+2y+z-2x-2y-2z&=-1 \\г&=1 \end {align}2x+2y+z-2(x+y+z)2x+2y+z-2x-2y-2zz=3-2(2)=-1=1
Это показывает новая система:
{x+y+z=2−2y+2z=2z=1\left\{\begin{matrix} x+y+z=2\\ -2y+2z=2\\ z= 1\\ \end{matrix}\right.⎩
⎨
⎧x+y+z=2−2y+2z=2z=1
Затем вычтите дважды третье уравнение из второго уравнения и упростите:
−2y+2z−2z=2−2y=0 \begin {выравнивание} -2y+2z-2z&=2-2 \\у&=0 \end {align}−2y+2z−2zy=2−2=0
Это показывает новую систему:
{x+y+z=2y=0z=1\left\{\begin{ матрица} x+y+z=2\\ y=0\\ z=1\\ \end{matrix}\right.⎩
⎨
⎧x+y+z=2y=0z=1
Наконец, вычтите третье и второе уравнение из первого уравнения, чтобы получить
x+y+z-y-z=2-0-1x=1\begin {align} x+y+z-y-z&=2-0-1 \\х&=1 \end {align}x+y+z−y−zx=2−0−1=1
Таким образом, окончательная решенная система будет следующей:
{x=1y=0z=1\left\ {\begin{matrix} x=1\\ y=0\\ z=1\\ \end{matrix}\right.
⎩
⎨
⎧x=1y=0z=1
Несовместимые и зависимые Системы с тремя переменными
Системы уравнений с тремя переменными бывают независимыми, зависимыми или несовместными; каждый случай может быть установлен алгебраически и представлен графически.
Цели обучения
Объясните графически, что означает, что системы уравнений с тремя переменными являются несовместимыми или зависимыми, а также как алгебраически распознать, когда это так. решения. Графически бесконечное количество решений находится на линии или плоскости, которая служит пересечением трех плоскостей в пространстве.
0=00 = 00=0
.
3=03 = 03=0
.Ключевые термины
- Независимая система : Система уравнений с единственным решением. Для систем уравнений с тремя переменными это решение представляет собой упорядоченную тройку
(x,y,z)(x, y, z)(x,y,z)
, который представляет единственную точку пересечения трех плоскостей. - Зависимая система : Система уравнений с бесконечным числом решений. Для систем уравнений с тремя переменными существует бесконечное число решений на прямой или плоскости, являющейся пересечением трех плоскостей в пространстве.
- Несовместимая система : Система уравнений без решения. Система уравнений с тремя переменными, не имеющая решений, представлена тремя плоскостями, не имеющими общих точек.
Идентификация зависимых и несогласованных систем
Напомним, что решение линейной системы — это такое присвоение чисел переменным, при котором одновременно выполняются все уравнения.
Решение системы уравнений с тремя переменными представляет собой упорядоченную тройку
(x,y,z)(x, y, z)(x,y,z)
и описывает точку пересечения трех плоскостей в пространстве .
Возможны три варианта решения системы трех уравнений с тремя переменными:
- Независимые системы имеют единственное решение. Решение системы методом исключения приводит к одной упорядоченной тройке
(x,y,z)(x, y, z)(x,y,z)
. Графически упорядоченная тройка определяет точку, являющуюся пересечением трех плоскостей в пространстве. - Зависимые системы имеют бесконечное число решений. Графически решения попадают на линию или плоскость, являющуюся пересечением трех плоскостей в пространстве.
- Непоследовательный 9Системы 0845 не имеют решения. Графически система без решения изображается тремя плоскостями, не имеющими общих точек.
Зависимые системы уравнений с тремя переменными
Из работы с системами уравнений с двумя переменными мы знаем, что зависимая система уравнений имеет бесконечное число решений.
То же верно и для зависимых систем уравнений с тремя переменными. Бесконечное количество решений может быть результатом нескольких ситуаций. Три плоскости могут быть одинаковыми, так что решение одного уравнения будет решением двух других уравнений. Все три уравнения могут быть разными, но они пересекаются на прямой, которая имеет бесконечные решения (графическое представление см. ниже). Или два уравнения могут быть одинаковыми и пересекать третье по прямой (см. пример задачи для графического представления).
Зависимые системы: Пример трех различных уравнений, пересекающихся на прямой.
Например, рассмотрим эту систему уравнений:
\left\\begin{matrix} \begin {выравнивание} 2x + y — 3z &= 0 \\ 4х + 2у — 6з &= 0 \\ х — у + г &= 0 \конец {выровнять} \end{матрица} \right.
Сначала умножьте первое уравнение на
−2-2−2
и добавьте его ко второму уравнению:
−2(2x+y−3z)+(4x+2y−6z)=0+0 (−4x+4x)+(−2y+2y)+(6z−6z)=00=0\begin {align} -2(2x + y — 3z) + (4x + 2y — 6z) &= 0 + 0 \\ (-4x + 4x) + (-2y + 2y) + (6z — 6z) &= 0 \\ 0 &= 0 \end {align}−2(2x+y−3z)+(4x+2y−6z)(−4x+4x)+(−2y+2y)+(6z−6z)0=0+0=0= 0
Нам не нужно продолжать.
В результате мы получаем тождество
0=00 = 00=0
, которое говорит нам, что эта система имеет бесконечное число решений. Есть и другие способы начать решать эту систему, например, умножить третье уравнение на
−2-2−2
и добавить его к первому уравнению. Затем мы проделаем те же шаги, что и выше, и получим тот же результат:
0=00 = 00=0
.
Если бы мы построили график каждого из трех уравнений, у нас были бы три плоскости, изображенные ниже. Обратите внимание, что две плоскости одинаковы и пересекают третью плоскость по прямой. Набор решений бесконечен, так как все точки вдоль линии пересечения будут удовлетворять всем трем уравнениям.
Зависимая система : Два уравнения представляют одну и ту же плоскость, и они пересекают третью плоскость по прямой.
Несовместные системы уравнений с тремя переменными
Так же, как и с системами уравнений с двумя переменными, мы можем столкнуться с несовместной системой уравнений с тремя переменными, а это означает, что она не имеет решения, удовлетворяющего всем трем уравнениям.
Уравнения могут представлять три параллельные плоскости, две параллельные плоскости и одну пересекающуюся плоскость или три плоскости, которые пересекают две другие, но не в одном и том же месте. Процесс исключения приведет к ложному утверждению, например,
3=73 = 73=7
или какое-то другое противоречие.
Несогласованные системы : Все три рисунка представляют системы три на три без решения. а) Три плоскости пересекаются друг с другом по трем различным параллельным прямым, не пересекающимся в одной точке. (b) Две плоскости параллельны и пересекаются с третьей плоскостью, но не друг с другом. в) Все три плоскости параллельны, поэтому точек пересечения нет.
Например, рассмотрим систему уравнений
\слева\\начать{матрицу} \begin {выравнивание} x — 3y + z &= 4\\ -х + 2у — 5з &= 3 \\ 5x — 13y + 13z &= 8 \конец {выровнять} \end{матрица} \right.
Используя метод исключения для решения системы уравнений с тремя переменными, обратите внимание, что мы можем сложить первое и второе уравнения, чтобы сократить
xxx
:
(x−3y+z)+(−x+2y− 5z)=4+3(x−x)+(−3y+2y)+(z−5z)=7−y−4z=7\begin {align}(x — 3y + z) + (-x + 2y — 5з)&=4+3\ (х — х) + (-3у + 2у) + (з-5з) &= 7 \\ -y — 4z &= 7 \end {выравнивание}(x−3y+z)+(−x+2y−5z)(x−x)+(−3y+2y)+(z−5z)−y−4z=4+3=7 =7
Затем умножьте первое уравнение на
−5-5−5
и добавьте к третьему уравнению:
−5(x−3y+z)+(5x−13y+13z)=−5 (4)+8(-5x+5x)+(15y-13y)+(-5z+13z)=-20+82y+8z=-12\begin {align} -5(x — 3y + z) + ( 5х — 13у + 13з) &= -5(4) + 8 \\ (-5x + 5x) + (15y — 13y) + (-5z + 13z) &= -20 + 8\ 2г + 8г &= -12 \end {align}−5(x−3y+z)+(5x−13y+13z)(−5x+5x)+(15y−13y)+(−5z+13z)2y+8z=−5(4 )+8=−20+8=−12
Теперь обратите внимание, что у нас есть система уравнений с двумя переменными:
\слева\\начать{матрицу}
\begin {выравнивание} -y — 4z &= 7 \\
2г + 8г &= -12
\конец {выровнять}
\end {матрица} \right.
Мы можем решить это, умножив верхнее уравнение на 2 и добавив его к нижнему уравнению:
2(−y−4z)+(2y+8z)=2(7)−12(−2y+2y) +(−8z+8z)=14−120=2\begin {align} 2(-y-4z) + (2y + 8z) &= 2(7) -12 \\ (-2у + 2у) + (-8з + 8з) &= 14 — 12\ 0 &= 2 \end {align}2(-y-4z)+(2y+8z)(-2y+2y)+(-8z+8z)0=2(7)-12=14-12=2
Окончательное уравнение
0=20 = 20=2
противоречие, поэтому делаем вывод, что система уравнений несовместна, а значит, не имеет решения.
Лицензии и атрибуции
Контент под лицензией CC, опубликованный ранее
- Курирование и доработка. Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права
Лицензионный контент CC, конкретная атрибуция
- Линейная алгебра/Решение линейных систем. Предоставлено : Wikibooks. Лицензия : CC BY-SA: Attribution-ShareAlike
- Система уравнений.
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - Безгранично. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- Обмен секретами — 3 точки. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/File:Secretsharing-3-point.png. Лицензия : Общественное достояние: неизвестно Copyright
- Система линейных уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Precalculus. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/precalculus/pages/1-introduction-to-functions. Лицензия : CC BY: Attribution
- Обмен секретами — 3 пункта. Предоставлено : Википедия.
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike 