Стенд 42 Колосовская А.А.
Ангелина Колосовская
Челябинская область, г. Троицк
МБОУ «Лицей №13», 11 класс
РАЗРАБОТКА ПРОГРАММЫ «КАЛЬКУЛЯТОР МАТРИЦ» НА VBA
Научный руководитель: Комарова Елена Сергеевна, Челябинская область, г. Троицк, Троицкий филиал ФГБОУ ВО «ЧелГУ», старший преподаватель кафедры математики, экономики и управления
Программа состоит из 11 листов. Главным является Лист1, на нем расположены 10 кнопок, при нажатии на которые выполняется действие. Все кнопки имеют свою функцию. Для начала работы пользователю нужно заполнить 2 матрицы любыми числами и в ячейку М1, под названием «Число», написать какое-нибудь число (Рис. 1). Для выполнения операций: обратная матрица, умножение матриц и вычисление определителя, матрицы должны быть второго или третьего порядка. Для всех остальных случаев, матрицы могут быть любого размера, но не превосходить десятого порядка.
Рис. 1. Главный лист программы
Для начала работы нужно нажать на кнопку «Запуск программы».
После чего появится диалоговое окно для ввода количества строк и столбцов двух матриц.
Сумма двух матриц. После этого мы можем выбрать любую операцию и нажать на соответствующую кнопку. Выберем кнопку «Сумма двух матриц». После нажатия нас переносит на Лист «Сумма». На нем расположена матрица С – сумма матриц А и В, также на каждом листе присутствует кнопка «Вернуться в начало», после её нажатия мы оказываемся на «Лист1» (Рис. 2).
Рис. 2. Сумма двух матриц
Если же размеры двух матриц будут разными, то программа выведет надпись «Для данных размеров матриц сумма не существует». Также, она будет появляться при умножении двух матриц разных размеров: «Для данных размеров матриц произведение не существует» (Рис. 3).
Рис. 3. Невозможность создать матрицу суммы из-за разности размеров матриц
Умножение матрицы на число. Выберем кнопку «Умножение матрицы на число». Программа открывает лист «Умножение», на нем мы видим уже умноженную матрицу на число (Рис.
4).
Рис. 4. Умножение матрицы на число
Произведение двух матриц. При нажатии на кнопку «Произведение двух матриц» программа открывает лист «Произведение», на котором присутствует матрица С – результат произведения матрицы А и В (Рис.5).
Рис. 5. Произведение двух матриц
Нахождение Min и Max элементов матрицы. При нажатии на кнопку «Min и Max элемент» нас переносит на лист «Max и Min элемент в матрице», на котором находятся два числа. Первое – Max элемент, а второе Min (Рис. 6).
Рис. 6. Min и Max элементы матрицы
Определитель матрицы. При нажатии на кнопку «Определитель матрицы» нас переносит на лист «Определитель», на котором находится определитель матрицы (Рис. 7).
Рис. 7. Определитель матрицы
Транспонирование матрицы. При нажатии на кнопку «Транспонирование матрицы» нас переносит на лист «Транспонирование матрицы», на котором находится транспонированная матрица (Рис.
8).
Рис. 8. Транспонированная матрица
Обратная матрица. При нажатии на кнопку «Обратная матрица» программа открывает лист «Обратная матрица», на котором находится обратная матрица (Рис. 9).
Рис. 9. Обратная матрица
Теория. При нажатии на эту кнопку высвечивается форма с краткой теорией (Рис. 10).
Рис. 10. Теория
Тестирование. Также, в программу входит лист «Тестирование», где можно потренироваться в выполнении операций над матрицами. Само тестирование состоит из 10 заданий. Чтобы начать, нужно нажать на кнопку «Начать тестирование», ответы писать в выделенную область под надписью «Ваш ответ», после выполнения заданий необходимо нажать на кнопку «Закончить тестирование», для проверки ваших ответов с правильными (Рис. 11).
Рис. 11. Тестирование
Игры с природой. Вы также можете решать задачи категории «статистические игры» с помощью нашей программы.
Вводим матрицу в поле, выделенное светло-желтым цветом (максимальный размер матрицы 10 x 10), в ячейку более темного цвета вводим коэффициент пессимизма, затем нажимаем кнопку «Начать работу» (Рис. 12).
Рис. 12. Статистические игры
Результаты будут представлены в виде таблицы (Рис. 13).
Рис. 13. Результаты
Тестирование программы проходило в Троицком филиале «ЧелГУ». В тестировании принимали участие студенты первого курса обучающиеся по направлению «Прикладная математика и информатика». Ими были сделаны замечания, касающиеся интерфейса, в частности они предложили написать правила работы с программой, и выделить цветом области, для ввода данных. Все их замечания, были исправлены (Рис. 14).
Рис.14. Окончательный интерфейс программы
Видео о проекте
Расписание работы автора проекта
2 апреля, пт
Диалог с экспертами
Ответы на вопросы
12:00
12:20
13:35 — 13:45
Петров А.
Б.
Белоножко П.П.
2 апреля, пт
12:40
13:00
13:20
Трудоношин В.А.
Хлебникова В.Л.
Оглоблин Д.И.
Задайте вопрос автору проекта
Обязанность отвечать на заданные вопросы остается полностью на участнике. Организаторы форума не несут ответственности за сроки получения ответа.
Заполняя данную форму Вы соглашаетесь с политикой конфиденциальности сайта.
Пообщайтесь с автором в режиме реального времени
Вы можете посмотреть диалог с экспертом и задать вопросы автору в форме вебинара.
Расписание сессий приведено выше
| Подключиться |
Союзная матрица онлайн решение — Линейная алгебра
Союзная матрица онлайн решение — Линейная алгебра | Удобный онлайн калькулятор.Главная
о проекте
Онлайн-калькуляторы
онлайн решение задач
Теория
статьи
Портфель
ваши задачи
Как это работает?
советы и инструкции
Разделы — Высшая математика — Линейная алгебра — Союзная матрица
Союзная матрица
Калькуляторы
Понравилось: 92 Просмотров: 28573
— удобный и бесплатный онлайн калькулятор, получить полное решение с помошью него очень просто и быстро, он детально распишет ход решения.
Сейчас решают задачи
Онлайн-калькулятор
Сокращения:
М — матрица
Нужно найти союзную матрицу Ms
Количество строк и столбцов матрицы М: 23456
Заполните матрицу M
| M = |
|
|---|
Введите цифры и буквы, изображенные на картинке (Регистр не важен): *
Определения
Матрица — математический объект, записываемый в виде прямоугольной таблицы чисел и допускающий алгебраические операции (сложение, вычитание, умножение) между ним и другими подобными объектами.
Союзная матрица — это матрица, полученная заменой ее элементов на их алгебраические дополнения.
Алгебраическим дополнением Аij элемента mij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца, то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.
Мне нравится Указать на ошибку
Другие калькуляторы из этого раздела
- Алгебраическое дополнение элемента матрицы
- Возведение матрицы в степень
- Матричный метод решения СЛАУ (метод обратной матрицы)
- Минор элемента матрицы
- Норма матрицы
- Обратная матрица
- Определитель матрицы 2-го порядка
- Определитель матрицы 3-го порядка
- Сложение и вычитание матриц
- Транспонирование матрицы
- Умножение матриц
- Умножение матрицы на число
- Формула Крамера
Добавить отзыв
Добавить отзыв
Имя
Сообщение ( Текст сообщения не должен содержать в себе каких-либо ссылок )
Введите цифры и буквы, изображенные на картинке (Регистр не важен): *
Главная
о проекте
Онлайн-калькуляторы
онлайн решение задач
Теория
статьи
Портфель
ваши задачи
Как это работает?
советы и инструкции
Калькулятор умножения матриц
Если вы имеете математическое образование
и ты наконец-то решил сделать карьеру в одном из стримов
связанных с математикой, будь то в области инженерии,
Архитектура или любой поток, связанный с коммерцией, здоровенная матрица
умножение — это то, что вам часто нужно делать.
Как проверить, можно ли перемножить две заданные матрицы?
Не каждые две матрицы можно перемножить.
Есть правило проверять и проверять; если две матрицы могут удовлетворить
это правило, то только вы можете умножать их друг на друга.
Это правило
заключается в следующем. Первое и главное условие для матрицы
умножение заключается в том, что количество столбцов в первой матрице
должно быть равно количеству строк во второй матрице.
После того, как вышеуказанное условие выполнено и вы можете выполнить умножение матриц, то результирующая матрица, полученная после умножение будет иметь то же количество строк, что и первое матрица и такое же количество столбцов, как вторая матрица в порядок умножения.
Пример — M1 (m, n) * M2 (o, p) = M3 (m, p), где M3 — результирующая матрица после умножения.
Преимущества калькулятора умножения матриц
Калькулятор умножения матриц уверен
быть вам на помощь всякий раз, когда вам нужно выполнить это утомительное
умножение матриц. Некоторые из причин, по которым вам необходимо
немедленно переключитесь на использование большого матричного умножения, как
следует — те, которые вы проверяете на указанные выше условия в своих матрицах
умножить, и условие выполняется тогда, вы можете
выполнить матричный расчет на них сейчас. Однако делать это очень
длинные лучше использовать матричное умножение для быстрых результатов.
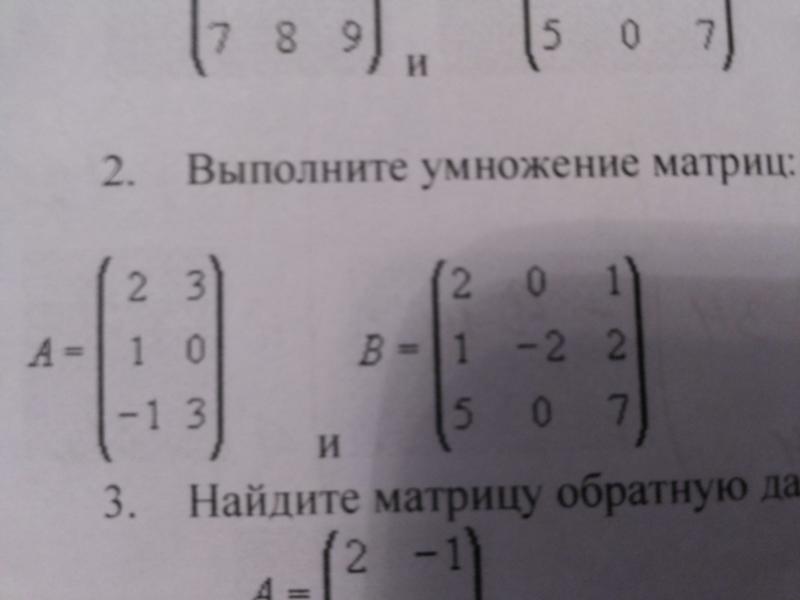Калькулятор матриц забирает
всю вашу боль от вспоминания этой типичной формулы и шаг за шагом
процедура для выполнения длинного матричного умножения, как вы только что
ввести значения двух матриц и оставить всю матрицу
Калькулятор умножения сделает за вас.Как пользоваться калькулятором умножения матриц?
- Здесь даны две матрицы выше
- Нажмите кнопку + и — минус рядом с ними, чтобы увеличить или уменьшить количество строк и столбцов.
- Нажмите на номер, который хотите изменить.
- После внесения изменений щелкните результат, чтобы начать интерактивное умножение матриц.
- Если вы хотите пройти каждый шаг, продолжайте нажимать «Далее».
- Или Чтобы сразу перейти к результату, нажмите кнопку «Конец».
Matrix Multiplication Calculator
Multiplication Of Matrices
Row11234567
x
Column11234567
Row21234567
x
Column21234567
Matrix — 1
Matrix — 2
Result
Matrix multiplication
Scalar multiplication :
Матрицы можно умножать на скалярное значение, умножая каждый элемент матрицы на скаляр.
Например, дана матрица A и скаляр c :
| A = | ; c = 5 |
The product of c and A is:
| 5 × | = |
|
Умножение матрицы на матрицу:
Умножение двух (или более) матриц требует больше усилий, чем умножение на скаляр. Чтобы перемножить две матрицы, количество столбцов в первой матрице должно совпадать с количеством строк во второй матрице. Например, можно умножить матрицу 2 × 3 на матрицу 3 × 4 , но нельзя умножить матрицу 2 × 3 на 4 × 3.
Можно умножить:
| A = |
| ; В = |
Cannot be multiplied:
Обратите внимание, что при умножении матриц A × B не обязательно равняется B × A × B . На самом деле, только потому, что А можно умножить на B не означает, что B можно умножить на A . Если матрицы имеют правильные размеры и могут быть умножены, матрицы умножаются путем выполнения так называемого скалярного произведения. Скалярное произведение включает в себя умножение соответствующих элементов в строке первой матрицы на элементы столбцов второй матрицы и суммирование результата, в результате чего получается одно значение. Скалярное произведение может быть выполнено только для последовательностей одинаковой длины. Поэтому количество столбцов в первой матрице должно совпадать с количеством строк во второй. Затем скалярный продукт становится значением в соответствующей строке и столбце новой матрицы, C . а 1,1 ×b 1,1 + а 1,2 ×b 2,1 + 3 1,3 b = 1,3 c 1,1 Скалярное произведение выполняется для каждой строки A и каждого столбца B до тех пор, пока все комбинации этих двух не будут завершены, чтобы найти значение соответствующих элементов в матрица С . Например, когда вы выполняете скалярное произведение строки 1 из A и столбец 1 из B , результатом будет c 1,1 матрицы C 68 68 68 68 68 68 68 68 Скалярное произведение строки 1 числа A и столбца 2 числа B будет равно c 1,2 матрицы
При перемножении двух матриц результирующая матрица будет иметь такое же количество строк, как и первая матрица, в данном случае A и такое же количество столбцов, как и во второй матрице, B . С A — 2 × 3 и B IS 3 × 4 , C будет 2 × 4 . Цвета здесь могут помочь определить, во-первых, можно ли перемножить две матрицы, а во-вторых, размеры результирующей матрицы. |
Например, в приведенном выше разделе матриц, которые можно перемножать, синяя строка в A умножается на синий столбец в B , чтобы определить значение в первом столбце первой строки матрицы . С . Это называется скалярным произведением строки 1 числа A и столбца 1 числа 9.0009 В :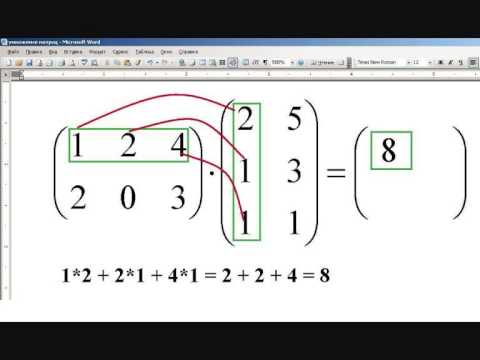
внизу: