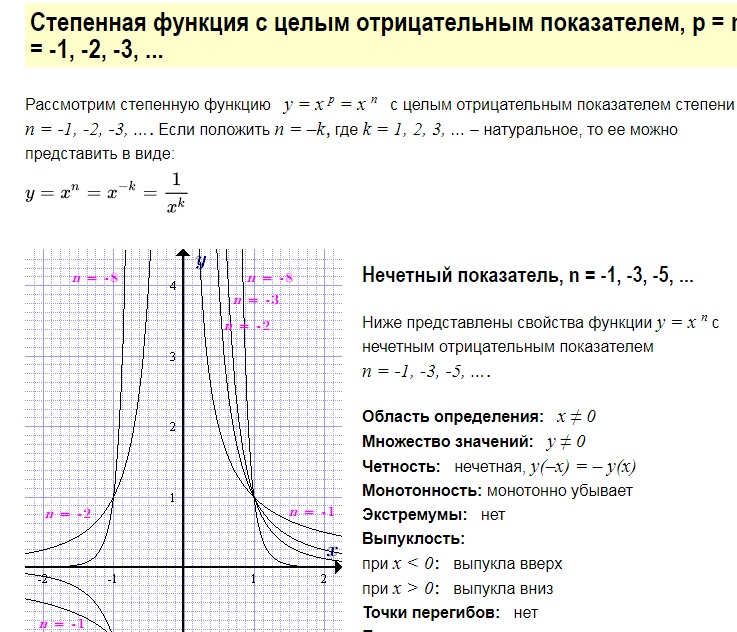
Берут ли в армию с плоскостопием 1,2,3 и 4 степени
До сих пор острым остается вопрос о том, берут ли в армию с плоскостопием. Все чаще врачи-ортопеды регистрируют данное заболевание у призывников, это негативно сказывается на качественном составе войск. Изначально болезнь развивается по причине недостаточной или избыточной нагрузки на ноги, и лишь небольшому количеству больных (3%) передается по наследству. В процессе подготовки к военной службе возникает множество споров на эту тему, поэтому важно до конца разобраться в данном вопросе.
Проверка плоскостопия в военкомате
Традиционно диагностика болезни осуществляется с использованием метода рентгенографии. Обследуемый находится в вертикальном положении, при этом стопы оказываются под давлением. Затем получают снимки разных проекций конечностей, что позволяет определить вид и степень отклонений. Привычным считается угол свода стопы равный 120–135° и величиной 39 мм. Если все показатели в норме, то юноша может готовиться к службе. Медицинская комиссия военкомата признает отклонением от нормы продольное и поперечное плоскостопие.
Если все показатели в норме, то юноша может готовиться к службе. Медицинская комиссия военкомата признает отклонением от нормы продольное и поперечное плоскостопие.
Встречаются случаи, когда заболевание скрывается под видом других не менее опасных патологий. Поэтому диагностировать плоскостопие может только квалифицированный врач-ортопед.
Возможна ли служба в армии
Само по себе заболевание редко вызывает болевые ощущения. Угрозу оно представляет лишь в том случае, если соответствует крайней степени сложности, главным является факт наличия артроза. В этом случае человек ощущает сильную боль, а конечность ограничена в движениях. Если эти два заболевания встречаются в совокупности, то служба в армии невозможна.
Чтобы определить, годен ли призывник к прохождению армейской подготовки, следует для начала узнать, какой степени плоскостопия соответствует состояние обследуемого. В основном у больных диагностируют комбинированное плоскостопие — продольно–поперечное.
Watch this video on YouTube
Отдельно специалисты выделяют следующие типы продольного плоскостопия.
Определение продольного плоскостопия
Первая степень
Соответствует категории годности «А». Угол внутреннего свода стопы составляет от 130° до 141°, а высота варьируется от 35 мм до 25 мм.
Вторая степень
Подходит под категорию «Б–3». Угол свода находится в пределах от 142° до 156°, высота должна составлять от 25 мм до 18 мм.
Третья степень
Категория «В». Внутренний свод расположен под углом от 157°, а высота его менее 18 мм.
Таким образом, призыву подлежат все молодые люди, имеющие первую и вторую степень болезни, но существуют исключения. Когда угол свода соответствует тяжести третьей степени, а высота совпадает с показателями второй, служба в армии возможна, но с незначительными ограничениями.
Определение поперечного плоскостопия
Помимо продольного, существует также поперечное плоскостопие.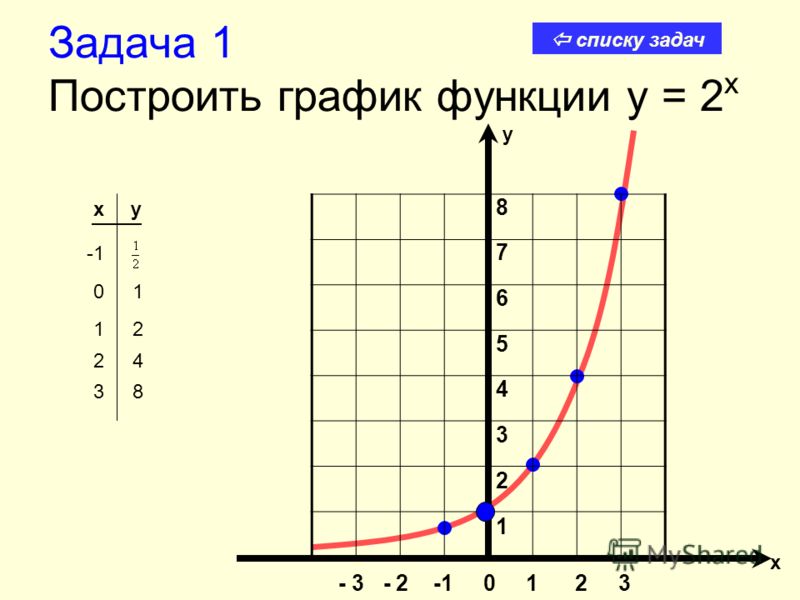 Это заболевание, при котором деформация стопы проявляется в виде уплотнения переднего отдела конечности, отдаления плюсневых костей на достаточно большом расстоянии друг от друга. Стопа укорочена, а первый палец отгибается наружу.
Это заболевание, при котором деформация стопы проявляется в виде уплотнения переднего отдела конечности, отдаления плюсневых костей на достаточно большом расстоянии друг от друга. Стопа укорочена, а первый палец отгибается наружу.
Специалисты выделяют 4 степени такой деформации.
Первая степень
Под ней понимается незначительное отклонение, при котором угол между плюсневыми костями составляет от 10° до 12°, а отклонения первого пальца в пределах от 15° до 20°.
Вторая степень
Соответствует категории годности «Б–3». Угол между костями от 13° до 16°, первый палец отклоняется на 20°–30°.
Третья степень
Величина угла между костями от 16° до 21°, а палец отклоняется на 30°–40°.
Четвертая степень
Соответствует категории годности «В». Между костями образуется угол от 20°, а первый палец отклоняется более чем на 40°.
Призывника относят к категории «не годен» в том случае, если степень плоскостопия составляет от 3 и выше. В зависимости от сложности заболевания призывник получает освобождение от службы в мирное или даже в военное время. Диагноз ставится только на основе исследований врача-ортопеда, после этого военный комиссар решает вопрос о возможности прохождения или отсрочки службы.
Диагноз ставится только на основе исследований врача-ортопеда, после этого военный комиссар решает вопрос о возможности прохождения или отсрочки службы.
Часто возникают спорные вопросы при прохождении комиссии:
- Военный комиссариат делает заключение о годности призывника, опираясь лишь на описания снимка, без консультации врача. Если же доктор не поставил окончательный диагноз, а решение уже вынесено, ситуация расценивается как отказ от предоставления человеку первой медицинской помощи. Юноши вправе обжаловать решение, обращаясь в высшие органы власти.
- Местный врач не смог представить заключение и направляет обследуемого в военкомат для окончательного решения вопроса. Обследуемый имеет право пожаловаться на доктора и добиваться полноправного лечения.
- Существуют подозрения о намеренной постановке специалистом диагноза, не соответствующего действительности. В таком случае стоит обратиться в другую поликлинику, а в крайнем случае подать жалобу, или обратиться в суд.

Важно отстаивать свои права, так как больным с диагнозом плоскостопие второй и третьей степени разрешается выполнять лишь допустимые физические нагрузки, а неправильно подобранное лечение может повлечь за собой вред для организма. К тому же иногда наличие патологии лишь на одной ноге может стать поводом не проходить военную службу.
Существуют методы лечения плоскостопия и в армейских условиях. Но самостоятельно избавится от заболевания невозможно, можно лишь обеспечить поддержание комфортного состояния стоп. Для того чтобы снизить нагрузку на суставы при ношении армейских сапог, рекомендуется подкладывать в обувь специальные ортопедические стельки. Но перед их приобретением следует проконсультироваться с ортопедом.
Большинство специалистов советуют носить стельки даже после окончания службы, для поддержания здорового состояния нижних конечностей и предотвращения развития плоскостопия.
Особенности поступления в другие ведомства
Согласно действующему законодательству, не исключается возможность прохождения службы в частях органов внутренних дел, но только при отсутствии отягощающих заболеваний, таких как артроз или наличия экзостозов стопы. Призывник вправе рассчитывать на службу в миграционной служебной части, материально-технической, военного обеспечения или хозяйственной части. Возможно поступление на службу МВД прочих типов: строительной, медицинской, финансовой, юридической и т.п.
Призывник вправе рассчитывать на службу в миграционной служебной части, материально-технической, военного обеспечения или хозяйственной части. Возможно поступление на службу МВД прочих типов: строительной, медицинской, финансовой, юридической и т.п.
При установлении плоскостопия второй степени и выше будет сложно попасть в Воздушно-десантные войска. Обусловлено это тем, что при прохождении службы сдаются сложные физические нормативы, которые трудноосуществимы для юношей с плоскостопием. Только если отсутствуют другие претензии по здоровью, а сам призывник является крепким и здоровым физически, предрасположен к занятию спортом и имеет спортивные разряды, то существует хороший шанс попасть на службу в десант.
В каких случаях освобождают от службы
На основании общепринятого в Российской Федерации документа Расписание болезней определяются все решения о прохождении или отсрочке службы для молодых людей, имеющих заболевания. Соответственно определяются и категории годности. Согласно статье 68 этого документа, призывники, имеющие продольное плоскостопие 3 степени либо поперечное 3 и 4 степени, на законных основаниях освобождаются от службы в армии, им присваивается категория «В» и выдается военный билет по здоровью.
Согласно статье 68 этого документа, призывники, имеющие продольное плоскостопие 3 степени либо поперечное 3 и 4 степени, на законных основаниях освобождаются от службы в армии, им присваивается категория «В» и выдается военный билет по здоровью.
Watch this video on YouTube
Призывники с плоскостопием 2 степени признаются пригодными или неспособными проходить службу в зависимости от наличия вторичных заболеваний нижних конечностей и общего состояния организма, а также физиологических особенностей человека.
3-8Экспоненциальные функции и их графики
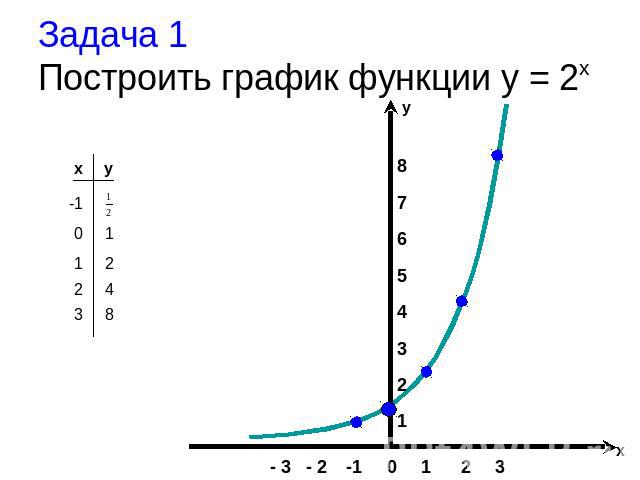
Экспоненциальные функции
На этом этапе нашего изучения алгебры мы начинаем рассматривать трансцендентные функции или функции, которые, кажется, «выходят за пределы» алгебры. Мы изучали функции с переменным основанием и постоянными показателями, такими как x2 или y−3. В этом разделе мы исследуем функции с постоянным основанием и переменными показателями. При заданном вещественном числе b>0, где b≠1, экспоненциальная функцияЛюбая функция с определением вида f(x)=bx, где b>0 и b≠1. имеет вид
Мы изучали функции с переменным основанием и постоянными показателями, такими как x2 или y−3. В этом разделе мы исследуем функции с постоянным основанием и переменными показателями. При заданном вещественном числе b>0, где b≠1, экспоненциальная функцияЛюбая функция с определением вида f(x)=bx, где b>0 и b≠1. имеет вид
f(x)=bx Экспоненциальная функция
Например, если основание b равно 2, то мы имеем экспоненциальную функцию, определяемую выражением f(x)=2x. Здесь мы видим, что показатель степени является переменной. До этого момента рациональные показатели были определены, а иррациональные — нет. Рассмотрим 27, где показатель степени — иррациональное число в диапазоне
2,64<7<2,65
Мы можем использовать эти границы для оценки 27,
22,64<27<22,656,23<27<6,28 97≈6,26
Следовательно, область определения любой экспоненциальной функции состоит из всех действительных чисел (−∞,∞). Выберите несколько значений для x , а затем определите соответствующие значения y .
xyf(x)=2xSolutions−214y=2−2=122=14(−2, 14)−112y=2−1=121=12(−1, 12)01y=20=1(0, 1) 12y=21=2(1, 2)24y=22=4(2, 4)76,26y=27≈6,26(2,65, 6,26)
Поскольку показатели степени определены для любого действительного числа, мы можем начертить график, используя непрерывную кривую через эти заданные точки:
Важно отметить, что когда x приближается к отрицательной бесконечности, результаты становятся очень маленькими, но никогда не достигают нуля. Например,
f(−5)=2−5=125≈0,03125f(−10)=2−10=1210≈0,0009766f(−15)=2−15=12−15≈.00003052
Это описывает горизонтальную асимптоту при y=0, ось x , и определяет нижнюю границу диапазона функции: (0,∞).
Основание b экспоненциальной функции влияет на скорость ее роста. Ниже мы изобразили y=2x, y=3x и y=10x на том же наборе осей.
Обратите внимание, что все эти экспоненциальные функции имеют одну и ту же точку пересечения y , а именно (0,1). Это связано с тем, что f(0)=b0=1 для любой функции, определенной с помощью формы f(x)=bx. Поскольку функции читаются слева направо, они интерпретируются как возрастающие или растущие экспоненциально. Кроме того, любая экспоненциальная функция этой формы будет иметь область определения, состоящую из всех действительных чисел (−∞, ∞), и диапазон, состоящий из положительных значений (0, ∞), ограниченных горизонтальной асимптотой при y = 0.
Поскольку функции читаются слева направо, они интерпретируются как возрастающие или растущие экспоненциально. Кроме того, любая экспоненциальная функция этой формы будет иметь область определения, состоящую из всех действительных чисел (−∞, ∞), и диапазон, состоящий из положительных значений (0, ∞), ограниченных горизонтальной асимптотой при y = 0.
Пример 1
Нарисуйте график и определите домен и диапазон: f(x)=10x+5.
Решение:
Основание 10 используется часто, особенно в экспоненциальном представлении. Следовательно, 10 называется общим основанием . На самом деле экспоненциальная функция y=10x настолько важна, что вы найдете кнопку 10x, посвященную ей, на большинстве современных научных калькуляторов. В этом примере мы нарисуем базовый график y=10x, а затем сдвинем его вверх на 5 единиц.
Обратите внимание, что горизонтальная асимптота базового графика y=10x была сдвинута вверх на 5 единиц до y=5 (показано пунктиром). Потратьте минуту, чтобы оценить несколько значений x с помощью калькулятора и убедитесь, что результат никогда не будет меньше 5.
Ответ:
Домен: (−∞,∞); Диапазон: (5,∞)
Далее рассмотрим экспоненциальные функции с дробными основаниями 0 xyf(x)=(12)xSolutions−24f(12)=(12)−2=1−22−2=2212=4(−2, 4)−12f(12)=(12)−1= 1−12−1=2111=2(−1, 2)01f(12)=(12)0=1(0, 1)112f(12)=(12)1=12(1, 12)214f(12 )=(12)2=14(2, 14) Количество точек на графике у нас есть, При чтении графика слева направо он интерпретируется как экспоненциально убывающий. База влияет на скорость, с которой экспоненциальная функция уменьшается или затухает. Ниже мы изобразили y=(12)x, y=(13)x и y=(110)x на одном и том же наборе осей. Напомним, что x−1=1x, поэтому мы можем выразить экспоненциальные функции с дробными основаниями, используя отрицательные показатели степени. Например, g(x)=(12)x=1x2x=12x=2−x. Кроме того, учитывая, что f(x)=2x, мы можем видеть, что g(x)=f(−x)=2−x и можем рассмотреть g является отражением f относительно оси y . Таким образом, при b>0 И для обоих случаев Домен:(−∞,∞)Диапазон:(0,∞)y-отрезок:(0,1)Асимптота:y= 0 Кроме того, обратите внимание, что графики проходят тест горизонтальной линии, и поэтому экспоненциальные функции являются взаимно однозначными. Мы используем эти базовые графики вместе с преобразованиями для построения графиков экспоненциальных функций. Нарисуйте график и определите домен и диапазон: f(x)=5−x−10. Решение: Начните с базового графа y=5−x и сдвиньте его вниз на 10 единиц. Точка пересечения y равна (0,−9), а горизонтальная асимптота равна y=−10. Ответ: Домен: (−∞,∞); Диапазон: (−10,∞) Примечание : Нахождение точки пересечения x графа в предыдущем примере оставлено для последующего раздела этой главы. Сейчас нас больше интересует общий вид экспоненциальных функций. Нарисуйте график и определите домен и диапазон: g(x)=−2x−3. Решение: Начните с базового графа y=2x и определите преобразования. y=2x Basic graphy=−2x Отражение относительно оси xy=−2x−3 Сдвиг вправо 3 единицы Обратите внимание, что горизонтальная асимптота остается одинаковой для всех преобразований. Чтобы закончить, мы обычно хотим включить и -intercept. Помните, что для нахождения точки пересечения и мы устанавливаем x=0. g(0)=-20-3=-2-3=-123=-18 Следовательно, точка пересечения y равна (0, -18). Ответ: Домен: (−∞,∞); Диапазон: (−∞,0) Попробуйте это! Нарисуйте график и определите домен и диапазон: f(x)=2x−1+3. Ответ: Домен: (−∞,∞); Диапазон: (3,∞) (нажмите, чтобы посмотреть видео) Некоторые числа часто встречаются в обычных приложениях. Одним из таких знакомых чисел является число пи (π), которое, как мы знаем, возникает при работе с кругами. Рисунок 7.1 Леонард Эйлер (1707–1783) На самом деле естественная экспоненциальная функция 9(−2)≈0,13534 После того, как вы научитесь пользоваться вашим конкретным калькулятором, теперь вы можете набросать график, нанеся точки. (Округлить до сотых.) xyf(x)=exSolutions−20,14f(−2)=e−2=0,14(−2, 0,14)−10,37f(−1)=e−1=0,37( −1, 0,37)01f(0)=e0=1(0, 1)12,72f(1)=e1=2,72(1, 2,72)27,39f(2)=e2=7,39(2, 7,39) Постройте точки и построить график. Обратите внимание, что функция аналогична графику y=3x. Домен состоит из всех действительных чисел, а диапазон состоит из всех положительных действительных чисел. Существует асимптота при y=0 и г — точка пересечения (0,1). Мы можем использовать преобразования, чтобы нарисовать график более сложных экспоненциальных функций. Нарисуйте график и определите домен и диапазон: g(x)=ex+2−3. Решение: Определите основные преобразования. y=ex Basic graphy=ex+2 Shift влево 2 unitsy=ex+2−3 Shift вниз 3 единиц g(0)=e0+2−3=e2−3≈4,39 Следовательно, г — точка пересечения равна (0,e2−3). Ответ: Домен: (−∞,∞); Диапазон: (−3,∞) Попробуйте это! Нарисуйте график и определите домен и диапазон: f(x)=e−x+2. Ответ: Домен: (−∞,∞); Диапазон: (2,∞) (нажмите, чтобы посмотреть видео) Экспоненциальные функции появляются в формулах, используемых для расчета процентов, заработанных на большинстве обычных сберегательных счетов. A(t)=P(1+rn)nt Здесь сумма A зависит от времени t в годах основная сумма P накапливает сложные проценты по годовой процентной ставке r . Значение n представляет количество начислений процентов в течение года. Инвестиция в размере 500 долларов США сделана в 6-летнюю депозитную карту, которая приносит 412% годовых и начисляется ежемесячно. Сколько будет стоить компакт-диск в конце 6-летнего срока? Решение: Здесь основная сумма долга P=500 долларов, процентная ставка r=412%=0,045, а поскольку проценты начисляются ежемесячно, n=12. A(t)=500(1+0,04512)12t Чтобы определить сумму на счете через 6 лет, оцените A(6) и округлите до ближайшего цента. A(6)=500(1+0,04512)12(6)=500(1,00375)72=654,65 Ответ: К концу 6-летнего срока компакт-диск будет стоить 654,65 доллара. Далее мы исследуем эффекты увеличения н в формуле. Для ясности примем P и r равными 1 и посчитаем соответственно. Продолжая эту схему, по мере того, как n увеличивается, скажем, увеличиваясь каждую минуту или даже каждую секунду, мы можем видеть, что результат стремится к натуральному основанию e≈2,71828. Начисление сложных процентов каждый момент приводит к формуле непрерывного начисления процентов Формула, которая дает сумму, накопленную за счет непрерывно начисленных процентов: A(t)=Pert., A(t)=Pert Здесь P представляет собой первоначальную вложенную основную сумму, r представляет собой годовую процентную ставку, а t представляет собой время в годах, в течение которого инвестиции позволяют непрерывно начислять сложные проценты. Инвестиция в размере 500 долларов США сделана в 6-летний депозитный сертификат, который приносит 412% годовых и непрерывно начисляется. Сколько будет стоить компакт-диск в конце 6-летнего срока? Решение: Здесь основная сумма долга P=500 долларов, а процентная ставка r=412%=0,045. Поскольку проценты начисляются непрерывно, мы будем использовать формулу A(t)=Pert. Инвестиции моделируются следующим образом: A(t)=500e0,045t Чтобы определить сумму на счете через 6 лет, оцените A(6) и округлите до ближайшего цента. A(6)=500e0,045(6)=500e0,27=654,98 Ответ: CD будет стоить 654,98 долларов в конце 6-летнего срока. Сравните два предыдущих примера и обратите внимание, что непрерывное начисление сложных процентов может быть не таким выгодным, как кажется. Хотя лучше начислять проценты чаще, разница не так велика. Конечно, процентная ставка является гораздо большим фактором в конечном результате. Попробуйте! Сколько будет стоить депозитный сертификат на 1200 долларов, приносящий 5,2% годовых с постоянным начислением сложных процентов, в конце 10-летнего срока? Ответ: $2 018,43 (нажмите, чтобы посмотреть видео) Оценить. f(x)=3x, где f(−2), f(0) и f(2). f(x)=10x, где f(−1), f(0) и f(1). g(x)=(13)x, где g(−1), g(0) и g(3). g(x)=(34)x, где g(-2), g(-1) и g(0). h(x)=9−x, где h(−1), h(0) и h(12). h(x)=4−x, где h(−1), h(−12) и h(0). f(x)=−2x+1, где f(−1), f(0) и f(3). f(x)=2−3x, где f(−1), f(0) и f(2). g(x)=10−x+20, где g(−2), g(−1) и g(0). g(x)=1−2−x, где g(−1), g(0) и g(1). Воспользуйтесь калькулятором, чтобы округлить следующее число до сотых. f(x)=2x+5, где f(2.5). f(x)=3x−10, где f(3.2). г(х)=4х, где г(2). г(х)=5х-1, где г(3). h(x)=10x, где h(π). h(x)=10x+1, где h(π3) f(x)=10−x−2, где f(1.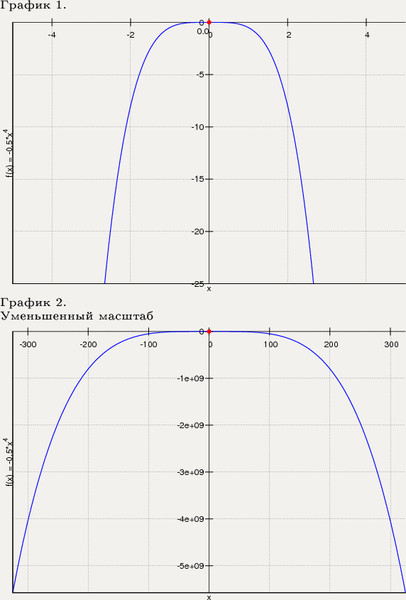
Пример 2
Пример 3

Natural Base e
 Это иррациональное число имеет специальную кнопку на большинстве калькуляторов π и округляется до пяти знаков после запятой, π≈3,14159.. Другое важное число и возникает при работе с моделями экспоненциального роста и распада. Это иррациональное число, округленное до пяти знаков после запятой, e≈2,71828. Эта константа естественным образом встречается во многих реальных приложениях и поэтому называется естественным основанием . Иногда e называют постоянной Эйлера в честь Леонарда Эйлера (произносится как «Ойлер»).
Это иррациональное число имеет специальную кнопку на большинстве калькуляторов π и округляется до пяти знаков после запятой, π≈3,14159.. Другое важное число и возникает при работе с моделями экспоненциального роста и распада. Это иррациональное число, округленное до пяти знаков после запятой, e≈2,71828. Эта константа естественным образом встречается во многих реальных приложениях и поэтому называется естественным основанием . Иногда e называют постоянной Эйлера в честь Леонарда Эйлера (произносится как «Ойлер»).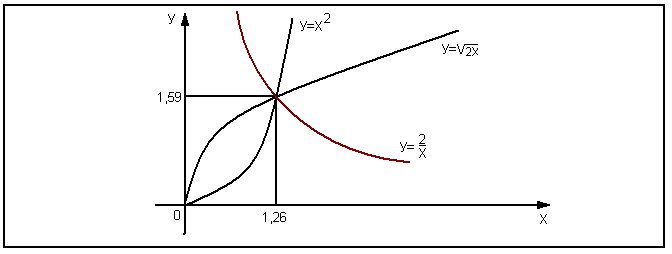
Пример 4
Формулы сложных процентов
 Сложные проценты возникают, когда проценты, накопленные за один период, добавляются к основной сумме инвестиций до расчета процентов за следующий период. Сумма, накопленная таким образом с течением времени, моделируется формулой сложных процентов. Формула, которая дает сумму, накопленную за счет получения процентов на основную сумму и процентов с течением времени: A(t)=P(1+rn)nt.:
Сложные проценты возникают, когда проценты, накопленные за один период, добавляются к основной сумме инвестиций до расчета процентов за следующий период. Сумма, накопленная таким образом с течением времени, моделируется формулой сложных процентов. Формула, которая дает сумму, накопленную за счет получения процентов на основную сумму и процентов с течением времени: A(t)=P(1+rn)nt.: Пример 5
 Инвестиции моделируются следующим образом:
Инвестиции моделируются следующим образом: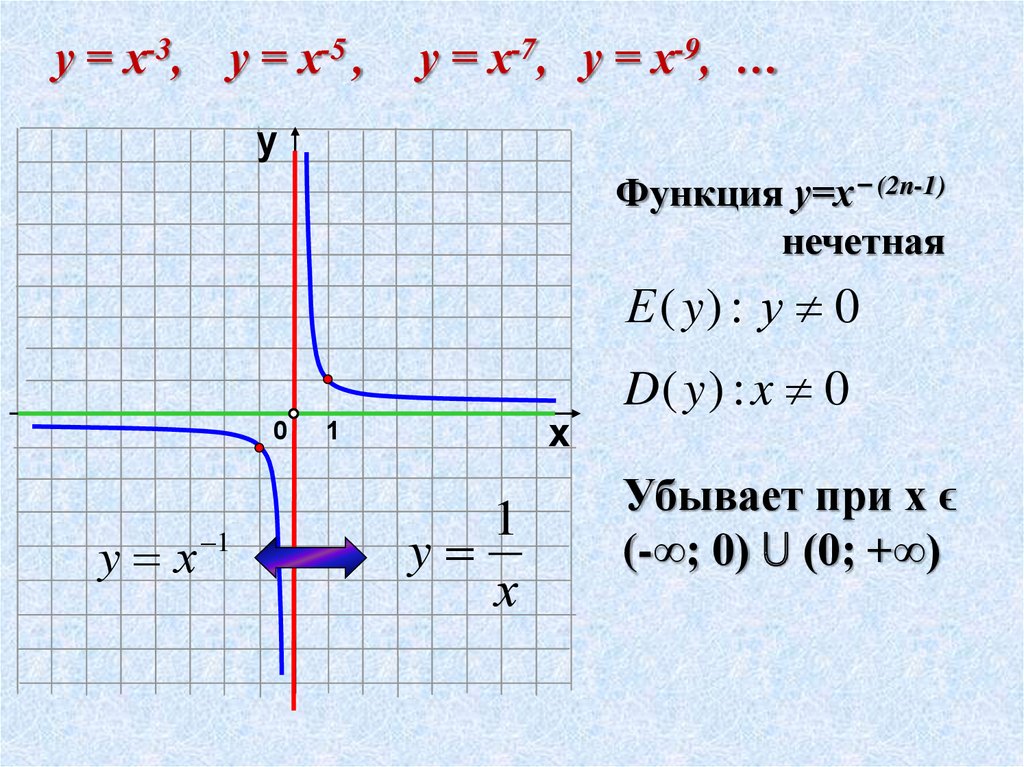
Пример 6
Ключевые выводы
 Область состоит из всех действительных чисел (−∞, ∞), а диапазон состоит из положительных чисел (0, ∞). Кроме того, все экспоненциальные функции этого вида имеют y — точка пересечения (0,1) и асимптотичны к оси x .
Область состоит из всех действительных чисел (−∞, ∞), а диапазон состоит из положительных чисел (0, ∞). Кроме того, все экспоненциальные функции этого вида имеют y — точка пересечения (0,1) и асимптотичны к оси x . Тематические упражнения
Часть A. Экспоненциальные функции

f(x)=5−x+3, где f(1.3).
f(x)=(23)x+1, где f(−2,7).
f(x)=(35)−x−1, где f(1.4).
f(x)=4x
г(х)=3х
ф(х)=4х+2
f(x)=3x−6
f(x)=2x−2
ф(х)=4х+2
f(x)=3x+1−4
f(x)=10x−4+2
ч(х)=2х-3-2
ч(х)=3х+2+4
г.
f(x)=(14)x
ч(х)=(13)х
f(x)=(14)x−2
ч(х)=(13)х+2
г(х)=2-х-3
г(х)=3−х+1
f(x)=6−10−x
г(х)=5−4−х
f(x)=5−2x
f(x)=3−3x
Нарисуйте функцию и определите область определения и диапазон. Нарисуйте горизонтальную асимптоту пунктирной линией.
ф(х)=ех+2
f(x)=ex−4
f(x)=5−3ex
f(x)=e−x+3
f(x)=1+e−x
f(x)=3−2e−x
f(x)=e−2x+2
f(x)=e−x2−1
f(x)=ex−3
ф(х)=ех+2
ф(х)=ех+1
f(x)=ex−3
f(x)=ex−2+1
f(x)=ex+2−1
г(х)=-ex
г(х)=е-х
ч(х)=-ех+1
ч(х)=-ех+3
Часть B: Натуральная основа
e Найдите f(−1), f(0) и f(32) для заданной функции. Используйте калькулятор, где это уместно, чтобы округлить до ближайшей сотой.
Используйте калькулятор, где это уместно, чтобы округлить до ближайшей сотой.
Нарисуйте функцию и определите домен и диапазон. Нарисуйте горизонтальную асимптоту пунктирной линией.
Джим инвестировал 750 долларов в 3-летний депозитный сертификат, который приносит 4,2% годовых, которые ежемесячно начисляются.
г. Сколько будет стоить компакт-диск в конце 3-летнего срока?
Сколько будет стоить компакт-диск в конце 3-летнего срока?Хосе инвестировал 2450 долларов в 4-летний депозитный сертификат, который приносит 3,6% годовых и начисляется каждые полгода. Сколько будет стоить компакт-диск в конце 4-летнего срока?
У Джейн есть сбережения в размере 5350 долларов на счете, приносящие 358% годовых, которые начисляются ежеквартально. Сколько будет на счете через 5 лет?
г.У Билла есть 12 400 долларов на обычном сберегательном счете, приносящий 423% годовых, который начисляется ежемесячно. Сколько будет на счете через 3 года?
Если 85 200 долларов инвестируются на счет, приносящий 5,8% годовых с ежеквартальным начислением процентов, то сколько процентов будет начислено за первые 3 года?
Если $124 000 инвестируются на счет, приносящий 4,6% годовых с ежемесячным начислением сложных процентов, то сколько процентов будет начислено за первые 2 года?
Билл инвестировал 1400 долларов в 3-летний депозитный сертификат, который приносит 4,2% годовых и постоянно начисляется.
 Сколько будет стоить компакт-диск в конце 3-летнего срока?
Сколько будет стоить компакт-диск в конце 3-летнего срока?Brooklyn инвестировал 2850 долларов в 5-летний депозитный сертификат, который приносит 5,3% годовых и постоянно начисляется. Сколько будет стоить компакт-диск в конце 5-летнего срока?
У Омара есть сбережения в размере 4200 долларов на счете, приносящие 438% годовых, которые постоянно начисляются. Сколько будет на счету через 212 лет?
У Нэнси есть сбережения в размере 8 325 долларов на счету, приносящие 578% годовых, которые постоянно начисляются. Сколько будет на счету через 512 лет?
Если 12 500 долларов вложены на счет, приносящий 3,8% годовых с постоянным начислением процентов, то сколько процентов будет начислено за первые 10 лет?
г.
 Если 220 000 долларов вложены на счет, приносящий 4,5% годовых с постоянным начислением процентов, то сколько процентов будет начислено за первые 2 года?
Если 220 000 долларов вложены на счет, приносящий 4,5% годовых с постоянным начислением процентов, то сколько процентов будет начислено за первые 2 года?Население небольшого городка растет в соответствии с функцией P(t)=12 500(1,02)t, где t представляет собой время в годах, прошедшее с момента последней переписи. Используйте функцию для определения численности населения в день переписи (когда t = 0) и оцените численность населения через 6 лет с этого времени.
г.Население небольшого городка уменьшается в соответствии с функцией P(t)=22 300(0,982)t, где t представляет собой время в годах с момента последней переписи. Используйте функцию для определения численности населения в день переписи (когда t = 0) и оцените численность населения через 6 лет с этого времени.
Уменьшение стоимости нового автомобиля в долларах моделируется по формуле V(t)=28 000(0,84)t, где t представляет количество лет после покупки автомобиля.
 Используйте формулу, чтобы определить стоимость автомобиля, когда он был новым ( t = 0) и стоимость через 4 года.
Используйте формулу, чтобы определить стоимость автомобиля, когда он был новым ( t = 0) и стоимость через 4 года.Количество уникальных посетителей веб-сайта колледжа может быть аппроксимировано формулой N(t)=410(1,32)t, где t представляет собой количество лет после 1997 года, когда был создан веб-сайт. Примерное количество уникальных посетителей сайта колледжа в 2020 году.
Если не остановить новый штамм вируса гриппа, он может очень быстро распространиться от одного человека к другому. Количество затронутых людей можно смоделировать по формуле P(t)=e0,22t, где t представляет собой количество дней, в течение которых вирус может беспрепятственно распространяться. Оцените количество людей, инфицированных вирусом через 30 дней и через 60 дней.
г.Если не контролировать, популяция из 24 диких английских кроликов может расти по формуле P(t)=24e0,19t, где время t измеряется в месяцах.
 Сколько кроликов будет через 312 лет?
Сколько кроликов будет через 312 лет?Население одного города в 1975 г. составляло 65 000 человек и росло в геометрической прогрессии со скоростью 1,7% в год. В то время рост населения моделировался по формуле P(t)=65 000e0,017t, где t представляет собой количество лет, прошедших с 1975 года. В 2000 году перепись определила, что фактическое население составляло 104 250 человек. Какое население предсказывала модель на 2000 год и какова была фактическая ошибка?
Из-за радиоактивного распада количество 10 миллиграммов йода-131 уменьшается в соответствии с формулой A(t)=10e−0,087t, где t представляет собой время, измеренное в днях. Какая часть образца остается через 10 дней?
г.Количество клеток в образце бактерий аппроксимируется логистической моделью роста N(t)=1,2×1051+9e−0,32t, где t представляет время в часах.
 Определите начальное количество клеток, а затем определите количество клеток через 6 часов.
Определите начальное количество клеток, а затем определите количество клеток через 6 часов.Рыночная доля продукта в процентах приблизительно рассчитывается по формуле P(t)=1002+e−0,44t, где t представляет собой количество месяцев после запуска агрессивной рекламной кампании. Насколько мы можем ожидать увеличения доли рынка после первых трех месяцев рекламы?
Часть C: Формулы сложных процентов
Почему b = 1 исключено как основание в определении показательных функций? Объяснять.
Объясните, почему экспоненциальная функция вида y=bx никогда не может быть отрицательной.
Исследуйте и обсудите вывод формулы сложных процентов.

Исследуйте и обсудите модель роста логистики. Дайте ссылку на дополнительную информацию по этой теме.
Исследуйте и обсуждайте жизнь и вклад Леонарда Эйлера.
Часть D: Дискуссионная доска
Ответы
f(−2)=19, f(0)=1, f(2)=9
г(-1)=3, г(0)=1, г(3)=127
ч(−1)=9, ч(0)=1, ч(12)=13
f(−1)=12, f(0)=0, f(3)=−7
г(-2)=120, г(-1)=30, г(0)=21
10,66
7.
 10
101385,46
−1,97
3,99
Домен: (−∞,∞); Диапазон: (0,∞)
Домен: (−∞,∞); Диапазон: (2,∞)
Домен: (−∞,∞); Диапазон: (0,∞)
Домен: (−∞,∞); Диапазон: (−4,∞)
Домен: (−∞,∞); Диапазон: (−2,∞)
Домен: (−∞,∞); Диапазон: (0,∞)
Домен: (−∞,∞); Диапазон: (−2,∞)
Домен: (−∞,∞); Диапазон: (−3,∞)
Домен: (−∞,∞); Диапазон: (−∞,6)
Домен: (−∞,∞); Диапазон: (−∞,5)
f(−1)≈2,37, f(0)=3, f(32)≈6,48
f(−1)≈3,90, f(0)=2, f(32)≈−8,45
f(−1)≈3,72, f(0)=2, f(32)≈1,22
f(−1)≈9,39, f(0)=3, f(32)≈2,05
Домен: (−∞,∞); Диапазон: (−3,∞)
Домен: (−∞,∞); Диапазон: (0,∞)
Домен: (−∞,∞); Диапазон: (1,∞)
Домен: (−∞,∞); Диапазон: (−∞,0)
Домен: (−∞,∞); Диапазон: (−∞,0)
г.
850,52 $
6 407,89 $
$16 066,13
1 588,00 $
4 685,44 $
$5778,56
Первоначальное население: 12 500 человек; Население 6 лет спустя: 14 077 91 813 человек.

Новый: 28 000 долларов США; Через 4 года: $13 940,40 91 813
Через 30 дней: 735 человек; Через 60 дней: 540 365 человек
г.- Модель
: 99 423 человека; ошибка: 4827 человек
Первоначально было 12 000 ячеек, а через 6 часов осталось 51 736 ячеек.
Ответ может отличаться
Ответ может отличаться
Ответ может отличаться
Степени, экспоненты и логарифмы
Степени, экспоненты и журналыОсновная силовая функция
|
 Вы знаете, как это можно расширить с помощью алгебры, чтобы определить
Вы знаете, как это можно расширить с помощью алгебры, чтобы определить
|
Откройте окно Maple и начертите функции
|
Можно (пока опустим логические подробности) «заполнить
в» определение, чтобы понять x b для любого действительного числа b
(по крайней мере, если x положителен).
Участок
|
Уравнение
|
Мы уже говорили о случаях y = x b (степенные функции ) и
|
 Сегодня нас в первую очередь интересуют более экзотические случаи:
Сегодня нас в первую очередь интересуют более экзотические случаи:Экспоненциальные функции: y = a x
График
|
Логарифмические функции:
|
Участок
|
 Синтаксис Maple: log[3](x) .) Поэкспериментируйте с другими значениями базы. (Почему случай a = 1 патологический?)
Синтаксис Maple: log[3](x) .) Поэкспериментируйте с другими значениями базы. (Почему случай a = 1 патологический?)Самый важный факт, который нужно запомнить об экспоненциальном и логарифмических функций состоит в том, что большинство этих функций ненужно запоминать!
Теорема: Существует число e 2,718 такое что
|
|
Следовательно, экспоненциальные и логарифмические функции относительно
произвольное основание a может быть исключено в пользу тех,
в отношении специальной базы, т.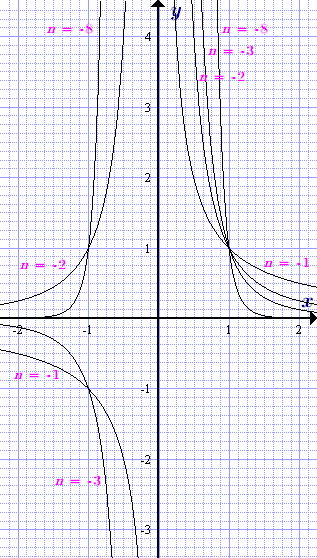 е.
е.
9х .)
Обозначения: e x также записывается как exp x. Тогда exp и ln рассматриваются как новые трансцендентные такие функции, как sin и cos. Как и в случае с триггерными функциями, скобки часто опускаются. аргументы этих функций при отсутствии неоднозначности:
|
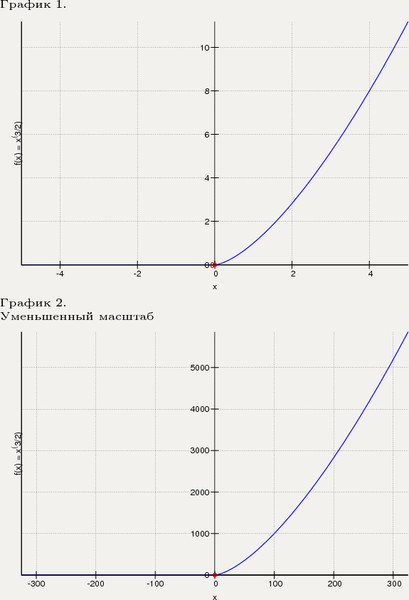
Функция e x увеличивается быстрее на бесконечности, чем любая степень функция.
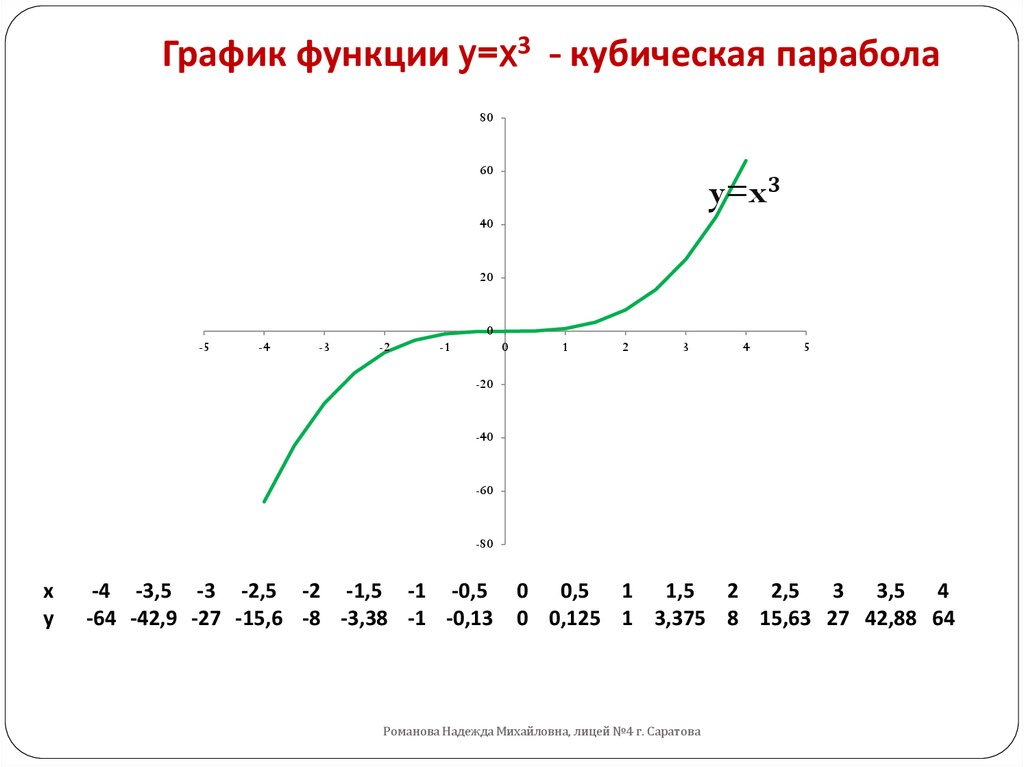
График y = e x и y = x 3 на тех же осях. Затем постройте y = e x и y = x 8 на тех же осях. Вы все еще верите этому утверждению? Сделайте масштаб x большим, а масштаб y огромным!
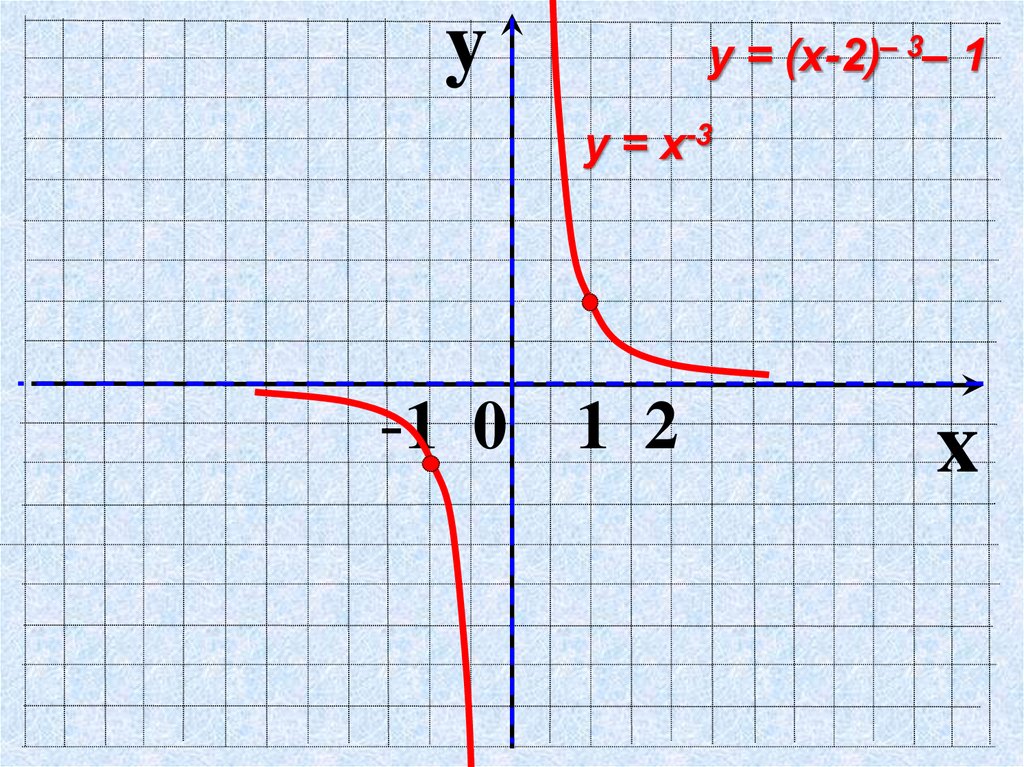
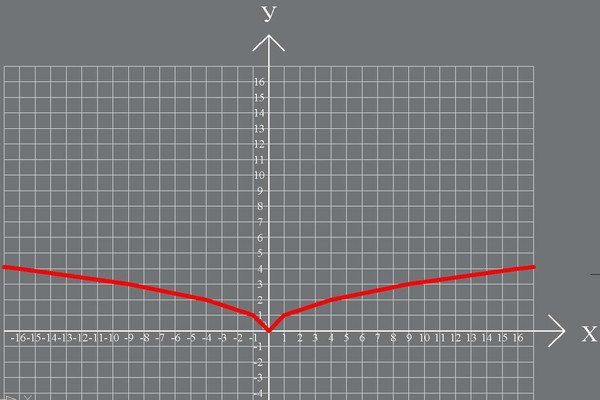
Функция e -x убывает на бесконечности быстрее, чем
любую отрицательную силу.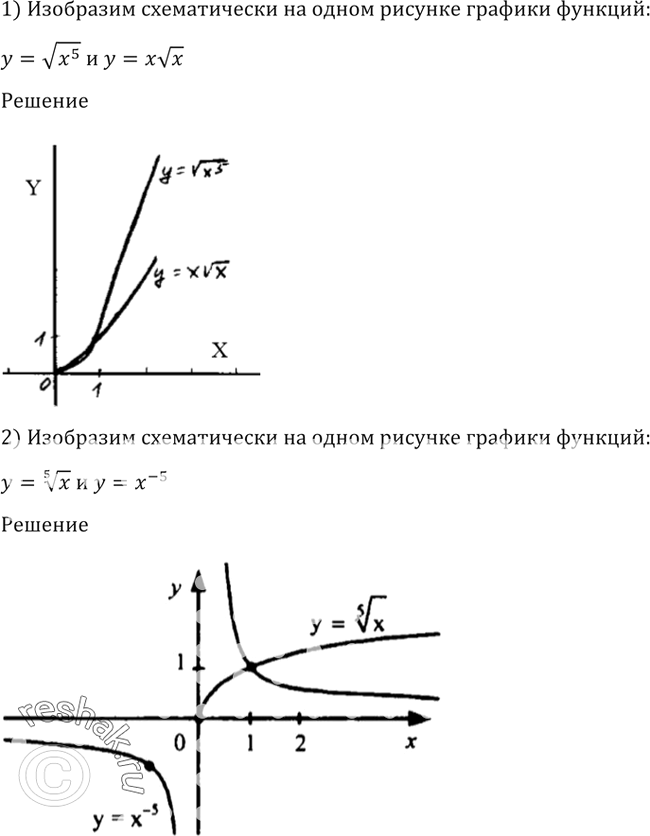
График y = e -x и y = x -2 на одних и тех же осях. Затем постройте y = e -x и y = x -20 на тех же осях; поэкспериментируйте с весами, чтобы найти точку пересечения.
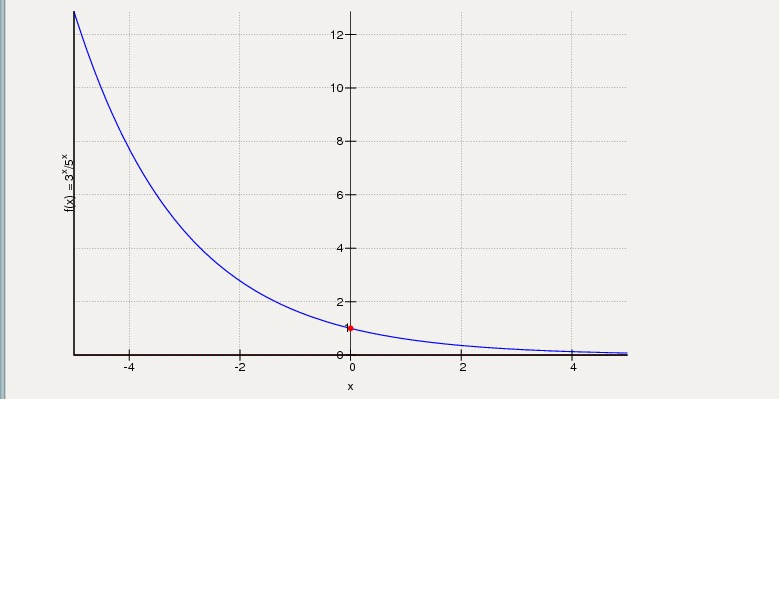
Функция ln x растет медленнее на бесконечности чем любая положительная (дробная) степень.
Постройте y = ln x и y = x 1/5 на тех же осях. Увеличивайте масштаб x, пока не найдете точку пересечения.
г. Когда x приближается к 0, функция — ln x увеличивается медленнее, чем любая отрицательная сила.
Постройте y = — ln x и y = x -1/5 на одних и тех же осях. Вы верите заявлению?
|
|
|
|
|
|
|

|
|
|
|
|
|
Файл переведен с T E X на T T H, версия 0.9(затем доработан вручную S.A.F.).
Обратная экспоненциальная функция — ChiliMath
В этом уроке я рассмотрю три примера , показывающих, как алгебраически определить обратную экспоненциальную функцию. Но прежде чем вы взглянете на рабочие примеры, я предлагаю вам сначала просмотреть предложенные ниже шаги, чтобы хорошо понять общую процедуру.
ШАГ 1: Замените f\left( x \right) на y.
\большой{е\влево(х\вправо) \в у}
ШАГ 2: Поменяйте местами \color{blue}x и \color{red}y в уравнении.
\large{x \to y}
\large{y \to x}
ШАГ 3: Выделите экспоненциальное выражение в одной части (левой или правой) уравнения.
Экспоненциальное выражение, показанное ниже, представляет собой общую форму, где b — основание, а N — показатель степени.
ШАГ 4. Удалите основание b экспоненциального выражения путем логарифмирования обеих частей уравнения.
- Чтобы упростить упрощение, возьмем логарифм обеих частей, используя основание самого экспоненциального выражения. 9{ — 1}}\left( x \right)
Применим предложенные выше шаги для решения некоторых проблем.
Примеры нахождения обратной экспоненциальной функции
Пример 1: Найдите обратную экспоненциальную функцию ниже.
Это должна быть простая задача, потому что экспоненциальное выражение в правой части уравнения уже выделено для нас.
Начните с замены обозначения функции f\left( x \right) на y.
Следующий шаг — поменять местами переменные \color{red}x и \color{red}y в уравнении.
 9{ — 1}}\влево( х \вправо). Это означает, что мы нашли обратную функцию.
9{ — 1}}\влево( х \вправо). Это означает, что мы нашли обратную функцию.Если мы изобразим исходную экспоненциальную функцию и обратную к ней на одной и той же плоскости XY, они должны быть симметричны относительно линии \large{\color{blue}y=x}. Какие они!
Пример 2: Найдите обратную экспоненциальную функцию ниже.
Единственное отличие этой задачи от предыдущей состоит в том, что экспоненциальное выражение имеет знаменатель 2. В остальном шаги будут такими же.
Мы меняем обозначение функции f\left( x \right) на y, после чего меняем местами переменные \color{red}x и \color{red}y.
На данный момент мы еще не можем выполнить шаг логарифмирования обеих частей. Причина в том, что экспоненциальное выражение в правой части не полностью само по себе. Сначала нам нужно избавиться от знаменателя 2.
Этого можно добиться, умножив обе части уравнения на 2. Левая часть умножится на 2, а знаменатель в правой части исчезнет! 9{ — 1}}\left( x \right) для обозначения того, что мы получили обратную функцию.

Как видите, графики экспоненциальной функции и обратной к ней симметричны относительно прямой \large{\color{green}y=x}.
Пример 3: Найдите обратную показательную функцию ниже.
Я вижу, что у нас есть экспоненциальное выражение, которое делится на другое. Хорошо, что экспоненциальные выражения имеют одно и то же основание, равное 3. Мы должны упростить это, используя правило деления экспоненты. Чтобы разделить экспоненциальные выражения, имеющие одинаковые основания, скопируйте общее основание, а затем вычтите их показатели степени. Ниже приведено правило. Предполагается, что b \ne 0,
Обратите внимание, как сильно упростилась исходная задача после применения правила деления экспоненты.
Теперь мы можем, как обычно, найти обратное. Перепишите f\left( x \right) как y, а затем поменяйте местами переменные \color{red}x и \color{red}y.
Прежде чем мы сможем получить журналы обеих частей, изолируем экспоненциальную часть уравнения, добавив обе части на 4.

Поскольку экспоненциальное выражение использует основание 3, мы берем журналы обеих частей уравнения с основанием 3. также! При этом показатель степени \color{blue}2y-1 в правой части упадет, поэтому мы можем продолжить поиск у, который является требуемой обратной функцией.
Подтверждает правильность нашего ответа, поскольку график заданной экспоненциальной функции и обратной к ней (логарифмической функции) симметричен относительно прямой \large{y=x}.
You might also be interested in:
Inverse of a 2×2 Matrix
Inverse of Absolute Value Function
Inverse of Constant Function
Inverse of Linear Function
Inverse of Logarithmic Function
Inverse of Квадратичная функция
Обратная рациональная функция
Обратная функция квадратного корня
Экспоненциальная функция — формула, асимптоты, область значений, диапазон
Экспоненциальная функция — это тип математической функции, которая помогает найти рост или уменьшение населения, денег, цен и т.
 д., которые растут или убывают экспоненциально. Джонатан читал новостную статью о последних исследованиях роста бактерий. Он читал, что был проведен эксперимент с одной бактерией. После первого часа бактерия удвоилась, и их стало две. После второго часа число было четыре. С каждым часом количество бактерий увеличивалось. Он думал, каково будет количество бактерий через 100 часов, если эта закономерность сохранится. Когда он спросил своего учителя о том же, ответом было понятие экспоненциальной функции.
д., которые растут или убывают экспоненциально. Джонатан читал новостную статью о последних исследованиях роста бактерий. Он читал, что был проведен эксперимент с одной бактерией. После первого часа бактерия удвоилась, и их стало две. После второго часа число было четыре. С каждым часом количество бактерий увеличивалось. Он думал, каково будет количество бактерий через 100 часов, если эта закономерность сохранится. Когда он спросил своего учителя о том же, ответом было понятие экспоненциальной функции.Давайте узнаем больше об экспоненциальной функции, а также о ее определении, уравнении, графиках, экспоненциальном росте, экспоненциальном затухании и т. д.
1. Что такое экспоненциальная функция? 2. Формула экспоненциальной функции 3. График экспоненциальной функции 4. Асимптоты экспоненциальной функции 5. 
Домен и диапазон экспоненциальной функции 6. Экспоненциальная серия 7. Правила экспоненциальной функции 8. Производная показательной функции 9. Интегрирование экспоненциальной функции 10. Часто задаваемые вопросы по экспоненциальной функции Что такое экспоненциальная функция?
Экспоненциальная функция, как следует из ее названия, включает показатели степени. Но обратите внимание, что экспоненциальная функция имеет константу в качестве основания и переменную в качестве ее показателя, но не наоборот (если функция имеет переменную в качестве основания и константу в качестве показателя степени, то это степенная функция, а не функция). экспоненциальная функция). Показательная функция может быть представлена в одной из следующих форм.
Экспоненциальная функция Определение
В математике экспоненциальная функция — это функция вида f (x) = a x , где «x» — переменная, а «a» — константа, которая называется основанием функции и оно должно быть больше 0.

Примеры экспоненциальной функции
Вот несколько примеров экспоненциальной функции.
- f(x) = 2 х
- f(x) = (1/2) х
- f(x) = 3e 2x
- f(x) = 4 (3) -0,5x
Формула экспоненциальной функции
Базовая экспоненциальная функция, согласно ее определению, имеет вид f(x) = b x , где b — константа, а x — переменная. Одной из популярных экспоненциальных функций является f(x) = e x , где e — «число Эйлера», а e = 2,718… Если мы расширим возможности различных экспоненциальных функций, экспоненциальная функция может включать в себя постоянная как кратная переменной по своей мощности. т. е. экспоненциальная функция также может иметь вид f(x) = e кх . Кроме того, он также может иметь вид f(x) = p e kx , где p — константа. Таким образом, экспоненциальная функция может быть в одной из следующих форм.

- f(x) = b х
- f(x) = ab х
- f(x) = ab сх
- f(x) = е х
- f(x) = e kx
- f(x) = p e kx
Здесь, кроме ‘x’, все остальные буквы являются константами, ‘x’ — переменная, а f(x) — экспоненциальная функция относительно x. Также обратите внимание, что основание каждой экспоненциальной функции должно быть положительным числом. т. е. в приведенных выше функциях b > 0 и e > 0. Также b не должно быть равно 1 (если b = 1, то функция f(x) = b x становится f(x) = 1, и в этом случае функция является линейной, но НЕ экспоненциальной).
Экспоненциальная функция возникает всякий раз, когда значение величины увеличивается при экспоненциальном росте и уменьшается при экспоненциальном затухании. Мы можем увидеть больше различий между экспоненциальным ростом и спадом вместе с их формулами в следующей таблице.
Экспоненциальный рост Экспоненциальный спад При экспоненциальном росте величина сначала медленно увеличивается, а затем быстро увеличивается. 
При экспоненциальном распаде величина сначала очень быстро убывает, а затем медленно. Формулы экспоненциального роста используются для моделирования роста населения, моделирования сложных процентов, определения времени удвоения и т. д. Экспоненциальный распад полезен для моделирования распада населения, определения периода полураспада и т. д. График функции в экспоненциальном росте увеличивается. График функции в экспоненциальном росте убывает. При экспоненциальном росте функция может иметь вид:
- f(x) = ab x , где b > 1.
- f(x) = a (1 + r) x
- Р = Р 0 е к т
Здесь b = 1 + r ≈ e k .
При экспоненциальном затухании функция может иметь вид:
г.- f(x) = ab x , где 0 < b < 1.
- f(x) = a (1 — r) x
- Р = Р 0 е -к т
Здесь b = 1 — r ≈ e — k .

В приведенных выше формулах
- a (или) P 0 = Исходное значение
- r = Скорость роста
- k = константа пропорциональности
- x (или) t = время (время может быть в годах, днях или (или) месяцах. Все, что мы используем, должно быть согласованным во всей задаче).
График экспоненциальной функции
Мы можем понять процесс построения графика экспоненциальной функции, взяв несколько примеров. Построим график двух функций f(x) = 2 x и g(x) = (1/2) x . Чтобы построить график каждой из этих функций, мы построим таблицу значений с некоторыми случайными значениями x, нанесем точки на график, соединим их кривой и продолжим кривую на обоих концах. Процесс построения графика экспоненциальной функции можно подробно изучить, нажав здесь.
Вот таблица значений, которые используются для построения графика экспоненциальной функции f(x) = 2 x .

Вот таблица значений, которые используются для построения графика экспоненциальной функции g(x) = (1/2) x .
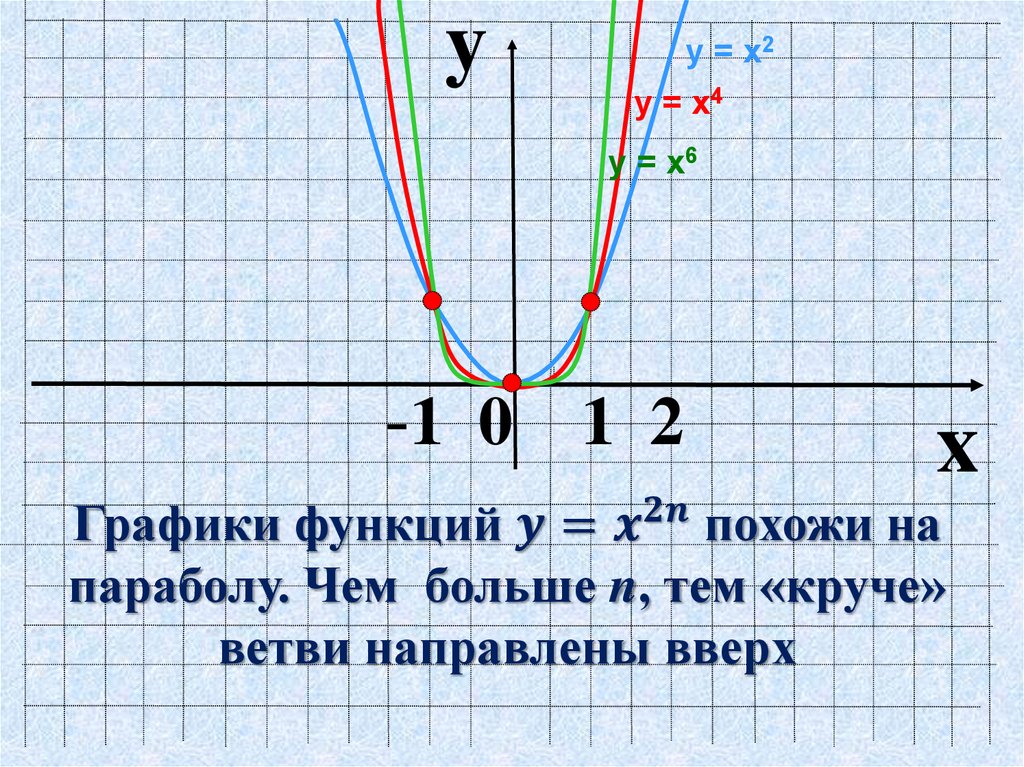
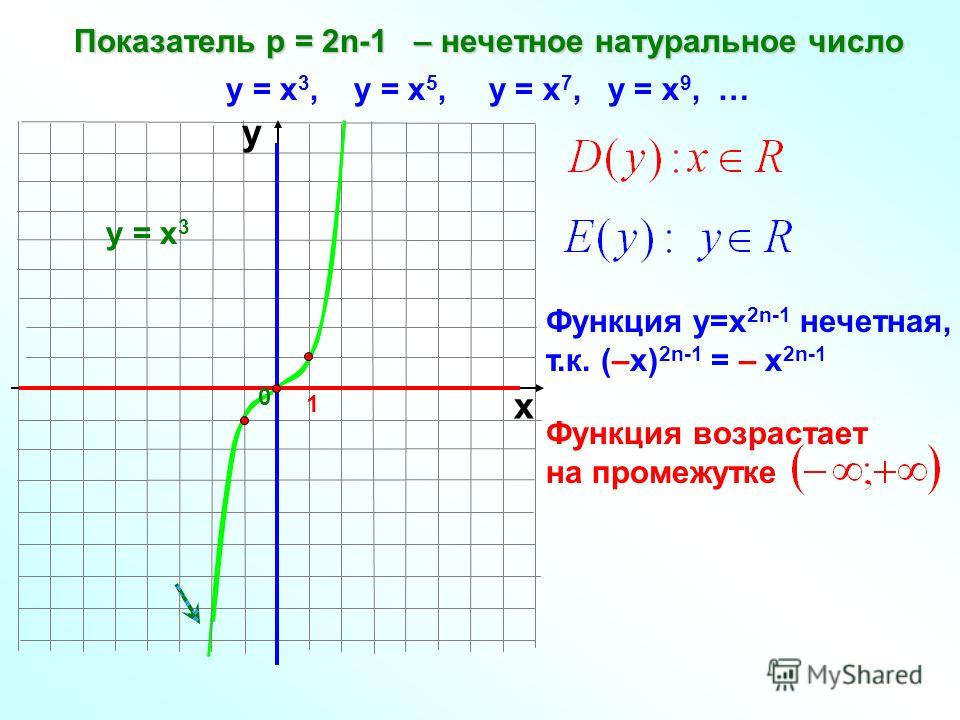
Примечание: Из двух приведенных выше графиков видно, что f(x) = 2 x увеличивается, тогда как g(x) = (1/2) x уменьшается. Таким образом, график показательной функции f(x) = b x .
- увеличивается, когда b > 1
- уменьшается, когда 0 < b < 1
Асимптоты экспоненциальной функции
Экспоненциальная функция не имеет вертикальной асимптоты, так как функция непрерывно возрастает/убывает. Но у него есть горизонтальная асимптота. Уравнение горизонтальной асимптоты экспоненциальной функции f(x) = ab x + c всегда равно y = c. т. е. это не что иное, как «у = константа, добавляемая к экспоненциальной части функции». На двух приведенных выше графиках (от f(x) = 2 x и g(x) = (1/2) x ), мы можем заметить, что горизонтальная асимптота равна y = 0, так как ничего не добавляется к показателю степени в обеих функциях.
 Таким образом,
Таким образом,- Показательная функция никогда не имеет вертикальной асимптоты.
- Горизонтальная асимптота показательной функции f(x) = ab x + c равна y = c.
Домен и диапазон экспоненциальной функции
Мы знаем, что область определения функции y = f(x) — это множество всех значений x (входных данных), где ее можно вычислить, а диапазон — это множество всех значений y (выходных данных) функции. Из графиков f(x) = 2 x и g(x) = (1/2) x в предыдущем разделе мы можем видеть, что показательная функция может быть вычислена при всех значениях x. Таким образом, областью определения экспоненциальной функции является множество всех действительных чисел (или) (-∞, ∞). Диапазон экспоненциальной функции можно определить по горизонтальной асимптоте графика, скажем, y = d, и по тому, находится ли график выше y = d или ниже y = d. Таким образом, для экспоненциальной функции f(x) = ab x ,
- Областью определения является множество всех действительных чисел (или) (-∞, ∞).

- Диапазон равен f(x) > d, если a > 0, и f(x) < d, если a < 0.
Чтобы понять это, вы можете увидеть пример ниже.
Экспоненциальная серия
Действительная экспоненциальная функция обычно может быть определена следующим степенным рядом: = 1 + (x/1) + (x 2 /2) + (x 3 /6) + …
Разложение некоторых других экспоненциальных функций дано, как показано ниже,
e = Σ n = 0 ∞ 1 n /n! = 1 + (1/1) + (1/2) + (1/6) + …
e -1 = Σ n = 0 ∞ (-1) n /n ! = 1 — (1/1) + (1/2) — (1/6) + …
Правила экспоненциальной функции
Правила экспоненциальной функции такие же, как правила экспоненты. Вот некоторые правила экспоненты.
- Закон нулевого показателя степени: a 0 = 1
- Закон продукта: м × a n = a m+n
- Закон частного: a m /a n = a m-n
- Закон Силы Силы: (a m ) n = a mn
- Закон силы продукта: (ab) m = a m b m
- Закон степени частного: (a/b) m = a m /b m
- Закон отрицательного показателя степени: a -м = 1/а м
Помимо этого, иногда нам нужно использовать формулу преобразования логарифмической формы в экспоненциальную, которая выглядит следующим образом:
- b x = a ⇔ log b a = x
Свойство равенства экспоненциальной функции
В соответствии со свойством равенства экспоненциальной функции, если две экспоненциальные функции с одинаковыми основаниями одинаковы, то их показатели также одинаковы.
 то есть
то естьб х 1 = б х 2 ⇔ х 1 = х 2
Производная экспоненциальной функции
Вот формулы дифференцирования, которые используются для нахождения производной экспоненциальной функции.
- д/дх (е х ) = е х
- d/dx (a x ) = a x · ln a.
Интегрирование экспоненциальной функции
г.Вот формулы интегрирования, которые используются для нахождения интеграла экспоненциальной функции.
- ∫ e x dx = e x + C
- ∫ a x dx = a x / (ln a) + C
Важные замечания по экспоненциальной функции:
- Область определения любой экспоненциальной функции — это множество всех действительных чисел.
- Показательная функция не имеет вертикальной асимптоты.
- Каждая экспоненциальная функция имеет одну горизонтальную асимптоту.

- График любой экспоненциальной функции либо возрастает, либо убывает.
☛ Связанные темы:
- Калькулятор экспоненциальной функции
- Логарифмические функции
- Экспоненциальные уравнения
Часто задаваемые вопросы об экспоненциальной функции
Что такое определение экспоненциальной функции?
Экспоненциальная функция — это тип математической функции, в которой используются показатели степени. Основная экспоненциальная функция имеет вид f(x) = b x , где b > 0 и b ≠ 1.
Какие формулы экспоненциальной функции?
В формулах показательной функции есть показатели степени. Показательное уравнение может быть представлено в одной из следующих форм.
- f(x) = ab cx
- f(x) = p e kx
Каковы правила экспоненциальной функции?
Поскольку экспоненциальная функция включает показатели степени, правила экспоненциальной функции такие же, как и правила показателей степени.
 Они равны:
Они равны:- a m × a n = a m+n
- a м /a n = a m-n
- а 0 = 1
- а -м = 1/а м
- ( м ) n = а млн
- (ab) м = а м б м
- (a/b) м = a м /b м
Как построить график экспоненциальной функции?
Чтобы построить график экспоненциальной функции y = f(x), создайте таблицу значений, взяв несколько случайных чисел в качестве x (обычно мы берем -2, -1, 0, 1 и 2), и подставьте каждое из них в функция, чтобы найти соответствующие значения y. Затем нанесите точки из таблицы и соедините их кривой. Наконец, удлините кривую на обоих концах. При рисовании графика обратите внимание на горизонтальную асимптоту.
Что такое область экспоненциальной функции?
Показательная функция f(x) = ab x определена для всех значений x и, следовательно, ее областью определения является множество всех действительных чисел, которые в интервальных обозначениях могут быть записаны как (-∞, ∞).

Каковы свойства экспоненциальной функции?
Свойства экспоненциальной функции могут быть представлены как
- а м /а н = а м-н
- а 0 = 1
- а -м = 1/а м
- (а м ) н = а мн
- (ab) м = а м б м
- (a/b) м = a м /b м
Для любой показательной функции вида f(x) = ab x , где b > 1, экспоненциальный график возрастает, а для любой показательной функции вида f(x) = ab x , где 0 < b < 1, график уменьшается.
Что такое диапазон экспоненциальной функции?
Диапазон экспоненциальной функции зависит от ее горизонтальной асимптоты, а также от того, лежит ли кривая выше или ниже горизонтальной асимптоты. т. е. для экспоненциальной функции f(x) = ab x диапазон равен
- f(x) > d, если a > 0 и
- f(x) < d, если a < 0,
где y = d — горизонтальная асимптота графика функции.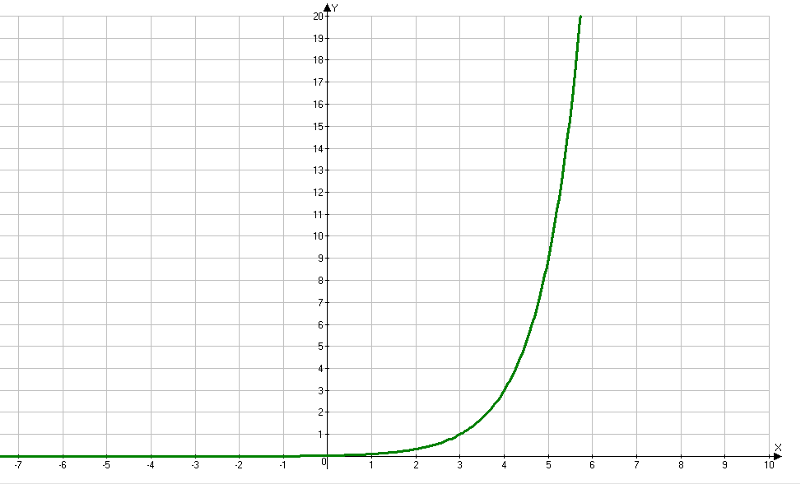




 Сколько будет стоить компакт-диск в конце 3-летнего срока?
Сколько будет стоить компакт-диск в конце 3-летнего срока? Сколько будет стоить компакт-диск в конце 3-летнего срока?
Сколько будет стоить компакт-диск в конце 3-летнего срока?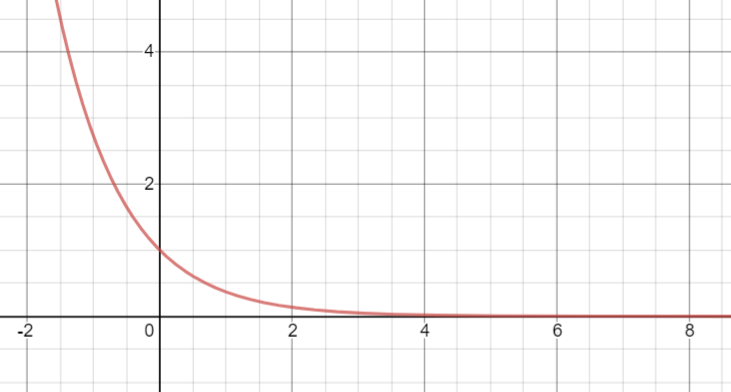 Если 220 000 долларов вложены на счет, приносящий 4,5% годовых с постоянным начислением процентов, то сколько процентов будет начислено за первые 2 года?
Если 220 000 долларов вложены на счет, приносящий 4,5% годовых с постоянным начислением процентов, то сколько процентов будет начислено за первые 2 года? Используйте формулу, чтобы определить стоимость автомобиля, когда он был новым ( t = 0) и стоимость через 4 года.
Используйте формулу, чтобы определить стоимость автомобиля, когда он был новым ( t = 0) и стоимость через 4 года.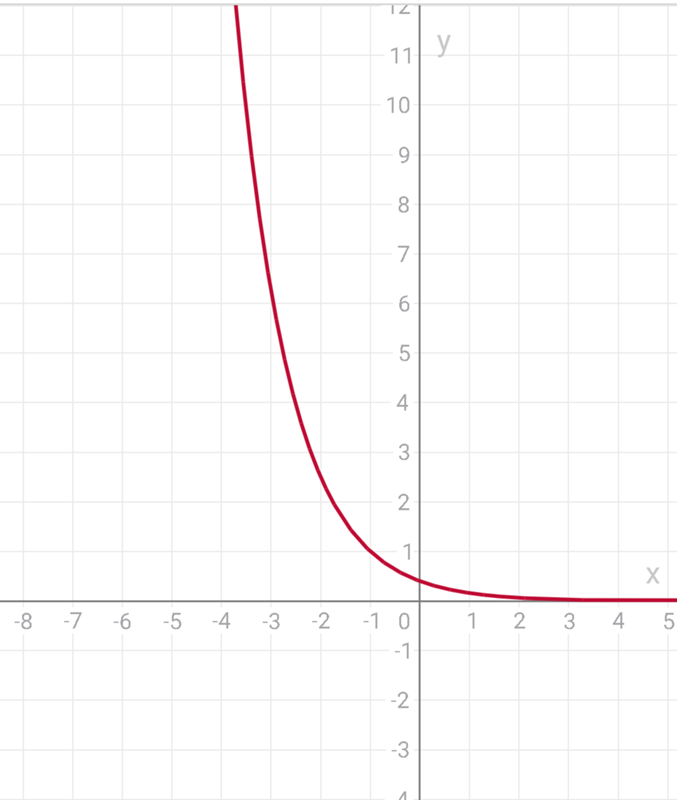 Сколько кроликов будет через 312 лет?
Сколько кроликов будет через 312 лет?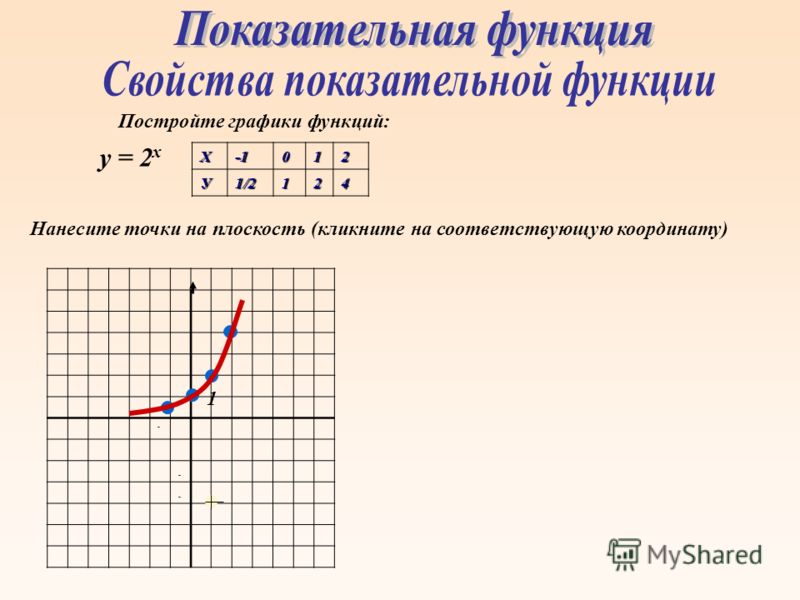 Определите начальное количество клеток, а затем определите количество клеток через 6 часов.
Определите начальное количество клеток, а затем определите количество клеток через 6 часов.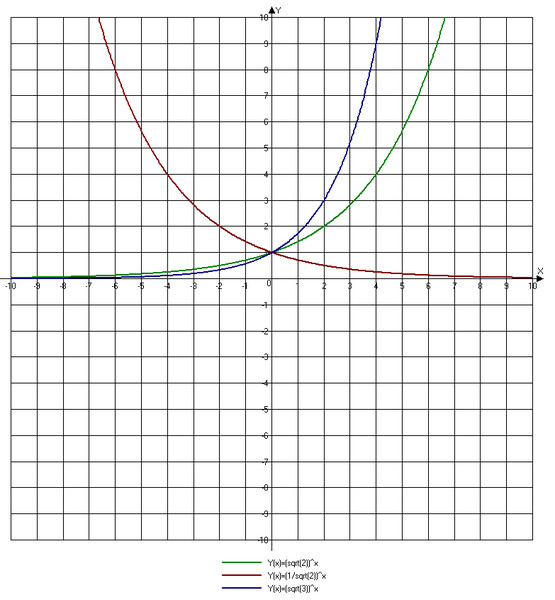
 10
10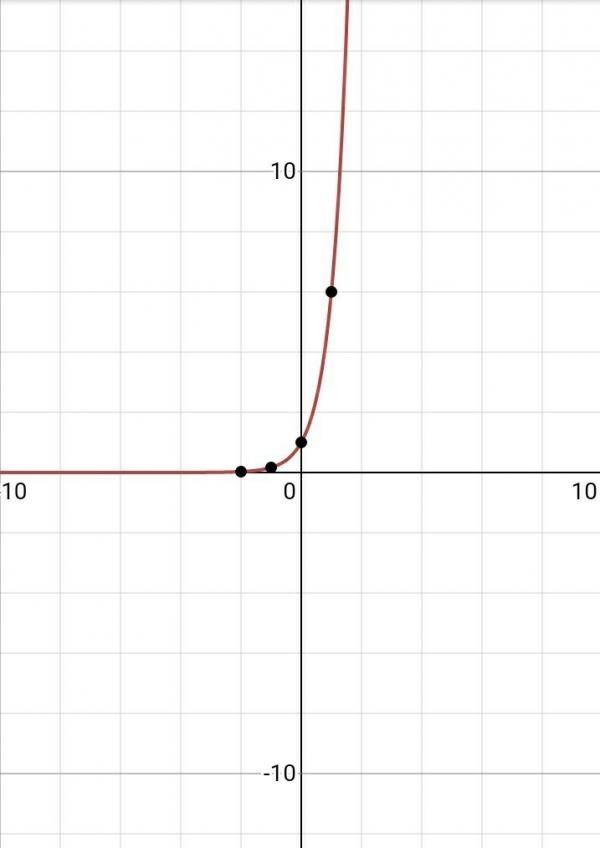
 9{ — 1}}\влево( х \вправо). Это означает, что мы нашли обратную функцию.
9{ — 1}}\влево( х \вправо). Это означает, что мы нашли обратную функцию.
 д., которые растут или убывают экспоненциально. Джонатан читал новостную статью о последних исследованиях роста бактерий. Он читал, что был проведен эксперимент с одной бактерией. После первого часа бактерия удвоилась, и их стало две. После второго часа число было четыре. С каждым часом количество бактерий увеличивалось. Он думал, каково будет количество бактерий через 100 часов, если эта закономерность сохранится. Когда он спросил своего учителя о том же, ответом было понятие экспоненциальной функции.
д., которые растут или убывают экспоненциально. Джонатан читал новостную статью о последних исследованиях роста бактерий. Он читал, что был проведен эксперимент с одной бактерией. После первого часа бактерия удвоилась, и их стало две. После второго часа число было четыре. С каждым часом количество бактерий увеличивалось. Он думал, каково будет количество бактерий через 100 часов, если эта закономерность сохранится. Когда он спросил своего учителя о том же, ответом было понятие экспоненциальной функции.




 Таким образом,
Таким образом,
 то есть
то есть
 Они равны:
Они равны: