Найти общее и частное решение дифференциального уравнения: Частное решение дифференциального уравнения

Содержание

Вариант № 21

Задача 1. Найти общее решение дифференциального уравнения

, (1) – дифференциальное уравнение с разделяющимися переменными

Интегрируя обе части уравнения, получим:

Общее решение уравнения (1):

Задача 2.Найти частные решения Дифференциального уравнения, удовлетворяющие начальным условиям.

Найдем общее решение дифференциального уравнения с разделяющимися переменными

Подставляем в полученное решение начальное условие:

Значит, искомое частное решение:

Задача 3. Решить дифференциальное уравнение (1)

Применим подстановку

Тогда:

Интегрируя, получим общий интеграл уравнения

В результате общий интеграл уравнения имеет вид:

Подставляя значение , получим общий интеграл уравнения (1):

Задача 4. Решить дифференциальное уравнение (1)

Составим определитель

Положим , гдеОпределяются из системы уравнений:

Положим в уравнении (1) ; Получим: ;

Применим подстановку ; Тогда:

Интегрируя обе части уравнения, получим:

Учитывая, что , получим общее решение уравнения (1):

Задача 5. Найти частные решения Дифференциального уравнения, удовлетворяющие начальным условиям.

Ищем общее решение линейного неоднородного дифференциального уравнения 1-го порядка

(1)

Найдем общее решение линейного однородного дифференциального уравнения 1-го порядка

Интегрируя обе части уравнения, получим:

Общее решение этого уравнения:

Применим метод вариации постоянных:

Дифференцируем

Y По X:

Подставляем полученные значения в уравнение (1):

Следовательно, общее решение линейного неоднородного дифференциального уравнения 1-го порядка:

Подставляем в полученное решение начальное условие:

Значит, искомое частное решение:

Задача 6. Найти частные решения Дифференциального уравнения, удовлетворяющие начальным условиям.

Ищем общее решение уравнения Бернулли: (1)

Применим подстановку

Подставляем в уравнение (1):

(2)

Требуем выполнения условия:

Подставляя полученное выражение в уравнение (2), получим:

Следовательно, общее решение уравнения Бернулли (1):

Подставляем в полученное решение начальное условие:

Значит, искомое частное решение:

Задача 7. Найти общий интеграл Дифференциального уравнения.

(1)

Так как , значит, мы имеем уравнение в полных дифференциалах

Находим

Общий интеграл Дифференциального уравнения

Задача 8. Определить тип дифференциального уравнения, найти общее решение и построить интегральную кривую, проходящую через точку М.

Найдем общее решение однородного дифференциального уравнения 1-го порядка с разделяющимися переменными

Следовательно, общим решением является семейство парабол:

Из условий в точке М найдем:

Отсюда искомая интегральная кривая:

Задача 9.

Решить дифференциальное уравнение (1) — явно не содержит

Полагая , имеем , тогда уравнение (1) принимает вид:

– уравнение с разделяющимися переменными относительно .

Общее решение этого уравнения:

Задача 10. Найти решение Дифференциального уравнения, удовлетворяющее заданным условиям.

Ищем общее решение дифференциального уравнения 2-го порядка:

Положим ,

Тогда уравнение преобразуется к виду:

Ищем общее решение уравнения Бернулли относительно р: (1)

Применим подстановку

Подставляем в уравнение (1):

(2)

Требуем выполнения условия:

Подставляя полученное выражение в уравнение (2), получим:

Следовательно, общее решение уравнения Бернулли (1):

Из условий и имеем:

Значит:

Из условия имеем

Значит, имеем частное решение Дифференциального уравнения, удовлетворяющее заданным условиям:

Задача 11. Найти общее решение дифференциального уравнения (1)

— линейное однородное уравнение 2 порядка с постоянными коэффициентами

Характеристическое уравнение:

Следовательно, фундаментальную систему решений уравнения (1) образуют функции

общее решение уравнения (1) имеет вид: .

Задача 12. Найти частное решение Дифференциального уравнения, удовлетворяющее указанным условиям.

Ищем решение линейного однородного уравнения 2 порядка с постоянными коэффициентами

(1)

Характеристическое уравнение:

общее решение однородного уравнения имеет вид: .

Продифференцируем:

Из указанных условий имеем:

Частное решение Дифференциального уравнения, удовлетворяющее указанным условиям:

Задача 13. Найти общее решение дифференциального уравнения (1)

— линейное неоднородное уравнение 2 порядка с постоянными коэффициентами и специальной правой частью

Ищем решение линейного однородного уравнения 2 порядка с постоянными коэффициентами

Характеристическое уравнение:

общее решение однородного уравнения имеет вид: .

Структура общего решения неоднородного уравнения (1) имеет вид: ;

где — общее решение однородного уравнения, а функция — частное решение неоднородного уравнения, которое ищем в виде:

Подставляем частное решение в неоднор. уравнение и находим неопределенный коэффициент:

Следовательно,

Общее решение неоднородного уравнения (1):

Задача 14. Найти общее решение дифференциального уравнения (1)

— линейное неоднородное уравнение 2 порядка с постоянными коэффициентами и специальной правой частью

Ищем решение линейного однородного уравнения 2 порядка с постоянными коэффициентами

Характеристическое уравнение:

общее решение однородного уравнения имеет вид: .

Применим принцип наложения решений (суперпозиции).

Структура общего решения неоднородного уравнения (1) имеет вид: ;

где — общее решение однородного уравнения, а функции — частные решения следующих уравнений:

;

Причём частные решения ищем в виде: ;

Подставляем поочередно частные решения в соответствующие уравнения и находим неопределенные коэффициенты:

Следовательно, Общее решение неоднородного уравнения (1):

Задача 15. Найти частное решение Дифференциального уравнения, удовлетворяющее указанным условиям.

Найдем решение линейного неоднородного уравнения 2 порядка с постоянными коэффициентами

Ищем решение линейного однородного уравнения 2 порядка с постоянными коэффициентами

(1)

Характеристическое уравнение: ; следовательно, фундаментальную систему решений уравнения (1) образуют функции

общее решение однородного уравнения (1) имеет вид: .

РЕшение линейного неоднородного уравнения ищем методом вариации произвольных постоянных: , а неизвестные функции определяем из системы уравнений:

Следовательно, Общее решение неоднородного уравнения (1):

Продифференцируем полученное решение

Из условий И Имеем:

Частное решение Дифференциального уравнения, удовлетворяющее указанным условиям:

Задача 16. Найти общее решение дифференциального уравнения (1)

— линейное неоднородное уравнение 3-го порядка с постоянными коэффициентами и специальной правой частью (многочлен)

Ищем решение линейного однородного уравнения 3 порядка с постоянными коэффициентами

Характеристическое уравнение:

Следовательно, фундаментальную систему решений уравнения (1) образуют функции

общее решение однородного уравнения имеет вид: .

Частное решение Ищем в виде: ;

Подставляем в неоднородное уравнение (1):

Следовательно,

Общее решение неоднородного уравнения (1):

Задача 17. Найти с помощью степенных рядов общее решение уравнения при указанных начальных условиях

(1)

Положим (2)

Имеем ;

Дифференцируя обе части уравнения (1), получим:

Подставим в выражение (2) и получим частноЕ решение уравнения при указанных начальных условиях:

Задача 18. Решить систему дифференциальных уравнений

Дифференцируя первое уравнение по , получим:

Из первого уравнения выразим значение

Значит:

(1)

Получили линейное неоднородное уравнение 2-го порядка с постоянными коэффициентами и специальной правой частью.

Ищем решение линейного однородного уравнения 2 порядка с постоянными коэффициентами:

Характеристическое уравнение:

Следовательно, общее решение однородного уравнения имеет вид: .

Частное решение Ищем в виде:

Подставляем в неоднородное уравнение (1):

Следовательно, Общее решение неоднородного уравнения (1):

Значение Выразим из:

< Предыдущая		Следующая >

Сообщество Экспонента

вопрос
22. 09.2022

Математика и статистика, Системы управления, Изображения и видео, Робототехника и беспилотники, Глубокое и машинное обучение(ИИ), Другое

Коллеги, добрый день. Необходимо использовать corrcoef, а массивы разной длины. Как сделать кол-во элементов одинаково?

7 Ответов

вопрос
20.09.2022

Другое, Встраиваемые системы, Цифровая обработка сигналов, Системы управления

Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…

Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т. ч. англоязычные форумы, не смог ничего найт…

MATLAB

20.09.2022

Публикация
15.09.2022

Системы управления, Другое

Видел видос на канале экспоненты по созданию топливной системы. Вопрос заключается в наличии более полного описания готового примера или соответсвующее документации. Я новичок в симулинке и ещё многого не знаю. Адекватных и раскрытых пособий по созданию гидрав…

Моделирование гидравлических систем в simulink

Публикация
10.09.2022

Системы управления, Электропривод и силовая электроника, Другое

Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов. В этой книге в научно-практическо-методической форме я план…

Публикация
24.08.2022

Цифровая обработка сигналов, Системы связи, Математика и статистика

&…

Здесь собрана литература по комбинированным методам множественного доступа, в которых используется разделение пользователей в нескольких ресурсных пространствах.

вопрос
23.08.2022

Математика и статистика, Радиолокация, Цифровая обработка сигналов

Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?

4 Ответа

ЦОС
цифровая обработка сигналов

23.08.2022

Публикация
23.08.2022

Цифровая обработка сигналов, Системы связи, Математика и статистика

&. ..

Здесь соборана литература по методам множественного доступа с поляризационным разделением и разделением по орбитальном угловому моменту.

Публикация
16.08.2022

Цифровая обработка сигналов, Системы связи, Математика и статистика

Здесь собрана литература по методам множественного доступа с пространственным разделением.

вопрос
22.07.2022

Изображения и видео, Цифровая обработка сигналов, Математика и статистика, Биология, Встраиваемые системы, Глубокое и машинное обучение(ИИ), Автоматизация испытаний, ПЛИС и СнК, Системы управления, Другое

Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например: file_1_1.txt file_1_2.txt file_1_3.txt file_1_4.txt fil…

2 Ответа

чтение

22.07.2022

вопрос
17.07.2022

Математика и статистика, Цифровая обработка сигналов

Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…

MATLAB
Signal Processing

17.07.2022

заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
написание лабораторных, рефератов и курсовых
выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

Форум, где посетители обмениваются идеями и помогают друг другу
Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
Аукцион, где цена за товар или услугу определяется в результате торгов
Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.
Выбрать платежную систему.
Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.

Методическая разработка занятия по предмету Элементы высшей математики по теме: «Определение обыкновенных дифференциальных уравнений. Общее и частное решение. Уравнения с разделенными переменными». | Методическая разработка по теме:

Методическая разработка

по предмету ЕН.01

ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ

по теме:

«Определение обыкновенных дифференциальных уравнений. Общее и частное решение. Уравнения с разделенными переменными»

Преподаватель математики:

Т.Н. Рудзина

Москва

2015 г.

ОТКРЫТЫЙ УРОК по теме:

Определение обыкновенных дифференциальных уравнений. Общее и частное решение. Уравнения с разделенными переменными.

«Великая книга природы написана на языке математики»

Галилей

Тип занятия: комбинированный, с элементами игры.

Формы занятия: индивидуальная, групповая, фронтальная.

Технология – игровая.

Оборудование: Кинофильм «Дифференциальные уравнения в науке и технике» (фрагменты), проектор, компьютер, доска, рабочие тетради.

Наглядные пособия. Таблица «Геометрическая интерпретация множества решений дифференциального уравнения».

Продолжительность занятия: 90 мин.

Цели занятия:

Дидактическая цель. Дать понятие о дифференциальном уравнении, его общем, частном решении. Показать геометрическую интерпретацию множества решений дифференциального уравнения. Учить решать дифференциальные уравнения с разделенными переменными.

Воспитательная цель. Формировать мировоззрение учащихся, раскрыв основные идеи математического моделирования, в котором дифференциальные уравнения играют большую роль. Активизировать учебную деятельность учащихся, рассказав о широком применении дифференциальных уравнений во многих отраслях науки и техники. Развивать любознательность и интерес к изучению математики, раскрывая прикладную направленность дифференциальных уравнений и приводя исторические сведения.

Методическая цель: Организация деятельностного подхода обучающихся на уроке.

Основные знания и умения. З н а т ь определения: дифференциального уравнения, его порядка, общего и частного решения. Иметь понятие о задаче Коши. У м е т ь геометрически иллюстрировать дифференциальные уравнения в простейших случаях; отличать дифференциальные уравнения от алгебраических.

Учебно-методическое обеспечение: тест, презентация преподавателя к открытому уроку (Приложение 1), задания для группового решения, задания для самостоятельной работы, кроссворд, лист оценки знаний студента

ПЛАН УРОКА.

Организационный момент (5 мин).
Сообщение темы и целей урока.

Мотивационная беседа с последующей постановкой цели (5 мин).

Актуализация опорных знаний:

1. Проверочная работа. (8 мин)

2. Отгадать имя ученого. (10 мин)

3. Историческая справка. (5 мин)

4. Просмотр научно-популярного фильма о применении дифференциальных уравнений. (6 мин)

Изучение нового материала. (20 мин)
Закрепление. (15 мин)
Домашнее задание. (2 мин)
Итог. (Решение кроссворда). (8 мин)
Рефлексия. (5 мин)

ХОД УРОКА.

I. Организационный момент.

Приветствие. Проверка готовности группы к уроку.

II. Сообщение темы и целей урока.

Тема нашего урока: Определение обыкновенных дифференциальных уравнений. Общее и частное решение. Уравнения с разделенными переменными.

Цель нашего занятия: познакомиться с понятием дифференциального уравнения, его общим и частным решением, знать, как определяется порядок ДУ, иметь понятие о задаче Коши. Понимать какое уравнение называется уравнением с разделенными переменными и учиться его решать.

Для достижения этой цели мы проведем проверочную работу с взаимопроверкой, чтобы быть готовыми воспринимать новый материал; решим задания, с помощью которых узнаем кто ввел термин «Дифференциальные уравнения» и это все будет у нас проходить в духе соревнования (поэтому мы разделились с вами на 3 группы). Посмотрим фильм советских времен о применении ДУ в науке и технике. Разберем новый материал, закрепим его и в заключении разгадаем кроссворд, который подведет итог нашего урока. Результаты оценивания знаний на разных этапах заносятся в лист оценки знаний каждого студента. В процессе занятия учитывается и индивидуальная, и групповая формы работы.

1. Мотивационная беседа с последующей постановкой цели.

Теория дифференциальных уравнений является заключительной темой после изучения дифференциально–интегрального исчисления. Тема эта очень сложная. Она является важной для получения фундаментального естественно – научного образования.

Для формирования представлений о математике, как о необходимой для каждого человека составляющей общих знаний о мире и понимания значимости этой науки для общественного прогресса.

«Математика – это то, посредством чего люди управляют природой и собой», – писал А.Н.Колмогоров (выдающийся математик современности).

III. Актуализация опорных знаний.

Проверочная работа. (8 мин)

(Слайд 2)

Найти производную.

I вариант II вариант

а) ; а)

б) б)

в) в)

г) г)

д) д) .

После решения нужно обменяться тетрадями и провести взаимопроверку по слайду. За каждый правильный ответ записываем себе 1 балл.

Ответы: (Слайд 3)

I вариант II вариант

а) ; а) ;

б) ; б) ;

в) ; в)

г) г)

д) д) .

2. Отгадать фамилию ученого.

(Слайд 4)

Кто ввел термин «ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ»?

Для этого решаете примеры на вычисление определенного интеграла, а затем по полученным результатам прочитаем слово (фамилию ученного).

Задание.

Вычислить определенный интеграл:

1. 2.

3. ; 4.

5. 6. 7. .

Проверим правильность решения примеров. С помощью таблицы определим, какой ответ решения определенного интеграла соответствует букве алфавита. С помощью полученных букв составим фамилию ученого, впервые применившего термин «Дифференциальные уравнения».

За каждый правильно вычисленный интеграл — 2 балла.

За составления фамилии ученого из полученных букв – 1 балл.

(Слайд 5)

Соответствие найденных значений определенных интегралов буквам алфавита.

7	6		8	0	1	2
Е	Н	Б	Ц	Й	Л	И

Историческая справка по применению дифференциальных уравнений.

Студенты группы подготовили свои сообщения по нашей теме. (Послушае м их).

При изучении тех или иных физических, биологических процессов, механических явлений, ученым удается составить дифференциальные уравнения этого процесса или явления. А затем, решая это уравнение, удается вывести функциональный закон описания изучаемого вопроса. Дифференциальные уравнения играют большую роль в деле изучения природы и различных физических, химических и других процессов.

Существует много процессов в природе, которые описываются дифференциальными уравнениями. Например, процесс размножения бактерий, явление органического роста, изменение давления при подъеме над уровнем моря, ток самоиндукции, протекающий в катушке после выключения постоянного напряжения.

Можно так же написать дифференциальные уравнение движения планеты вокруг Солнца, искусственного спутника вокруг земли. Решая дифференциальные уравнения движения планет и их спутников (эти уравнения весьма сложны, т. к. планеты притягиваются не только к Солнцу, но и друг к другу), ученые предсказывают их будущее движение, узнают моменты солнечного и лунного затмений. Когда однажды оказалось, что планета Уран отклоняется от заранее вычисленной орбиты, ученые нисколько не сомневались в «правильности» математики. В середине 19 века французский астроном Леверье и английский астроном Джон Адамс одновременно и независимо один от другого сделали смелое предположение, что отклонение Урана вызывается притяжением к нему новой, до сих пор неизвестной планеты. С помощью дифференциальных уравнений они вычислили положение этой новой планеты и указали, где нужно искать ее на небе. Точно в указанном месте эта планета (её назвали НЕПТУН) была затем обнаружена. О ней говорят, что она открыта «на кончике пера» (путем вычислений).

Возникнув в XVI в. на базе задач математики и физики, теория дифференциальных уравнений как самостоятельная дисциплина сложилась к концу XVIII в. В настоящее время теория дифференциальных уравнений продолжает развиваться и является одной из важнейших частей математики.

Тот факт, что самые различные явления описываются одинаковыми дифференциальными уравнениями, часто используется на практике.

Просмотр научно-популярного фильма советских времен о применении дифференциальных уравнений. (Cлайд 6)

IV. Объяснение нового материала:

Мотивация: в школьном курсе встречались с различными уравнениями: алгебраическими, показательными, тригонометрическими и т.д. Во всех этих уравнениях неизвестными являются числа.

В математике и ее приложениях иногда приходиться рассматривать функциональные уравнения, решениями которых служат неизвестные функции (или семейство функций). (Вспомним, что же такое функция? Ответ: Это зависимость, когда каждому значению переменной x ставится в соответствие единственное значение y).

К функциональным уравнениям относятся дифференциальные уравнения.

Рассмотрим некоторую функцию . Обозначим через ее первую производную, — вторую и т.д., а дифференциалы функций и аргумента обозначим соответственно и .

В дифференциальных уравнениях всегда присутствует производные или дифференциалы функции и аргумента. Это отличительный признак дифференциальных уравнений.

Например, , – дифференциальные уравнения.

Выполним задание. (Слайд 7)

Установить, какое из указанных уравнений являются дифференциальными:

а) ; б) ; в) ;

г) ; д) ; е) .

Ответ: а), г), е) — дифференциальные уравнения.

Определение:

(Слайд 8)

Дифференциальным уравнением называется уравнение, содержащее производные искомой функции или ее дифференциалы.

(Слайд 9)

Решить дифференциальное уравнение — значит найти такую функцию, подстановка которой в это уравнение обращает его в тождество. Эта функция называется решением дифференциального уравнения.

Даны функции: , , . Какие из них являются решениями дифференциального уравнения ? (Слайд 10)

Ответ: .

(Слайд 11)

Решение, содержащее постоянную C, называется общим решением дифференциального уравнения.

Решение, в которое подставлено числовое значение C, называется частным решением дифференциального уравнения.

Значение С вычисляется при подстановке начальных данных в общее решение. Геометрически частное решение представляется одной интегральной кривой, общее решение – совокупностью интегральных кривых.

(Слайд 12)

Зная, что функция является общим решением уравнения , определить его частное решение, если .

Решение:

Подставив в общее решение заданные начальные условия , , получим , откуда . Теперь подставим значение

в общее решение и найдем искомое частное решение .

Таким образом, при решении дифференциальных уравнений сначала получается общее решение. Затем, если известны начальные данные, то можно получить частное решение.

(Слайд 13)

Для этого нужно:

подставить начальные данные в общее решение и вычислить С;
полученное числовое значение С подставить в общее решение.

(Слайд 14)

Задача нахождения частного решения дифференциального уравнения по начальным данным называется задачей Коши.

При вычислении неопределенных интегралов мы имеем дело с дифференциальным уравнением. Нахождение неопределенного интеграла по заданному дифференциалу некоторой функции сводиться к решению дифференциального уравнения.

Найти решение дифференциального уравнения , удовлетворяющего условию .

Общее решение этого уравнения находим интегрированием:

Подставив начальные данные и определив , найдем частное решение (решение задачи Коши) .

(Слайд 15)

Символически дифференциальное уравнение записывается так:

, , .

(Слайд 16)

Определение:

Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.

(Слайд 17)

Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение.

– дифференциальное уравнение I порядка, т.к. наивысший порядок производной – I.

– дифференциальное уравнение II-го порядка.

– дифференциальное уравнение III-го порядка.

, где – дифференциальное уравнение II-го порядка. (Определить порядок — на слайде 17)

К дифференциальным уравнениям I-го порядка относятся уравнения, в которые входят производные (или дифференциалы) не выше первого порядка.

Общий вид дифференциального уравнения I-го порядка

(Слайд 18)

Если это уравнение можно разрешить относительно , то оно примет вид .

Дифференциальные уравнения I порядка с разделенными переменными.

(Слайд 19)

Определение:

Уравнение вида , где и – данные функции, называется уравнением с разделенными переменными.

Это уравнение можно переписать в виде:

и рассмотреть, как равенство двух дифференциалов.

Каждая часть уравнения с разделенными переменными представляет собой произведение некоторого выражения, зависящего от одной переменной, на дифференциал этой переменной.

(Слайд 20)

Пример:

— уравнения с разделенными переменными. Решение таких уравнений выполняется непосредственным интегрированием.

Решить уравнение: .

Здесь переменные разделены.

Интегрируя, получим:

Так как – произвольно, то обозначим через , тогда

— общее решение или общий интеграл данного дифференциального уравнения.

С геометрической точки зрения получим семейство концентрических окружностей с центром в начале координат и радиусом равным C.

(Слайд 21)

V. Закрепление.

Решить уравнение

Здесь , .

, интегрируя обе части

– общее решение, его можно записать в явной форме:

Решить уравнение

Решить уравнение

— общее решение.

Найти частное решение дифференциального уравнения , если , .

Имеем:

– частное решение.

Решить уравнение , если , при

— частное решение.

(Слайд 22)

VI. Домашнее задание:

;

;

;

Ответы: 1) 3)

2) 4) .

VII. Итог.

(Слайд 23)

Решение кроссворда.

КРОССВОРД

По горизонтали:

Решение дифференциального уравнения, которое можно получить, если известны начальные данные.
Что показывает старшая производная дифференциального уравнения?
Действие нахождения общего решения ДУ.

7. Нахождение конкретного частного решения по начальным данным – это задача … .

По вертикали:

4. Найти решение ДУ, значит, найти … .

5. Ученый, который ввел термин «Дифференциальные уравнения».

6. Дифференциальным уравнением называется уравнение, содержащее … .

8. Название ДУ, если искомая функция зависит от одного независимого переменного.

Теперь необходимо подсчитать количество баллов (индивидуально и по командам) соответственно таблице.

Таблица баллов

№ п/п	За что начисляются баллы	Количество	Максимальное количество баллов за данный пункт	Мои БАЛЛЫ
1	Решение проверочной работы	По 1 баллу за каждый правильно решенный пример	5
2	Решение заданий «Отгадай фамилию»	По 2 баллу за каждый правильно решенный пример	14
3	За составление фамилии ученого	1 балл	1
4	Историческая справка	1 балл	1
5	Участие в объяснении нового материала	По 1 баллу за каждый правильный ответ	1
6	Решение примеров на закрепление материала	3-5 баллов	5
7	Ответы на кроссворд	За каждое отгаданное слово – 1 балл	8

(Слайд 25).

КРИТЕРИИ ОЦЕНОК

Количество баллов	Оценка
18-20	5
13-17	4
8-12	3

VIII. Рефлексия. (Слайд 26)

1. «Я узнал много нового» —

2. «Мне это пригодится в жизни» —

3. «На уроке было над чем подумать» —

4. «На все вопросы, возникающие в ходе урока, я получил ответы» —

5. «На уроке я работал добросовестно и цели урока достиг» —

Поднимите руки, кто поставил 5 плюсов, а затем те, кто поставил 4 и три плюса.

5 –

4 –

3 –

2 –

Частное решение дифференциального уравнения

LearnPracticeDownload

Частное решение дифференциального уравнения – это единственное решение вида y = f(x), которое удовлетворяет дифференциальному уравнению. Частное решение дифференциального уравнения получается путем присвоения значений произвольным константам общего решения дифференциального уравнения.

Давайте узнаем больше о частном решении дифференциального уравнения, о том, как найти решение дифференциального уравнения и о разнице между частным решением и общим решением дифференциального уравнения.

1.	Что такое частное решение дифференциального уравнения?
2.	Как найти частное решение дифференциального уравнения?
3.	Частное решение против общего решения дифференциального уравнения
4.	Примеры частного решения дифференциального уравнения
5.	Практические вопросы
6.	Часто задаваемые вопросы о частном решении дифференциального уравнения

Что такое частное решение дифференциального уравнения?

Частным решением дифференциального уравнения является уравнение вида y = f(x), не содержащее произвольных констант и удовлетворяющее дифференциальному уравнению. Уравнение или функция вида y = f(x), имеющие определенные значения x, которые удовлетворяют этому уравнению и называются решениями этого уравнения. Для дифференциального уравнения d ² y/dx ² + 2dy/dx + y = 0, значения y, удовлетворяющие этому дифференциальному уравнению, называются решением дифференциального уравнения.

Здесь y = f(x), представляющий прямую или кривую, является решением дифференциального уравнения, которое удовлетворяет дифференциальному уравнению. Решение вида y = ax ² + bx + c является общим решением дифференциального уравнения, так как оно содержит произвольные константы a, b, c. Далее, если решение имеет значения, присвоенные этим произвольным константам, или если решение не содержит произвольных констант, то решение называется частным решением дифференциального уравнения.

Как найти частное решение дифференциального уравнения?

Частное решение дифференциального уравнения может быть вычислено из общего решения дифференциального уравнения. Общее решение дифференциального решения будет иметь форму y = f(x), которая может быть любой параллельной линией или кривой, и, определив точку, которая удовлетворяет одной из этих линий или кривых, мы можем найти точное уравнение вида y = f(x), которое является частным решением дифференциального уравнения.

Следующие шаги помогут найти частное решение дифференциального уравнения.

Данное дифференциальное уравнение решается путем разделения переменных и интегрирования с обеих сторон для получения общего решения дифференциального уравнения.
Для дифференциальных уравнений, которые нелегко решить, используются различные методы, чтобы найти общее решение дифференциального уравнения.
Общее решение дифференциального уравнения содержит произвольные константы, которым необходимо присвоить подходящие значения, чтобы получить частное решение дифференциального уравнения.
Определена точка, которая поможет заменить значения произвольных констант, чтобы получить частное решение дифференциального уравнения.
У дифференциального уравнения может быть несколько частных решений, основанных на различных значениях произвольной константы.

Частное решение против общего решения дифференциального уравнения

Частное решение дифференциального уравнения получается из общего решения дифференциального уравнения. Дифференциальное уравнение имеет одно общее решение и множество частных решений, основанных на различных значениях произвольных констант общего решения.

Общее решение дифференциала представляет собой семейство кривых или линий на координатной плоскости. Эти кривые или линии представляют набор параллельных линий или кривых, и каждая из этих линий или кривых может быть идентифицирована как частное решение дифференциальное уравнение.

Общее решение дифференциального уравнения имеет вид y = ax + b, но частным решением дифференциального уравнения может быть y = 3x + 4, y = 5x + 7, y = 2x + 1. Эти частные решения дифференциального уравнения были получены путем присвоения различных значений произвольным константам a, b в общем решении дифференциального уравнения.

Связанные темы

Следующие темы помогут лучше понять конкретное решение дифференциального уравнения.

Порядок и степень дифференциального уравнения
Линейное дифференциальное уравнение
Дифференциальные уравнения
Однородное дифференциальное уравнение

Примеры частного решения дифференциального уравнения

Пример 1: Определить, является ли уравнение y = e ^-2x частным решением дифференциального уравнения d ² y/dx ² + dy/dx -2y = 0.
Данное уравнение решения дифференциального уравнения имеет вид y = e ^-2x .
Дифференцируя приведенное выше уравнение решения в обе стороны, мы получаем следующее выражение.
dy/dx = -2e ^-2x
Далее, дифференцируя это по x для второго дифференцирования, мы имеем:
d ² y/dx ² = 4e ^-2x
Применяя это в дифференциальном уравнении, чтобы проверить, удовлетворяет ли оно заданное выражение.
Данное дифференциальное уравнение:
D ² Y/DX ² + DY/DX -2Y = 0
4E ^-2X -2E ^-2X -2E ^-2X = 0.
Следовательно, уравнение y = e ^-2x является решением дифференциального уравнения d ² y/dx ² + dy/dx -2y = 0,
Пример 2: Проверить, является ли функция y = acosx + bsinx частным решением дифференциального уравнения y» + y = 0?
Решение:
Данной функцией является y = aCosx + bSinx.
Возьмем вторую производную этой функции.
y’ = -aSinx + bCosx
y» = -aCosx — bSinx
Далее мы можем подставить это значение второй производной в нижеследующее дифференциальное уравнение.
y» + y = 0
(-aCosx — bSinx) + (aCosx + bSinx.) = 0
-aCosx — bSinx + aCosx + bSinx. = 0
-aCosx + aCosx -bSinx +bSinx = 0
Следовательно, функция y = acosx + bsinx является решением дифференциального уравнения y» + y = 0,

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, зачем нужна математика, с нашими сертифицированными экспертами

Запишитесь на бесплатный пробный урок

Практические вопросы по частному решению дифференциального уравнения

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о частном решении дифференциального уравнения

Что такое частное решение дифференциального уравнения?

А частным решением дифференциального уравнения является решение вида y = f(x), не имеющее произвольных констант. Общее решение дифференциального уравнения имеет вид y = f (x) или y = ax + b и имеет a, b в качестве произвольных констант. Присвоение значений этим произвольным константам приводит к частным решениям, таким как y = 2x + 1, y = 3x + 4, y = 5x + 2.

В чем разница между общим решением и частным решением дифференциального уравнения?

Частные решения были получены из общих решений. Общее решение дифференциального уравнения имеет произвольные константы, а решения без произвольных констант называются частными решениями дифференциального уравнения. Общее решение дифференциального уравнения представляет собой семейство кривых или набор параллельных прямых, и каждая из этих прямых или кривых может быть членом как частное решение дифференциального уравнения.

Как определить конкретное решение дифференциального уравнения?

Частное решение дифференциального уравнения легко определить, так как оно не имеет произвольных констант. Решения y = 3x + 3, y = x ² + 11x + 7 являются примерами частного решения дифференциального уравнения.

Какая польза от частного решения дифференциального уравнения?

Частное решение дифференциального уравнения полезно для нахождения точного решения, удовлетворяющего дифференциальному уравнению, в определенной точке или для определенного значения независимой переменной.

Рабочие листы по математике и визуальные учебные программы

Общие и частные решения

Здесь мы научимся находить общее решение дифференциального уравнения, и использовать это общее решение, чтобы найти частное решение. Мы будем также применим это к задачам ускорения, в которых мы используем ускорение и начальные условия объекта, чтобы найти положение функция.

Пример 1: поиск конкретного решения

Найти частное решение дифференциального уравнения, удовлетворяющее заданному начальному условию:

Сначала нужно найти общее решение. Для этого нам нужно интегрировать обе стороны, чтобы найти y:

Это дает нам общее решение. Чтобы найти конкретное решение, нам нужно применить начальные условия, заданные для нас (y = 4, x = 0) и решить для C:

После того, как мы решим для C, мы получим частное решение.

Пример 2: Поиск частного решения

Найдите частное решение дифференциального уравнения, удовлетворяющее заданному начальному условию:

Сначала нам нужно проинтегрировать обе части, что дает нам общее решение:

9003

Теперь мы применяем начальные условия (x = 1, y = 4) и находим C, который мы используем для создания нашего частного решения:

Пример 3: Поиск частного решения

Найдем частное решение дифференциального уравнения, удовлетворяющее заданному начальному условию:

Сначала найдем общее решение, интегрируя обе части:

Теперь, когда у нас есть общее решение, мы можем применить начальные условия и найти частное решение:

Скорость и ускорение

Здесь мы будем применять конкретные решения, чтобы найти функции скорости и положения по ускорению объекта.

Пример 4: Функция поиска позиции

Найдите функцию положения движущейся частицы с заданным ускорением, начальным положением и начальной скоростью:

У нас есть функция ускорения, начальная скорость 10 и начальное положение 5, и ищут функция положения. Мы знаем, что интеграл ускорения равен скорость, так что давайте начнем с этого:

Теперь мы имеем общее решение скорости функция. Чтобы получить частное решение, нам нужна начальная скорость. Поскольку это начальная скорость, это скорость в момент времени t = 0; следовательно, наше начальное условие v = 10, t = 0:

Теперь, когда у нас есть частное решение скорости, мы можем интегрировать его, чтобы найти положение:

Теперь мы можем применить наши начальные условия к этому общее решение, чтобы получить частное решение, которое является положением функцию, которую мы хотим. Как и раньше, x ₀ — это начальное положение
, что означает, что время t = 0, а x = 5:

Это функция положения частицы.

Пример 5: Поиск функции положения

У нас есть уравнение для ускорения, начальное скорость 7 и начальное положение 0. Первый шаг — найти частное решение скорости частицы:

Теперь мы можем использовать функцию скорости, чтобы найти функция положения. Помните, нам нужно будет найти конкретное решение функции положения, а не только общее решение:

Пример 6. Применение дифференциального уравнения

Здесь мы будем использовать пример из реальной жизни, чтобы применить то, что мы только что узнали.

Мяч бросают прямо вниз с начальной со скоростью 20 футов/с с вершины здания высотой 300 футов. Пренебрегая трением воздуха, доу через какое время мяч достигнет земли и с какой скоростью он попал?

Чтобы решить эту проблему, нам нужно положить в терминах, которые мы можем понять. Единицы даны в футах и футов/секунду; ускорение свободного падения в этих единицах равно -32 фут/с ² .

Мы знаем, что мяч был брошен вниз с начальной скоростью (t = 0) 20 футов/с; поскольку он идет вниз, скорость будет отрицательной (v ₀ = -10).

Наконец, здание достигает 300 футов в высоту, и мяч брошен сверху. Поскольку мяч начинается с места вверх от уровня земли, начальное положение будет положительным 300 (x ₀ = 300). Подставим все это в уравнение, аналогичное предыдущим примерам:

Теперь мы получаем где-то! Вопрос задает о мяче, когда он падает на землю. Чтобы быть в состоянии выяснить информация о том, когда он упадет на землю, нам нужно знать, который час хиты. Уравнение, связывающее положение со временем, есть положение функция, которую мы уже знаем, как получить из предыдущих примеров:

Теперь, когда у нас есть функция положения, мы можем начните вычислять время, за которое мяч коснется земли, и скорость, с которой он попадает. Для каждого из этих уравнений необходимо знать время; например, если мы подставим 2 вместо t в функцию скорости, это даст нам скорость в момент t = 2, или 2 секунды после броска мяча. Нам нужно знать, который час мяч падает на землю; для этого нам нужно задать позицию функцию, равную 0, и решить для t. Мяч стартовал в 300 футах от земли, и мы использовали 300 в качестве исходное положение. Если мы установим нашу позицию равной 0, это скажет нам когда мяч коснется земли:

Мы получаем два значения для t: -5 и 3,75. Мы можем выбросить -5, так как у нас не может быть отрицательного ценность для времени. Следовательно, время, за которое мяч достигнет земля составляет 3,75 секунды. Чтобы найти скорость в момент удара мяча о земли, мы просто подставим 3,75 вместо t в наше уравнение скорости и решим:

Скорость мяча при ударе о землю составляет -140 футов/с

Пример 7. Применение дифференциального уравнения

Тормоза автомобиля включаются, когда он движется со скоростью 60 км/ч, обеспечивая постоянное замедление 12 м/с ² . Какое расстояние проезжает автомобиль до остановки и сколько времени это занимает?

Хорошо, давайте разберемся. Мы знаем, что ускорение равно -12 м/с ² . Начальная скорость 60 км/ч; это нужно будет преобразовать в м/с (у нас не может быть проблем с разными единицами измерения):

Начальная скорость автомобиля составляет 16,7 м/с. Мы также можем назвать начальное положение x = 0, так как это когда автомобиль начинает замедляться. Все вместе:

Мы знаем, что нам понадобится функция положения в в какой-то момент, так как нам нужно выяснить, какое расстояние проедет машина до подходит к остановке, так что давайте уберем это с дороги:

Теперь нам нужно выяснить, в какое время машина подходит к остановке. Мы не знаем, в каком положении будет машина. этой точке, но мы знаем, что скорость будет равна 0. Чтобы узнать когда скорость равна 0, нам нужно установить скорость равной 0 и решить:

Автомобиль останавливается через 1,4 секунды после подачи тормоза. Какое расстояние он проходит до остановки? Нам нужно подставить t = 1,4 к функции положения, чтобы узнать:

Автомобиль проезжает 11,6 метра до остановки

Найти общие и частные решения с использованием разделения переменных Вопрос дня Карточки Учитесь по концепции

Исчисление AB Справка » Дифференциальные уравнения » Поиск общих и частных решений с использованием разделения переменных

Что такое разделение переменных?

Возможные ответы:

Взятие производной от двух переменных

Причудливая формулировка для разложения на множители

Интегрирование с двумя переменными

Использование алгебры для переписывания дифференциального уравнения так, чтобы две разные переменные находились на правильных сторонах

5 ответ:

Использование алгебры для перезаписи дифференциального уравнения так, чтобы две разные переменные находились на противоположных сторонах

Объяснение:

Когда мы пытаемся интегрировать дифференциальное уравнение, иногда нам приходится использовать метод, называемый разделением переменных. Это связано с тем, что нам нужно интегрировать по каждой переменной, но мы не можем этого сделать, когда они находятся на одной стороне. Когда мы можем получить каждую переменную на разных сторонах с их соответствующим дифференциалом (т. е. или ), тогда мы можем интегрировать каждую сторону по каждой переменной.

Сообщить об ошибке

Когда нужно использовать разделение переменных?

Возможные ответы:

Когда мы решаем функцию с двумя разными переменными в определенной точке

Когда нам нужно найти производную дифференциального уравнения

На самом деле нам никогда не приходится использовать разделение переменных, это просто ярлык

Когда нам нужно проинтегрировать дифференциальное уравнение с двумя разными переменными

Правильный ответ:

Когда нам нужно проинтегрировать дифференциальное уравнение с двумя разными переменными

Объяснение:

Используя разделение переменных, мы можем интегрировать, чтобы решить дифференциальное уравнение.

Сообщить об ошибке

Используйте разделение переменных для решения следующего дифференциального уравнения:

Возможные ответы:

Правильный ответ:

Объяснение:

Мы должны манипулировать этим дифференциальным уравнением, чтобы получить каждую переменную и ее собственную часть с ее дифференциалом. Как только мы это сделаем, мы должны соответствующим образом интегрировать каждую сторону.

(разделенные и умноженные на)

(только перестройка)

(Let)

(это только постоянная, поэтому мы переименуем)

Сообщайте о ошибке

Правильный ответ:

Объяснение:

(умноженные на и умноженные на)

(Let)

(Let).

Сообщить об ошибке

Использовать разделение переменных для решения следующих дифференциальных уравнений:

Возможные ответы:

Правильный ответ:

Объяснение:

(умноженное на)

(расширение)

(Let)

(это постоянная, так и назовите)

Отчет о ошибке

ИЗ решить дифференциальное уравнение по частному решению.

Возможные ответы:

Верно

Ложно

Правильный ответ:

Верно

Объяснение:

Так же, как интегрирование для функции одной переменной в конкретном решении. Мы также можем решить, используя разделение переменных и интеграцию для нашего конкретного решения.

Сообщить об ошибке

Найдите общее решение следующего дифференциального уравнения в точке .

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала мы должны использовать разделение переменных для решения общего уравнения, тогда мы сможем найти общее решение.

(умноженное на)

(Let)

Теперь мы подключаем к нашему решению для нашего константа

. 0003

и поэтому наше решение —

Сообщайте о ошибке

Найдите общее решение следующего уравнения дифференциального уравнения в точке.

Возможные ответы:

Правильный ответ:

Объяснение:

(умножение на и умножение на )

(Let)

(это только постоянная, так что переименовать)

Теперь мы подключаем нашу точку, чтобы решить.

Таким образом, наше решение на этой точке:

Отчет о ошибке

Найдите конкретное решение для использования точки следующего дифференциального уравнения.

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала мы должны использовать разделение переменных для решения общего уравнения, тогда мы сможем найти частное решение.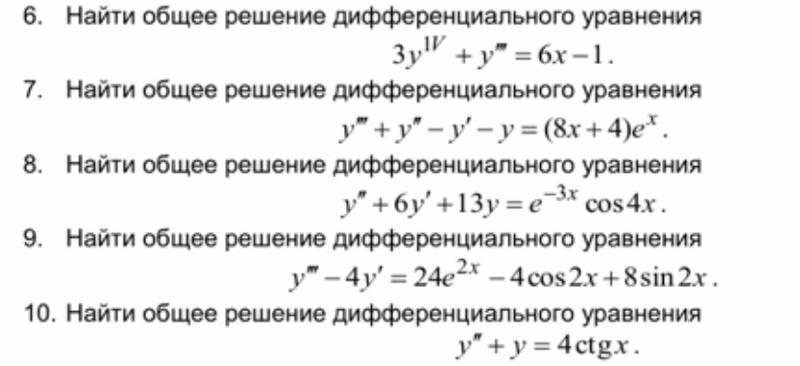

(умножение на)

(Let)

Теперь мы подключаем наше начальное условие, что нам дали

Теперь мы решим, когда

. Назовите дифференциальное уравнение, которое можно решить, используя разделение переменных.

Возможные ответы:

отделимые производные

отделимые частичные

разделимые уравнения

они не имеют специального названия

Правильный ответ:

разделимые уравнения

Пояснение:

Разделимые уравнения — это то, что мы называем дифференциальными уравнениями, которые мы можем решить, используя разделение переменных.

Сообщить об ошибке

Уведомление об авторских правах

Все ресурсы Calculus AB

45 Практические тесты Вопрос дня Карточки Учитесь по концепции

Дифференциальные уравнения — Неопределенные коэффициенты

Онлайн-заметки Пола
Главная / Дифференциальные уравнения / DE второго порядка / Неопределенные коэффициенты

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 3-9: Неопределенные коэффициенты

В этом разделе мы рассмотрим первый метод, который можно использовать для нахождения частного решения неоднородного дифференциального уравнения.

\[y» + p\left( t \right)y’ + q\left( t \right)y = g\left( t \right)\]

Одним из основных преимуществ этого метода является то, что он сводит задачу к задаче по алгебре. Иногда алгебра может запутаться, но для большинства задач она не будет слишком сложной. Еще одна приятная особенность этого метода заключается в том, что дополнительное решение не требуется явно, хотя, как мы увидим, в некоторых случаях потребуется знание дополнительного решения, и поэтому мы обычно находим и это.

Этот метод имеет два недостатка. Во-первых, это будет работать только для довольно небольшого класса \(g(t)\). Класс \(g(t)\), для которых работает метод, включает в себя некоторые из наиболее распространенных функций, однако существует множество функций, для которых неопределенные коэффициенты просто не будут работать. Во-вторых, это обычно полезно только для дифференциальных уравнений с постоянными коэффициентами.

Метод достаточно прост. Все, что нам нужно сделать, это посмотреть на \(g(t)\) и сделать предположение о форме \(Y_{P}(t)\), оставив коэффициент(ы) неопределенным (и, следовательно, имя метод). Подставьте предположение в дифференциальное уравнение и посмотрите, сможем ли мы определить значения коэффициентов. Если мы можем определить значения для коэффициентов, значит, мы угадали правильно, если мы не можем найти значения для коэффициентов, значит, мы угадали неправильно. 9{5т}}\]

Показать решение

Суть здесь в том, чтобы найти конкретное решение, однако первое, что мы собираемся сделать, это найти дополнительное решение этого дифференциального уравнения. Напомним, что дополнительное решение получается из решения

\[у» — 4у’ — 12у = 0\]

Характеристическое уравнение для этого дифференциального уравнения и его корни. 9{6т}}\]

На этом этапе причина, по которой нужно сделать это в первую очередь, не будет очевидной, однако мы хотим, чтобы вы привыкли находить ее до того, как мы начнем работу по поиску конкретного решения. В конце концов, как мы увидим, полезно иметь под рукой дополнительное решение, и поэтому лучше иметь привычку сначала находить его, прежде чем выполнять работу с неопределенными коэффициентами.

Теперь приступим к поиску конкретного решения. Как упоминалось перед началом этого примера, нам нужно сделать предположение о форме конкретного решения этого дифференциального уравнения. Поскольку \(g(t)\) является экспонентой, а мы знаем, что экспоненты никогда не появляются и не исчезают в процессе дифференцирования, кажется, что наиболее вероятной формой конкретного решения будет 9{5t}}\end{выравнивание*}\]

Итак, чтобы наша догадка была решением, нам нужно выбрать \(A\) так, чтобы коэффициенты экспонент по обе стороны от знака равенства были одинаковыми. Другими словами, нам нужно выбрать \(A\) так, чтобы

\[ — 7A = 3\hspace{0.25in} \Rightarrow \hspace{0.25in}A = — \frac{3}{7}\]

Хорошо, мы нашли значение коэффициента. Это значит, что мы угадали правильно. Тогда частным решением дифференциального уравнения будет 9{5т}}\]

Прежде чем двигаться дальше, давайте еще раз отметим, что мы начали решение выше, найдя дополнительное решение. Технически это не является частью метода неопределенных коэффициентов, однако, как мы в конечном итоге увидим, наличие этого метода до того, как мы сделаем предположение о конкретном решении, может сэкономить нам много работы и / или головной боли. Поиск дополнительного решения первым — это просто хорошая привычка, поэтому мы постараемся выработать у вас эту привычку в ходе следующих нескольких примеров. На данный момент не беспокойтесь о том, почему это хорошая привычка. Со временем мы поймем, почему это хорошая привычка.

Теперь вернемся к работе. Обратите внимание, что в последнем примере мы все время говорили «конкретное решение», а не «конкретное решение». Это потому, что есть и другие возможности для конкретного решения, которое нам только что удалось найти. Любой из них будет работать, когда дело доходит до записи общего решения дифференциального уравнения.

Говоря об этом… Этот раздел посвящен поиску частных решений, и большинство примеров будут посвящены поиску только частных решений. Тем не менее, мы должны сделать хотя бы один полноценный IVP, чтобы убедиться, что мы можем сказать, что сделали его. 9{5t}}\hspace{0.25in}\hspace{0.25in}y\left( 0 \right) = \frac{{18}}{7}\hspace{0.25in}y’\left( 0 \right) = — \фракция{1}{7}\]

Показать решение

Мы знаем, что общее решение будет иметь вид

\[y\left( t \right) = {y_c}\left( t \right) + {Y_P}\left( t \right)\]

, и у нас уже есть как дополнительное, так и частное решение из первого примера, поэтому нам не нужно выполнять дополнительную работу для этой задачи.

Одна из наиболее частых ошибок в этих задачах состоит в том, чтобы найти дополнительное решение, а затем, поскольку мы, вероятно, привыкли это делать, применить начальные условия к дополнительному решению, чтобы найти константы. Однако это неверно. Дополнительное решение — это только решение однородного дифференциального уравнения, и мы ищем решение неоднородного дифференциального уравнения, и начальные условия должны удовлетворять этому решению, а не дополнительному решению. 9{5t}}\end{выравнивание*}\]

Теперь применим к ним начальные условия.

\[\begin{align*}\frac{{18}}{7} = y\left( 0 \right) & = {c_1} + {c_2} — \frac{3}{7}\\ — \frac {1}{7} = y’\left( 0 \right) & = — 2{c_1} + 6{c_2} — \frac{{15}}{7}\end{align*}\]

Решение этой системы дает \(c_{1} = 2\) и \(c_{2} = 1\). Фактическое решение тогда.

\[y\left( t \right) = 2{{\bf{e}}^{ — 2t}} + {{\bf{e}}^{6t}} — \frac{3}{7}{ {\bf{e}}^{5t}}\]

Это будет единственная IVP в этом разделе, поэтому не забывайте, как это делается для неоднородных дифференциальных уравнений!

Давайте рассмотрим еще один пример, который даст второй тип \(g(t)\), для которого будут работать неопределенные коэффициенты.

Пример 3. Найдите частное решение следующего дифференциального уравнения. \[y» — 4y’ — 12y = \sin \left( {2t} \right)\]

Показать решение

Опять же, давайте отметим, что нам, вероятно, следует найти дополнительное решение, прежде чем мы перейдем к угадыванию конкретного решения. Однако, поскольку однородное дифференциальное уравнение для этого примера такое же, как и для первого примера, мы не будем здесь этим заниматься.

Теперь давайте возьмем опыт из первого примера и применим его здесь. В первом примере была экспоненциальная функция в \(g(t)\), и наше предположение было экспоненциальным. Это дифференциальное уравнение имеет синус, поэтому давайте попробуем следующее предположение для конкретного решения.

\[{Y_P}\left( t \right) = A\sin \left( {2t} \right)\]

Дифференцирование и подстановка в дифференциальное уравнение дает,

\[ — 4A\sin \left( {2t} \right) — 4\left( {2A\cos \left( {2t} \right)} \right) — 12\left( {A\sin \left( { 2t} \right)} \right) = \sin \left( {2t} \right)\]

Сбор одинаковых терминов дает

\[ — 16A\sin \left( {2t} \right) — 8A\cos \left( {2t} \right) = \sin \left( {2t} \right)\]

Нам нужно выбрать \(A\) так, чтобы мы получили одну и ту же функцию по обе стороны от знака равенства.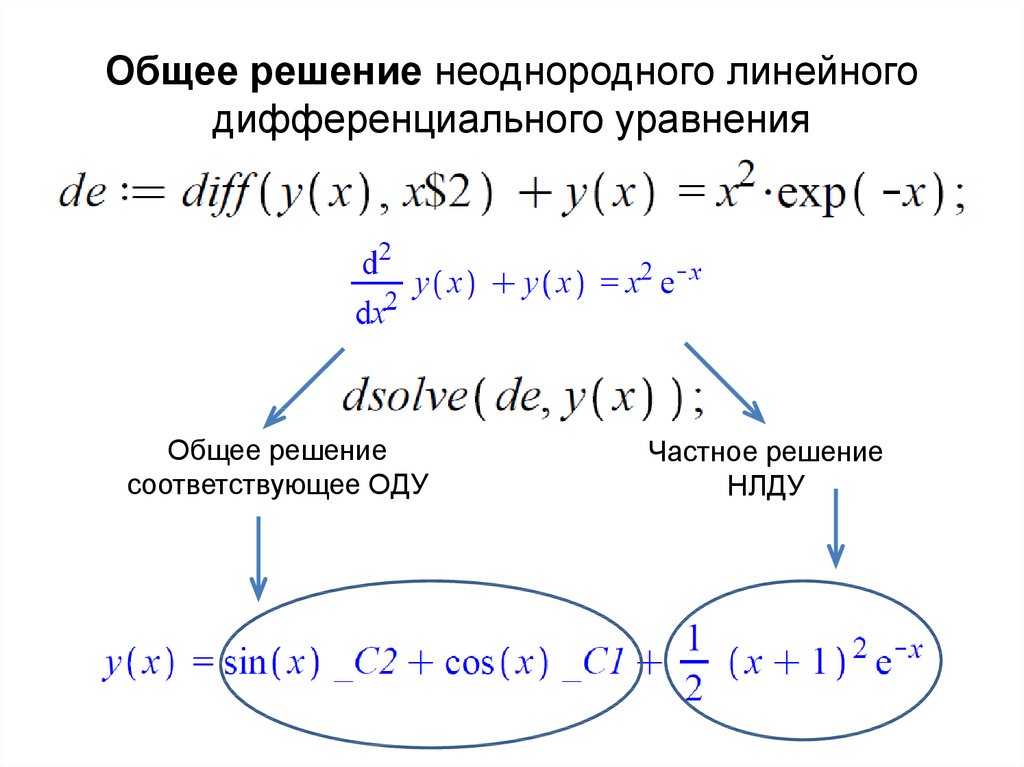 Это означает, что коэффициенты синусов и косинусов должны быть равны. Или

\[\begin{align*}& \cos \left( {2t} \right)\,: & — 8A & = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}A = 0\\ & \ sin \left( {2t} \right)\,:& — 16A & = 1\hspace{0.25in} \Rightarrow \hspace{0.25in}A = — \frac{1}{{16}}\end{align *}\]

Обратите внимание на две вещи. Во-первых, поскольку в правой части нет косинуса, это означает, что коэффициент должен быть равен нулю на этой стороне. Что еще более важно, у нас есть серьезная проблема здесь. Чтобы косинус выпадал, как и должно быть, чтобы догадка удовлетворяла дифференциальному уравнению, нужно положить \(A = 0\), но если \(A = 0\), синус тоже выпадет выходит, и этого не может быть. Аналогичным образом, выбор \(A\) для сохранения синуса также сохранит косинус.

Это означает, что наша первоначальная догадка была неверной. Если мы получаем несколько значений одной и той же константы или не можем найти значение константы, значит, мы ошиблись.

Одним из приятных аспектов этого метода является то, что когда мы ошибаемся, наша работа часто предлагает исправление. В данном случае проблема заключалась в возникшем косинусе. Итак, чтобы противостоять этому, давайте добавим косинус к нашему предположению. Наша новая догадка:

. \[{Y_P}\left( t \right) = A\cos \left( {2t} \right) + B\sin \left( {2t} \right)\]

Подстановка этого в дифференциальное уравнение и сбор подобных членов дает,

\[\begin{align*} — 4A\cos \left( {2t} \right) — 4B\sin \left( {2t} \right) — 4\left( { — 2A\sin \left( {2t} \right) + 2B\cos \left( {2t} \right)} \right) — \\ 12\left( {A\cos \left( {2t} \right) + B\sin \left( {2t} \right)} \right) & = \sin \left( {2t} \right)\\ \left( { — 4A — 8B — 12A} \right)\cos \left( {2t} \right) + \left ( { — 4B + 8A — 12B} \right)\sin \left( {2t} \right) & = \sin \left( {2t} \right)\\ \left( { — 16A — 8B} \right) \cos \left( {2t} \right) + \left( {8A — 16B} \right)\sin \left( {2t} \right) & = \sin \left( {2t} \right)\end{ выровнять*}\]

Теперь установите коэффициенты равными

\[\begin{align*} & \cos \left( {2t} \right)\,: &- 16A — 8B & = 0\\ & \sin \left( {2t} \right)\,: & 8A — 16В & = 1\конец{выравнивание*}\]

Решение этой системы дает нам

\[A = \frac{1}{{40}}\hspace{0,25 дюйма}\hspace{0,25 дюйма}B = — \frac{1}{{20}}\]

Мы нашли константы и на этот раз угадали правильно. Тогда частным решением дифференциального уравнения будет

\[{Y_P}\left( t \right) = \frac{1}{{40}}\cos \left( {2t} \right) — \frac{1}{{20}}\sin \left( {2t} \справа)\]

Обратите внимание, что если бы в последнем примере у нас был косинус вместо синуса, то наше предположение было бы таким же. На самом деле, если появились и синус, и косинус, мы увидим, что то же самое предположение также будет работать.

Давайте рассмотрим третий и последний тип базового \(g(t)\), который у нас может быть. Существуют и другие типы \(g(t)\), которые мы можем иметь, но, как мы увидим, все они вернутся к двум типам, которые мы уже сделали, а также к следующему. 93} — т + 3\]

Показать решение

Еще раз, опять же, мы обычно хотим сначала получить дополнительное решение, но снова мы работаем с одним и тем же однородным дифференциальным уравнением (в конце концов вы поймете, почему мы продолжаем работать с одной и той же однородной задачей), поэтому мы снова просто обратитесь к первому примеру.

В этом примере \(g(t)\) является кубическим полиномом. Для этого нам понадобится следующая догадка для частного решения.

9{\ бета т}} \) \(а\cos\влево({\бета т} \вправо)\) \(A\cos\left({\beta t}\right) + B\sin\left({\beta t}\right)\) \(b\sin\left({\beta t}\right)\) \(A\cos\left({\beta t}\right) + B\sin\left({\beta t}\right)\) \(a\cos\left({\beta t}\right) + b\sin\left({\beta t}\right)\) \(A\cos \left( {\beta t} \right) + B\sin \left({\beta t} \right)\) 9{n — 1}} + \cdots {A_1}t + {A_0}\)

Обратите внимание, что на самом деле существует только три типа функций, приведенных выше. Если вы думаете об этом, функции одиночного косинуса и одиночного синуса — это действительно частные случаи случая, когда присутствуют и синус, и косинус. Кроме того, мы еще не обосновали догадку для случая, когда присутствуют и синус, и косинус. Мы обосновываем это позже.

Теперь нам нужно перейти к более сложным функциям. Более сложные функции получаются путем произведения и суммы основных видов функций. Давайте сначала посмотрим на продукты. 9{4т}}\]

Показать решение

Вы, наверное, устали от вступительного комментария, но опять же, найти дополнительное решение сначала действительно хорошая идея, но опять же, мы уже сделали работу в первом примере, поэтому мы не будем делать это снова здесь. Мы обещаем, что со временем вы поймете, почему мы продолжаем использовать одну и ту же однородную задачу и почему мы считаем хорошей идеей иметь в запасе дополнительное решение. На данный момент все, что мы пытаемся сделать, это укрепить привычку сначала находить дополнительное решение. 9{4t}}\left( {At + B} \right)\]

Однако с этим у нас будут проблемы. Как мы увидим, когда мы подставим наше предположение в дифференциальное уравнение, мы получим из него только два уравнения. {4t}}\left( {ACt + BC} \ Правильно)\] 9{4т}}\]

Этот последний пример иллюстрирует общее правило, которому мы будем следовать, когда произведение содержит экспоненциальную величину. Когда произведение включает экспоненту, мы сначала удаляем экспоненту и записываем предположение для части функции без экспоненты, затем мы вернемся назад и добавим экспоненту без какого-либо ведущего коэффициента.

Рассмотрим еще несколько продуктов. В интересах краткости мы просто запишем догадку для конкретного решения и не будем вдаваться во все подробности нахождения констант. Кроме того, поскольку мы не собираемся приводить реальное дифференциальное уравнение, мы не можем сначала найти дополнительное решение. 9{7t}}\sin \left( {10t} \right)\) Показать решение

Итак, у нас есть экспонента в функции. Помните правило. Мы проигнорируем экспоненту и запишем предположение для \(16\sin \left( {10t} \right)\), а затем вернем экспоненту.

Предположение для синуса:

\[A\cos \left( {10t} \right) + B\sin \left( {10t} \right)\]

Теперь, для фактического предположения для конкретного решения, мы возьмем приведенное выше предположение и прикрепим к нему экспоненту. Это дает 92} + BEt + CE} \right)\sin t\end{массив}\]

Обратите внимание, что везде, где встречается одна из неизвестных констант, она находится в произведении неизвестных констант. Это означает, что если бы мы прошли и использовали это как наше предположение, система уравнений, которую нам нужно было бы решить для неизвестных констант, содержала бы в себе произведения неизвестных. Такие типы систем, как правило, очень трудно решить.

Итак, чтобы избежать этого, мы сделаем то же самое, что и в предыдущем примере. Везде, где мы видим произведение констант, мы будем переименовывать его и называть одной константой. Догадка, которую мы будем использовать для этой функции, будет. 9{ — 2t}}\left( {3 — 5t} \right)\cos \left( {9t} \right)\) Показать решение

Эта заключительная часть состоит из всех трех частей. Во-первых, мы проигнорируем экспоненту и запишем предположение для.

\[ — \left( {3 — 5t} \right)\cos \left( {9t} \right)\]

Знак минус также можно игнорировать. Предположение для этого

\[\left( {At + B} \right)\cos \left( {9{ — 2t}}\left( {Ct + D} \right)\sin \left( {9t} \right)\]

Обратите внимание, что мы поставили экспоненту на оба члена.

Есть несколько общих правил, которые нужно помнить для продуктов.

Если \(g(t)\) содержит экспоненту, игнорируйте ее и запишите предположение для остатка. Затем верните экспоненту обратно без ведущего коэффициента.
Для произведения полиномов и триггерных функций сначала запишите предположение только для полинома и умножьте его на соответствующий косинус. Затем добавьте новое предположение для многочлена с другими коэффициентами и умножьте его на соответствующий синус.

Если вы помните эти два правила, вы не ошибетесь с продуктами. Записывать догадки по продуктам обычно не так уж и сложно. Трудность возникает, когда вам действительно нужно найти константы.

Теперь давайте посмотрим на суммы основных компонентов и/или произведения основных компонентов. Для этого нам понадобится следующий факт.

Факт

Если \(Y_{P1}(t)\) является частным решением для

\[y» + p\left( t \right)y’ + q\left( t \right)y = {g_1}\left( t \right)\]

и если \(Y_{P2}(t)\) является частным решением для

\[y» + p\left( t \right)y’ + q\left( t \right)y = {g_2}\left( t \right)\]

тогда \(Y_{P1}(t)\) + \(Y_{P2}(t)\) является частным решением для

\[y» + p\left( t \right)y’ + q\left( t \right)y = {g_1}\left( t \right) + {g_2}\left( t \right)\]

Этот факт можно использовать как для нахождения частных решений дифференциальных уравнений, в которых есть суммы, так и для записи предположений для функций, в которых есть суммы. {4t}}\]

Давайте рассмотрим еще пару примеров. Как и в случае с продуктами, здесь мы просто будем делать предположения и не будем беспокоиться о фактическом нахождении коэффициентов.

Пример 8 Запишите форму частного решения \[y» + p\left( t \right)y’ + q\left( t \right)y = g\left( t \right)\]

для следующих \(g(t)\).

\(g\left( t \right) = 4\cos \left( {6t} \right) — 9\sin \left( {6t} \right)\) 9{ — 3t}}\cos \left( {6t} \right) — \sin \left( {6t} \right)\)

Показать все решения Скрыть все решения

a \(g\left( t \right) = 4\cos \left( {6t} \right) — 9\sin \left( {6t} \right)\) Показать решение

Этот первый мы уже рассказали вам, как это сделать. Это в таблице основных функций. Однако мы хотели обосновать догадку, которую мы там изложили. Используя факт о суммах функций, у нас возникло бы искушение записать предположение для косинуса и предположение для синуса. Это даст.

\[\ underbrace {A\cos \left( {6t} \right) + B\sin \left( {6t} \right)}_{{\mbox{угадай косинус}}} + \ underbrace {C\ cos \left( {6t} \right) + D\sin \left( {6t} \right)}_{{\mbox{угадай синус}}}\]

Итак, мы получили бы косинус от каждого предположения и синус от каждого предположения. Проблема с этим предположением заключается в том, что мы собираемся решить только два уравнения после подключения к дифференциальному уравнению, и все же у нас есть 4 неизвестных. Мы никогда не сможем решить для каждой из констант.

Чтобы исправить это замечание, мы можем объединить некоторые термины следующим образом.

\[\left( {A + C} \right)\cos \left( {6t} \right) + \left( {B + D} \right)\sin \left( {6t} \right)\]

После этого мы видим, что у нас действительно есть один косинус с коэффициентом и один синус с коэффициентом, поэтому мы можем просто использовать

\[{Y_P}\left( t \right) = A\cos \left( {6t} \right) + B\sin \left( {6t} \right)\]

Общее эмпирическое правило записи предположений для функций, включающих суммы, состоит в том, чтобы всегда объединять одинаковые члены в отдельные члены с одиночными коэффициентами. Это значительно упростит работу по нахождению коэффициентов.

b \(g\left( t \right) = — 2\sin t + \sin \left( {14t} \right) — 5\cos \left( {14t} \right)\) Показать решение

Для этого мы получим два набора синусов и косинусов. Это произойдет, потому что у нас есть два разных аргумента в них. Мы получим один набор для синуса только с \(t\) в качестве аргумента, и мы получим другой набор для синуса и косинуса с 14\(t\) в качестве аргументов. 9{ — 8t}}\]

Заметьте, однако, что если бы мы умножили экспоненту во втором члене, мы бы получили два члена, которые по существу одинаковы и должны быть объединены. Это тот случай, когда догадка для одного термина полностью содержится в догадке для другого термина. Когда это происходит, мы просто отбрасываем догадку, которая уже включена в другой термин.

Итак, догадка здесь на самом деле.

\[{Y_P}\left( t \right) = A{{\bf{e}}^t} + \left( {Bt + C} \right){{\bf{e}}^{ — 8t} }\] 9{ — 3t}}\left( {B\cos \left( {6t} \right) + C\sin \left( {6t} \right)} \right) + D\cos \left( {6t} \right ) + E\sin\left( {6t} \right)\]

Мы можем комбинировать предположения только в том случае, если они идентичны с точностью до константы. Итак, мы не можем объединить первую экспоненту со второй, потому что вторая на самом деле умножается на косинус и синус, и поэтому две экспоненты на самом деле являются разными функциями. Точно так же последний синус и косинус не могут быть объединены с синусом и косинусом в среднем члене, потому что синус и косинус в среднем члене на самом деле умножаются на экспоненту и поэтому различны.

Таким образом, при работе с суммами функций убедитесь, что вы ищете идентичные догадки, которые могут содержаться или не содержаться в других догадках, и комбинируете их. Это упростит вашу работу в дальнейшем.

У нас есть еще одна тема в этом разделе, которую необходимо обсудить. В первых нескольких примерах мы постоянно твердили о пользе дополнительного решения, прежде чем угадывали конкретное решение. Мы никогда не давали никаких оснований для этого другим, которые «доверяют нам». Настало время понять, почему полезно сначала иметь под рукой дополнительное решение. Лучше всего это показать на примере, так что давайте перейдем к нему. 9{6т}}\]

Показать решение

Эта задача кажется слишком простой, чтобы приводить ее в конце раздела. Это особенно верно, учитывая простоту нахождения частного решения для \(g\)(\(t\)) , которые являются просто экспоненциальными функциями. Кроме того, поскольку цель этого примера состоит в том, чтобы проиллюстрировать, почему, как правило, неплохо иметь сначала под рукой дополнительное решение, давайте продолжим и сначала вспомним дополнительное решение. Вот оно, 9{6t}}\end{выравнивание*}\]

Хммм…. Что-то здесь кажется неправильным. Ясно, что экспонента не может быть равна нулю. Итак, что пошло не так? Наконец, нам нужно дополнительное решение. Обратите внимание, что второй член в дополнительном решении (перечисленном выше) является в точности нашим предположением о форме частного решения, а теперь вспомним, что обе части дополнительного решения являются решениями однородного дифференциального уравнения

. \[у» — 4у’ — 12у = 0\] 9{6т}}\]

Итак, что мы узнали из этого последнего примера. Хотя технически нам не нужно дополнительное решение для неопределенных коэффициентов, вы можете проделать большую работу только для того, чтобы в конце выяснить, что вам нужно добавить \(t\) к предположению, потому что оно появилось в комплементарное решение. Этой работы можно избежать, если мы сначала найдем дополнительное решение, сравним наше предположение с дополнительным решением и посмотрим, не появится ли какая-либо часть вашего предположения в дополнительном решении.

Если часть вашего предположения появляется в дополнительном решении, нам нужно изменить эту часть предположения, добавив \(t\) к той части предположения, которая вызывает проблемы. Однако нам нужно быть немного осторожными и убедиться, что мы добавляем \(t\) в правильном месте. Следующий набор примеров покажет вам, как это сделать.

Пример 10 Запишите предположение для частного решения данного дифференциального уравнения. Не найти коэффициенты. 9{10t}} + \left( {Et + F} \right)\cos t + \left( {Gt + H} \right)\sin t\]

Обратите внимание, что если мы умножим экспоненциальный член через круглые скобки, мы получим часть дополнительного решения. Поскольку проблемная часть возникает из первого члена, всего первого члена будут умножены на \(t\). Со вторым и третьим терминами все в порядке.

Правильное предположение о форме конкретного решения в этом случае. 9{ — 2t}}\left( {A\cos \left( {\frac{t}{2}} \right) + B\sin \left({\frac{t}{2}} \right)} \ справа) + \ слева ( {Ct + D} \ справа) \ соз \ слева ( {\ гидроразрыва {t} {2}} \ справа) + \ слева ( {Et + F} \ справа) \ грех \ слева ( { \frac{t}{2}} \right)\]

В этом случае и второе, и третье слагаемые содержат части дополнительного решения. Однако первый член этого не делает, поскольку при умножении и синус, и косинус будут иметь экспоненту с ними, а это не является частью дополнительного решения. Нам нужно беспокоиться о членах, появляющихся в дополнительном решении, только если единственная разница между членом дополнительного решения и конкретным термином предположения заключается в константе перед ними. 9{ — 2t}}\left( {A\cos \left( {\frac{t}{2}} \right) + B\sin \left({\frac{t}{2}} \right)} \ справа) + \ слева ( {Ct + D} \ справа) \ соз \ слева ( {\ гидроразрыва {t} {2}} \ справа) + \ слева ( {Et + F} \ справа) \ грех \ слева ( { \frac{t}{2}} \right)\]

На этот раз, однако, первый термин вызывает проблемы, а не второй или третий. На самом деле первое слагаемое — это в точности дополнительное решение, поэтому для него потребуется \(t\). Напомним, что у нас будет проблема с членом в нашем предположении только в том случае, если оно отличается от дополнительного решения только на константу. Во втором и третьем членах в нашем предположении нет экспоненты, и поэтому они не отличаются от дополнительного решения только на константу. 9{ — 4t}}\]

При умножении ни один из членов не находится в дополнительном решении, так что все будет в порядке.

Как показал этот последний набор примеров, мы действительно должны иметь на руках дополнительное решение, прежде чем даже записывать первое предположение для конкретного решения. Делая это, мы можем сравнить наше предположение с дополнительным решением, и если какой-либо из терминов из вашего конкретного решения появится, мы будем знать, что у нас будут проблемы. Как только проблема определена, мы можем добавить \(t\) к термину(ам) проблемы и сравнить наше новое предположение с дополнительным решением. Если проблем нет, мы можем перейти к проблеме, если есть проблемы, добавить еще одну \(t\) и снова сравнить.

Можете ли вы увидеть общее правило относительно того, когда потребуется \(t\) и когда потребуется t ² для дифференциальных уравнений второго порядка?

Общие и частные решения дифференциального уравнения

Автор Swapnil Nanda
Последнее изменение 19-07-2022

Автор Свапнил Нанда
Последнее изменение 19-07-2022

Общие и частные решения дифференциального уравнения: Функции дифференциального уравнения часто описывают физические величины, тогда как производные выражают скорость изменения физических величин. Дифференциальное уравнение – это связь, которая существует между функцией и ее производными. Эти уравнения появляются в широком диапазоне приложений, включая физику, химию, биологию, антропологию, геологию и экономику. В результате глубокое понимание дифференциальных уравнений стало критически важным во всех текущих научных исследованиях.

В этой статье мы узнаем об общем решении и методе нахождения частного решения из общего решения дифференциального уравнения. Мы также научимся решать начальные задачи и несколько способов найти решение дифференциальных уравнений первого порядка и первой степени.

Решение дифференциального уравнения

Решение дифференциального уравнения — это связь, которая удовлетворяет дифференциальному уравнению между участвующими переменными. Когда такое отношение и полученные из него производные заменяются в дифференциальном уравнении, левая и правая части равны. 92}}} + у = 0\)

Это показывает, что \(y = A\,\cos\,x + B\,\sin\,x\) удовлетворяет дифференциальному уравнению \((i)\), указывающему, что это решение дифференциального уравнения, представленного в \((я)\).

Просто проверить, что \(y = 3\,\cos \,x + 2\,\sin \,x,\,y = A\,\cos \,x,\,y = B\,\ sin \,x\) и другие решения также решения дифференциального уравнения, заданного в \((i)\). Мы обнаружили, что решение \(y = 3\,\cos \,x + 2\,\sin \,x\) не имеет случайных констант, тогда как решения \(y = A\,\cos \,x,\ ,y = B\,\sin\,x\) имеют только один. Решение \(y = A\,\cos \,x + B\,\sin \,x\) содержит две произвольные константы, поэтому оно известно как общее решение \((i)\), тогда как все остальные решения являются частными решениями. 93} + c\), где \(c\) — произвольная константа, как показано на рисунке ниже.

Частное решение дифференциального уравнения

Частное решение дифференциального уравнения — это решение, полученное путем присвоения заданных значений произвольным константам в общем решении.
Критерии для вычисления значений произвольных констант могут быть даны нам как задача с начальными значениями или как граничные условия.

Особое решение

Сингулярное решение дифференциального уравнения также является частным решением, но оно не может быть получено из общего решения путем определения значений произвольных констант.

Проблемы с начальным значением

Мы видели, что дифференциальное уравнение первого порядка представляет семейство кривых с одним параметром, дифференциальное уравнение второго порядка представляет семейство кривых с двумя параметрами и так далее. Поэтому, если мы хотим указать конкретного члена такого семейства кривых, то в дополнение к дифференциальному уравнению нам потребуются некоторые другие условия для задания параметра (параметров). 9\простое}(0) =\, – 2\)

Из вышеизложенного следует, что для задания конкретного члена семейства кривых нам требуется

дифференциальное уравнение, представляющее данное семейство кривых
значения зависимой переменной
ее производные различного порядка в некоторой точке области определения.

Эти значения обычно задаются только в одной точке области определения независимой переменной и обычно называются начальными значениями или начальными условиями.

Решение дифференциальных уравнений первого порядка и первой степени

Дифференциальное уравнение первого порядка и первой степени можно записать как

\(f\left( {x,\,y} \right)dx + g\left( {x,\,y} \right)dy = 0\)

\( \Стрелка вправо \frac{{dy}}{{dx}} = \frac{{f(x,\,y)}}{{g(x,\,y)}} = \phi (x, \,у)\)

, где \(f(x,\,y)\) и \(g(x,\,y)\) являются функциями \(x\) и \(y\).

Решение таких уравнений не всегда выполнимо. Только когда такое дифференциальное уравнение подходит под категорию некоторых стандартных форм, его можно решить. Обсудим некоторые стандартные формы и методы получения их решений.

Дифференциальное уравнение типа \(\frac{{dy}}{{dx}} = f\left( x \right)\)

Рассмотрим

\(\frac{{dy}}{{dx}} = f(x)\)

\(\стрелка влево dy = f(x)dx\)

Интегрируя обе части, получаем

\(\int d y = \int f (x)dx + C\)

\( \Стрелка вправо y = \int f (x)dx + C\)

Это общее решение дифференциального уравнения.

Дифференциальное уравнение типа \(\frac{{dy}}{{dx}} = f(y)\)

Рассмотрим

\(\frac{{dy}}{{dx}} = f(y)\)

\( \Rightarrow \frac{{dx}}{{dy}} = \frac{1}{{f(y)}}\), при условии \(f(y) \ne 0\)

\( \Стрелка вправо dx = \frac{1}{{f(y)}}dy\)

Объединяя обе стороны, получаем

\(\ int d x = \ int {\ frac {1} {{f (y)}}} dy + C \)

\( \Rightarrow x = \int {\frac{1}{{f(y)}}} dy + C\), что дает общее решение дифференциального уравнения.

Решенные примеры – общее и частное решения дифференциального уравнения 92}} \right)y = 0\)

Следовательно, данная функция является решением данного дифференциального уравнения.

Q.4. Убедитесь, что функция, заданная формулой \(y = \sin\,x – \cos \,x,\,x \in R\), является решением задачи с начальным значением \(\frac{{dy}}{{dx }} = \sin \,x + \cos \,x,\,y(0) =\, — 1\).
Ответ : Дано, \(y = \sin\,x – \cos\,x,\,x \in R\)
\(\Rightarrow \frac{{ay}}{{dx}} = \ cos \,x + \sin \,x\), которое является заданным дифференциальным уравнением.
Таким образом, \(y = \sin \,x – \cos \,x\) удовлетворяет заданному дифференциальному уравнению и, следовательно, является решением. Также при \(x = 0,\,y = \sin\,0 – \cos \,0 = 0 – 1 = – 1\) т.е. \(y(0) =\, – 1\). 92}}}} dy\)
\( \Rightarrow x = \frac{1}{{2y}} + C\, \ldots \ldots (i)\)
Дано, что \(y(1) = 1\) т.е. \(y = 1\), когда \(x = 1\).
Подставляя \(x = 1\) и \(y = 1\) в \((i)\), мы получаем
\(1 = \frac{1}{2} + C \Rightarrow C = \frac{ 1}{2}\)
Подставляя \(C = 12\) в \((i)\), мы получаем
\(x = \frac{1}{{2y}} + \frac{1}{2 }\)
\( \Rightarrow y = \frac{1}{{2x – 1}}\), что является искомой кривой решения.

Резюме

Решения дифференциальных уравнений в основном бывают двух типов: общее решение и частное решение. Доступное решение дифференциального уравнения содержит столько произвольных констант, сколько порядка дифференциального уравнения. Частное решение дифференциального уравнения достигается путем присвоения определенных значений произвольным константам в общем решении. Метод решения этих произвольных констант включает начальные задачи, и мы изучили технику нахождения общего решения дифференциальных уравнений первого порядка и первой степени с помощью интегрирования.

Часто задаваемые вопросы (FAQ)

Q.1. Что такое общее и частное решение дифференциального уравнения?
Ответ: Общее решение дифференциального уравнения состоит из такого количества произвольных констант, которое соответствует порядку дифференциального уравнения.
Частное решение дифференциального уравнения — это решение, вычисленное путем присвоения заданных значений произвольным константам в общем решении.

Q.2. Как поля наклона связаны с общими и частными решениями дифференциальных уравнений?
Ответ: Визуальное изображение дифференциального уравнения вида \(\frac{{dy}}{{dx}} = f(x,\,y)\) называется полем наклона. Существует крошечный отрезок линии, наклон которого равен значению \(f\) в каждой точке выборки \(\left({x,\,y} \right)\).

Q.3. В чем разница между общим и частным решением дифференциального уравнения?
Ответ: Частное решение — это всего лишь решение, которое решает все ОДУ; общее решение, с другой стороны, является полным решением ОДУ, которое представляет собой сумму дополнительных и частных решений.

Q.4. Сколько решений имеет дифференциальное уравнение?
Ответ: Дифференциальное уравнение, как мы видели, часто имеет неограниченное число решений. Общее решение — это имя, данное такому решению. Существует только одно решение связанной проблемы с начальными значениями. Частным решением является такое решение, в котором не осталось неизвестных констант.

Q.5. В чем смысл решения дифференциального уравнения?
Ответ: Функция \(y = f\left( x \right)\), которая удовлетворяет дифференциальному уравнению при подстановке вместе со своими производными, называется решением дифференциального уравнения.

Узнайте все о дифференциальных уравнениях

Мы надеемся, что эта подробная статья об общих и частных решениях дифференциального уравнения была вам полезна. Если у вас есть какие-либо сомнения, сообщите нам о них в разделе комментариев ниже. Наша команда постарается решить ваши вопросы в кратчайшие сроки.

Сокращение глупых ошибок; Пройдите бесплатные пробные тесты, связанные с дифференциальным уравнением

17Вычисление дифференциальных уравнений — Частные решения

Когда мы решаем дифференциальные уравнения, мы обычно используем интегрирование. Как вы помните из интеграции, если у вас нет начальных условий, вы получите общую неизвестную константу в своем ответе в качестве заполнителя, указывающую, что на самом деле существует бесконечное количество решений. То же понятие возникает при решении дифференциальных уравнений.

Краткий ответ — — Терминология относится к тому, есть ли в нашем окончательном ответе неизвестная константа. Для общего решения неизвестная константа ЯВЛЯЕТСЯ частью решения, указывающей на бесконечное число решений. В частном решении нет неизвестной константы, и решение, которое мы имеем, является единственным решением.

Подробный ответ — — Когда вы решаете дифференциальное уравнение, вы используете интегрирование, которое вводит неизвестную константу.
В общем решении остается неизвестная константа, и у вас недостаточно информации, чтобы определить, что это за константа. Следовательно, у вас есть бесконечное количество решений.
В частном решении вы начинаете с поиска общего решения, но затем вам даются начальные условия, которые вы используете для определения значения константы. Эти начальные условия на самом деле являются точками, через которые проходит решение дифференциального уравнения. В конце концов, у вас есть только одно решение без каких-либо неизвестных констант.

общее решение		частное решение
бесконечное число решений		только одно решение
содержит неизвестные константы		НЕ содержит неизвестных констант
не задано (или слишком мало) начальных условий		заданы начальные условия; используется для решения констант

Чтобы найти общее решение , просто решите дифференциальное уравнение и оставьте все неизвестные константы в своем окончательном ответе.
Чтобы найти частное решение , сначала найдите общее решение, затем подставьте начальные условия и найдите константы.

Примечания
1. При определении частного решения вам будет дано такое же количество начальных условий, как и порядок дифференциального уравнения. В зависимости от того, как заданы начальные условия, вам может потребоваться останавливаться после каждого интегрирования и решать для отдельных констант, или вам может потребоваться подождать, пока вы не закончите полностью, и решить для всех констант сразу. Вы почувствуете это, когда будете решать практические задачи.
2. Для общего решения, если не заданы начальные условия или задано меньше порядка дифференциального уравнения, мы не можем определить все неизвестные константы, поскольку каждое интегрирование вводит другую константу.
3. Когда вы впервые изучали интеграцию, вы, вероятно, столкнулись с проблемами начального значения. На самом деле это были дифференциальные уравнения, где вас просили найти конкретное решение.

Практика

93 \) и найти значение \(с\), при котором решение удовлетворяет начальному условию \(у(2) = 6\).

Решение

MIP4U — 3656 Видео

Видео по MIP4U

Войдите, чтобы оценить эту проблему, и чтобы увидеть, что он актете.

Убедитесь, что \( y=c_1 \sin(2x) + c_2 \cos(2x) + 1 \) является общим решением \( y» + 4y = 8 \) и найдите \(c_1\) и \(c_2\), если \(y(0) = 5\) и \(y'(0) = -1\).

Постановка задачи

Убедитесь, что \( y=c_1 \sin(2x) + c_2 \cos(2x) + 1 \) является общим решением \( y» + 4y = 8 \) и найдите \( c_1\) и \(c_2\), если \(y(0) = 5\) и \(y'(0) = -1\).

Решение

blackpenredpen — 3657 решение для видео

видео от blackpenredpen

Войдите, чтобы оценить текущий рейтинг этой проблемы и оценить ее. x — 3x — 3 \) является общим решением \( dy/dx = 3x + y \) и найдите \(C\), если \(y(0) = — 1\). 9x — 3x — 3 \) является общим решением \(dy/dx = 3x + y \) и решить для \(C\), если \(y(0) = -1\).

Решение

Blackpenredpen — 3658 Видеореал

Видео Blackpenredpen

Log In Screat Thating Thatule Tract.

Решение

MIP4U

Видео по MIP4U

Войдите, чтобы оценить эту проблему, и чтобы увидеть, что он актете.

9{6t} \), где \(а\) и \(Ь\) — константы.
No related posts.
Навигация по записям
Предыдущая статьяЗадание 1 по математике: 1 задание ЕГЭ по математике профильного уровня 2023: теория и практика
Следующая статьяГрафик 3 в степени х 1: Mathway | Популярные задачи
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт
Найти:
Рубрики
© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»
Карта сайта

Вариант № 21

Сообщество Экспонента

заказ решений на аукционе за минимальную цену с максимальным качеством

Объединение сервисов в одну систему

Принцип работы

За счет чего будет развиваться сервис

Преимущества для заказчиков

Преимущества для решающих задания

Преимущества для владельца сервиса

Что необходимо для создания сервиса

Частное решение дифференциального уравнения

Что такое частное решение дифференциального уравнения?

Как найти частное решение дифференциального уравнения?

Частное решение против общего решения дифференциального уравнения

Примеры частного решения дифференциального уравнения

Практические вопросы по частному решению дифференциального уравнения

Часто задаваемые вопросы о частном решении дифференциального уравнения

Что такое частное решение дифференциального уравнения?

В чем разница между общим решением и частным решением дифференциального уравнения?

Как определить конкретное решение дифференциального уравнения?

Какая польза от частного решения дифференциального уравнения?

Общие и частные решения

Найти общие и частные решения с использованием разделения переменных Вопрос дня Карточки Учитесь по концепции

Все ресурсы Calculus AB

Дифференциальные уравнения — Неопределенные коэффициенты

Раздел 3-9: Неопределенные коэффициенты

Факт

Общие и частные решения дифференциального уравнения

Решение дифференциального уравнения

Частное решение дифференциального уравнения

Особое решение

Проблемы с начальным значением

Решение дифференциальных уравнений первого порядка и первой степени

Дифференциальное уравнение типа \(\frac{{dy}}{{dx}} = f\left( x \right)\)

Решенные примеры – общее и частное решения дифференциального уравнения 92}} \right)y = 0\)

Резюме

Часто задаваемые вопросы (FAQ)

17Вычисление дифференциальных уравнений — Частные решения

Добавить комментарий Отменить ответ