График арксин: Элементарная математика

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )
17	Найти точное значение	sec(30 град. )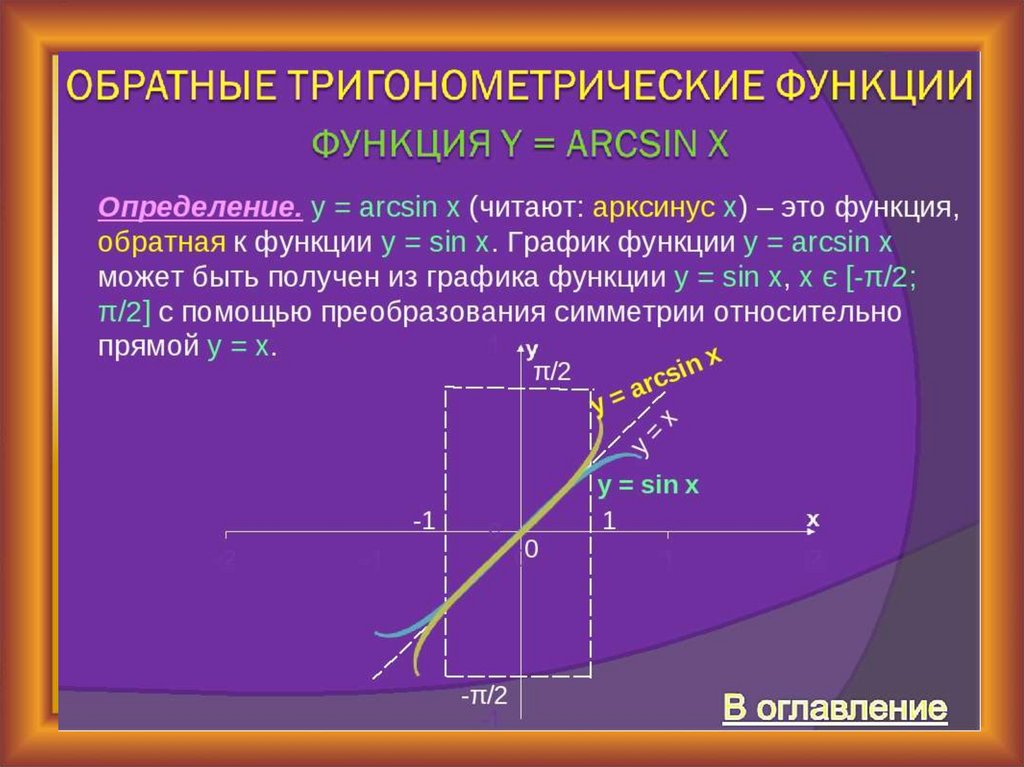
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )
23	Найти точное значение	arctan(- квадратный корень из 3)
24	Найти точное значение	csc(60 град. )
25	Найти точное значение	sec(45 град. )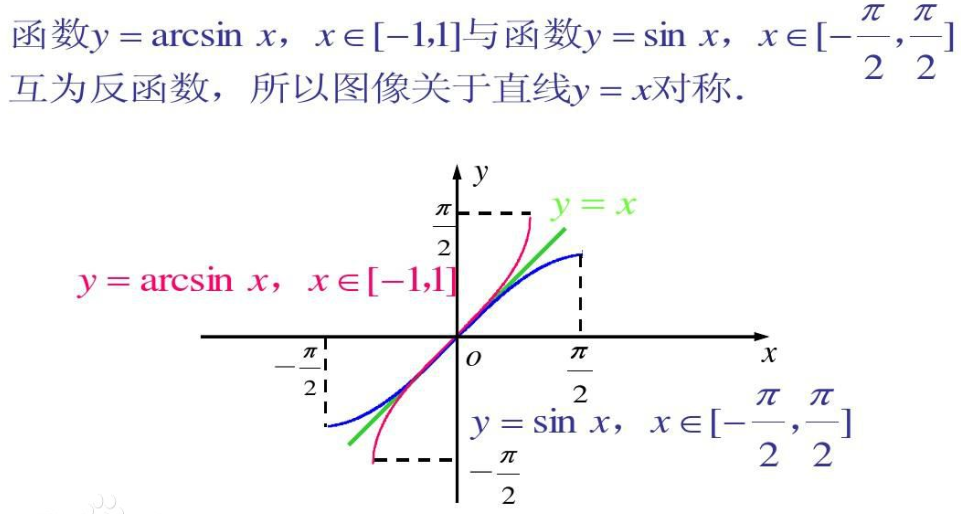
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )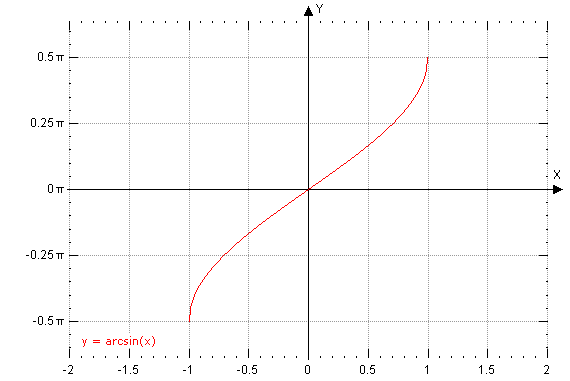
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )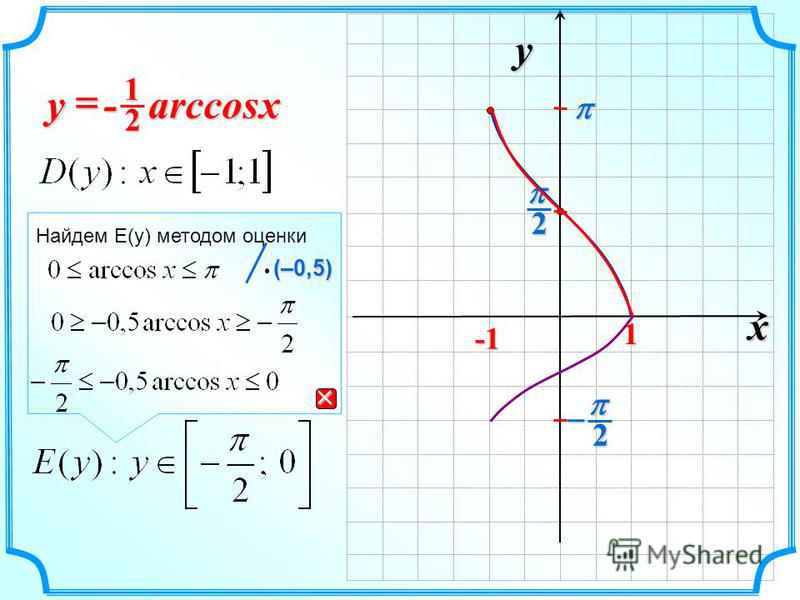
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень из 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень из 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень из 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень из 2)/2)
100	Преобразовать из градусов в радианы	88 град.

Арксинус числа a. Функция y = arcsin x, её свойства и график. Выражения с арксинусом

12+

6 месяцев назад

Математика от Баканчиковой300 подписчиков

Тригонометрия 8-11 класс. Что такое арксинус числа? Как найти арксинус любого числа? Как построить график функции y = arcsin x? Какие свойства есть у функции y = arcsin x? Сегодня мы ответим на эти вопросы. Если Вы не видели наши предыдущие уроки по теме: «Функция y=sin x, её график и свойства» и «Обратная функция, её свойства и график», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. Мы покажем Вам, как получается график функции y = arcsin x, и почему область определения функции y = arcsin x ограничена отрезком [-1; 1], а область значений – отрезком [-π/2; π/2]. Обратим особое внимание на то, что арксинус – это угол поворота, а не просто число. Дадим Вам два определения арксинуса числа а. Напомним Вам, какую задачу решает график функции y = sin x, и поясним, какую задачу решает график функции y = arcsin x. Особо отметим две характерные ошибки, которые допускают ученики при вычислении арксинуса. На примере 7 упражнений покажем Вам нюансы вычисления арксинуса числа и выражений с арксинусами.

Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео. 00:00 Начало видео. 00:39 Что нужно вспомнить? 01:38 Как получается график функции y = arcsin x? 02:02 Какую задачу решает график функции y = sin x? 03:49 Строим график обратного соответствия функции y = sin x. 05:39 Будет ли функцией обратное соответствие функции y = sin x? 09:53 На каком отрезке у функции y = sin x будет обратная функция? 10:28 Какую задачу решает график функции y = arcsin x? 11:57 График функции y = arcsin x. 12:44 Область определения функции y = arcsin x. 13:03 Область значений функции y = arcsin x. 13:39 Так что же такое арксинус? 16:00 Определение арксинуса и примеры упражнений. 17:25 Доказать, что а) arcsin ½ = π/6. 18:09 Доказать, что б) arcsin (-√2/2) = -π/4. 18:47 Арксинус на единичной окружности. 21:09 Доказать, что в) arcsin(- ½) = -30°. 22:21 Второе определение арксинуса. 23:00 Доказать, что г) arcsin 0,809 = 54°. 25:18 Характерные ошибки при вычислении арксинуса. 28:49 Вычисление выражений с арксинусом. 32:15 На следующем уроке … Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео: Единицы измерения углов. Часть 2. Радиан. Тригонометрия 8-11 класс. https://rutube.ru/video/3a3a7b21273aaaff03296fdc700df9b5/ Обратная функция, её свойства и график. Как найти функции обратные данным и построить график. Алгебра 8-11 класс. https://youtu.be/Gr53TGYtBO8 Функция y = sin x, её график и свойства. Тригонометрия 8-11 класс. https://rutube.ru/video/a0f98530ee52e1303236e975c6a826f8/ Функция y = cos x, её график и свойства. Тригонометрия 8-11 класс. https://rutube.ru/video/79a7a2ce60eefcab7aea2ee136a00bb2/ Функция y = tg x, её график и свойства. Тригонометрия 8-11 класс. https://rutube.ru/video/054662ce7a2196ad6a2d199f1e895585/ Функция y = sin x, график функции и способы задания функции. Тригонометрия 8-11 класс. https://rutube.ru/video/f067b3cda83df006306963e40f30b5ab/ Определение синуса, косинуса, тангенса и котангенса на единичной окружности.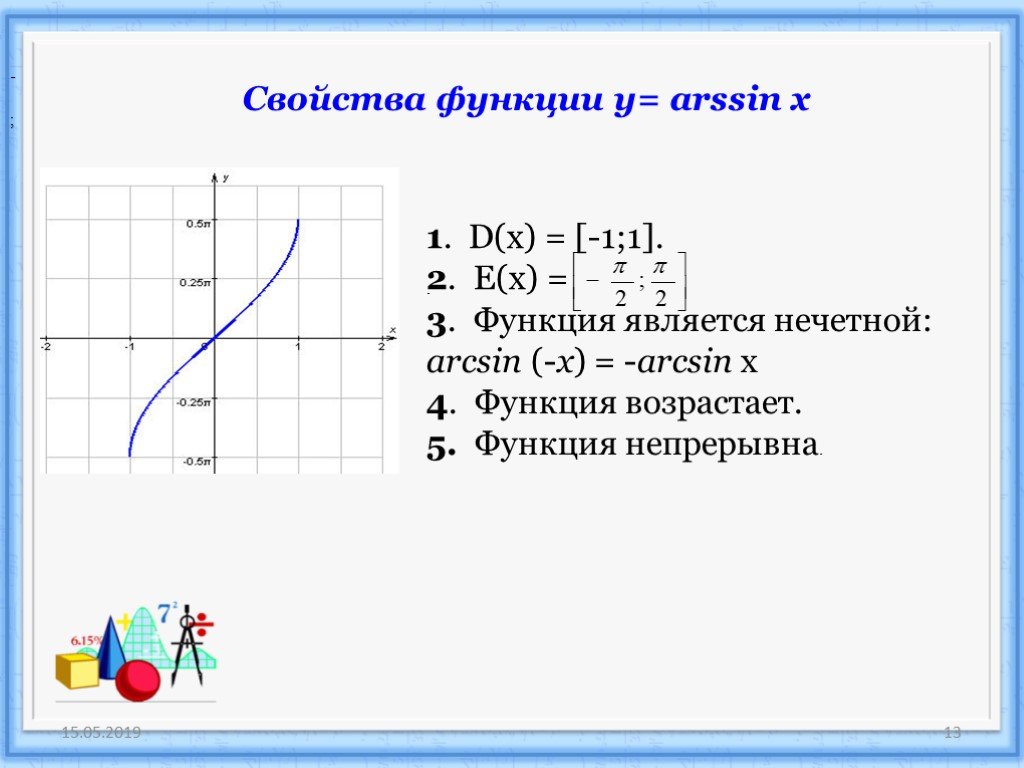 Шпаргалка по тригонометрии. Алгебра 10 класс. https://rutube.ru/video/4a839b2f5c0a7656b8b41b6e5e67ddc4/ Определение тангенса и котангенса на единичной окружности. Алгебра 10 класс. https://rutube.ru/video/f2494d81bfa2dcc2e9562060c1f5690f/ Графический способ задания функции. График функции. Определение. https://youtu.be/9v-Geo6pOoo Все уроки по теме «Функция и её свойства» можно найти в плейлисте: https://rutube.ru/plst/57182 #обратныетригонометрическиефункции #арксинусчисла #графикарксинуса #графикarcsin #областьопределенияarcsin #областьзначенийarcsin #найтиarcsin #вычислитьarcsin #определениеарксинуса #значениевыраженияarcsin #арксинусэто #алгебратригонометрическиефункции #тригонометрическиефункцииалгебра10 #МатематикаОтБаканчиковой тригонометрия, алгебра тригонометрические функции, тригонометрические функции алгебра 10, обратные тригонометрические функции, арксинус числа, график арксинуса, график arcsin, область определения arcsin, область значений arcsin, найти arcsin, вычислить arcsin, определение арксинуса, значение выражения arcsin, арксинус это

Arcsin — Формула, График, Домен и Диапазон, Примеры

Arcsin — одна из шести основных обратных тригонометрических функций. Это обратная тригонометрическая функция синуса. Арксинус также называется обратным синусом и математически записывается как arcsin x или sin ^-1 x (читается как синус, обратный x). Важно отметить, что sin ^-1 x не то же самое, что (sin x) ^-1 , то есть sin ^-1 x не является обратной функцией sin x. В обратной тригонометрии у нас есть шесть обратных тригонометрических функций: arccos, arcsin, arctan, arcsec, arccsc и arccot.

Arcsin x определяет угол, соответствующий отношению перпендикуляра к гипотенузе прямоугольного треугольника. В этой статье мы рассмотрим понятие арксинуса и выведем его формулу. Мы также обсудим область значений и диапазон значений arcsin x и, следовательно, построим их график. Мы также решим различные примеры, используя тождества arcsin x, чтобы лучше понять его приложения и концепцию.

1.	Что такое арксинус?
2.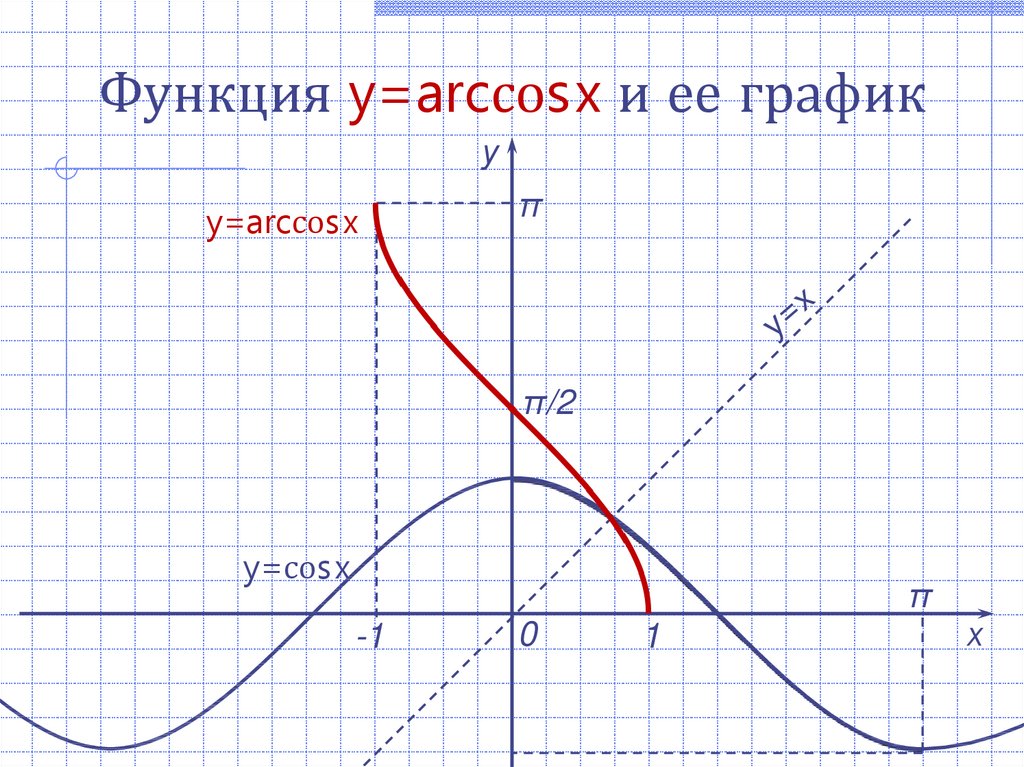	Arcsin x Формула
3.	Диаграмма арксинуса
4.	Домен и диапазон Arcsin
5.	Идентификационные данные Arcsin
6.	Часто задаваемые вопросы по Arcsin

Что такое арксинус?

Арксинус является обратной тригонометрической функцией синуса. Он дает меру угла для соответствующего значения функции синуса. Мы обозначаем функцию арксинуса для действительного числа x как arcsin x (читается как арксинус x) или sin ^-1 x (читается как инверсия синуса x), которая является обратной величиной sin y. Если sin y = x, то мы можем записать это как y = arcsin x. Arcsin — одна из шести важных обратных тригонометрических функций. Шесть обратных тригонометрических функций:

• Arcsin: функция, обратная синусу, обозначается arcsin x или sin ^-1 x
• Arccos: функция, обратная косинусу, обозначается arccos x или cos ^-1 x
• Arctan: функция, обратная тангенсу, обозначается arctan x или tan ^-1 х
• Arccot: Функция, обратная котангенсу, обозначается arccot ​​x или cot ^-1 x
• Arcsec: функция, обратная секансу, обозначается arcsec x или sec ^-1 x
• Arccsc: Функция, обратная косекансу, обозначается arccsc x или csc ^-1 x

Функция arcsin помогает нам найти меру угла, соответствующую значению функции синуса.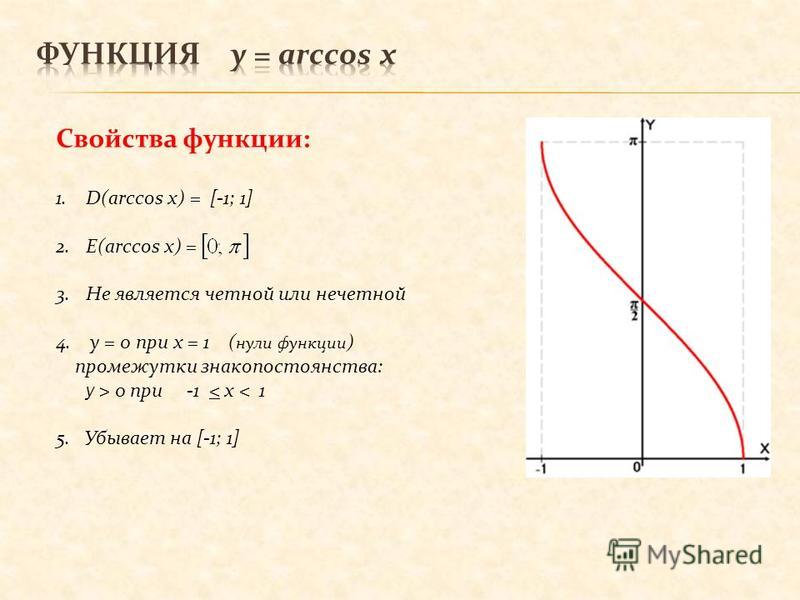 Давайте посмотрим на несколько примеров, чтобы понять его функционирование. Мы знаем значения функции синуса для некоторых конкретных углов, используя тригонометрическую таблицу.

• Если sin 0 = 0, то arcsin 0 = 0
• sin π/6 = 1/2 подразумевает arcsin (1/2) = π/6
• sin π/3 = √3/2 подразумевает arcsin (√3/2) = π/3
• Если sin π/2 = 1, то arcsin (1) = π/2

Arcsin x Формула

Мы можем использовать формулу арксинуса, когда задано значение синуса угла, и мы хотим вычислить точную величину угла. Рассмотрим прямоугольный треугольник. Мы знаем, что sin θ = Противоположная сторона / Гипотенуза. Поскольку arcsin является обратной функцией синуса, поэтому мы имеем θ = arcsin (противоположная сторона / гипотенуза). Следовательно, формула для arcsin x такова:

θ = арксинус (противоположная сторона / гипотенуза)

Мы также можем использовать закон синусов для получения формулы арксинуса. Для треугольника ABC со сторонами AB = c, BC = a и AC = b имеем sin A/a = sin B/b = sin C/c. Тогда, взяв два за раз, мы имеем

sin A / a = sin B / b

⇒ sin A = (a/b) sin B

⇒ A = arcsin [(a/b) sin B]

Точно так же мы можем найти величину углов B и C, используя тот же метод.

График дугового синуса

Теперь, когда мы знаем формулу арксинуса, построим график арксинуса x, используя некоторые его точки. Как обсуждалось функционирование arcsin, мы знаем значения функции синуса для некоторых конкретных углов и, используя тригонометрические формулы, имеем

• sin 0 = 0 подразумевает arcsin 0 = 0 → (0, 0)
• sin π/6 = 1/2 подразумевает arcsin (1/2) = π/6 → (1/2, π/6)
• sin π/3 = √3/2 подразумевает arcsin (√3/2) = π/3 → (√3/2, π/3)
• sin π/2 = 1 подразумевает arcsin (1) = π/2 → (1, π/2)
• sin (-π/4) = -1/√2 подразумевает arcsin (-1/√2) = -π/4 → (-1/√2, -π/4)
• sin (-π/6) = -1/2 подразумевает arcsin (-1/2) = -π/6 → (-1/2, -π/6)

Теперь, нанеся указанные выше точки на график, мы получим приведенный ниже график арксинуса:

Домен и диапазон Arcsin

Поскольку мы знаем, что две функции являются обратными друг другу, если они взаимно однозначны, а область определения и область определения функции становятся соответственно областью определения и областью определения обратной функции.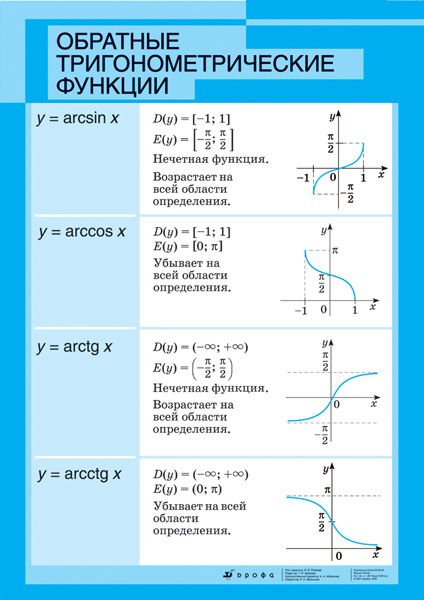 Мы знаем, что областью определения sin x являются все действительные числа, а его диапазон равен [-1, 1]. Но с этой областью sin x не является биективным. Итак, мы ограничиваем область определения синусоидальной функции до [–π/2, π/2], тогда sin x становится биективным с областью определения [–π/2, π/2] и диапазоном [-1, 1]. Когда область определения sin x ограничена [–3π/2, –π/2], [–π/2, π/2] или [π/2, 3π/2] и т. д., и диапазон [ -1, 1], то sin x биективен и, следовательно, соответственно мы можем определить arcsin с областью определения [-1, 1] и диапазоном [–3π/2, –π/2], [–π/2, π/2 ] или [π/2, 3π/2] и так далее.

Мы получаем разные ветви функции arcsin для каждого интервала. Ветвь arcsin, соответствующая домену [-1, 1] и диапазону [–π/2, π/2], называется ветвью главного значения. Итак, arcsin определяется как arcsin: [-1, 1] → [–π/2, π/2]. Следовательно, домен и диапазон arcsin:

• Домен Arcsin: [-1, 1]
• Диапазон арксинуса: [–π/2, π/2]

Идентификация Arcsin

Теперь мы обсудим некоторые важные свойства и тождества функции арксинуса, которые помогают нам упростить и решить различные задачи тригонометрии.

• sin (arcsin x) = x, если x находится в [-1, 1]
• arcsin (sin x) = x, если x находится в [–π/2, π/2]
• arcsin (1/x) = arccsc x, если x ≤ -1 или x ≥ 1
• arcsin (–x) = — arcsin x, если x ∈ [-1, 1]
• arcsin x + arccos x = π/2, если x ∈ [-1, 1]
• 2 arcsin x = arcsin (2x √(1 — x ² )), если -1/√2 ≤ x ≤ 1/√2
• 2 arccos x = arcsin (2x √(1 — x ² )), если 1/√2 ≤ x ≤ 1
• arcsin x + arcsin y = arcsin [x√(1 — y ² ) + у√(1 — х ² )]

Важные примечания по арксинусу

• Арксинус является функцией, обратной функции синуса.
• Домен и диапазон arcsin равны [-1, 1] и [–π/2, π/2] соответственно.
• Производная арксинуса равна 1/√(1 — x²).
• Интеграл от arcsin равен ∫arcsin x dx = x sin ^-1 x + √(1 — x ² ) + C

☛ Похожие темы:

• Sin 1 в градусах
• Обратные тригонометрические соотношения
• Обратные триггерные производные

 

Арксинус Примеры

1. Пример 1: Докажите формулу арксинуса 2 arcsin x = arcsin (2x √(1 — x ² )), если -1/√2 ≤ x ≤ 1/√2.

   Решение: Предположим, что arcsin x = y, тогда мы имеем sin y = x. Рассмотрим RHS

   RHS = arcsin (2x √(1 — x ² ))

   = arcsin [2 sin y √(1 — sin ² y)]

   = arcsin [2 sin y √(cos ² y)] — [Используя тригонометрическую формулу sin ² A + cos ² A = 1, откуда следует cos ² А = 1 — sin ² A]

   = arcsin [2 sin y cos y]

   = arcsin [sin2y] — [используя тригонометрическую формулу sin2A = 2 sinA cosA]

   = 2y

   = 2 арксинус х — [Потому что arcsin x = y]

   Ответ: Следовательно, мы доказали, что 2 arcsin x = arcsin (2x √(1 — x ² )), если -1/√2 ≤ x ≤ 1/√2

2. Пример 2: Найдите значение arcsin (sin 3π/5).

   Решение: Мы знаем, что arcsin (sin x) = x, поэтому мы имеем arcsin (sin 3π/5) = 3π/5, но 3π/5 ∉ [–π/2, π/2]. Итак, нам нужно найти значение, эквивалентное sin 3π/5, такое, что угол лежит в интервале [–π/2, π/2]. Используя тригонометрическую формулу sin x = sin (π — x), мы имеем

   sin (3π/5) = sin (π — 3π/5)

   = sin (5π/5 — 3π/5)

   = sin (2π/5)

   Также обратите внимание, что 2π/5 ∈ [–π/2, π/2].

   Итак, у нас есть arcsin (sin 3π/5) = 2π/5

   Ответ: arcsin (sin 3π/5) = 2π/5

3. Пример 3: Докажите, что arcsin (3/5) – arcsin (8/17) = arccos (84/85)

   Решение: Предположим, что A = arcsin (3/5) и B = arcsin (8/ 17), тогда мы имеем sin A = 3/5 и sin B = 8/17. Затем, используя тригонометрическую формулу, sin ² x + cos ² x = 1, имеем

   cos A = √ (1 — sin ² A)

   = √ (1 — (3/5) ² )

   = √(1 — 25 сентября )

   = √(16/25)

   = 4/5

   cos B = √ (1 — sin ² B)

   = √ (1 — (8/17) ^{2 9000 6 )}

   = √(1 — 64/289)

   = √(225/289)

   = 15/17

   Теперь, используя формулу cos (A — B) = cos A cos B + sin A sin B

   = 4 /5 × 15/17 + 3/5 × 8/17

   = 60/85 + 24/85

   = 84/85

   ⇒ A — B = arccos (84/85)

   ⇒ arcsin (3/5) – arcsin (8/17) = arccos (84/85) — [A = arcsin ( 3/5) и B = arcsin (8/17)]

   Ответ: Таким образом, мы доказали, что arcsin (3/5) – arcsin (8/17) = arccos (84/85)

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по Arcsin Questions

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по Arcsin

Что такое арксинус в тригонометрии?

Арксинус является обратной тригонометрической функцией синуса. Мы обозначаем функцию арксинуса для действительного числа x как arcsin x (читается как арксинус x) или sin ^-1 x (читается как обратный синус x). Это одна из шести основных обратных тригонометрических функций: arccos, arcsin, arctan, arcsec, arccsc и arccot. Важно помнить, что грех ^-1 х не является обратной величиной синуса.

Что такое формула арксинуса?

Формула для арксинуса определяется следующим образом: θ = арксинус (противоположная сторона/гипотенуза), где θ — угол в прямоугольном треугольнике. Функция arcsin помогает нам найти меру угла, соответствующую значению функции синуса.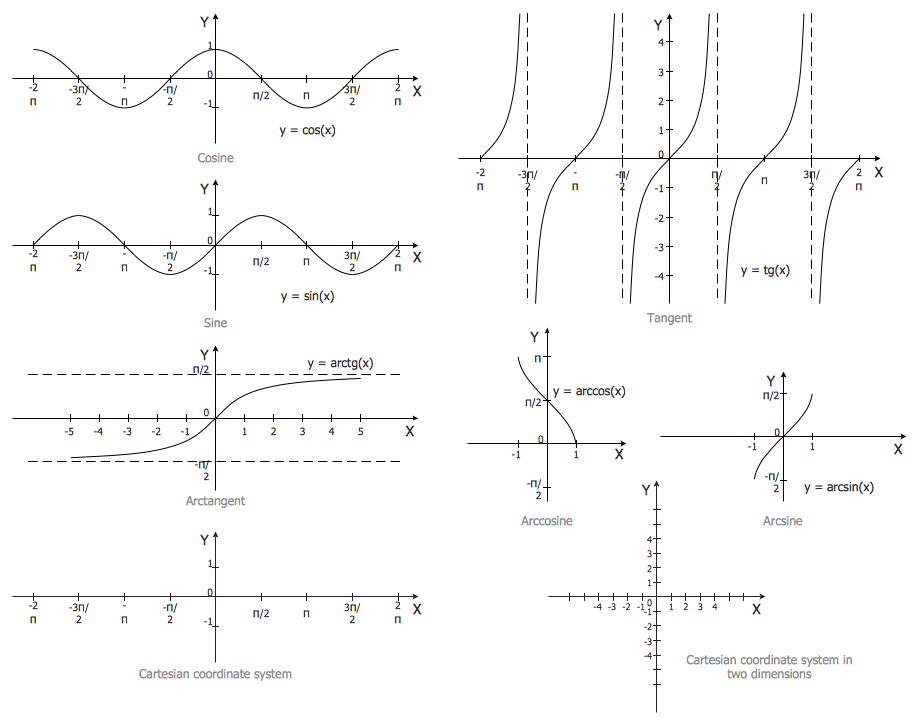 Мы также можем найти меру угла в треугольнике, используя формулу арксинуса, полученную с использованием закона синусов.

Что такое производная от Arcsin x?

Производная arcsin определяется как d/dx(arcsin x) = 1/√(1 — x²). Мы можем вывести эту формулу, используя первый принцип производных и метод дифференцирования по цепному правилу.

Как интегрировать Arcsin?

Интеграл от arcsin определяется выражением ∫arcsin x dx = x sin ^-1 x + √(1 — x ² ) + C, где C — постоянная интегрирования. Его можно получить с помощью различных методов, таких как интегрирование по частям и метод замещения с последующим интегрированием по частям.

Что такое домен и диапазон Arcsin?

Домен и диапазон arcsin:

• Домен Arcsin: [-1, 1]
• Диапазон арксинуса: [–π/2, π/2]

Мы ограничиваем область определения функции синуса до [–π/2, π/2], чтобы сделать ее биективной, и, следовательно, определяем функцию арксинуса как две функции, обратные друг другу, если они взаимно однозначны.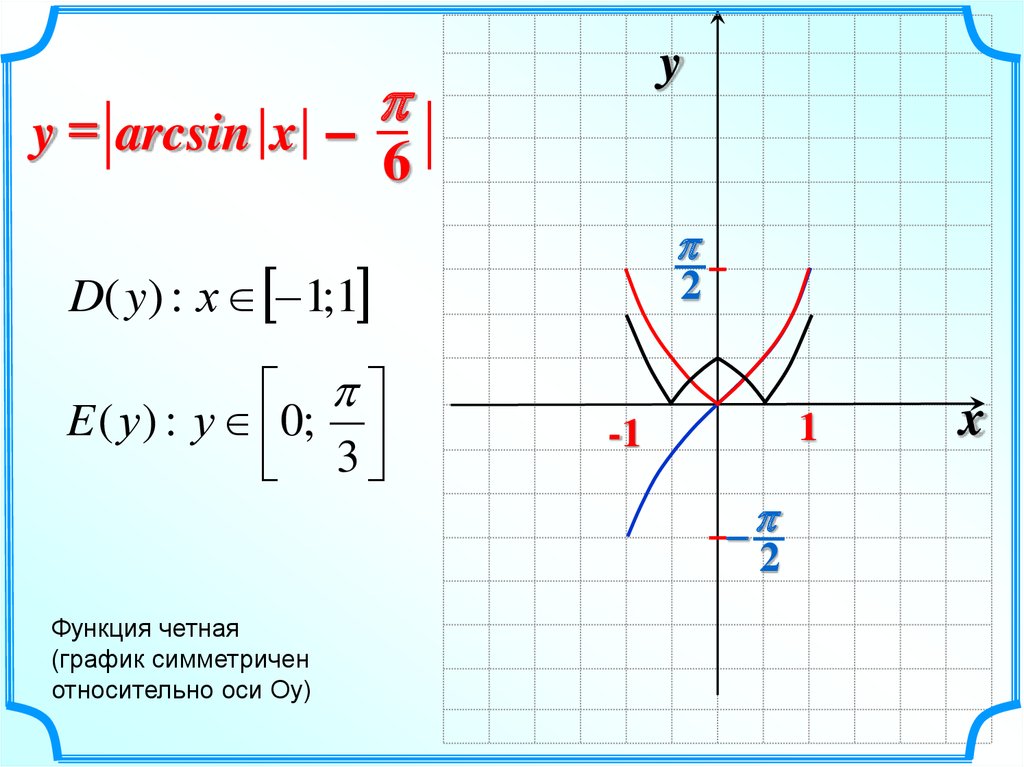 Ветвь arcsin, соответствующая домену [-1, 1] и диапазону [–π/2, π/2], называется ветвью главного значения.

Как построить график арксинуса?

Используя определение и функционирование арксинуса, мы можем нанести некоторые точки на график с помощью тригонометрической таблицы. Некоторые из пунктов:

• sin 0 = 0 подразумевает arcsin 0 = 0 → (0, 0)
• sin π/6 = 1/2 подразумевает arcsin (1/2) = π/6 → (1/2, π/6)
• sin π/3 = √3/2 подразумевает arcsin (√3/2) = π/3 → (√3/2, π/3)
• sin π/2 = 1 подразумевает arcsin (1) = π/2 → (1, π/2)
• sin (-π/4) = -1/√2 подразумевает arcsin (-1/√2) = -π/4 → (-1/√2, -π/4)
• sin (-π/6) = -1/2 подразумевает arcsin (-1/2) = -π/6 → (-1/2, -π/6)

Затем, нанеся эти точки на график и соединив их кривой, мы получим график арксинуса.

Является ли Arcsin обратной стороной Sin?

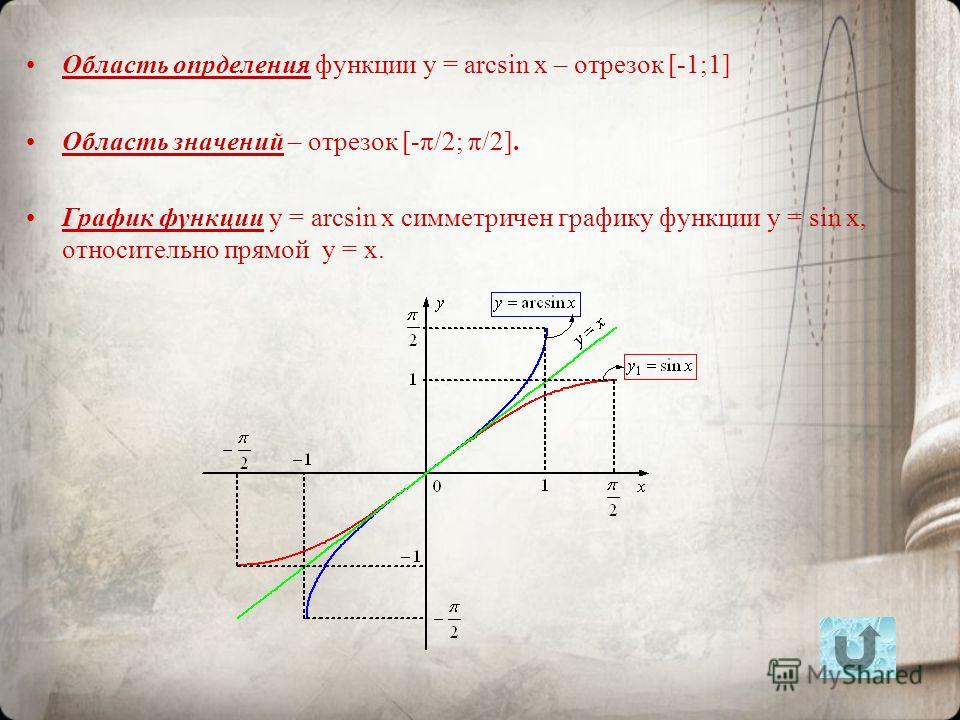
Arcsin является обратной тригонометрической функцией sin. Когда функция arcsin определяется как arcsin: [-1, 1] → [–π/2, π/2], мы говорим, что она обратна sin: [–π/2, π/2] → [ -1, 1].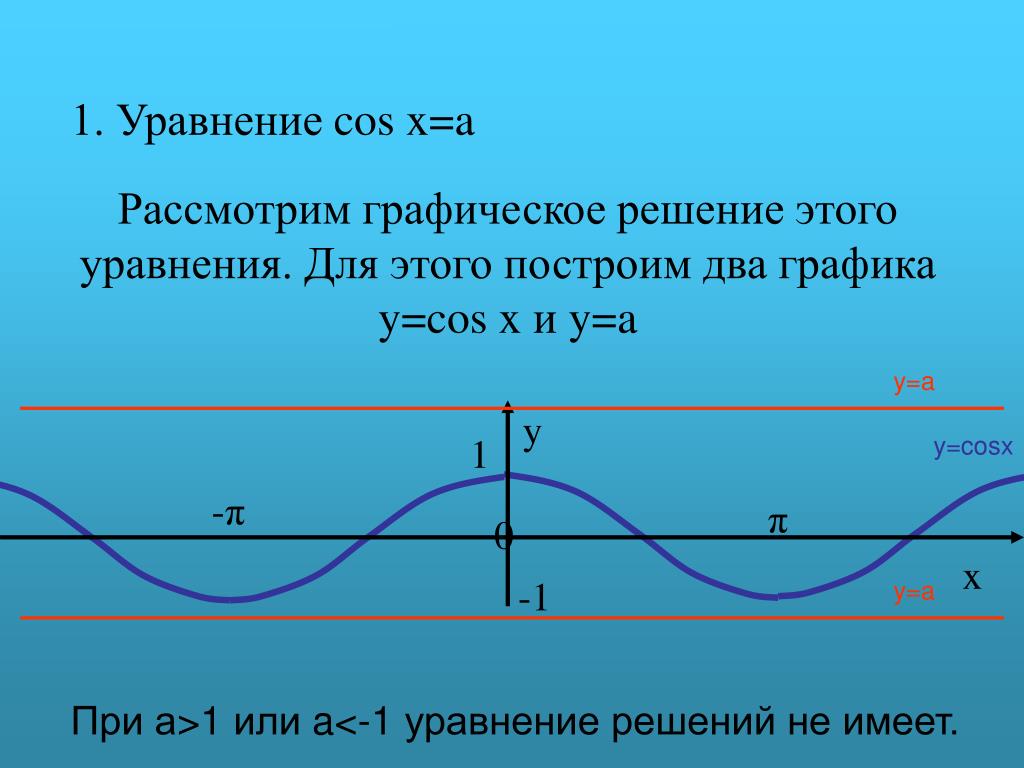

В чем разница между Sin и Arcsin?

Синус — это тригонометрическая функция, которая отображает вещественное число в угол, тогда как арксинус является обратной функцией синуса. Обе функции определяются как arcsin: [-1, 1] → [–π/2, π/2], тогда мы говорим, что это обратная функция sin: [–π/2, π/2] → [-1 , 1] и являются обратными друг другу.

Почему Arcsin (-2) не определен?

Arcsin (-2) не определен, поскольку область определения arcsin ограничена [-1, 1], а -2 не лежит в интервале [-1, 1].

Каковы личности Arcsin?

Вот некоторые важные формулы и тождества arcsin:

• sin (arcsin x) = x, если x находится в [-1, 1]
• arcsin (sin x) = x, если x находится в [–π/2, π/2]
• arcsin (1/x) = arccsc x, если x ≤ -1 или x ≥ 1
• arcsin (–x) = — arcsin x, если x ∈ [-1, 1]
• arcsin x + arccos x = π/2, если x ∈ [-1, 1]
• 2 arcsin x = arcsin (2x √(1 — x ² )), если -1/√2 ≤ x ≤ 1/√2

Что такое арксинус греха?

Формула для arcsin от sin дается следующим образом: arcsin (sin x) = x, если x находится в [–π/2, π/2].

угловой синус(х) | функция обратного синуса

arcsin(x) | функция обратного синуса

Главная›Математика›Тригонометрия› Arcsin

arcsin(x), sin ^-1 (x), функция обратного синуса.

• Определение углового синуса
• График угловых синусов
• Правила Arcsin
• Таблица угловых углов
• Калькулятор арксинуса

Определение арксинуса

Арксинус x определяется как функция обратного синуса x, когда -1≤x≤1.

Когда синус y равен x:

sin y = x

Тогда арксинус x равен обратному синусу x, который равен y:

arcsin x = sin ^-1 x = y

Пример

arcsin 1 = sin ^-1 1 = π /2 рад = 90°

График арксинуса

Правила Arcsin

Имя правила	Правило
Синус арксинуса	sin( arcsin х ) = х
Арксинус синуса	угловых синусов (sin х ) = х +2 к π, когда к ∈ℤ ( к целое число)
Арксинус отрицательного аргумента	arcsin(- x ) = — arcsin x
Дополнительные уголки	arcsin x = π/2 — arccos x = 90° — арккос х
Сумма арксинуса	arcsin α + arcsin( β ) = arcsin( α√ (1- β 2 ) + β√ (1- α 2 ) )
Разница арксинуса	arcsin α — arcsin( β ) = arcsin( α√ (1- β 2 ) — β√ (1- α 2 ))
Косинус арксинуса
Тангенс арксинуса
Производная арксинуса
Неопределенный интеграл арксинуса

Стол арксинуса

x	arcsin(x) (рад)	угловой синус(х) (°)
-1	-π/2	-90°
-√3/2	-π/3	-60°
-√2/2	-π/4	-45°
-1/2	-π/6	-30°
0	0	0°
1/2	№/6	30°
√2/2	№/4	45°
√3/2	№/3	60°
1	π/2	90°

 

---

См.