Нахождение тангенса синуса косинуса: Синус, косинус, тангенс и котангенс

Содержание

Определение синуса, косинуса, тангенса и котангенса

Прогнозирующий результат:

I-группа — должны показать оперативность применения знаний

II-группа — должны уметь применять знания на практике, выполнять задания обязательного уровня.

Сценарий урока:

Наглядные пособия:

1. на доске таблицы:

2. на доске модель окружности с радиусом 20см и подвижным радиусом ОА

3. у каждого ученика модель окружности с R=4см и радиусом ОА

4. заготовлена таблица на доске и у ребят в тетрадях

?	30^o	45^o	60^o	90^o	180 o	0 ^o	270^o	360^o
sin
cos
tg
ctg

Класс разбит на разноуровневые группы:

в группе

— 3 ученика, которые учатся на “3”

— 2 ученика, которые учатся на “4 и 5”.

Цель урока вырабатывается вместе с учениками.
Проверка домашнего задания —

На дом было задано:
- повторить из курса геометрии определение синуса, косинуса, тангенса в прямоугольном треугольнике 7 п. 62. п.67 (А. Погорелов)
- значение синуса, косинуса, тангенса для 0^o, 30^o ,45^o , 60^o , 90^o .
Фронтальная проверка по вопросам
Устно.
- каждой группе задаётся вопрос, ученик отвечает и заполняется заготовка таблицы значений тригонометрических функций.
- вопросы
  - значения sin 30^o , cos 60^o , tg 45^o и т.д.
  - столбец для 180^o и 270^o остался пустой.
Фронтально — устно:
- ответить на вопросы
  - что называется синусом угла в прямоугольном треугольнике
  - что называется косинусом угла в прямоугольном треугольнике
  - что называется тангенсом угла в прямоугольном треугольнике

Учитель в своих записях отмечает учеников, которые верно ответили.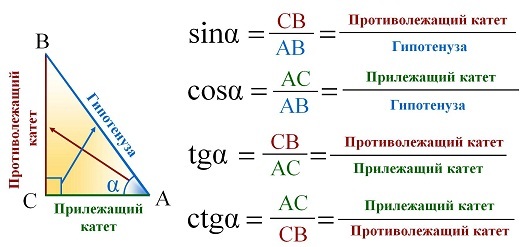

У доски выполнить задание: задание ученик выполняет с комментариями
- вычислить:
  - 2cos 60^o + sin30^o
  - 2cos 30^o + 2sin45^o

Ученики выполняют эти задания в тетрадях.

Сильные ученики работают по карточкам из 10 заданий выполнить по выбору 5.
- Карточка: вычислить:
  2cos 60^o + 3cos30^o
  5sin30^o – ctg45^o
  2sin60^o + 6cos60^o– 4tg45^o
  12sin60^o • cos60^o
  3tg45^o • tg60^o
  4tg60^o • sin60^o
  2sin60^o • tg60^o
  2sin45^o – 4cos30^o
  7tg30^o •cos30^o
  6tg30^o – 2sin60^o

Проверка через проектор, каждый проверяет свою работу и ставит баллы, за каждое задание – 1 балл.

В это время остальные выполняют диктант в тетрадях:
- вычислить:
  2cos60^o
  sin30^o + cos60^o
  cos90^o + sin45^o
  2sin30^o + 2tg45^o
  3tg60^o

Ученики меняются работами, и проверяют. Решение записано на доске. Выставляют отметки. Заполняется учётный лист “самооценка”

Объяснение по теме:

У каждого ученика модель окружности с подвижным радиусом. Работаем с этой окружностью. Повернём радиус ОА на угол 60^o — этот угол называется углом поворота. У доски на модели тоже показывают этот угол. Если радиус ОА повернуть около точки О по часовой стрелке, то угол поворота считают отрицательным; против часовой стрелки – положительным.

В группах ребята работают самостоятельно: на модели покажите углы 45^o , 100^o, 120^o, -45^o, -100^o , -120^o , -60^o.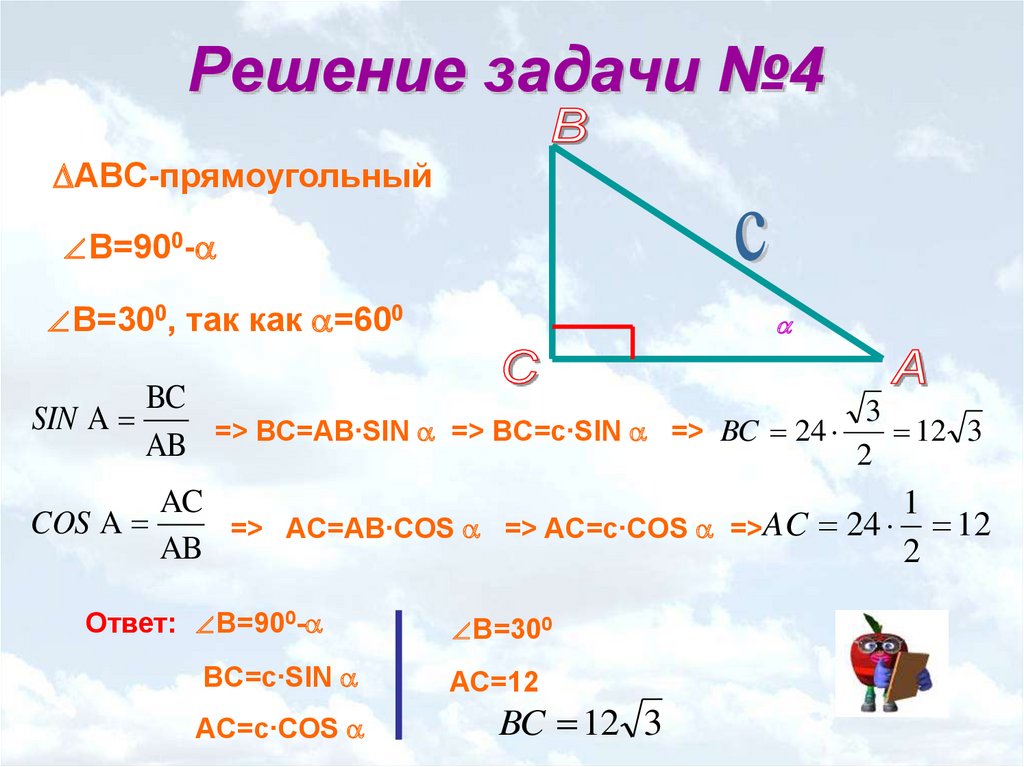

В курсе геометрии мера угла выражается от 0^o до 180^o . Угол поворота может выражаться от — до + . На модели у доски показан угол 300^o. Отработать углы поворота 0^o, 90^o, 180^o, 270^o, 360^o.Показать угол 400^o=360^o+40^o.

Работа у доски:

к доске приглашается ученик, он показывает угол, а ребята выполняют на месте (обсуждают вместе). Показать угол поворота и указать четверть, в которой он расположен: 283

o, 700^o, -150^o , 190^o , 270^o , 80^o, 100^o, 4220^o, 325^o, -20^o, 800^o.

из каждой группы выходит один ученик и выполняет два задания.

Объяснения учителя:

Отметим на окружности угол , рассмотрим треугольник ОАС.

А ( х; у ), С = 90^o , АС = у,

ОС = х, ОА = R.

Вырабатывается вместе с ребятами определение синуса угла : sin = AC/OA = у/R

Вырабатывается вместе с ребятами определение косинуса угла : cos= AC/OA = х/R

tg= AC/OC = у/х , ctg = OC/AC = х/у.

Рассмотрим определение синуса, косинуса, тангенса и котангенса.

Ребята в группах прорабатывают определение синуса, косинуса, тангенса и котангенса по учебнику.

В тетрадях записывают: sin = у/R , cos = х/R , tg = у/х , ctg = х/у.

Фронтальная работа:

На окружности показать угол поворота 90^o , найти sin90^o , cos90^o , tg90^o , ctg не имеет смысла для 90^o .

2 таблица значений.

Вывод:

выражение sin и cos определены при любом ;
tg определён при любом кроме +90?, +270?, +450? .
ctg определён при любом , кроме 0?, +180? , +360? .

В тетрадях сделать эту запись.

Каждому значению соответствует единственное значение sin, cos, tg , ctg . Поэтому синус, косинус, тангенс и котангенс являются функциями угла ?. Их называют тригонометрическими функциями.

Область значений синуса и косинуса является [-1; 1], тангенса и котангенса ? ( — , +).

Фронтальное закрепление:

Ученики выполняют в тетрадях, один ученик работает у доски:

Указать наибольшее значение выражения 1 + sin . ( в тетрадях: 1 + sin принимает наибольшее значение 2 )
Какое наименьшее значение имеет выражение 1 + sin
Какое наибольшее и наименьшее значение имеет выражение 2 — cos

Устно:

может ли sin принимать значения 2 , 2 , 1 / 2 , 3 , 3 – 1 , 3 / 2 , 1 + 3.
Вопрос задан группе, ученик из группы отвечает и объясняет кратко.
может ли cos , sin принимать значения (1 + 3)/ 2 ; (1 — 3)/2 .
Ученики объясняют.

Закрепление:

Найти значение выражения:
Все работают с учеником, который работает у доски с комментариями. У доски проработали три ученика и получили отметки.

Ребята пересели по парам.

Самостоятельная работа:
В “самооценке” отмечают столбик “Как я понял тему”:
О – “хорошо”
[] — не всё;
V — плохо.

I — В II — В

1. Углом какой четверти является угол :

= 130^o , = 200^o , = 490^o
.
= 170^o , = 280^o , = 700^o .
1 балл

2. Вычислить:

sin 0^o + 2cos60^o
tg 60^o •sin60^o •ctg30^o
4sin90^o ? 3cos180^o
3ctg90^o • 3sin270^o

3 балл

3. Найти значение выражения sin + cos, если

= 0^o
= 90^o
= 45^o
= 180^o

1 балл

Каждое задание дано в баллах; ученики выполняют задание по выбору, работа выполняется в тетрадях под копирку.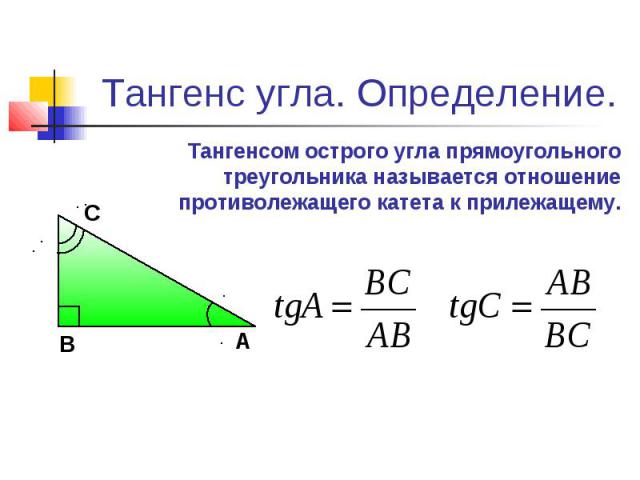 Листочки с работой ученики сдают, а работу ученики проверяют сами, готовое решение на доске. И оценивают. Заполняют “самооценку”.

Домашнее задание:
определение sin, cos , tg , ctg .

№ 717, 770.

“Самооценка”

Ф.И. ученика

диктант

тема

самостоятельная

(своя оценка)

самостоятельная

(учитель)

за урок

1. Соколов Н.
4

О

5

5

5

2. Аношина А.
5

О

5

5

5

3. Зуева О.

3

[]

3

3

3

4. Белов К.
4

[]

4

3

4

5. Гриненко К.
5

О

5

4

5

За диктант – ставит учитель.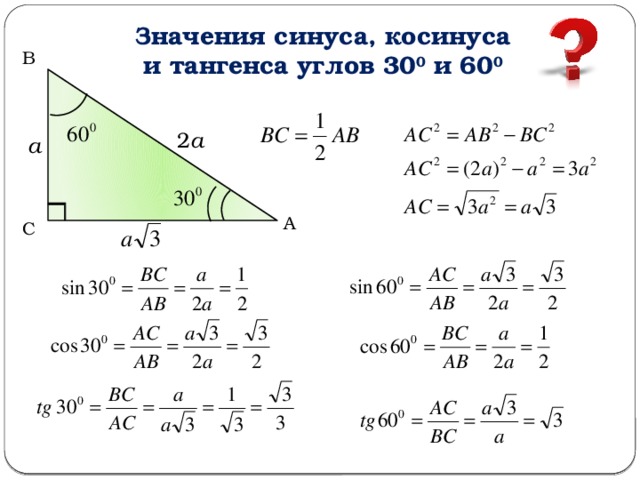
За урок выводится общая оценка
Синус и косинус. Запомнить навсегда!
Бизнес с Oriflame — рост и РАЗВИТИЕ!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2012-10-01
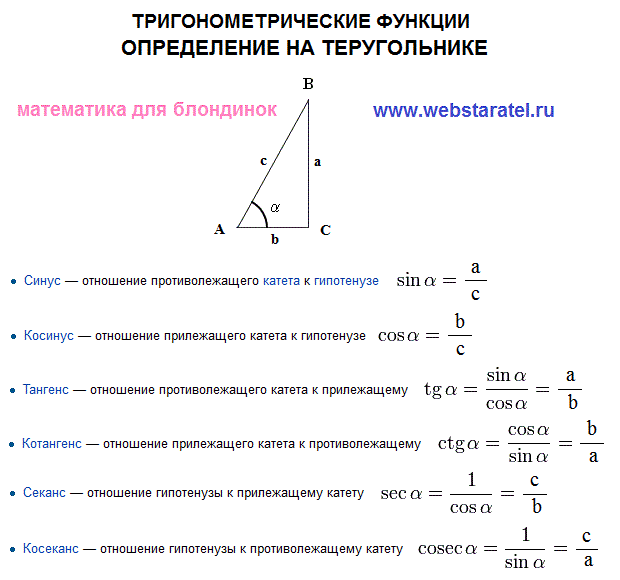
Синус косинус, определение. Друзья! В прошлой статье, где были рассмотрены задачи на решение прямоугольного треугольника, я пообещал изложить приём запоминания определений синуса и косинуса. Используя его, вы всегда быстро вспомните – какой катет относится к гипотенузе (прилежащий или противолежащий). Решил в «долгий ящик не откладывать», необходимый материал ниже, прошу ознакомиться 😉
Дело в том, что я не раз наблюдал, как учащиеся 10-11 классов с трудом вспоминают данные определения. Они прекрасно помнят, что катет относится к гипотенузе, а вот какой из них — забывают и путают. Цена ошибки, как вы знаете на экзамене – это потерянный бал.
Информация, которую я представлю непосредственно к математике не имеет никакого отношения. Она связана с образным мышлением, и с приёмами словесно-логической связи.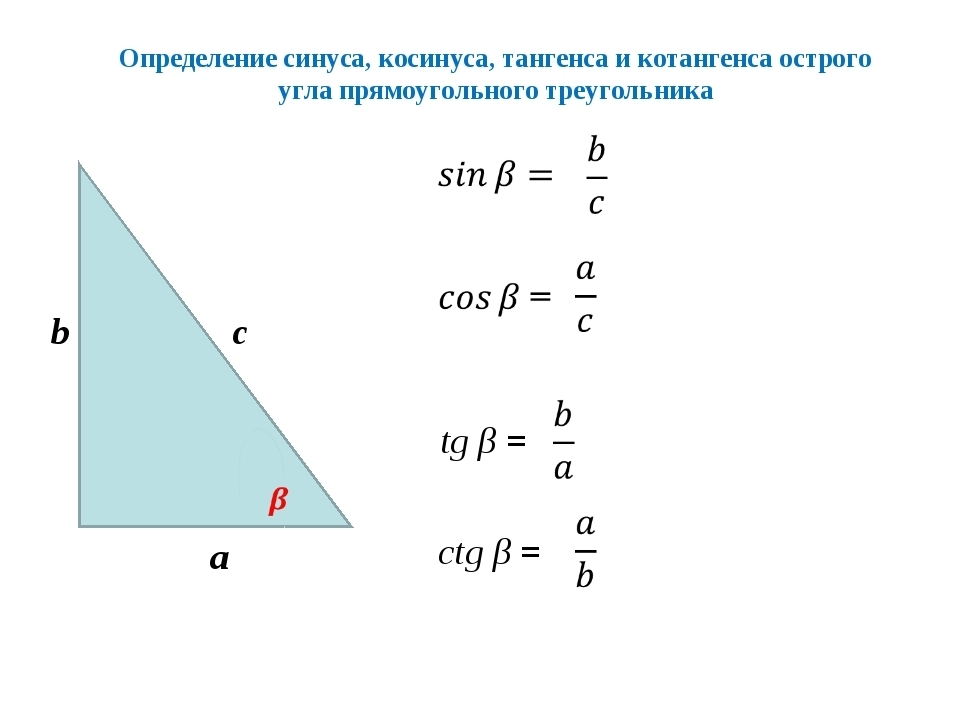 Именно так, я сам, раз и на всегда запомнил данные определения. Если вы их всё же забудете, то при помощи представленных приёмов всегда легко вспомните.
Напомню определения синуса и косинуса в прямоугольном треугольнике:
Косинус острого угла в прямоугольном треугольнике —   это отношение прилежащего катета к гипотенузе:
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Итак, какие ассоциации у вас вызывает слово косинус?
Наверное, у каждого свои 😉   Запоминайте связку:
Таким образом, у вас сразу в памяти возникнет выражение –
«… отношение ПРИЛЕЖАЩЕГО катета к гипотенузе».
Проблема с определением косинуса решена.
Если нужно вспомнить определение синуса в прямоугольном треугольнике, то вспомнив определение косинуса, вы без труда установите, что синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе.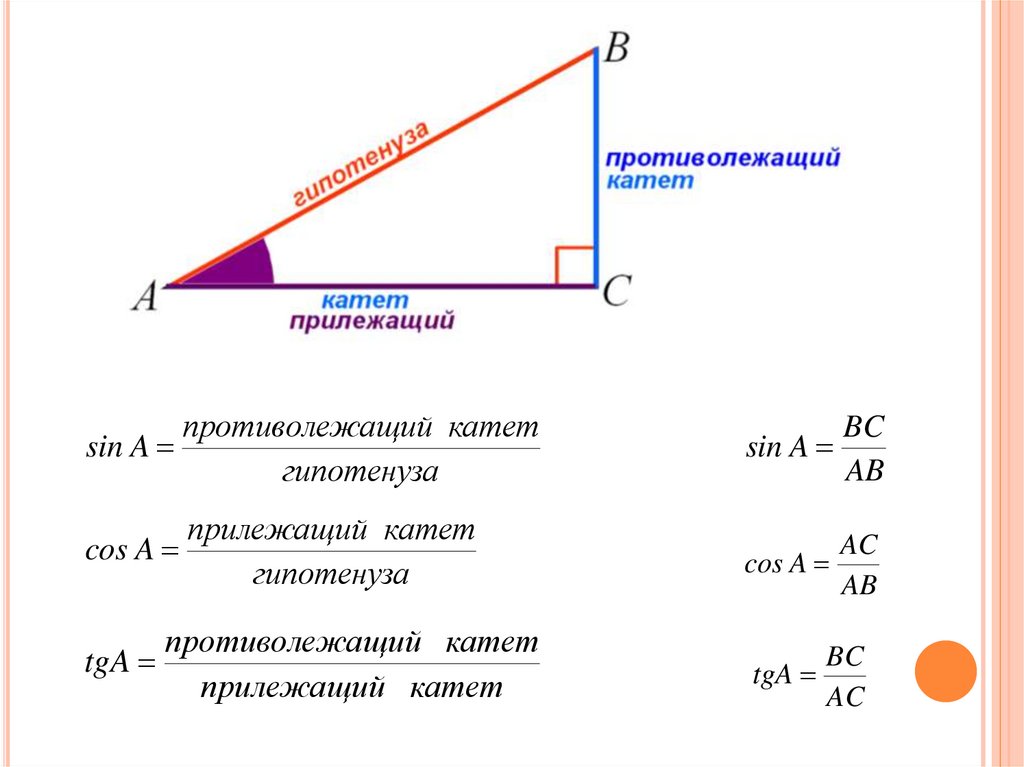 Ведь катетов всего два, если прилежащий катет «занят» косинусом, то синусу остаётся только противолежащий.
Как быть с тангенсом и котангенсом? Путаница та же. Учащиеся знают, что это отношение катетов, но проблема вспомнить какой к которому относится – то ли противолежащий к прилежащему, то ли наоборот.
Определения:
Тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему:
Котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему:
Как запомнить? Есть два способа. Один так же использует словесно-логическую связь, другой – математический.
СПОСОБ МАТЕМАТИЧЕСКИЙ
Есть такое определение – тангенсом острого угла называется отношение синуса угла к его косинусу:
*Запомнив формулу, вы всегда сможете определить, что тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему.
Аналогично. Котангенсом острого угла называется отношение косинуса угла к его синусу:
Итак! Запомнив указанные формулы вы всегда сможете определить, что:
— тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему
— котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему.
СПОСОБ СЛОВЕСНО-ЛОГИЧЕСКИЙ
О тангенсе. Запомните связку:
То есть если потребуется вспомнить определение тангенса, при помощи данной логической связи, вы без труда вспомните, что это
«… отношение противолежащего катета к прилежащему»
Если речь зайдёт о котангенсе, то вспомнив определение тангенса вы без труда озвучите определение котангенса –
«… отношение прилежащего катета к противолежащему»
Есть интересный приём по запоминанию тангенса и котангенса на сайте «Математический тандем», посмотрите.
СПОСОБ УНИВЕРСАЛЬНЫЙ
Можно просто зазубрить.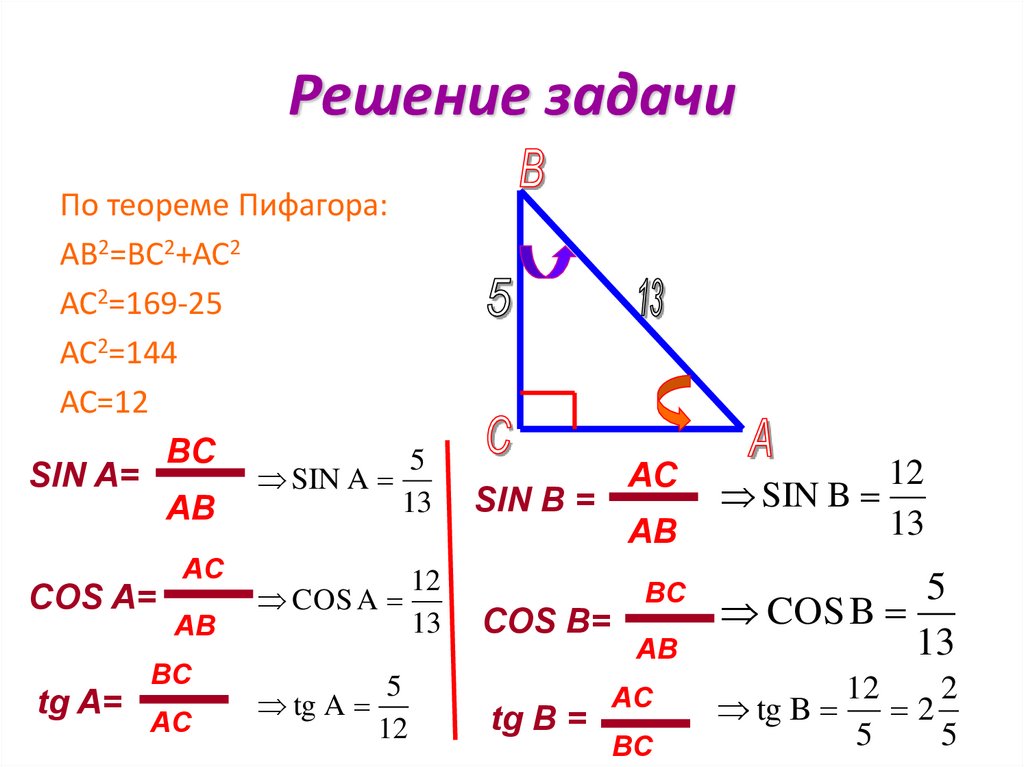 Но как показывает практика, благодаря словесно-логическим связкам человек запоминает информацию надолго, и не только математическую.
Надеюсь, материал был вам полезен.
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Приёмы | Как запомнитьФормулы
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

тригонометрия — Как вычислить синус косинус или тангенс угла (простое объяснение)
Я думаю, что здесь действительно два вопроса:
Как Архимед нашел длину стороны прямоугольного треугольника, противоположной заданному углу ?
Как калькулятор вычисляет триггерные функции?
Для №1: Честно говоря, я думаю, что он просто нарисовал и измерил. Это приводит к вопросу: «Как вообще они измеряли длину?» и, может быть, это на самом деле то, что вы спрашивали. В те дни измерения длины часто основывались на частях тела. См. здесь для получения дополнительной информации, включая другие методы/устройства.
Для № 2: Подробный ответ довольно технический и сложный, поэтому я постараюсь максимально упростить.
Как указано в другом ответе, калькуляторы используют ряды Тейлора для оценки триггерных функций. По сути, ряд Тейлора — это способ выражения функции с помощью четырех основных операций сложения, вычитания, умножения и деления.
Каждый компьютер и каждый калькулятор (с электроприводом) имеет центральный процессор, для краткости называемый ЦП. Процессор состоит из пучка крошечных проводов, по которым проходит электрический ток. Когда мы отдаем компьютеру или калькулятору команды (например, открываем или сохраняем файл, нажимаем кнопки на клавиатуре или калькуляторе), электричество проходит по проводам таким образом, что эти команды действительно выполняются.
Самые основные операции, которые мы можем выполнять с этой электрической разводкой, — это сложение и вычитание. Умножение и деление должны выполняться с соответствующими комбинациями сложения и вычитания. Иными словами, мы можем выполнять операции сложения и вычитания по одному электрическому маршруту. Но для чего-то более сложного потребуется не один маршрут. Например, когда вы говорите своему калькулятору сделать $4 + 5$, для этого требуется только один маршрут. Но если вы скажете своему калькулятору сделать 4 доллара умножить на 5 долларов, электричество, проходящее по проводам, на самом деле составит 4 доллара + 4 + 4 + 4 + 4 доллара, что занимает четыре маршрута (по одному на каждое добавление, а у нас есть четыре добавления). ).
То же самое относится и к более сложным операциям и функциям. Им также требуется более одного электрического маршрута, где каждый электрический маршрут в основном представляет собой сложение или вычитание. В этом нам поможет ряд Тейлора. Ряд Тейлора говорит нам, как вычислять эти функции с помощью сложения, вычитания, умножения и деления. И помните, что умножение и деление сами по себе «определяются» (в электрической схеме ЦП) с помощью сложения и вычитания. Поэтому, когда вы говорите своему калькулятору вычислить синус некоторого числа, электричество проходит по проводам, так что он фактически вычисляет выражение, данное рядом Тейлора.
Обратите внимание, что ряд Тейлора — это бесконечный ряд, который, конечно, не может для процессора вычислить в точности как в общем случае, но калькуляторы и компьютеры имеют фиксированное количество цифр, которые они могут отображать в любом случае. Поэтому достаточно просто использовать первые несколько членов ряда Тейлора.
Это заметает много деталей под ковер, но я надеюсь, что это хоть немного проясняет ситуацию. Если вам нужна дополнительная информация, Coursera в настоящее время проводит действительно хороший курс по этому вопросу. Это бесплатно. Есть еще один на EdX, но я думаю, что он немного более продвинутый. Я изучал этот материал в школе 12 лет назад, и в настоящее время я использую оба из них для освежения знаний, прежде чем перейти к более продвинутым исследованиям. Курс Coursera был действительно полезен для освоения основ, поэтому я определенно рекомендую хотя бы взглянуть на него.
Удачи и поддерживайте интеллектуальное любопытство!
Как рассчитываются синус, косинус и тангенс?
Тригонометрия — это раздел математики, изучающий соотношение сторон и углов в треугольнике. С помощью тригонометрии возможно определение высоты больших гор или башен, а также в астрономии, она используется для определения расстояния между звездами или планетами и широко используется в физике, архитектуре и системах GPS-навигации. Тригонометрия основана на принципе, что «Если два треугольника имеют одинаковое множество углов, то их стороны находятся в одинаковом отношении» . Длина сторон может быть разной, но соотношение сторон одинаковое.
Прямоугольный треугольник
Тригонометрические отношения определены только для прямоугольного треугольника.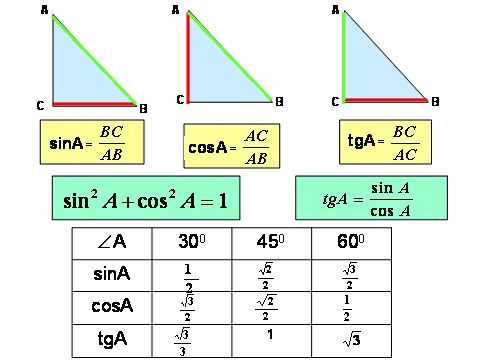 В прямоугольном треугольнике есть угол 90 °, а два других угла меньше 90 °, относительно этих углов каждая сторона называется перпендикулярным основанием и гипотенузой. Давайте посмотрим, что такое перпендикуляр, основание и гипотенуза прямоугольного треугольника,
Гипотенуза: Сторона, противоположная 90°. это самая большая сторона.
Перпендикуляр: Сторона перед углом или напротив угла перпендикулярна.
Основание: Основание — это одна из сторон, которая касается угла,
Примечание Гипотенуза никогда не может рассматриваться как основание или перпендикуляр.
В прямоугольном треугольнике угол, отличный от 90°, образован двумя сторонами, одна из которых является гипотенузой. другая сторона, которая содержит угол или касается угла, является основанием, а сторона, которая не касается угла, перпендикулярна.
Как показано на диаграмме выше, для того же треугольника, если рассматривать угол 30°, перпендикуляром является сторона PQ, но если рассматривать угол 60°, перпендикуляром является сторона QR.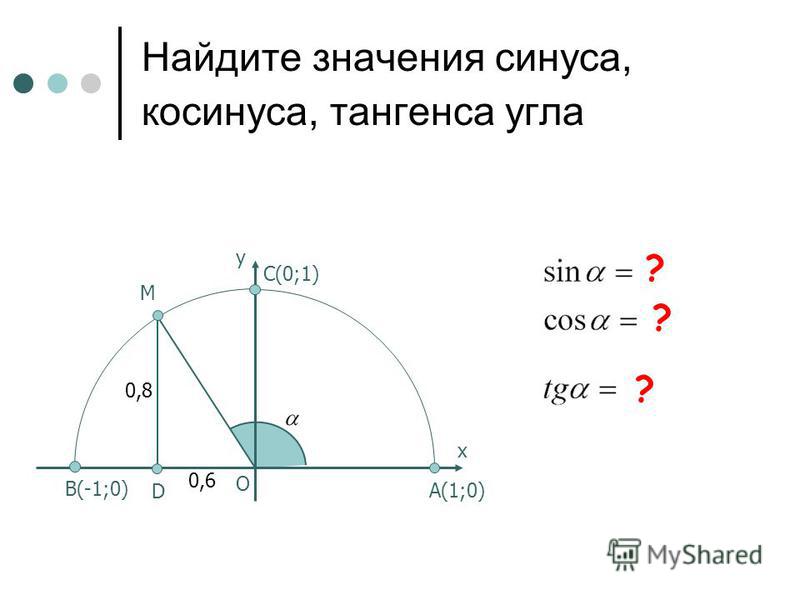
Тригонометрические функции
Тригонометрические функции также называются круговыми функциями или тригонометрическими отношениями. являются отношениями сторон прямоугольного треугольника, Они показывают отношения между углом и сторонами, и они являются основой тригонометрии . Существует шесть тригонометрических функций: синус, косинус, тангенс, косеканс, секанс, котангенс. Представления сторон для шести соотношений:
sin A = Перпендикуляр / Гипотенуза
cos A = Основание / Гипотенуза
tan A = Перпендикуляр / Основание
cot A = Основание / Перпендикуляр
sec A = Гипотенуза / Основание
cosec.
Как рассчитываются синус, косинус и тангенс?
Синус, косинус и тангенс, также называемые sin, cos и tan соответственно, являются наиболее часто используемыми тригонометрическими отношениями, остальные 3 являются обратными им.
Sin – Синус угла A – это отношение длин перпендикуляра к гипотенузе.
sin A = Перпендикуляр / Гипотенуза
Cos – Cos угла A – это отношение длины основания к гипотенузе.
cos A = Основание / Гипотенуза
Тангенс – Тангенс угла А представляет собой отношение длин перпендикуляров к основанию.
tan A = Перпендикулярно / Основание
Чтобы рассчитать эти отношения, найдите длину сторон треугольника и затем возьмите соответствующие отношения. Чтобы найти длину, если известна одна из сторон и угол, можно легко найти остальные стороны через синус, косинус и тангенс угла. Ниже приведены тригонометрические значения некоторых важных углов.
Углы (в градусах)    0°       9 60°
Sin θ 0 124 1/√2 √3/2 1
Cos θ 1 √3/2 1 1/2 0
Тан θ 0 1/√3 1 √3 ∞ 9 Co 0034 ∞ √3 1 1/√3 0
Сек. 120 Cosec θ ∞ 2 √2 √ 3/2 1
Примеры задач
Вопрос 1: Рассмотрите следующий треугольник и ответьте на следующий вопрос?
Найдите значение sin, cos и tan для угла 30°
Решение:
= 2см.
Sin(30°) = (п/ч) = 1/2.
Cos(30°) = (ч/ч) = √3/2.
tan(30°) = (p/b) = 1/2.
Вопрос 2. Для той же фигуры в вопросе 1 найдите значение sin, cos и tan для угла 60°
Решение:
Для угла 60°
перпендикуляр = √3см, основание = 1см , гипотенуза = 2 см.
Sin(60°) = (п/ч) = √3/2.
Cos(60°) = (ч/ч) = 1/2.
тангенс (60°) = (p/b) = √3/1.
Вопрос 3: В прямоугольном треугольнике основание до угла 30° равно 18 м. Найдите длину гипотенузы.
No related posts.