График четной функции: Чётные и нечётные функции — урок. Алгебра, 9 класс.

Четный график и нечетный. Как определять четные и нечетные функции

Определение 1. Функцияназываетсячетной (нечетной ), если вместе с каждым значением переменной
значение –х также принадлежит
и выполняется равенство

Таким образом, функция может быть четной или нечетной только тогда, когда ее область определения симметрична относительно начала координат на числовой прямой (числа х и –х одновременно принадлежат
). Например, функция
не является четной и нечетной, так как ее область определения
не симметрична относительно начала координат.

Функция
четная, так как
симметрична относительно начала координат и.

Функция
нечетная, так как
и
.

Функция
не является четной и нечетной, так как хотя
и симметрична относительно начала координат, равенства (11.1) не выполняются. Например,.

График четной функции симметричен относительно оси Оу , так как если точка

тоже принадлежит графику.

График нечетной функции симметричен относительно начала координат, так как если
принадлежит графику, то и точка
тоже принадлежит графику.

При доказательстве четности или нечетности функции бывают полезны следующие утверждения.

Теорема 1. а) Сумма двух четных (нечетных) функций есть функция четная (нечетная).

б) Произведение двух четных (нечетных) функций есть функция четная.

в) Произведение четной и нечетной функций есть функция нечетная.

г) Если f – четная функция на множествеХ , а функцияg определена на множестве
, то функция
– четная.

д) Если f – нечетная функция на множествеХ , а функцияg определена на множестве
и четная (нечетная), то функция
– четная (нечетная).

Доказательство . Докажем, например, б) и г).

б) Пусть
и
– четные функции. Тогда, поэтому. Аналогично рассматривается случай нечетных функций
и
.

г) Пусть f – четная функция. Тогда.

Остальные утверждения теоремы доказываются аналогично. Теорема доказана.

Теорема 2. Любую функцию
, заданную на множествеХ , симметричном относительно начала координат, можно представить в виде суммы четной и нечетной функций.

Доказательство . Функцию
можно записать в виде

.

Функция
– четная, так как
, а функция
– нечетная, поскольку. Таким образом,
, где
– четная, а
– нечетная функции. Теорема доказана.

Определение 2. Функция
называетсяпериодической , если существует число
, такое, что при любом
числа
и
также принадлежат области определения
и выполняются равенства

Такое число T называетсяпериодом функции
.

Из определения 1 следует, что если

Т – период функции
, то и число –Т тоже является периодом функции
(так как при заменеТ на –Т равенство сохраняется). С помощью метода математической индукции можно показать, что еслиТ – период функцииf , то и
, тоже является периодом. Отсюда следует, что если функция имеет период, то она имеет бесконечно много периодов.

Определение 3. Наименьший из положительных периодов функции называется ееосновным периодом.

Теорема 3. ЕслиТ – основной период функцииf , то остальные периоды кратны ему.

Доказательство . Предположим противное, то есть что существует периодфункцииf (>0), не кратныйТ . Тогда, разделивнаТ с остатком, получим
, где
. Поэтому

то есть – период функцииf

, причем
, а это противоречит тому, чтоТ – основной период функцииf . Из полученного противоречия следует утверждение теоремы. Теорема доказана.

Хорошо известно, что тригонометрические функции являются периодическими. Основной период
и
равен
,
и
. Найдем период функции
. Пусть
— период этой функции. Тогда

(так как
.

илиилиили
.

Значение T , определяемое из первого равенства, не может быть периодом, так как зависит отх , т.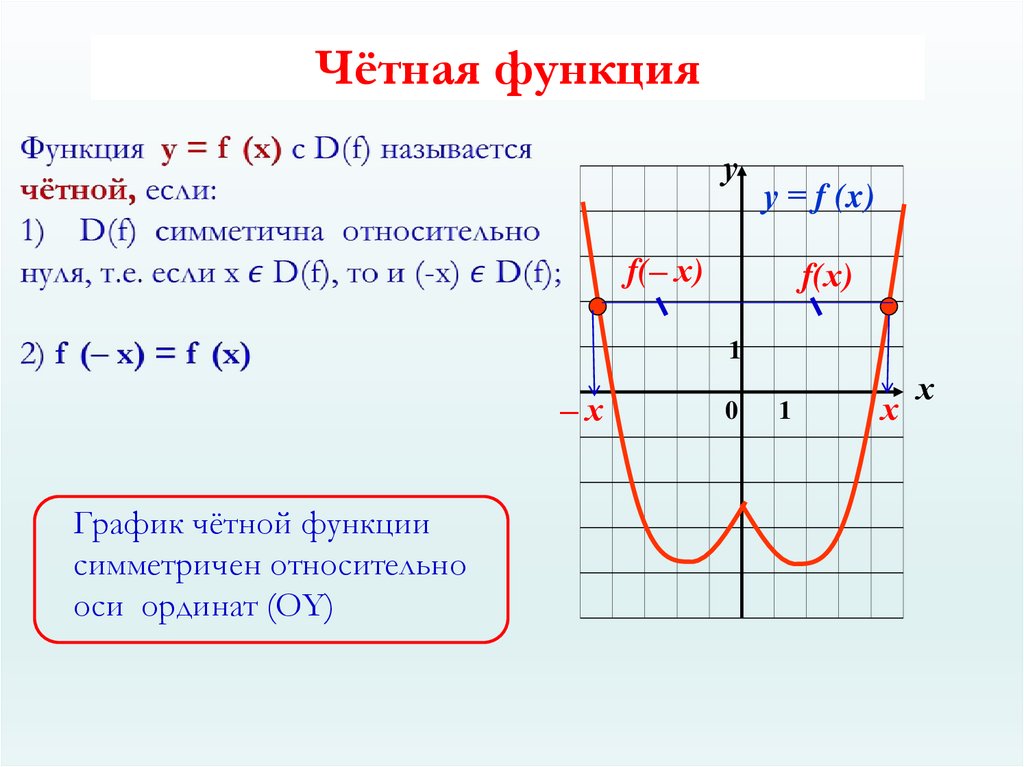 е. является функцией отх , а не постоянным числом. Период определяется из второго равенства:
. Периодов бесконечно много, при
наименьший положительный период получается при
:
. Это – основной период функции
.

Примером более сложной периодической функции является функция Дирихле

Заметим, что если T

– рациональное число, то
и
являются рациональными числами при рациональномх и иррациональными при иррациональномх . Поэтому

при любом рациональном числе T . Следовательно, любое рациональное числоT является периодом функции Дирихле. Ясно, что основного периода у этой функции нет, так как есть положительные рациональные числа, сколь угодно близкие к нулю (например, рациональное числоможно сделать выборомn сколь угодно близким к нулю).

Теорема 4. Если функцияf задана на множествеХ и имеет периодТ , а функцияg задана на множестве
, то сложная функция
тоже имеет периодТ .

Доказательство . Имеем, поэтому

то есть утверждение теоремы доказано.

Например, так как cos x имеет период
, то и функции
имеют период
.

Определение 4. Функции, не являющиеся периодическими, называютсянепериодическими .

В июле 2020 года NASA запускает экспедицию на Марс. Космический аппарат доставит на Марс электронный носитель с именами всех зарегистрированных участников экспедиции.

Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.

Один из этих вариантов кода нужно скопировать и вставить в код вашей веб-станицы, желательно между тегами

и или же сразу после тега . По первому варианту MathJax подгружается быстрее и меньше тормозит страницу. Зато второй вариант автоматически отслеживает и подгружает свежие версии MathJax. Если вставить первый код, то его нужно будет периодически обновлять. Если вставить второй код, то страницы будут загружаться медленнее, зато вам не нужно будет постоянно следить за обновлениями MathJax.

Подключить MathJax проще всего в Blogger или WordPress: в панели управления сайтом добавьте виджет, предназначенный для вставки стороннего кода JavaScript, скопируйте в него первый или второй вариант кода загрузки, представленного выше, и разместите виджет поближе к началу шаблона (кстати, это вовсе не обязательно, поскольку скрипт MathJax загружается асинхронно). Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.

Очередной канун Нового Года… морозная погода и снежинки на оконном стекле… Все это побудило меня вновь написать о… фракталах, и о том, что знает об этом Вольфрам Альфа. По этому поводу есть интересная статья , в которой имеются примеры двумерных фрактальных структур. Здесь же мы рассмотрим более сложные примеры трехмерных фракталов.

Фрактал можно наглядно представить (описать), как геометрическую фигуру или тело (имея ввиду, что и то и другое есть множество, в данном случае, множество точек), детали которой имеют такую же форму, как и сама исходная фигура. То есть, это самоподобная структура, рассматривая детали которой при увеличении, мы будем видеть ту же самую форму, что и без увеличения. Тогда как в случае обычной геометрической фигуры (не фрактала), при увеличении мы увидим детали, которые имеют более простую форму, чем сама исходная фигура. Например, при достаточно большом увеличении часть эллипса выглядит, как отрезок прямой. С фракталами такого не происходит: при любом их увеличении мы снова увидим ту же самую сложную форму, которая с каждым увеличением будет повторяться снова и снова.

Бенуа Мандельброт (Benoit Mandelbrot), основоположник науки о фракталах, в своей статье Фракталы и искусство во имя науки написал: «Фракталы — это геометрические формы, которые в равной степени сложны в своих деталях, как и в своей общей форме.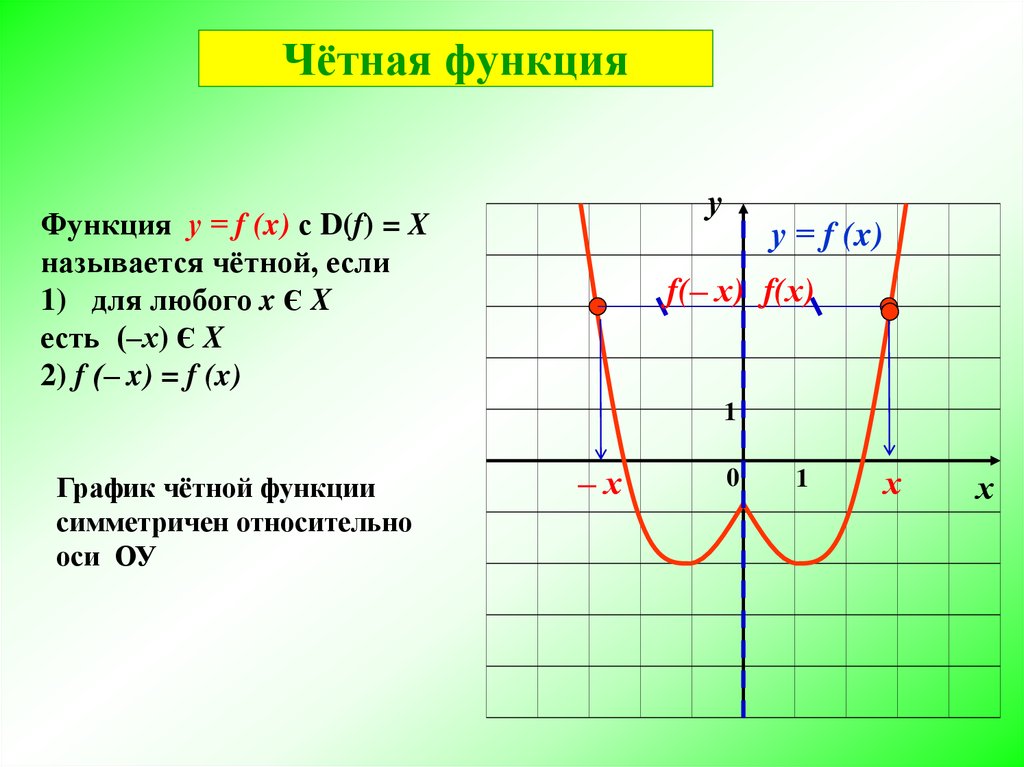

То есть, если часть фрактала будет увеличена до размера целого, она будет выглядеть, как целое, или в точности, или, возможно, с небольшой деформацией».

Нули функции
Нулём функции называется то значение х , при котором функция обращается в 0, то есть f(x)=0.

Нули – это точки пересечения графика функции с осью Ох.

Четность функции
Функция называется чётной, если для любого х из области определения выполняется равенство f(-x) = f(x)

Четная функция симметрична относительно оси Оу

Нечетность функции
Функция называется нечётной, если для любого х из области определения выполняется равенство f(-x) = -f(x).

Нечетная функция симметрична относительно начала координат.
Функция которая не является ни чётной,ни нечётной называется функцией общего вида.

Возрастание функции
Функция f(x) называется возрастающей, если большему значению аргумента соответствует большее значение функции, т.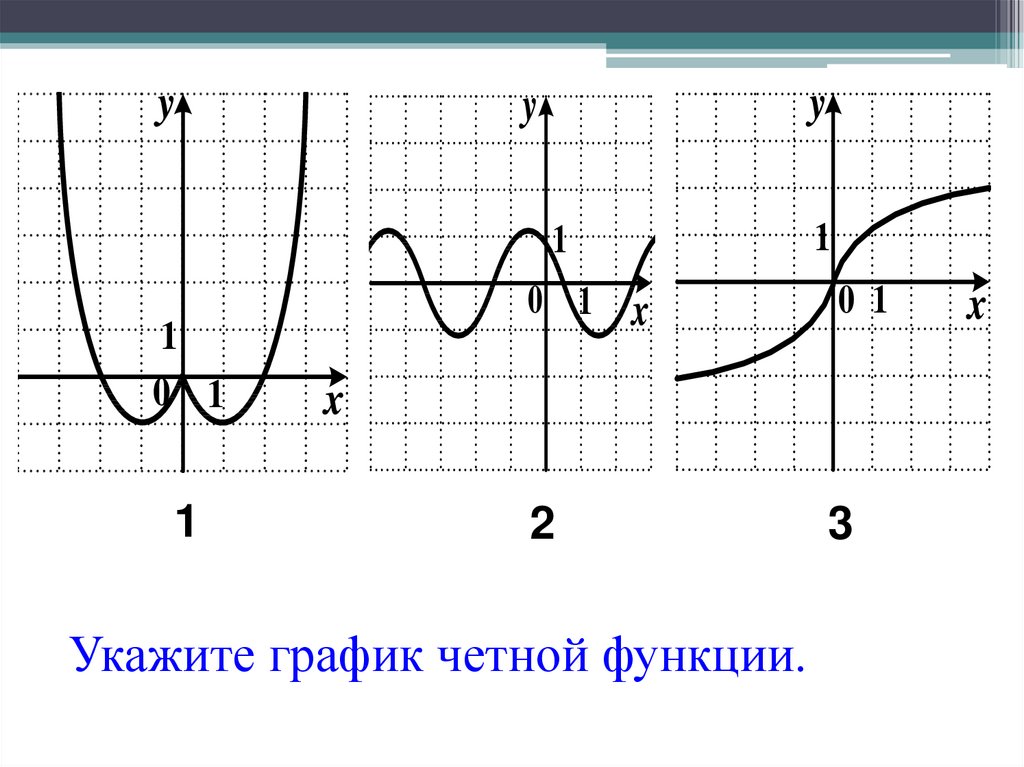 е. x 2 >x 1 → f(x 2)>f(x 1)

Убывание функции
Функция f(x) называется убывающей, если большему значению аргумента соответствует меньшее значение функции, т.е. x 2 >x 1 → f(x 2)
Промежутки, на которых функция либо только убывает, либо только возрастает, называются промежутками монотонности . Функция f(x) имеет 3 промежутка монотонности:
(-∞ x 1), (x 1 , x 2), (x 3 ; +∞)

Находят промежутки монотонности с помощью сервиса Интервалы возрастания и убывания функции

Локальный максимум
Точка х 0 называется точкой локального максимума, если для любого х из окрестности точки

х 0 выполняется неравенство: f(x 0) > f(x)

Локальный минимум
Точка х 0 называется точкой локального минимума, если для любого х из окрестности точки х 0 выполняется неравенство: f(x 0)
Точки локального максимума и точки локального минимума называются точками локального экстремума.

x 1 , x 2 — точки локального экстремума.

Периодичность функции
Функция f(x) называется периодичной, с периодом Т , если для любого х выполняется равенство f(x+T) = f(x) .

Промежутки знакопостоянства
Промежутки, на которых функция либо только положительна, либо только отрицательна, называются промежутками знакопостоянства.

f(x)>0 при x∈(x 1 , x 2)∪(x 2 , +∞), f(x)

Непрерывность функции
Функция f(x) называется непрерывной в точке x 0 , если предел функции при x → x 0 равен значению функции в этой точке, т.е. .

Точки разрыва
Точки, в которых нарушено условие непрерывности называются точками разрыва функции.

x 0 — точка разрыва.

1. Найти область определения функции D(y).
2. Найти точки пересечения графика функций с осями координат.
3. Исследовать функцию на четность или нечетность.
4. Исследовать функцию на периодичность.
5. Найти промежутки монотонности и точки экстремума функции.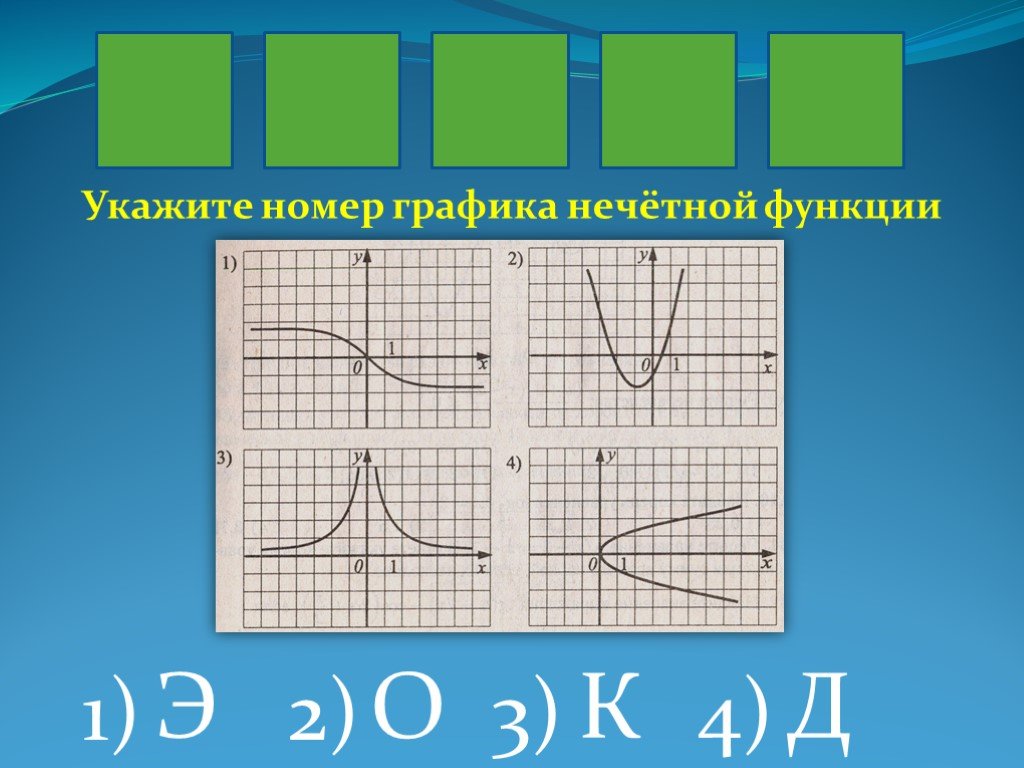
6. Найти промежутки выпуклости и точки перегиба функции.
7. Найти асимптоты функции.
8. По результатам исследования построить график.

Пример: Исследовать функцию и построить ее график: y = x 3 – 3x
8) По результатам исследования построим график функции:

Четная функция.

Четной называется функция, знак которой не меняется при изменении знака x .

x выполняется равенство f (–x ) = f (x ). Знак x не влияет на знак y .

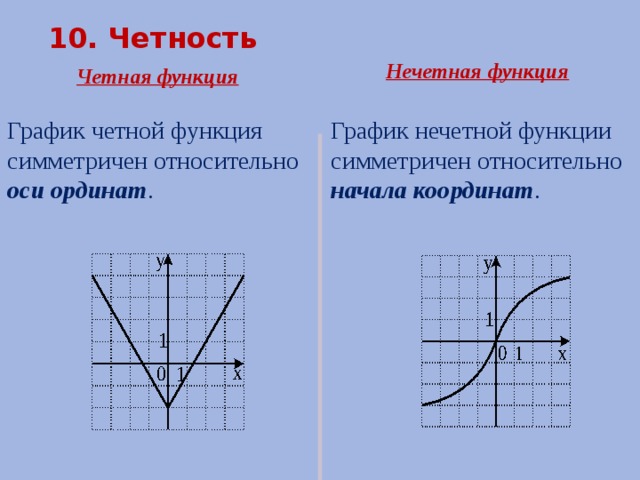
График четной функции симметричен относительно оси координат (рис.1).

Примеры четной функции:

y = cos x

y = x 2

y = –x 2

y = x 4

y = x 6

y = x 2 + x

Пояснение:
Возьмем функцию y = x 2 или y = –x 2 .
При любом значении x функция положительная. Знак x не влияет на знак y . График симметричен относительно оси координат. Это четная функция.

Нечетная функция.

Нечетной называется функция, знак которой меняется при изменении знака x .

Говоря иначе, для любого значения x выполняется равенство f (–x ) = –f (x ).

График нечетной функции симметричен относительно начала координат (рис.2).

Примеры нечетной функции:

y = sin x

y = x 3

y = –x 3

Пояснение:

Возьмем функцию y = –x 3 .
Все значения у в ней будут со знаком минус. То есть знак x влияет на знак y . Если независимая переменная – положительное число, то и функция положительная, если независимая переменная – отрицательное число, то и функция отрицательная: f (–x ) = –f (x ).
График функции симметричен относительно начала координат.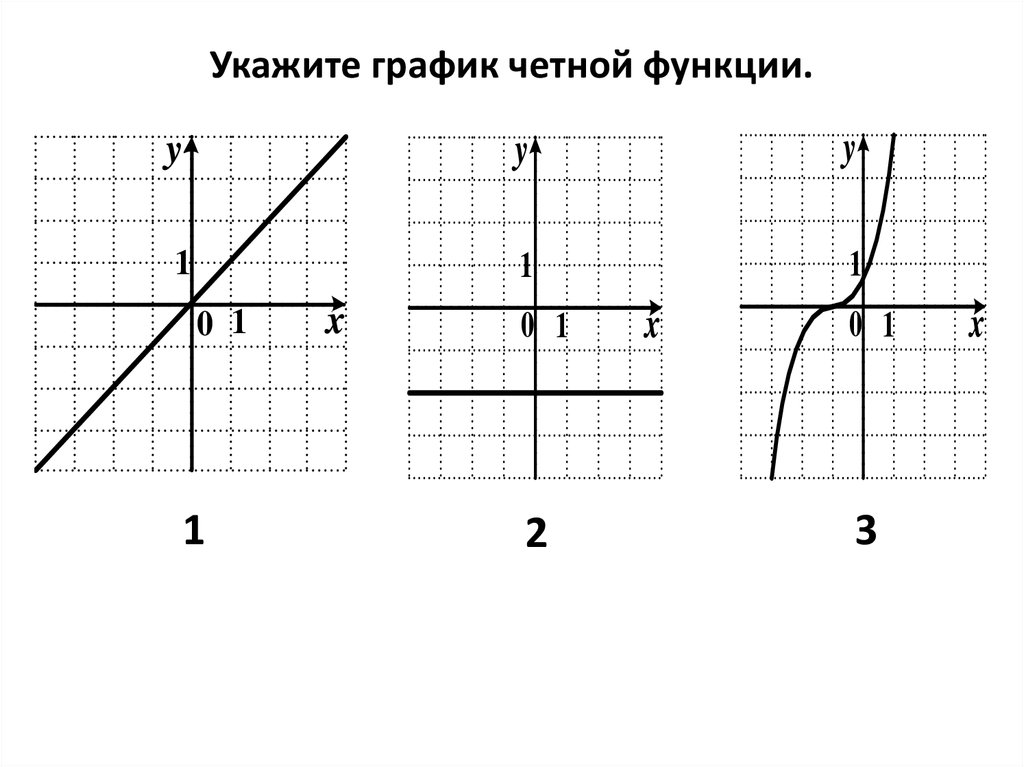 Это нечетная функция.

Свойства четной и нечетной функций:

ПРИМЕЧАНИЕ:

Не все функции являются четными или нечетными. Есть функции, которые не подчиняются такой градации. К примеру, функция корня у = √х не относится ни к четным, ни к нечетным функциям (рис.3). При перечислении свойств подобных функций следует давать соответствующее описание: ни четна, ни нечетна.

Периодические функции.

Как вы знаете, периодичность – это повторяемость определенных процессов с определенным интервалом. Функции, описывающие эти процессы, называют периодическими функциями . То есть это функции, в чьих графиках есть элементы, повторяющиеся с определенными числовыми интервалами.

— (матем.) Функция у = f (x) называется чётной, если она не меняется, когда независимое переменное изменяет только знак, то есть, если f (x) = f (x). Если же f (x) = f (x), то функция f (x) называется нечётной. Например, у = cosx, у = x2… …

F(x) = x пример нечётной функции.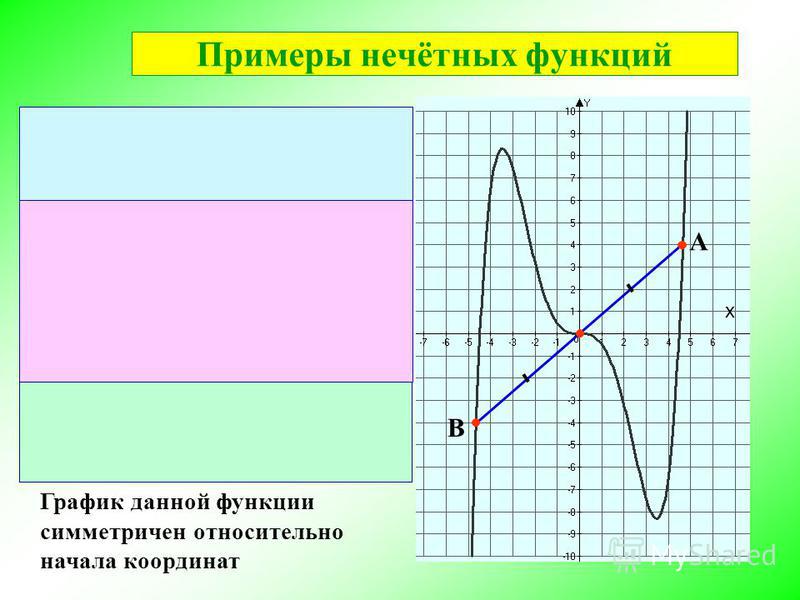 f(x) = x2 пример чётной функции. f(x) = x3 … Википедия

Функция, удовлетворяющая равенству f (x) = f (x). См. Чётные и нечётные функции … Большая советская энциклопедия

F(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия

F(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия

F(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия

F(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия

Специальные функции, введённые французским математиком Э. Матье (E. Mathieu) в 1868 при решении задач о колебании эллиптической мембраны. М. ф. применяются также при изучении распространения электромагнитных волн в эллиптическом цилиндре … Большая советская энциклопедия

Запрос «sin» перенаправляется сюда; см. также другие значения. Запрос «sec» перенаправляется сюда; см. также другие значения. Запрос «Синус» перенаправляется сюда; см. также другие значения … Википедия

Математика: Справ. материалы

Математика: Справ. материалы

Гусев В. А., Мордкович А. Г. Математика: Справ. материалы: Кн. для учащихся.— М.: Просвещение, 1988.— 416 с. В книге дано краткое изложение основных разделов школьных курсов алгебры и начал анализа, геометрии. Книга окажет помощь в систематизации и обобщении знаний по математике. Оглавление СЛОВО К УЧАЩИМСЯ ГЛАВА I. ЧИСЛА § 1. Натуральные числа 2. Арифметические действия над натуральными числами. 3. Деление с остатком. 4. Признаки делимости. 5. Разложение натурального числа на простые множители. 6. Наибольший общий делитель нескольких натуральных чисел. 7. Наименьшее общее кратное нескольких натуральных чисел. 8. Употребление букв в алгебре. Переменные. § 2. Рациональные числа 10. Равенство дробей. Основное свойство дроби. Сокращение дробей. 11. Приведение дробей к общему знаменателю. 12. Арифметические действия над обыкновенными дробями. 13. Десятичные дроби. 14. Арифметические действия над десятичными дробями. 15. Проценты. 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь. 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь. 18. Координатная прямая. 19. Множество рациональных чисел. § 3. Действительные числа 21. Действительные числа. Числовая прямая. 22 Обозначения некоторых числовых множеств. 23. Сравнение действительных чисел. 25. Числовые промежутки. 26. Модуль действительного числа. 27. Формула расстояния между двумя точками координатной прямой. 28. Правила действий над действительными числами. 29. Свойства арифметических действий над действительными числами. 30. Пропорции. 31. Целая часть числа. Дробная часть числа. 32. Степень с натуральным показателем. 33. Степень с нулевым показателем. Степень с отрицательным целым показателем. 34. Стандартный вид положительного действительного числа. 35. Определение арифметического корня. 36. Корень нечетной степени из отрицательного числа. 37. Степень с дробным показателем. 38. Свойства степеней с рациональными показателями. 39. Приближенные значения чисел. Абсолютная и относительная погрешности. 40. Десятичные приближения действительного числа по недостатку и по избытку. 41. Правило извлечения квадратного корня из натурального числа. 42. Понятие о степени с иррациональным показателем. 43. Свойства степеней с действительными показателями. § 4. Комплексные числа 45. Арифметические операции над комплексными числами. 46. Алгебраическая форма комплексного числа. 47. 3. 112. Построение графика функции y = f(x-m)+n 113. График квадратичной функции. 114. Способы построения графика квадратичной функции 115. Построение графика функции y = f(kx). 116. Сжатие и растяжение графиков тригонометрических функций. 117. График гармонического колебания ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ § 12. Преобразование выражений, содержащих переменную под знаком логарифма 119. Определение логарифма положительного числа по данному основанию. 120. Свойства логарифмов. 121. Переход к новому основанию логарифма. 122. Логарифмирование и потенцирование. 123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма. § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений 125. Формулы сложения и вычитания аргументов. 126. Формулы приведения. 127. Соотношения между тригонометрическими функциями одного и того же аргумента. 128. Формулы двойного угла. 129. Формулы понижения степени. 130. Преобразование суммы тригонометрических функций в произведение. 131. Преобразование произведения тригонометрических функций в сумму. 132. Преобразование выражения a cos t + b sin t к виду A sin (t + a). 133. Примеры преобразований выражений, содержащих обратные тригонометрические функции. ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ § 14. Уравнения с одной переменной 135. Равносильность уравнений. 136. Линейные уравнения. 137. Квадратные уравнения. 138. Неполные квадратные уравнения. 139. Теорема Виета. 140. Системы и совокупности уравнений. 141. Уравнения, содержащие переменную под знаком модуля. 142. Понятие следствия уравнения. Посторонние корни. 143. Уравнения с переменной в знаменателе. 144. Область определения уравнения. 145. Рациональные уравнения. 146. Решение уравнения p(x) = 0 методом разложения его левой части на множители. 147. Решение уравнений методом введения новой переменной. 148. Биквадратные уравнения. 149. Решение задач с помощью составления уравнений. 150. Иррациональные уравнения. 151. Показательные уравнения. 152. Логарифмические уравнения. 153. Примеры решения показательно-логарифмических уравнений. 154. Простейшие тригонометрические уравнения. 155. Методы решения тригонометрических уравнений. 156. Универсальная подстановка (для тригонометрических уравнений). 157. Метод введения вспомогательного аргумента (для тригонометрических уравнений). 158. Графическое решение уравнений. 159. Уравнения с параметром. § 15. Уравнения с двумя переменными 161. График уравнения с двумя переменными. 162. Линейное уравнение с двумя переменными и его график. § 16. Системы уравнений 164. Решение систем двух уравнений с двумя переменными методом подстановки. 165. Решение систем двух уравнений с двумя переменными методом сложения. 167. Графическое решение систем двух уравнений с двумя переменными. 168. Исследование системы двух линейных уравнений с двумя переменными. 169. Решение систем двух уравнений с двумя переменными методами умножения и деления. 170. Системы показательных и логарифмических уравнений. 171. Системы тригонометрических уравнений с двумя переменными. 172. Системы трех уравнений с тремя переменными. 173. Решение задач с помощью составления систем уравнений. Глава VI. НЕРАВЕНСТВА § 17. Решение неравенств с переменной 175. Графическое решение неравенств с одной переменной. 176. Линейные неравенства с одной переменной. 177. Системы неравенств с одной переменной. 178. Совокупность неравенств с одной переменной. 179. Дробно-линейные неравенства. 180. Неравенства второй степени. 181. Графическое решение неравенств второй степени. 182. Неравенства с модулями. 183. Решение рациональных неравенств методом промежутков. 184. Показательные неравенства. 185. Логарифмические неравенства. 186. Иррациональные неравенства. 187. Решение тригонометрических неравенств. 188. Неравенства и системы неравенств с двумя переменными. § 18. Доказательство неравенств 190. Синтетический метод доказательства неравенств. 191. Доказательство неравенств методом от противного. 192. Использование неравенств при решении уравнений. ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 19. Числовые последовательности 194. Способы задания последовательности. 195. Возрастание и убывание последовательности. 196. Определение арифметической прогрессии. 197. Свойства арифметической прогрессии 198. Определение геометрической прогрессии. 199. Свойства геометрической прогрессии. 200. Понятие о пределе последовательности. 201. Вычисление пределов последовательностей. 202. Сумма бесконечной геометрической прогрессии при |q| § 20. Предел функции 204. Вычисление пределов функции при х->оо. 205. Предел функции в точке. Непрерывные функции. 206. Вертикальная асимптота. 207. Вычисление пределов функций в точке. § 21. Производная и ее применения 209. Определение производной. 210. Формулы дифференцирования. Таблица производных. 211. Дифференцирование суммы, произведения, частного. 212. Сложная функция и ее дифференцирование. 213. Физический смысл производной. 214. Вторая производная и ее физический смысл. 215. Касательная к графику функции. 216. Применение производной к исследованию функций на монотонность. 217. Применение производной к исследованию функций на экстремум. 218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке. 219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке. 220. Задачи на отыскание наибольших или наименьших значений величин. 221. Применение производной для доказательства тождеств. 222. Применение производной для доказательства неравенств. 223. Общая схема построения графика функции. § 22. Первообразная и интеграл 225. Таблица первообразных. 226. Правила вычисления первообразных. 227. Интеграл. 228. Связь между интегралов и первообразной (формула Ньютона—Лейбница). 229. Правила вычисления интегралов. 230. Использование интеграла для вычисления площадей плоских фигур. ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ 2. Точка. Прямая. 3. Определения. Аксиомы. Теоремы. § 2. Основные свойства простейших геометрических фигур 5. Луч. 6. Окружность. Круг. 7. Полуплоскость. 8. Угол. Градусная мера угла. 9. Смежные и вертикальные углы. 10. Центральные и вписанные углы. 11. Параллельные прямые. 12. Признаки параллельности прямых. 13. Перпендикулярные прямые. 14. Касательная к окружности. 15. Треугольники. 16. Равенство треугольников. 17. Равнобедренный треугольник. 18. Сумма углов треугольника. 19. Прямоугольный треугольник. Теорема Пифагора. 20. Окружности, вписанные в треугольник и описанные около треугольника. § 3. Геометрические построения на плоскости 22. Простейшие задачи на построение. 23. Геометрическое место точек на плоскости. § 4. Четырехугольники 25. Параллелограмм. 26. Прямоугольник. Ромб. Квадрат. 27. Трапеция. § 5. Многоугольники 29. Выпуклые многоугольники. 30. Правильные многоугольники. 31. Длина окружности. § 6. Решение треугольников 33. Соотношения между сторонами и углами в прямоугольном треугольнике. 34. Теорема косинусов. Теорема синусов. 35. Решение треугольников. § 7. Площади плоских фигур 37. Площади многоугольников. 38. Площади подобных фигур. 39. Площадь круга. ГЛАВА II. Прямые и плоскости в пространстве § 9. Параллельность прямых и плоскостей 42. Параллельность прямой и плоскости. 43. Параллельные плоскости. § 10. Перпендикулярность прямых и плоскостей 45. Перпендикуляр и наклонная к плоскости. 46. Перпендикулярность плоскостей. ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ § 11. Многогранники 48. Многогранные углы. Многогранники. 49. Призма. Параллелепипед. Куб. 50. Пираприда. 51. Правильные многогранники. § 12. Тела вращения 53. Конус. 54. Шар. § 13. Изображение пространственных фигур на плоскости 56. Ортогональное проектирование. 57. Геометрическое место точек в пространстве. § 14. Объемы тел 59. Объем параллелепипеда, призмы и пирамиды. 60. Объем цилиндра и конуса. 61. Общая формула объемов тел вращения. § 15. Площади поверхностей тел 63. Понятие площади поверхности. 64. Площади поверхностей тел вращения. ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ § 16. Координаты на плоскости и в пространстве 66. Координаты середины отрезка. § 17. Уравнения фигур на плоскости 68. Пересечение двух окружностей. 69. Уравнение прямой. 70. Пересечение прямой и окружности. § 18. Уравнения фигур в пространстве 72. Уравнение сферы. 73. Взаимное расположение сферы и плоскости. 74. Пересечение двух сфер. ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР 76. Понятие движения. § 20. Подобие фигур 78. Подобные фигуры. ГЛАВА VI. ВЕКТОРЫ 80. Понятие вектора. 81. Координаты вектора. § 22. Операции над векторами 83. Умножение вектора на число. Коллинеарные векторы. 84. Скалярное произведение векторов. ПРИЛОЖЕНИЯ ГЕОМЕТРИЯ

2.9 Четные и нечетные функции

Оглавление

Четные функции

Функция $y=f(x)$, определенная на интервале $(-a,a)$, называется четной , если при изменении знака любого значения $x$ принадлежащий этому интервалу, значение функции не меняется, а именно:

\[
f(-x)=f(x)\qquad\text{для каждого }x\text{ в интервале}(- а, а).
\]

Рис. 1: График четной функции симметричен относительно оси $y$

 

Если функция четная, ее график симметричен относительно оси $y$ . {2}$ и $y=\cos x$ (см. рис. 2). 9{2}$ (c) График $y=\cos x $ Рис. 2 $x$ принадлежащих этому интервалу, меняется только знак (а не абсолютное значение) функции, а именно
\[
f(-x)=-f(x)\qquad\text{для каждого }x\text {в интервале}(-а,а).
\]

Если функция нечетная, ее график равен 9{3}$ (б) График $y=1/x $ (c) График $y=\sin x $

Рисунок 4

• Если нечетная функция $f$ определена при $x=0$, то ее значение должно быть там равно нулю:
  \[
  f(0)=0.
  \] [Предположим, что $f(0)=b$. Поскольку точка $(0,b)$ лежит на графике $f$, а $f$ нечетна, $(0,-b)$ также должна лежать на графике $f$. Следовательно, мы должны иметь $ b=0$, иначе $f$ присвоила бы два разных значения $\pm b$ $x=0$, что невозможно.] 9{2}=г(х).
  \]

  (c) Эта функция не является ни четной, ни нечетной, поскольку
  \[
  h(-x)=1+\sin(-x)=1-\sin x\neq\begin{cases}
  1+\sin x=g (x)\\
  -(1+\sin x)=-g(x)
  \end{case}
  \]

  Обзор тригонометрических функций см. в разделе 3.3.
  

  Mathwords: четная функция

  Mathwords: четная функция

  индекс: нажмите на букву индекс: предметные области
  	Четная функция Функция с графиком, который симметричен с относительно оси Y. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт