Как решать двоичную систему: Двоичная система счисления

Головоломки Бакуро, двоичные числа — Робикс кружок робототехники

Головоломки Бакуро — отличный способ научить детей переводить числа в двоичную систему счисления и выполнять в ней арифметические операции.

Рис. 1 Пример головоломки Бакуро. Как ее решать — расскажем ниже

Головоломки Бакуро похожи на головоломки Судоку, мы должны определить , какие числа стоит вписать в пустые ячейки. Только в отличие от Судоку, это могут быть только числа являющиеся степенью двойки , а двоичная система позволит нам их быстро и правильно рассчитать.

В этой статье вы найдете алгоритм для решения подобных головоломок, примеры головоломок Бакуро и полезные ссылки на другие ресурсы по этой теме.

Что такое двоичная система счисления?

Бинарные числа это способ представления известных всем нам чисел (из привычной десятичной системы счисления) с помощью единиц (1) и нулей (0) . Вес единиц и нулей меняется в зависимости от того, на какой позиции они находится.
Итак, у каждой позиции есть свой вес. Считаем слева — направо: 1, 2, 4, 8, 16 и так далее, каждый следующий шаг в два раза больше предыдущего.
Для перевода числа из двоичной системы в десятичную мы должны умножить вес позиции на стоящее на нем число.

4	3	2	1	0	позиция(начнем с нуля)
16	8	4	2	1	вес (степени двойки)

Информация для учеников которые умеют возводить в степень: как не трудно заметить вес позиции это двойка (2) возведенная в степень номера позиции.

Перевод двоичного числа в десятичное

Давайте разберемся на примере, попробуем перевести двоичные числа в десятичные.

двоичное число	складываем (каждое число умноженное на вес справа — налево)	результат (десятичное число)
00001	1 + 0 + 0 + 0 + 0	1
00011	1 + 2 + 0 + 0 + 0	3
00111	1 + 2 + 4 + 0 + 0	7
01111	1 + 2 + 4 + 8 + 0	15
11111	1 + 2 + 4 + 8 +16	31

Обратите внимание, что получаемое в результате сложения число, в каждом случае на один меньше , чем вес следующей позиции. Эти двоичные числа — интересная штука!

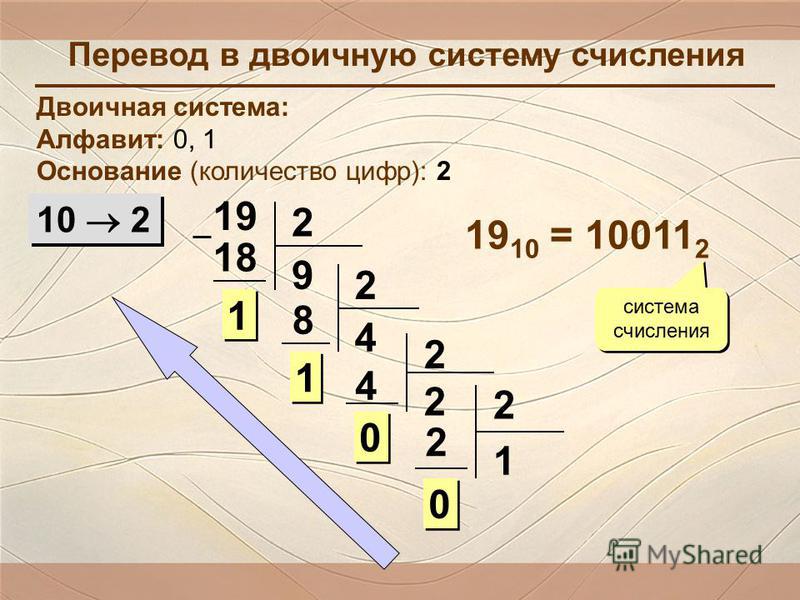
Перевод десятичного числа в двоичное

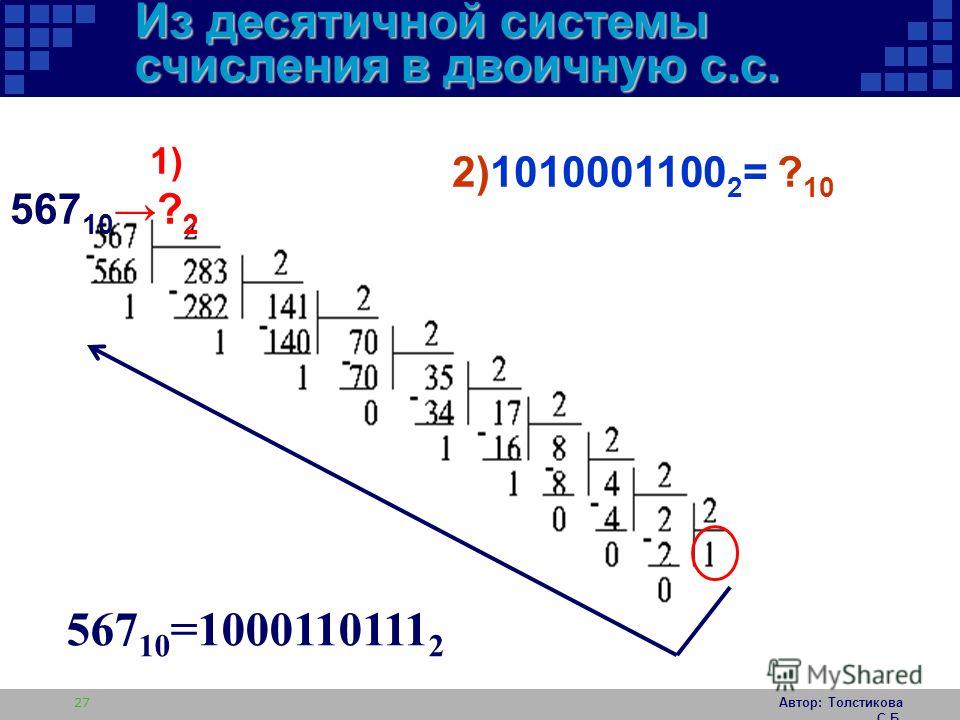
Теперь разберемся как перевести двоичное число в десятичное. Для этого удобно воспользоваться методом деления в столбик. Мы делим число на 2 максимально возможное число раз и запоминаем остатки от этих делений. Это и будет искомое двоичное число. Чтобы не переписывать здесь всю последовательность действий при делении, просто оставим для Вас полезную ссылку где все расписано очень подробно.

Как решить простейшую головоломку Бакуро

Теперь, когда мы знаем как переводить двоичные числа мы можем решить простейшую головоломку Бакуро. Давайте сделаем это!

Рис. 2 Головоломка Бакуро в простейшем виде.

Правило № 1: в головоломке Бакуро пустые ячейки должны быть заплонены числами которые составляют являются степенями числа два. Они же, вес позиции. При этом , если в двоичных числах всего 4 знака, эти числа не могут быть больше восьми. (два в третьей степени).

Правило № 2: как и в Судоку, сумма чисел записанных в пустые ячейки должна быть равна заданной ячейке по горизонтали и по вертикали. Например, в нашем случае, во втором ряду мы должны получить в сумме 12, а во втором столбце — 6.

Правило № 3: если пораскинуть головой, можно догадаться, что из заданного двоичного числа можно вывести числа, которые мы должны записать в связанные с ним ячейки. Например , двоичное число 1001 (9) включает в себя 1 в четвертой позиции, то есть 8 и 1 в первой позиции, то есть 1. Осталось понять, как их распределить в ячейках в первом столбце.

Правило № 4: Числа записанные в столбцах и в строках должны сходиться. То есть сумма в первом столбце должна равняться 9, а в первой строке — 3. В нашем примере, это поможет нам определить, куда записаться 1 , а куда 8. Так как сумма в первой строке должна равняться 3, записать туда 8 мы точно не можем, значит записываем туда единицу.

Рис. 3 Правильное решение на головоломку Бакуро

Подсказки

Если вы немного подумаете, вы ведите еще много интересных подсказок, которые следуют из двоичной записи чисел в этой головоломке, например:

1. Если число нечетное, очевидно , что где-то в ячейках должна быть записана единица, так как при сложении четных чисел — всегда получается четное число.
2. Существует не так много способов разбить число на числа являющиеся степенями числа 2, часто такой способ всего один.

Мы не будем делиться с вами всеми секретами. 🙂 Попробуйте решить эти задачки самостоятельно, мы уверены, они помогут вам лучше разобраться в двоичных числах и переводах из одной системы счисления в другую.

Полезные ссылки

1. Больше информации о том, что такое Бакуро головоломки и как их решать (на английском) https://teachinglondoncomputing.org/bakuro/
2. Примеры головоломок Бакуро № 1 https://teachinglondoncomputing.files.wordpress.com/2015/11/puzzlesheet-bakuro2.pdf
3. Примеры головоломок Бакуро № 2 https://teachinglondoncomputing.files.wordpress.com/2015/11/puzzlesheet-bakuro11.pdf
4. Слайды с подсказками https://teachinglondoncomputing.files.wordpress.com/2015/11/slides-bakuro.pdf

Другие головоломки на нашем сайте

Если вы занимаетесь робототехникой и программированием и вам нравится решать головоломки, посмотрите на подборку наших авторских ребусов и задачек:

1. Задачка на конструкторе Знаток с мотором и пропеллером
2. Задачка на конструкторе Знаток с семисегментным индикатором

Сохраните или поделитесь

Как перевести в двоичную?

Статьи › Код › Как перевести буквы в двоичный код?

Для того, чтобы преобразовать число из десятичной системы счисления в двоичную, необходимо выполнить следующие действия.

• Делим десятичное число на 2 и записываем остаток от деления.
• Результат деления вновь делим на 2 и опять записываем остаток.
• Повторяем операцию до тех пор пока результат деления не будет равен нулю.

1. Как перевести число в двоичную систему алгоритм?
2. Как перевести из десятичной системы в двоичную систему?
3. Как перевести целое число из десятичной системы в двоичную?
4. Как перевести отрицательное число в двоичную систему счисления?
5. Как перевести число в двоичную систему пример?
6. Как записать число в двоичную систему?
7. Как перевести из десятичной в любую?
8. Как перевести 12 из десятичной в двоичную?
9. Как перевести число с запятой в двоичную систему?
10. Как перевести 121 из десятичной в двоичную?
11. Как перевести 126 из десятичной в двоичную?
12. Как перевести 90 из десятичной в двоичную?
13. Как быстро перевести в двоичную систему счисления?
14. Как решить двоичную систему счисления?
15. Как перевести число 9 в двоичную систему?
16. Как перевести число 123 в двоичную систему?
17. Как перевести из 4 в 2 систему счисления?
18. Как перевести число 42 в двоичную систему?
19. Как перевести 105 из десятичной в двоичную?
20. Как перевести 120 из десятичной в двоичную?
21. Как перевести 123 из десятичной в двоичную?
22. Как перевести число 11 в двоичную систему?

Как перевести число в двоичную систему алгоритм?

Таким образом, для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на 2 до тех пор, пока не получим частное, которое будет равно нулю.

Как перевести из десятичной системы в двоичную систему?

Алгоритм перевода целого десятичного числа в двоичное:

• последовательно выполнять деление целого десятичного числа и получаемых целых частных на 2 до тех пор, пока не получится частное, меньшее 2;
• записать полученные остатки в обратной последовательности.

Как перевести целое число из десятичной системы в двоичную?

Перевод целых десятичных чисел в любую другую системы счисления осуществляется делением числа на основание новой системы счисления до тех пор, пока в остатке не останется число меньшее основания новой системы счисления.

Как перевести отрицательное число в двоичную систему счисления?

Для перевода отрицательного числа в двоичный дополнительный код нужно перевести положительное число в двоичную систему, потом поменять нули на единицы и единицы на нули. Затем прибавить к результату 1.

Как перевести число в двоичную систему пример?

Для перевода числа из восьмеричной системы счисления в двоичную необходимо каждую цифру этого числа записать трехразрядным двоичным числом (триадой).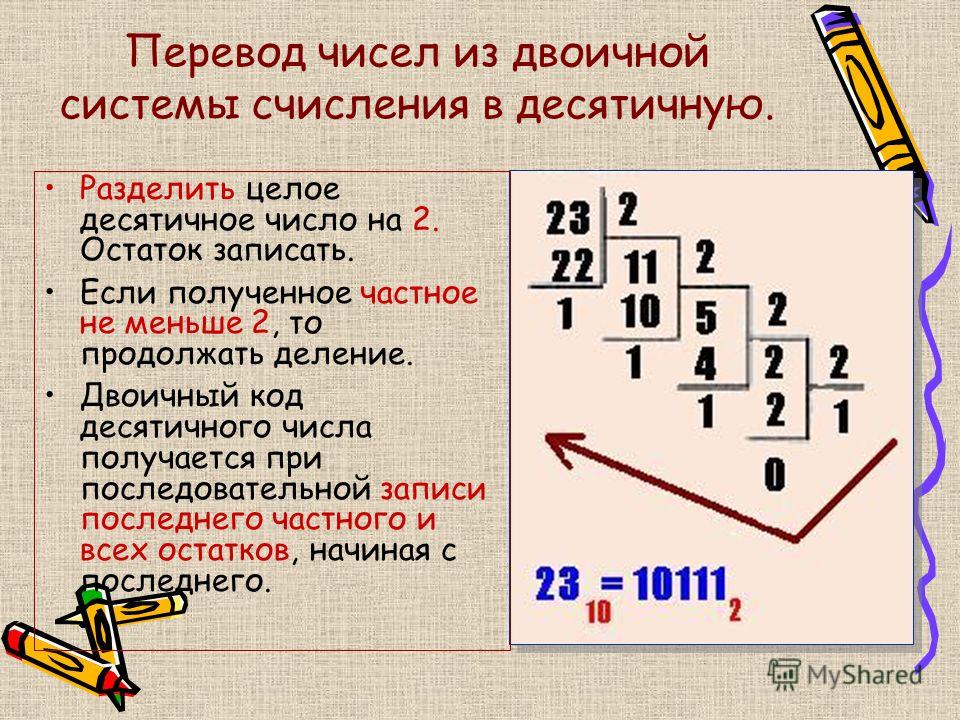 Пример: записать число 16,24(8) в двоичной системе счисления. Ответ: 16,24(8)= 1110,0101(2).

Как записать число в двоичную систему?

В двоичной системе счисления числа записываются с помощью двух символов (0 и 1). Чтобы не путать, в какой системе счисления записано число, его снабжают указателем справа внизу. Например, число в десятичной системе 510, в двоичной 1012.

Как перевести из десятичной в любую?

Перевод из десятичной системы счисления в любую другую.

Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания.

Как перевести 12 из десятичной в двоичную?

Двоичная система счисления — позиционная система счисления с основанием 2. Шестнадцатеричная система счисления — позиционная система счисления по целочисленному основанию 16.Числовые системы

Десятичное число (положительное)	Двоичное число
12	1100
13	1101
14	1110
15	1111

Как перевести число с запятой в двоичную систему?

Умножаем последовательно число на основание искомой системы счисления — \(2\). Умножаем до тех пор, пока не получим единицу в целой части. Записываем выделенные на схеме числа в прямом порядке и получаем в итоге двоичное число \(111010,001\).

Как перевести 121 из десятичной в двоичную?

Решение. Представим число 121 в виде разности: 121 = 128 − 7. Теперь переведём отдельно два числа и вычтем результаты в двоичной системе счисления: 128 = 10000000; 7 = 111. Следовательно, 121 = 1111001.

Как перевести 126 из десятичной в двоичную?

Решение. Представим 126 в виде суммы степеней двойки: 126 10 = 1 · 26 + 1 · 25 + 1 · 24 + 1 · 23 + 1 · 22 + 1 · 21 = 11111102. Ответ: 1111110.

Как перевести 90 из десятичной в двоичную?

Двоичная система — 1011010.

Как быстро перевести в двоичную систему счисления?

Чтобы быстро переводить числа из десятичной системы счисления в двоичную, нужно хорошо знать числа «2 в степени». Например, 210=1024 и т. д. Это позволит решать некоторые примеры на перевод буквально за секунды.

Как решить двоичную систему счисления?

Для перевода десятичного числа в двоичное надо разделить его на 2 и собрать остатки, начиная с последнего частного. Для перевода двоичного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания двоичной системы счисления на соответствующие цифры в разрядах двоичного числа.

Как перевести число 9 в двоичную систему?

Шестнадцатеричная система — 9. Двоичная система — 1001.

Как перевести число 123 в двоичную систему?

Шестнадцатеричная система — 7b. Двоичная система — 1111011.

Как перевести из 4 в 2 систему счисления?

Цифры исходного числа четверичной системы счисления заменяются (слева направо) на соответствующие (по таблице пар) пары цифр двоичной системы счисления. Незначащий нуль первой (самой левой) пары опускается (отбрасывается).

Как перевести число 42 в двоичную систему?

Шестнадцатеричная система — 2a. Двоичная система — 101010.

Как перевести 105 из десятичной в двоичную?

Шестнадцатеричная система — 69. Двоичная система — 1101001.

Как перевести 120 из десятичной в двоичную?

Перевод 120 в двоичную систему — решение, подробно.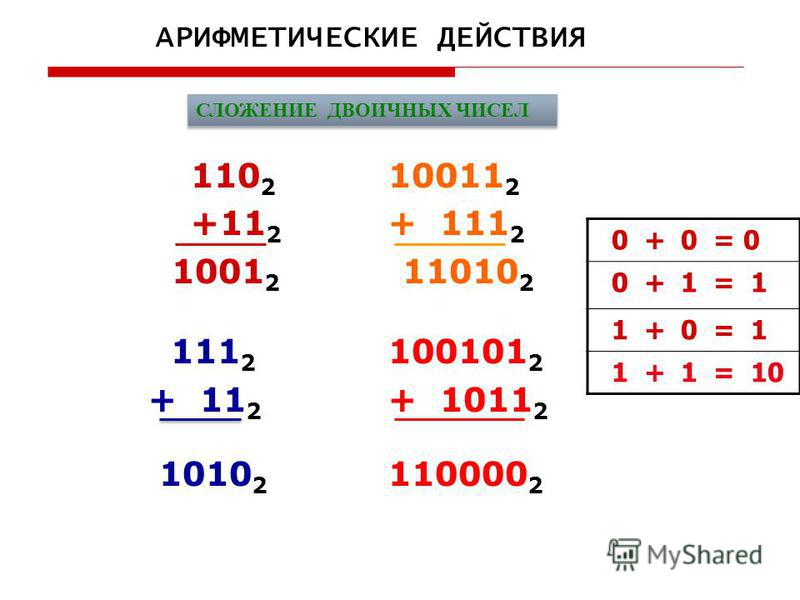

Ответ: 12010(в десятичной) равно = 11110002(в двоичной).

Как перевести 123 из десятичной в двоичную?

Для перевода десятичного числа 123 в двоичную систему счисления, необходимо его последовательно делить на 2 до тех пор, пока остаток не станет меньше чем 2.

Как перевести число 11 в двоичную систему?

Двоичная система счисления — позиционная система счисления с основанием 2. Шестнадцатеричная система счисления — позиционная система счисления по целочисленному основанию 16.Числовые системы

Десятичное число (положительное)	Двоичное число
10	1010
11	1011
12	1100
13	1101

Основы счисления: введение и двоичные числа

Основание-4 и основание-7Восьмеричное и шестнадцатеричное

Purplemath

Преобразование между различными системами счисления на самом деле довольно просто, но поначалу мысли, лежащие в основе этого, могут показаться немного запутанными. И хотя тема различных систем счисления может показаться вам несколько бессмысленной, появление компьютеров и компьютерной графики увеличило потребность в знании того, как работать с различными (недесятичными) системами счисления, особенно с двоичными системами (единицы и нули) и шестнадцатеричные системы (числа от нуля до девяти, за которыми следуют буквы от A до F).

Содержание продолжается ниже

MathHelp.com

В нашей обычной десятичной системе у нас есть цифры для чисел от нуля до девяти. У нас нет однозначного числа «десять». (Римляне так и сделали, в их иероглифе «X».) Да, мы пишем «10», но это означает «1 десяток и 0 единиц». Это две цифры; у нас нет ни одной одиночной цифры, обозначающей «десять».

Вместо этого, когда нам нужно сосчитать на единицу больше девяти, мы обнуляем столбец единиц и добавляем единицу к столбцу десятков. Когда мы становимся слишком большими в столбце десятков — когда нам нужно на единицу больше, чем девять десятков и девять единиц («99″), мы обнуляем столбцы десятков и единиц и прибавляем единицу к столбцу десяти умножить на десять, или сотням. Следующий столбец — это столбец десять умножить на десять, или тысяч. и так далее, причем каждый больший столбец в десять раз больше предыдущего. Мы помещаем цифры в каждый столбец, говоря нам, сколько копий этой степени десяти нам нужно. другие основания не таковы, что вы занимаетесь счислением с основанием десять с детства. И (почти) каждая цивилизация использовала математику с основанием десять, вероятно, по той простой причине, что у нас десять пальцев. Если бы вместо этого мы жили в мультипликационный мир, где у нас было бы только четыре пальца на каждой руке (считайте их в следующий раз, когда вы смотрите телевизор или читаете комиксы), тогда «естественной» базовой системой, вероятно, была бы восьмеричная система счисления.

Двоичный

Давайте посмотрим на числа с основанием два или двоичные. Как бы вы написали, например, 12 ₁₀ («двенадцать, основание десять») в виде двоичного числа? Вам нужно будет преобразовать в столбцы с основанием два, аналог столбцов с основанием десять.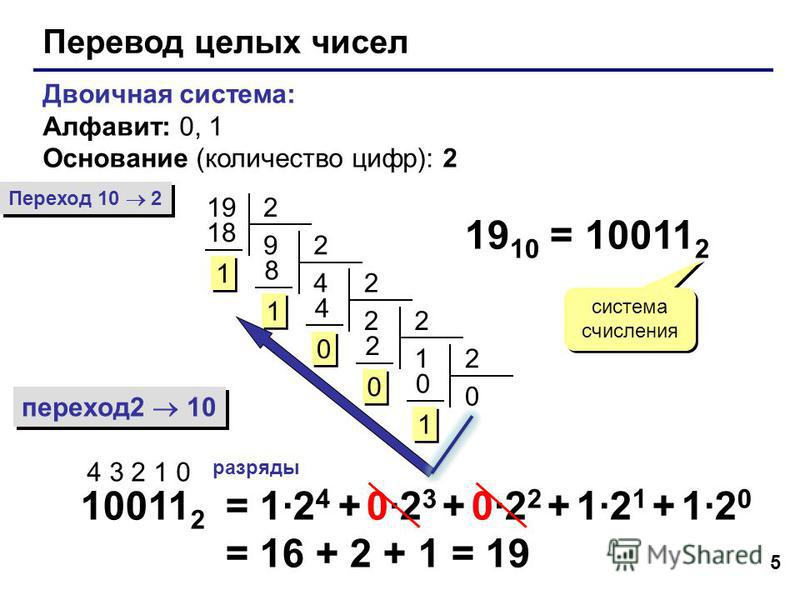 В базе десять у вас есть столбцы или «места» для 10 ⁰ = 1, 10 ¹ = 10, 10 ² = 100, 10 ³ = 1000 и так далее. Точно так же в базе два у вас есть столбцы или «места» для 2 ⁰ = 1, 2 ¹ = 2, 2 ² = 4, 2 ³ = 8, 2 ⁴ = 16 и так далее.

Первый столбец в математике с основанием два — это столбец единиц. Но только «0» или «1» могут быть в столбце единиц. Когда вы дойдете до «два», вы обнаружите, что нет ни одной одиночной цифры, обозначающей «два» в математике с основанием два. Вместо этого вы помещаете «1» в столбец «двойки» и «0» в столбец «единицы», указывая на «1 два и 0 единиц». Основание десять «два» (2 ₁₀ ) записывается в двоичном виде как 10 ₂ .

«Три» по основанию два на самом деле «1 два и 1 один», поэтому оно записывается как 11 ₂ . «Четыре» на самом деле дважды два, поэтому мы обнуляем столбец двоек и столбец единиц и ставим «1» в столбец четверок; 4 ₁₀ записывается в двоичной форме как 100 ₂ .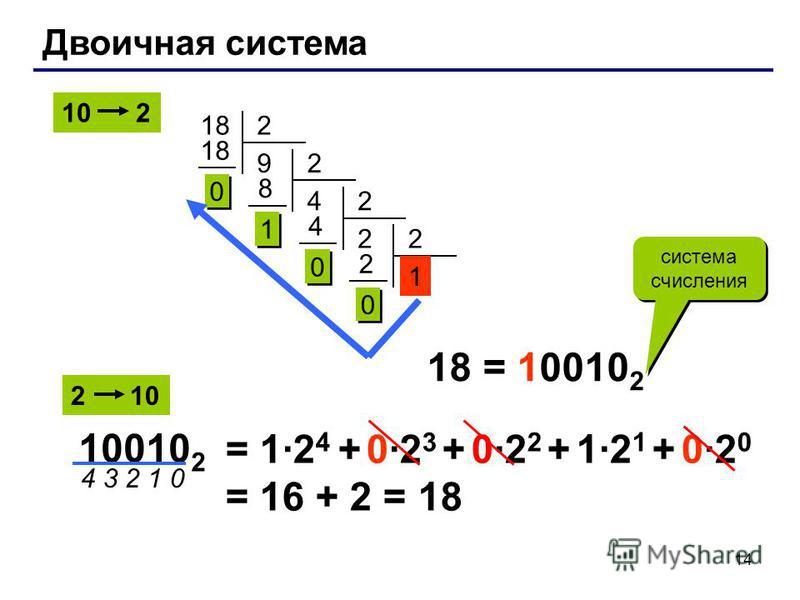 Вот список первых нескольких чисел:

Преобразование между двоичными и десятичными числами довольно просто, если вы помните, что каждая цифра в двоичном числе представляет собой степень двойки.

Я перечислю цифры по порядку, как они появляются в номере, который мне дали. Затем в другом ряду я буду считать эти цифры СПРАВА, начиная с нуля:

Первая строка выше (обозначенная как «цифры») содержит цифры двоичного числа; вторая строка (обозначенная как «нумерация») содержит степень числа 2 (основание), соответствующую каждой цифре. Я буду использовать этот список для преобразования каждой цифры в степень двойки, которую она представляет:

1×2 ⁸ + 0×2 ⁷ + 1×2 ⁶ + 1×2 ⁵ + 0× 2 ⁴ + 0×2 ³ + 1×2 ² + 0×2 ¹ + 1×2 ⁰

= 1×256 + 0×128 + 1×364 + 1×364 + 0×16 + 0×8 + 1×4 + 0×2 + 1×1

= 256 + 64 + 32 + 4 + 1

= 357

Тогда 101100101 ₂ преобразуется в 357 ₁₀ .

---

Преобразование десятичных чисел в двоичные почти так же просто: просто разделите на 2.

Чтобы выполнить это преобразование, мне нужно несколько раз делить на 2, отслеживая остатки по ходу дела. Смотрите ниже:

Приведенный выше рисунок анимирован на «живой» веб-странице.

Как видите, после многократного деления на 2 я получил следующие остатки:

Эти остатки говорят мне, что такое двоичное число. Я читал числа снаружи деления, начиная сверху с конечного значения и его остатка, и двигался по правой стороне последовательного деления вниз. Затем:

357 ₁₀ преобразуется в 101100101 ₂ .

---

---

Этот метод преобразования подходит для преобразования в любую недесятичную систему счисления. Только не забудьте включить эту первую цифру вверху, перед списком остатков. Если вам интересно, объяснение того, почему этот метод работает, доступно здесь.

Вы можете преобразовать десятичную систему счисления в любую другую. Когда вы будете изучать эту тему в классе, вы, вероятно, будете преобразовывать числа в различные другие системы счисления, поэтому давайте рассмотрим еще несколько примеров…

---

URL: https://www.purplemath.com/modules/numbbase .htm

Стр. 2 Стр. 3

Двоичная формула с примерами решения

Двоичная система счисления — это система чисел, имеющая основание 2 и использующая только две цифры, «0 и 1». Это один из четырех типов систем счисления, который чаще всего используется компьютерными языками, такими как Java и C++. «Би» в слове «двоичный» означает «два». Некоторые примеры двоичных чисел: (11) ₂ , (1110) ₂ , (10101) ₂ и так далее. Здесь 2 — основание двоичного числа, а каждая цифра называется битом. Двоичное число может быть преобразовано в другие три системы счисления, то есть в десятичную систему счисления, восьмеричную систему счисления и шестнадцатеричную систему счисления. В этой статье мы обсудим арифметические операции над двоичными числами и формулы преобразования двоичных чисел в другие три системы счисления.

Двоичная формула

Чтобы понять двоичную систему счисления, мы должны сначала понять ее действие. Двоичные числа широко используются в электронных схемах, где реализованы логические элементы, а также в микроконтроллерах для логических вычислений. Двоичное число использует только две цифры, «0 и 1», где каждая цифра известна как бит. Ввод данных в компьютер сначала преобразуется в двоичный язык с помощью назначенного кода ASCII. Кроме того, информация преобразуется из бинарного языка в язык пользователя и представляется в виде выходных данных.

Арифметическая операция над двоичными числами

Двоичное сложение

Сложение двоичных чисел немного отличается от обычного сложения, но довольно просто. Выполняя сложение двух двоичных чисел, мы должны складывать их цифра за цифрой. Сложение двух двоичных чисел также является двоичным числом. Взгляните на приведенную ниже таблицу, чтобы понять сложение двоичных чисел.

Двоичный номер 1	Binary number 2	Sum	Carry
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

.

Здесь нет переноса, как при сложении двоичных чисел, но требуется заимствование, когда мы вычитаем более высокую цифру из меньшей цифры. Взгляните на приведенную ниже таблицу, чтобы понять вычитание двоичных чисел.

.0176

Binary number 1	Binary number 2	Difference	Borrow
0	0	0	0
0	1	1	1
17
133 9000 3
33333333 1339393 13919193199939 9000 3	0	1	0
1	1	0	0

Binary Multiplication

Binary multiplication is similar к умножению нормальных чисел. Взгляните на приведенную ниже таблицу, чтобы понять умножение двоичных чисел.

Двоичный номер 1	Binary number 2	Multiplication
0	0	0
0	1	0
1	0	0
1	1	1

Двоично-десятичная формула

Десятичное число чаще всего используется в нашей повседневной жизни. Десятичное число имеет основание 10, и для его представления используются цифры от 0 до 9. Некоторые примеры десятичных чисел: (14)10, (245)10, (1456)10 и т. д. Теперь, чтобы преобразовать двоичное число «a _n-1 ….a ₃ a ₂ a ₁ a ₀ «, умножьте каждую цифру данного двоичного числа на степени 2.  

Если двоичное число с n цифрами равно B = a _n-1 ….a ₃ a ₂ a ₁ a ₀ ,

Теперь десятичное число равно D = (1n 9002 -1 × 2 ^n-1 ) +…+(а ₃ × 2 ³ ) + (а ₂ × 2 ² ) + (а ₁ × 3 2 1 900) (а ₀ × 2 ⁰ ).

Десятичное число	Двоичное число	Десятичное число	Binary number
1	001	11	1011
2	010	12	1100
3	011	13	1101
4	100	14	1110
5	101	15	1111
6	110	16	10000
7	111	17	10001
8	1000	18	10010
9	1001	19	10011
10	1010	20	10100

2 ₂ в десятичном формате.

Решение:

Данное двоичное число равно (1101011) ₂ .

(11001)2 = (1 × 2 ⁶ ) + (1 × 2 ⁵ ) + (0 × 2 ⁴ ) + (1 × 2 ³ ) + (0 × 2 ² ) ) + (1 × 2 ¹ ) + (1 × 2 ⁰ )

= 64 + 32 + 0 + 8 + 0 + 2 + 1 = 107

Следовательно, двоичное число (1101011) ₂ равно десятичному числу (107) ₁₀ .

Преобразование десятичного числа в двоичное

Десятичное число можно преобразовать в двоичное путем непрерывного деления заданного числа на 2, пока мы не получим частное, равное 1, и записать числа снизу вверх.

Пример: преобразовать десятичное число (39) ₁₀ в двоичное.

Решение: 

Чтобы преобразовать (39) ₁₀ в двоичное число, мы должны последовательно делить 39 на 2, пока не получим частное 1,9. 0003

 

Таким образом, (39) ₁₀ в двоичной системе счисления равно (100111) ₂ .

Двоично-восьмеричная формула

Восьмеричное число — это система счисления, имеющая основание 8 и использующая цифры от 0 до 7. Восьмеричная система счисления первоначально использовалась как язык компьютерного программирования в раннем возрасте. В восьмеричной системе счисления после 7 идут числа от 10 до 17, затем от 20 до 27 и так далее. Они не содержат цифр, таких как 8 и 9. У нас есть два типа методов преобразования двоичного числа в восьмеричное, т. е. путем прямого преобразования двоичного числа в восьмеричное, а другой — преобразования двоичного числа в десятичное, а затем преобразования полученное десятичное число в восьмеричное.

Binary number	Octal Number	Binary number	Octal Number
000	0	1000	10
001	1	1001	11
0002 010	2	1010	12
011	3	1011	13
100	4	1100	14
101	5	1101	15
110	6	1110	16
111	7	1111	17

Например, преобразуйте (10110110) ₂ в восьмеричное число.

Решение:

Метод 1:

Шаг 1: Начиная с правого конца, разделите заданное двоичное число на пару из трех цифр.

 10-110-110

Шаг 2: Мы можем заметить, что в первой группе нет трех цифр. Поэтому добавьте нули слева. Теперь подставьте в него значение восьмеричного числа.

010-110-110

(010) ₂ = (2) ₈

(110) ₂ = (6) ₈

(110) ₂ = (6)

(110) ₂ = (6)

(110) ₂ = (6) ₈

Шаг 3: Теперь объедините все цифры.

010-110-110 = 2-6-6 = 266

Следовательно, двоичное число (10110110) ₂ в восьмеричной системе равен 266.

Метод 2:

Это долгий процесс, так как мы должны выполнить два преобразования, то есть из двоичного в десятичное и снова из десятичного в восьмеричное.

Шаг 1: Преобразование двоичного числа (10110110) ₂ в десятичное

(1 × 2 ⁷ ) + (0 × 2 ⁶ ) + (3 × 1 4 9002) × 2 ⁴ ) + (0 × 2 ³ ) + (1 × 2 ² ) + (1 × 2 ¹ ) + (0 × 2 ⁰ )

= 128 + 0 + 32 + 16 + 0 + 4 + 2 + 0 = (182) ₁₀

Шаг 2: Теперь разделим полученное десятичное число на 8. 0 0 2 3 

, двоичное число (10110110)

₂ в восьмеричной системе равно 266.

Преобразование из двоичной системы в шестнадцатеричную Формула

Шестнадцатеричная система счисления — это система счисления, имеющая основание 16 и использующая числа от 0 до 7 и алфавиты. от A до F, где алфавиты от A до F представляют числа от 10 до 15 десятичной системы счисления. Некоторыми примерами шестнадцатеричной системы счисления являются AF16, 7BF, B2A1 и т. д. У нас есть два типа методов для преобразования двоичного числа в шестнадцатеричное, т.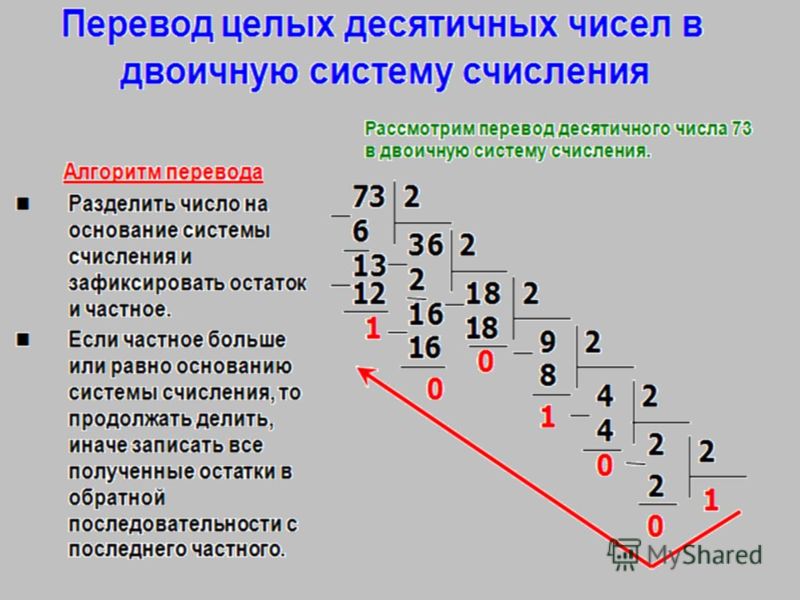 е. путем прямого преобразования двоичного в шестнадцатеричное, а другой — преобразования двоичного в десятичное. , а затем преобразование полученного десятичного числа в шестнадцатеричное.

Decimal number	Binary number	Hexadecimal Number	Decimal number	Binary number	Hexadecimal number
0	0000	0	8	1000	8 169
1	0001	1	9	1001	9
2	0010	2	10	1010	A
3	0011	3	11	1011	B
4	0100	4	12	1100	C
5	0101	5	13	1101	D
6	0110	6	14	1110	E
7	0111	7	15	1111	F

Например, преобразуйте (1101010) ₂ в шестнадцатеричное число.

Решение:

Метод 1:

Шаг 1: Начиная с правого конца, разделите заданное двоичное число на пару из четырех цифр.

1101010 ⇒ 110-1010

Шаг 2: Мы можем заметить, что в первой группе нет четырех цифр. Поэтому добавьте нули слева. Теперь подставьте в него значение шестнадцатеричного числа.

110-1010 ⇒ 0110-1010

(0110) ₂ = (6) ₁₆

(1010) ₂ = (А) ₁₆

Шаг 3: Теперь объедините все цифры.

0110-1010 = 6 – А = (6А) ₁₆

Таким образом, двоичное число (1101010) ₂ в шестнадцатеричной системе равно 6А.

Метод 2:

Это долгий процесс, так как мы должны выполнить два преобразования, то есть из двоичного в десятичное и снова из десятичного в шестнадцатеричное.

Шаг 1: Преобразование двоичного числа (1101010) ₂ в десятичное

(1 × 2 ⁶ ) + (1 × 2 ⁵ ) + (0 × 2 ⁴ ) + (1 × 2 ³ ) + (0 × 2 ² ) + (1 × 2 ¹ ) + (0 × 2 ⁰ )

= 64 + 32 + 0 + 8 + 0 + 2 + 0 = (106) ₁₀

Шаг 2: Разделите полученное десятичное число число на 16.

 

Мы знаем, что в шестнадцатеричной системе 10 равно A. Таким образом, шестнадцатеричное число равно 6A.

Следовательно, двоичное число (1101010) ₂ в шестнадцатеричной системе равно 6А.

Решенные примеры двоичной формулы

Пример 1. Преобразование десятичного числа (73) ₁₀ в двоичное.

Решение:

Чтобы преобразовать (73) ₁₀ в двоичное число, мы должны непрерывно делить его на 2, пока не получим частное от 1. 10 в двоичной системе счисления равно (1001001) ₂ .

Пример 2. Преобразование двоичного числа (110010101) ₂ в восьмеричное.

Решение:

Чтобы преобразовать двоичное число в восьмеричное, сначала мы должны разделить данное двоичное число на пару из трех цифр, начиная с правого конца. Теперь подставьте в него значение восьмеричного числа.

110010101 ⇒ 110 – 010 – 101

6 – 2 – 5 = 625

Следовательно, двоичное число (110010101) ₂ в восьмеричной системе равен 625.

Пример 3: Преобразование двоичного числа (10110110) ₂ в шестнадцатеричное.

Решение: 

Чтобы преобразовать двоичное число в шестнадцатеричное, мы сначала должны разделить данное двоичное число на пару из четырех цифр, начиная с правого конца. Теперь подставьте в него значение шестнадцатеричного числа.

10110110 ⇒ 1011 – 0110

(1011) ₂ = (Б) ₁₆

(0110) ₂ = (6) ₁₆

SO, (10110110) ₂ = (B6) ₁₆

Следовательно, бинарный номер (10110110). .

Пример 4: Добавьте (1011010) ₂ и (1101011) ₂ .

Решение:

Отсюда (1011010) ₂ + (1011010) ₂ = 2 92 2

01.

Пример 5: Умножьте (110) ₂ и (101) ₂ .

Решение:

Таким образом, (110) ₂ × (101) ₂ = (11110) _{2 9002.}

Часто задаваемые вопросы о двоичной формуле

Вопрос 1: Дайте определение двоичной системе счисления.

Ответ:

Двоичная система счисления — это система счисления, имеющая основание 2 и использующая только две цифры «0 и 1». Это один из четырех типов систем счисления, который чаще всего используется компьютерными языками, такими как Java и C++. «Би» в слове «двоичный» означает «два». Некоторые примеры двоичных чисел: (11) ₂ , (1110) ₂ , (10101) ₂ и так далее.

Вопрос 2: Что такое формула для преобразования двоичного числа в десятичное число?

Ответ:

Для преобразования двоичного числа «a _n-1 ….

a ₃ a ₂ a _{1 1 цифра} a 0 со степенями двойки.

Если двоичное число из n цифр равно B = a _n-1 ….a ₃ a ₂ a ₁ a ₀ ,

Теперь десятичное число равно D = (a _n-1 × 2 ^n-1 ) +… ³ ) + (а ₂ × 2 ² ) + (а ₁ × 2 ¹ ) + (а ₀ × 2 ⁰ ).

Вопрос 3: Какова формула преобразования двоичного числа в шестнадцатеричное?

Ответ:

У нас есть два типа методов для преобразования двоичного числа в шестнадцатеричное число, т. е. непосредственное преобразование двоичного числа в шестнадцатеричное, а другой — преобразование двоичного числа в десятичное, а затем преобразование полученного десятичное в шестнадцатеричное. Чтобы преобразовать двоичное число в шестнадцатеричное, мы сначала должны разделить данное двоичное число на пару из четырех цифр, начиная с правого конца.

No related posts.