Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3.  ВЫЧИТАНИЕ§ 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5. 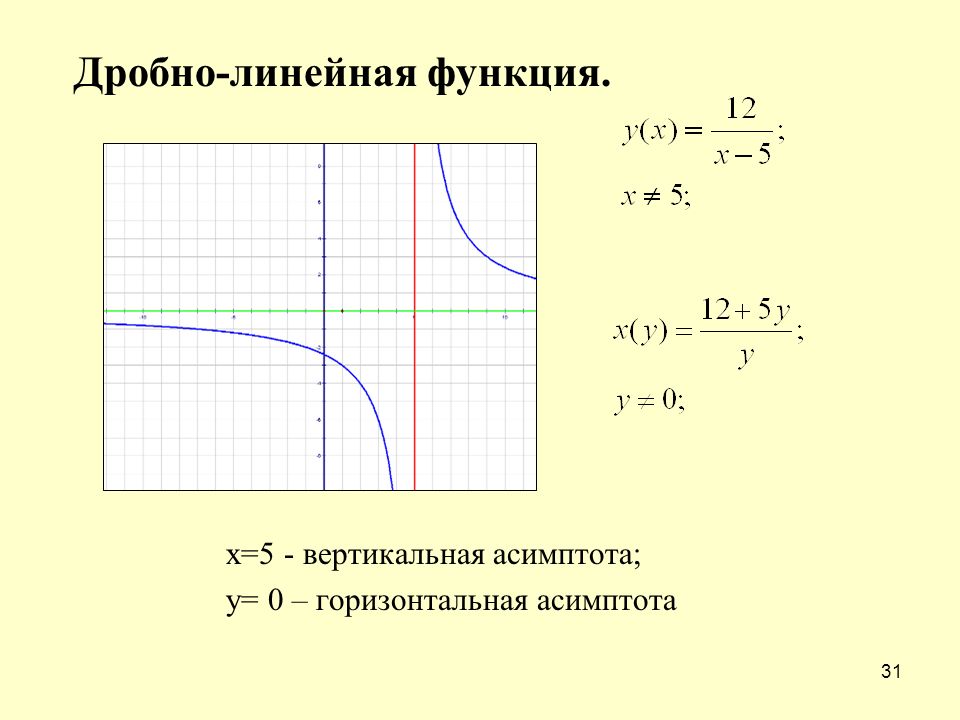 СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ§ 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5. ОДНОЧЛЕНЫ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ § 5. СТЕПЕНЬ ДРОБИ Контрольные вопросы ГЛАВА VI § 1.  ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ§ 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3. 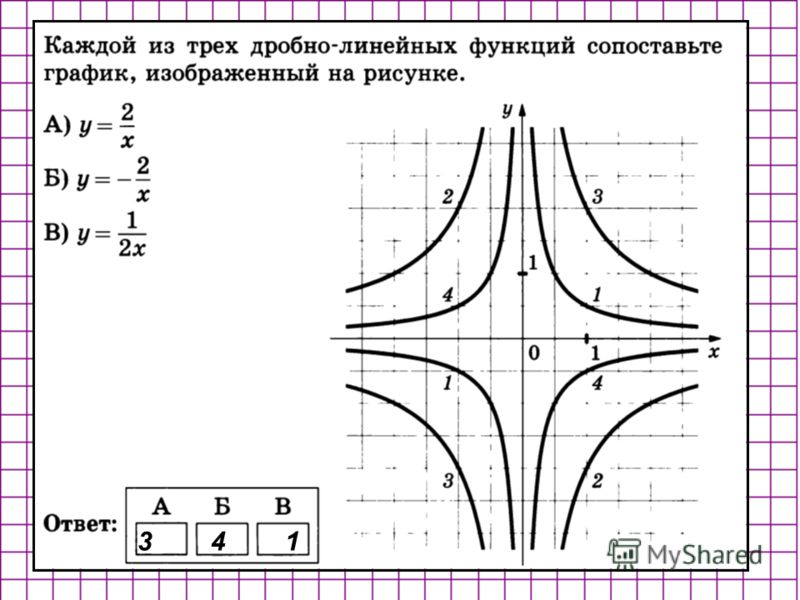 КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК§ 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4.  СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросыГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4. 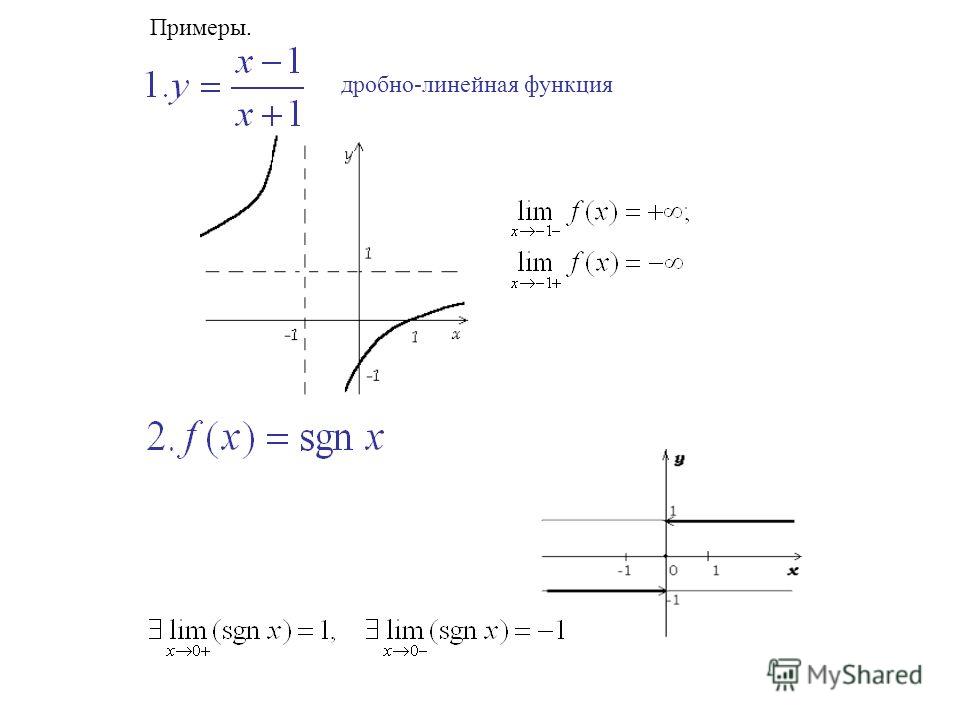 СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК§ 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2. 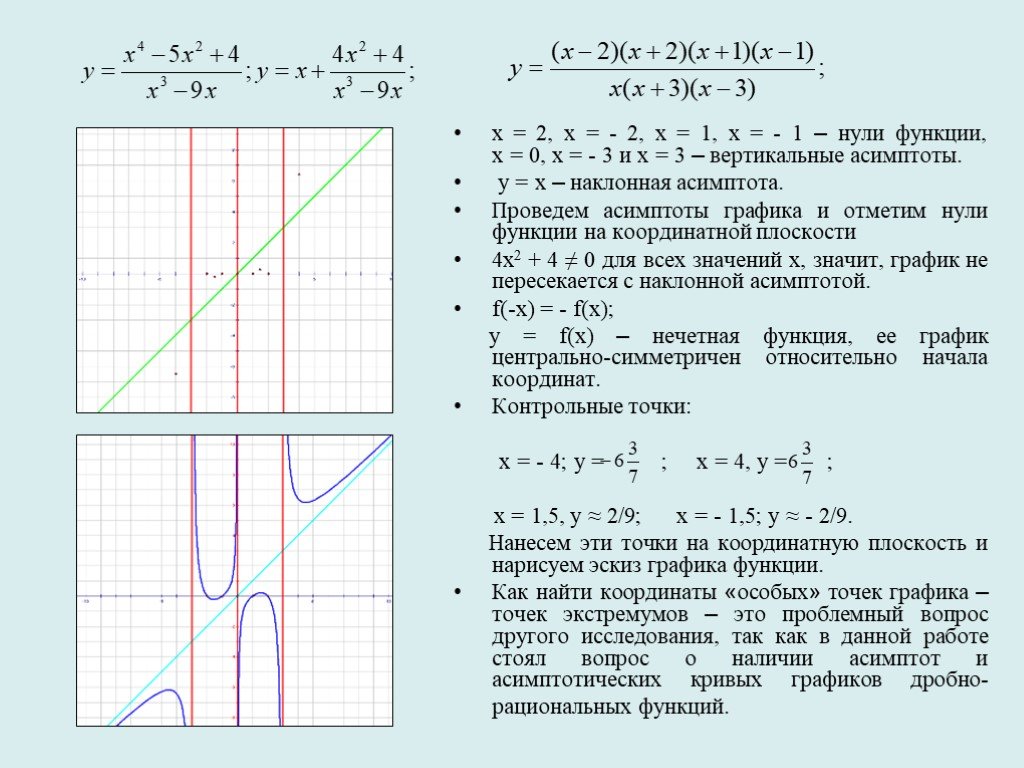 ПРЕДЕЛ ФУНКЦИИ§ 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ Контрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1. 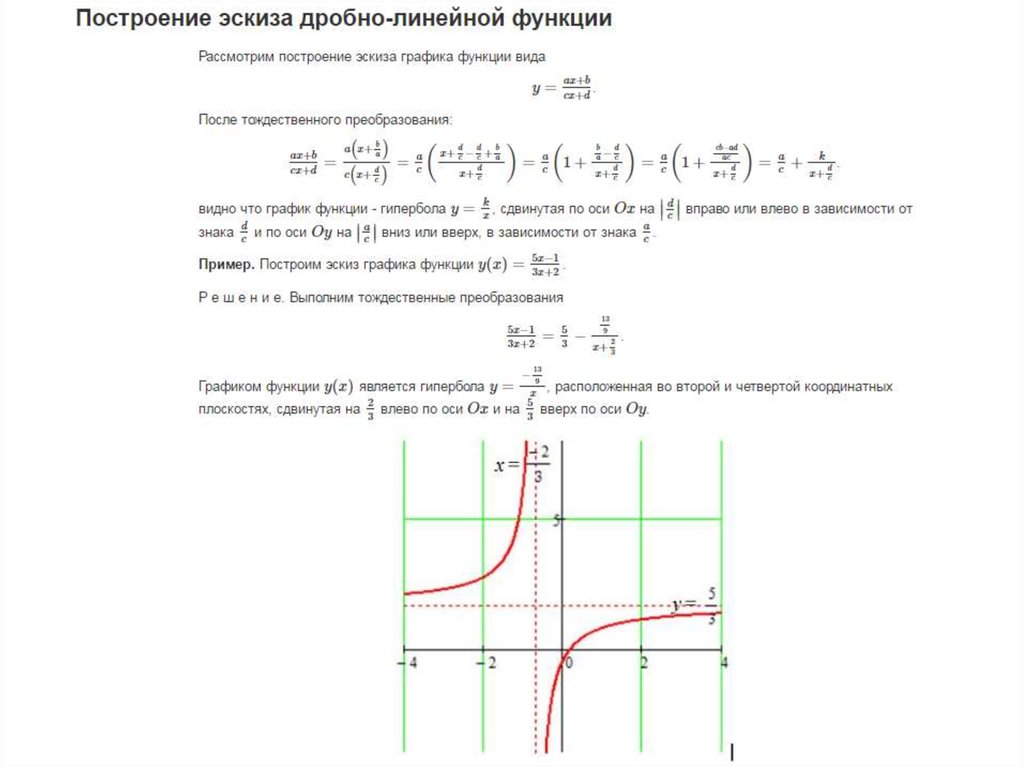 ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК§ 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1.  ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА§ 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5. Задачи на проценты 6. Задачи на смеси (сплавы) 7. Задачи на разбавление |
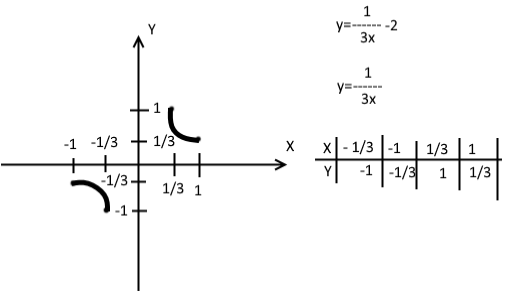
Дробно-рациональной функцией называется отношение двух многочленов:
, коэффициенты при степенях x -действительные числа, причём, будем предполагать, что числитель и знаменатель дроби не имеют общих линейных сомножителей. При построении графика дробно-рациональной функции надо исследовать поведение функции на бесконечности, а также вблизи нулей знаменателя, которые определяют вертикальные асимптоты графика. Рассмотрим поведение функции на . Возможны 4 случая. 1) n<m . Если степень числителя меньше степени знаменателя, то дробно-рациональная функция стремится к нулю при стремлении x к . 2) n=m . В этом случае предел функции на равен отношению старших коэффициентов, это значит, что у функции будет горизонтальная асимптота . 3) n=m+1 . В этом случае у функции будет наклонная асимптота y=kx+b , которая получается в результате деления числителя дроби на знаменатель: . 4) n≥m+2 . Значения функции стремятся к при стремлении аргумента x к . Знак бесконечности легко определяется по степеням старших членов n,m и коэффициентам an ,bm при старших степенях, а именно, на +
∞ знак определяется знаком произведения an·bm , а на —
∞ — знаком выражения (-1)n-m·an·bm . Теперь рассмотрим поведение дробно-рациональной функции вблизи точек разрыва, т.е. нулей знаменателя. Пусть — корень знаменателя кратности k . Это значит, что при разложении знаменателя на множители одним из сомножителей будет двучлен . При приближении аргумента x к числитель дроби представляет некую константу, отличную от нуля, а знаменатель стремится к нулю, а значит, дробь будет неограниченно возрастать по абсолютной величине, стремясь к . Таким образом, прямая будет вертикальной асимптотой графика функции. Знак бесконечности, к которой стремится функция слева и справа от , можно определить непосредственно подстановкой вместо x в выражение функции числа, близкого к числу с недостатком (слева) или с избытком (справа), но обычно этот знак определяется по методу интервалов, если нам известны корни числителя и знаменателя. Рассмотрим частный случай дробно-рациональной функции: дробно-линейную функцию , в числителе и знаменателе которой линейные функции. Рассмотрим примеры.
|
Графиком дробно-линейной функции является гипербола.
Расположение гиперболы определяется вертикальной асимптотой и горизонтальной асимптотой. Вертикальная асимптота — это нуль знаменателя,
то есть прямая , а горизонтальная асимптота-прямая ( случай 2 : n=m). Заметим, что рассматривая дробно-линейную функцию, мы предполагаем, что с ≠ 0 , иначе функция будет линейной, и её графиком будет прямая линия.Как построить график рациональных функций? Узнайте здесь!
ПримерДругой примерДело с дыркой
Purplemath
Как построить график рациональной функции?
Для построения рациональной функции:
- Разложите числитель и знаменатель на множители.
- Найдите множители для их нулей; имейте в виду, что нули знаменателя создают вертикальные асимптоты
- Найдите x — и y -перехваты, если они есть.
- Найдите любую горизонтальную или наклонную (то есть наклонную) асимптоту.
- Нанесите на график достаточное количество точек, чтобы увидеть, что происходит на графике.
- Нарисуйте свой график.
Содержание продолжается ниже
MathHelp.com
Как только вы поймете ход событий, рациональные функции на самом деле довольно просто изобразить в виде графика. Давайте проработаем несколько примеров.
- Нарисуйте следующее:
Сначала я найду вертикальные асимптоты, если они есть, для этой рациональной функции. Поскольку я не могу построить график там, где функция не существует, и поскольку функция не будет существовать там, где в знаменателе был бы ноль, я приравняю знаменатель к нулю, чтобы найти любые запрещенные точки:
х — 1 = 0
х = 1
Таким образом, я не могу иметь x = 1, и поэтому у меня есть вертикальная асимптота.
Я нарисую это на своем графике:
Далее я найду горизонтальную или наклонную асимптоту. Поскольку числитель и знаменатель имеют одинаковую степень (они оба линейные), асимптота будет горизонтальной, а не наклонной, а горизонтальная асимптота будет результатом деления старших коэффициентов:
y = 2 / 1 = 2
Я обозначу эту асимптоту штрихом:
(Если вы не уверены в том, как я нашел эти асимптоты, просмотрите урок об асимптотах. Прежде чем продолжить построение графика, вам нужно хорошо изучить эту тему. рациональные числа.)
Далее я найду любые x или y пересечений.
y -пересечение (таким образом, x = 0):
(0 + 5) / (0 − 1)
06 0 5 = −5 = y
x -интерцепт (SO y = 0):
0 = (2 x + 5) / ( x + 5) / ( x ) / ( x ) / ( x / ( x + 5) / ( x + 5) / ( x + 5)
0 = 2 x + 5
−5 = 2 x
−2,5 = x
Тогда точки пересечения находятся в точках (0, –5) и (–2,5, 0).
Я нарисую эти точки в:
Теперь я выберу еще несколько x значений, вычислите соответствующие значения y и нанесите еще несколько точек.
| х | y = (2 х + 5)/( х — 1) |
|---|---|
| −6 | (2(−6) + 5)/((−6) − 1) = −7/−7 = 1 |
| −1 | (2(−1) + 5)/((−1) − 1) = (−2 + 5)/(−2) = (3)/(−2) = −1,5 |
| 2 | (2(2) + 5)/((2) — 1) = (4 + 5)/(1) = (9)/(1) = 9 |
| 3 | (2(3) + 5)/((3) − 1) = (6 + 5)/(2) = (11)/(2) = 5,5 |
| 6 | (2(6) + 5)/((6) − 1) = (12 + 5)/(5) = (17)/(5) = 3,4 |
| 8 | (2(8) + 5)/((8) — 1) = (16 + 5)/(7) = (21)/(7) = 3 |
| 15 | (2(15) + 5)/((15) − 1) = (30 + 5)/(14) = (35)/(14) = 2,5 |
В основном я выбирал значения x ближе к середине графика.
Из-за горизонтальной асимптоты у меня уже есть хорошее представление о том, что делает график по бокам.
(В любом случае может быть хорошей идеей сделать пару точек рядом с концами для проверки вашей работы.) намеки на то, что происходит с графиком, мне нужно было больше точек, чтобы показать мне, что происходит.
Теперь я нанесу эти точки:
И теперь я могу соединить точки:
Когда вы рисуете график, убедитесь, что вы показываете график, продолжающийся в стороны. Не останавливайтесь только в точке, которую вы нарисовали, потому что это создаст впечатление, что график действительно останавливается в этой точке.
Могу ли я просто скопировать график моего калькулятора?
Предупреждение. Ваш калькулятор может отображать вводящий в заблуждение график для заданной рациональной функции. Когда вы рисуете, вы наносите несколько точек, а затем соединяете их; ваш калькулятор делает то же самое. Но вы достаточно умны, чтобы не пересекать вертикальную асимптоту; твой калькулятор не такой умный.
Если ваш калькулятор затеняет пиксель в нижней части экрана, а затем следующий затеняемый пиксель находится в верхней части экрана, то калькулятор, скорее всего, весело нарисует красивую вертикальную линию, соединяющую две точки, вот так:
По этой причине вы можете переключить режим построения графика с «линейный» на «точечный» (или аналогичный параметр для вашей модели калькулятора; см. руководство пользователя). В точечном режиме вы получите график, который выглядит следующим образом:
Я выделил несвязанные точки красным цветом. Весь график состоит из точек, но большинство точек расположены рядом друг с другом, поэтому они выглядят как линия. Если вы сохраните режим построения графика как «линейный», вам необходимо помнить, что то, что отображается на экране, может быть несколько неправильным при построении графика рациональных чисел.
URL: https://www.purplemath.com/modules/grphrtnl.htm
Стр. 2 Стр. 3 Стр. 4
Графики рациональных функций: определение, примеры
Знаете ли вы, как легко построить график простых рациональных функций? ? Вы все должны быть знакомы с дробями.
Верхняя часть дроби называется числителем, а нижняя — знаменателем. Числитель рациональной функции показывает x-пересечение графика. С другой стороны, знаменатель показывает вертикальные асимптоты графика. Множители числителя имеют целые степени больше единицы в многочленах.
Можете ли вы угадать, какая из следующих рациональных функций изображена на графике ниже? Вертикальные асимптоты, связанные с факторами знаменателя, будут отражать одну из двух обратных функций. Вы должны знать, что когда степень множителя в знаменателе нечетна, график направлен на положительную бесконечность вверх по одной стороне вертикальной асимптоты. Напротив, другая сторона обращена к отрицательной бесконечности.
Графики рациональных функций — 1/x 2 Вот еще один пример. Можете ли вы еще раз угадать, какая из следующих рациональных функций изображена на графике ниже? Вы должны знать, когда степень знаменателя четна; характеристический график либо стремится к положительной бесконечности с обеих сторон вертикальной асимптоты, либо к отрицательной бесконечности с обеих сторон.
Давайте разберем приведенный выше график рациональной функции на примере. Предположим, дробь равна f (x) = (x + 1) 2 (x – 3)/(x + 3) 2 (x – 2), то график функции будет таким:
Этот график рисуется путем подстановки 1, 2,… и т.д. получить значения функции для построения графика. Вот ключевые моменты, которые можно извлечь из приведенного выше графика:
Вы, должно быть, заметили, что на пересечении x = -1, соответствующем фактору (x + 1) 2 , присутствующему в числителе, график постоянно отскакивает. с квадратичным характером фактора.
Следует также отметить, что на точке пересечения x = 3, соответствующей (x-3) множителю числителя, график проходит через ось, как и в случае линейного множителя.
Также на вертикальной асимптоте x = -3, соответствующей (x + 3) 2 множителю знаменателя, график согласуется с поведением функции f (x) = 1/x 2 . Благодаря этому график направлен вверх по обеим сторонам асимптоты.
Наконец, на вертикальной асимптоте x = 2, соответствующей (x – 2) множителю в знаменателе, наблюдается согласованное поведение функции f (x) = 1/x. График стремится к положительной бесконечности с левой стороны асимптоты и к отрицательной бесконечности с правой стороны.
Как построить график рациональных функций? – Ключевые советы, которым нужно следоватьЕсли у вас есть сложности с построением графиков рациональных функций, то пришло время следовать этим ключевым советам, перечисленным ниже:
- Вы должны оценить функцию в первую очередь. Оцените его как 0, чтобы найти точку пересечения по оси y.
- Далее вам нужно разложить числитель и знаменатель.
- После разложения на множители для множителей в числителе, не являющихся общими со знаменателем, необходимо определить, где каждый множитель равен нулю, чтобы найти точки пересечения x.
- После выполнения шага 3 найдите кратности пересечений x. Вы делаете этот шаг, чтобы определить поведение графика в этих точках.
- Необходимо отметить кратность нулей, чтобы определить локальное поведение множителей в знаменателе. Это помогло бы найти вертикальные асимптоты для необычных множителей числителя. Для этого вам нужно установить эти коэффициенты равными нулю, а затем решить их.
- После получения нулей на шаге 5 необходимо найти устранимые разрывы, приравняв эти множители к 0. Это нужно сделать для множителей в знаменателе, общих с множителями в числителе.
- Теперь сравните числитель и знаменатель в градусах, чтобы определить наклонную или горизонтальную асимптоты.
- Наконец, вы можете нарисовать график, который хотели.
Давайте научимся строить графики простых рациональных функций на примере.
Пример. Нарисуйте график функции f (x) = (x + 2) (x – 3)/(x + 1) 2 (x -2) .
Решение: Вы можете выполнить следующие действия, чтобы начертить график для следующей функции:
Шаг 1: Первым шагом наброска графика является факторизация функции.
Поскольку функция уже учтена, она сохраняет ваш первый шаг.
Шаг 2: Вам нужно найти записи. Оцените функцию в нуле, чтобы получить точку пересечения с осью y, как показано:
f (0) = (0 + 2) (0 – 3)/(0 + 1) 2 (0 – 2) = 3.
Шаг 3: Получив точку пересечения по оси Y, чтобы найти точку пересечения по оси X, определите значение, когда числитель функции равен нулю. Установите каждый фактор равным нулю, затем найдите точки пересечения x при x = -2 и x = 3. Вы увидите, что поведение функции является линейным (кратность 1) вместе с графиком через точку пересечения.
Шаг 4: Теперь у вас есть точки пересечения x и y как (-2, 0) и (3, 0) и (0, 3) соответственно.
Шаг 5: Далее, чтобы получить вертикальные асимптоты, нужно сохранить значение знаменателя равным нулю. Это произойдет, когда x + 1 = 0 и x – 2 = 0, что даст значение для вертикальных асимптот при x = -1 и x = 2. Поскольку в числителе и знаменателе нет общих множителей, не будет устранимых разрывов.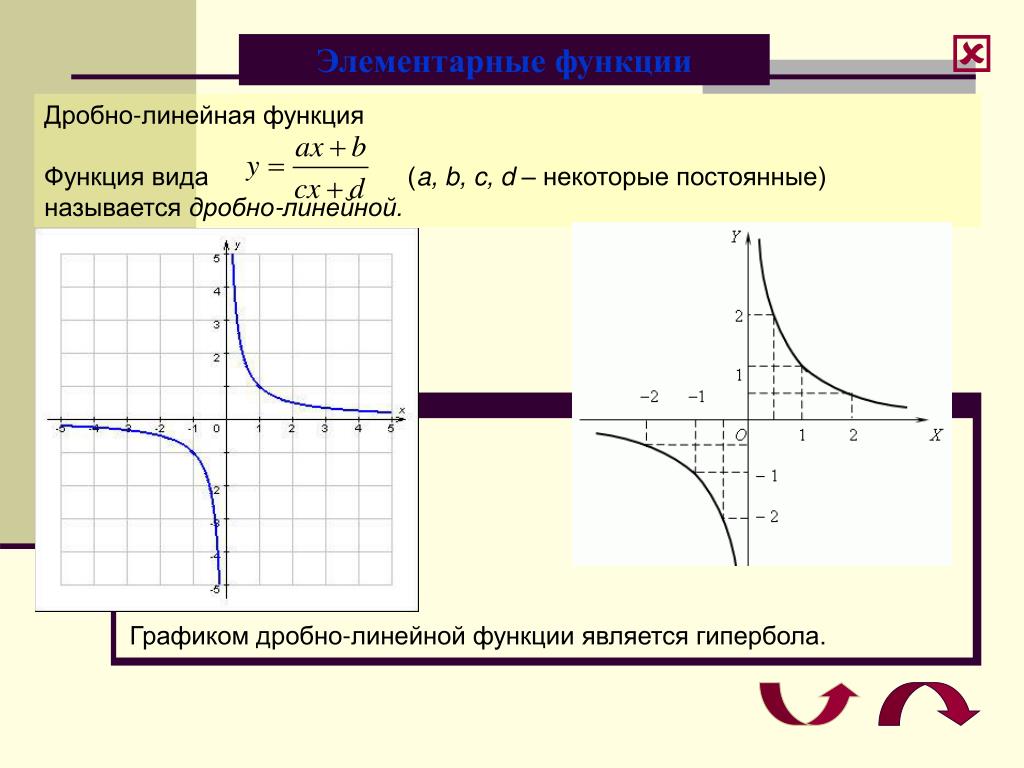
.
Шаг 6: Наконец, степень знаменателя больше степени числителя, что говорит о том, что график имеет горизонтальную асимптоту при y = 0,
Шаг 7: Чтобы набросать график, вам нужно построить три точки пересечения. Поскольку вы знаете, что точка пересечения с осью Y положительна, а точка пересечения с осью X между вертикальными асимптотами отсутствует, вы узнаете, что функция должна оставаться положительной между асимптотами. Это позволит вам заполнить среднюю часть графика.
Шаг 8: Коэффициент, связанный с вертикальной асимптотой при x = -1, возводится в квадрат, поэтому вы знаете, что поведение такой функции будет одинаковым с обеих сторон асимптоты. График стремится к положительной бесконечности, когда входные данные приближаются к асимптоте справа. Таким образом, график также будет стремиться к положительной бесконечности слева.
Шаг 9: Фактор не возводится в квадрат вертикальной асимптоты при x = 2. Следовательно, график будет иметь противоположное поведение по обе стороны от асимптоты.
После того, как график пройдет точку пересечения x, вы увидите, что график выровняется до нулевого выхода. Однако на это указывала горизонтальная асимптота.
Попробуйте сами!
Пример 2: Можете ли вы начертить график функции: f (x) = 4x + 12x + 1?
Ответ:
Пример 3. Постройте график функции: 2x + 5x – 1,
Ответ:
После построения графика рациональных функций, как их записать?Если вам дан график рациональной функции и вам нужно написать функцию, вы должны в первую очередь проверить точки пересечения. Если рациональная функция имеет точки пересечения по оси x в точках x = x1, x2, x3…, xn, вертикальные асимптоты в точках x = v1, v2, …vm и нет xi = любой vj, то функция может быть записана в виде:
f (x) = a(x – x1)p1 (x – x2)p2… (x – xn)pn(x – v1)q1(x – v2)q2… (x – vm)qn
Там, где поведение графика может найти степени пи или qi для каждого фактора на соответствующем пересечении или асимптоте, вы также можете найти коэффициент растяжения «а» из заданного значения функции, отличной от точки пересечения х или горизонтальной асимптотой, если она отлична от нуля.
Шаги по написанию функции после построения графика простых рациональных функций показаны ниже:
Шаг 1: Вам необходимо определить множители числителя. Исследуйте поведение графика на точках пересечения x, чтобы найти нули и их кратности. На этом шаге легко найти простейшую функцию с небольшими кратностями, например 1 или 3. Он усложняется, когда используются большие числа, например 8 или 9., входите в картину.
Шаг 2: Далее необходимо определить множители знаменателя. Изучите поведение обеих сторон каждой вертикальной асимптоты, чтобы определить факторы и их мощности.
Шаг 3: После выполнения шагов 1 и 2 последним шагом будет использование любой четкой точки на графике для определения коэффициента растяжения.
Крайне важно научиться строить графики рациональных функций, поскольку они могут быть полезными инструментами для представления реальных ситуаций, когда вам нужно найти решения сложных проблем.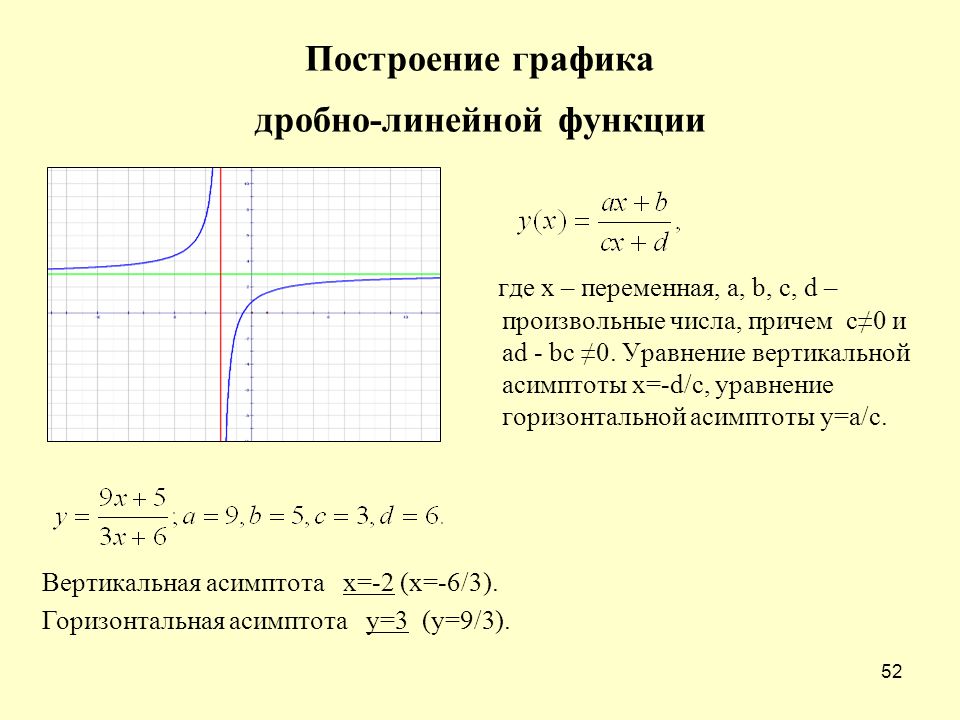
Уравнения, представляющие обратную, прямую или совместную вариацию, представляют собой рациональные формулы, которые могут моделировать многие реальные жизненные ситуации. Следовательно, было бы полезно, если бы вы попрактиковались в построении графиков рациональных функций.
Часто задаваемые вопросы
1. Что такое определение рациональной функции?
Ответ. Рациональная функция — это функция вида f(x) = p(x)/q(x), где p(x) и q(x) — многочлены. Рациональные функции важны, потому что их можно выразить как частное двух многочленов, что упрощает их факторизацию.
2. Как узнать, рациональна ли функция?
Ответ. Если вы хотите узнать, является ли функция рациональной, вы можете посмотреть на ее график или на ее уравнение. Если график функции содержит только вертикальные и горизонтальные линии, то он рациональный. Если уравнение содержит только целые числа, то оно рационально.
3. Как построить график рациональной функции?
Ответ.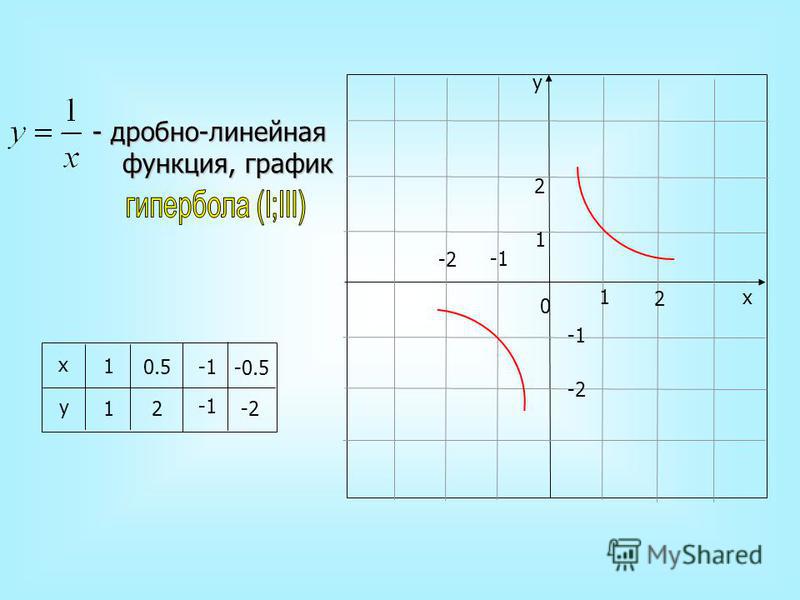
Вы можете построить график рациональных функций, используя тест вертикальной линии. Тест вертикальной линии — это способ определить, определена ли рациональная функция в данной точке. Он основан на том факте, что если вы начертите на графике две разные точки функции, а затем нарисуете вертикальную линию, соединяющую их, вы получите прямую линию, если функция определена в этих точках.
4. Как найти асимптоты рациональных функций?
Ответ. Асимптоты рациональных функций являются корнями знаменателя, и они всегда являются целыми числами. Чтобы найти асимптоты рациональной функции, сначала изолируйте знаменатель, вынеся его за скобки. Затем проверьте, чтобы все корни этого знаменателя были целыми числами. Если вы нашли целочисленный корень, значит, вы нашли свою асимптоту.
5. Каковы приложения рациональной функции?
Ответ. Рациональные функции являются наиболее распространенным типом полиномиальных функций, и их можно применять по-разному.