Радикальные функции — Уроки Византа
Радикальные функции содержат
функции с корнями. В большинстве примеров речь идет о квадратных корнях.
Построение графика радикальных функций может быть затруднено, потому что
область почти всегда должна учитываться.
Построим график следующей функции:
Сначала мы должны рассмотреть область определения функции. Мы должны отметить, что мы не можем
иметь отрицательное значение под знаком квадратного корня, иначе мы получим комплексное число. Следовательно,
мы устанавливаем все, что находится под корневым знаком больше или равно 0.
Помните, что когда мы делим на отрицательное число, мы переворачиваем неравенство. Этот результат
означает, что область значений x или входных данных представляет собой любое значение, меньшее или равное от
до 2.
Затем мы можем продолжить и нанести наши точки, но мы должны быть осторожны, чтобы не нанести точки
Метод, который мы можем 9Использование 0003 состоит в том, чтобы установить функцию, равную различным положительным целым числам, чтобы увидеть, каково их значение x.
Например, мы хотим узнать, какое значение x дает значение y, равное 4, мы можем спросить себя:
«Квадратный корень из какого значения дает нам 4?» Мы знаем, что это 16. Затем мы можем спросить: «Какое значение
при вычитании из 2 дает нам 16?» Мы видим 2 – (-14) = 16 . Следовательно,
, чтобы получить значение y, равное 4, нам нужно значение x, равное -14.
Мы можем видеть, почему x не может быть больше 2 на графике, и мы также можем видеть, почему
нет отрицательных значений y. Если x больше 2, мы получим комплексное число
, и мы не сможем получить отрицательное значение y из выражения с квадратным корнем
Мы также можем видеть, что это выглядит как боковая парабола с опущенными отрицательными значениями
y.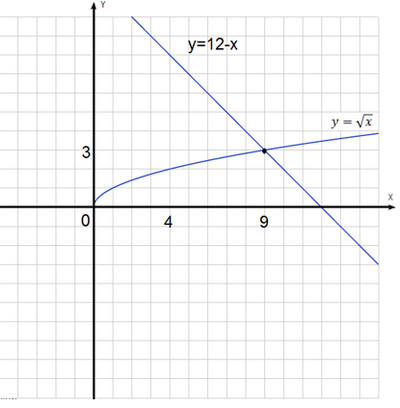
Это верно, и если мы возведем в квадрат обе части функции и
изолируем x, мы получим уравнение параболы относительно y.
Таким образом, наш диапазон не ограничивается только положительными значениями y. Однако мы должны понимать, что это уравнение отличается от исходной функции, потому что оно на самом деле не является функцией. Напомним, чтобы быть функцией, изображение должно пройти тест
вертикальных линий.
Важно помнить об этом различии и понимать, как радикальные функции
в терминах x алгебраически и геометрически соотносятся с уравнениями в терминах y.
Далее построим график функций:
Помните, первое, что нам нужно сделать, это посмотреть, есть ли у нас какие-либо ограничения для нашего домена
. У нас не может быть отрицательного значения внутри квадратного корня, поэтому мы можем установить оба выражения внутри корня больше или равным 0.
Вместо этого мы можем изобразить
оба выражения внутри корня как функции на графике и посмотреть, любые
значения x дают отрицательное значение y.
Мы можем видеть график g(x) = x 2 +9 всегда выше оси x,
означает, что для всех значений x функции дают положительные значения y. Так как у нас
всегда будет положительное значение y для этой функции, то ограничений
на наш домен нет.
График f(x) = x 2 -9 опускается ниже оси x между -3 и
и х = 3 .
При работе с
полиномами внутри корневого знака построение графика полиномиальной функции является
самым простым способом увидеть, где функция опускается ниже оси x, и найти точки пересечения x.
Везде, где график отрицателен по оси абсцисс, есть ограничение на область
исходной функции.
Чтобы построить график функций, нам нужно иметь в виду домен для f(x) и график
точек меньше -3 и больше 3. Для графика g(x) мы можем
построить любое значение x, которое захотим. Мы можем сделать это, составив таблицу xy или вставив уравнения
в графический калькулятор.
Если мы посмотрим на характер графиков, они очень похожи на две разные
без их отрицательных значений y. Мы можем произвести некоторые манипуляции и увидеть, что функции
могут быть представлены в виде гиперболических уравнений.
Каждая радикальная функция будет частью
конического сечения. Это потому, что когда мы манипулируем функцией, чтобы она была в
терминах как x, так и y, у нас всегда будет y 2 . Давайте сделаем еще один пример
, иллюстрирующий этот момент.
Далее постройте график функции:
Во-первых, мы проверяем домен, изображая выражение внутри корня и устанавливая
равно y.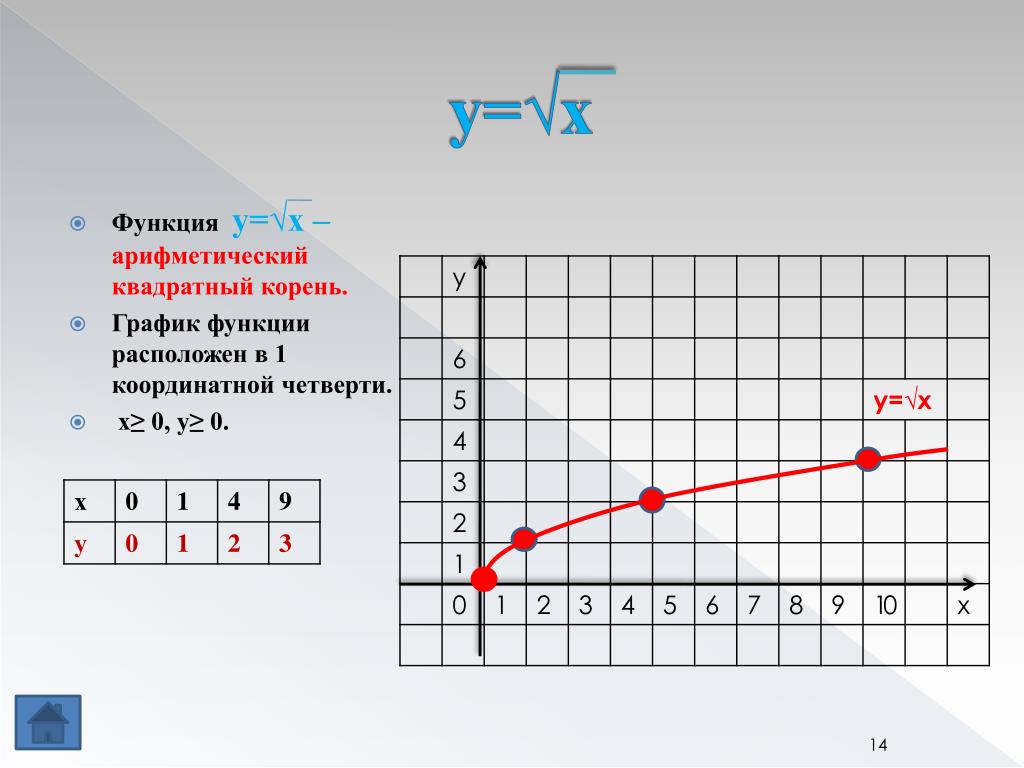
Мы видим, что точки пересечения x равны (-4,0) и (4,0) , и когда x на
меньше -4 и больше положительного 4 , у нас отрицательный y ценности.
Это наши ограничения.
Давайте построим нашу исходную функцию с учетом ограничений нашей области (другими словами,
слов, точки графика между x = -4 и x = 4).
Мы должны заметить, что это полукруг, в котором отсутствуют отрицательные значения y. Немного поработав с
, мы можем составить уравнение окружности с радиусом 4.
Высшие корни
Мы оценили радикальные функции, включающие квадратные корни. При построении графиков этих
функций мы должны знать предметную область, прежде чем рисовать их. Некоторые радикальные функции, например
, никогда не будут иметь доменных ограничений. Рассмотрим функцию кубического корня.
В качестве примера нарисуйте график функции кубического корня:
Ограничений домена нет, потому что мы можем взять кубический корень из отрицательного числа
. Следовательно, наша область определения — «все действительные числа», и мы можем построить любое значение x
, которое захотим.
Что если у нас есть функция с 4-м корнем, например
У нас не может быть отрицательного значения y для любого входа. Например, (2) 4 и
(-2) 4 оба дают положительное число 16. Если мы подставим -16 вместо x, мы получим комплексное число
. Это означает, что нам нужно подумать о нашей области, прежде чем строить график.
Мы можем сделать вывод, что для любой радикальной функции
Если n равно нечетному , наш домен не ограничен.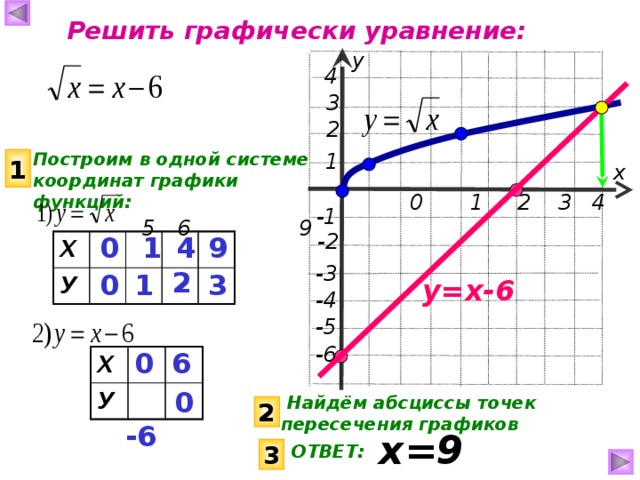
, мы должны учитывать ограничения для нашего домена.
В следующем примере мы хотим найти домен функции:
Мы можем построить график внутренних функций, но давайте установим выражение внутри радикала
больше или равное 0.
Затем мы можем исправить домен как [-∞,-3] U [3,∞] , чтобы указать, что домен
представляет собой любое значение x меньше -3 и больше 3.
Нет решения
Иногда область определения радикальной функции не будет иметь положительных значений y,
и поэтому для действительных чисел графика не будет.
Например, найдите домен и решение для следующей функции
.
Мы уже можем видеть при проверке, что выражение внутри квадратного корня
У нас не может быть квадратного корня из отрицательного значения, поэтому домен не определен, и, следовательно,
образ функции не определен на реальной плоскости xy. Мы также можем проверить на
графическое изображение выражения и установка его равным y.
Нахождение нулей радикальных функций
Поиск нулей — это еще один способ сказать поиск корней. Нахождение нулей
радикальных функций уникально, потому что иногда найденные нами корни на самом деле
не удовлетворяют функции. Эти корни называются посторонними нулями .
Стратегия нахождения корней подкоренных функций состоит в том, чтобы изолировать подкоренное выражение
даст нам тот же результат, если мы возведем в квадрат ее противоположность, которая не удовлетворяет исходной функции
.
Как мы уже видели в первых трех примерах, уравнение , которое мы получили, когда решили и x, и y, отличается от исходной функции
, которая у нас была. Из-за этого мы всегда должны проверять наши результаты при нахождении
корней.
Наконец, давайте посмотрим на функцию:
Во-первых, чтобы найти наш домен, мы устанавливаем каждое выражение под радикалом больше или равно
равным 0.
Поскольку у нас есть два ограничения, мы берем то, которое является наиболее ограничивающим, и, таким образом,
Чтобы найти наши пересечения x, мы устанавливаем функцию равной 0 и находим x.
У нас есть два корня – х = 3 и х = -2 . Давайте подключим их и проверим
, чтобы увидеть, удовлетворяют ли они этой функции.
Поскольку наша функция равна 0, 3 является корнем.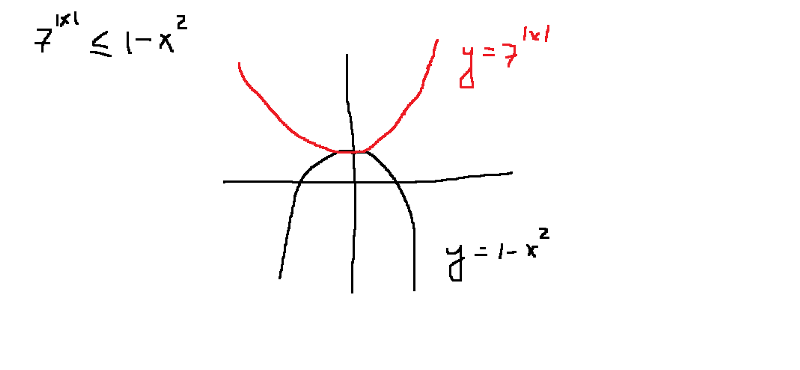
Поскольку наша функция не равна 0, -2 не является корнем.
Глядя на нашу функцию, мы можем ясно видеть наш перехват x и наше ограничение домена.
Радикальные функции — Джастин Скайчак 93 } = \sqrt{ -64 }$
Как следствие, график $f$ остается пустым для отрицательных значений $x$ слева от оси y.
При этом другие подкоренные функции иногда могут принимать отрицательные входные данные, которые преобразуются в положительные числа перед применением подкореня.
Например, $x=-4$ является допустимым входом для $f(x)=\sqrt{-x}$, потому что операция внутри корня преобразует отрицательный ввод в положительный, и мы можем взять корень из положительные числа.
Но операция также преобразует положительные входные данные в отрицательные, поэтому положительная часть графика исчезает.
Функции кубического корня
В отличие от функций квадратного корня, функции кубического корня, такие как $f(x)=\ sqrt[3]{x}$ может принимать как положительные, так и отрицательные входные данные, поскольку кубические корни определены как для положительных, так и для отрицательных чисел.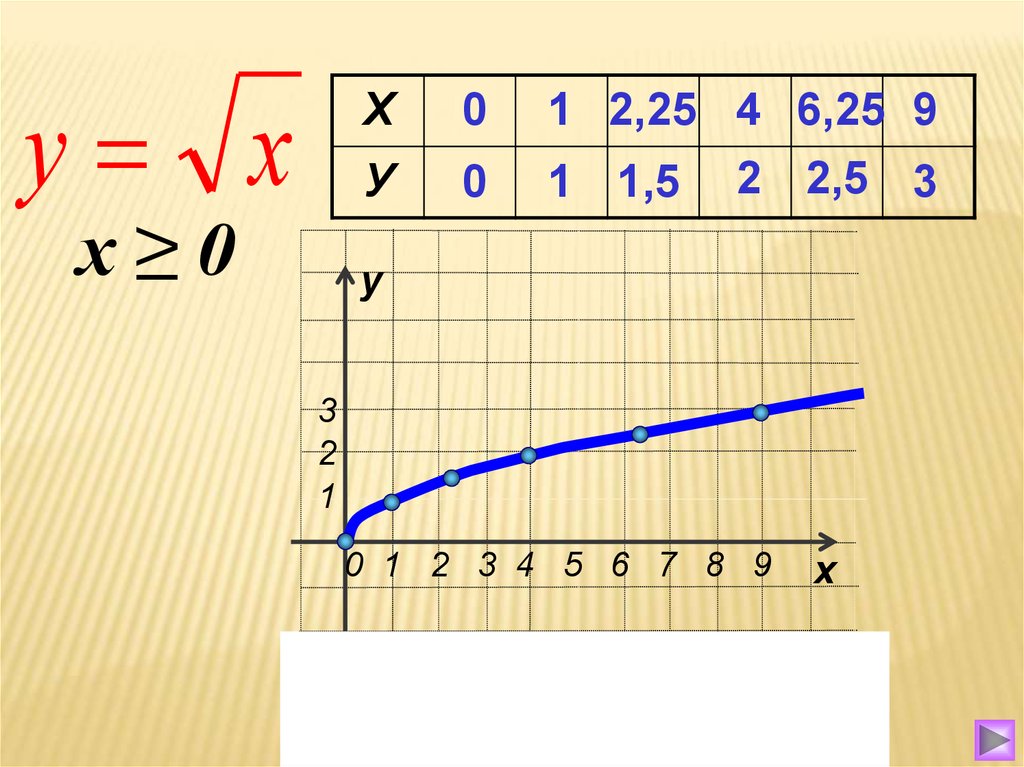
В общем, то, покрывает ли радикальная функция весь граф или только его часть, зависит от того, является ли корень четным или нечетным.
- • Четные корни НЕ определены для отрицательных чисел, поэтому график остается пустым для любого входного значения $x$, которое делает внутреннюю часть корня отрицательной.
- • Нечетные корни определены для отрицательных чисел, поэтому граф существует для любых входных данных $x$, даже если это делает внутреннюю часть корня отрицательной.
Просто помните, что является ли значение x допустимым входом для корневой функции, зависит не только от знака значения x, но и от того, что функция делает с входным значением x перед применением корня.
Посторонние решения
При решении радикальных уравнений допустимые алгебраические шаги иногда могут привести к решениям, которые на самом деле неверны.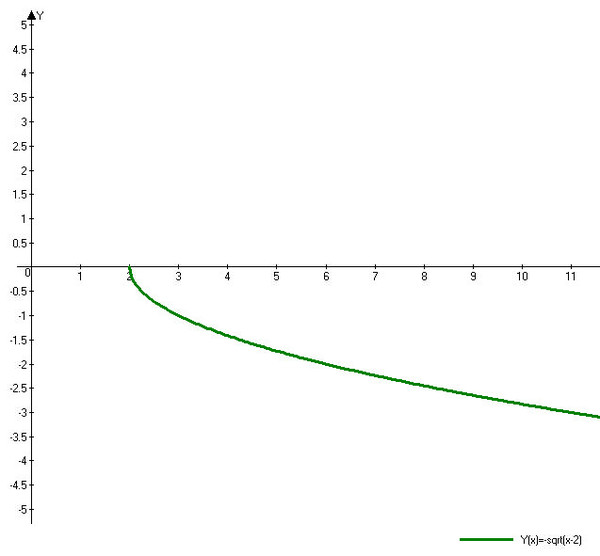
Например, возведение в квадрат обеих частей уравнения $\sqrt{x}=-2$ дает $x=4$. Однако, когда мы вводим $x=4$ в уравнение для проверки решения, мы получаем $\sqrt{4}=-2$, что упрощается до $2=-2$, что неверно.
Поэтому мы говорим, что решение $x=4$ является лишним , а уравнение $\sqrt{x}=-2$ на самом деле не имеет решений в действительных числах. 92$.
Аналогичная проблема возникает, когда мы возводим обе части уравнения в четвертую, шестую, восьмую или любую четную степень — возведение в четную степень превращает отрицательные числа в положительные, поэтому вводится дополнительное решение, соответствующее отрицательному корню .
С другой стороны, возведение обеих частей уравнения в третью, пятую, седьмую или любую нечетную степень не меняет знак ни одного числа, поэтому не приводит к посторонним решениям.
Главный вывод 92-x=0 \\ \text{Множественный полином} \hspace{.5cm} &\Bigg| \hspace{.5cm} x(2x-1)(4x+1)=0 \\ \text{Решить} \hspace{.