Урок по геометрии в 9-м классе по теме «Площадь многоугольника»
Цель:
- закрепить понятие площади.
- вывести формулу площади правильного многоугольника.
- провести лабораторно-исследовательскую работу на тему: “Какой многоугольник имеет наибольшую площадь”.
Ход урока
Устно(5-7 минут). 1. Какая фигура изображена на рисунке? ( многоугольник)
Обсуждается с классом, что уже известно о многоугольниках:
а) какая фигура называется многоугольником;
б) виды многоугольников (выпуклый, невыпуклый, правильный, неправильные)
Определить на каждом рисунке вид многоугольника.
- В какую фигуру обычно вписывают многоугольники? (0кружность).
- Какой многоугольник называется вписанным? (Если
все его вершины являются точками окружности).

- Какой многоугольник называется описанным? (Если все стороны многоугольника касаются окружности).
Мы уже на протяжении нескольких уроков изучаем площади различных четырехугольников и треугольника, а на этом уроке рассмотрим общий случай.
Как вычислить площадь произвольного многоугольника? Как вы думаете, площадь какого многоугольника проще всего посчитать?
Проведем лабораторно-исследовательскую работу.
Предлагаю изобразить невыпуклый, выпуклый неправильный, выпуклый правильный пятиугольник.
Как посчитать площадь каждого? Поскольку мы знаем, как вычисляются площади треугольника и четырехугольников, то есть предложение разбить каждый пятиугольник на известные нам фигуры.
Невыпуклый пятиугольник разбили на два разных треугольника, надо считать площадь каждого треугольника и складывать.
Выпуклый неправильный пятиугольник
Аналогичное решение.
Правильный пятиугольник разбивается на равные треугольники. Достаточно найти площадь одного треугольника и умножить на их количество.
Значит проще всего находить площадь правильного многоугольника.
Но ученые не остановились на этом, они вывели формулу площади для правильного многоугольника. Эту теорему мы сейчас докажем.
Теорема. Площадь правильного многоугольника равна половине произведения периметра многоугольника на радиус вписанной окружности.
Дано: А1…….Аn — многоугольник правильный,
А1А2=А2А3=………=Аn-1Аn,
Все углы равны.
Доказать: S = Pr
Доказательство:
Правильный многоугольник делится на равные равнобедренные треугольники.
Рассмотрим треугольник A1OA2: угол А1ОА2-
центральный (как его вычислить?) .
Все треугольники равны по двум сторонам и углу между ними. Найдем площадь треугольника. Для этого проведем высоту. Эта высота будет радиусом вписанной окружности. Так как треугольники равнобедренные, то высота является медианой и биссектрисой.
S= h A1An. Всего треугольников N штук.
S= hА1А2n=Pr. Что и требовалось доказать
Вопросом о вычислении площади люди заинтересовались ещё с древнейших времен. Наиболее известная задача — это задача Дидоны.
Финикийская царица Дидона спасалась от своего
брата, тирана Пигмалиона. Она отплыла из города
Тира в 825 году до нашей эры. После долгого
путешествия корабль пристал к берегам Африки.
Дидоне понравилась земля. Она обратилась к
местному предводителю нумидийцев Ярбу с
просьбой продать кусок земли. Ярб заломил
баснословную цену за клочок земли, который можно
окружить бычьей шкурой. Но Дидона не растерялась
и согласилась.
Итак, какую задачу так блестяще решила Дидона? Эта задача звучит так: “Какую наибольшую площадь можно окружить веревкой заданной длины?”
В геометрии эта задача звучит так: Какая геометрическая фигура с одинаковым периметром имеет наибольшую площадь?
Попытаемся и мы ответить на этот вопрос.
Проведем лабораторно-исследовательскую работу.
Класс разбивается на три группы. Каждая группа выбирает себе один из видов треугольника (разносторонний, равнобедренный, равносторонний). Р = 18см.
Задание каждой группе: вычислить площадь
треугольника.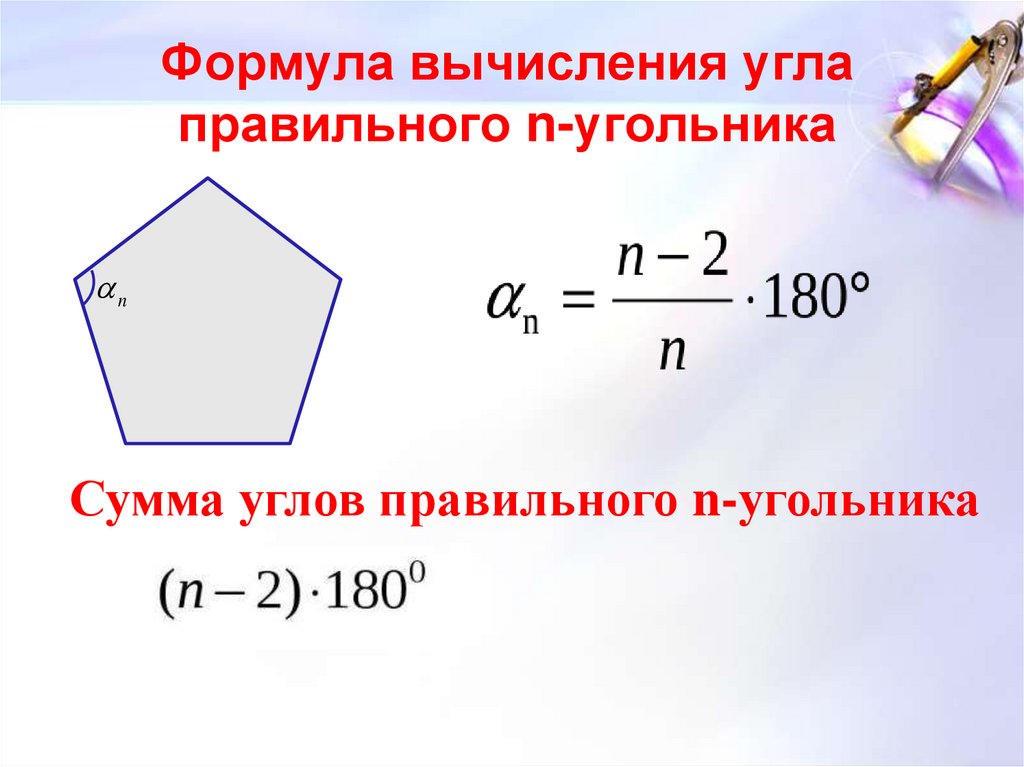
Здесь очень важно обратить внимание учеников на составление треугольника с данным периметром. (Должно выполняться условие, чтобы треугольник существовал, надо, чтобы сумма двух сторон были больше длины третьей стороны).
Пример. 1. Разносторонний треугольник. Р=18см.
а = 3, б = 8, с = 7, тогда S== == 6.
а = 5, в=7, с= 6, тогда S= = 6=.
а =4, в=8, с=6, тогда S= = .
(приведены несколько примеров разносторонних треугольников с периметром 18см.)
Пример2. Равнобедренный треугольник, Р=18см.
а= 5, в=5, с=8, тогда S== 12 или
а=4, в=7, с=7, тогда S= =6=или
а=2, в=8, с=8, тогда S==
Пример3. Равносторонний треугольник.
а=в=с=6, тогда S= =
Из всех приведенных примеров видно, самая
большая площадь получилась у равностороннего
треугольника. Учащиеся при выполнении работы
сами сравнивают получившиеся результаты каждой
группы и делают вывод.
Может возникнуть вопрос: выполняется ли это для четырехугольников?
Учащимся предлагается тем же способом провести исследование для параллелограмма, прямоугольника, квадрата.
Пример1. Параллелограмм. Р=20см.
АВ= 1см, ВС= 9см, /_В= 30°, тогда S= 1*9*sin30°= 9*0,5=4,5см2
АВ= 2см, ВС= 8см, угол В=30°, тогда S= 2*8*sin30°= 16*0,5=8см2
АВ= 3см, ВС=7см, угол В=30°, тогда S= 3*7*sin30°=21*0,5=10,5см2
АВ=4см, ВС=6см, тогда S= 4*6*sin30°= 24*0,5=12см2.
Пример2. Прямоугольник. Р= 20см.
А= 1см, В= 9см, тогда S=9*1=9см2 или
А= 2см, В= 8см, Тогда S= 2*8=16см2 или
А=3см, В= 7см, тогда S= 3*7=21см2 или
А= 4, В= 6, тогда S= 4*6=24см2
Пример3. Квадрат. Р=20см.
А= 5см, тогда S=5*5=25см2
Вывод: здесь мы видим ту же картину наибольшая
площадь у правильного четырехугольника то есть у
квадрата.
Учащиеся делают заключение: наибольшую площадь будет иметь правильный многоугольник.
А если у этого многоугольника бесконечно много сторон, то он будет похож на окружность. Следовательно, максимальную площадь занимает круг. Как посчитать площадь круга вы узнаете на следующем уроке.
Площадь многоугольника. Свойства площадей — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1.
 Тема: Площадь многоугольникаЦель:
Тема: Площадь многоугольникаЦель:Повторение формул для вычисления
площадей многоугольников; изучение
формулы Пика; применение формул при
решении практических задач и задач из
вариантов ОГЭ.
2. Сформулируйте свойства площадей
1. Равные многоугольники имеют равныеплощади.
2. Если многоугольник составлен из
нескольких многоугольников, то его площадь
равна сумме этих многоугольников.
3. Площадь квадрата равна квадрату его
стороны.
3. Найдите площадь прямоугольника
Задания для устного счетаНайдите площадь
прямоугольника
15 дм
3м
Правильный ответ: 450 дм2
4. Найдите площадь прямоугольника
32 см2Правильный ответ: 64 см2
5. Найдите площадь прямоугольника
11 см2
Правильный ответ: 88 см2
6. Найдите площадь квадрата
1,7 смПравильный ответ: 2,89 см2
7. Найдите площадь параллелограмма
11 см15 см
Правильный ответ: 165 см2
8.
 Найдите площадь параллелограмма20 см
Найдите площадь параллелограмма20 см13 см
Правильный ответ: 360 см2
9. Найдите площадь ромба
10 см13 см
Правильный ответ: 65 см2
10. Найдите площадь треугольника
1,2 дм4 дм
Правильный ответ: 2,4 см2
11. Найдите площадь треугольника
9 см14 см
Правильный ответ: 63 см2
12. Найдите площадь трапеции
9 см9 см
15 см
Правильный ответ: 108 см2
13. Как измерить площадь фигуры, формула для которой неизвестна?
14. Метод разбиения (метод сложения)
15. Метод достраивания (метод вычитания)
16. Вычисление площадей многоугольников с целочисленными вершинами
Определение: Точкакоординатной плоскости
называется целочисленной,
если обе её координаты
целые числа.
Вывод новой формулы для вычисления
площадей с целочисленными вершинами
Выполните задание на компьютере в
программе «Живая математика»
B
Спрятать точки на границе
8
Спрятать точки на границе
Спрятать внутренние точки
Показать внутренние точки
P1
6
A
C
D
4
E
2
-15
-10
-5
Показать измеренная площадь
5
-2
1.
 Посчитать количество целочисленных точек, лежащих внутри фигуры (В)
Посчитать количество целочисленных точек, лежащих внутри фигуры (В)-4
Вычисления записать в тетрадь
2. Посчитать количество целочисленных точек, лежащих на границе фигуры (Г)
3. Вычислить Г/2
4. Вычислить площадь средствами программы
-6
5. Найти закономерность между вычислениями в пунктах 1-3 и площадью
-8
10
Показать измеренная площадь
15
Площадь многоугольника с целочисленными
вершинами равна
Г
–1
B +
2
где
В — количество целочисленных точек внутри
многоугольника, а
Г — количество целочисленных точек на границе
многоугольника.
Формула Пика была открыта австрийским
математиком Георгом Пиком в 1899г.
20. Георг Пик
ГЕОРГ ПИКГеорг Алекса́ндр Пик (10 августа 1859 — 13 июля 1942) —
австрийский математик, родился в еврейской семье.
Мать — Йозефа Шляйзингер, отец — Адольф Йозеф Пик.
В 16 лет Георг закончил школу и поступил в Венский
университет.
В 20 лет получил право преподавать физику и математику.
Шестнадцатого апреля 1880 года под руководством Лео
Кёнигсбергера Пик защитил докторскую диссертацию «О
классе абелевых интегралов».
В Немецком университете в Праге в 1888 году Пик получил
место экстраординарного профессора математики, затем в
1892-м стал ординарным профессором. В 1900—1901 годах
занимал пост декана философского факультета.
С его именем связаны матрица Пика, интерполяция Пика —
Неванлинны, лемма Шварца — Пика. 13 июля 1942 года Пик
был депортирован в созданный нацистами в северной
Чехии лагерь Терезиенштадт, где умер две недели спустя в
возрасте 82 лет.
Выполните на компьютере следующее задание:
1. Вычислить площадь заданных многоугольников по формуле
Пика
2. Проверить ответ средствами программы «Живая математика»
E
F
C
O
J
L
Творческое задание:
1.
2.
3.
Создать макет витража для школьного музея для экспозиции
«Метрогородок». Использовать маркеры трех цветов.

Найти площадь фигур одного цвета по формуле Пика.
Рассчитать стоимость материалов.
Витраж должен состоять из
многоугольников
разного цвета с вершинами в узлах
сетки.
Посчитайте площади
многоугольников
одного цвета и стоимость витража
по исходным данным.
1 клетка соответствует 100 см2
Стоимость 1 м2 :
Желтое стекло 4000 руб
Красное стекло 4000 руб
Синее стекло 5000 руб
Фиолетовое 5000 руб
Зеленое стекло 6000 руб
Розовое стекло 6000 руб
23. Подведение итогов: Работа с интеллект- картой, создание синквейна.
ПОДВЕДЕНИЕ ИТОГОВ:РАБОТА С ИНТЕЛЛЕКТ- КАРТОЙ,
СПАСИБО ЗА УРОК!
При создании презентации использовались
Интернет- ресурсы:
https://infourok.ru
https://ru.wikipedia.org
http://journals.org
http://oknamin.ru
https://сommons.wikimedia.org
English Русский Правила
Площадь неправильных многоугольников
Площадь неправильных многоугольниковПоказать рекламу
Скрыть рекламу
О рекламе
Введение
Я просто решил поделиться с вами умной техникой, которую я когда-то использовал для нахождения площади обычных многоугольников.
Многоугольник может быть правильным (все углы равны и все стороны равны) или неправильным
| Обычный | Нестандартный |
Пример многоугольника
Возьмем этот многоугольник в качестве примера:
Координаты
Первый шаг — превратить каждую вершину (угол) в координату, как на графике:
3 Площадь 9 Под единицей Line Segment
Теперь для каждого линейного сегмента вычислите площадь до оси x .
Итак, как рассчитать каждую площадь?
Усредните две высоты, затем умножьте на ширину
Пример: Для фигуры, выделенной выше, мы берем две высоты (координаты «y» 2,28 и 4,71) и вычисляем среднюю высоту:
(2,28 +4,71)/2 = 3,495
Вычислите ширину (разница между координатами «x» 2,66 и 0,72)
2,66-0,72 = 1,94
Площадь ширина×высота:
1,903 × 3,4953
Добавить их всех
Теперь сложите их все!
Но хитрость заключается в том, чтобы складывать, когда они идут вперед (положительная ширина), и вычитать, когда они идут назад (отрицательная ширина).
Если всегда ходить вокруг многоугольника по часовой стрелке и всегда вычитать первую координату «x» из второй, получается естественно, вот так:
| Из | отдо | |||||
|---|---|---|---|---|---|---|
| х | лет | х | и | Средняя высота | Ширина (+/-) | Площадь (+/-) |
| 0,72 | 2,28 | 2,66 | 4,71 | 3,495 | 1,94 | 6.7803 |
| 2,66 | 4,71 | 5 | 3,5 | 4.105 | 2,34 | 9.6057 |
| 5 | 3,5 | 3,63 | 2,52 | 3.01 | -1,37 | -4.1237 |
| 3,63 | 2,52 | 4 | 1,6 | 2,06 | 0,37 | 0,7622 |
| 4 | 1,6 | 1,9 | 1 | 1,3 | -2,1 | -2,7300 |
| 1,9 | 1 | 0,72 | 2,28 | 1,64 | -1,18 | -1,9352 |
| Всего: | 8. 3593 3593 | |||||
Вы также можете пойти в другом направлении. Если вы получили отрицательную область, просто сделайте ее положительной.
А выглядит это так:
Вот так! Площадь 8.3593
Площадь инструмента многоугольника
Рад, что вы дочитали до этого места! В награду вы получите ссылку на инструмент рисования области многоугольника, который может сделать все это за вас. Он также принимает ручной ввод координат.
Copyright © 2017 MathsIsFun.com
Вычисление площади многоугольника
Все математические ресурсы GMAT
22 Диагностические тесты 693 практических теста Вопрос дня Карточки Learn by Concept
GMAT Math Help » Проблемные вопросы » Геометрия » Полигоны » Вычисление площади многоугольника
Периметр правильного шестиугольника равен 72 сантиметрам. Чему равна его площадь с точностью до квадратного сантиметра?
Возможные ответы:
Правильный ответ:
Пояснение:
Этот правильный шестиугольник можно представить как состоящий из шести равносторонних треугольников, каждый из которых образован стороной и двумя радиусами; каждая имеет боковую длину в сантиметрах. Площадь одного треугольника равна
Площадь одного треугольника равна
Таких треугольников шесть, умножьте это на 6:
Сообщить об ошибке
Какова максимально возможная площадь четырехугольника с периметром 48?
Возможные ответы:
Правильный ответ:
Пояснение:
Четырехугольник с максимальной площадью при заданном периметре является квадратом. Поскольку у квадрата четыре равные стороны, максимальная площадь равна
Сообщить об ошибке
Человек хочет спроектировать комнату таким образом, чтобы при взгляде сверху она выглядела как трапеция с прикрепленным к ней квадратом (показано ниже). Площадь всей комнаты должна быть 100 квадратных метров. Показанная красная линия делит пополам пунктирную линию и имеет длину 15. Сколько из следующих ответов являются возможными значениями длины одной стороны квадрата?
a) 5
b) 6
c) 7
d) 8
Изображение выполнено не в масштабе, но трапециевидная фигура будет похожа по размерам на изображенную.
Возможные ответы:
Правильный ответ:
Пояснение:
Обозначим длину одной стороны квадрата. Это также вершина трапеции. Обозначим основание трапеции. Наконец, пусть будет высота трапеции. Тогда площадь трапеции равна площади квадрата.
Тогда общая площадь равна 100, поэтому:
Теперь мы знаем, что красная линия имеет длину 15. — это область этой линии, которая находится в трапеции. Однако мы замечаем, что остаток в точности равен длине одной стороны квадрата. Итак, или
Переписав предыдущее уравнение:
Теперь это уравнение с двумя переменными, и мы можем легко вычеркнуть ответы, подставив возможные значения. То, что мы находим, это для , соответственно. Ибо мы получаем , что слишком мало (должно быть больше ). Ведь мы получаем.
Сообщить об ошибке
Какова площадь правильного восьмиугольника со стороной 10?
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь правильного многоугольника равна половине произведения его апофемы — расстояния по перпендикуляру от центра до стороны — и его периметра.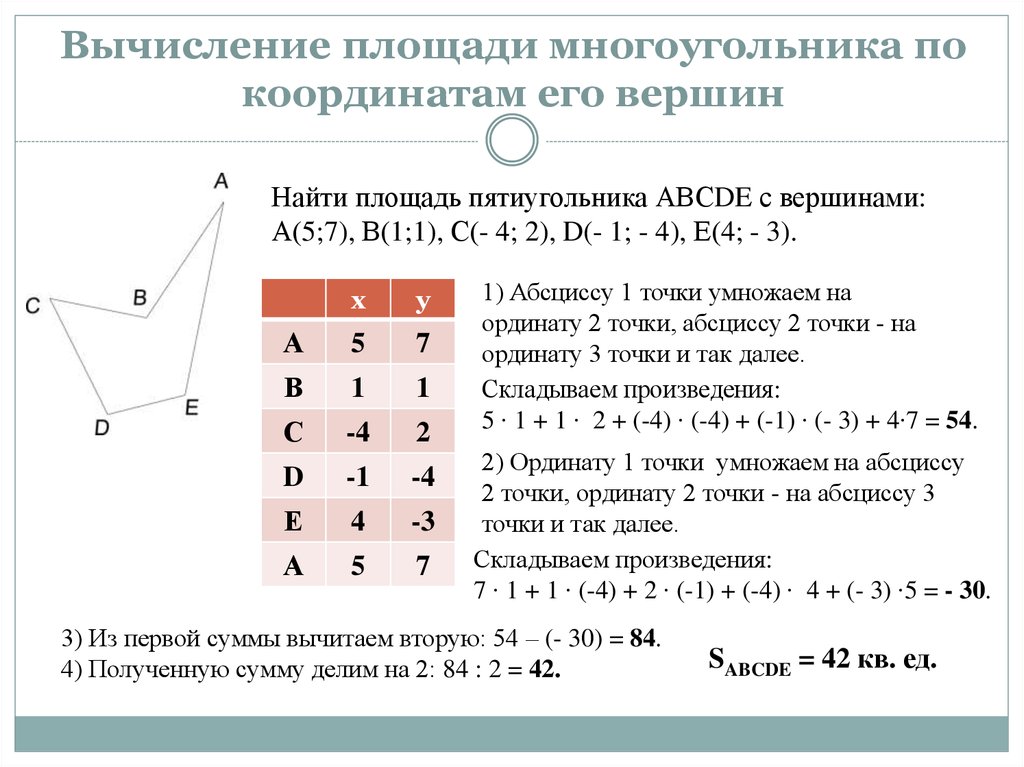
Периметр восьмиугольника
На приведенной ниже диаграмме апофема восьмиугольника .
является половиной длины стороны, или 5. можно рассматривать как длину катета треугольника с гипотенузой 10, или
Это апофема .
Следовательно, площадь равна
Сообщить об ошибке
Какова площадь правильного шестиугольника со стороной 10?
Возможные ответы:
Правильный ответ:
Пояснение:
Правильный шестиугольник можно представить как составную часть шести равносторонних треугольников, каждая из сторон которых равна длине стороны шестиугольника:
Каждый из треугольников имеет площадь
Подставьте , чтобы получить
Умножьте это на 6: , площадь шестиугольника.
Сообщить об ошибке
Какова площадь фигуры с вершинами ?
Возможные ответы:
Правильный ответ:
Объяснение:
Эту фигуру можно рассматривать как составную часть двух простых фигур: прямоугольника с вершинами и треугольника с вершинами.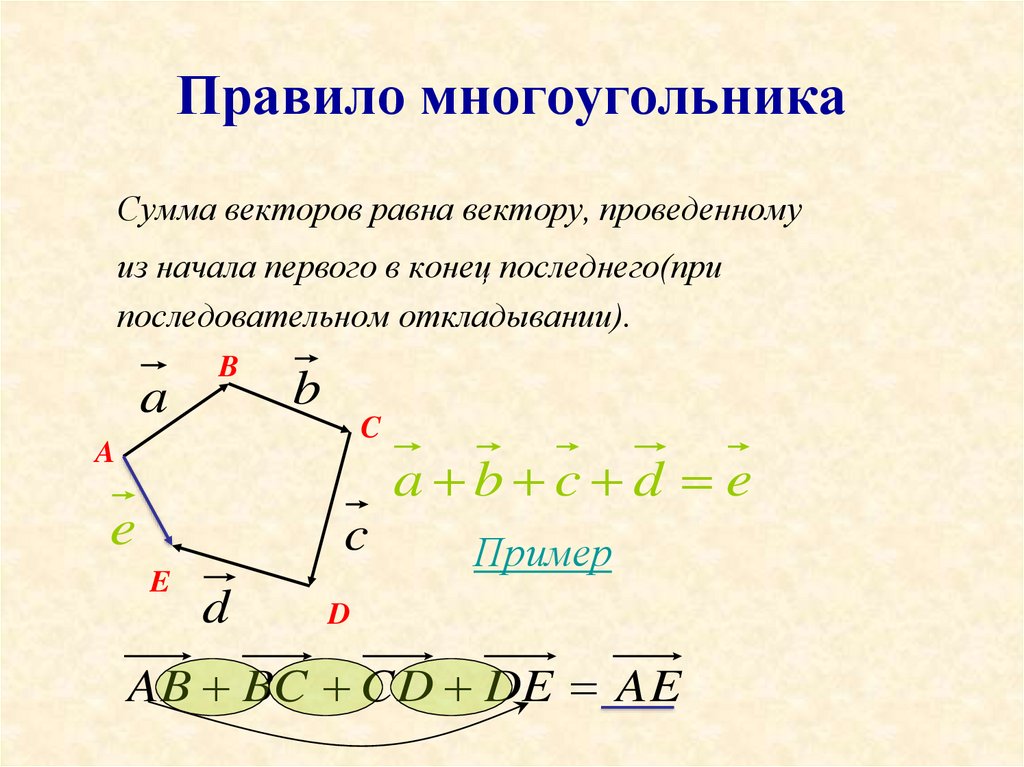
Прямоугольник имеет длину и высоту , поэтому его площадь равна произведению этих размеров или .
Основанием треугольника является длина горизонтального отрезка, соединяющего и , то есть ; его высота — это расстояние по вертикали от другой вершины до этого сегмента, которое равно . Площадь этого треугольника равна половине произведения основания на высоту, то есть .
Сложите площади прямоугольника и треугольника, чтобы получить общую площадь:
Сообщить об ошибке
Примечание. Рисунок НЕ выполнен в масштабе
Какова площадь приведенного выше рисунка?
Предположим, что все углы, показанные на рисунке, прямые.
Возможные ответы:
Недостаточно информации для ответа на вопрос.
Правильный ответ:
Пояснение:
Эту фигуру можно рассматривать как меньший прямоугольник, вырезанный из большего; см. диаграмму ниже.
диаграмму ниже.
Мы можем заполнить недостающие длины сторон, используя тот факт, что противоположные стороны прямоугольника конгруэнтны. Как только это будет сделано, мы можем умножить длину на высоту обоих прямоугольников, чтобы получить площадь каждого из них, и вычесть площади:
квадратных футов
Сообщить об ошибке
На следующем рисунке изображен сад, окруженный стеной. Сад представлен серой областью; а стена представлена белой областью.
и являются квадратами, а площадь сада равна площади стены.
Длина составляет .
Найдите площадь стены.
Возможные ответы:
Правильный ответ:
Объяснение:
Длина AB равна 7, поэтому площадь ABCD равна:
.
Площадь сада (EFGH) равна площади стены.
Итак,
,
поэтому
.

