Построение графика квадратичной функции
«Построение графика квадратичной функции» (9 класс)
Урок 2
Цели урока:
- Образовательные: научиться построению графика квадратичной функции и использованию графика для получения её свойств.
- Развивающие: развивать логическое мышление, алгоритмическую культуру, внимание, навыки самостоятельной работы с источником информации и самоконтроля, поддерживать интерес к математике.
- Воспитательные: воспитывать последовательность, ответственность, самостоятельность, настойчивость, дисциплинированность.
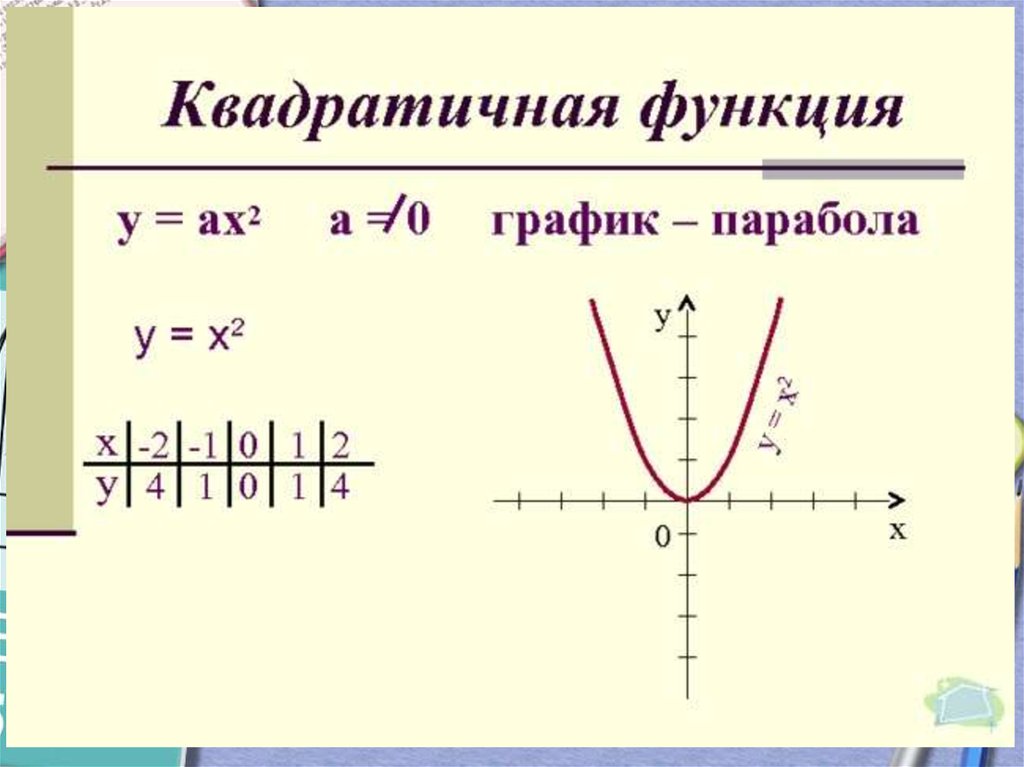
Квадратичной функцией называется функция, которую можно задать формулой вида y=ax²+bx+c , где х — независимая переменная, a, b и с -некоторые числа (причём а≠0).
Например: у = 5х²+6х+3,
у = -7х²+8х-2,
у = 0,8х²+5,
у = ¾х²-8х,
у = -12х²
— квадратичные функции
 к. а=2, а0 ). Например: у= -7 х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а у 0 х у 0 х «
к. а=2, а0 ). Например: у= -7 х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а у 0 х у 0 х «
Графиком квадратичной функции является парабола , ветви которой направлены вверх (если а0) или вниз (если а
- у= 2 х ²+4х-1 – графиком является парабола, ветви которой направлены вверх (т.к. а=2, а0 ).
Например:
- у= -7 х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а
у
0
х
у
0
х
Чтобы построить график функции надо:
1. Описать функцию:
название функции,
что является графиком функции,
куда направлены ветви параболы.
Пример: у = х ²-2х-3 – квадратичная функция, графиком является парабола, ветви которой направлены вверх (т.к. а=1, а0)
Чтобы построить график функции надо:
Пример: у = х ²-2х-3 (а = 1; b = -2; с = -3) Найдём координаты вершины параболы
n = 1²-2·1-3 = -4
А(1;-4) – вершина параболы.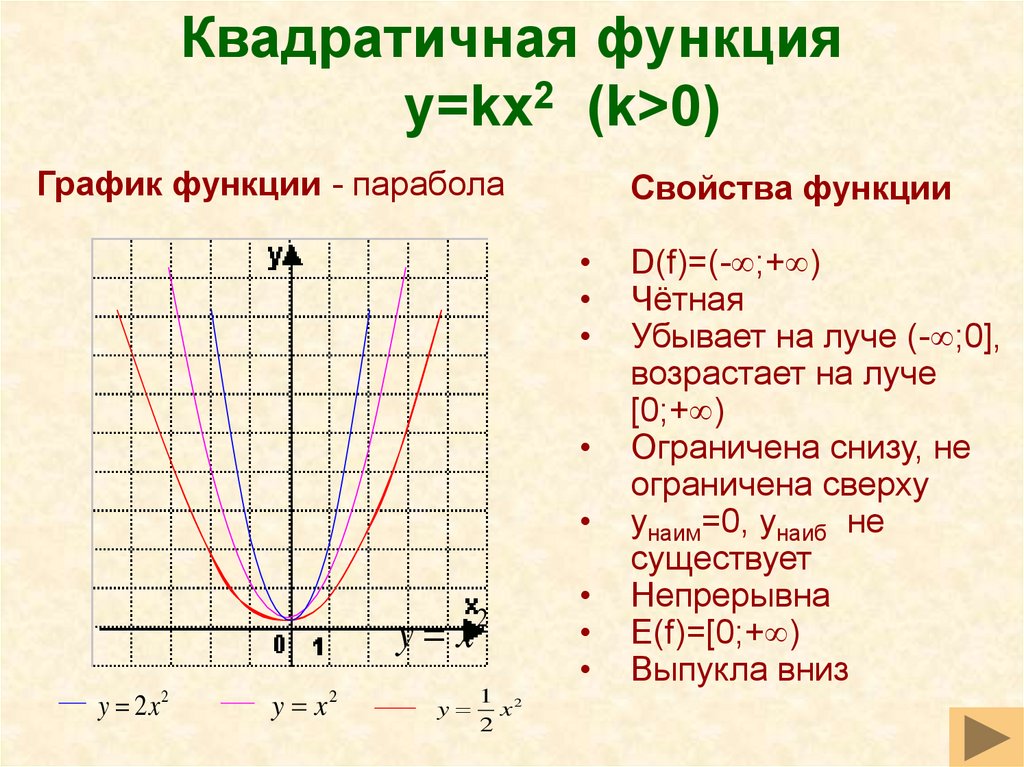
х=1 – ось симметрии параболы.
2. Найти координаты вершины параболы А( m;n) по формулам:
;
или n = у(m) т.е. подставить найденное значение абсциссы m в формулу, которой задана функция и вычислить значение.
Прямая x=m является ось ю симметрии параболы.
Чтобы построить график функции надо:
3. Заполнить таблицу значений функции:
Прямая x=m является осью симметрии параболы, т.е. точки графика симметричны относительно этой прямой.
В таблице расположить вершину в середине таблицы и взять соседние симметричные значения х. Например, следующим образом:
*- посчитать значение функции в выбранных значениях х.
Пример: у = х ²-2х-3
А(1;- 4) – вершина параболы
х=1 – ось симметрии параболы.
Составим таблицу значений функции:
Х
у
— 1
0
0
— 3
1
— 4
2
— 3
3
0
Х
у
m-2
*
m-1
*
m
m+1
n
*
m+2
*
Чтобы построить график функции надо:
4. Построить график функции: — отметить в координатной плоскости точки, координаты которых указаны в таблице; — соединить их плавной линией.
Построить график функции: — отметить в координатной плоскости точки, координаты которых указаны в таблице; — соединить их плавной линией.
х
у
-1
0
0
-3
1
-4
2
-3
3
0
У
4
-4
3-3
2
-2
1
-1
у = х ²-2х-3
0
-2
1
-1
-3
2
3
-4
4
-5
5
6
х
Попробуйте ответить на контрольные вопросы:
- Сформулируйте определение квадратичной функции.
- Что представляет собой график квадратичной функции?
- Куда могут быть направлены ветви параболы и от чего это зависит?
- В какой последовательности нужно строить график квадратичной функции?
Стоит немного отдохнуть от компьютера.
Попробуйте построить в тетради график функции
у = -2х²+8х-3
Постройте график функции у = -2х ²+8х-3 План построения графика квадратичной функции:
1.
- название функции; что является графиком функции; куда направлены ветви параболы
- название функции;
- что является графиком функции;
- куда направлены ветви параболы
2. Найти координаты вершины параболы А( m;n)
по формулам:
или n = у(m)
3. Заполнить таблицу значений функции.
4. Построить график функции:
- отметить в координатной плоскости точки, координаты которых указаны в таблице; соединить их плавной линией.
- отметить в координатной плоскости точки, координаты которых указаны в таблице;
- соединить их плавной линией.
Проверьте себя. Ваше задание должно быть выполнено следующим образом:
у = -2х ²+8х-3 — квадратичная функция, графиком является парабола, ветви которой направлены вниз (т.к. а=-2, а
Найдём координаты вершины параболы
n = -2·2²+8·2-3 =5
А ( 2; 5 ) – вершина параболы.
х=5 ось симметрии параболы.
Составим таблицу значений функции.
у = -2х ²+8х-3
у
7
6
5
4
-3
3
-2
2
-1
1
0
-1
1
-2
-3
2
3
-4
4
5
6
х
Х
у
0
-3
1
3
2
3
5
3
4
-3
Если у вас получилось тоже самое – вы молодец и мы вас поздравляем!!! Вы можете перейти к следующей странице .
Если вы допустили ошибку – не огорчайтесь. У вас всё ещё впереди! Вы можете заглянуть в свой учебник (п.7)
Рассмотрим свойства этой квадратичной функции. (листаем свойства по щелчку мыши)
- Область определения функции (-∞;+∞)
Область значений функции (-∞;5]
- Нули функции х =0,5 и х =3,5
- у 0 на промежутке (0,5;3,5)
y
- Функция возрастает на промежутке (-∞;2]
функция убывает на промежутке [2;+∞)
- Наибольшее значение функции равно 5
у
7
6
5
4
3
у = -2х ²+8х-3
2
-1
1
0
-2
1
-1
2
-3
3
-4
4
х
Перед продолжением работы запишите домашнее задание,
№ 122, 124(а),
244(б,в)
Далее выполните тест.
- прочитайте задание;
- выполните его устно или, сделав записи в тетради;
- и выберите правильный ответ
Выполните тест
1 вопрос: Выберите квадратичную функцию а)
б)
в)
г)
Выполните тест
2 вопрос: Куда направлены ветви параболы ?
- Вверх
- Вниз
Выполните
3 вопрос: Укажите координаты вершины параболы
а) А(3;6)
б) А(-1;-17)
в) А(1;-5)
г) А(1;-1)
Выполните тест
у
У
У
0 6
х
-6 0
х
-6 0
х
4 вопрос:
На рисунке показаны графики квадратичных функций. Выберите график функции
у= — 4х²-16х+1, подведите к нему стрелку и нажмите левую кнопку мыши .
у
у
17
5
у
1
0 2,5
х
-2 х
2,5
6
0
х
Выполните тест
5 вопрос: Укажите формулу квадратичной функции, график которой изображён на рисунке.
- у = -x 2 +6x
- у = — 3х²+8х-11
- у = — 4х²-16х+1
- у = х²-6х
- у = х²+6х
- у = 1,2х²-6х+5
У
-6 0
х
Выполните следующую работу в тетрадях по вариантам. Постройте графики функций:
- I вариант
у = -х ²+6х-8
Укажите свойства функции.
- II вариант
у = х ²-6х-7
Укажите свойства функции.
Описание графика квадратичной функции. I случай, классическая парабола
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Задания на свойства и графики квадратичной функции вызывают, как показывает практика, серьезные затруднения. Это довольно странно, ибо квадратичную функцию проходят в 8 классе, а потом всю первую четверть 9-го класса «вымучивают» свойства параболы и строят ее графики для различных параметров.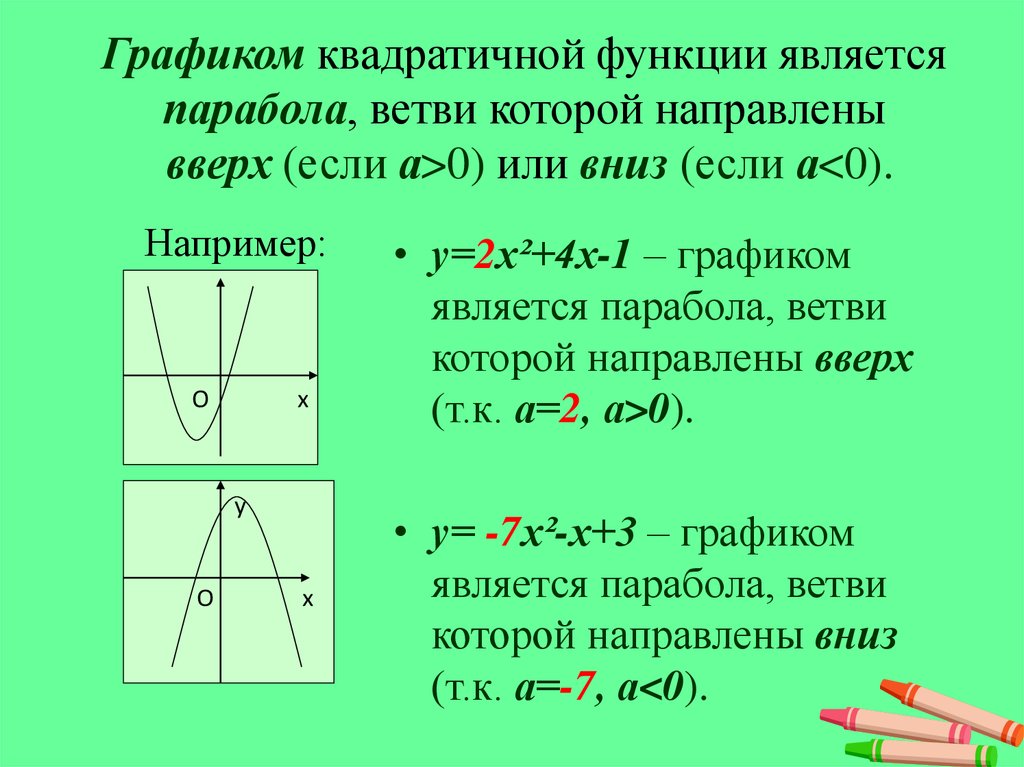
Это связано с тем, что заставляя учащихся строить параболы, практически не уделяют времени на «чтение» графиков, то есть не практикуют осмысление информации, полученной с картинки. Видимо, предполагается, что, построив десятка два графиков, сообразительный школьник сам обнаружит и сформулирует связь коэффициентов в формуле и внешний вид графика. На практике так не получается. Для подобного обобщения необходим серьезный опыт математических мини исследований, которым большинство девятиклассников, конечно, не обладает. А между тем, в ГИА предлагают именно по графику определить знаки коэффициентов.
Не будем требовать от школьников невозможного и просто предложим один из алгоритмов решения подобных задач.
Итак, функция вида y = ax 2 + bx + c называется квадратичной, графиком ее является парабола. Как следует из названия, главным слагаемым является ax 2 . То есть а не должно равняться нулю, остальные коэффициенты (b и с ) нулю равняться могут.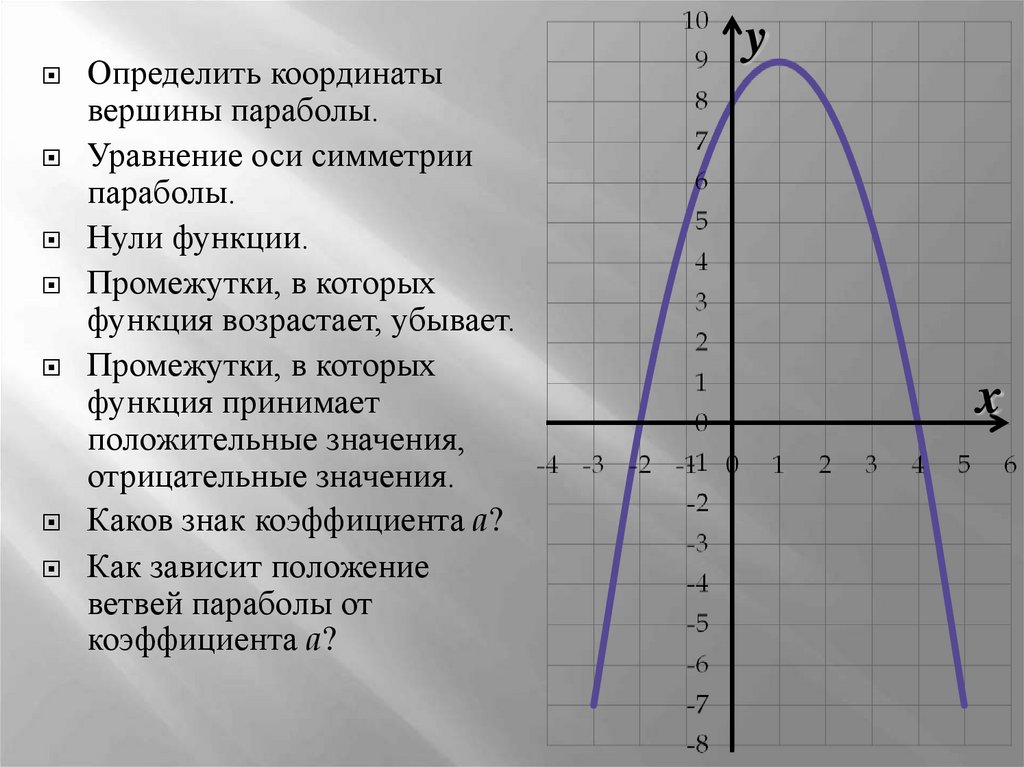
Посмотрим, как влияют на внешний вид параболы знаки ее коэффициентов.
Самая простая зависимость для коэффициента а . Большинство школьников уверенно отвечает: » если а > 0, то ветви параболы направлены вверх, а если а а > 0.
y = 0,5x 2 — 3x + 1
В данном случае а = 0,5
А теперь для а
y = — 0,5×2 — 3x + 1
В данном случае а = — 0,5
Влияние коэффициента с тоже достаточно легко проследить. Представим, что мы хотим найти значение функции в точке х = 0. Подставим ноль в формулу:
y = a 0 2 + b 0 + c = c . Получается, что у = с . То есть с — это ордината точки пересечения параболы с осью у. Как правило, эту точку легко найти на графике. И определить выше нуля она лежит или ниже. То есть с > 0 или с
с > 0:
y = x 2 + 4x + 3
с
y = x 2 + 4x — 3
Соответственно, если с = 0, то парабола обязательно будет проходить через начало координат:
y = x 2 + 4x
Сложнее с параметром b .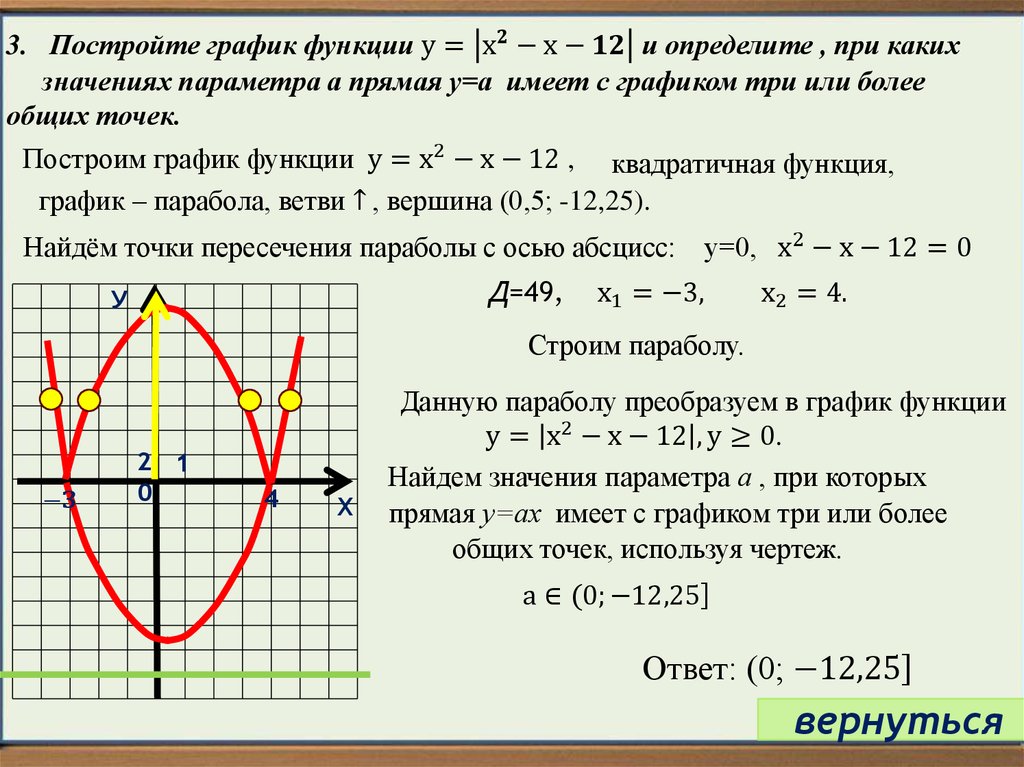 Точка, по которой мы будем его находить, зависит не только от b но и от а . Это вершина параболы. Ее абсцисса (координата по оси х ) находится по формуле х в = — b/(2а) . Таким образом, b = — 2ах в . То есть, действуем следующим образом: на графике находим вершину параболы, определяем знак ее абсциссы, то есть смотрим правее нуля (х в > 0) или левее (х в
Точка, по которой мы будем его находить, зависит не только от b но и от а . Это вершина параболы. Ее абсцисса (координата по оси х ) находится по формуле х в = — b/(2а) . Таким образом, b = — 2ах в . То есть, действуем следующим образом: на графике находим вершину параболы, определяем знак ее абсциссы, то есть смотрим правее нуля (х в > 0) или левее (х в
Однако это не все. Надо еще обратить внимание на знак коэффициента а . То есть посмотреть, куда направлены ветви параболы. И только после этого по формуле b = — 2ах в определить знак b .
Рассмотрим пример:
Ветви направлены вверх, значит а > 0, парабола пересекает ось у ниже нуля, значит с х в > 0. Значит b = — 2ах в = -++ = -. b а > 0, b с
Во многих задачах требуется вычислить максимальное или минимальное значение квадратичной функции. Максимум или минимум можно найти, если исходная функция записана в стандартном виде: или через координаты вершины параболы: f (x) = a (x − h) 2 + k {\displaystyle f(x)=a(x-h)^{2}+k}
. {2}}
следующим образом:
{2}}
следующим образом:
- В функции коэффициенты a = 1 {\displaystyle a=1}
и b = 10 {\displaystyle b=10}
- x = − 10 (2) (1) {\displaystyle x=-{\frac {10}{(2)(1)}}}
- x = − 10 2 {\displaystyle x=-{\frac {10}{2}}}
- В качестве второго примера рассмотрим функцию . Здесь a = − 3 {\displaystyle a=-3}
и b = 6 {\displaystyle b=6}
. Поэтому координату «x» вершины параболы вычислите так:
- x = − b 2 a {\displaystyle x=-{\frac {b}{2a}}}
- x = − 6 (2) (− 3) {\displaystyle x=-{\frac {6}{(2)(-3)}}}
- x = − 6 − 6 {\displaystyle x=-{\frac {6}{-6}}}
- x = − (− 1) {\displaystyle x=-(-1)}
- x = 1 {\displaystyle x=1}
Найдите соответствующее значение f(x). Подставьте найденное значение «x» в исходную функцию, чтобы найти соответствующее значение f(x). Так вы найдете минимум или максимум функции.
- В первом примере f (x) = x 2 + 10 x − 1 {\displaystyle f(x)=x^{2}+10x-1}
вы вычислили, что координата «х» вершины параболы равна x = − 5 {\displaystyle x=-5}
.
 {2}+6x-4}
значение a {\displaystyle a}
отрицательное, поэтому вы нашли максимум. Вершина параболы лежит в точке с координатами (1 , − 1) {\displaystyle (1,-1)}
, а максимальное значение функции равно − 1 {\displaystyle -1}
.
{2}+6x-4}
значение a {\displaystyle a}
отрицательное, поэтому вы нашли максимум. Вершина параболы лежит в точке с координатами (1 , − 1) {\displaystyle (1,-1)}
, а максимальное значение функции равно − 1 {\displaystyle -1}
.
Определите направление параболы. Для этого посмотрите на знак коэффициента a {\displaystyle a} . Если коэффициент a {\displaystyle a} положительный, парабола направлена вверх. Если коэффициент a {\displaystyle a} отрицательный, парабола направлена вниз. Например:
- . Здесь a = 2 {\displaystyle a=2} , то есть коэффициент положительный, поэтому парабола направлена вверх.
- . Здесь a = − 3 {\displaystyle a=-3} , то есть коэффициент отрицательный, поэтому парабола направлена вниз.
- Если парабола направлена вверх, нужно вычислить минимальное значение функции. Если парабола направлена вниз, необходимо найти максимальное значение функции.
Найдите минимальное или максимальное значение функции.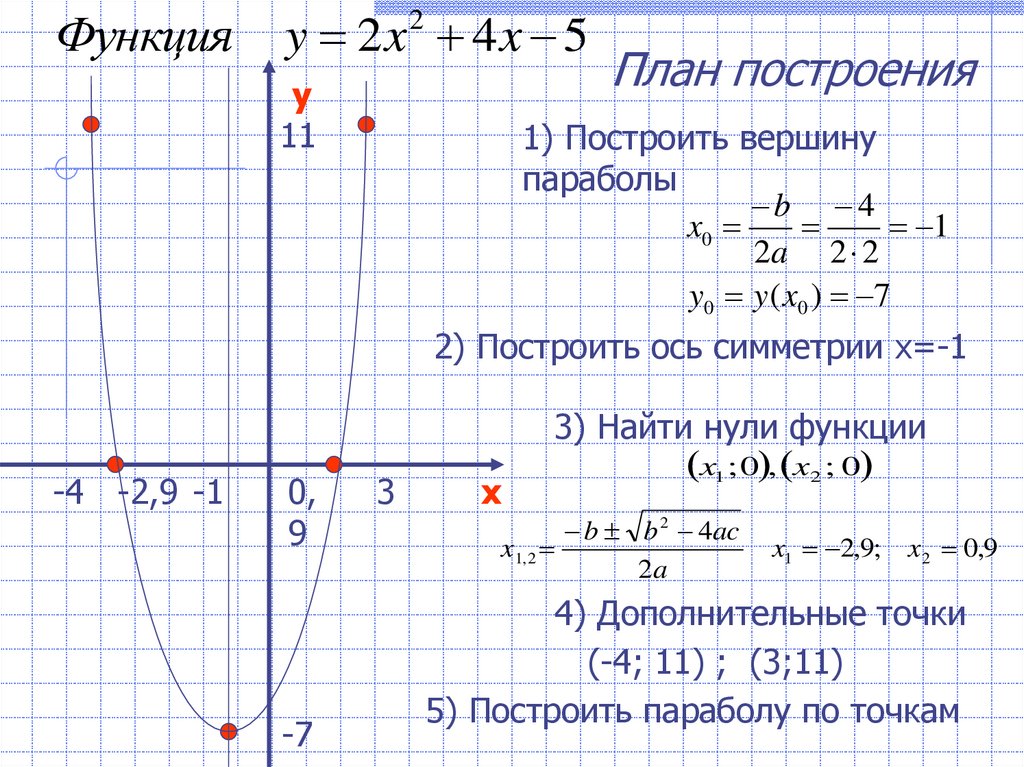 {\prime }(x)=4x-4}
{\prime }(x)=4x-4}
Производную приравняйте к нулю. Напомним, что производная функции равна угловому коэффициенту функции в определенной точке. В минимуме или максимуме угловой коэффициент равен нулю. Поэтому, чтобы найти минимальное или максимальное значение функции, производную нужно приравнять к нулю. В нашем примере.
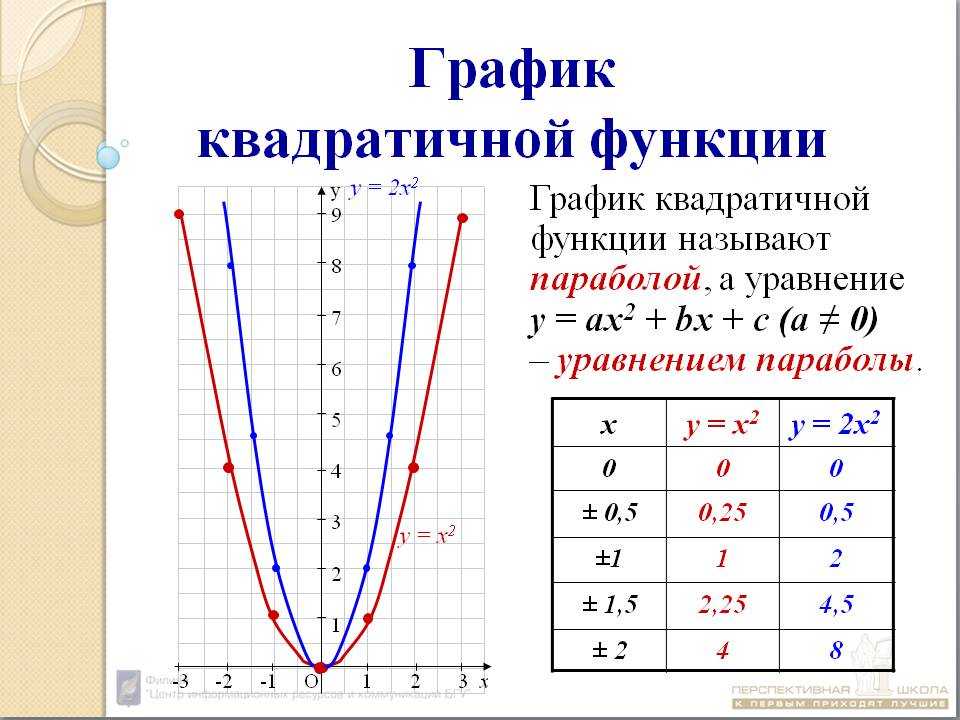
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
Пример.
Построить график функции y=x²+2x-3.
Решение:
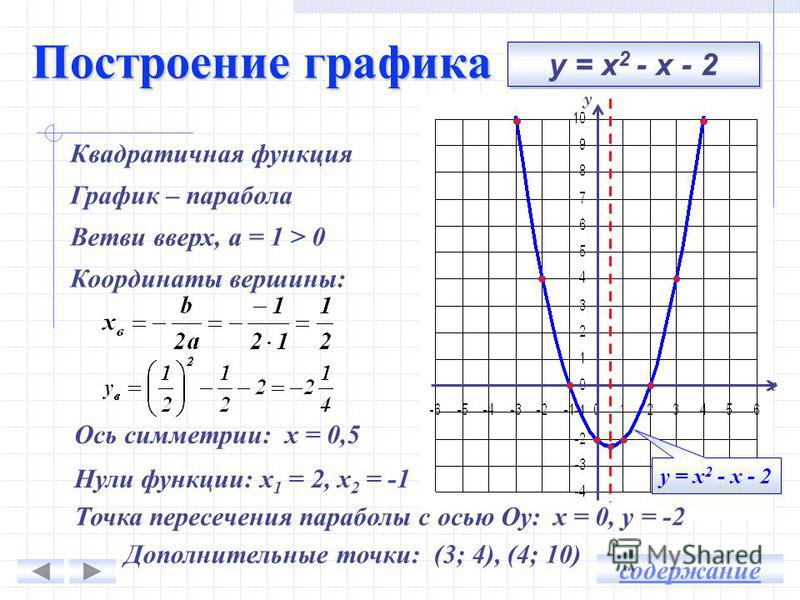
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх.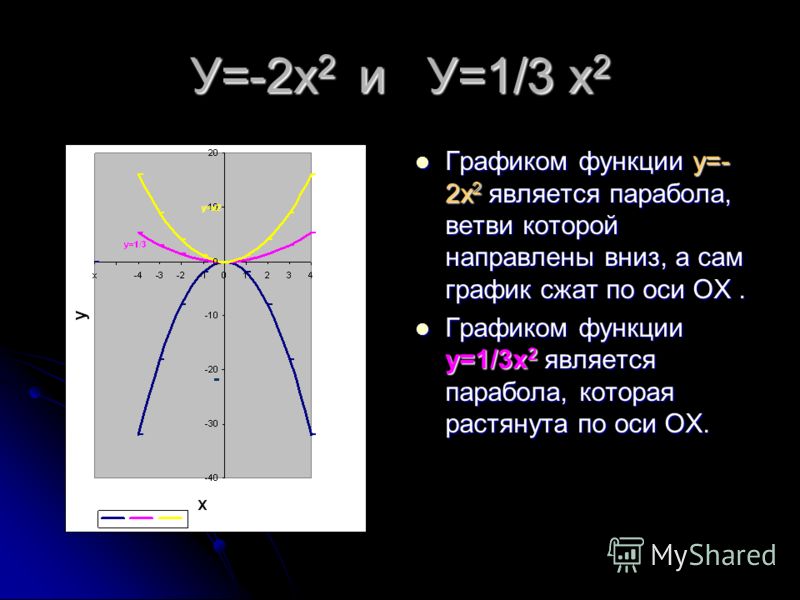 Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем . В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Построить график функции y= -x²-3x.
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Рубрика: |
На уроках математики в школе Вы уже познакомились с простейшими свойствами и графиком функции y = x 2 .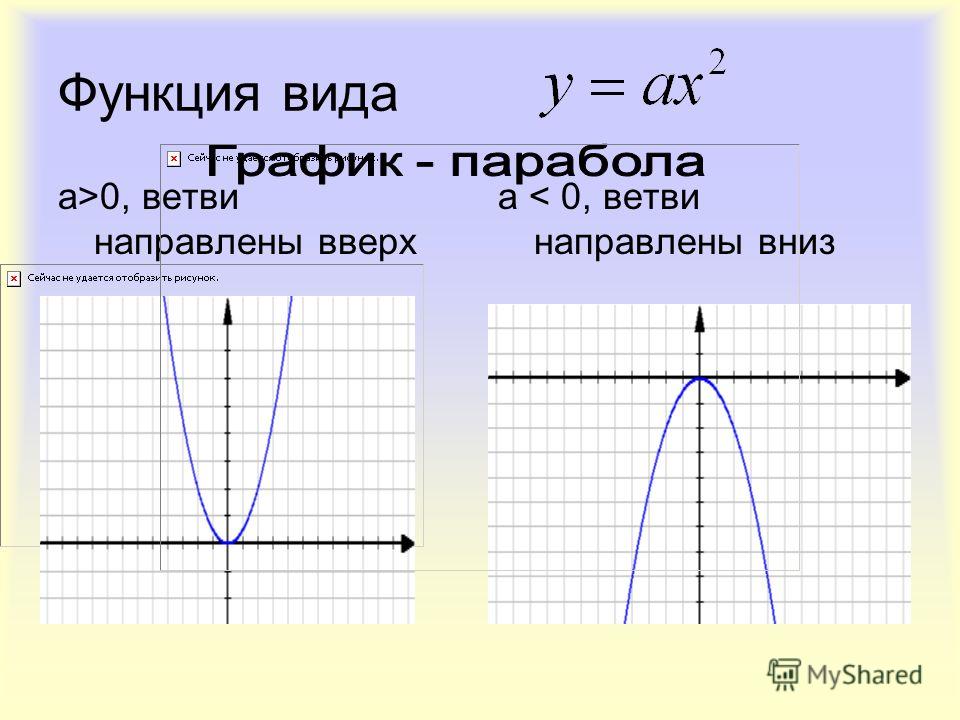 Давайте расширим знания по квадратичной функции .
Давайте расширим знания по квадратичной функции .
Задание 1.
Построить график функции y = x 2 . Масштаб: 1 = 2 см. Отметьте на оси Oy точку F (0; 1/4). Циркулем или полоской бумаги измерьте расстояние от точки F до какой-нибудь точки M параболы. Затем приколите полоску в точке M и поверните ее вокруг этой точки так, чтобы она стала вертикальной. Конец полоски опустится немного ниже оси абсцисс (рис. 1) . Отметьте на полоске, насколько она выйдет за ось абсцисс. Возьмите теперь другую точку на параболе и повторите измерение еще раз. Насколько теперь опустился край полоски за ось абсцисс?
Результат: какую бы точку на параболе y = x 2 вы не взяли, расстояние от этой точки до точки F(0; 1/4) будет больше расстояния от той же точки до оси абсцисс всегда на одно и то же число – на 1/4.
Можно сказать иначе: расстояние от любой точки параболы до точки (0; 1/4) равно расстоянию от той же точки параболы до прямой y = -1/4. Эта замечательная точка F(0; 1/4) называется фокусом параболы y = x 2 , а прямая y = -1/4 – директрисой этой параболы. Директриса и фокус есть у каждой параболы.
Эта замечательная точка F(0; 1/4) называется фокусом параболы y = x 2 , а прямая y = -1/4 – директрисой этой параболы. Директриса и фокус есть у каждой параболы.
Интересные свойства параболы:
1. Любая точка параболы равноудалена от некоторой точки, называемой фокусом параболы, и некоторой прямой, называемой ее директрисой.
2. Если вращать параболу вокруг оси симметрии (например, параболу y = x 2 вокруг оси Oy), то получится очень интересная поверхность, которая называется параболоидом вращения.
Поверхность жидкости во вращающемся сосуде имеет форму параболоида вращения. Вы можете увидеть эту поверхность, если сильно помешаете ложечкой в неполном стакане чая, а потом вынете ложечку.
3. Если в пустоте бросить камень под некоторым углом к горизонту, то он полетит по параболе (рис. 2).
4. Если пересечь поверхность конуса плоскостью, параллельной какой-либо одной его образующей, то в сечении получится парабола (рис. 3) .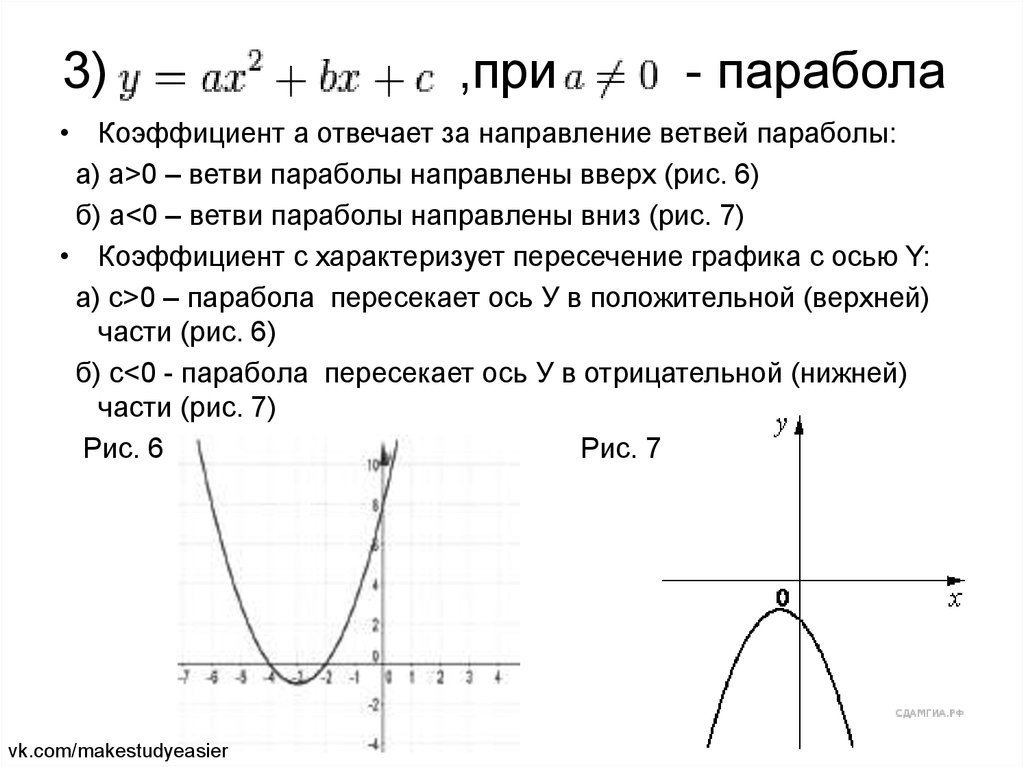
5. В парках развлечений иногда устраивают забавный аттракцион «Параболоид чудес». Каждому, из стоящих внутри вращающегося параболоида, кажется, что он стоит на полу, а остальные люди каким-то чудом держаться на стенках.
6. В зеркальных телескопах также применяют параболические зеркала: свет далекой звезды, идущий параллельным пучком, упав на зеркало телескопа, собирается в фокус.
7. У прожекторов зеркало обычно делается в форме параболоида. Если поместить источник света в фокусе параболоида, то лучи, отразившись от параболического зеркала, образуют параллельный пучок.
Построение графика квадратичной функции
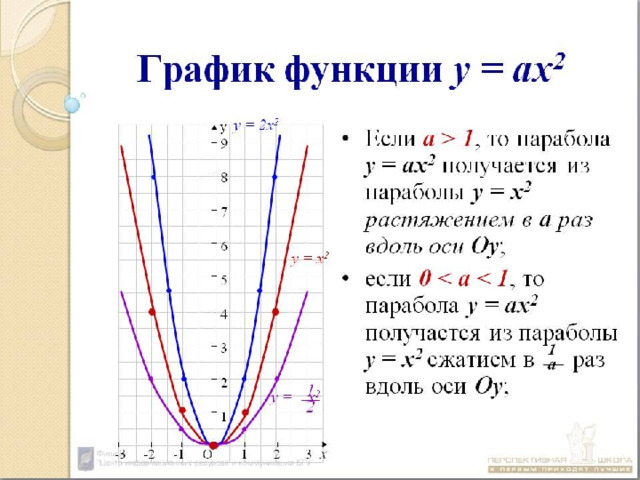
На уроках математики вы изучали получение из графика функции y = x 2 графиков функций вида:
1) y = ax 2 – растяжение графика y = x 2 вдоль оси Oy в |a| раз (при |a| рис. 4 ).
2) y = x 2 + n – сдвиг графика на n единиц вдоль оси Oy, причем, если n > 0, то сдвиг вверх, а если n
3) y = (x + m) 2 – сдвиг графика на m единиц вдоль оси Ox: если m 0, то влево, (рис.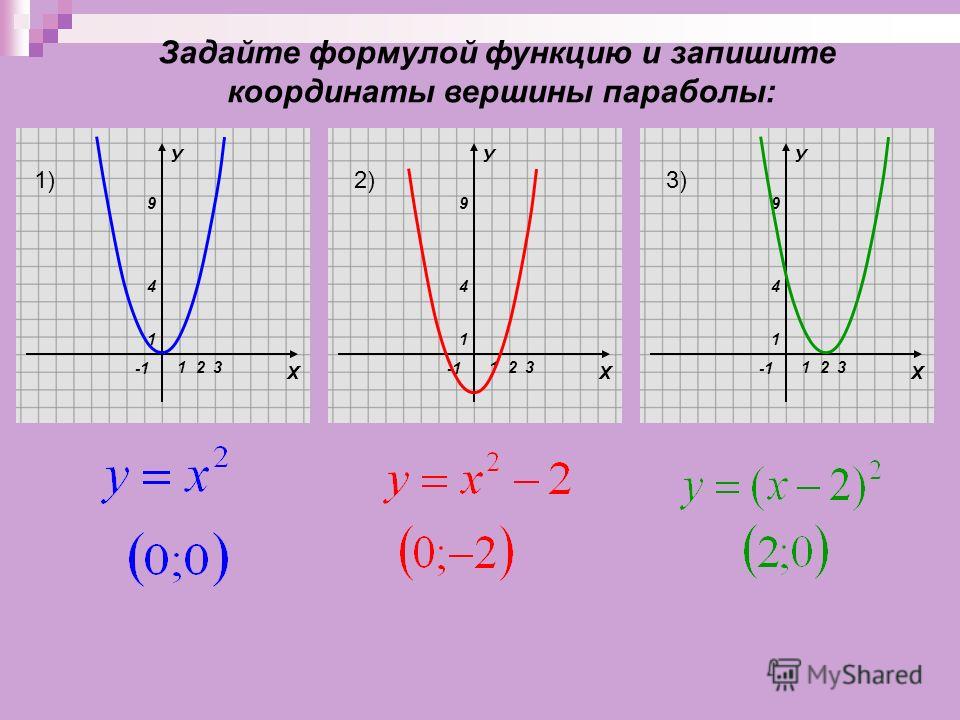 5) .
5) .
4) y = -x 2 – симметричное отображение относительно оси Ox графика y = x 2 .
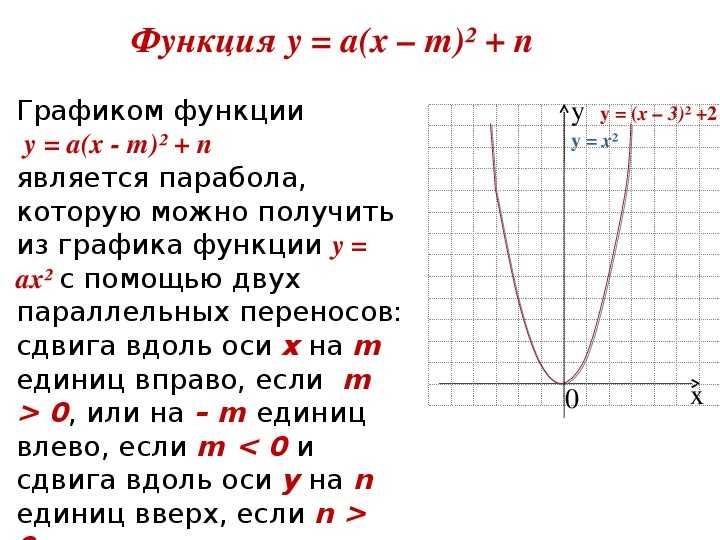
Подробнее остановимся на построении графика функции y = a(x – m) 2 + n .
Квадратичную функцию вида y = ax 2 + bx + c всегда можно привести к виду
y = a(x – m) 2 + n, где m = -b/(2a), n = -(b 2 – 4ac)/(4a).
Докажем это.
Действительно,
y = ax 2 + bx + c = a(x 2 + (b/a) x + c/a) =
A(x 2 + 2x · (b/a) + b 2 /(4a 2) – b 2 /(4a 2) + c/a) =
A((x + b/2a) 2 – (b 2 – 4ac)/(4a 2)) = a(x + b/2a) 2 – (b 2 – 4ac)/(4a).
Введем новые обозначения.
Пусть m = -b/(2a) , а n = -(b 2 – 4ac)/(4a) ,
тогда получим y = a(x – m) 2 + n или y – n = a(x – m) 2 .
Сделаем еще замены: пусть y – n = Y, x – m = X (*).
Тогда получим функцию Y = aX 2 , графиком которой является парабола.
Вершина параболы находится в начале координат. X = 0; Y = 0.
Подставив координаты вершины в (*), получаем координаты вершины графика y = a(x – m) 2 + n: x = m, y = n.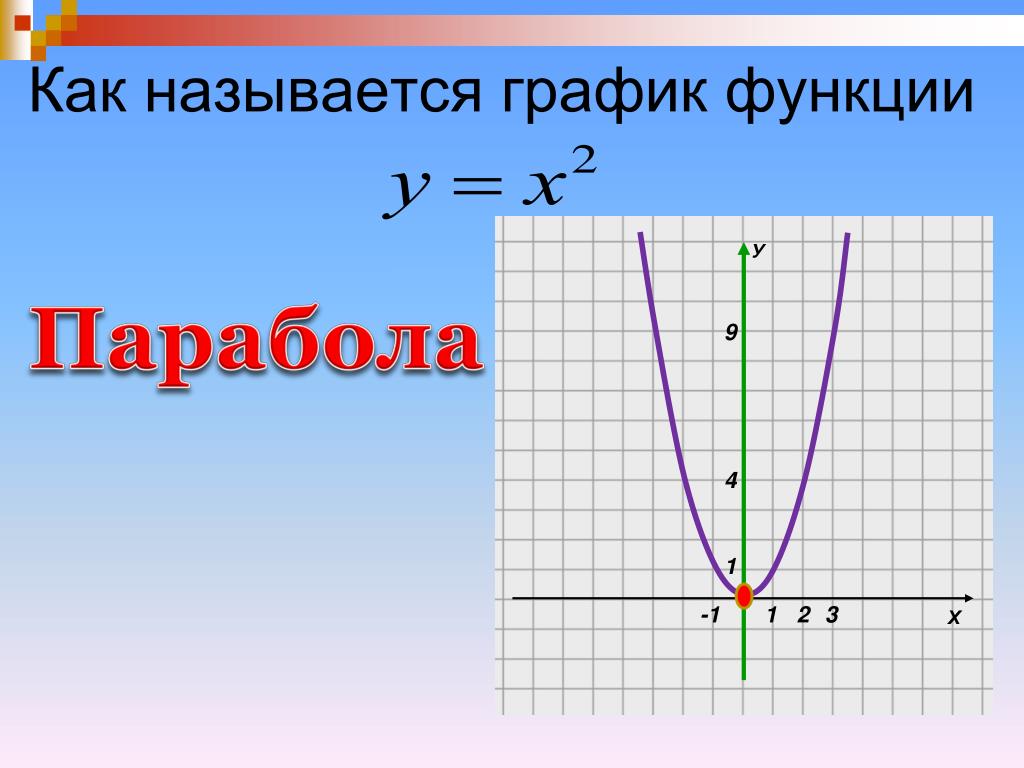
Таким образом, для того, чтобы построить график квадратичной функции, представленной в виде
y = a(x – m) 2 + n
путем преобразований, можно действовать следующим образом:
a) построить график функции y = x 2 ;
б) путем параллельного переноса вдоль оси Ox на m единиц и вдоль оси Oy на n единиц – вершину параболы из начала координат перевести в точку с координатами (m; n) (рис. 6) .
Запись преобразований:
y = x 2 → y = (x – m) 2 → y = a(x – m) 2 → y = a(x – m) 2 + n.
Пример.
С помощью преобразований построить в декартовой системе координат график функции y = 2(x – 3) 2 – 2.
Решение.
Цепочка преобразований:
y = x 2 (1) → y = (x – 3) 2 (2) → y = 2(x – 3) 2 (3) → y = 2(x – 3) 2 – 2 (4) .
Построение графика изображено на рис. 7 .
Вы можете практиковаться в построении графиков квадратичной функции самостоятельно.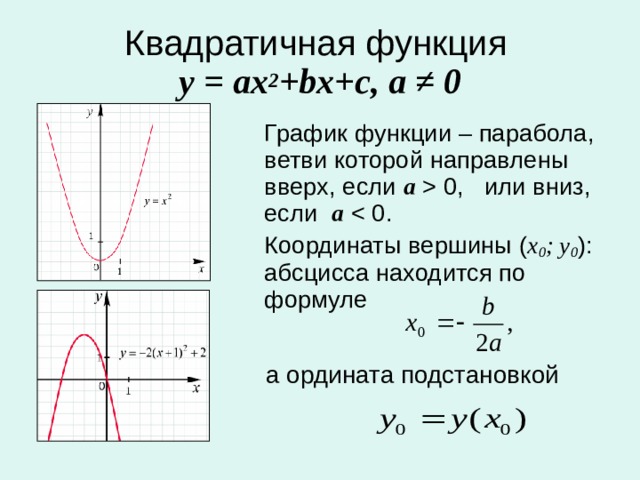 Например, постройте в одной системе координат с помощью преобразований график функции y = 2(x + 3) 2 + 2. Если у вас возникнут вопросы или же вы захотите получить консультацию учителя, то у вас есть возможность провести бесплатное 25-минутное занятие с онлайн репетитором после регистрации . Для дальнейшей работы с преподавателем вы сможете выбрать подходящий вам тарифный план.
Например, постройте в одной системе координат с помощью преобразований график функции y = 2(x + 3) 2 + 2. Если у вас возникнут вопросы или же вы захотите получить консультацию учителя, то у вас есть возможность провести бесплатное 25-минутное занятие с онлайн репетитором после регистрации . Для дальнейшей работы с преподавателем вы сможете выбрать подходящий вам тарифный план.
Остались вопросы? Не знаете, как построить график квадратичной функции?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
графиков квадратичных функций | Колледж Алгебра
Результаты обучения
- Распознавание характеристик парабол.
- Поймите, как график параболы связан с ее квадратичной функцией.
Изогнутые антенны, подобные показанным на фото, обычно используются для фокусировки микроволн и радиоволн для передачи телевизионных и телефонных сигналов, а также спутниковой и космической связи.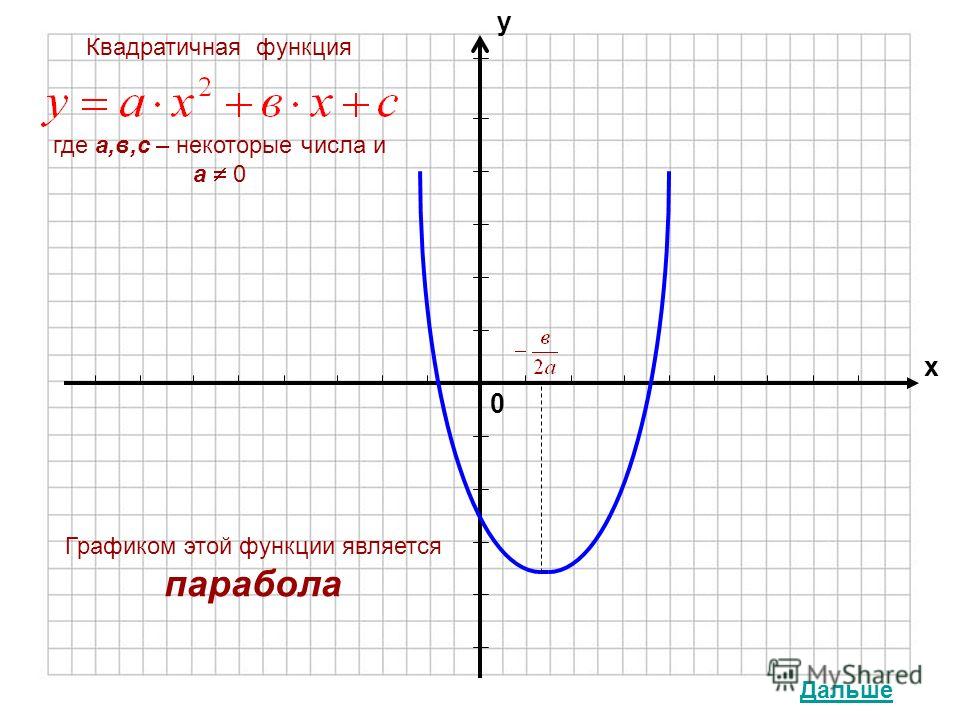 Поперечное сечение антенны имеет форму параболы, которую можно описать квадратичной функцией.
Поперечное сечение антенны имеет форму параболы, которую можно описать квадратичной функцией.
Набор спутниковых антенн. (кредит: Мэтью Колвин де Валье, Flickr)
Характеристики парабол
График квадратичной функции представляет собой U-образную кривую, называемую параболой . Одной из важных особенностей графа является то, что он имеет крайнюю точку, называемую вершиной . Если парабола раскрывается, вершина представляет собой самую низкую точку на графике или минимальное значение квадратичной функции. Если парабола направлена вниз, вершина представляет собой самую высокую точку на графике или максимальное значение . В любом случае вершина является поворотной точкой на графе. Граф также является симметричным с вертикальной линией, проведенной через вершину, называемую осью симметрии .
Точка пересечения [latex]y[/latex] — это точка, в которой парабола пересекает ось [latex]y[/latex].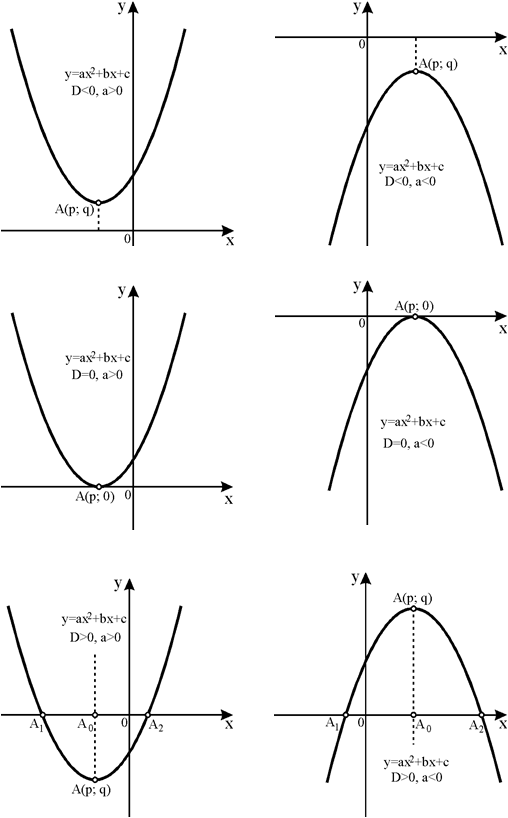 {2}+bx+c[ /латекс] 9{2}+4x+3[/латекс]. В этой форме [латекс]а=1,\текст{ }b=4[/латекс] и [латекс]с=3[/латекс]. Поскольку [latex]a>0[/latex], парабола открывается вверх. Ось симметрии: [латекс]x=-\dfrac{4}{2\left(1\right)}=-2[/latex]. Это также имеет смысл, поскольку на графике видно, что вертикальная линия [latex]x=-2[/latex] делит график пополам. Вершина всегда находится вдоль оси симметрии. Для параболы, которая открывается вверх, вершина находится в самой нижней точке графика, в данном случае [латекс]\влево(-2,-1\вправо)[/латекс]. [latex]x[/latex]-перехваты, те точки, где парабола пересекает [latex]x[/latex]-ось, находятся в [latex]\left(-3,0\right)[/latex] и [латекс]\влево(-1,0\вправо)[/латекс]. 9{2}+k[/latex]
{2}+bx+c[ /латекс] 9{2}+4x+3[/латекс]. В этой форме [латекс]а=1,\текст{ }b=4[/латекс] и [латекс]с=3[/латекс]. Поскольку [latex]a>0[/latex], парабола открывается вверх. Ось симметрии: [латекс]x=-\dfrac{4}{2\left(1\right)}=-2[/latex]. Это также имеет смысл, поскольку на графике видно, что вертикальная линия [latex]x=-2[/latex] делит график пополам. Вершина всегда находится вдоль оси симметрии. Для параболы, которая открывается вверх, вершина находится в самой нижней точке графика, в данном случае [латекс]\влево(-2,-1\вправо)[/латекс]. [latex]x[/latex]-перехваты, те точки, где парабола пересекает [latex]x[/latex]-ось, находятся в [latex]\left(-3,0\right)[/latex] и [латекс]\влево(-1,0\вправо)[/латекс]. 9{2}+k[/latex]
, где [latex]\left(h,\text{ }k\right)[/latex] — вершина. Поскольку вершина появляется в стандартной форме квадратичной функции, эта форма также известна как вершинная форма квадратичной функции .
Учитывая квадратичную функцию в общем виде, найдите вершину параболы.

Одна из причин, по которой мы можем захотеть идентифицировать вершину параболы, заключается в том, что эта точка сообщит нам, где происходит максимальное или минимальное значение вывода, [latex]k[/latex], и где оно происходит, [latex]h [/латекс]. Если нам дан общий вид квадратичной функции: 92+bx+c[/latex]
Мы можем определить вершину [latex](h,k)[/latex], выполнив следующие действия:
- Идентифицировать [latex]a[/latex], [latex] ]b[/латекс] и [латекс]с[/латекс].
- Найдите [latex]h[/latex], координату [latex]x[/latex] вершины, подставив [latex]a[/latex] и [latex]b[/latex] в [latex]h =-\dfrac{b}{2a}[/latex].
- Найдите [latex]k[/latex], [latex]y[/latex]-координату вершины, оценивая [latex]k=f\left(h\right)=f\left(-\dfrac{ б}{2а}\справа)[/латекс] 9{2}-6x[/latex], напишите уравнение в общем виде, а затем в стандартном виде.
Показать решение
Нахождение области определения и диапазона квадратичной функции
Любое число может быть входным значением квадратичной функции.
 Следовательно, областью определения любой квадратичной функции являются все действительные числа. Поскольку параболы имеют максимум или минимум в вершине, диапазон ограничен. Так как вершина параболы будет либо максимальной, либо минимальной, диапазон будет состоять из всех [latex]y[/latex]-значений, больших или равных [latex]y[/latex]-координате вершины или меньше или равно [latex]y[/latex]-координате в точке поворота, в зависимости от того, открывается ли парабола вверх или вниз. 9{2}+bx+c[/latex] с положительным значением [latex]a[/latex] равно [latex]f\left(x\right)\ge f\left(-\frac{b}{2a} \right)[/latex], или [латекс]\left[f\left(-\frac{b}{2a}\right),\infty \right)[/latex]; диапазон квадратичной функции, записанной в общем виде с отрицательным значением [latex]a[/latex] , равен [latex]f\left(x\right)\le f\left(-\frac{b}{2a}\ right)[/latex], или [latex]\left(-\infty ,f\left(-\frac{b}{2a}\right)\right][/latex].
Следовательно, областью определения любой квадратичной функции являются все действительные числа. Поскольку параболы имеют максимум или минимум в вершине, диапазон ограничен. Так как вершина параболы будет либо максимальной, либо минимальной, диапазон будет состоять из всех [latex]y[/latex]-значений, больших или равных [latex]y[/latex]-координате вершины или меньше или равно [latex]y[/latex]-координате в точке поворота, в зависимости от того, открывается ли парабола вверх или вниз. 9{2}+bx+c[/latex] с положительным значением [latex]a[/latex] равно [latex]f\left(x\right)\ge f\left(-\frac{b}{2a} \right)[/latex], или [латекс]\left[f\left(-\frac{b}{2a}\right),\infty \right)[/latex]; диапазон квадратичной функции, записанной в общем виде с отрицательным значением [latex]a[/latex] , равен [latex]f\left(x\right)\le f\left(-\frac{b}{2a}\ right)[/latex], или [latex]\left(-\infty ,f\left(-\frac{b}{2a}\right)\right][/latex].Диапазон квадратичной функции записывается в стандартной форме [латекс]f\left(x\right)=a{\left(xh\right)}^{2}+k[/latex] с положительным значением [latex]a[/latex] равно [ латекс]f\left(x\right)\ge k[/latex]; диапазон квадратичной функции, записанной в стандартной форме с отрицательным значением [latex]a[/latex] , равен [latex]f\left(x\ справа)\le k[/латекс].

Как: Для заданной квадратичной функции найти домен и диапазон.
- Область определения любой квадратичной функции, как и всех действительных чисел.
- Определите, является ли [латекс]а[/латекс] положительным или отрицательным. Если [latex]a[/latex] положительно, парабола имеет минимум. Если [latex]a[/latex] отрицательно, парабола имеет максимум.
- Определите максимальное или минимальное значение параболы [latex]k[/latex].
- Если парабола имеет минимум, диапазон задается как [латекс]f\влево(х\вправо)\ge k[/латекс] или [латекс]\влево[к,\infty \вправо)[/латекс] . Если парабола имеет максимум, диапазон задается как [латекс]f\влево(х\вправо)\le k[/латекс] или [латекс]\влево(-\infty ,k\вправо][/латекс] 92 [/latex]
Величина [latex]a[/latex] указывает на растяжение графика. Если [latex]|a|>1[/latex], точка, связанная с конкретным [latex]x[/latex]-значением, смещается дальше от оси [latex]x[/latex] – , поэтому график кажется, становится уже, и есть вертикальное растяжение.
 Но если [latex]|a|<1[/latex], точка, связанная с конкретным значением [latex]x[/latex], смещается ближе к оси [latex]x[/latex] – , поэтому график кажется шире, но на самом деле происходит сжатие по вертикали. 9{2}}{4a} \end{align}[/latex]
Но если [latex]|a|<1[/latex], точка, связанная с конкретным значением [latex]x[/latex], смещается ближе к оси [latex]x[/latex] – , поэтому график кажется шире, но на самом деле происходит сжатие по вертикали. 9{2}}{4a} \end{align}[/latex]Однако на практике обычно легче запомнить, что [latex]h[/latex] – это выходное значение функции, когда входное значение [ латекс]h[/латекс], поэтому [латекс]f\left(h\right)=f\left(-\dfrac{b}{2a}\right)=k[/latex].
Попробуйте
Координатная сетка наложена на квадратичную траекторию баскетбольного мяча на рисунке ниже. Найдите уравнение траектории мяча. Стрелок попадает в корзину?
(кредит: модификация работы Дэна Мейера)
Показать раствор
Ключевые понятия
- Полиномиальная функция второй степени называется квадратичной функцией.
- График квадратичной функции представляет собой параболу. Парабола представляет собой U-образную кривую, которая может открываться как вверх, так и вниз.

- Ось симметрии — вертикальная линия, проходящая через вершину.
- Квадратичные функции часто записывают в общем виде. Стандартная или вершинная форма полезна для простого определения вершины параболы. Любая форма может быть записана из графа.
- Вершина может быть найдена из уравнения, представляющего квадратичную функцию.
- Областью определения квадратичной функции являются все действительные числа. Диапазон зависит от функции.
Глоссарий
- ось симметрии
- вертикальная линия, проведенная через вершину параболы, относительно которой парабола симметрична; он определяется как [latex]x=-\dfrac{b}{2a}[/latex].
- общий вид квадратичной функции 92+ 5x + 3` 123456-1-2-35-5-10-15-20-25-30xyОткрыть изображение на новой странице
n-образная парабола
Рисование парабол
Чтобы нарисовать график квадратного уравнения, мы делаем следующие шаги:
(a) Проверьте, является ли `a > 0` или `a < 0`, чтобы решить, является ли он U-образным или n-образным.



 {2}+6x-4}
значение a {\displaystyle a}
отрицательное, поэтому вы нашли максимум. Вершина параболы лежит в точке с координатами (1 , − 1) {\displaystyle (1,-1)}
, а максимальное значение функции равно − 1 {\displaystyle -1}
.
{2}+6x-4}
значение a {\displaystyle a}
отрицательное, поэтому вы нашли максимум. Вершина параболы лежит в точке с координатами (1 , − 1) {\displaystyle (1,-1)}
, а максимальное значение функции равно − 1 {\displaystyle -1}
. Следовательно, областью определения любой квадратичной функции являются все действительные числа. Поскольку параболы имеют максимум или минимум в вершине, диапазон ограничен. Так как вершина параболы будет либо максимальной, либо минимальной, диапазон будет состоять из всех [latex]y[/latex]-значений, больших или равных [latex]y[/latex]-координате вершины или меньше или равно [latex]y[/latex]-координате в точке поворота, в зависимости от того, открывается ли парабола вверх или вниз. 9{2}+bx+c[/latex] с положительным значением [latex]a[/latex] равно [latex]f\left(x\right)\ge f\left(-\frac{b}{2a} \right)[/latex], или [латекс]\left[f\left(-\frac{b}{2a}\right),\infty \right)[/latex]; диапазон квадратичной функции, записанной в общем виде с отрицательным значением [latex]a[/latex] , равен [latex]f\left(x\right)\le f\left(-\frac{b}{2a}\ right)[/latex], или [latex]\left(-\infty ,f\left(-\frac{b}{2a}\right)\right][/latex].
Следовательно, областью определения любой квадратичной функции являются все действительные числа. Поскольку параболы имеют максимум или минимум в вершине, диапазон ограничен. Так как вершина параболы будет либо максимальной, либо минимальной, диапазон будет состоять из всех [latex]y[/latex]-значений, больших или равных [latex]y[/latex]-координате вершины или меньше или равно [latex]y[/latex]-координате в точке поворота, в зависимости от того, открывается ли парабола вверх или вниз. 9{2}+bx+c[/latex] с положительным значением [latex]a[/latex] равно [latex]f\left(x\right)\ge f\left(-\frac{b}{2a} \right)[/latex], или [латекс]\left[f\left(-\frac{b}{2a}\right),\infty \right)[/latex]; диапазон квадратичной функции, записанной в общем виде с отрицательным значением [latex]a[/latex] , равен [latex]f\left(x\right)\le f\left(-\frac{b}{2a}\ right)[/latex], или [latex]\left(-\infty ,f\left(-\frac{b}{2a}\right)\right][/latex].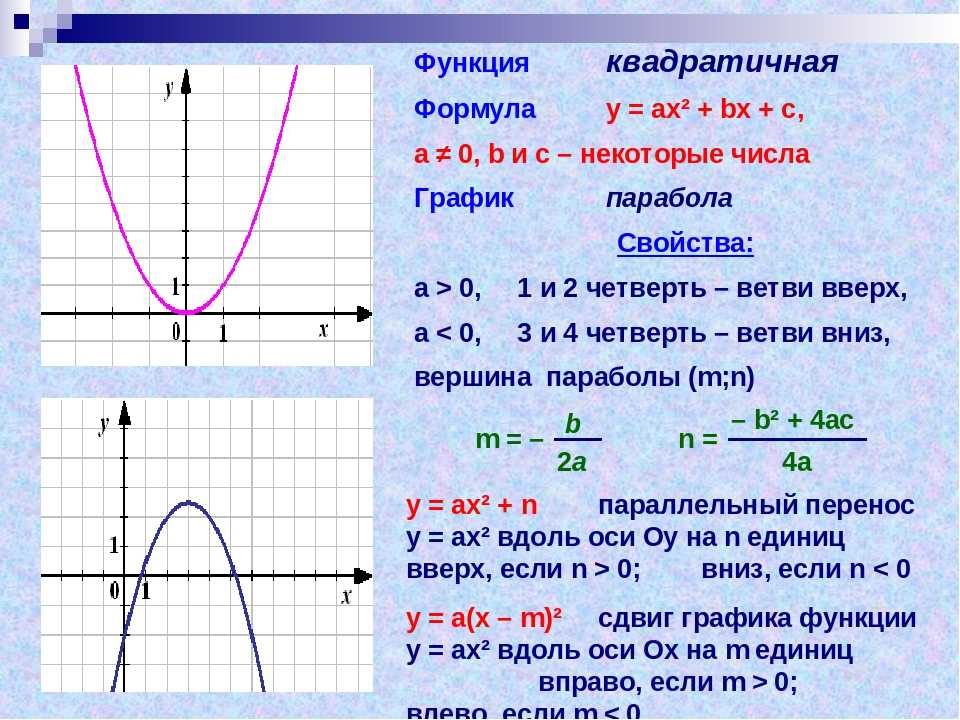
 Но если [latex]|a|<1[/latex], точка, связанная с конкретным значением [latex]x[/latex], смещается ближе к оси [latex]x[/latex] – , поэтому график кажется шире, но на самом деле происходит сжатие по вертикали. 9{2}}{4a} \end{align}[/latex]
Но если [latex]|a|<1[/latex], точка, связанная с конкретным значением [latex]x[/latex], смещается ближе к оси [latex]x[/latex] – , поэтому график кажется шире, но на самом деле происходит сжатие по вертикали. 9{2}}{4a} \end{align}[/latex]