векторы площадь параллелограмма
Вы искали векторы площадь параллелограмма? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и выразить площадь проекции параллелограмма на векторах, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «векторы площадь параллелограмма».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как векторы площадь параллелограмма,выразить площадь проекции параллелограмма на векторах,вычислите площадь параллелограмма построенного на векторах,вычислить диагонали и площадь параллелограмма построенного на векторах,вычислить площадь параллелограмма построенного на векторах,вычислить площадь параллелограмма построенного на векторах a и b,вычислить площадь параллелограмма построенного на векторах a и b онлайн,вычислить площадь параллелограмма построенного на векторах а и b,вычислить площадь параллелограмма построенного на векторах а и в,вычислить площадь параллелограмма построенного на векторах и,как вычислить площадь параллелограмма построенного на векторах,как найти площадь параллелограмма построенного на векторах,как найти площадь параллелограмма построенного на векторах а и в,найдите площадь параллелограмма построенного на векторах,найти высоту параллелограмма построенного на векторах,найти площадь параллелограмма диагоналями которого служат векторы,найти площадь параллелограмма построенного на векторах,найти площадь параллелограмма построенного на векторах онлайн,обчислити площу паралелограма побудованого на векторах,онлайн калькулятор площадь параллелограмма построенного на векторах,онлайн найти площадь параллелограмма построенного на векторах,параллелограмм построен на векторах a и b,площадь параллелограмма векторы,площадь параллелограмма на векторах,площадь параллелограмма по векторам,площадь параллелограмма построенного на векторах,площадь параллелограмма построенного на векторах найти онлайн,площадь параллелограмма построенного на векторах онлайн калькулятор,площадь параллелограмма через вектора,площадь параллелограмма через векторы,пользуясь параллелограммом построенным на векторах a и b,построить параллелограмм на векторах.
Решить задачу векторы площадь параллелограмма вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Площадь параллелограмма, построенного на векторах, заданных своими координатами на плоскости — Студопедия
Поделись с друзьями:
Предположим, что заданы координаты векторов :
.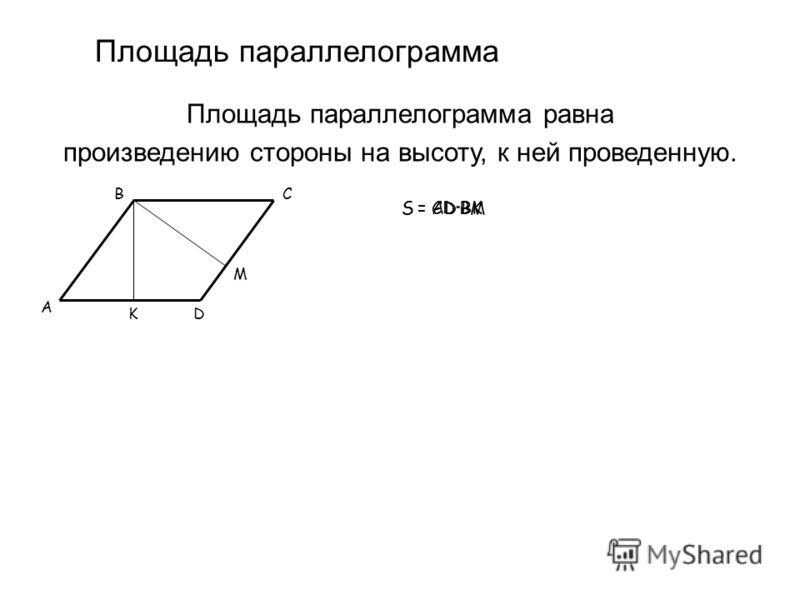 Тогда
Тогда
Можно доказать, что , если пара векторов — правая, и , если пара векторов — левая.
Аналог смешанного произведения для векторов плоскости
Для векторов на плоскости операция, аналогичная смешанному произведению, будет операцией над двумя векторами.
Если два вектора на плоскости имеют координаты: , то естественно определить аналог смешанного произведения как число равное определителю:
Ввиду доказанной формулы для , получим геометрический смысл этой операции: , если пара векторов — правая и , если эта пара левая.
Аналогия простирается и дальше на пространство любой размерности.
Задача
Докажите, что аналог векторного произведения для векторов плоскости – это операция, совершаемая над одним вектором (результат обозначим ). Она сводится к повороту этого вектора на против часовой стрелки.
Указание
Определите координаты вектора из условия:
для любого вектора
То есть мы как бы «делим» скалярно «смешанное произведение» на вектор .
ЗАДАНИЯ УПРАЖНЕНИЙ
1. Даны координаты точек на плоскости . Найти
а) координаты вектора ,
б) координаты точки — середины отрезка ,
в) координаты точки , если ,
г) координаты точки , если ,
д) координаты точки , если .
2. Даны координаты векторов
Найти а) координаты ,
б) координаты ,
в) координаты .
3. Даны длины векторов и угол между ними
Найти а) скалярное произведение ,
б) скалярное произведение ,
в) длину вектора ,
г) проекцию вектора на направление другого вектора ,
д) угол между векторами и .
4. Даны координаты векторов
Выполнить задания пунктов а) — д) предыдущей задачи.
5. При каком значении параметра векторы и будут перпендикулярны?
6. При каких значениях и векторы и будут параллельны?
7. Даны длины векторов и угол между ними
Найти а) длину векторного произведения ,
б) длину векторного произведения .
8. Даны координаты векторов
Найти координаты векторного произведения .
9. Даны координаты вершин треугольника на плоскости
. Найти площадь треугольника .
10. Даны координаты вершин треугольника в пространстве
. Найти площадь треугольника .
11. Даны координаты векторов в пространстве
Найти смешанное произведение .
12. Даны координаты вершин пирамиды в пространстве
. Найти а) объём пирамиды ,
б) длину высоты .
13. При каком значении параметра векторы , , будут компланарны?
14. При каком значении параметра точки будут лежать в одной плоскости?
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
2)=кв.(0+1+9)=кв.10#.Итак, #KL=MN#
Направление #KL# — это вектор #vecv#, такой как:
#vecv=(x_K-x_L,y_K-y_L,z_K-z_L)=(0,1,3 )#.
Направление #MN# — это вектор #vecw#, такой как:
#vecw=(x_M-x_N,y_M-y_N,z_M-z_N)=(0,1,3)#.
Итак, #vecv# параллелен #vecw#.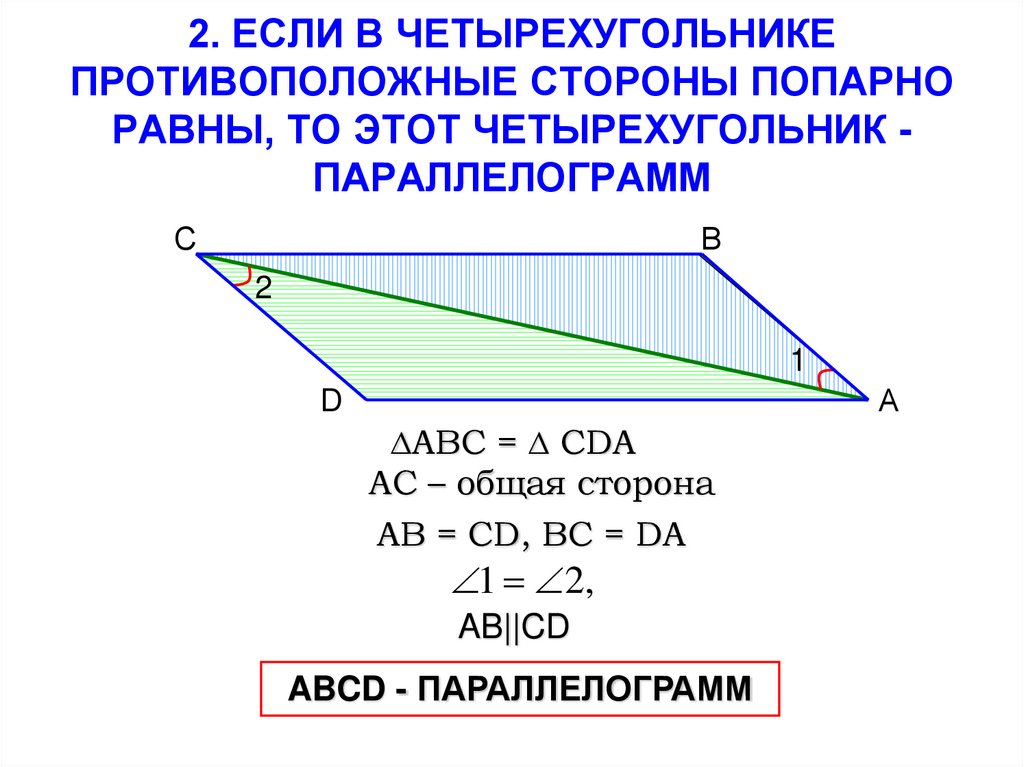
Итак, поскольку #KL=MN# и #KL# параллелен #MN#, фигура является параллелограммом.
Площадь параллелограмма: #A=b*h#.
Можно считать, что основание #b# равно #KL=sqrt10#, но найти высоту сложнее, т.к. это расстояние между двумя линиями #r#, содержащими #K и L#, и #s# , который содержит #M и N#.
Плоскость, перпендикулярная прямой, может быть записана:
#a(x-x_P)+b(y-y_P)+c(z-z_P)=0#,
где #vecd(a,b ,c)# — любой вектор, перпендикулярный плану, а #P# — любая точка, лежащая на плане.
Чтобы найти #pi#, то есть план, перпендикулярный #r#, можно предположить, что #vecd=vecv# и #P=K#.
Итак:
#pi: 0(x-1)+1(y-2)+3(z-3)=0rArry+3z-11=0#.
Строка может быть записана как система трех уравнений в параметрической форме:
#x=x_P+at#
#y=y_P+bt#
#z=z_P+ct#
Где #P# — любая точка линии, а #vecd(a,b,c)# — любой вектор, направление линии.
Чтобы найти #s#, мы можем предположить, что #P=M# и #vecd=vecw#.
Итак #s#:
#x=3+0t#
#y=8+1t#
#z=6+3t#
или:
#x=3#
#y=8+t #
#z=6+3t#.
Теперь, решая систему между #pi# и #s#, мы можем найти #Q#, цоколь высоты, проведенной из #K# в #s#. 92)=кв.(4+81/4+9/4)=кв.((16+81+9)/4)=кв.кв.106/2#.
Наконец, область:
#A=sqrt10sqrt106/2=sqrt1060/2=sqrt(4*265)/2=sqrt265#.
Второй.
Мы можем помнить, что векторное произведение двух векторов — это вектор, длина которого равна площади параллелограмма, у которого два вектора являются двумя сторонами.
Вектор: #vec(KL)=(0,1,3)#,
вектор #vec(KM)=(2,6,3)#.
А теперь нам нужно сделать: #vec(KL)xxvec(KM)#
Мы можем построить матрицу:
первая строка: #[i,j,k]#,
вторая строка #[0,1,3]#,
третья строка#[2,6,3]#.
Определитель — это вектор: #-15veci+6vecj-2veck#, а его длина: #sqrt(225+36+4)=sqrt265#, то есть запрашиваемая область.
Найти площадь параллелограмма, заданного векторами
х
- 1
Задайте математический вопрос
Выполнение домашних заданий может помочь улучшить оценки.

- 2
Объясните математический вопрос
Домашнее задание является необходимой частью школы, которая помогает учащимся повторять и практиковать то, что они узнали в классе.
- 3
Решить математические задачи
Если вы хотите получить лучшие ответы на домашнее задание, вам нужно задавать правильные вопросы.
- 4
Лучшие эксперты
Решение математических задач может быть интересным и сложным!
Площадь параллелограмма
В этом видеоруководстве по исчислению 3 объясняется, как найти площадь параллелограмма, используя два вектора и метод векторного произведения, учитывая
`
Определитель и площадь параллелограмма
Проблема решена! Вы получите подробное решение от эксперта в предметной области, который поможет вам изучить основные понятия.
Площадь параллелограмма, определяемая двумя векторами Пример
Таким образом, площадь вашего параллелограмма в квадрате равна определителю матрицы, векторы-столбцы которой составляют этот параллелограмм. равно
Получить исследование
Get Study — отличный способ улучшить свои оценки.
Получите самое полезное решение для домашних заданий
Математика — это изучение чисел, форм и закономерностей.
Решайте словесные вопросы тоже
Математика — это способ определения взаимосвязей между числами, фигурами и другими математическими объектами.