Функции «один к одному» и «вкл» | nool
Перейти к основному содержанию
Домашняя страница Технологического института Онтарио
nool
Концепция взаимно однозначных функций необходима для понимания концепции обратных функций.
Функции «один к одному»
Если функция не имеет двух упорядоченных пар с разными первыми координатами и одной и той же второй координатой, то функция называется однозначной. Звучит запутанно, поэтому давайте рассмотрим следующее:
В однозначной функции для любого y существует только один x, который может быть сопряжен с данным y.
График функции можно также использовать для определения того, является ли функция взаимно однозначной, используя тест горизонтальной линии:
Если каждая горизонтальная линия пересекает график функции не более чем в одной точке, то функция является однозначной.
Рассмотрим графики следующих двух функций:
На каждом графике функция выделена синим цветом, а горизонтальная линия — красным. Для первого графика (слева) функция не является взаимно однозначной, поскольку можно провести горизонтальную линию, дважды пересекающую график. Однако второй график (справа) является взаимно однозначной функцией, поскольку невозможно провести горизонтальную линию, пересекающую график более одного раза.
Пример: Определите, является ли следующая функция однозначной:
f = {(1,2), (3, 4), (5, 6), (8, 6), (10, -1)}
Решение: Эта функция не является однозначной, поскольку упорядоченные пары (5, 6) и (8, 6) имеют разные первые координаты и одну и ту же вторую координату.
Онто-функции
Онто-функция такова, что для каждого элемента в домене кодов существует элемент в домене, который отображается на него. Опять же, это звучит запутанно, поэтому давайте рассмотрим следующее:
Функция f из A в B вызывается, если для всех b в B существует a в A такое, что f( a ) = b .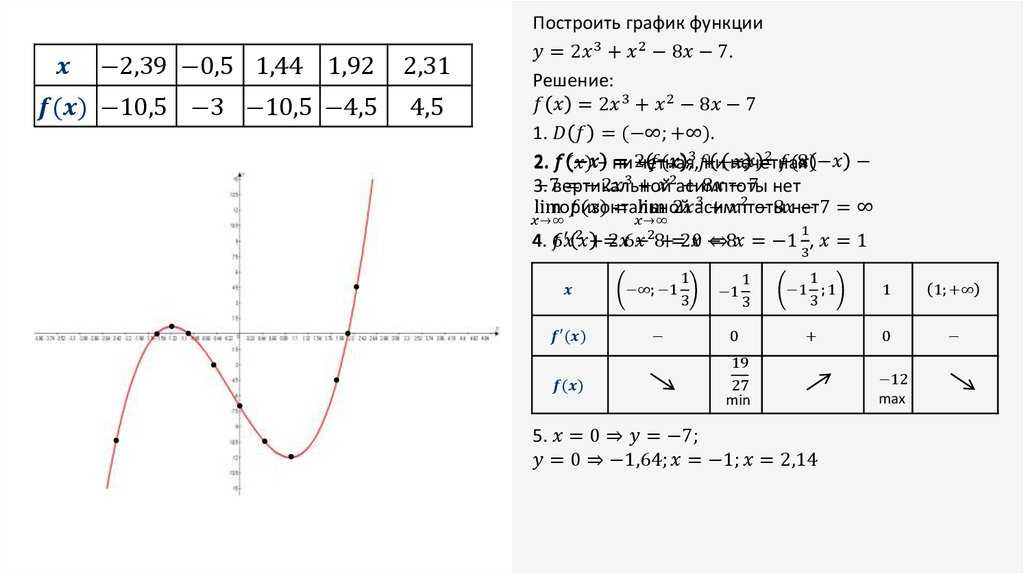
Определение родительских функций (вербально/графически) | Техасский шлюз
Давайте изучим различные родительские функции и узнаем, как определить, представляет ли график или уравнение линейную или квадратичную функцию.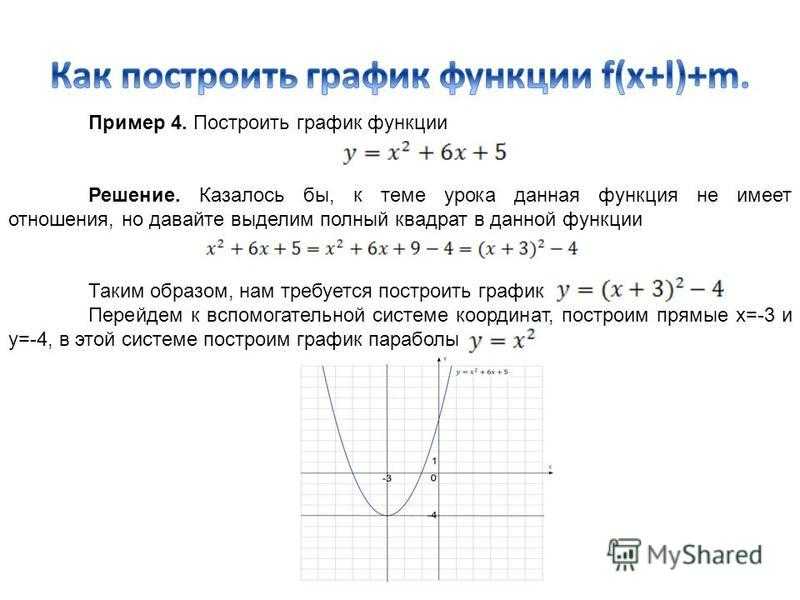
Стандарты TEKS и ожидания учащихся
A(3) Линейные функции, уравнения и неравенства. Учащийся применяет стандарты математического процесса при использовании графиков линейных функций, ключевых функций и связанных преобразований для представления различными способами и решения уравнений, неравенств и систем уравнений с использованием технологий и без них. Ожидается, что учащийся:
A(3)(C) начертит линейные функции на координатной плоскости и определит ключевые функции, включая
x — точка пересечения, y — точка пересечения, нули и наклон в математических и реальных задачах
A(7) Квадратичные функции и уравнения. Учащийся применяет стандарты математического процесса при использовании графиков квадратичных функций и связанных с ними преобразований для представления различными способами и определения с помощью технологий и без них решений уравнений.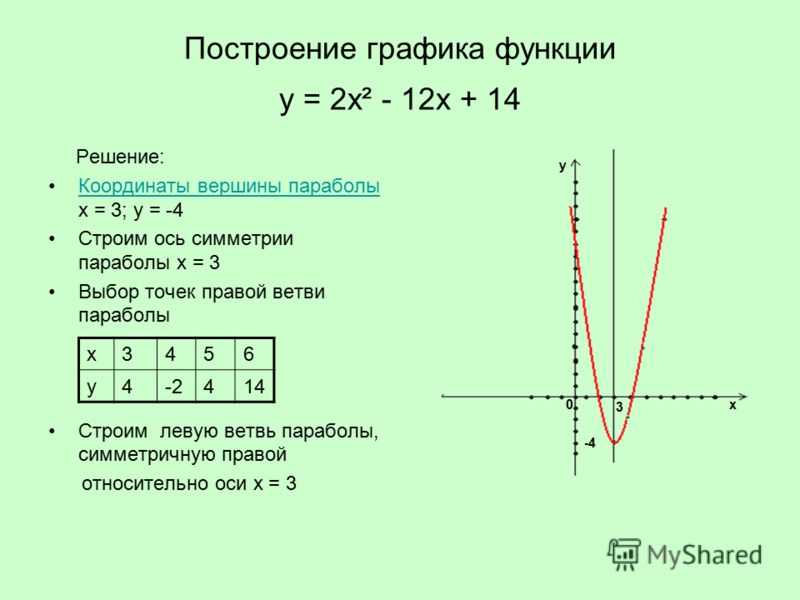
A(7)(A) нарисует квадратичные функции на координатной плоскости и использует график для определения ключевых атрибутов, если это возможно, включая x — точка пересечения, y — точка пересечения, нули, максимальное значение, минимальные значения, вершина и уравнение оси симметрии линейная или квадратичная родительская функция.
Основные вопросы
Как линейная функция выглядит в виде графика и уравнения?
Как выглядит квадратичная функция в виде графика и уравнения?
Словарь
- Родительская функция
- Линейная функция
- Квадратичная функция
Наша цель — научиться распознавать линейную и квадратичную родительские функции по графическому или словесному описанию.
Что такое родительская функция?
Родительская функция — это самая основная форма функции.
Он обладает теми же основными свойствами, что и другие, подобные ему, но он не был перемещен или растянут в каком-либо направлении или перекошен каким-либо образом.
Какое нам дело?
Родительские функции позволяют нам быстро сказать определенные черты их «детей». Например, у моих родителей карие глаза, а у меня карие глаза. Большинство людей могли бы угадать цвет моих глаз, познакомившись с моими родителями.
Важно помнить, что вы должны знать, связаны ли свойства функции с линейной ( y = x ) или квадратичной ( y = x 2 ) родительской функцией.
Для получения информации о линейной родительской функции можно использовать графический онлайн-калькулятор или приведенный ниже апплет графической утилиты.
Направления:
1. В апплете ниже (или на веб-сайте) введите значение x для уравнения « y ( x ) = ____» и нажмите «График». Это линейная родительская функция.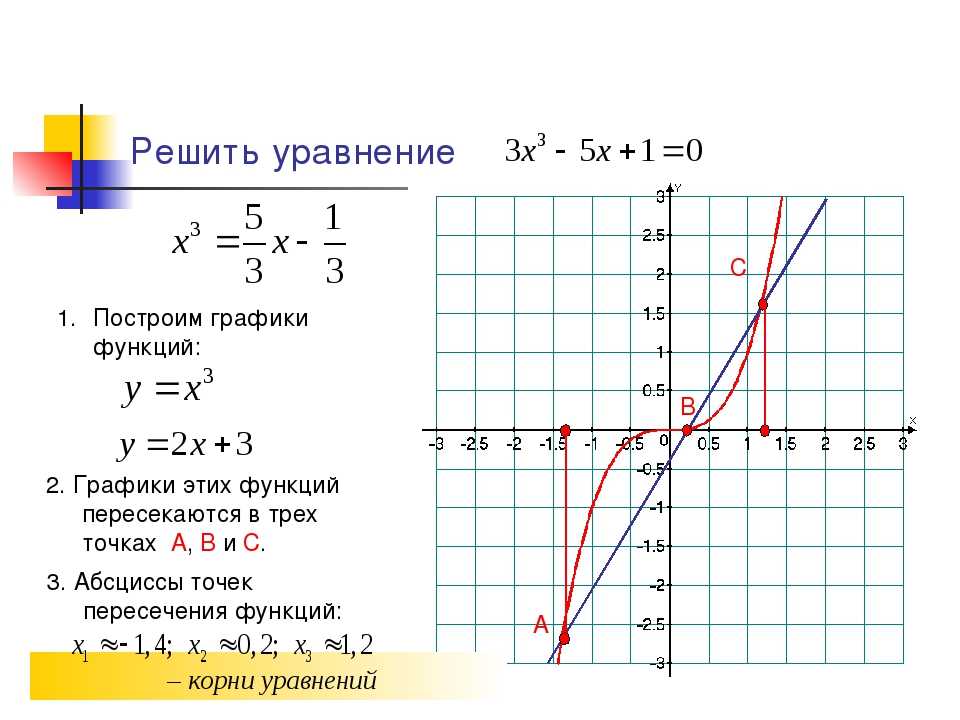
2. Исследуйте графики линейных функций, добавляя или вычитая значения x (например, y ( x ) = x + 2) или умножая x на константу (например, у ( х ) = 3 х ). Помните, что линейная функция родительского элемента равна y ( x ) = x . Это самая основная и простая форма функции.
На этой странице вы будете использовать графический онлайн-калькулятор или графический апплет для получения информации о квадратичной родительской функции.
Направления:
1. Введите x 2 под кнопкой редактора уравнений «Y=» на графическом калькуляторе или » y ( x ) = ____» в ссылке графического апплета. Нажмите «График». Это квадратичная родительская функция. На изображении ниже показано, как будет выглядеть действие.
2. Исследуйте квадратичную родительскую функцию и то, как другие квадратичные функции могут быть сформированы путем преобразования родительской функции.