По математике корень: Квадратный корень — все что нужно для сдачи ОГЭ и ЕГЭ

Как репетитор по математике снимает проблему понимания записи корней — Колпаков Александр Николаевич

По всем существующим программам тема «квадратный корень» рассматривается в 8 классе и является началом изучения одного из важнейших разделов математики — квадратного трехчлена. От того насколько аккуратно репетитор по математике объяснит восьмикласснику новое и часто очень сложное для него понятие, зависит не только скорость усвоения новых видов уравнений и следующих за ними текстовых задач, но и уровень понимания геометрии, в которой к этому моменту (по учебнику Атанасяна) «запускаются» площади. Какие проблемы обычно встречает репетитор по математике в процессе работы с данной и какие решения можно найти в той или иной ситуации? Рассмотрим эти вопросы подробнее.
Стоит отметить, что в 8 классе ученик впервые сталкивается с «невидимой» математикой, которую тяжело объяснять на рисунках. Действительно, как репетитору по математике показать координатной оси число ? Если раньше в 5 – 7 классах для объяснения записи достаточно было сказать ученику: «Представь себе, что единичный отрезок разделен на 3 равные части и отложено 2 таких кусочка», то с квадратными корнями так просто из положения выйти не получится. А выход искать надо, ибо главная проблема заключается в том, что ребенок не может сопоставить записи с реальными объектами. Система объяснений репетитора по математике для таких ситуаций должна, как мне кажется, основываться на практических соответствиях, а не на сложной и непонятной в 8 классе арифметике (аксиоматики) действий с действительными числами. Коротко опишу свой метод, которым часто пользуюсь.

Как репетитор по математике объясняет смысл записи ?

Сначала нужно убедить школьника в необходимости изучения корней. Это можно сделать при помощи стандартной демонстрации рисунка квадрата со стороной 1см, на диагонали которого строится новый квадрат с площадью в 2 кв.см. Некоторые репетиторы по математике ограничиваются только этим фактом и сформированным представлением ученика о методах вычисления площадей прямоугольников. В объяснениях репетитора формула используется как абсолютная и неоспоримая. Тогда получается, что длина нового квадрата должна при возведении в квадрат давать число 2. Однако, действие умножение вводилось в математике начальных классов совершенно иначе, а именно как заменитель повторений слагаемых, и связывалось с площадями только в случае натуральных значений сторон (или рациональных, как программе 6 класса). Если репетитор по математике объясняет ученику, что длина стороны выражается совершенно новым видом числа и использует для этого операцию, введенную с натуральными измерениями, то допускает некую ошибку. Конечно, она не заметна будет 99,999% школьников, но от этого репетитору не легче. Ребенок пропустит не только сам обман, но и всю логику, которую ему пытаются объяснить.

Лучше всего сказать, что новые числа (и действия с ними) были введены математиками для того, чтобы создать единые правила вычисления различных величин, одной из которых является площадь. Ох, как было бы удобно, если бы площадь всегда вычислялась одинаково (для всех размеров сторон), то есть при помощи одного и того же арифметического действия, по одним и тем же правилам и свойствам (известных для рациональных чисел). Кроме этого необходимо соответствовать зрительному представлению о величине площадей в простых ситуациях. То есть если по рисунку видно, что площадь равна 2, значит и в действии «умножение» должно получиться 2. По сути вводится совершенно новое арифметическое действие (с использованием известного знака » «), которое для рациональных чисел имеет то же самый смысл, как и «старое умножение», а для нового вида чисел отождествляется с площадью прямоугольника, имеющего указанные множителями размеры! В этом случае репетитору по математике запросто удастся объяснить законы сложения и умножения, которые распространяются в том числе и на иррациональные числа.

Можно показать работу распределительного закона умножения через свойство аддитивности площади прямоугольника. Рисунок, при помощи которого репетитор по математике убеждает ученика в верности свойства показан справа.

Обязательно нужно сказать, что „новые“ числа должны жить со „старыми“ по одним и тем же правилам (свойствам), так как отрезки можно последовательно откладывать на одной прямой и заново измерять.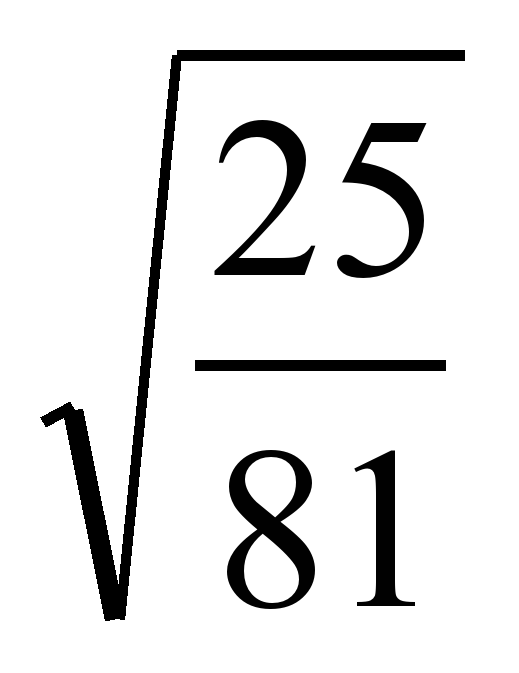 Получаются новые отрезки, соответствующие арифметическим суммам. Передача репетитором по математике смысла записи легко реализуется при помощи несложных и разумных рассуждений — вопросов: «Мы водим в математику новые числа. Они будут использоваться вместе со старыми, например, для измерения отрезков. Можно ли последовательно соединить какие-нибудь два из них, например, соответствующие числам см и 3 см? Конечно. Тогда возникает проблема измерения (записи) полученного расстояния. Логично было бы назвать его суммой и использовать знакомый уже знак «+». Ровно так математики и делают. Они пишут , а в голове держат отрезок, который получается при соединении частей см и 3 см. Мы тоже будем использовать такую форму». Репетитор по математике развивает мысль дальше: «Каждый ли отрезок можно разделить пополам? Конечно. А как записать полученную длину? Оказывается, что для нее нет никакой другой записи из известных нам. Тогда договоримся использовать ту же форму с числителем и знаменателем, как и раньше». Репетитор по математике проводит черту дроби между рассматриваемой суммой и число 2 и тем самым снимает проблему восприятия новых форм записи чисел. Ученик начинает понимать, что нагромождения радикалов и дробей имеют непосредственное воплощение в реальные величины и явления. Приходит осознание того, что означает в математике дробная запись с корнями и слагаемыми (любые части отрезков должны обозначаться точными символами).

Репетитор продолжает: «Для новых чисел оказываются верными те же самые свойства и правила, которыми мы используемся для рациональных чисел: правила раскрытия скобок, правила приведения дробей к общему знаменателю и т.д. Почему? Это происходит из-за сохранения переместительных, сочетательных и распределительных законов сложения и умножения». (репетитор по математике возвращается к свойству аддитивности площади — см. рисунок с прямоугольником).

О методике работы с темой «квадратные корни» можно говорить и говорить. Проблема с восприятием «синтаксиса» радикалов — лишь одна из проблем, открывающаяся перед репетитором по математике. Нужно заниматься выработкой навыков счета и преобразований, адаптацией строгих математических правил к особенностям детского восприятия и запоминания, визуальным сопровождением к объяснениям, подготовкой индивидуальных материалов многим другим. Будет время — напишу о своих правилах, наблюдениях и подходах к работе с темой.

Александр Николаевич, репетитор по математике — Москва / Строгино. .

Корень (в математике) — «Энциклопедия»

КОРЕНЬ в математике,

1) степени n из числа а, число х такое, что хⁿ = а. Действие нахождения корня называется извлечением корня. В области действительных чисел существует ровно один корень нечётной степени из любого действительного числа, причём корень из положительного числа положителен, а из отрицательного отрицателен. Корень чётной степени из положительного числа имеет два значения, равные по абсолютной величине и противоположные по знаку. Корень чётной степени из отрицательного числа в области действительных чисел не существует, потому что чётная степень любого действительного числа положительна. Положительный корень степени n из положительного числа а называется арифметическим корнем и обозначается ⁿ√а (√а при n = 2). Второй, отрицательный корень, существующий при чётном n, обозначается ⁿ√а. Если же рассматриваются оба значения корня, то перед знаком радикала ставится двойной знак, например √4= +2. В этом случае говорят об алгебраических значениях корня. Существует ровно один арифметический корень данной степени из данного положительного числа. Для числа 0 существует ровно один корень любой степени и он равен 0.

Реклама

В области комплексных чисел при а≠0 существует n различных корней степени n. Например, значениями ³√8 являются числа 2, -1 + i√3, -1 — i√3, где i — мнимая единица. Корень степени n из единицы, т. е. решение уравнения хⁿ = 1, можно записать в виде

Формулу для корней n-й степени из любого комплексного числа z = r (cos φ + i sin φ), r > 0, 0 ≤ φ < 2π, смотри в статье Комплексное число. Все эти корни находятся на комплексной плоскости в вершинах правильного n-угольника с центром в точке нуль, одна из вершин которого находится в точке ⁿ√r(cos(φ/n) + i sin(φ/n)).

К нахождению корней математиков древности приводили различные геометрические задачи. Среди вавилонских клинописных текстов (2-е тысячелетие до нашей эры) имеются описания приближённого нахождения корня и таблицы квадратных корней, а в египетских папирусах встречается и особый знак для извлечения корня. Древнегреческие математики установили несоизмеримость стороны квадрата с его диагональю (равной а√2, если а — его сторона), что позднее привело к открытию иррациональных чисел. Индийский учёный Ариабхата (5 век нашей эры) описал правила для извлечения квадратных и кубических корней. Омар Хайям, арабский учёный аль-Каши (15 век), немецкий математик М. Штифель (16 век) извлекали корни высших степеней, исходя из формулы для (а + b)

2) Корни алгебраического уравнения

a₀xⁿ + а₁

— число с, которое при подстановке его вместо х обращает левую часть уравнения в нуль. Корень этого уравнения называется также корнем многочлена

f_n(x) = а₀хⁿ + а₁x^n-1 + … +а_n.

Если число с является корнем многочлена f_n(х), то f_n(х) делится без остатка на х-с. Смотри также Алгебраическое уравнение.

Real and Complex – LearnDataSci

Автор: Alfie Grace
Data Scientist

Быстрый способ получить квадратный корень из значения — использовать оператор возведения в степень **

3 в качестве второго параметра с 0 параметром. См. ниже краткий пример:

 4**0,5 

Выход:

  2,0 

Использование ** — не единственный и не самый точный способ вычисления квадратного корня в Python. Мы рассмотрим, как можно вычислить квадратный корень значения с помощью возведения в степень, а также math и numpy sqrt() функций, а также рассмотрим преимущества каждого варианта.

Использование оператора возведения в степень ** — это простой способ получить квадратный корень из числа. Этот оператор возводит первый операнд в степень второго операнда.

Чтобы получить квадратный корень, вам нужно использовать 0,5 в качестве второго операнда, как показано во введении.

В следующем фрагменте показан еще один пример использования **0,5 для вычисления квадратного корня для диапазона значений:

 значений = [16, 25, 36, 49, 64]
для x в значениях:
    х_кварт = х**0,5
    print(f'value: {x} квадратный корень {x_sqrt}') 

 value: 16 квадратный корень 4. 0
значение: 25 квадратный корень 5.0
значение: 36 квадратный корень 6.0
значение: 49 квадратный корень 7.0
значение: 64 квадратный корень 8,0 

 -4**0,5 

 -2,0 

  (-4)**0,5 

 (1,2246467991473532e-16+2j) 

Обратите внимание, что вторым операндом ** может быть любое действительное число. Таким образом, вы используете только 0,5 при поиске квадратного корня. Ниже приведены некоторые другие примеры значений, которые можно вычислить с помощью 9.0012 ** :

 х = 4
печать (f' x квадрат: {x ** 2}')
print(f' x в кубе: {x**3}')
print(f' x в степени -1 (x/x в квадрате): {x**-1}')
print(f' x в степени -2 (x/x в кубе): {x**-2}') 

Выход:

 x в квадрате: 16
 х в кубе: 64
 x в степени -1 (x/x в квадрате): 0,25
 x в степени -2 (x/x в кубе): 0,0625 

Альтернативным способом вычисления квадратного корня значения является использование функции math.sqrt() из библиотеки math . В приведенном ниже примере показано, как мы можем применить math.sqrt() функция к примеру, используемому в разделе **0. 5 :

 import math
значения = [16, 25, 36, 49, 64]
для x в значениях:
    x_sqrt = math.sqrt(x)
    print(f'value: {x} квадратный корень {x_sqrt}') 

Out:

 value: 16 квадратный корень 4.0
значение: 25 квадратный корень 5.0
значение: 36 квадратный корень 6.0
значение: 49 квадратный корень 7.0
значение: 64 квадратный корень 8.0 

Как показывают результаты, использование math.sqrt() дает те же результаты, что и **0.5 . Преимущество использования **0.5 в начале этой статьи заключается в том, что ** не требует импорта, как это делает math.sqrt() .

С другой стороны, многие утверждают, что math.sqrt() обычно выполняется быстрее; см. эту страницу переполнения стека для разбивки скоростей.

Использование отрицательного значения с math. sqrt() вызовет ошибку ValueError: math domain error , как показано ниже:

 math.sqrt(-4) 

Out:

 ----- -------------------------------------------------- --------------------
ValueError Traceback (последний последний вызов)
 в <модуль>
----> 1 math.sqrt(-4)
ValueError: ошибка математической области 

В зависимости от того, как вы хотите обрабатывать квадратные корни из отрицательных значений, обработка ValueError может быть предпочтительнее. В качестве альтернативы мы можем избежать этого, используя cmath.sqrt() , как мы увидим в следующем разделе.

Вы также можете вычислить квадратный корень из отрицательных и комплексных чисел, используя библиотеку cmath . См. пример ниже:

 import cmath
с = (12 + 16j)
cmath.  sqrt(с) 

Out:

 (4+2j) 

Отличный способ избежать получения ValueError: ошибка математической области использует cmath.sqrt() для обработки исключений.

Например, мы можем сделать это с помощью следующего скрипта:

 import math
импортировать cmath
значения = [16, -25, 36, -49, 64]
для x в значениях:
    пытаться:
        x_sqrt = math.sqrt(x)
    кроме ValueError:
        x_sqrt = cmath.sqrt(x)
        
    print(f'value: {x} квадратный корень {x_sqrt}') 

Выход:

 значение: 16 квадратный корень 4.0
значение: -25 квадратный корень 5j
значение: 36 квадратный корень 6.0
значение: -49 квадратный корень 7j
значение: 64 квадратный корень 8.0 

Если вы работаете с массивами NumPy, у вас также есть возможность использовать

numpy. sqrt()

Использование этой функции с массивом создаст новый массив, содержащий все квадратные корни исходного массива. В приведенном ниже примере показано, как мы можем создать массив, используя список из предыдущих примеров, а затем применить np.sqrt() :

 импортировать numpy как np
values_array = np.array ([16, 25, 36, 49, 64])
sqrt_array = np.sqrt (массив_значений)
print(f'values: {values_array} квадратный корень значений: {sqrt_array}') 

Out:

 значений: [16 25 36 49 64] квадратный корень значений: [4. 5. 6. 7. 8.] 

Стоит отметить, что вы также можете использовать

Вычислить квадратный корень значения в Python просто, используя оператор возведения в степень ** или math. sqrt() . Стоит отметить, что math.sqrt() обычно быстрее из двух и что с помощью cmath.sqrt() можно получить квадратный корень из комплексного числа. При работе с массивами у вас также есть возможность использовать функцию numpy.sqrt() для вычисления квадратного корня каждого значения.

Начните учиться бесплатно

Познакомьтесь с авторами

Альфи Грейс Data Scientist

Алфи получила степень магистра машиностроения в Университетском колледже Лондона. В настоящее время он работает специалистом по данным в Square Enix. Найдите его в LinkedIn.

Редактор: Брендан Мартин
Основатель LearnDataSci

Вернуться к оглавлению блога

терминология — Почему название «квадратный корень»?

Этот вопрос недавно появился на сайте English Language and Usage StackExchange (здесь). Я воспроизведу здесь ответ, который я дал там.

Короче говоря, корень является переводом латинского слова radix , которое само по себе является неправильным переводом арабского слова jadhr. Это слово имеет несколько значений в арабском языке, одно из которых действительно является корнем . Но арабоязычные математики ¹ , которые ввели его, использовали его в другом значении: «основа», «фундамент», «низшая часть».

^{1 Я говорю «говорящих по-арабски», потому что некоторые из них не были арабами и писали на арабском языке, на лингва-франка своего времени и места. Например, Мухаммад ибн Муса аль-Хорезми, которого традиционно считают основателем алгебры, был персом. В частности, слово алгебра происходит от арабского слова al-jabr , «уравновешивание», которое фигурирует в названии его самой известной работы.}

Обсуждение

Согласно Encyclopaedia Britannica,

В IX веке арабские писатели обычно называли один из равных множителей числа jadhr («корень»), а их средневековые европейские переводчики использовали латинское слово radix (от которого происходит прилагательное радикал).

Но почему авторы математических трактатов на арабском языке использовали слово jadhr ?

Причина связана с различием между «конкретными» и «абстрактными» числами (см., например, здесь), которое, по-видимому, было очень важно для математиков того времени:

конкретное число: число, относящееся к определенному предмету или предметам, например, три собаки, десять человек0008

Словарь Коллинза, здесь и здесь

(в настоящее время эти проблемы обычно переживают в науках и инженерии, под названием анализ измерения.)

Кажется, что была традиция мышления, возвращаясь к древним Египет, что, чтобы вычислить, например. площадь прямоугольника, нельзя просто перемножить два абстрактных числа, обозначающих длины сторон прямоугольника. Скорее, одно из этих чисел должно быть сначала умножено на «основу» площади (я не уверен, есть ли какое-либо концептуальное различие между такого рода «основой» и современным понятием единицы измерения). Именно этот «базис» арабоязычные математики называли джадр , арабское слово, означающее «основа», «основа», «низшая часть». Однако jadhr также означает «корень», и многие переводчики арабских слов на другие языки (включая латынь и китайский) ошибочно полагали, что jadhr используется в текстах в этом значении. Вот соответствующая выдержка из источника, который я процитирую ниже:

.

Таким образом, египтянин вычислил квадрат, сначала умножив одну сторону (9 90 216 ккет 90 217 ) на квадратную единицу. Это был квадрат — основание ( jadhr ) умножить на другую сторону, представляя чистое число. Тот же самый процесс описан также аль-Ховаризми, который говорит: «И в каждой квадратной фигуре одна из ее сторон, умноженная на квадратную единицу, равна ее джазр … и мы делаем другую сторону, а именно hj , три, и это число его джадр ».

                                               С. Гандз, О происхождении термина «корень». Вторая статья ,
                                                     Американский математический ежемесячник, том. 35, с. 74, 1928.

Расширенное обсуждение

Следующее взято из статьи О происхождении термина «корень» С. Гандз (The American Mathematical Monthly vol. 33, 261–265, 1926; доступно в открытом доступе здесь ):

Термин «корень» имеет арабское происхождение. «Латинские произведения, переведенные с арабский язык имеет оснований для общего термина, а унаследованные от Римская цивилизация имеет 90 216 latus 90 217». ² Radix («корень») — это арабское jadhr, , а latus (греческое, πλευρά, pleura, означает «ребро» или «сторона») — сторона геометрического квадрата. .

^{2 См. Smith, History of Mathematics, vol. II, с. 150.}

Конечно, довольно странно, что в этом связь. Это предполагает, что если основное число является корнем, квадрат может быть куст и так далее в своего рода математическом саду.

Китайцы действительно используют слово kun для обозначения корня, травы и куста, а также Индусы также используют слово мула для обозначения корня растения, но это было очень вероятно, из-за арабского влияния, которое так часто наблюдается в Китае и которое мог распространиться в Индию через Китай. Однако факт, что таким образом до сих пор у нас нет удовлетворительного объяснения того, почему этот ботанический термин должен нашли свое место в теории чисел. …

Поэтому стоящая перед нами проблема, как уже ясно изложено профессором Смитом, состоит в том, чтобы выяснить, были ли правы средневековые латинские авторы в своем переводе арабского слова 9.0216 jadhr по основанию («корень»). …

Поэтому писатель начал исследовать истинное значение слова слово jadhr , не зависящее от лексиконов или латинских версий тринадцатого века, но ищущее значение, как оно появляется в рукописях самих старых арабских математиков.

Мухаммад ибн Муса аль-Хорезми (ок. 825 г.) — старейший арабский математик, пользующийся большой известностью.0217, который дал Европе и название, и основные принципы алгебры. Его глава Баб аль Мисаха («о геометрии») начинается так: «Знай, что значение выражения «один в одном» есть «площадь»; и его значение — один локоть (длиной) в одном локте ( в ширину). И всякая крыша с равными сторонами и углами, которая имеет один локоть с каждой стороны, является (квадратной) единицей. Но если она имеет два локтя с каждой стороны и имеет равные стороны и углы, то вся крыша в четыре раза больше крыша, которая имеет один локоть в одном локте… И в каждой квадратной крыше с равными сторонами одна из ее сторон (умноженная) в квадратной единице равна ее джадр ; или если то же самое умножить на два (квадратные единицы), то оно будет как два из его джадхров , будет ли эта крыша мала или велика». …

Джадр означает не только «корень», но также «основу», «основу», «низшую часть». Мухаммед ибн Муса… начинает свою главу о площадях с введения нового понятия квадратной единицы. Затем он говорит, что для того, чтобы получить площадь любой фигуры, мы должны сначала умножить одну сторону на квадратную единицу; затем это основание умножается на другую сторону. Умножаем не одну сторону на одну сторону, а одну jadhr , представляющий квадратную основу, с одной стороны, представляющей число. То же самое определение и идея можно найти и в других местах его алгебры. …

Термин [ джадхр ] означает не «корень», а «квадратный базис», то, умножением которого мы получаем площадь квадрата. По этой причине джадр использовалось более поздними авторами, такими как Омар Хайям, в качестве основного числа квадратного числа. Последний больше ничего не знал об изначальном значении числа 9.0216 jadhr , и он использовал это слово в широком смысле для dil’ (греч. πλευρά ), что означает «ребро» или «сторона». Но он, как и аль-Ховаризми, все же знал, что это конкретное число в противовес абстрактному числу.

Ко времени Беха Эддина (ок. 1600 г.) первоначальное значение было полностью забыто. В своей книге Kholdsat al-Hisdb («Сущность арифметики») он говорит: «То, что умножается само на себя, в арифметике называется джадр , в геометрии диль’ («сторона»), а шай’ («вещь», «причина») в алгебре». Он определенно понимал под jadhr абстрактный «корень». В этой неправильно понятой форме термин jadhr попал в средневековую латынь как radix .

И в О происхождении термина «корень». Вторая статья того же автора (The American Mathematical Monthly, vol. 35, 67–75, 1928; здесь), мы находим дальнейшее объяснение:

Теперь интересно обнаружить, что этот довольно странный процесс возведения площади в квадрат сохранился в математическом папирусе Райнда как древнейший метод вычисления площади, использовавшийся египтянами еще в 1650 г. до н.э. Таким образом, вполне возможно, что формулируя это геометрическое определение джадр ал-Ховаризми был подсказан не только математическими соображениями, но и давними историческими воспоминаниями о египетской геометрии.

Египетская единица измерения длины земли была Хет в 100 локтей. Самой распространенной единицей площади был сетат или квадрат Кхет , который содержал 10 000 квадратных локтей. Для практических целей в измерении земли они использовали единицу, называемую локтем земли или локтем-полосой. Это была узкая полоска земли длиной в сто локтей и шириной в один локоть. Меньшие порции щетинок при были выражены в таких локтях-полосках. Чтобы получить площадь прямоугольника, в хете иногда умножали его длину в локтях на ширину. Это дало им правильный ответ в локтях. Тем не менее, более ясно мы видим в задаче 48, что для умножения 8 хет на 8 хет и 9 хет на 9 хет «действительно написанная работа выглядит как умножение 9′ setat на чистое число 9».

Таким образом, египтянин вычислил квадрат, сначала умножив одну сторону (9 Kket ) в квадратной единице. Это был квадрат — основание ( джадр ), которое нужно было умножить на другую сторону, представляя собой чистое число. Тот же самый процесс описан также аль-Ховаризми, который говорит: «И у каждой квадратной фигуры одна из ее сторон, умноженная на квадратную единицу, есть ее джазхр… и мы делаем другую сторону, а именно, hj , три, и это число его джадра ».

Этот архаичный способ вычисления квадрата находит свое оправдание не только в «своеобразной египетской системе умножения», но и в самой природе первобытных вычислений. Древние египтяне не вычисляли площади и не измеряли свои поля по абстрактным правилам. Первоначально они находили площадь экспериментально-практическим путем, взяв маленькую квадратную мерку и попробовав, сколько раз она содержалась на измеряемом поле, «как сегодня мы измеряем сукно в ярдах». Для этой цели простая мера длины, Хет или шнур, толку от него не было. Таким образом, они должны были создать квадратную единицу, локтевую полосу, Хет в длину и один локоть в ширину. Это был первый джадхр с квадратным основанием, использовавшийся в практической жизни.

Эта локтевая полоса, по всей вероятности, также могла быть основной идеей египетской концепции квадратного корня. Идея квадратного корня существовала в Египте, и технический термин для нее был Knbt , буквально «угол» или «угол». Пит объясняет это тем, что длина каждой из двух сторон квадрата, содержащего любой его угол, равна его квадратному корню. Однако не чистая, одномерная сторона содержит «угол», а только jadhr , сторона, умноженная на квадратную единицу, содержит «угол». «Угол» или «угол» — это примитивное слово, обозначающее небольшую квадратную единицу. Аполлоний (ок. 225 г. до н. э.) определяет угол как сужение поверхности в одной точке под ломаной линией. Поскольку слово «угол», «краеугольный камень» обычно подразумевает также значение «низшая часть», «основа, основание», мы можем видеть в египетском Knbt источник и происхождение греческого pythmenes (основания), арабского жопа и джадр, иврит иккар и аш и индус мула .

No related posts.