| 1 | Оценить с использованием заданного значения | квадратный корень 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | y=x+4 | ||
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень 1 | |
| 69 | Упростить | квадратный корень 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
График функции y 5x 4.
Постройте график функции y=Разберем как строить график с модулем.
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=— (x-3)-(— (x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3).
Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=— (x-3)-(+ (x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+ (x-3)-(+ (x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4.
Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.
Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U и возрастает на промежутке }
Показательная функция, ее свойства и график
1. «Показательная функция, ее свойства и график»
2. Свойства показательной функции:
Функцию вида y=ax, где а>0, a≠1, х – любое число,называют показательной функцией.
Область определения показательной функции: D (y)=R –
множество всех действительных чисел.
Область значений показательной функции: E (y)=R+ множество всех положительных чисел.
Показательная функция y=ax возрастает при a>1.
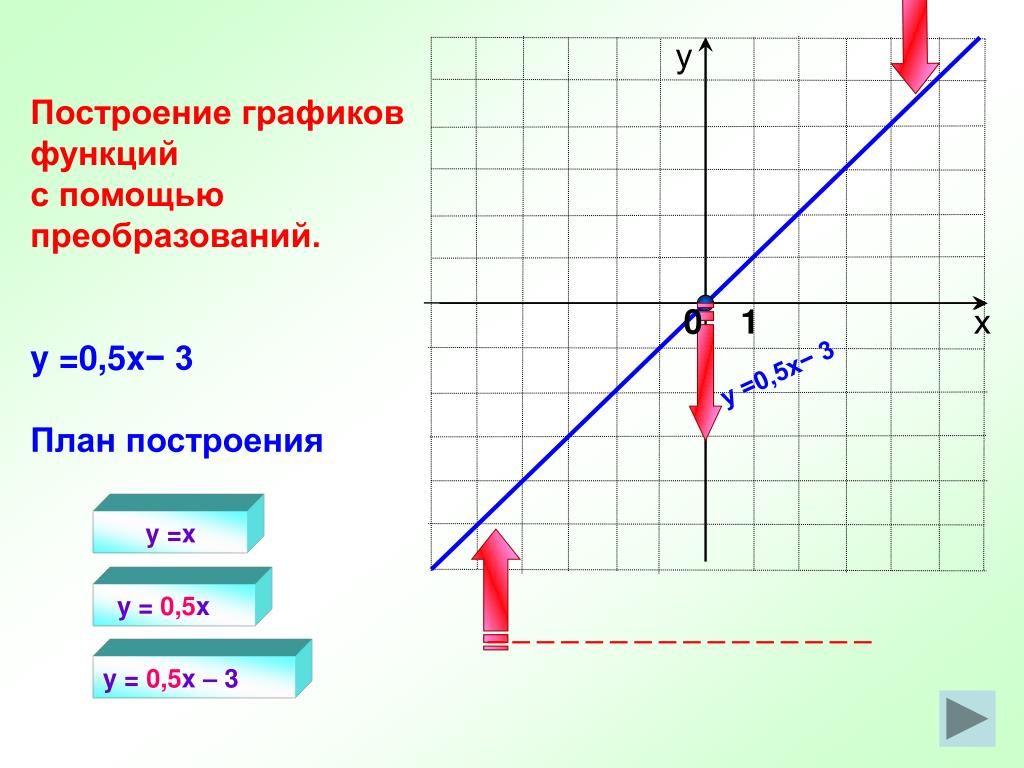
Показательная функция y=ax убывает при 0
3. Графики показательной функции:
4. К общим свойствам показательной функции как при 0 < a < 1, так и при a > 1 относятся:
К общим свойствам показательной функции как при 01 относятся:
5. Построить графики функций: у= (0,5)х и у=2х.
6. В одной координатной плоскости построить графики функций: y=2x, y=3x, y=5x, y=10x. Сделать выводы.
В одной координатной плоскости построить графики функций:y=2x, y=3x, y=5x, y=10x. Сделать выводы.
1) Переменная х может принимать любое
значение (D (y)=R), при этом значение у
всегда будет больше нуля (E (y)=R+).
2) Графики всех данных функций
пересекают ось Оу в точке (0; 1),
3) Все данные функции являются
возрастающими, так как большему
значению аргумента соответствует и
большее значение функции.
7. В одной координатной плоскости построить графики функций: y=(1/2)x, y=(1/3)x, y=(1/5)x, y=(1/10)x.
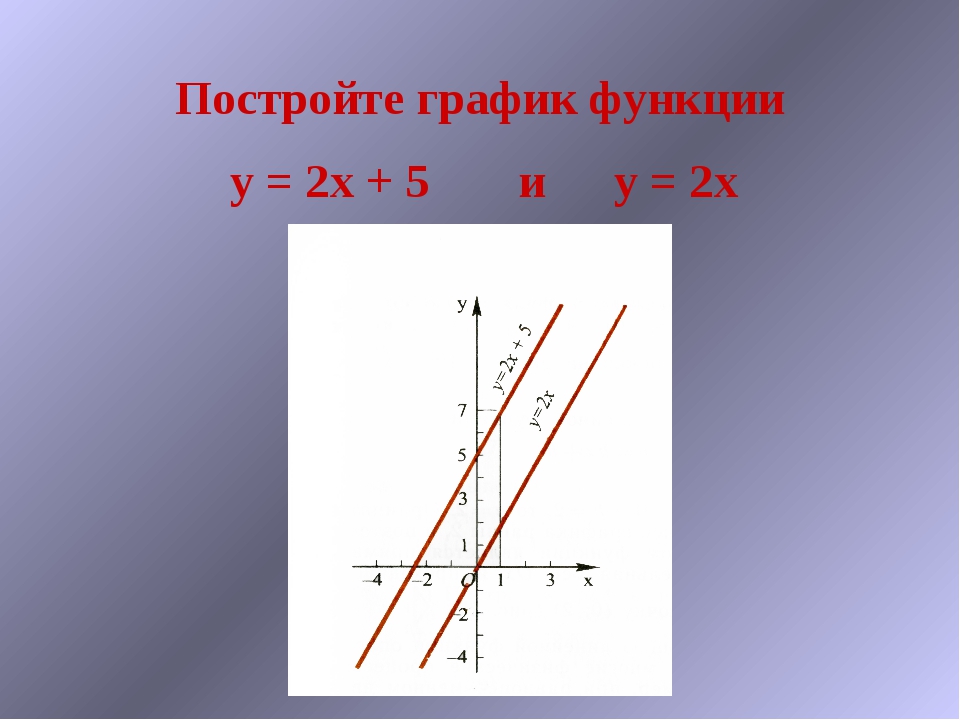Сделать выводы.. В одной координатной плоскости построить графики функций:y=(1/2)x, y=(1/3)x, y=(1/5)x, y=(1/10)x. Сделать выводы..
1) Переменная х может принимать любое
значение (D (y)=R), при этом значение у
всегда будет больше нуля (E (y)=R+).
2) Графики всех данных функций
пересекают ось Оу в точке (0; 1),
3) Все эти функции являются
убывающими, так как большему
значению аргумента соответствует
меньшее значение функции .
8. Решить графически уравнения: 1) 3x=4-x, 2) 0,5х=х+3.
Решить графически уравнения:1) 3x=4-x, 2) 0,5х=х+3.
9. Найти область значений функции: 1) y=-2x; 2) y=(1/3)x+1; 3) y=3x+1-5.
Найти область значений функции: 1) y=-2x; 2) y=(1/3)x+1; 3) y=3x+1-5.x
1)y=3
x+1-5. x
2) y=-2
y=(1/3)
+1;
Область
значений
показательной
функции y=2x – все
х∙3-5.
Запишем
функцию
в
виде:
у=3
x
0
ко всем частям
положительные
числа,прибавляя
т.
е.0
двойного
0
умножаем все части двойного неравенства на 3:
0+1
Значит, умножая каждую часть двойного неравенства на
0∙3
(-1),
получаем:
1
из всех частей двойного неравенства вычитаем 5:
—
∞
Ответ:
Е(у)=(1; +∞).
0-5
Ответ: Е(у)=(-∞; 0).
— 5
Ответ: Е(у)=(-5; +∞).
10. Домашнее задание:
Параграф 11 стр 72№ 196 (чет) стр 76
№ 197 (чет) стр 76
Построение графиков функций в Excel
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
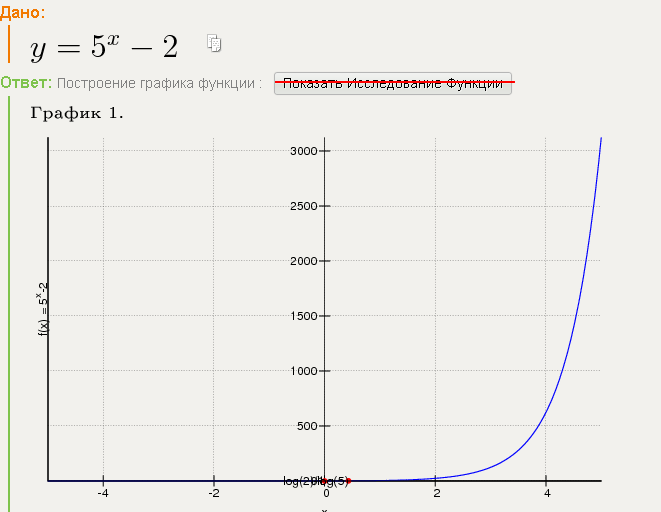
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам.
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2x2-2
Параболу по двум точкам уже не построить, в отличии от прямой.
2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Получим:
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: [-4;0) и (0; 4].
Подготовим две таблички, где х изменяется с шагом 0,2:
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
Получаем график функции y=1/x
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Спасибо за внимание!
на Ваш сайт.
Взаимное расположение графиков линейных функций. 7-й класс
Класс: 7
Тип урока: урок изучения нового материала
Цели урока:
Образовательные:
- Повторить свойства линейной функции;
- Отработать навык построения графиков линейной функции;
- Определить влияние коэффициентов к и в на взаимное расположение графиков линейных функций;
- Отработать знания и умения определять взаимное расположение графиков линейных функций заданных аналитически.
Развивающие:
- Работать над развитием понятийного аппарата;
- Развивать навыки самоконтроля;
- Развивать познавательную активность;
- Развивать культуру учебной деятельности;
- Развивать осмысленное отношение к своей деятельности;
- Развивать самостоятельность мышления, видеть
общую закономерность и делать обобщенные выводы.
Воспитательные:
- Воспитывать ответственное отношение к учению;
- Воспитывать волю и настойчивость для достижения конечных результатов;
- Воспитывать аккуратность;
- Воспитывать культуру общения.
Формы работы: индивидуальная работа, самостоятельная практическая работа, фронтальный, индивидуальный опрос.
Структура урока:
- Организационный момент
- Актуализация опорных знаний
- Введение в тему, постановка учебных задач
- Изучение нового материала в ходе выполнения практической работы
- Первичное осмысление и закрепление учебного материала
- Рефлексия
- Запись и обсуждение домашнего задания
- Подведение итога урока, анкетирование
Ход урока
Организационный момент
Учитель приветствует учащихся, проверка
присутствующих на уроке и проверка готовности к
уроку, наличие учебных принадлежностей.
Настрой
учащихся на учебную деятельность.
Актуализация опорных знаний.
Фронтальный устный опрос:
- Какие функции вам известны? (линейная функция, прямая пропорциональность)
- Какой формулой задается каждая из этих функций? (y=kx+b; y=kx)
- Как называется переменная x и y в формуле, задающий функцию? (абсцисса, независимая переменная, функция, зависимая переменная)
- Что является графиком этих функций? В чем их сходство и различие? (графиком линейной функции и прямой пропорциональности является прямая, но у прямой пропорциональности график проходит через начало координат)
- Как влияет коэффициент k на график функции? (если k>0,то прямая возрастающая, если k<0, то прямая убывающая)
- Каким образом мы сможем построить графики этих функций? (необходимо знать координаты двух точек, прямая пропорциональность проходит через точку (0;0))
- Среди записанных на доске формул выберите те,
которые задают линейную функцию, прямую
пропорциональность
- y=5x-7
- y=-2x
- y=2/x
- y=5x+2
- y=-2x+7
- y=-3
- y=x/2
- y=3,6x
- y=x-4
- y= (5x-1) + (8x+9)
- Функция задана формулой y=2x+5. Найдите значение
функции, соответствующее значению аргумента,
равному -3;0;5
- Функция задана формулой y=4x-9. Найдите значение аргумента, при котором функция принимает значение -1;0;3
- Принадлежат ли графику функции y=-2xточки с координатами А(4;-8), В(-10,20), С(0,5; -2),Т (-?;?)
Найдите значение
функции, соответствующее значению аргумента,
равному -3;0;5Введение в тему. Постановка учебных задач.
Известно, что графиком линейной функции и прямой пропорциональности являются прямые. Ребята, вспомните из курса геометрии, каким может быть взаимное расположение двух прямых (параллельны, пересекаются, совпадают). А теперь нам предстоит выяснить, от чего зависит взаимное расположение двух прямых. Для этого мы выполним следующую практическую работу.
Изучение нового материала в ходе выполнения практической работы.
Сейчас Вы выполните графическую практическую работу, которая поможет ответить на следующие вопросы: от чего зависит параллельность, пересечение, совпадение графиков линейных функций? Как по аналитическому заданию функций определить взаимное расположение их графиков?
Задание №1
- В одной системе координат постройте графики функций: y=2x-3; y=2x+4; y=2x-7
Задание №2
- В одной системе координат постройте графики функций: y=2x-3; y=-x+4; y=5x+1
Задание №3
В одной системе координат постройте графики функций: y=2x-3 y=-x-3 y=5x-3
В итоге выполнения задания у Вас в тетради
должно получиться три системы координат, в
каждой из которых построено три графика.
Первичное осмысление и закрепление изученного. Обсуждение результатов практической работы.
- Посмотрите на формулы, задающие графики в задании №1, что Вы можете сказать про коэффициенты? (k- одинаковы, b- различны)
- Обратите внимание на то, как расположены графики функций в задании №1 (графики данных функций параллельны)
- Посмотрите на формулы, задающие графики в задании №2, что Вы можете сказать про коэффициенты? (k-различны, b- различны)
- Обратите внимание на то, как расположены графики функций в задании №2? (графики данных функций пересекаются)
- Посмотрите на формулы, задающие графики в задании №3, что Вы можете сказать про коэффициенты? (k- различны, b- одинаковы)
- Обратите внимание на то, как расположены графики функций в задании №3? (графики данных функций пересекаются в точке с координатой (0;3))
- Какой вывод можно сделать, сопоставив
аналитическое задание функций и взаимное
расположение их графиков?
- (когда коэффициенты k одинаковы, а b различны, то прямые параллельны;
- когда коэффициенты k различны, и b различны, то прямые пересекаются;
- когда коэффициенты k различны, а b одинаковы, то
прямые пересекаются в точке с координатой (0;b)).
Записать полученные выводы в тетрадь.
Задание №4
Среди функций, заданных формулами y=x+0,5; y=-0,5x+4; y=5x-1; y=1+0,5x; y=-3+0,5x выделите те, графики которых параллельны графику функции y=0,5x+4
Задание №5
Пересекаются ли графики функций: y=2-7x и y=-7x-3; y=2x+5 и y=3-4x; y=3x и y=-5+3x.
Задание №6
Приведите примеры трех функций, графики которых параллельны графику функции y=5x+2и примеры трех функций, графики которых пересекаются с графиком функции y=5x+2
Рефлексия.
Фронтальное обсуждение вопросов: какова цель прошедшего урока? Что мы делали, чтобы достигнуть цели? Что нового узнали?
Запись и обсуждение домашнего задания.
Задайте формулой линейную функцию, если
известно, что k=-3 и график проходит через точку
A(-2;3). Приведите примеры трех функций, графики
которых параллельны данной, а также примеры трех
функций, графики которых пересекают данный
график.
Подведение итогов урока и выставление оценок. Анкетирование
Анкета “Как прошел урок?”
- Доволен ли ты тем, как прошел урок?
- Было ли тебе интересно на уроке?
- Сумел ли ты получить новые знания?
- Ты был активен на уроке?
- Ты сумел показать свои знания?
- Учитель был внимателен к тебе?
- Ты с удовольствием будешь выполнять домашнее задание?
Как построить график функции
В этой статье разобран самый простой метод получения графика функции.
Суть метода: найти несколько точек принадлежащих графику, расставить их на координатной плоскости и соединить. Этот способ не лучший (лучший – построение графиков с помощью элементарных преобразований), но если вы все забыли или ничего не учили, то знайте, что у вас всегда есть план Б – возможность построить график по точкам.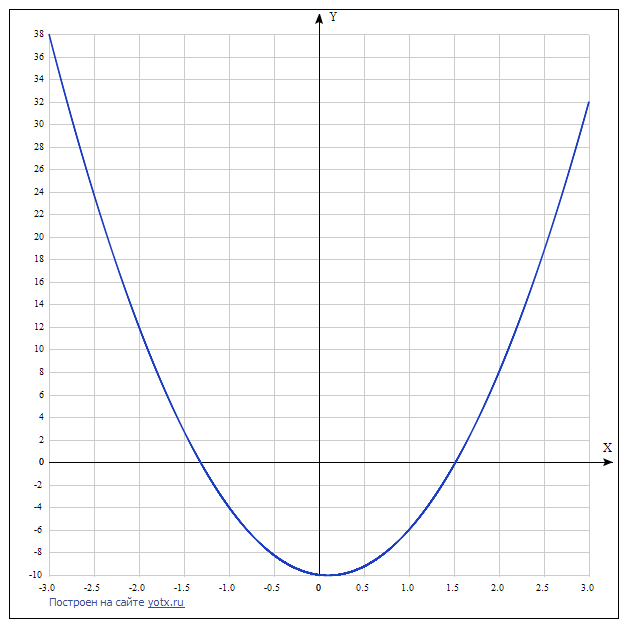
Итак, алгоритм по шагам:
1. Представьте, как выглядит ваш график.
Строить гораздо легче, если вы понимаете, что примерно должны получить в итоге. Поэтому сначала посмотрите на функцию и представьте, как примерно должен выглядеть ее график. Все виды графиков элементарных функций вы можете найти здесь. Этот пункт желательный, но не обязательный.
Пример: Построить график функции \(y=-\)\(\frac{2}{x}\)
Данная функция — гипербола с ветвями расположенными во второй и четвертой четверти. Её график выглядит как-то так:
2. Составьте таблицу точек, принадлежащих графику:
Теперь подставим разные значения «иксов» в функцию, и для каждого икса посчитаем значение «игрека».
Пример: \(y=-\)\(\frac{2}{x}\)
|
при \(x=-1\) |
\(y=-\)\(\frac{2}{-1}\)\(=2\) |
|
|
при \(x=0\) |
\(y\) — не существует (делить на ноль нельзя) |
|
|
при \(x=1\) |
\(y=-\)\(\frac{2}{1}\)\(=-2\) |
|
|
при \(x=2\) |
\(y=-\)\(\frac{2}{2}\)\(=-1\) |
|
|
при \(x=3\) |
\(y=-\)\(\frac{2}{3}\) |
|
|
при \(x=4\) |
\(y=-\)\(\frac{2}{4}\)\(=-\)\(\frac{1}{2}\) |
Результат вычислений удобно представлять в виде таблицы, примерно такой:
|
\(x\) |
\(-1\) |
\(0\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
|
\(y\) |
\(2\) |
\(-\) |
\(-2\) |
\(-1\) |
\(-\)\(\frac{2}{3}\) |
\(-\)\(\frac{1}{2}\) |
Как вы могли догадаться, полученные пары «икс» и «игрек» — это точки, лежащие на нашем графике.
4. Постройте координатную плоскость и отметьте на ней точки из таблицы.
Пример:
5. Если нужно, найдите еще несколько точек и нанесите их на координатную плоскость.
Пример: Чтобы построить график мне не хватает нескольких точек из отрицательной части, а также рядом с осью игрек, поэтому я добавлю столбцы с \(x=-2\), \(x=-4\), \(x=\)\(\frac{1}{2}\) и \(x=-\)\(\frac{1}{2}\)
|
при \(x=-2\) |
\(y=-\)\(\frac{2}{-2}\)\(=1\) |
|
|
при \(x=-4\) |
\(y=-\)\(\frac{2}{-4}\)\(=\)\(\frac{1}{2}\) |
|
|
при \(x=\)\(\frac{1}{2}\) |
\(y=-\)\(\frac{2}{\frac{1}{2}}\)\(=-2:\)\(\frac{1}{2}\)\(=-2 \cdot 2=-4\) |
|
|
при \(x=-\)\(\frac{1}{2}\) |
\(y=-\)\(\frac{2}{-\frac{1}{2}}\)\(=-2:(-\)\(\frac{1}{2}\)\()\)\(=-2 \cdot (-2)=4\) |
|
\(x\) |
\(-1\) |
\(0\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(-2\) |
\(-4\) |
\(\frac{1}{2}\) |
\(-\)\(\frac{1}{2}\) |
|
\(y\) |
\(2\) |
\(-\) |
\(-2\) |
\(-1\) |
\(-\)\(\frac{2}{3}\) |
\(-\)\(\frac{1}{2}\) |
\(1\) |
\(\frac{1}{2}\) |
\(-4\) |
\(4\) |
6.
Постройте график
Теперь аккуратно и плавно соединяем точки.
Готово!
Скачать статью
Преобразование графиков функций
Преобразование графиков функций
В этой статье я познакомлю вас с линейными преобразованиями графиков функций и покажу, как с помощью этих преобразований из графика функции получить график функции
Линейным преобразованием функции называется преобразование самой функции и/или ее аргумента к виду , а также преобразование, содержащее модуль аргумента и/или функции.
Наибольшие затруднения при построении графиков с помощью линейных преобразований вызывают следующие действия:
- Вычленение базовой функции, собственно, график которой мы и преобразовываем.
- Определения порядка преобразований.
Именно на этих моментах мы и остановимся подробнее.
Рассмотрим внимательно функцию
В ее основе лежит функция .
Назовем ее базовой функцией.
При построении графика функции мы совершаем преобразования графика базовой функции .
Если бы мы совершали преобразования функции в том же порядке , в каком находили ее значение при определенном значении аргумента, то
Рассмотрим какие виды линейных преобразований аргумента и функции существуют, и как их выполнять.
Преобразования аргумента.
1. f(x) f(x+b)
1. Строим график фунции
2. Сдвигаем график фунции вдоль оси ОХ на |b| единиц
- влево, если b>0
- вправо, если b<0
Построим график функции
1. Строим график функции
2. Сдвигаем его на 2 единицы вправо:
2. f(x) f(kx)
1. Строим график фунции
2. Абсциссы точек графика делим на к, ординаты точек оставляем без изменений.
Построим график функции .
1. Строим график функции
2. Все абсциссы точек графика делим на 2, ординаты оставляем без изменений:
3.
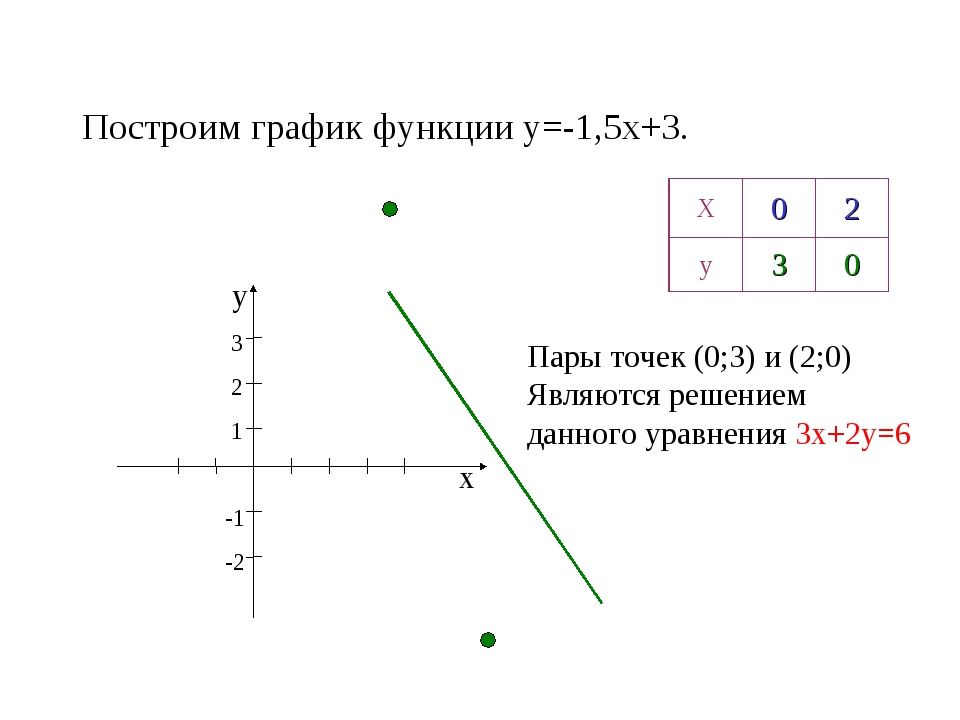f(x) f(-x)
1. Строим график фунции
2. Отображаем его симметрично относительно оси OY.
Построим график функции .
1. Строим график функции
2. Отображаем его симметрично относительно оси OY:
4. f(x) f(|x|)
1. Строим график функции
2. Часть графика, расположенную левее оси ОY стираем, часть графика, расположенную правее оси ОY Достраиваем симметрично относительно оси OY:
График функции выглядит так:
Построим график функции
1. Строим график функции (это график функции , смещенный вдоль оси ОХ на 2 единицы влево):
2. Часть графика, расположенную левее оси OY (x<0) стираем:
3. Часть графика, расположенную правее оси OY (x>0) достраиваем симметрично относительно оси OY:
Важно! Два главных правила преобразования аргумента.
1. Все преобразования аргумента совершаются вдоль оси ОХ
2.
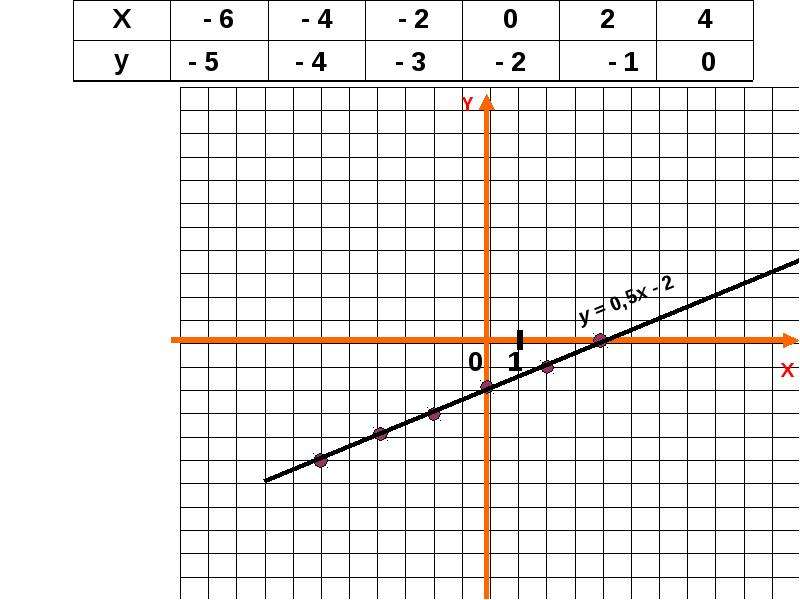Все преобразования аргумента совершаются «наоборот» и «в обратном порядке».
Например, в функции последовательность преобразований аргумента такая:
1. Берем модуль от х.
2. К модулю х прибавляем число 2.
Но построение графика мы совершали в обратном порядке:
Сначала выполнили преобразование 2. — сместили график на 2 единицы влево (то есть абсциссы точек уменьшили на 2, как бы «наоборот»)
Затем выполнили преобразование f(x) f(|x|).
Коротко последовательность преобразований записывается так:
Теперь поговорим о преобразовании функции. Преобразования совершаются
1. Вдоль оси OY.
2. В той же последовательности, в какой выполняются действия.
Вот эти преобразования:
1. f(x)f(x)+D
1. Строим график функции y=f(x)
2. Смещаем его вдоль оси OY на |D| единиц
- вверх, если D>0
- вниз, если D<0
Построим график функции
1.
Строим график функции
2. Смещаем его вдоль оси OY на 2 единицы вверх:
2. f(x)Af(x)
1. Строим график функции y=f(x)
2. Ординаты всех точек графика умножаем на А, абсциссы оставляем без изменений.
Построим график функции
1. Построим график функции
2. Ординаты всех точек графика умножим на 2:
3. f(x)-f(x)
1. Строим график функции y=f(x)
2. Отображаем его симметрично относительно оси ОХ.
Построим график функции .
1. Строим график функции .
2. Отображаем его симметрично относительно оси ОХ.
4. f(x)|f(x)|
1. Строим график функции y=f(x)
2. Часть графика, расположенную выше оси ОХ оставляем без изменений, часть графика, расположенную ниже оси OX, отображаем симметрично относительно этой оси.
Построим график функции
1. Строим график функции . Он получается смещением графика функции вдоль оси OY на 2 единицы вниз:
2.
Теперь часть графика, расположенную ниже оси ОХ, отобразим симметрично относительно этой оси:
И последнее преобразование, которое, строго говоря, нельзя назвать преобразованием функции, поскольку результат этого преобразования функцией уже не является:
y=f(x) |y|=f(x)
1. Строим график функции y=f(x)
2. Часть графика, расположенную ниже оси ОХ стираем, затем часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.
Построим график уравнения
1. Строим график функции :
2. Часть графика, расположенную ниже оси ОХ стираем:
3. Часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.
И, наконец, предлагаю вам посмотреть ВИДЕОУРОК в котором я показываю пошаговый алгоритм построения графика функции
График этой функции выглядит так:
И.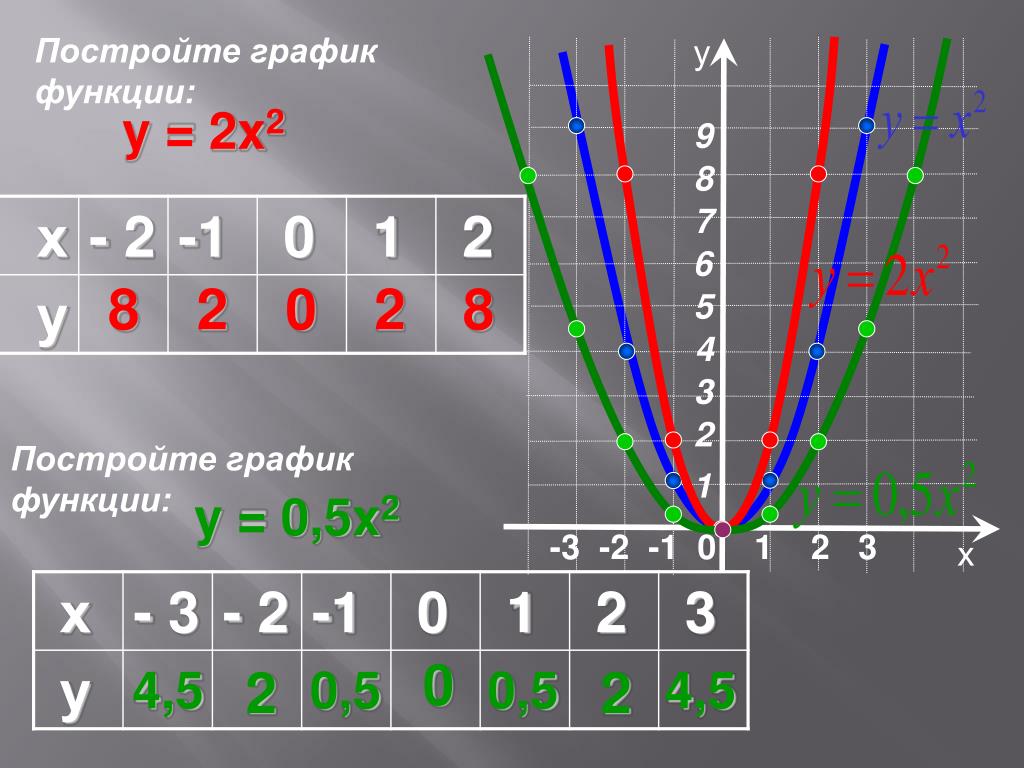
В. Фельдман, репетитор по математике.
Нарисуйте график функции y = 5x Считайте с графика значение y, когда 1) x = 5 2) х = 6
Линейная взаимосвязь — это взаимосвязь между переменными, при которой при нанесении на координатную плоскость точки лежат на одной линии. Давайте начнем с рассмотрения ряда точек в квадранте I на координатной плоскости.Посмотрите на пять упорядоченных пар (и их координаты x и y) ниже. Вы видите какой-либо образец расположения точек? Если эта модель продолжится, какие еще точки могут быть на линии?

Вы, вероятно, определили, что если этот шаблон продолжится, следующая упорядоченная пара будет в (5, 10).Это имеет смысл, потому что точка (5, 10) «совпадает» с другими точками в серии — она буквально находится на той же линии, что и другие. Применяя ту же логику, вы можете определить, что упорядоченные пары (6, 12) и (7, 14) также принадлежали бы, если бы эта координатная плоскость была больше; они тоже будут соответствовать другим пунктам.
Эти серии точек также могут быть представлены в виде таблицы. В таблице ниже записаны координаты x и y каждой упорядоченной пары на графике.
Координата x
Координата Y
0
0
1
2
2
4
3
6
4
50002 8
6
12
7
14
Обратите внимание, что каждая координата y в два раза больше соответствующего значения x. Все эти значения x и y следуют одному и тому же шаблону, и при размещении на координатной плоскости все они совпадают.
Когда вы знаете шаблон, который связывает значения x и y, вы можете найти значение y для любого значения x, которое лежит на линии. Таким образом, если правило этого шаблона состоит в том, что каждая координата y в два раза больше соответствующего значения x, тогда упорядоченные пары (1.5, 3), (2.5, 5) и (3.5, 7) также должны появиться в строке. , верный? Посмотрите, что происходит.

Если бы вы продолжали добавлять упорядоченные пары (x, y), где значение y было в два раза больше значения x, вы бы получили такой график.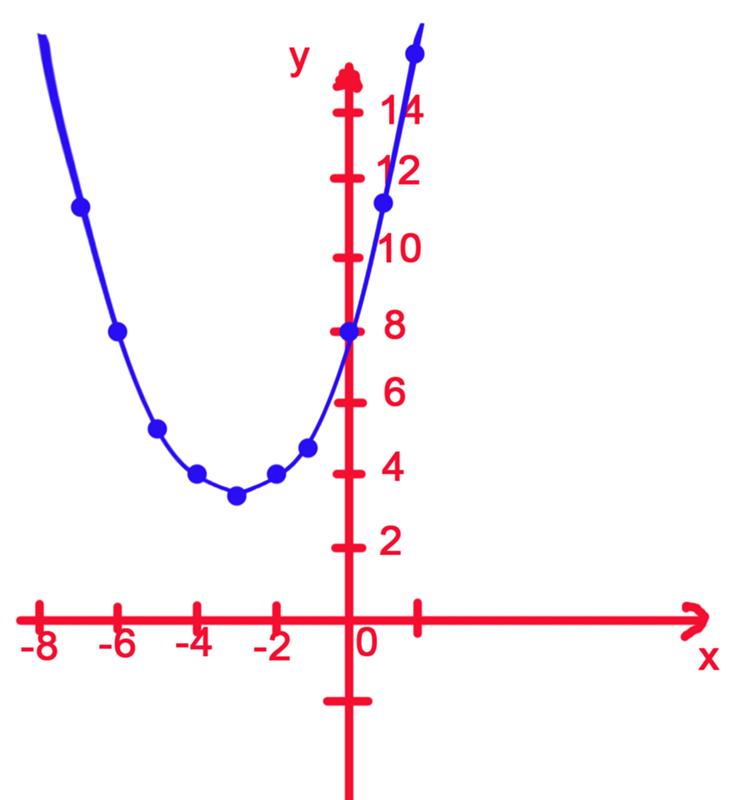

Посмотрите, как все точки сливаются вместе, образуя линию. Таким образом, вы можете представить себе линию как набор из бесконечного числа отдельных точек, которые имеют одно и то же математическое отношение. В этом случае отношение состоит в том, что значение y в два раза больше значения x.
Есть несколько способов представить линейную зависимость — таблица, линейный график, а также линейное уравнение. Линейное уравнение — это уравнение с двумя переменными, упорядоченные пары которых изображены в виде прямой линии.
Есть несколько способов создать график из линейного уравнения. Один из способов — создать таблицу значений для x и y, а затем нанести эти упорядоченные пары на координатную плоскость. Для определения линии достаточно двух точек. Однако всегда рекомендуется наносить более двух точек, чтобы избежать возможных ошибок.
Затем вы проводите линию через точки, чтобы показать все точки, которые находятся на линии.
Стрелки на каждом конце графика показывают, что линия бесконечно продолжается в обоих направлениях.Каждая точка в этой строке является решением линии
| Начало алгебры Урок 21: Построение графиков линейных уравнений Цели обучения
Введение
Учебник
Практические задачи
Нужна дополнительная помощь по этим темам? |
В этом уроке мы будем дополнять это, посмотрев
при построении графиков линейных уравнений путем нанесения точек, которые
решения.
По сути, когда вы строите график, вы строите решения и соединяете точки с
получать
ваш график. Конкретно,
когда вы построите график линейных уравнений, вы получите прямой
линия.
Посмотрим, что вы можете сделать с этими линейными уравнениями.
) Вы
хочу, чтобы это было как можно проще. Ниже приведена диаграмма
Я закончил после подключения значений, которые я упомянул для x .
Это позволит вам проверить и понять, понимаете ли вы
эти
типы проблем. Math работает так же, как
что-нибудь
иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться
Это.
Даже лучшие спортсмены и музыканты получали помощь и много
практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте. На самом деле не бывает слишком много практики.
Решите Свойства прямой y = 5x-25 Tiger Algebra Solver
Переставьте:
Переставьте уравнение, вычтя то, что находится справа от знака равенства с обеих сторон уравнения:
y- (5 * x-25) = 0
Шаг 1:
Уравнение прямой линии
1.
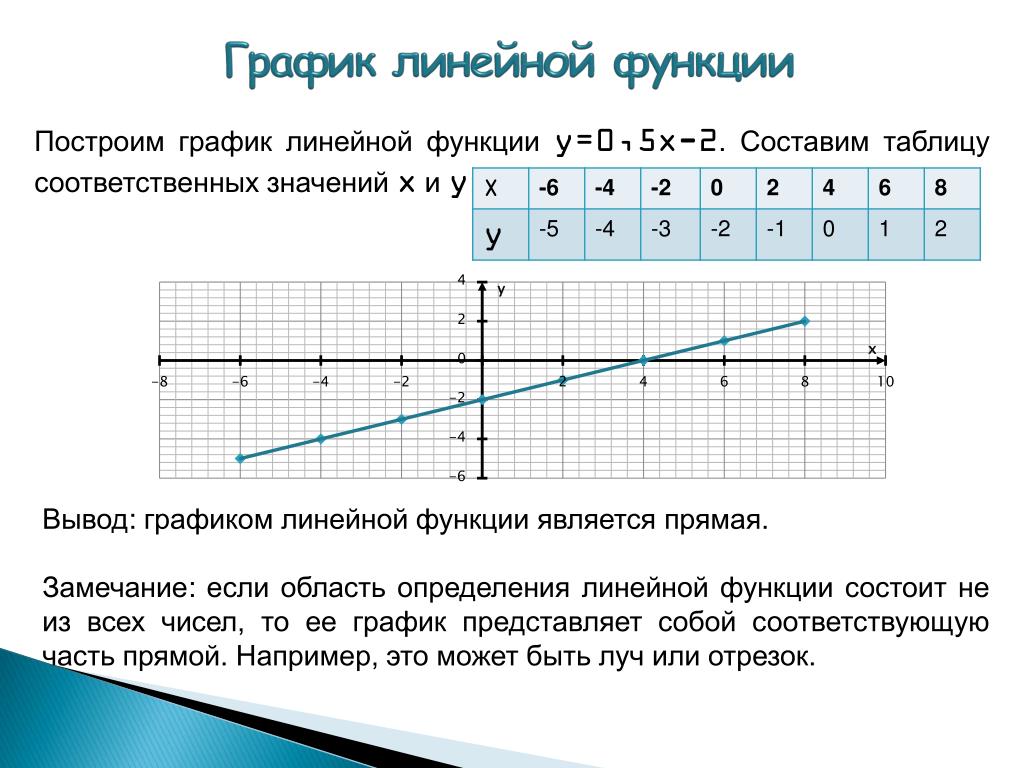1 Решите y-5x + 25 = 0
Тигр понимает, что здесь есть уравнение прямой.Такое уравнение обычно записывается y = mx + b («y = mx + c» в Великобритании).
«y = mx + b» — это формула прямой линии, проведенной в декартовой системе координат, в которой «y» — вертикальная ось, а «x» — горизонтальная ось.
В этой формуле:
y указывает нам, как далеко идет линия.
x сообщает нам, как далеко вдоль
м находится наклон или градиент, т.е. насколько крутой является линия.
b является точкой пересечения оси Y, т.е. Ось Y
Пересечения по осям X и Y и наклон называются свойствами линии.Теперь мы построим график линии y-5x + 25 = 0 и вычислим ее свойства
График прямой линии:
Вычислите точку пересечения Y:
Обратите внимание, что при x = 0 значение y равно -25 / 1, поэтому эта линия «обрезает» ось y в точке y = -25.00000
Y-intercept = -25/1 = -25.00000
Вычислить пересечение по оси X:
Когда y = 0, значение x равно 5 / 1 Таким образом, наша линия «разрезает» ось x в точке x = 5,00000
x-intercept = 25/5 = 5
Вычислите наклон:
Наклон определяется как изменение y, деленное на изменение x.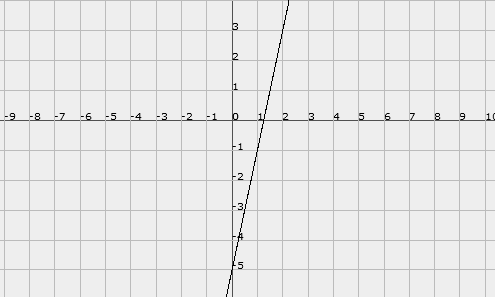
Отметим, что для x = 0 значение y равно -25,000, а для x = 2,000 значение y равно -15,000. Таким образом, при изменении x на 2.000 (изменение x иногда называют «RUN») мы получаем изменение на -15.000 — (-25.000) = 10.000 по y. (Изменение y иногда называют «ПОДЪЕМ», а наклон равен m = ПОДЪЕМ / ПЕРЕДАЧА)
Наклон = 10.000 / 2.000 = 5.000
Геометрическая фигура: прямая
- Наклон = 10.000 / 2.000 = 5.000
- пересечение по оси x = 25/5 = 5
- пересечение по оси y = -25/1 = -25.00000
Как построить график функции y 5x + 1 математика для класса 11 CBSE
Подсказка: Найдите две (минимум) или более точек, которые удовлетворяют заданному уравнению, например, $ y = 5x + 1 $ Изобразите их на миллиметровой бумаге, а затем соедините их с помощью прямой линии. Полный пошаговый ответ —
Поскольку данное уравнение является линейной формой уравнения с двумя переменными, вы получите прямую линию.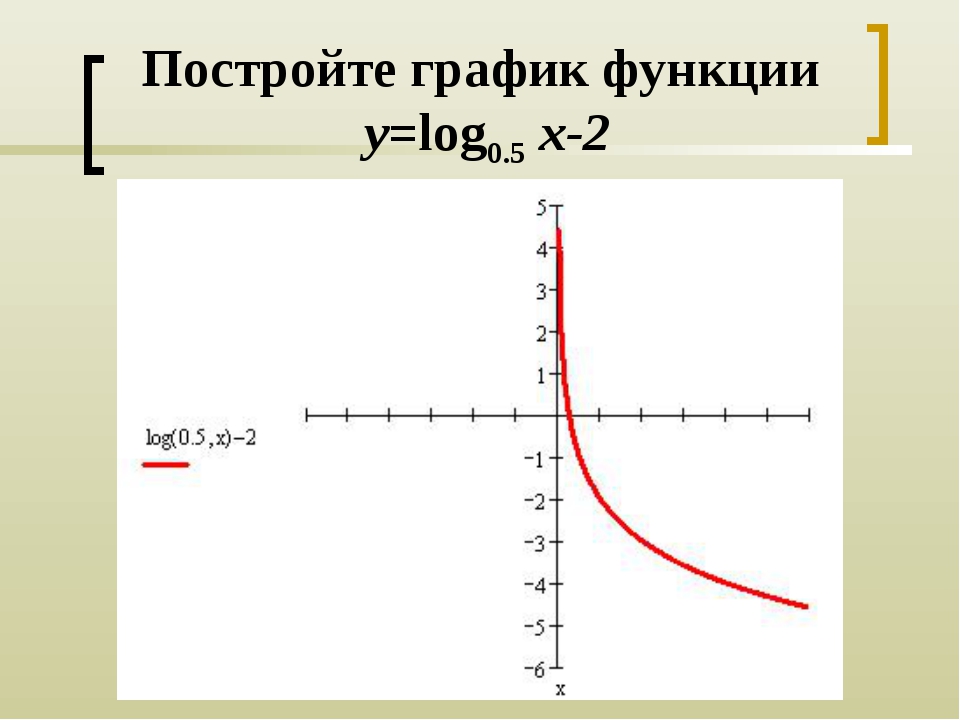
Дано-
$ y = 5x + 1 $
При x = 0 $; $ y = 5 (0) + 1 $ $ = 1 $
Таким образом, мы получили нашу первую точку, которая будет удовлетворять уравнению (0,1). Это Y-образный перехват.
При $ y = 0 $; $ 5x + 1 = 0 $
$ \ Rightarrow x = \ dfrac {{- 1}} {5} $
Следовательно, мы получили еще одну точку, которая будет удовлетворять уравнению и равна ( $ \ left ({- \ dfrac {1} {5}, 0} \ right) $
Поскольку это дробь, мы попытаемся найти другую точку, координаты которой имеют два целых числа.
При $ y = 6 $; $ 5x + 1 = 6 $
$ \ Rightarrow x = \ dfrac {5} {5} = 1 $
Следовательно, вторая требуемая точка — это (1,6).
Отметьте точки (0,1) и (1,6) на листе графика. Соедините эти две точки, и вы получите требуемый график.
Примечание — Координаты могут варьироваться в зависимости от вашего выбора, но все точки должны удовлетворять заданному уравнению прямой.
Вы в одном шаге от ответа!
Подпишитесь бесплатно!
Регистрируясь, вы также получаете БЕСПЛАТНЫЙ доступ к тысячам решенных вопросов, викторин
и загружаемым PDF-файлам!
систем линейных уравнений
систем линейных уравнений Часто бывает необходимо посмотреть на несколько функций одного и того же независимого
Переменная.
Рассмотрим предыдущий пример, где x — количество произведенных товаров.
и продано, была независимой переменной в трех функциях: функции затрат,
функция дохода и функция прибыли.
В целом там может быть:
n уравнений
v переменные
Решение систем уравненийЕсть четыре метода решения систем линейных уравнений:
а.графическое решение
б. алгебраическое решение
c. метод исключения
d. метод замещения
Пример 1
даны являются два следующих линейных уравнения:
f (x) = y = 1 + 0,5x
f (x) = y = 11 — 2x
Постройте первое уравнение для первого уравнения , найдя две точки данных.Установив сначала x, а затем y равны нулю, можно найти точку пересечения y на вертикальная ось и точка пересечения x на горизонтальной оси.
Если x = 0,
тогда f (0) = 1 + .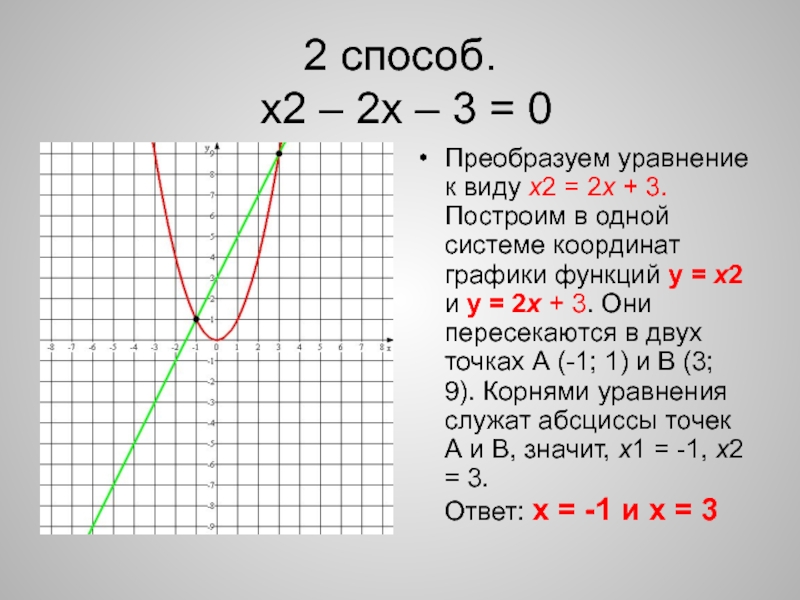
5 (0) = 1
Если y = 0, тогда f (x) = 0 = 1 + .5x
-,5x = 1
х = -2
Результирующий точки данных: (0,1) и (-2,0)
Постройте график второго уравнения , найдя две точки данных.От установив сначала x, а затем y равным нулю, можно найти точку пересечения y по вертикальной оси и точка пересечения x по горизонтальной оси.
Если x = 0, тогда f (0) = 11-2 (0) = 11
Если y = 0, тогда f (x) = 0 = 11 — 2x
2x = 11
х = 5,5
Результирующий точки данных: (0,11) и (5.5,0)
В точке пересечения двух уравнений x и y имеют одинаковые значения.
На графике эти значения можно прочитать как x = 4 и y = 3.
Пример 2
даны являются два следующих линейных уравнения:
f (x) = y = 15 — 5x
f (x) = y = 25 — 5x
Постройте первое уравнение для первого уравнения , найдя две точки данных.
Установив
сначала x, а затем y равны нулю, можно найти точку пересечения y на
вертикальная ось и точка пересечения x на горизонтальной оси.
Если x = 0, тогда f (0) = 15-5 (0) = 15
Если y = 0, тогда f (x) = 0 = 15 — 5x
5x = 15
х = 3
Результирующий точки данных: (0,15) и (3,0)
Постройте график второго уравнения , найдя две точки данных.От установив сначала x, а затем y равным нулю, можно найти точку пересечения y по вертикальной оси и точка пересечения x по горизонтальной оси.
Если x = 0, тогда f (0) = 25-5 (0) = 25
Если y = 0, тогда f (x) = 0 = 25 — 5x
5x = 25
х = 5
Результирующий точки данных: (0,25) и (5,0)
Из графика видно, что эти линии не пересекаются.Они параллельны. У них одинаковый наклон. Нет однозначного решения.
Пример 3
даны являются два следующих линейных уравнения:
21x — 7y = 14
-15x + 5y = -10
Перепишите
уравнения, поместив их в форму пересечения наклона.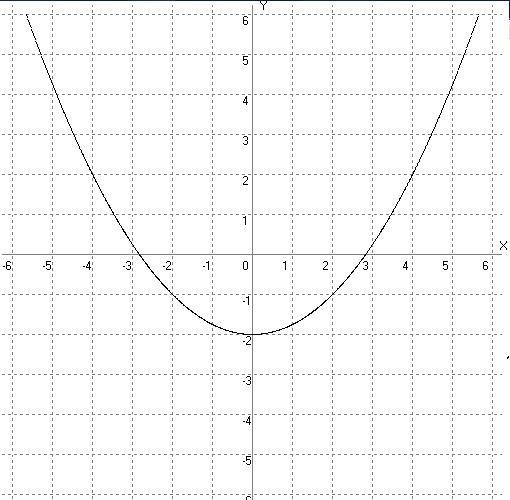
Первый уравнение становится
7y = -14 + 21x
у = -2 + 3х
Второй уравнение становится
5лет = -10 + 15x
у = -2 + 3х
Изобразите любое уравнение, найдя две точки данных.Установив сначала x, а затем y равный нулю, можно найти точку пересечения y по вертикали ось и точку пересечения x на горизонтальной оси.
Если x = 0, тогда f (0) = -2 +3 (0) = -2
Если y = 0, тогда f (x) = 0 = -2 + 3x
3x = 2
х = 2/3
Результирующий точки данных: (0, -2) и (2 / 3,0)
Из графика видно, что эти уравнения эквивалентны.Там — бесконечное количество решений.
Алгебраическое решение
Этот метод будет проиллюстрирован с помощью анализа спроса и предложения. Этот Тип анализа заимствован из работ великого английского экономиста Альфреда Маршалл.
Q = количество и P = цена
P (s) = функция предложения и P (d) = функция спроса
При построении графика цена откладывается на вертикальной оси.
Таким образом, цена — это
зависимая переменная.Было бы логичнее рассматривать количество как
зависимая переменная, и этот подход использовал великий французский экономист,
Леон Вальрас. Однако по соглашению экономисты продолжают строить графики, используя
Анализ Маршалла, который называют крестом Маршалла.
Цель состоит в том, чтобы найти равновесную цену и количество, т. Е. Решение где цена и количество будут иметь одинаковые значения в функции предложения и функция цены.
Q E = равновесная величина P E = равновесная цена
Для равновесия
предложение = спрос
или P (s) = P (d)
Учитывая следующие функции
П (т) = 3Q + 10 и P (d) = -1 / 2Q + 80
Приравняйте уравнения друг к другу и решите относительно Q.
P (т) = 3Q + 10 = -1 / 2Q + 80 = P (d)
3.5Q = 70
Q = 20 Равновесное количество 20.
Подставьте это значение вместо Q в любое уравнение и решите для P.
P (т) = 3 (20) + 10
П (т) = 70
П (г) = -1/2 (20) + 80
П (г) = 70 Цена равновесия — 70.
Метод исключения
Этот метод включает удаление переменных из уравнений. Переменные удаляются последовательно, пока не останется только одна последняя переменная, т.е. пока не будет одно уравнение с одним неизвестным. Затем это уравнение решается для одного неизвестного. Затем решение используется для нахождения второго последняя переменная. Процедура повторяется, добавляя обратно переменные в качестве их решений. найдены.
Пример 1
2х + 3у = 5
-5x — 2y = 4
Порядок действий: удалить y.Коэффициенты при y не совпадают в
два уравнения, но если бы они были, можно было бы сложить два
уравнения и члены y будут сокращаться. Однако это возможно через
умножение каждого уравнения, чтобы заставить члены y иметь
одинаковые коэффициенты в каждом уравнении.
Шаг 1: Умножьте первое уравнение на 2, а второе уравнение умножьте на 3. Это дает
4х + 6у = 10
-15x — 6y = 12
Шаг 2: Сложите два уравнения.Это дает
-11x = 22
х = -2
Шаг 3: Решить относительно y в любом из исходных уравнений
2 (-2) + 3у = 5
3 года = 9
г = 3 или
-5 (-2) — 2y = 4
10 — 2y = 4
2y = 6
г = 3
Альтернативная процедура: удалить x.Коэффициенты при x не совпадают в двух уравнениях, но если бы они были, можно было бы добавить два уравнения и члены y будут сокращаться. Однако возможно путем умножения каждого уравнения, чтобы заставить члены x равняться имеют одинаковые коэффициенты в каждом уравнении.
Шаг 1:
Умножьте первое уравнение на 5, а второе уравнение умножьте на 2.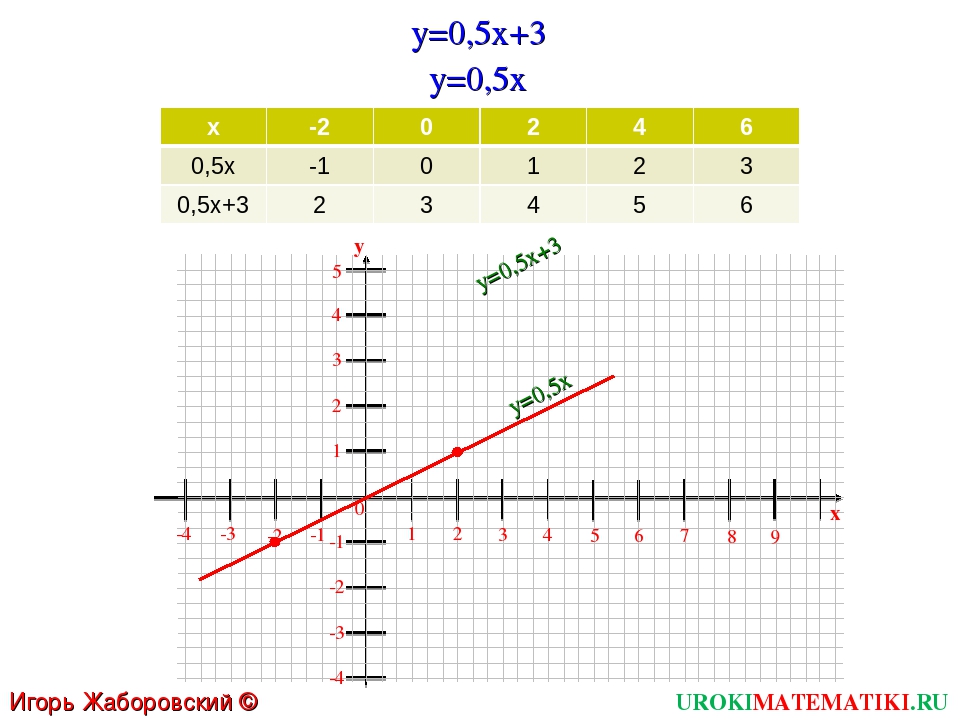
Это дает
10x + 15y = 25
-10x — 4y = 8
Шаг 2: Сложите два уравнения.Это дает
11лет = 33
y = 3
Шаг 3: Решить относительно x в любом из исходных уравнений
2x + 3 (3) = 5
2x = -4
х = -2 или
-5x — 2 (3) = 4
— 5x = 10
х = -2
Пример 2
2x 1 + 5x 2 + 7x 3 = 2
4x 1 — 4x 2 — 3x 3 = 7
3x 1 — 3x 2 — 2x 3 = 5
В этом примере есть три переменные: x 1 , x 2 и
x 3 .Одна из возможных процедур — удалить первый x 1 , , чтобы исключить следующие x 2 , а затем найти x 3 .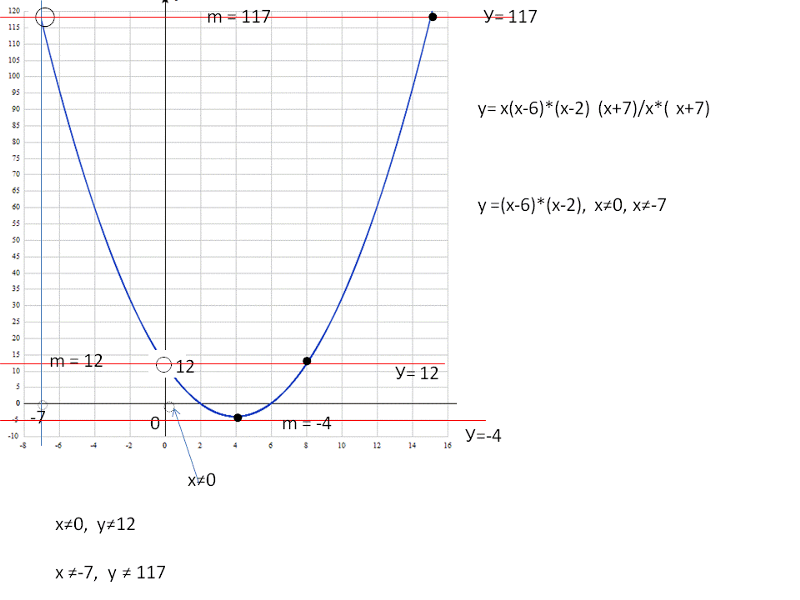
Значение, полученное для x 3 , используется для решения x 2 и
наконец, значения, полученные для x 3 и x 2 , используются для
решить относительно x 1 .
Процедура Часть A Сначала удалите x 1 .
Шаг 1 Умножение первое уравнение на 2 и вычтите второе уравнение из первого уравнение.Это дает
4x 1 + 10x 2 + 14x 3 = 4 первое уравнение
4x 1 — 4x 2 — 3x 3 = 7 второе уравнение
14x 2 + 17x 3 = -3 второе уравнение вычитается из первого
Шаг 2 Умножение первое уравнение на 3, третье уравнение умножьте на 2 и вычтите третье уравнение из первого уравнения.Это дает
6x 1 + 15x 2 + 21x 3 = 6 первое уравнение
6x 1 — 6x 2 — 4x 3 = 10 третье уравнение
21x 2 + 25x 3 = -4 третье уравнение вычитается из первого
Процедура, часть B Второе удаление x 2 .
Из Части А осталось два уравнения. Из этих двух уравнений исключить
x 2 .
14x 2 + 17x 3 = -3 первое уравнение
21x 2 + 25x 3 = -4 второе уравнение
Шаг 1 Умножение первое уравнение на 21, второе уравнение умножьте на 14. и вычтите второе уравнение из первого уравнения.Это дает
294x 2 + 357x 3 = -63 первое уравнение
294x 2 + 350x 3 = -56 второе уравнение
7x 3 = -7 второе уравнение вычитается из первого
x 3 = -1
Часть C Решите относительно x 2 , вставив значение, полученное для x 3 в любое уравнение из части B.
14x 2 + 17 (-1) = -3
1 4x 2 = 14
х 2 = 1 или
21x 2 + 25 (-1) = -4
21x 2 = 21
х 2 = 1
Часть D
Решите относительно x 1 , вставив полученные значения x 2 andx 3 в любом из трех исходных уравнений.
2x 1 + 5x 2 + 7x 3 = 2 первое исходное уравнение
2x 1 + 5 (1) + 7 (-1) = 2
2x 1 = 4
x 1 = 2 или
4x 1 — 4x 2 — 3x 3 = 7 секунд исходное уравнение
4x 1 — 4 (1) — 3 (-1) = 7
4x 1 = 8
х 1 = 2 или же
3x 1 — 3x 2 — 2x 3 = 5 третье исходное уравнение
3x 1 — 3 (1) -2 (-1) = 5
3x 1 = 6
х 1 = 2
Метод замещения
Это включает выражение одной переменной через другую, пока не будет
одно уравнение с одним неизвестным.Затем это уравнение решается для этого
один неизвестный. Затем результат используется для поиска переменной, которая была
выражается через переменную, решение которой было только что найдено.
Пример
12x — 7лет = 106 первое уравнение
8x + У = 82 второе уравнение
Решите второе уравнение для y, а затем подставьте полученное значение y в первое уравнение.
г = 82 — 8x второе уравнение, решенное относительно y
12x — 7 (82 — 8х) = 106 первое уравнение переписано в x
12x — 574 + 56x = 106
68x = 680
х = 10
Подставьте полученное значение x в любое из исходных эквивалентов.
12x — 7лет = 106 первое уравнение
12 (10) — 7лет = 106
7лет = 14
г = 2
8 (10) + У = 82 второе уравнение
г = 2
[индекс]
линейных функций
линейных функций Линейная функция популярна в экономике.Это привлекательно, потому что это
просто и легко обрабатывать математически. У него много важных приложений.
Линейные функции — это функции, график которых представляет собой прямую линию.
Линейная функция имеет следующий вид
y = f (x) = a + bx
Линейная функция имеет одну независимую переменную и одну зависимую переменную. Независимая переменная — это x, а зависимая переменная — это y.
a — постоянный член или точка пересечения по оси y.Это ценность зависимого переменная при x = 0.
b — коэффициент независимой переменной. Он также известен как наклон и дает скорость изменения зависимой переменной.
Построение линейной функцииЧтобы построить график линейной функции:
1. Найдите 2 точки, которые удовлетворяют уравнению
2. Участок
3. Соедините точки прямой линией
Пример:
y = 25 + 5x
пусть x = 1
, тогда
y = 25 + 5 (1) = 30пусть x = 3
, тогда
y = 25 + 5 (3) = 40
Простой пример линейного уравнения
Компания имеет постоянные затраты на установку и оборудование в размере 7000 долларов США, а также переменные
стоимость 600 долларов за каждую единицу продукции.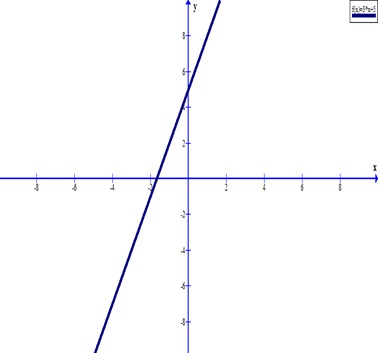
Какова общая стоимость при различных уровнях выпуска?
пусть x = единицы продукции
пусть C = общая стоимость
C = постоянные затраты плюс переменные затраты = 7000 + 600 x
| выход | Итого |
| 15 шт. | C = 7000 + 15 (600) = 16000 |
| 30 шт. | C = 7000 + 30 (600) = 25000 |
Линейные уравнения можно складывать, умножать или делить.
Простой пример сложения линейных уравнений
C (x) — функция стоимости
C (x) = фиксированные затраты + переменные затраты
R (x) — функция дохода
R (x) = продажная цена (количество проданных единиц)
прибыль равна выручке за вычетом затрат
P (x) — функция прибыли
P (x) = R (x) — C (x)
x = количество произведенных и проданных единиц
Данные:
Компания получает 45 долларов за каждую проданную единицу продукции.
Имеет переменную стоимость
25 долларов США за единицу и фиксированная стоимость 1600 долларов США.
Какова его прибыль, если он продаст (а) 75 предметов, (б) 150 предметов и (в) 200 предметов?
R (x) = 45x С (х) = 1600 + 25x P (x) = 45x — (1600 + 25x) = 20x — 1600
| пусть x = 75 | P (75) = 20 (75) — 1600 = -100 а потеря |
| пусть x = 150 | П (150) = 20 (150) — 1600 = 1400 |
| пусть x = 200 | П (200) = 20 (200) — 1600 = 2400 |
[индекс]
алгебра колледжа — симметрия
В общих чертах, двумерный график считается симметричным относительно определенной линии, если часть графика на одной стороне линии является зеркальным отображением той части графика, которая по другую сторону линии.
Например, график ниже считается симметричным относительно оси y (линия x = 0), потому что четверть круга слева от оси y является зеркальным отображением четверти круга справа от оси y. ось. Фактически, если бы вы могли сложить эту страницу по оси Y, две четверти круга идеально совпали бы.
Нас интересуют четыре типа симметрии:
(1) симметрия относительно оси y
(2) симметрия относительно оси x
(3) симметрия относительно начала координат
(4) симметрия относительно линии y = x
Почему кого-то волнует симметрия?
Одна из причин заключается в том, что знание того, что график симметричен относительно линии, уменьшает объем работы, которую нужно сделать, чтобы описать кривую.Если вы пытаетесь описать, где на графике есть пик, впадина или разрыв, вам нужно будет исследовать только одну половину графика — другая половина графика (ее зеркальное отображение) будет просто дубликатом.
Это может быть особенно полезно, если вы работаете в трехмерном пространстве, как это делается в многомерном исчислении.
Есть несколько уровней понимания симметрии, которые мы собираемся развивать в этом классе:
(1) общее понимание концепции, чтобы вы могли взглянуть на двумерный график и составить мнение относительно его возможной симметрии (относительно оси y, оси x, начала координат или y = x)(2) пространственная перспектива, позволяющая нарисовать эскиз графика, который был бы симметричен данному графику
(3) способность проверить уравнение графика на симметрию, прежде чем вы когда-либо увидите график.Последний особенно полезен, когда мы переходим к трехмерным графам, и симметрию сложнее определить, глядя на фигуру.
Это чтение предназначено, чтобы помочь вам развить интуитивное понимание симметрии в основу тестов на симметрию, которые мы используем для уравнений.
Графическое представление симметрии
Взгляните на этот график из пяти точек.
Черная точка представляет исходную точку, а цветные точки демонстрируют четыре типа симметрии.
Черная и красная точки симметричны относительно оси y.
Черная и синяя точки симметричны относительно оси x.
Черная и зеленая точки симметричны относительно начала координат
Черная и розовая точки симметричны относительно y = x
Симметрия относительно оси Y
Посмотрите еще раз на черную и красную точки.Обратите внимание, что x-координаты являются аддитивно обратными друг другу. То есть, если b — координата x одной точки, то — b — координата x другой точки. Таким же образом мы проверяем уравнение кривой, чтобы убедиться, что кривая симметрична относительно оси y.
Проверка симметрии относительно оси Y: замените x на (-x). Упростите уравнение. Если полученное уравнение эквивалентно исходному уравнению, тогда график симметричен относительно оси y.
Пример: Используйте тест на симметрию относительно оси y, чтобы определить, симметричен ли график y — 5x 2 = 4 относительно оси y.
исходное уравнение: y — 5x 2 = 4тест: y — 5 (-x) 2 = 4
упростить: y — 5x 2 = 4
Заключение: Поскольку результирующее уравнение эквивалентно исходному уравнению, график симметричен относительно оси Y
Симметрия относительно оси x
Проверка на симметрию относительно оси x аналогична предыдущей проверке.Посмотрите еще раз на черные и синие точки. Обратите внимание, что теперь y-координаты аддитивно инвертируют друг друга. То есть, если c — координата y одной точки, то — c — координата y другой точки. Таким же образом мы проверяем уравнение кривой, чтобы убедиться, что кривая симметрична относительно оси x.
Проверка симметрии относительно оси x: замените y на (-y). Упростите уравнение. Если полученное уравнение эквивалентно исходному уравнению, тогда график симметричен относительно оси x.
Пример: Используйте тест на симметрию относительно оси x, чтобы определить, является ли график y — 5x 2 = 4 симметричным относительно оси x.
исходное уравнение: y — 5x 2 = 4тест: (-y) — 5x 2 = 4
упростить: — y — 5x 2 = 4
Заключение: Поскольку результирующее уравнение НЕ эквивалентно исходному уравнению, график НЕ является симметричным относительно оси x
Вот набросок кривой.Тот факт, что кривая симметрична z относительно оси y и НЕ симметрична относительно оси y, довольно очевиден.
Симметрия относительно начала координат
Тест на симметрию относительно начала координат также имеет сходство с предыдущими тестами. Посмотрите на черные и зеленые точки. Обе координаты x и y являются аддитивно обратными. То есть (b, c) и (-b, -c) симметричны относительно начала координат.
Вы можете думать о симметрии относительно начала координат как о отражении относительно оси y, а также оси x. Тест на симметрию относительно начала координат объединяет элементы из первых двух тестов.
Проверка симметрии относительно начала координат: замените y на (-y) И x на (-x). Упростите уравнение. Если полученное уравнение эквивалентно исходному уравнению, тогда график симметричен относительно начала координат.
Пример: Используйте тест на симметрию относительно начала координат, чтобы определить, симметричен ли график xy — 5x 2 = 4 относительно начала координат.
исходное уравнение: xy — 5x 2 = 4тест: (-x) (- y) — 5 (-x) 2 = 4
упростить: xy — 5x 2 = 4
Заключение: Поскольку результирующее уравнение эквивалентно исходному уравнению, график симметричен относительно начала координат.
Вот набросок кривой.
Мы должны сначала решить для y (в терминах x), чтобы использовать графический калькулятор.
На этот раз симметрию не так легко увидеть на эскизе.
Симметрия относительно прямой y = x
Для последней симметрии вернемся к черной и розовой точкам. В этом случае координаты x и y поменялись местами на . То есть (b, c) и (c, b) симметричны относительно прямой y = x. Большая часть нашей более поздней работы с этим типом симметрии будет связана с функциями.В этом случае нас будет интересовать создание уравнения, график которого симметричен (относительно y = x) с заданным графиком. Мы делаем это, меняя местами
x и y.Пример: Создайте уравнение графика, которое будет симметричным
(около y = x) с графиком y = x 3 ,для x> или = 0.исходное уравнение: y = x 3
новое уравнение: x = y 3
решить относительно y: y = x 1/3 , x> or = 0
Вот два графика.