Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
10.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
На экзамене 20 билетов, Андрей не выучил 1 из них.
Можно ли силу 8 Н разложить на две по 5 Н каждая? Можно ли ту же силу разложить на две по 9 Н?
Дан вектор m{1;2;2}.Найдите координаты единичного вектора е ,сонаправленного с вектором
Решено
В треугольнике ABC известно что AB=3 BC=8 AC=7. Найдите косинус (COS) угла ABC. Помогите пожалуйста с решением-очень очень нужно. Спасибо.
Помогите составить условия задачи, не решения, а условия. В школьный буфет привезли 36 кг яблок по 9 кг в каждом ящике, сколько ящиков привезли в буфет?
Пользуйтесь нашим приложением
Шаг за шагом Решение:
Шаг 1:
Шаг 2:
Вытягивая, как термины:
2.
1 Вытягиваем, как факторы:
-x 2 -2 2 . 6x — 5 = -1 • (x 2 + 6x + 5) 2,2 Факторинг x 2 + 6x + 5 Первый термин — x + 2 2 . Пыхая фактор, разделяя средний термин
Средний член равен +6x, его коэффициент равен 6 .
Последний член, «константа», равен +5
Шаг 1. Умножьте коэффициент первого члена на константу среднего члена, который равен 6 .
| -5 | + | -1 | = | -6 | |||||||||||||||||||
| -1 | + | -1 | + | + | + | 9000.
| -6 | ||||||
| 1 | + | 5 | = | 6 | Это |
Шаг -3: повторно с использованием Среднего, с использованием Среднего, с использованием средних факторов.
На шаге 2 выше, 1 и 5
x 2 + 1x + 5x + 5
Шаг-4: Складка первых 2 терминов, вытягивая, как факторы:
x • (x + 1)
Сбалоть последние 2 термина, вытягивание общих множителей :
5 • (x+1)
Шаг-5: Сложите четыре члена шага 4:
(x+5) • (x+1)
, что является желаемой факторизацией
Уравнение в конце шага 2:
(-х - 5) • (х + 1) = 0
Шаг 3 :
Теория – корни произведения:
3.1 Произведение нескольких членов равно нулю.
Если произведение двух или более слагаемых равно нулю, то хотя бы одно из слагаемых должно быть равно нулю.
Теперь мы будем решать каждый термин = 0 отдельно
Другими словами, мы собираемся решить столько уравнений, сколько членов в произведении
Любое решение термина = 0 также решает произведение = 0.
Решение единого переменного уравнения:
3.2 Решение: -x-5 = 0
Добавить 5 к обеим сторонам уравнения:
-x = 5
Умножение обеих сторон уравнения (-1): x = x = 5
.
-5
Решение уравнения с одной переменной:
3.3 Solve : x+1 = 0
Subtract 1 from both sides of the equation :
x = -1
Supplement : Solving Quadratic Equation Directly
Solving x 2 +6x+5 = 0 directly
Ранее мы разложили этот полином на множители, разделив средний член. давайте теперь решим уравнение, заполнив квадрат и используя квадратную формулу
парабола, найдя вершину:
4.1 найдите вершину y = x 2 +6x+5
Параболы имеют самую высокую или самую низкую точку, называемую вершиной. Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум). Мы знаем это еще до того, как начертили «у», потому что коэффициент первого члена, 1 , положителен (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух точек пересечения x (корней или решений) параболы.
То есть, если парабола действительно имеет два действительных решения.
Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх через некоторый период времени. Вершина параболы может предоставить нам такую информацию, как максимальная высота, на которую может подняться объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы, Ax 2 +Bx+C, x-координата вершины определяется как -B/(2A) . В нашем случае координата x равна -3,0000
Подставив в формулу параболы -3,0000 вместо x, мы можем вычислить координату y:
y = 1,0 * -3,00 * -3,00 + 6,0 * -3,00 + 5,0
или y = -4,000
Графики Vertex и X -Пересечения:
Корневой график для: y = x 2 +6x+5
Ось симметрии (пунктирная) {x}={-3,00}
Вершина в {x,y} = {-3,00,-4,00}
x -Пересечения (корни):
Корень 1 в точке {x,y} = {-5,00, 0,00}
Корень 2 в точке {x,y} = {-1,00, 0,00}
Решить квадратное уравнение, заполнив квадрат
4.
2 Решение x 2 +6x+5 = 0, заполнив квадрат.
Вычтите 5 из обеих частей уравнения:
x 2 +6x = -5
Теперь немного хитрости: возьмите коэффициент x , равный 6 , разделите на два, получите 3, и, наконец, возведите его в квадрат, получив 9
Добавьте 9 к обеим частям уравнения:
В правой части имеем:
-5 + 9 или, (-5/1)+(9/1)
Общий знаменатель двух дробей равен 1. Сложение (-5/1)+(9/1) дает 4/1
Таким образом, складывая обе части, мы окончательно получаем:
x 2 +6x+9 = 4
Добавление 9 завершило левую часть в полный квадрат:
x 2 +6x+9 =
(x+3)• (x+3) =
(x+3) 2
Вещи, которые равны к одному и тому же и равны друг другу. Поскольку
x 2 +6x+9 = 4 и
x 2 +6x+9 = (x+3) 2
тогда, согласно закону транзитивности,
(x+3) 2 = 4
#4.2.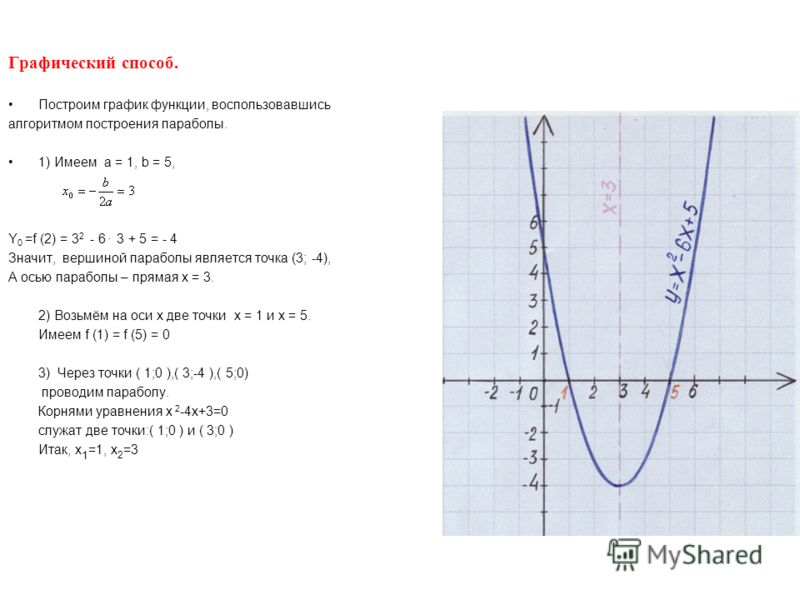
1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(x+3) 2 равен
(x+3) 2/2 =
(x+3) 1 = x+9 Принцип квадратного корня в уравнении #4.2.1 получаем:
x+3 = √ 4
Вычтем 3 с обеих сторон, чтобы получить:
x = -3 + √ 4
Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное
x 2 + 6x + 5 = 0
имеет два решения:
x = -3 + √ 4
или
x = -3 — √ 4
Решить квадратное уравнение с помощью квадратичной формулы
Согласно квадратичной формуле, x , решение для Ax 2 +bx +c = 0, где A, B и C являются числами, часто называемыми коэффициентами, определяется:
-B ± √ B 2 -4AC
x = ————————————————————————————————————————————————————————————— ——
2A
В нашем случае A = 1
B = 6
C = 5
Соответственно, B 2 — 4AC =
36 — 20 =
16
Применение формулы квадрата:
-6 ± √ 16
x = —————
2
Можно ли упростить 6 √?
Да! Разложение числа 16 на простые множители равно
2•2•2•2
Чтобы иметь возможность удалить что-то из-под корня, должно быть 2 этих экземпляра (потому что мы берем квадрат, т.