График функции y 2x в квадрате рисунок: как построить график функции y 2x в квадрате

Работа № 4. Вариант 2. № 4. ГДЗ Алгебра 9 класс Кузнецова. Помогите выяснить, проходит ли график через точку – Рамблер/класс

Работа № 4. Вариант 2. № 4. ГДЗ Алгебра 9 класс Кузнецова. Помогите выяснить, проходит ли график через точку – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

а) Постройте график функции у = 2х — 4.

б) Проходит ли график через точку В(-45; -86)?
 

ответы

a) y = 2x — 4.
График — прямая.
 
б)   B (-45; -86).
y(-45) = 2 ∙ (-45) — 4 = -90 — 4 = -94; -94 ≠ -86.
Равенство неверно, т. о. точка В не принадлежит графику.
 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

ЕГЭ

10 класс

11 класс

Химия

похожие вопросы 5

Напишите гдз по алгебре Мордкович 7 класс! Надо решить №32.20!

Решите уравнение:
●32.20.    а) х2 — 3x + 2 = 0;          в) х2 — 6x + 8 = 0;
б) x2 + 8х + 15 = 0;                      г) x2 (Подробнее…)

ГДЗАлгебраМордкович А.Г.7 класс

Будет ли введено устное собеседование по русскому языку на ГИА?

Подскажите, будет ли введено устное собеседование по русскому языку на ГИА? Как это будет проходить? (Подробнее. ..)

НовостиГИАЭкзамены9 классРусский язык

3. Вычислите… 6 класс А.П. Ершова Математика. К 2. Вариант А 1

3.
Вычислите: (Подробнее…)

ГДЗМатематика6 классЕршова А.П.

Радиус основания цилиндра равен 2. В этот цилиндр наклонно к оси вписан квадрат со стороной 4 так, что все вершины его находятся на окружностях осн

Радиус основания цилиндра равен 2. В этот цилиндр наклонно к оси вписан квадрат со стороной 4 так, что все вершины его находятся на (Подробнее…)

ВыпускнойЕГЭГДЗ

Помогите упростить № 443 ГДЗ Математика 6 класс Никольский С.М.

Упростите запись по образцу (Подробнее…)

ГДЗМатематика6 классНикольский С.М.

Написать уравнение линейной функции по графику прямой | Колледж Алгебра |

Графики линейных функций

Напомним, что в разделе «Линейные функции» мы написали уравнение для линейной функции по графику. Теперь мы можем расширить наши знания о построении графиков линейных функций для более тщательного анализа графиков. Начните с рассмотрения рисунка 8. Мы сразу видим, что график пересекает ось y в точке (0, 4), так что это y -перехват.

Рисунок 8

Затем мы можем рассчитать наклон, найдя подъем и уклон. Мы можем выбрать любые две точки, но давайте посмотрим на точку (-2, 0). Чтобы добраться от этой точки до перехвата y- , мы должны продвинуться на 4 единицы вверх (подъем) и вправо на 2 единицы (бег). Таким образом, наклон должен быть

м=подъем=42=2м=\frac{\text{подъем}}{\text{прогон}}=\frac{4}{2}=2\\m=подъем=24=2

Подстановка наклона и пересечения y- в форму пересечения наклона линии дает

у=2х+4у=2х+4\\у=2х+4

Как: Имея график линейной функции, найдите уравнение, описывающее эту функцию.

1. Определите точку пересечения y- уравнения.
2. Выберите две точки для определения уклона.
3. Замените точку пересечения y- и наклон в форму линии с пересечением наклона.

Пример 4. Сопоставление линейных функций с их графиками

Сопоставьте каждое уравнение линейных функций с одной из линий на рисунке 9.

1. f(x)=2x+3f\влево(x\вправо)=2x+3\\f(x)=2x+3

2. g(x)=2x−3g\left(x\right)=2x — 3\\g(x)=2x−3

3. h(x)=−2x+3h\left(x\right)=-2x+3\\h(x)=−2x+3

4. j(x)=12x+3j\left(x\right)=\frac{1}{2}x+3\\j(x)=21​x+3

Рисунок 9

Решение

Проанализируйте информацию для каждой функции.

1. Эта функция имеет наклон 2 и y — точка пересечения 3. Она должна проходить через точку (0, 3) и наклоняться вверх слева направо. Мы можем использовать две точки, чтобы найти наклон, или мы можем сравнить его с другими перечисленными функциями. Функция g  имеет тот же наклон, но другую точку пересечения y-. Линии I и III имеют одинаковый наклон, потому что они имеют одинаковый наклон. Строка III не проходит через (0, 3), поэтому f должна быть представлена ​​линией I.
2. Эта функция также имеет наклон 2, но y
   — пересечение –3. Он должен проходить через точку (0, –3) и наклоняться вверх слева направо. Он должен быть представлен линией III.
3. Эта функция имеет наклон –2 и точку пересечения y-, равную 3. Это единственная функция, указанная с отрицательным наклоном, поэтому она должна быть представлена ​​линией IV, поскольку она наклонена вниз слева направо.
4. Эта функция имеет наклон

   12\frac{1}{2}\\21​

   и точку пересечения y- 3. Она должна проходить через точку (0, 3) и наклоняться вверх слева направо . Линии I и II проходят через (0, 3), но наклон j меньше наклона f , поэтому линия для j должна быть более плоской. Эта функция представлена ​​линией II.

Теперь мы можем перемаркировать линии, как показано на рисунке 10.

Рисунок 10

Нахождение пересечения линии размером x

До сих пор мы находили точки пересечения y- функции: точки, в которых график функции пересекает ось y . Функция также может иметь x — точка пересечения, — координата x точки пересечения графика функции с осью x . Другими словами, это входное значение, когда выходное значение равно нулю.

Чтобы найти точку пересечения x , установите функцию f ( x ) равной нулю и найдите значение x . Например, рассмотрим показанную функцию.

f(x)=3x−6f\влево(x\вправо)=3x — 6\\f(x)=3x−6

Установить функцию равной 0 и найти x .

{0=3x−66=3×2=xx=2\begin{cases}0=3x — 6\qquad \\ 6=3x\qquad \\ 2=x\qquad \\ x=2\qquad \end{cases }\\⎩

⎨

⎧​0=3x−66=3×2=xx=2​

График функции пересекает ось x в точке (2, 0).

Вопросы и ответы

Все ли линейные функции имеют x точек пересечения?

Нет. Однако линейные функции вида y  = c , где c — ненулевое действительное число, являются единственными примерами линейных функций без пересечения x .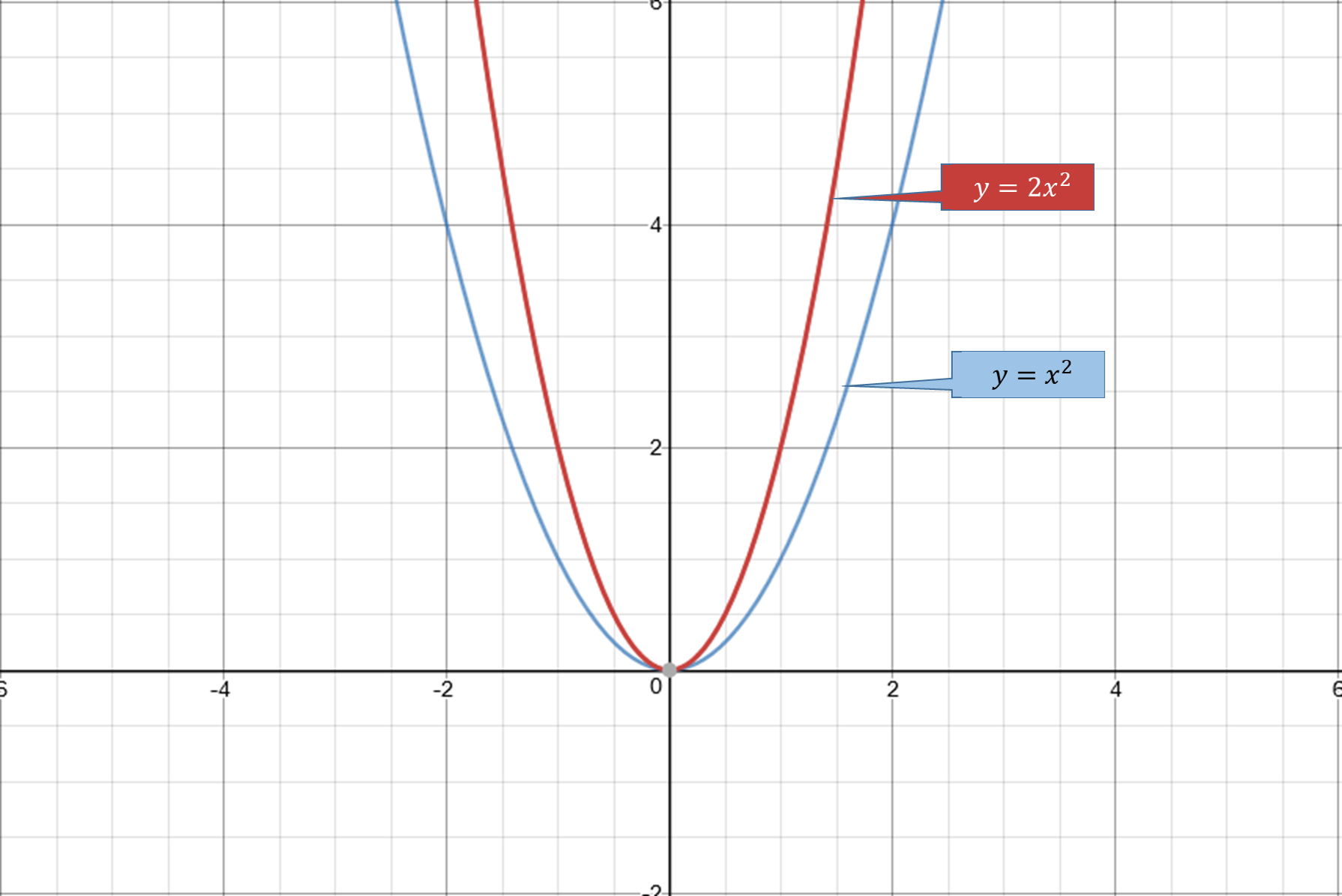 Например,

y = 5 — это горизонтальная линия, расположенная на 5 единиц выше оси x . Эта функция не имеет x -перехватов .

Рисунок 11

A Общее примечание:

x — точка пересечения

78 ф ( x ) = 0. Его можно решить с помощью уравнения 0 = m x + b .

Пример 5: Нахождение точки пересечения

x

Нахождение точки пересечения x

f(x)=12x−3f\left(x\right)=\frac{1}{2}x — 3 \\f(x)=21​x−3

.

Решение

Установите функцию равной нулю для решения x .

{0=12x−33=12×6=xx=6\begin{case}0=\frac{1}{2}x — 3\\ 3=\frac{1}{2}x\\ 6=x \\ х=6\конец{случаи}\\⎩

⎨

⎧​0=21​x−33=21​x6=xx=6​

График пересекает ось x в точке (6, 0).

Рис. 12.  График линейной функции

f(x)=12x−3f\left(x\right)=\frac{1}{2}x — 3\\f(x)=21​ х-3

.

Попробуйте 4

Найдите точку пересечения x

f(x)=14x−4f\left(x\right)=\frac{1}{4}x — 4\\f(x) =41​x−4

. Решение

Описание горизонтальных и вертикальных линий

Есть два особых случая линий на графике — горизонтальные и вертикальные линии. Горизонтальная линия указывает постоянный выход или y -значение. На рисунке 13 мы видим, что выход имеет значение 2 для каждого входного значения. Таким образом, изменение объема производства между любыми двумя точками равно 0. В формуле наклона числитель равен 0, поэтому наклон равен 0. Если мы используем m  = 0 в уравнении

f(x)=mx+bf \left(x\right)=mx+b\\f(x)=mx+b

, уравнение упрощается до

f(x)=bf\left(x\right)=b\\f(x)=b

. Другими словами, значение функции является константой. Этот график представляет функцию

f(x)=2f\left(x\right)=2\\f(x)=2

.

Рис. 13.  Горизонтальная линия, представляющая функцию

f(x)=2f\left(x\right)=2\\f(x)=2

.

Рисунок 14

Вертикальная линия указывает на постоянное значение или значение x . Мы видим, что входное значение для каждой точки на линии равно 2, но выходное значение меняется. Поскольку это входное значение сопоставляется более чем с одним выходным значением, вертикальная линия не представляет функцию. Обратите внимание, что между любыми двумя точками изменение входных значений равно нулю. В формуле наклона знаменатель будет равен нулю, поэтому наклон вертикальной линии не определен.

Обратите внимание, что вертикальная линия, такая как на рис. 15 , , имеет точку пересечения x , но не имеет точки пересечения y-, если это не линия x = 0. Этот график представляет линию x = 2.

Рис. 15. Вертикальная линия x = 2, которая не представляет функцию.

A Общее примечание: горизонтальные и вертикальные линии

Линии могут быть горизонтальными или вертикальными.

A горизонтальная линия — это линия, заданная уравнением вида

f(x)=bf\left(x\right)=b\\f(x)=b

.

Вертикальная линия — это линия, заданная уравнением вида

x=ax=a\\x=a

.

Пример 6. Написание уравнения горизонтальной линии

Напишите уравнение линии, изображенной на рисунке 16. Рис. 160078 г = –4.

Пример 7. Написание уравнения вертикальной линии

Напишите уравнение линии, изображенной на рисунке 17.

Рисунок 17

Раствор

Константа x -значение равно 7, поэтому уравнение x = 7.

Лицензии и атрибуты

Контент по лицензии CC, совместно используемый ранее

• Precalculus. Автор : Джей Абрамсон и др. Предоставлено : ОпенСтакс. Расположен по адресу : https://openstax.org/books/precalculus/pages/1-introduction-to-functions. Лицензия : CC BY: Attribution . Условия лицензии.

  Привет Меня зовут Женева, и у меня возникли проблемы с графическим отображением уравнений типа y=2x+1, что является моей домашней работой. Я не знаю, как это сделать. Я учусь в 8 классе, изучаю курс алгебры 9 класса I. Спасибо   Привет Женева, Иногда, особенно после небольшого опыта, вы можете сказать по «форме» уравнения, какова «форма» графика. Если вы можете определить форму, это упрощает построение графика, но сейчас давайте просто попробуем построить его, не зная формы заранее. Для этого я буду использовать таблицу значений. Я собираюсь выбрать некоторые значения для переменной x, вычислить соответствующее значение y и затем записать свои результаты в таблицу. Так, например, когда x = 1, то y = 2 1 + 1 = 3, а когда x = 2, то y = y = 2 2 + 1 = 5. Вот моя таблица, включающая эти два значения x и еще несколько. х и 1 3 2 5 3 7 0 1 -1 -1 -2 -3 Теперь я нанес эти точки на свой график. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт