Найдите вероятность того что случайно выбранное целое число из первого миллиона: Национальный исследовательский университет «Высшая школа экономики»

Вычисление вероятности — Умскул Учебник

На этой странице вы узнаете

• Как кот может быть одновременно жив и мертв? 
• Можно ли всегда выигрывать спор с монеткой? 
• Если рандомно ответить на вопрос теста, какой шанс угадать ответ?

Какова вероятность выиграть в лотерею? Исследователи подсчитали: один на восемь миллионов. «Или выиграю, или проиграю», — решаю я, покупая лотерейный билет. Так понятие вероятности преследует нас в обычной жизни. И не только в лотерее. Давайте разберемся подробнее.

Вероятность

Выходя утром из дома, мы задумываемся: брать ли с собой зонт? Проверяем прогноз погоды — вероятность выпадения осадков 2%. Зонтик нам сегодня вряд ли понадобится. В пути нас настигает ливень…

Прогноз погоды — самый яркий пример вероятности. Он не всегда бывает точный, не всегда сбывается. Мы не можем с уверенностью сказать, что будет завтра. Зато можем по совокупности факторов определить, на какую погоду стоит ориентироваться.  

Теория вероятности — один из разделов математики, в котором изучаются модели случайных экспериментов. 

Случайными экспериментами называются такие, результаты которых неизвестны заранее. Подбрасывая монетку, мы не знаем, что выпадет — орел или решка. Только поймав монетку, мы узнаем результат. 

Как кот может быть одновременно жив и мертв?  Ученый по имени Эрвин Шредингер провел мысленный эксперимент. Он поместил кота в закрытый ящик, в котором был расположен механизм, содержащий атомное ядро и ёмкость с ядовитым газом.  По эксперименту с вероятностью 0,5 ядро распадется, емкость с газом откроется и кот умрет. Но при этом с вероятностью 0,5 ядро не распадается и кот останется жив.  Пока ящик закрыт, мы не знаем результат эксперимента — такой эксперимент в математике можно назвать случайным.  Тем временем кот находится одновременно в двух состояниях: он и жив, и мертв.

Рассмотрим чуть подробнее пример с монеткой. Есть всего два варианта, какое событие может произойти:

• выпадет орел;
• выпадет решка. 

Эти два события образуют множество элементарных событий. 

Множество элементарных событий — множество всех возможных результатов случайного эксперимента. 

В случае выше их всего два. А если мы будем подбрасывать игральную кость, то их будет уже 6. Множество элементарных событий будет менять в зависимости от ситуации. 

Допустим, мы поспорили с друзьями, что выпадет орел. Для нас это событие будет благоприятным, поскольку мы выиграем спор. Второе событие будет неблагоприятным, потому что спор будет проигран. 

Как найти вероятность, что мы выиграем спор? Нужно разделить число благоприятных событий на общее число событий. Таким образом, мы получили классическое определение вероятности. 

Вероятность — отношение количества благоприятных событий к количеству всех возможных событий. 

Пусть m — количество благоприятных исходов, а n — количество всех событий. Получаем следующую формулу. 

\(P = \frac{m}{n}\)

Вероятность можно обозначить, как P(x), где х — некоторое событие. 

Заметим, что количество благоприятных исходов должно быть либо меньше, либо равно количеству всех исходов. Если благоприятных событий больше, чем всех, значит, мы нашли не все множество элементарных событий.

Когда вероятность равна 1, то такое событие точно наступит. Иначе говоря, мы можем быть уверены на 100% — оно произойдет.

Можно ли всегда выигрывать спор с монеткой? Можно, если хитро сформулировать условия. Например: «Орел — я выиграл, решка — ты проиграл». Вероятность выигрыша в этом случае будет равна \(P = \frac{2}{2} = 1\), то есть мы точно выиграем спор.  Однако вероятность не так проста, и даже здесь подготовила ловушку.  В редких случаях есть и третий вариант событий — монетка встанет на ребро. Вероятность такого события составляет  \(\frac{1}{6000}\). То есть за миллион бросков это может случиться 150 раз или 1 раз в 2 дня, если подкидывать монету каждый день по 8 часов в течение года. Чтобы монета встала на ребро два раза подряд, придется подбрасывать ее в том же темпе около 35 лет.

Вероятность всегда будет меньше или равна 1. Но ее можно выразить и через проценты. Для этого достаточно умножить полученный результат на 100%. 

Пример 1. На ресепшене одного из отелей стоит ваза с конфетами. В вазе 56 яблочных конфет, 49 апельсиновых и 35 малиновых. Гость отеля наугад тянет конфету. Какова вероятность, что ему попадется апельсиновая конфета?

Решение. Найдем, сколько всего конфет в вазе: 56 + 49 + 35 = 140. Вероятность вытащить апельсиновую конфету будет равна 
\(\frac{49}{140} = 0,35\)

Выразим в процентах:  
0,35 * 100% = 35%

Задача решена. Обычно в ответе пишут значение вероятности через дробное число, а не проценты. Поэтому получаем следующий ответ.  

Ответ: 0,35

Чтобы выразить вероятность через проценты в одно действие, достаточно воспользоваться следующей формулой. 

\(P = \frac{m}{n} * 100%\)

Но что, если нам нужно найти вероятность для более сложных экспериментов? Первым делом нужно определить, какие события перед нами.

Равновозможные и противоположные события

Когда мы бросаем игральную кость, вероятность выпадения любого из чисел равна 16. То есть вероятности выпадения чисел равны между собой. Такие события называются равновозможными. 

Равновозможные события — такие события, что по условиям опыта ни одно из них не является более возможным, чем другие. 

Вероятности появления событий равны. 

Для игрального кубика существует всего шесть событий, которые могут произойти: выпадет число 1, 2, 3, 4, 5 или 6. Все эти события образуют полную группу событий. 

Полная группа событий — такая группа событий, если в результате опыта обязательно появится хотя бы одно из них.  

В результате подбрасывания монеты выпадет либо орел, либо решка. То есть полная группа событий состоит из двух событий. 

Мы подбросили монету и выпал орел. Следовательно, не выпала решка. 

А если не выпадет орел? Обязательно выпадет решка. Эти события будут называться противоположными. 

Противоположные события — такие события, если при не наступлении одного обязательно наступает второе. 

Обозначим событие “выпала решка” как A. Противоположное ему событие “выпал орел” обозначим как \(\overline{A}\). 

Заметим, что вероятность события A равняется 12, как и вероятность события \(\overline{A}\). Чему равна их сумма?

\)\frac{1}{2} + \frac{1}{2} = 1\) 

Так мы вывели связь между противоположными событиями. Поскольку они всегда образуют полную группу событий, то сумма их вероятностей будет равна 1. 

\(P(A) + P(\overline{A}) = 1\)

Какие еще примеры противоположных событий можно назвать? Ясная и дождливая погода. Если наступает одно из этих событий, то второе уже не может наступить. 

Объединение и пересечение событий 

Допустим, у нас есть два события: сегодня пойдет снег и сегодня пойдет дождь. Что будет, если мы их объединим? 

Объединение событий — событие, состоящее из всех элементарных исходов, благоприятствующих хотя бы одному из событий. 

В этом случае мы получим событие, которое будет выполняться при любом из исходов: и если пойдет снег, и если не пойдет снег. 

Объединение событий обозначается знаком \(\cup\). Объединение событий А и В можно записать как \(A \cup B\). 

Рассмотрим немного другой пример. В первое событие входит, что Илья получит пятерку по физике, а второе событие — Антон получит пятерку по физике. А как можно назвать событие, если оба мальчика получат пятерку по физике?

Пересечение событий — событие, состоящее из всех элементарных исходов, благоприятствующих обоим событиям. 

Пересечение событий обозначается знаком \(\cap\). Пересечение событий А и В можно записать как \(A \cap B\). 

Несовместные и совместные события

Рассмотрим два события: “чайник исправно работает” и “чайник сломался”. Могут ли эти события существовать одновременно? Нет, поскольку появление одного из них исключает появление другого.

Такие события называются несовместными. Название само говорит, что события не могут существовать одновременно. 

Несовместные события — такие события, появление одного из которых исключает появление другого. 

Решим небольшую задачу. На экзамене есть несколько билетов. С вероятностью 0,5 попадется билет по планиметрии. С вероятностью 0,3 попадется билет по экономике. При этом не существует билетов, которые включают обе эти темы. С какой вероятностью на контрольной попадется билет по одной из этих тем?

Представим билеты в виде схемы. Заметим, что нам нужно объединить два из трех кругов, то есть сложить их вероятности.  

Следовательно, вероятность будет равна 0,5 + 0,3 = 0,8.

Сформулируем определение суммы вероятностей двух несовместных событий. 

Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей:

\(P(A \cup B) = P(A) + P(B)\)

Если существуют несовместные события, то существуют и совместные. 

Совместные события — события, наступление одного из которых не исключает наступления другого. 

В магазине работают два консультанта. Один из них занят общением с клиентом. Означает ли это, что второй консультант тоже занят?  Нет, поскольку они работают независимо друг от друга. Если занят первый консультант, второй может быть как занят, так и нет. 

Подбросим игральный кубик и рассмотрим два вида событий. Пусть событие А — это “выпадет число 2”, событие В — “выпадет четное число”. 

Найдем вероятность события А: \(\frac{1}{6}\). 

Для события В всего три благоприятных исхода из шести: выпадет число 2, 4 или 6. Тогда вероятность наступления события В равна \(\frac{3}{6} = \frac{1}{2}\)

Исключают ли события А и В друг друга? Нет, поскольку если произойдет событие А, произойдет и событие В. Когда произойдет событие В, есть вероятность, что произойдет и событие А. 

Найдем объединение совместных событий на примере кругов. Если мы наложим их друг на друга, то в середине получится как бы два слоя. Проверить это можно, если наложить друг на друга два листа бумаги. 

А нужно получить вот такую картину:

Поэтому для объединения двух кругов нам нужно будет исключить одну из серединок. 

Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения:

\(P(A \cup B) = P(A) + P(B) — P(A \cap B)\)

В каких случаях нужно пользоваться формулой со сложением? Достаточно, чтобы задачу можно было сформулировать с помощью “или”. Например, нужно, чтобы выпали темы по планиметрии или по экономике.  

Независимые и зависимые события 

Прогуляемся в магазин за булочками. В упаковке две булочки, а сама упаковка непрозрачная, то есть увидеть булочки до вскрытия упаковки мы не можем. 

Известно, что на заводе, где изготавливаются булочки, 5 из 100 булочек подгорают. Значит, 95 из 100 булочек не подгорают. По классическому определению вероятности находим, что вероятность каждой булочки не подгореть равна \(\frac{95}{100} = 0,95\). 

Какова вероятность, что в упаковке попадутся только не подгорелые булочки? Как найти вероятность сразу для двух булочек?

Ответим на вопрос: зависят ли булочки друг от друга? 

Если подгорит одна из булочек в упаковке, не обязательно подгорит другая. Следовательно, булочки не зависят друг от друга. Такие события называются независимыми. 

Независимые события — такие события, появление одного из которых не зависит от появления другого события.  

Определим вероятность независимых событий. 

Пусть вероятность, что подгорела первая булочка, будет равна Р(А) = 0,95, а вероятность для второй булочки будет равна Р(В) = 0,95. 

А чтобы найти вероятность независимых событий, нужно воспользоваться следующей формулой:

\(P(A \cap B) = P(A) * P(B)\)

Тогда вероятность, что булочки в одной упаковке не подгорят, равняется P = 0,95 * 0,95 = 0,9025. 

В каком случае нужно пользоваться этой формулой? Нужно подставить союз “и”. 

Мы хотим, чтобы в упаковке первая булочка была не подгорелой и вторая булочка была не подгорелой. 

Приведем еще один пример. В здании два автомата с кофе на разных этажах. Даже если сломается один из них, работа второго не будет зависеть от первого. 

Но если автоматы стоят  рядом и включены в одну розетку, то при поломке одного из них есть вероятность выхода из строя розетки, а значит, и второй автомат тоже сломается. Такие события будут зависимыми: появление одного из них зависит от появления другого.  

Предположим, что в мешке лежит семь кубиков: два из них оранжевые, а пять — фиолетовые. Из мешка дважды вытаскивают кубики. Какова вероятность, достать во второй раз именно фиолетовый кубик?

Нужная последовательность может быть в двух случаях:

• сначала вытащат фиолетовый кубик и потом снова фиолетовый;
• сначала вытащат оранжевый кубик, а потом фиолетовый. 

Разберем первый случай. Вероятность в первый раз вытащить фиолетовый кубик равна \(\frac{5}{7}\). После этого в мешке останется шесть кубиков, четыре из которых будут фиолетовые. 

Вероятность вытащить во второй раз фиолетовый кубик равна \(\frac{5}{7} * \frac{4}{6} = \frac{20}{42} = \frac{10}{21}\). 

Теперь рассмотрим второй случай. Вероятность в первый раз достать оранжевый кубик равна \(\frac{2}{7}\). В мешке останется шесть кубиков, пять из которых будут фиолетовыми. 

Вероятность вытащить во второй раз фиолетовый кубик будет уже равна \(\frac{2}{7} * \frac{5}{6} = \frac{10}{42} = \frac{5}{21}\).  

В этом примере очень наглядно видно, что вероятность напрямую зависит от того, какой кубик попался первым. Следовательно, эти события зависимы. 

Как отличить зависимые и независимые события? Если после наступления первого события меняется количество благоприятных и всех исходов, то такие события — зависимые. Если количество благоприятных и всех исходов не меняется, то события независимые.

Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А. 

Условная вероятность обозначается P(B|A). В нашем примере условной вероятностью будет вычисление, что во второй раз попадется именно фиолетовый кубик.   

Найдем вероятность двух зависимых событий. Формула похожа на ту, что используется для независимых событий. Но в этот раз нам нужно применить условную вероятность. 

Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило:

\(P(A \cap B) = P(A) * P(B | A)\)

Формула Бернулли

Рассмотрим случаи, когда испытание повторяется многократно. 8} \approx 0,1\) 

Фактчек

• Вероятность — отношение количества благоприятных событий к количеству всех возможных событий. 
• События могут быть противоположными. Противоположные события — такие события, если при не наступлении одного обязательно наступает второе. 
• События можно разделить на совместные и несовместные. Несовместные события — такие события, появление одного из которых исключает появление другого. Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей: P(A \(\cup) B) = P(A) + P(B). Совместные события — события, наступление одного из которых не исключает наступления другого. Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения: P(A \cup B) = P(A) + P(B) — P(A \cap B).
• События также можно разделить на независимые и зависимые. Независимые события — такие события, появление одного из которых не зависит от появления другого события. Вероятность независимых событий можно найти по формуле P(A \cap B) = P(A) * P(B). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. P(A \cap B) = P(A) * P(B | A). 
• Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А. 

Проверь себя

Задание 1. 
Какие события являются несовместными?

1. Подбрасывание монетки.
2. Брак батареек в одной упаковке.
3. “Миша идет” и “Миша стоит”.
4. Случайное вытаскивание конфет из вазы. 

Задание 2. 
Алена делает ошибку при решении задач по математике с вероятностью 0,17. С какой вероятностью она не сделает ошибку при решении задачи?

1. 0,17
2. 1
3. 0,83
4. 1,17 

Задание 3.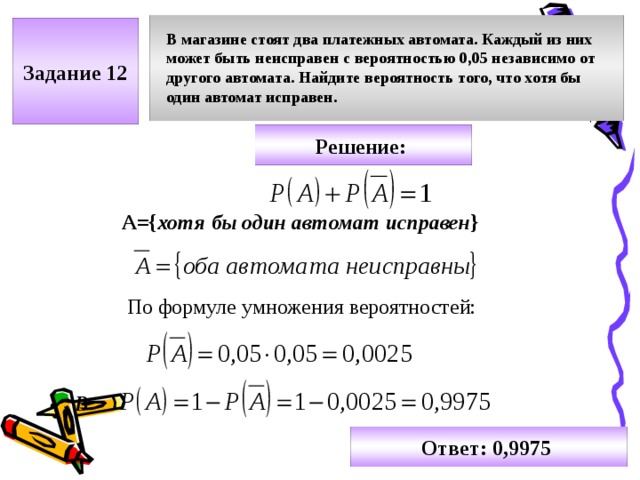  
Артем решал задачи на вероятность. Ниже приведены его ответы. В какой из задач он точно совершил ошибку?

1. 1
2. 0,216
3. 0,45
4. 1,5 

Задание 4. 
В упаковке три шариковые ручки. С вероятностью 0,1 такая ручка не будет писать. Найдите вероятность, что все три ручки в упаковке пишут. 

1. 0,3
2. 0,001
3. 2,7
4. 0,729 

Задание 5. 
Перед Дашей лежит несколько карточек. Она случайно переворачивает одну из них. С вероятностью 0,5 на карточке окажется рисунок природы. С вероятностью 0,27 на карточке окажется мотивационная цитата. Карточек и с рисунком, и с цитатой нет. Найдите вероятность, что Дана перевернет карточку или с рисунком, или с цитатой. 

1. 0,77
2. 0,135
3. 0,23
4. -0,23

Ответы: 1. — 3 2. — 3 3. — 4 4. — 4 5. — 1

Вероятность с использованием перестановок и комбинаций

Результаты обучения

• Вычисление условной вероятности события
• Используйте теорему Байе для вычисления условной вероятности
• Рассчитать ожидаемое значение события

Мы можем использовать перестановки и комбинации, чтобы помочь нам ответить на более сложные вопросы вероятности.

примеры

Выбран 4-значный PIN-код. Какова вероятность того, что нет повторяющихся цифр?

Показать решение

Попробуйте

Пример

В лотерее одного штата 48 шаров с номерами от 1 до 48 помещаются в автомат, и шесть из них вытягиваются случайным образом. Если шесть выпавших номеров совпадают с номерами, выбранными игроком, игрок выигрывает 1 000 000 долларов. В этой лотерее порядок выпадения номеров не имеет значения. Вычислите вероятность того, что вы выиграете приз в миллион долларов, если купите один лотерейный билет.

Показать решение

 

Пример

В лотерее штата из предыдущего примера, если пять из шести выпавших номеров совпадают с номерами, выбранными игроком, игрок выигрывает второй приз в размере 1000 долларов. Вычислите вероятность того, что вы выиграете второй приз, если купите один лотерейный билет.

Показать решение

Предыдущие примеры показаны в следующем видео.

примера

Вычислите вероятность случайного извлечения пяти карт из колоды и получения ровно одного туза.

Показать решение

Пример

Вычислите вероятность случайного извлечения пяти карт из колоды и получения ровно двух тузов.

Показать решение

Просмотрите следующее для дальнейшей демонстрации этих примеров.

Попробуйте

Давайте сделаем паузу, чтобы рассмотреть известную задачу теории вероятностей:

Предположим, у вас есть комната, полная 30 человек. Какова вероятность того, что есть хотя бы один общий день рождения?

Угадайте ответ на приведенную выше задачу. Было ли ваше предположение довольно низким, около 10%? Это кажется интуитивным ответом (возможно, 30/365?). Давайте посмотрим, стоит ли нам прислушиваться к своей интуиции. Однако начнем с более простой задачи.

пример

Предположим, в комнате находятся три человека. Какова вероятность того, что у этих трех человек есть хотя бы один общий день рождения?

Показать решение

---

Предположим, в комнате находятся пять человек. Какова вероятность того, что среди этих пяти человек есть хотя бы один общий день рождения?

Показать решение

---

Предположим, в комнате 30 человек. Какова вероятность того, что среди этих 30 человек есть хотя бы один общий день рождения?

Показать решение

Ниже подробно рассматривается проблема дня рождения.

Если вам нравится делать ставки, и если вы можете убедить 30 человек раскрыть свои дни рождения, вы можете выиграть немного денег, поспорив с другом, что в комнате будет по крайней мере два человека с одинаковым днем ​​​​рождения в любое время. вы находитесь в комнате на 30 и более человек. (Конечно, вам нужно убедиться, что ваш друг не изучал вероятность!) Вы не гарантированно выиграете, но вы должны выигрывать более чем в половине случаев.

Это один из многих противоречивых результатов теории вероятностей; то есть это идет вразрез с нашими внутренними инстинктами.

Попробуйте

Предположим, в комнате находятся 10 человек. Какова вероятность того, что среди этих 10 человек есть хотя бы один общий день рождения?

3.2.2 Вероятностная выборка

Содержание

Текст начинается

Тематическая навигация

• 3 Сбор и обработка данных
  • 3. 2 Отбор проб
    • 3.2.1 Отбор проб
    • 3.2.2 Вероятностная выборка
    • 3.2.3 Невероятностная выборка

Под вероятностной выборкой понимается отбор выборки из совокупности, когда этот отбор основан на принципе рандомизации, то есть случайного отбора или случайности. Вероятностная выборка более сложна, требует больше времени и обычно дороже, чем невероятностная выборка. Однако, поскольку единицы из совокупности выбираются случайным образом и можно рассчитать вероятность выбора каждой единицы, можно получить надежные оценки и сделать статистические выводы о совокупности.

Существует несколько различных способов выбора вероятностной выборки.

При выборе плана вероятностной выборки цель состоит в том, чтобы свести к минимуму ошибку выборки оценок наиболее важных переменных обследования, одновременно сводя к минимуму время и затраты на проведение обследования. Некоторые операционные ограничения также могут повлиять на этот выбор, например, характеристики инструментария обследования.

В данном разделе каждый из этих методов будет кратко описан и проиллюстрирован примерами.

Простая случайная выборка

В простой случайной выборке (SRS) каждая единица выборки совокупности имеет равные шансы быть включенной в выборку. Следовательно, каждая возможная выборка также имеет равные шансы быть отобранной. Чтобы выбрать простую случайную выборку, вам необходимо перечислить все единицы в генеральной совокупности обследования.

Пример 1

Чтобы взять простую случайную выборку из телефонной книги, каждая запись должна быть последовательно пронумерована. Если бы в телефонной книге было 10 000 записей и размер выборки составлял 2 000, то компьютер должен был бы случайным образом сгенерировать 2 000 номеров от 1 до 10 000. Все числа будут иметь одинаковые шансы быть сгенерированными компьютером. 2000 телефонных записей, соответствующих 2000 сгенерированным компьютером случайным числам, составили бы выборку.

SRS можно сделать с заменой или без. SRS с заменой означает, что существует вероятность того, что выбранная телефонная запись может быть выбрана дважды или более. Обычно подход SRS проводится без замены, поскольку он более удобен и дает более точные результаты. В остальной части текста

SRS будет использоваться для обозначения SRS без замены, если не указано иное.

СРС является наиболее часто используемым методом. Преимущество этого метода заключается в том, что он не требует никакой информации об инструментарии обследования, кроме полного списка единиц обследуемой совокупности вместе с контактной информацией. Кроме того, поскольку SRS является простым методом и его теория хорошо известна, существуют стандартные формулы для определения размера выборки, оценок и т. д., и эти формулы просты в использовании.

С другой стороны, этот метод требует списка всех единиц совокупности. Если такого списка еще не существует, а целевая аудитория велика, его создание может быть очень дорогим или нереалистичным. Если список уже существует и содержит вспомогательную информацию по объектам, то

SRS не использует информацию, позволяющую повысить эффективность других методов (например, стратифицированной выборки). Если сбор должен производиться лично, SRS может предоставить выборку, которая слишком распределена по нескольким регионам, что может увеличить затраты и продолжительность обследования.

Пример 2

Представьте, что у вас есть кинотеатр, и вы предлагаете специальный фестиваль фильмов ужасов в следующем месяце. Чтобы решить, какие фильмы ужасов показать, вы опрашиваете кинозрителей, какие из перечисленных фильмов им нравятся больше всего. Чтобы составить список фильмов, необходимых для вашего опроса, вы решаете выбрать 10 из 100 лучших фильмов ужасов всех времен.

Один из способов выбрать образец — написать все названия фильмов на листках бумаги и поместить их в пустую коробку. Затем нарисуйте 10 названий, и у вас будет образец. Используя этот подход, вы обеспечите равную вероятность выбора каждого фильма. Вы даже можете рассчитать эту вероятность выбора, разделив размер выборки (n=10) на размер совокупности 100 лучших фильмов ужасов всех времен (N=100). Эта вероятность будет равна 0,10 (10/100) или 1 из 10.

Систематическая выборка

Систематическая выборка означает наличие пробела или интервала между каждой выбранной единицей в выборке. Например, вы можете выполнить следующие действия:

1. Пронумеруйте единицы на вашем кадре от 1 до N (где N — это общая численность населения).
2. Определите интервал выборки ( K ), разделив количество единиц в совокупности на желаемый размер выборки. Например, чтобы выбрать выборку в 100 человек из совокупности в 400 человек, вам потребуется интервал выборки 400/100 = 4.
   Следовательно, K = 4. Вам нужно будет выбрать одну единицу из каждых четырех единиц, чтобы получить в общей сложности 100 единиц в вашей выборке.
3. Случайным образом выберите число от 1 до K . Это число называется , случайное начало , и это будет первое число, включенное в вашу выборку. Если вы выберете 3, третья единица на вашем кадре будет первой единицей, включенной в вашу выборку; если вы выберете 2, ваша выборка начнется со второго устройства на вашей раме.
4. Выберите каждые Kth (в данном случае, каждую четвертую) единицу после этого первого числа. Например, выборка может состоять из следующих единиц, чтобы составить выборку из 100: 3 (случайное начало), 7, 11, 15, 19 … 395, 399 (до N , что в данном случае равно 400). ).

В приведенном выше примере вы можете видеть, что можно выбрать только четыре возможных образца, соответствующих четырем возможным случайным стартам:

1, 5, 9, 13 … 393, 397

2, 6, 10, 14 … 394, 398

3, 7, 11, 15 … 395, 399

4, 8, 12, 16 … 396, 400

Каждый член населения принадлежит только к одному из четыре образца, и каждый образец имеет одинаковый шанс быть выбранным. Из этого мы видим, что каждая единица имеет один шанс из четырех быть выбранным в выборке. Это такая же вероятность, как если бы была выбрана простая случайная выборка из 100 единиц. Основное отличие состоит в том, что в случае SRS любая комбинация из 100 единиц может составить выборку, в то время как при систематической выборке имеется только четыре возможных выборки. Порядок единиц в кадре будет определять возможные выборки для систематической выборки. Если совокупность случайным образом распределена в основе, систематическая выборка должна давать результаты, аналогичные простой случайной выборке.

Этот метод часто используется в промышленности, где изделие выбирается для испытаний с производственной линии, чтобы гарантировать, что машины и оборудование имеют стандартное качество. Например, тестер на заводе-изготовителе может выполнять проверку качества каждого 20-го продукта на сборочной линии. Тестер может выбрать случайное начало между числами 1 и 20. Это определит первый тестируемый продукт; после этого каждый 20-й продукт будет протестирован.

Интервьюеры могут использовать этот метод выборки при опросе людей для выборочного обследования. Исследователь рынка может выбрать, например, каждого 10-го человека, который входит в конкретный магазин, после случайного выбора первого человека. Инспектор может опросить жителей каждого пятого дома на улице после случайного выбора одного из первых пяти домов.

Преимущества систематической выборки заключаются в том, что отбор выборки не может быть проще: вы получаете только одно случайное число, случайное начало, а остальная часть выборки следует автоматически. Самым большим недостатком метода систематической выборки является то, что если в способе размещения совокупности в списке есть какой-либо периодический признак, и этот периодический признак каким-то образом совпадает с интервалом выборки, возможные выборки могут не быть репрезентативными для совокупности. Это можно увидеть на следующем примере:

Пример 3

Предположим, вы управляете большим продуктовым магазином и у вас есть список сотрудников в каждом отделе. Продуктовый магазин разделен на следующие 10 секций: гастроном, пекарня, кассы, склад, мясной прилавок, продукты, аптека, фотосалон, цветочный магазин и химчистка. В каждой секции работает 10 сотрудников, включая менеджера (всего 100 сотрудников). Ваш список упорядочен по разделам, где сначала указан менеджер, а затем остальные сотрудники в порядке убывания старшинства.
Если вы хотите опросить своих сотрудников о том, что они думают об их рабочей среде, вы можете выбрать небольшую выборку, чтобы ответить на ваши вопросы. Если вы используете метод систематической выборки и ваш интервал выборки равен 10, вы можете выбрать только руководителей или только новых сотрудников в каждом разделе. Этот тип выборки не даст вам полной или адекватной картины мыслей ваших сотрудников.

Выборка с вероятностью, пропорциональной размеру

Вероятностная выборка требует, чтобы каждый член обследуемой совокупности имел известную вероятность включения в выборку, но не требует, чтобы эта вероятность была одинаковой для всех. Если в основе имеется информация о размере каждой единицы (например, количество работников для каждого предприятия) и если эти единицы различаются по размеру, эту информацию можно использовать при формировании выборки для повышения эффективности. Это известно как 9Выборка 0099 с вероятностью, пропорциональной размеру (PPS). При использовании этого метода чем больше размер единицы, тем выше вероятность ее включения в выборку. Для повышения эффективности этого метода необходимо, чтобы измерение размера было точным. Это более сложный метод выборки, который не будет подробно обсуждаться здесь.

Стратифицированная выборка

При использовании стратифицированной выборки совокупность делится на однородные взаимоисключающие группы, называемые стратами, а затем из каждой страты отбираются независимые выборки. Любой из методов выборки, упомянутых в этом разделе, может быть использован для выборки внутри каждой страты. Метод выборки может варьироваться от одной страты к другой. Совокупность может быть стратифицирована по любой переменной, значение которой доступно для всех единиц основы выборки до формирования выборки (например, возраст, пол, провинция проживания, доход).

Зачем создавать слои? Есть много причин, главная из которых заключается в том, что это может сделать стратегию выборки более эффективной. В предыдущем разделе упоминалось, что для оценки определенной точности требуется больший размер выборки для характеристики, которая сильно варьируется от одной единицы к другой, чем для характеристики с меньшей изменчивостью. Например, если бы каждый человек в совокупности имел одинаковую заработную плату, то выборки одного человека было бы достаточно, чтобы получить точную оценку средней заработной платы.

В этом заключается идея повышения эффективности, полученного с помощью стратификации. Если вы создаете страты, в которых единицы имеют сходные характеристики и значительно отличаются от единиц в других стратах, вам потребуется только небольшая выборка из каждой страты, чтобы получить точную оценку общего дохода для этой страты. Затем вы можете объединить эти оценки, чтобы получить точную оценку общего дохода для всего населения. Если бы вы использовали SRS для всего населения без стратификации, выборка должна была бы быть больше, чем сумма всех размеров выборок страты, чтобы получить оценку общего дохода с тем же уровнем точности.

Еще одним преимуществом является то, что стратифицированная выборка обеспечивает достаточный размер выборки для представляющих интерес подгрупп населения. При стратификации совокупности каждая страта становится независимой совокупностью, и для каждой из них рассчитывается размер выборки.

Пример 4

Предположим, вы хотите оценить, сколько старшеклассников работают неполный рабочий день на национальном уровне и уровне провинции. Если бы вы выбрали простую случайную выборку из 25 000 человек из списка всех старшеклассников в Канаде (при условии, что такой список был доступен для выбора), вы бы получили немногим более 100 человек с Острова Принца Эдуарда, поскольку они составляют менее 0,5% населения Канады. Эта выборка, вероятно, не будет достаточно большой для подробного анализа, который вы планировали. Разделение вашего списка по провинциям, а затем определение размера выборки, необходимого для каждой провинции, позволит вам получить требуемый уровень точности для Острова Принца Эдуарда, а также для каждой из других провинций.

Стратификация наиболее полезна, когда стратифицирующие переменные

• просты в работе,
• легко заметить,
• тесно связаны с темой опроса.

Кластерная выборка

Иногда слишком дорого иметь слишком разбросанную географическую выборку. Командировочные расходы могут стать дорогими, если интервьюерам приходится опрашивать людей из одного конца страны в другой. Чтобы сократить расходы, статистики могут выбрать 9Метод кластерной выборки 0099 .

Кластерная выборка делит совокупность на группы или кластеры. Несколько кластеров выбираются случайным образом для представления общей совокупности, а затем все единицы внутри выбранных кластеров включаются в выборку. В выборку не включены единицы из невыбранных кластеров. Они представлены представителями выбранных кластеров. Это отличается от стратифицированной выборки, когда некоторые единицы выбираются из каждой страты. Примерами кластеров являются фабрики, школы и географические районы, такие как избирательные округа.

Пример 5

Предположим, вы представитель спортивной организации и хотите узнать, в каких видах спорта участвуют учащиеся 11-х (или 4-х) классов по всей Канаде. Было бы слишком дорого и долго опрашивать каждого канадца в 11-м классе или даже пару учеников из каждого класса 11-го класса в Канаде. Вместо этого случайным образом выбираются 100 школ со всей Канады. Эти 100 школ являются отобранными кластерами. Затем опрашиваются все учащиеся 11-х классов во всех 100 кластерах.

Кластерная выборка создает «карманы» единиц выборки, а не распределяет выборку по всей территории, что позволяет снизить затраты на операции по сбору. Еще одна причина использования кластерной выборки заключается в том, что иногда список всех единиц генеральной совокупности недоступен, в то время как список всех кластеров либо доступен, либо его легко создать.

В большинстве случаев кластерная выборка менее эффективна, чем SRS . Это главный недостаток метода. По этой причине обычно лучше обследовать большое количество небольших скоплений, а не небольшое количество больших скоплений. Почему? Поскольку соседние единицы имеют тенденцию быть более похожими, в результате получается выборка, которая не отражает весь спектр мнений или ситуаций, присутствующих в генеральной совокупности. В примере 5 учащиеся одной и той же школы, как правило, занимаются одними и теми же видами спорта, то есть теми, для которых в их школе имеются возможности.

Еще один недостаток кластерной выборки заключается в том, что у вас нет полного контроля над окончательным размером выборки. Поскольку не во всех школах одинаковое количество учащихся 11-х классов, и вы должны опросить каждого учащегося в своей выборке, окончательный размер может быть больше или меньше, чем вы ожидали.

Многоэтапная выборка

Многоэтапная выборка аналогична кластерной выборке, за исключением того, что она включает выборку в каждом выбранном кластере, а не включает все единицы из выбранных кластеров. Этот тип выборки требует как минимум двух этапов. На первом этапе выявляются и отбираются большие кластеры. На втором этапе единицы выбираются из выбранных кластеров с использованием любого из методов вероятностной выборки. В этом контексте кластеры называются первичными единицами выборки (ПЕВ), а единицы внутри кластеров называются вторичными единицами выборки (ВЕВ). При наличии более двух этапов в рамках SSE выбираются третичные единицы выборки (TSU), и процесс продолжается до тех пор, пока не будет получена окончательная выборка.

Пример 6

В примере 5 кластерная выборка будет выбирать 100 школ, а затем опрашивать каждого учащегося 11 класса из этих школ. Вместо этого вы можете выбрать больше школ, получить список всех учащихся 11-х классов из этих выбранных школ и выбрать случайную выборку учащихся 11-х классов из каждой школы. Это будет двухэтапный план выборки. Школы будут иметь PSU , а учащиеся — SSU .

Вы также можете получить список всех классов 11 класса в выбранных школах, выбрать случайную выборку классов из каждой из этих школ, получить список всех учащихся в выбранных классах и, наконец, выбрать случайную выборку учащихся из каждого выбранного класса. Это будет трехэтапный план выборки. Школы были бы PSU , классы будут иметь номер SSU , а студенты будут иметь номер TSU . Каждый раз, когда добавляется этап, процесс усложняется.

Теперь представьте, что в каждой школе учится в среднем 80 11-классников. Тогда кластерная выборка даст вашей организации выборку из примерно 8000 учащихся (100 школ x 80 учащихся). Если вам нужна большая выборка, вы можете выбрать школы с большим количеством учащихся. Для меньшей выборки вы можете выбрать школы с меньшим количеством учащихся. Одним из способов контроля размера выборки может быть разделение школ на большие, средние и малые размеры (с точки зрения количества учащихся 11-х классов) и выборка школ из каждой страты. это называется стратифицированная кластерная выборка .

В качестве альтернативы можно использовать трехэтапную схему. Вы должны выбрать выборку из 400 школ, затем выбрать два класса 11 класса в каждой школе и, наконец, выбрать 10 учащихся в классе. Таким образом, вы все равно получите выборку из примерно 8000 учащихся (400 школ x 2 класса x 10 учащихся), но выборка будет более разбросанной.

Из этого примера видно, что при многоступенчатой ​​выборке у вас все еще есть преимущество более концентрированной выборки для снижения затрат. Однако выборка не такая концентрированная, как кластерная выборка, и размер выборки, необходимый для получения заданного уровня точности, все равно будет больше, чем для 9-кратной выборки.0135 SRS , так как этот метод менее эффективен. Тем не менее, многоэтапная выборка может сэкономить много времени и усилий по сравнению с SRS , поскольку вам не нужно иметь список всех учащихся 11-х классов. Все, что вам нужно, это список классов из 400 школ и список учеников из 800 классов.

Многоэтапная выборка

Многоэтапная выборка собирает основную информацию из большой выборки единиц, а затем собирает более подробную информацию для подвыборки этих единиц. Наиболее распространенной формой многоэтапной выборки является двухэтапная выборка (или двойная выборка), но также возможны три или более этапов.

Многоэтапный отбор проб сильно отличается от многоступенчатого отбора проб, несмотря на схожесть их названий. Хотя многоэтапная выборка также включает в себя получение двух или более выборок, все выборки берутся из одного и того же кадра. Выбор подразделения на втором этапе обусловлен его выбором на первом этапе. Единица, не выбранная на первом этапе, не будет частью выборки на втором этапе. Как и в случае многоэтапной выборки, чем больше фаз используется, тем сложнее план выборки и ее оценка.

Многоэтапная выборка полезна, когда в основе выборки отсутствует вспомогательная информация, которую можно было бы использовать для стратификации совокупности или для исключения части совокупности.

Пример 7

Предположим, что организации требуется информация о животноводческих фермах в Альберте, но в инструментарии обследования перечислены все типы ферм — крупного рогатого скота, молочные, зерновые, свиноводческие, птицеводческие и сельскохозяйственные. Ситуация усложняется тем, что инструментарий обследования не предоставляет никакой вспомогательной информации по перечисленным там хозяйствам.

Простой опрос, единственным вопросом которого будет «Часть или вся ваша ферма посвящена животноводству?» можно было провести. При наличии только одного вопроса это обследование должно иметь низкую стоимость интервью (особенно если оно проводится по телефону) и, следовательно, организация должна быть в состоянии составить большую выборку. После того, как первая выборка составлена, можно взять вторую, меньшую выборку среди фермеров, занимающихся выращиванием крупного рогатого скота, и задать этим фермерам более подробные вопросы. Используя этот метод, организация избегает затрат на съемочные единицы, которые не входят в эту конкретную область (например, фермеры, не занимающиеся животноводством).

В примере 7 данные, собранные на первом этапе, использовались для исключения единиц, не входящих в целевую совокупность. В другом контексте эти данные можно было бы использовать для повышения эффективности второй фазы, например, путем создания пластов. Многоэтапная выборка также может использоваться для уменьшения нагрузки на респондентов или в случае очень разных затрат, связанных с разными вопросами опроса, как показано в следующем примере.

Пример 8

В ходе обследования состояния здоровья участникам задают несколько основных вопросов об их питании, привычках курения, физических упражнениях и употреблении алкоголя. Кроме того, опрос требует, чтобы респонденты подвергали себя некоторым прямым физическим тестам, таким как бег на беговой дорожке или измерение артериального давления и уровня холестерина.

Заполнение анкет или опрос участников являются относительно недорогими процедурами, но медицинские тесты требуют наблюдения и помощи квалифицированного врача, а также использования оборудованной лаборатории, что может быть довольно дорогостоящим.