График х 4: График y = f(x) = x^(4/3) (х в степени (4 делить на 3)) постройте график функции и изобразите его. Исследуйте данную функцию. [Есть ОТВЕТ!]

Содержание

Построение графиков уравнений, содержащих модули

Туезова Лариса Николаевна, учитель математики

Разделы: Математика, Конкурс «Презентация к уроку»

Презентация к уроку

Загрузить презентацию (3 МБ)

Тип урока: Урок формирования новых знаний.

Цели урока:

Формировать умение строить графики уравнений содержащих модули.
Развитие логического мышления, познавательного интереса.
Развитие общеучебных навыков и умений – организационных, интеллектуальных и коммуникативных.

Оборудование: мультимедиа проектор, доска.

I. Орг. момент.

II. Устный счет.

Вычислите. (слайд 1)
Решите уравнение. (слайд 2)

III.

Объяснение нового материала.

1. Построить график уравнения (слайд 3)

Решение. (слайд 4)

По определению модуля имеем:

Построим график уравнения: (слайд 5)

х=2у, если у≥0
х=0, если у<0
Получили график уравнения

2. Построить график уравнения .(слайд 6)

Решение. (слайд 7)

По определению модуля имеем:

Если у=0, то х – любое.

Выполним построение. (слайд 8)

х = 1, если у>0;
x = — 1, если у<0;

Построить график уравнения (слайд 9)

Решение. (слайд 10)

По определению модуля имеем:

При х≥0, у≥0, уравнение х+у=4;
При х≥0, у<0, уравнение х-у=4;
При х<0, у≥0, уравнение –х+у=4;
При х<0, у<0, уравнение –х-у=4.

(слайд 11)

Построить график уравнения (слайд 12)

Решение. (слайд 13)

По определению модуля имеем:

При х≥0, у≥0, уравнение х-у=4;
При х≥0, у<0, уравнение х+у=4;
При х<0, у≥0, уравнение –х-у=4;
При х<0, у<0, уравнение –х+у=4.

(слайд 14)

IV. Закрепление. Решение задач.

Построить график уравнения.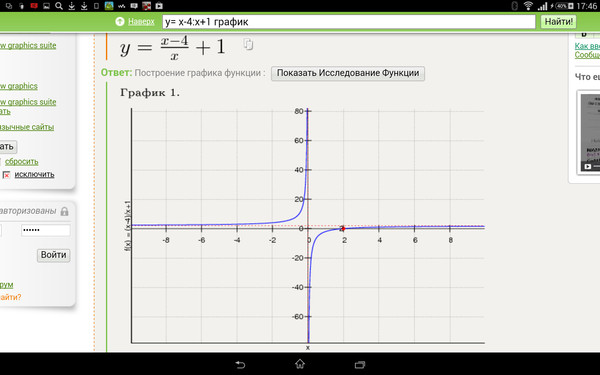 (слайд 15)

а) |x|+|y|=2;

б)|x|-|y|=3.

Проверка (слайд ) (слайд 16)

(слайд 17)

V. Итог урока.

Домашнее задание. (слайд 18)

Построить графики уравнений: а) |y|=1-|x|; б)|y|=|x|+3.

28.04.2014

47 Постройте график функции у = |x — 4|

47 Постройте график функции у = |x — 4| — 5. Мордкович алгебра 8 класс – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

47 Постройте график функции у = |x — 4| — 5.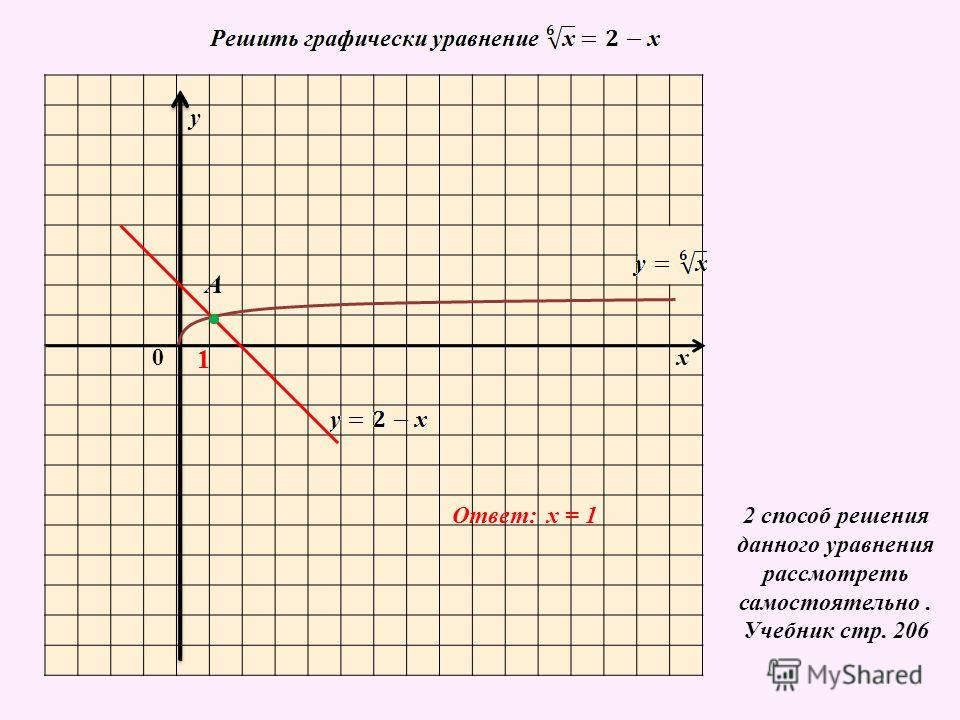 Найдите:
а)    наименьшее значение функции;
б)    промежутки монотонности функции;
в)     нули функции;
г)     значения аргумента, при которых у > 0, у < 0.

ответы

что нам стоит график построить?)

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы

Психология

ЕГЭ

10 класс

9 класс

похожие вопросы 4

Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра

10. При каких значениях р уравнение -х 2 + 6х — 2 = р:
а) не имеет корней;
б) имеет один корень; (Подробнее…)

ГДЗМордкович А.Г.Алгебра8 класс

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее.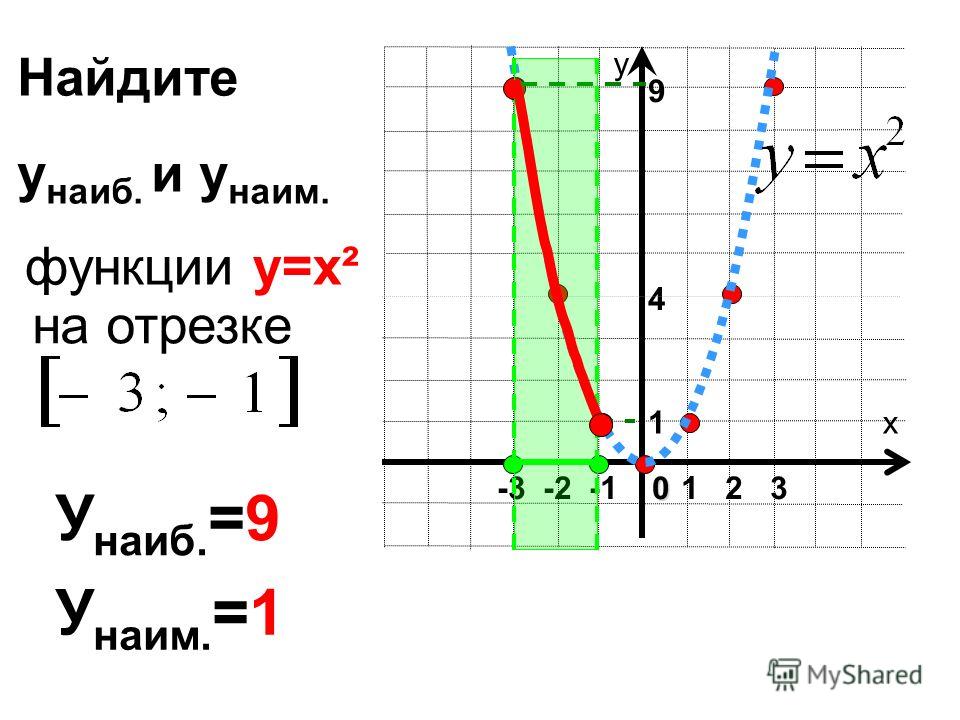

..)

ГДЗ11 классКолмогоров А.Н.Алгебра

Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.

Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)

ГДЗШкола8 классХимияГабриелян О.С.

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

3-8 9 Оценить квадратный корень из 12

10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

линий графика

Графики линейных уравнений

График уравнения с двумя переменными представляет все возможные комбинации

x и y , которые удовлетворяют уравнению.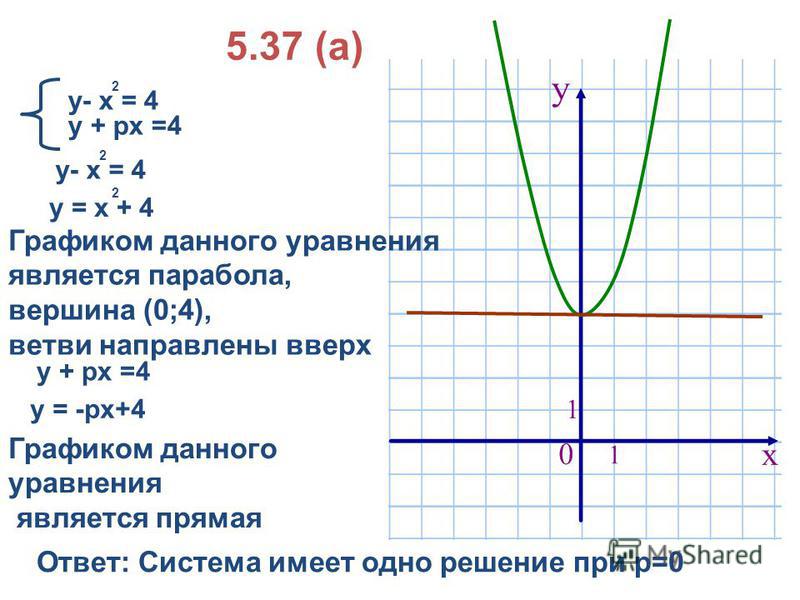

Другими словами, точки на графике имеют координаты ( x , y ), которые делают утверждение уравнения верным. В зависимости от характера уравнения и показателей переменных каждое уравнение имеет свой график.

График любого уравнения с двумя переменными, обе из которых имеют степень 1, не умножаются друг на друга и не входят в знаменатель какой-либо дроби, представляет собой прямую линию.
Например, график 2y — x + 4= 0 представляет собой линию. Это означает, что если мы найдем все возможные комбинации x и y, которые работают в уравнении, и изобразим их в системе координат, результатом будет линия. Поскольку две точки определяют линию, если мы распознаем уравнение как линейное уравнение, нам нужны только два набора x и y (точек), которые удовлетворяют уравнению для графика. Способов найти эти точки много, и их бесконечное множество. Мы рассмотрим линии графика, используя их точки пересечения по осям x и y. Это точки, в которых линия пересекает ось x и ось y соответственно.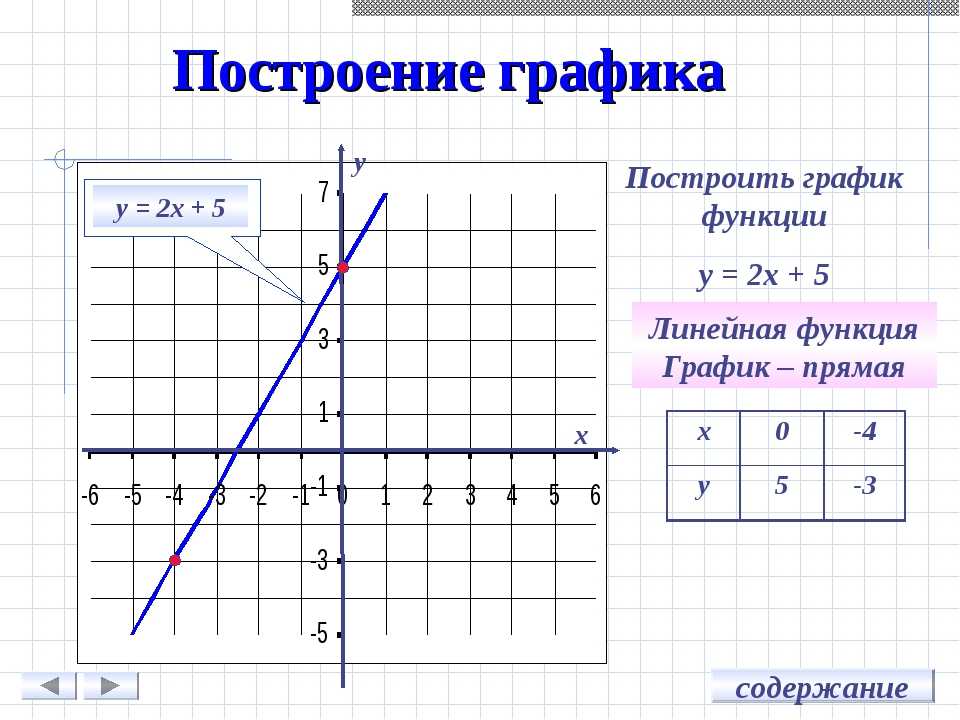
Причина, по которой мы выбираем эти точки, заключается в том, что с ними легче работать. Точка пересечения линии по оси X является точкой на оси X и, следовательно, имеет нулевую координату Y. А точка пересечения линии по оси y — это точка на оси y с нулевой координатой x . Мы собираемся использовать эти факты, чтобы найти недостающие координаты каждой точки.
Сначала мы подставим ноль вместо y и найдем соответствующее x , а затем подставим ноль вместо x и найдем соответствующее y .
Пример 1) График 2 y — х + 4 = 0
Если мы подставим 0 вместо
x , то получим:
2 y — 0 + 4 = 0 Вычтем 4 с обеих сторон:
2 y = -4 и разделив на 2, получим y = -2, поэтому у нас есть (0,-2), это и -перехват.
Далее подставляем ноль вместо y :
2(0) — x + 4 = 0 Вычитаем по 4 с обеих сторон:
— x = -4 или x = 4, получаем наша вторая точка (4,0), это x -intercept
Теперь наносим точки и соединяем их. Результирующая линия представляет все x,y комбинаций, которые работают в данном уравнении.
Каждая линия имеет крутизну, которая обозначается как наклоном . Крутизна линии или ее наклон — это отношение подъема линии (насколько далеко вверх или вниз мы должны идти, чтобы достичь другой точки) к ее длине (насколько далеко вперед или назад мы должны пройти). Для приведенной выше линии наклон равен 2/4 или 1/2, поскольку нам нужно подняться на 2 единицы вверх, а затем на 4 единицы, чтобы добраться из одной точки в другую. Мы также можем найти наклон, решив наше уравнение для
и первый. Тогда коэффициент наклона будет равен x (а оставшееся число — точка пересечения с осью y):
Сначала мы прибавим x к обеим сторонам и вычтем 4: 2 y = x — 4
Затем мы разделим обе стороны на 2: y = x /2 — 2 (это называется формой пересечения наклона линии)
Таким образом, наклон равен 1/2, а пересечение по оси Y равно -2.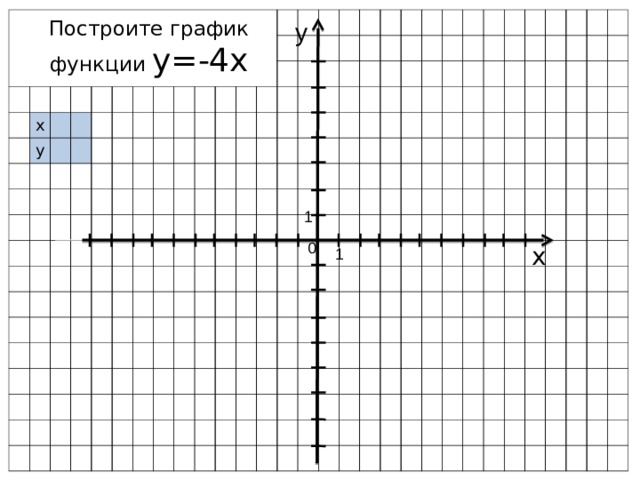 Эта информация может оказаться полезной в некоторых случаях.

Пример 2) График 4y + 5x = 20
Подставляя ноль вместо x, мы получаем:
4y = 20 или y = 5
Таким образом, мы получаем y-intercept (0,5)
Подставляя ноль вместо y, мы получаем:
5x = 20 или x = 4
Таким образом, x-пересечение равно (4,0)
.
Обратите внимание, что наклон этой линии равен -5/4, так как нам нужно спуститься на 5 единиц вниз и пройти на 4 единицы вперед, чтобы добраться из одной точки в другую.
И если мы решим для y (изменим на форму пересечения наклона ), мы сначала должны вычесть 5x с обеих сторон:
4y = -5x + 20, а затем разделить на 4:
y = -5/4 x + 5
Что также показывает, что наклон равен -5/4, а y-перехват должен быть 5.

Особые случаи:

Иногда нам может понадобиться отобразить уравнения только с одной переменной в системе координат.
Например, y = 4 или x = -2 являются уравнениями, которые содержат только одну переменную, но их можно изобразить в виде линий.
No related posts.