График квадратичной функции примеры: Построение графика квадратичной функции — урок. Алгебра, 8 класс.

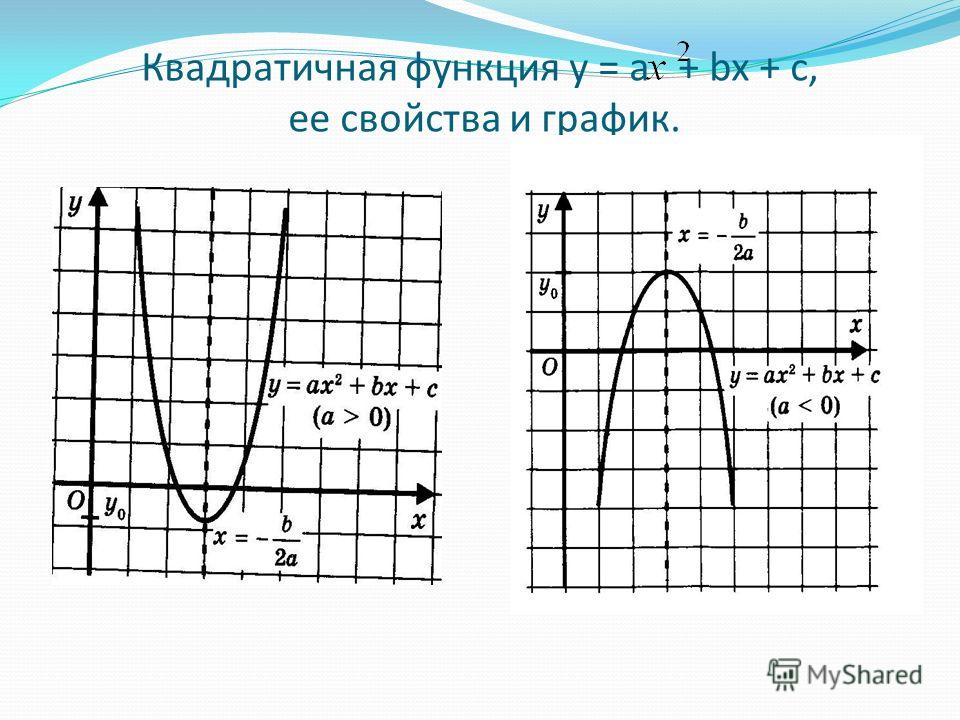
Квадратичная функция, ее свойства, примеры и график

Функция y = ax² + bx + c, где a, b и c — заданные числа, a ≠ 0, x — переменная, называется квадратичной функцией. Другими словами, квадратичная функция – это зависимость, содержащая аргумент в квадрате. Отсюда и ее название.

При этом многочлен ax² + bx + c называют квадратным трехчленом. Числа a, b и c называются коэффициентами квадратного трехчлена: a — первым коэффициентом, b — вторым,                        c — свободным членом. Значения x, при которых квадратный трехчлен обращается в нуль, называются корнями квадратного трехчлена.

Для нахождения корней квадратного трехчлена нужно решить квадратное уравнение                 ax² + bx + c = 0. Рассмотрим пример, найдем корни квадратного трехчлена x² — x — 2. Решая уравнение x² — x — 2 = 0, получаем: x₁ = -1, x₂ = 2.

Число корней квадратного уравнения ax² + bx + c = 0 зависит от знака его дискриминанта                     D = b² — 4ac, а значит и квадратный трехчлен:

• имеет два различных корня, если D > 0;
• имеет один корень (два равных корня), если D = 0;
• не имеет действительных корней, если D < 0.

Рассмотрим пример, квадратный трехчлен 3x² — 8x + 5 имеет два различных корня, так как          D = 8² — 4* 3*5 = 4 > 0, корни этого трехчлена: x₁ = 5/3,  x₂ = 1.

Квадратный трехчлен 4x² — 4x + 1 имеет один корень, так как D = 4² — 4*4*1 = 0, корень этого трехчлена  х = 1/2.

Квадратный трехчлен 2x² — 5x + 6 не имеет действительных корней, так как                                       D = 5² — 4*2*6 = — 23 < 0.

Рассмотрим самую простую квадратичную функцию

y = x², т.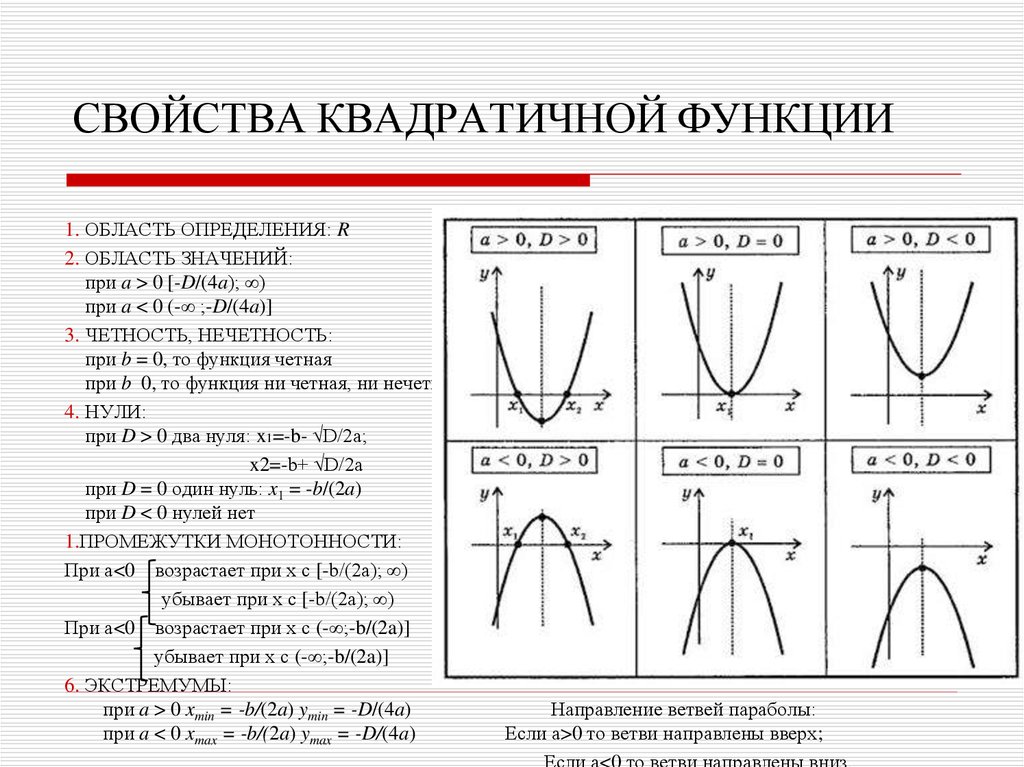 е. функцию y = ax² + bx + c, при a = 1, b = c = 0. Для построения графика этой функции составим таблицу ее значений.

х	-2	-1	0	1	2
у	4	1	0	1	4

Отметим точки на координатной плоскости и соединим их плавной линией.

Кривая, являющаяся графиком функции y = x², называется параболой. Ось ординат является осью симметрии параболы. Точку пересечения параболы с ее осью симметрии называют вершиной параболы. Вершиной параболы y = x² является начало координат.

Рассмотрим функцию вида y = 2x², чтобы построить график составим таблицу значений.

x	-2	-1	0	1	2
y	8	2	0	2	8

Сравним графики функций y = 2х² и y = х². При одном и том же х значение функции y = 2х² в 2 раза больше значения функции y = х². Это значит, что каждую точку графика y = 2х² можно получить из точки графика функции y = х² с той же абсциссой увеличением ее ординаты в 2 раза. Говорят, что график функции y = 2х² получается растяжением графика функции y = х² в 2 раза вдоль оси ординат.

Рассмотрим функцию вида y = 1/2x², чтобы построить график составим таблицу значений.

х	-2	-1	0	1	2
y	2	0.5	0	0.5	2

Сравним графики функций y = 1/2x² и y = х². Каждую точку графика y = 1/2x² можно получить из точки графика функции  y = х² с той же абсциссой уменьшением ее ординаты в 2 раза.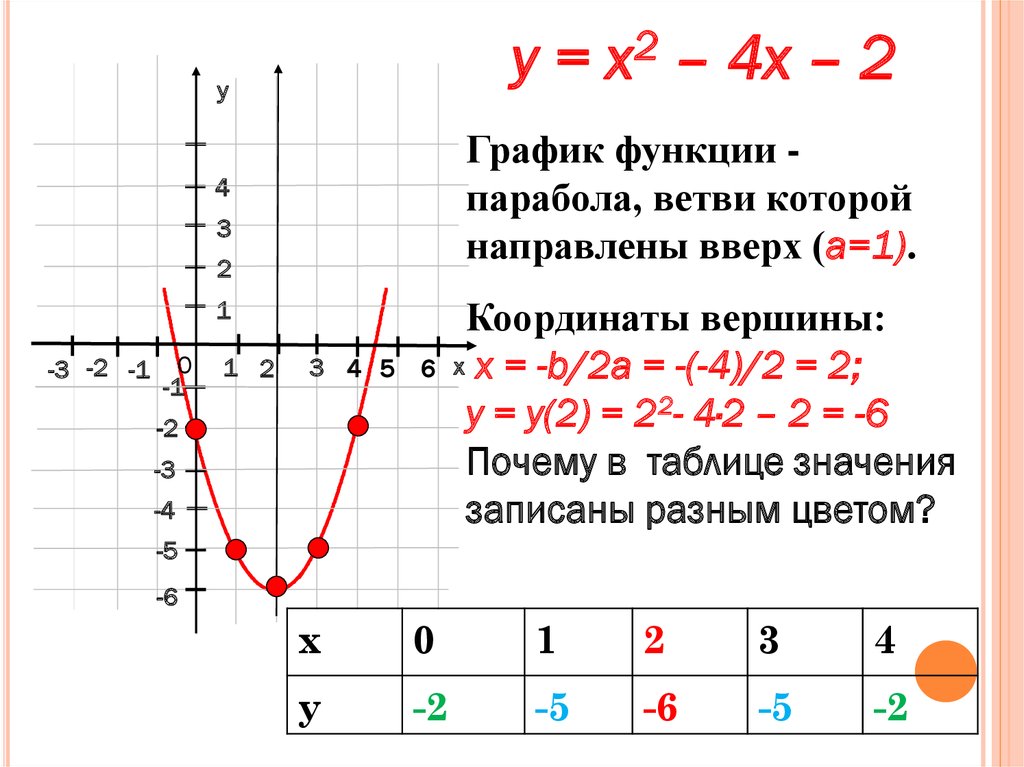 Говорят, что график функции y = 1/2x² получается сжатием графика функции y = х² в 2 раза вдоль оси ординат.

Рассмотрим функцию вида y = —x²,  и сравним с функцией y = х². При одном и том же значении х значения этих функций равны по модулю и противоположны по знаку. Следовательно, график функции 

y = —x² можно получить симметрией относительно оси абсцисс графика функции  y = х². Составим таблицу значений.

х	-2	-1	0	1	2
у	-4	-1	0	-1	-4

Говорят, что ветви параболы y = х² направлены вверх, а ветви параболы y = —x² направлены вниз. Аналогично график функции y = -2х² симметричен графику функции y = 2х² относительно оси абсцисс.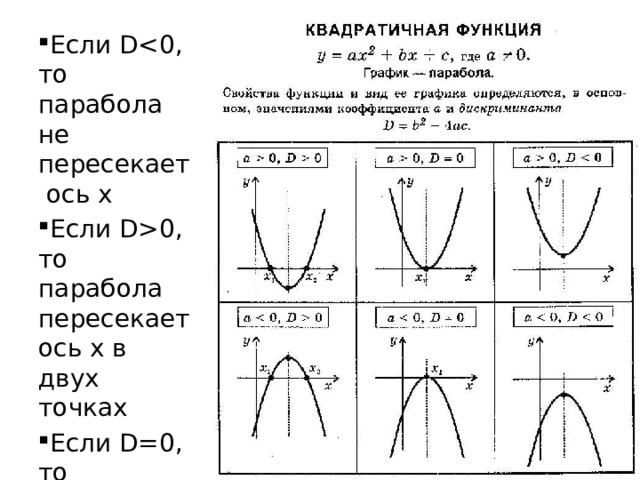 График функции y = -1/2х² симметричен графику функции y = 1/2х² относительно оси абсцисс. График функции y = ах² при любом а ≠ 0 также называют параболой. При а >

 0 ветви параболы направлены вверх, а при а < 0 вниз.

Рассмотрим функцию вида y = x² — 2х — 3, чтобы построить график составим таблицу значений.

х	-2	-1	0	1	2	3	4
у	5	0	-3	-4	-3	0	5

 

Вообще, графиком функции y = ax² + bx + c является парабола, получаемая сдвигом параболы      y = ax² вдоль координатных осей. Равенство y = ax² + bx + c называют уравнением параболы.

Построение графика квадратичной функции

Урок 8. Алгебра 9 класс ФГОС

На этом уроке вводиться алгоритм построения графика квадратичной функции.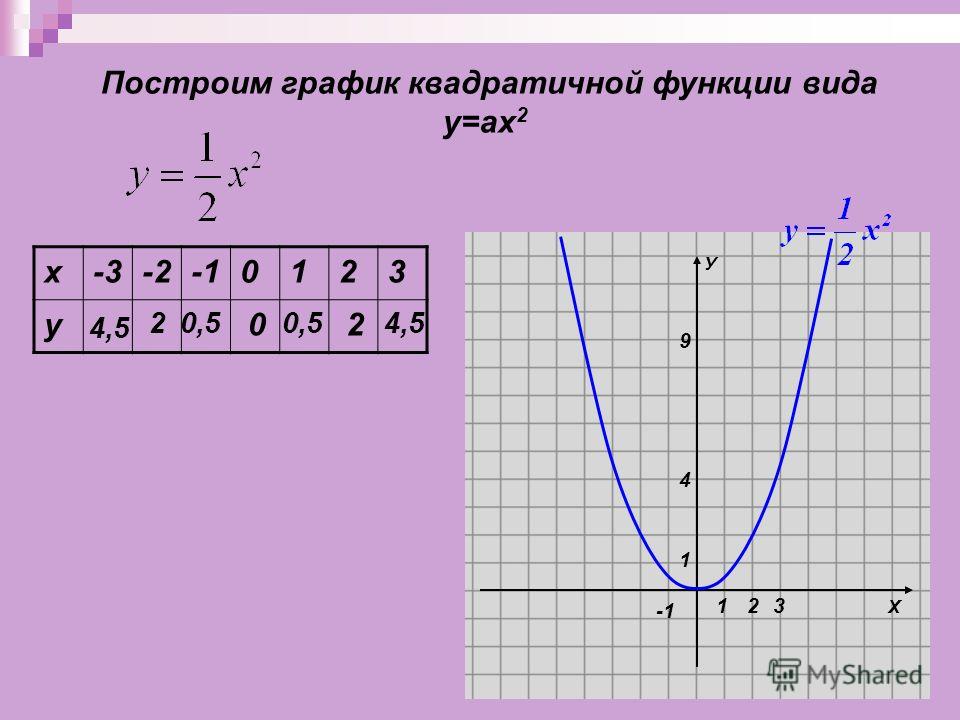 Рассматриваются примеры построения графиков квадратичных функций вида y=a(x-m)2+n и y=ax2+bx+c.

Конспект урока «Построение графика квадратичной функции»

Графиком любой квадратичной функции является парабола. У каждой параболы есть вершина, при изображении графика важно знать её координаты. Вершина параболы  имеет координаты (m,n).

Определите координаты вершин для парабол:

Определим координаты вершины параболы, которая является графиком квадратичной функции записанной в виде .

Преобразуем квадратный трёхчлен, выделим из него квадрат двучлена:

Второе слагаемое представим в виде удвоенного произведения:

Выделим квадрат суммы:

После сокращения получаем:

Отсюда запишем, что:

Вывод.

Графиком функции  является парабола, которую можно получить из параболы с помощью двух параллельных переносов: сдвига относительно оси x и сдвига относительно оси

y. Данная парабола имеет вершину с координатами (m,n), где , . Осью симметрии является прямая x=m.

Пример.

Найти координаты вершины параболы .

Вершина будет иметь координаты (m,n), каждую из которых можно получить по формуле. Подставим коэффициенты квадратичной функции в формулу и найдём эти значения:

Вершина параболы имеет координаты (-2,-5).

Воспользуемся наиболее простым способом: сначала найдём m вершины по формуле. И учитывая, что вершина принадлежит графику функции, подставим m вместо аргумента в функцию:

Получили вершину, которая имеет координаты (-2,-5).

Алгоритм построения графика квадратичной функции:

1.     Определить направление ветвей парабола. Если a>0, то ветви направлены вверх, если

a<0, то — вниз.

2.     Найти координаты вершины параболы и отметить её на координатной плоскости.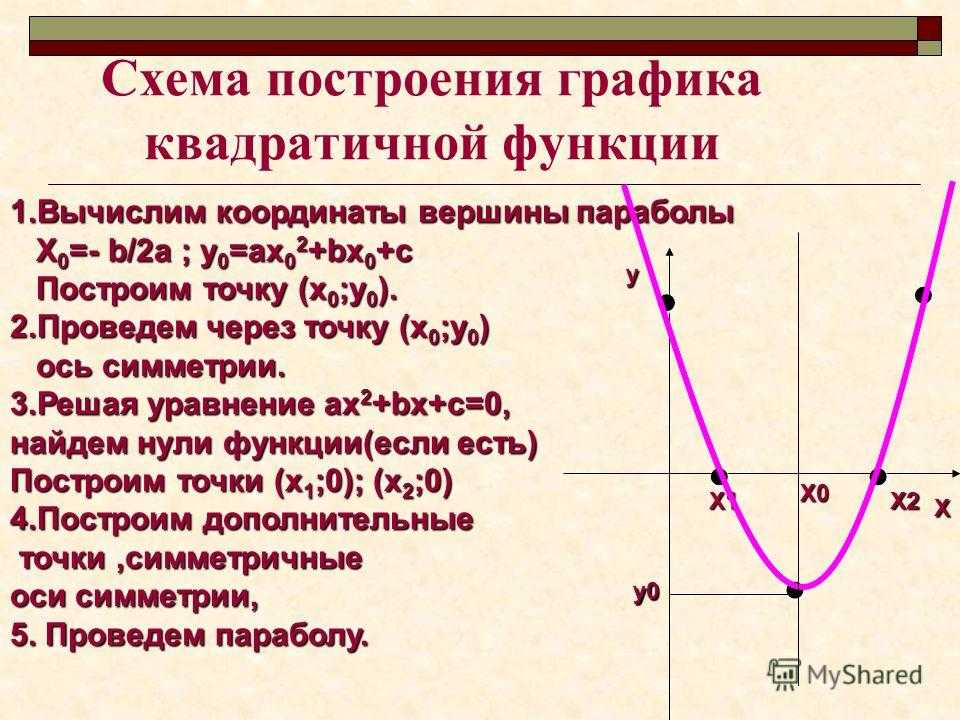 Применив формулу , найдём абсциссу вершины параболы, и, подставив это значение в формулу, задающую функцию, найдем ординату этой точки.

3.     Определить ось симметрии x=m.

4.     Построить ещё несколько точек принадлежащих параболе, составив таблицу значений функции с учётом оси симметрии.

5.     Соединить отмеченные точки плавной линией.

Пример.

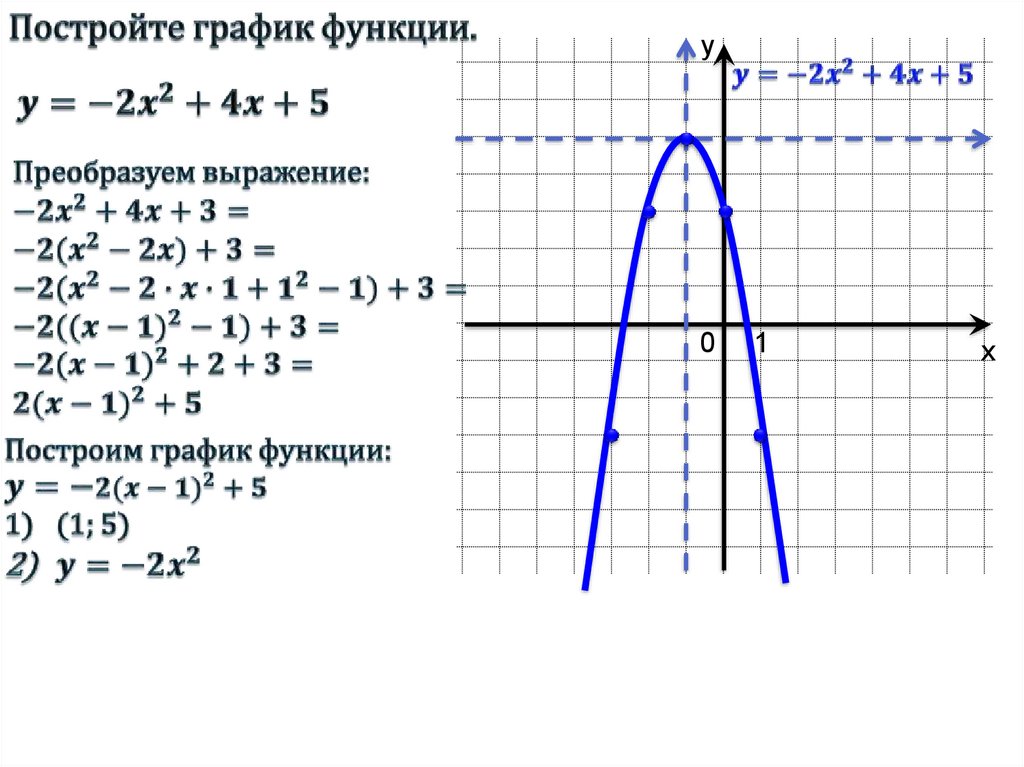
Изобразить график функции .

1.                Определим направление ветвей параболы:

2.                Найдём координаты вершины:

Получили вершину с координатами (-2, -3).

3.                Определим ось симметрии:

4.                Составим таблицу значений:

Выбранные значения симметричны относительно оси симметрии.

5.                Отметим и соединим полученные точки на координатной плоскости:

Получили параболу, которая является графиком функции.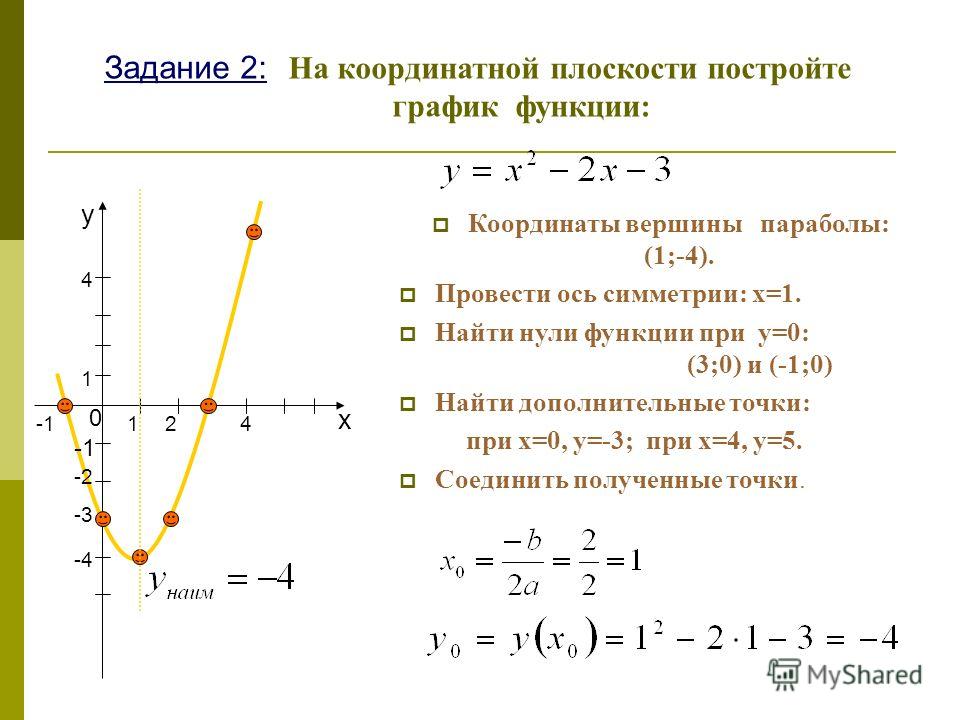 n

Получите полный комплект видеоуроков, тестов и презентаций Алгебра 9 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Квадратичные функции и их графики

Цели обучения

• Квадратичные функции
  • Корни или нули квадратичной функции
  • Характеристики параболы
    • вершина
    • ось симметрии
    • x/y — пересечения
• Классификация решений квадратных уравнений
  • Дискриминант

Изогнутые антенны, подобные показанным на фото, обычно используются для фокусировки микроволн и радиоволн для передачи телевизионных и телефонных сигналов, а также спутниковой и космической связи. Поперечное сечение антенны имеет форму параболы, которую можно описать квадратичной функцией.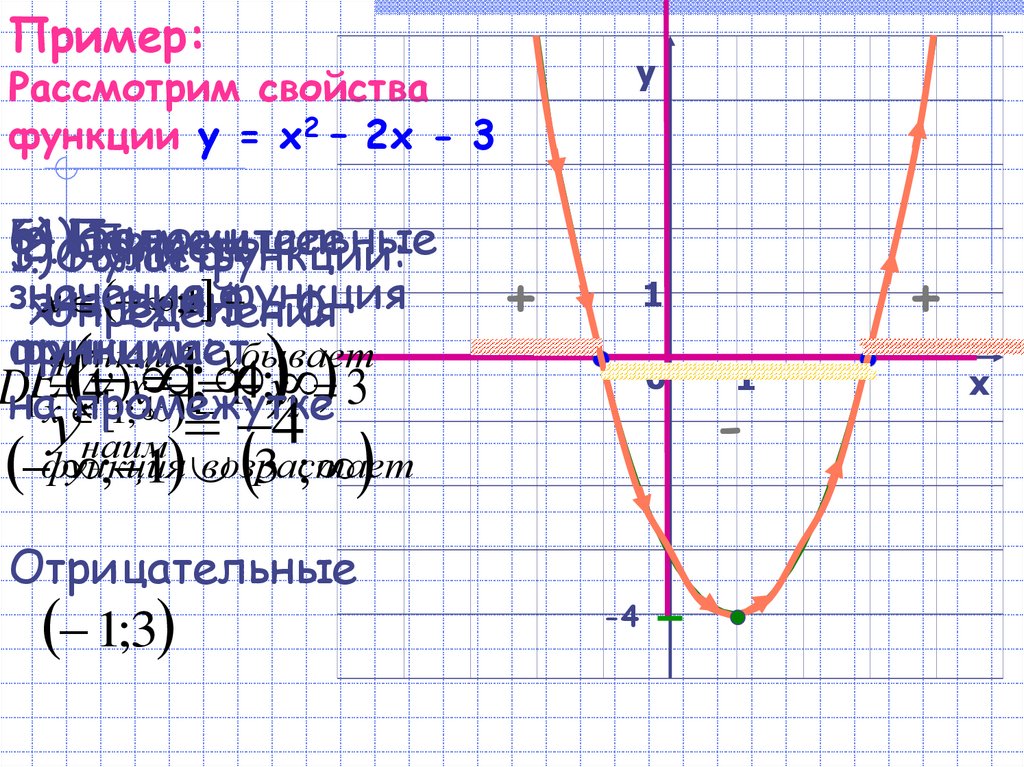

Набор спутниковых антенн. (кредит: Мэтью Колвин де Валле, Flickr)

Характеристики парабол

График квадратичной функции представляет собой U-образную кривую, называемую параболой . Одной из важных особенностей графа является то, что он имеет крайнюю точку, называемую вершиной . Если парабола раскрывается, вершина представляет собой самую низкую точку на графике или минимальное значение квадратичной функции. Если парабола направлена ​​вниз, вершина представляет собой самую высокую точку на графике или максимальное значение . В любом случае вершина является поворотной точкой на графе. График также симметричен, вертикальная линия проходит через вершину, называемую осью симметрии .

Точка пересечения y — это точка, в которой парабола пересекает ось y . Точки пересечения x — это точки, в которых парабола пересекает ось x . Если они существуют, x -перехватов представляют собой нулей или корни квадратичной функции, значения x  при которых y  = 0.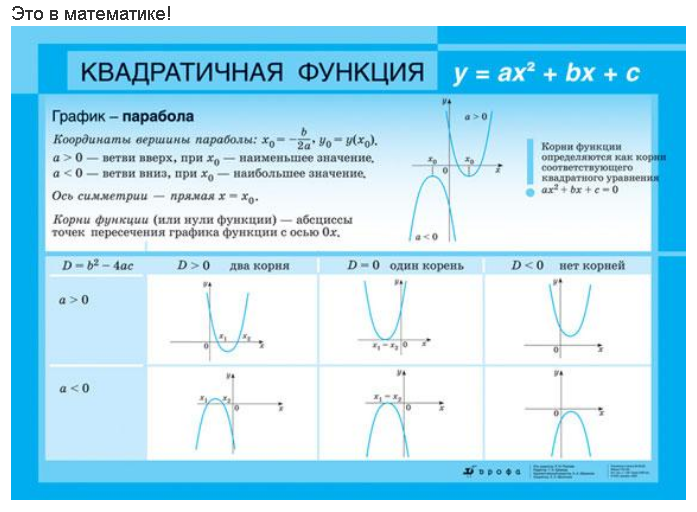

Пример: Определение характеристик параболы

Определить вершину, ось симметрии, нули и y 90 017 — точка пересечения параболы, показанной ниже.

Решение

Попробуйте

Общие и стандартные формы квадратичных функций

Общая форма квадратичной функции представляет функцию в виде 9{2}+4x+3[/латекс]. В этой форме [латекс]а=1,\текст{ }b=4[/латекс] и [латекс]с=3[/латекс]. Поскольку [latex]a>0[/latex], парабола открывается вверх. Ось симметрии: [латекс]x=-\frac{4}{2\left(1\right)}=-2[/latex]. Это также имеет смысл, поскольку на графике видно, что вертикальная линия [latex]x=-2[/latex] делит график пополам. Вершина всегда находится вдоль оси симметрии. Для параболы, которая открывается вверх, вершина находится в самой нижней точке графика, в данном случае [латекс]\влево(-2,-1\вправо)[/латекс]. 9{2}+k[/latex]

, где [latex]\left(h,\text{ }k\right)[/latex] — это вершина. Поскольку вершина появляется в стандартной форме квадратичной функции, эта форма также известна как вершинная форма квадратичной функции .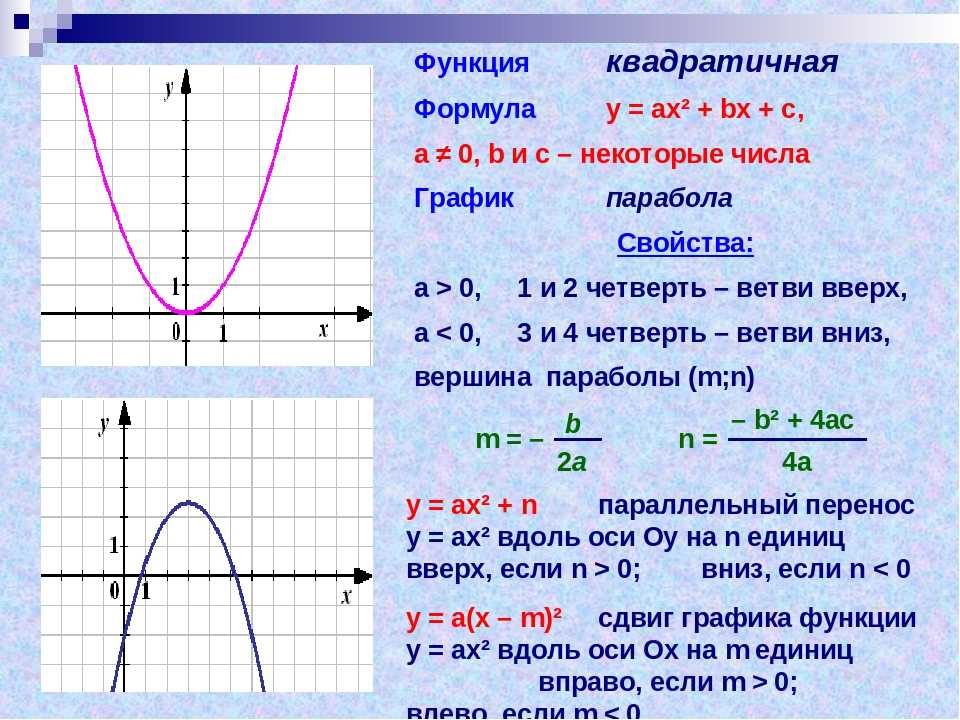

Для заданной квадратичной функции в общем виде найдите вершину параболы.

Одна из причин, по которой мы можем захотеть идентифицировать вершину параболы, заключается в том, что эта точка сообщит нам, где происходит максимальное или минимальное значение выходного сигнала ( 92+bx+c[/latex]

Мы можем определить вершину [latex](h,k)[/latex], выполнив следующие действия:

• Идентифицировать a , b и c .
• Найдите h , координату x вершины, подставив a и b  в [latex]h=-\frac{b}{2a}[/latex].
• Найдите k , y -координату вершины, оценивая [latex]k=f\left(h\right)=f\left(-\frac{b}{2a}\right)[/ латекс] 9{2}-6x[/latex], напишите уравнение в общем виде, а затем в стандартном виде.

  Решение

  В этом разделе мы продолжим изучение квадратичных функций, в том числе решим задачи, связанные с площадью и движением снаряда. Работа с квадратичными функциями может быть менее сложной, чем работа с полиномиальными функциями более высокой степени, поэтому они предоставляют хорошую возможность для детального изучения поведения функции.

  Классификация решений квадратных уравнений

  Как и в предыдущих прикладных задачах, нам также необходимо найти точки пересечения квадратных уравнений для графического построения парабол. Напомним, что мы находим y — пересечение квадратичного уравнения путем оценки функции на входе, равном нулю, и мы находим x — пересечений в местах, где выход равен нулю. Обратите внимание, что количество перехватов размером x может варьироваться в зависимости от расположения графика.

  Количество пересечений параболы по оси x

  Математики также определяют x пересечений как корни квадратичной функции.

  Как: Имея квадратичную функцию [латекс]f\влево(х\вправо)[/латекс], найдите 9{2}+5x — 2[/латекс].

  Решение

  В Примере: Нахождение y – и x – точек пересечения параболы, квадратичное уравнение было легко решено путем разложения на множители. {2}+4x — 4[/latex ]. 9{2}-4ac<0[/latex], то число под радикалом будет отрицательным. Поскольку вы не можете найти квадратный корень из отрицательного числа, используя действительные числа, реальных решений нет. Однако вы можете использовать мнимые числа. Тогда у вас будет два сложных решения: одно путем добавления мнимого квадратного корня, а другое путем его вычитания.

Важные термины

ось симметрии

вертикальная линия, проведенная через вершину параболы, относительно которой парабола симметрична; он определяется как [latex]x=-\frac{b}{2a}[/latex]. 92-4ac[/latex], который говорит, имеет ли квадратное число действительные или комплексные корни

вершина

точка, в которой парабола меняет направление, соответствующее минимальному или максимальному значению квадратичной функции

нули

в заданной функции значения x , при которых y = 0, также называемые корнями

Графики квадратичных функций | Колледж Алгебра

Результаты обучения

• Распознавание характеристик парабол.
• Поймите, как график параболы связан с ее квадратичной функцией.

Изогнутые антенны, подобные показанным на фото, обычно используются для фокусировки микроволн и радиоволн для передачи телевизионных и телефонных сигналов, а также спутниковой и космической связи. Поперечное сечение антенны имеет форму параболы, которую можно описать квадратичной функцией.

Набор спутниковых антенн. (кредит: Мэтью Колвин де Валле, Flickr)

Характеристики парабол

График квадратичной функции представляет собой U-образную кривую, называемую параболой . Одной из важных особенностей графа является то, что он имеет крайнюю точку, называемую вершиной . Если парабола раскрывается, вершина представляет собой самую низкую точку на графике или минимальное значение квадратичной функции. Если парабола направлена ​​вниз, вершина представляет собой самую высокую точку на графике или максимальное значение .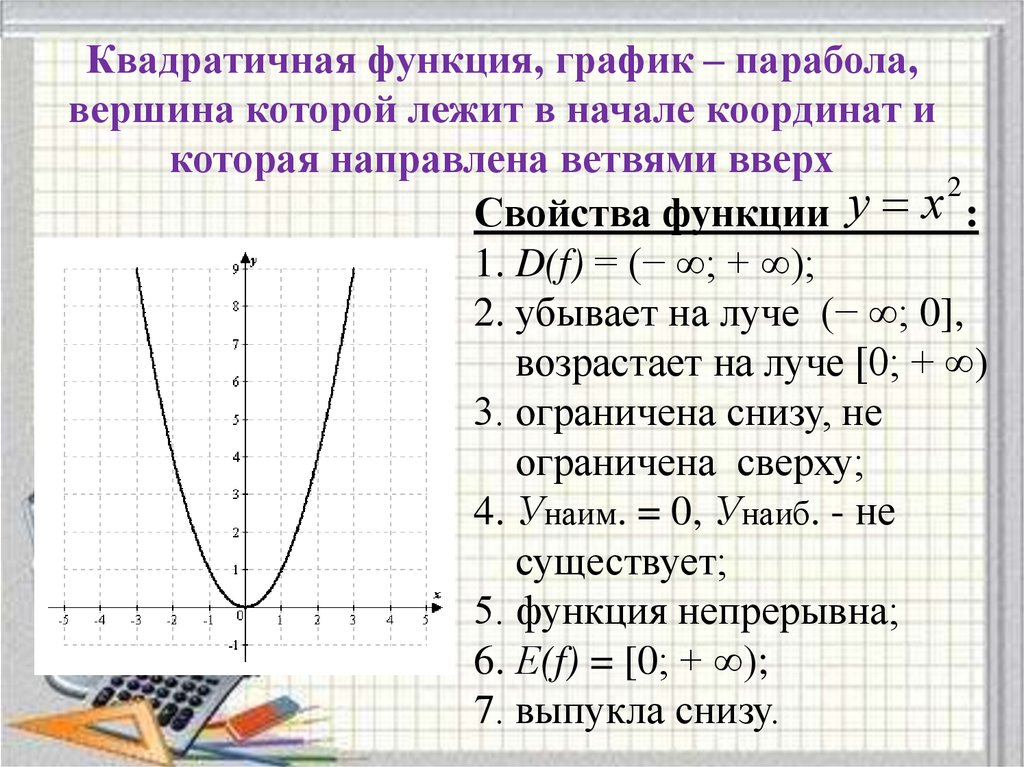 {2}+bx+c[ /латекс] 9{2}+4x+3[/латекс]. В этой форме [латекс]а=1,\текст{ }b=4[/латекс] и [латекс]с=3[/латекс]. Поскольку [latex]a>0[/latex], парабола открывается вверх. Ось симметрии: [латекс]x=-\dfrac{4}{2\left(1\right)}=-2[/latex]. Это также имеет смысл, поскольку на графике видно, что вертикальная линия [latex]x=-2[/latex] делит график пополам. Вершина всегда находится вдоль оси симметрии. Для параболы, которая открывается вверх, вершина находится в самой нижней точке графика, в данном случае [латекс]\влево(-2,-1\вправо)[/латекс]. [latex]x[/latex]-перехваты, те точки, где парабола пересекает [latex]x[/latex]-ось, находятся в [latex]\left(-3,0\right)[/latex] и [латекс]\влево(-1,0\вправо)[/латекс]. 9{2}+k[/latex]

, где [latex]\left(h,\text{ }k\right)[/latex] — это вершина. Поскольку вершина появляется в стандартной форме квадратичной функции, эта форма также известна как вершинная форма квадратичной функции .

Учитывая квадратичную функцию в общем виде, найдите вершину параболы.

Одна из причин, по которой мы можем захотеть идентифицировать вершину параболы, заключается в том, что эта точка сообщит нам, где происходит максимальное или минимальное значение вывода, [latex]k[/latex], и где оно происходит, [latex]h [/латекс]. Если нам дан общий вид квадратичной функции: 92+bx+c[/latex]

Мы можем определить вершину [latex](h,k)[/latex], выполнив следующие действия:

• Идентифицировать [latex]a[/latex], [latex] ]b[/латекс] и [латекс]с[/латекс].
• Найдите [latex]h[/latex], координату [latex]x[/latex] вершины, подставив [latex]a[/latex] и [latex]b[/latex] в [latex]h =-\dfrac{b}{2a}[/latex].
• Найдите [latex]k[/latex], [latex]y[/latex]-координату вершины, оценивая [latex]k=f\left(h\right)=f\left(-\dfrac{ б}{2а}\справа)[/латекс] 9{2}-6x[/latex], напишите уравнение в общем виде, а затем в стандартном виде.

  Показать раствор

  Нахождение области определения и диапазона квадратичной функции

  Любое число может быть входным значением квадратичной функции. Следовательно, областью определения любой квадратичной функции являются все действительные числа. Поскольку параболы имеют максимум или минимум в вершине, диапазон ограничен. Так как вершина параболы будет либо максимальной, либо минимальной, диапазон будет состоять из всех [latex]y[/latex]-значений, больших или равных [latex]y[/latex]-координате вершины или меньше или равно [latex]y[/latex]-координате в точке поворота, в зависимости от того, открывается ли парабола вверх или вниз. 9{2}+bx+c[/latex] с положительным значением [latex]a[/latex] равно [latex]f\left(x\right)\ge f\left(-\frac{b}{2a} \right)[/latex], или [латекс]\left[f\left(-\frac{b}{2a}\right),\infty \right)[/latex]; диапазон квадратичной функции, записанной в общем виде с отрицательным значением [latex]a[/latex] , равен [latex]f\left(x\right)\le f\left(-\frac{b}{2a}\ right)[/latex], или [latex]\left(-\infty ,f\left(-\frac{b}{2a}\right)\right][/latex].

  Диапазон квадратичной функции записывается в стандартной форме [латекс]f\left(x\right)=a{\left(xh\right)}^{2}+k[/latex] с положительным значением [latex]a[/latex] равно [ латекс]f\left(x\right)\ge k[/latex]; диапазон квадратичной функции, записанной в стандартной форме с отрицательным значением [latex]a[/latex] , равен [latex]f\left(x\ справа)\le k[/латекс].

  Как: Для заданной квадратичной функции найти домен и диапазон.

  1. Область определения любой квадратичной функции, как и всех действительных чисел.
  2. Определите, является ли [латекс]а[/латекс] положительным или отрицательным. Если [latex]a[/latex] положительно, парабола имеет минимум. Если [latex]a[/latex] отрицательно, парабола имеет максимум.
  3. Определите максимальное или минимальное значение параболы [latex]k[/latex].
  4. Если парабола имеет минимум, диапазон задается как [латекс]f\влево(х\вправо)\ge k[/латекс] или [латекс]\влево[к,\infty \вправо)[/латекс] . Если парабола имеет максимум, диапазон задается как [латекс]f\влево(х\вправо)\le k[/латекс] или [латекс]\влево(-\infty ,k\вправо][/латекс] 92 [/latex]

     Величина [latex]a[/latex] указывает на растяжение графика. Если [latex]|a|>1[/latex], точка, связанная с конкретным значением [latex]x[/latex], смещается дальше от оси [latex]x[/latex] – , поэтому график кажется, становится уже, и есть вертикальное растяжение. Но если [latex]|a|<1[/latex], точка, связанная с конкретным значением [latex]x[/latex], смещается ближе к оси [latex]x[/latex] – , поэтому график кажется шире, но на самом деле происходит сжатие по вертикали. 9{2}}{4a} \end{align}[/latex]

     На практике, однако, обычно легче запомнить, что [latex]h[/latex] – это выходное значение функции, когда входное значение [ латекс]h[/латекс], поэтому [латекс]f\left(h\right)=f\left(-\dfrac{b}{2a}\right)=k[/latex].

     Попробуйте

     Координатная сетка наложена на квадратичную траекторию баскетбольного мяча на рисунке ниже. Найдите уравнение траектории мяча. Стрелок попадает в корзину?

     (кредит: модификация работы Дэна Мейера)

     Показать решение

     Ключевые понятия

     • Полиномиальная функция второй степени называется квадратичной функцией.
     • График квадратичной функции представляет собой параболу. Парабола представляет собой U-образную кривую, которая может открываться как вверх, так и вниз.

       No related posts.