Фанпарк Бобровый лог
FUNCUP: Итоги любительских стартов сезона 2022*23
26 марта в Фанпарке «Бобровый лог» прошел заключительный в этом горнолыжном сезоне этап соревнований среди любителей горных лыж и сноуборда FUNCUP. Третий этап проходил в формате параллельной гонки – участники стартовали парами в два заезда, меняясь курсами. Это, конечно, добавило соревнованиям и зрелищности, и азарта, и помогло участникам в полной мере ощутить дух соперничества на трассе.
Любительский спортивный сезон завершен, все баллы подсчитаны и подведены результаты.
Напомним, FUN CUP – любительские соревнования среди горнолыжников и сноубордистов в личном зачете в возрасте от 14 лет и старше, у спортсменов-любителей есть две попытки на то, чтобы продемонстрировать свою технику и доказать превосходство. Длина трассы – 400 метров.
Имена победителей и призёров III этапа FUNCUP:
Горные лыжи/ Женщины:
1 место – Анастасия Каплунова
2 место – Диана Морозова
3 место – Кира Поливаева
протокол
Горные лыжи/ Мужчины:
1 место – Дмитрий Кудин
2 место – Дмитрий Гришин
3 место – Дмитрий Каторгин
протокол
Горные лыжи/ Женщины 50+:
1 место – Ирина Кузема
протокол
Горные лыжи/ Мужчины 50+:
1 место – Дмитрий Величка
2 место – Андрей Должников
3 место – Дмитрий Чабан
протокол
Горные лыжи/ Женщины PRO:
1 место – Дарья Андриянова
2 место – Елена Колосова
3 место – Елизавета Рычкова
протокол
Горные лыжи/ Мужчины PRO:
1 место – Кирилл Бугаев
2 место – Георгий Бутор
3 место – Артем Жавнер
протокол
Сноуборд/ Женщины:
1 место – Марина Жидкова
2 место – Амайя Клинова
3 место – Елена Копытова
протокол
Сноуборд/ Мужчины:
1 место – Дмитрий Миханошин
2 место – Александр Помазанов
3 место – Роман Парамонов
протокол
Сноуборд/ Женщины PRO:
1 место – Анастасия Ушенина
протокол
Сноуборд/ Мужчины PRO:
1 место – Роман Морозов
2 место – Андрей Кибисов
3 место – Дмитрий Кибисов
протокол
Абсолютными победителями Кубка FUN CUP сезона 2022*23, набравшими максимальное количество баллов по сумме трех этапов соревнований, стали:
Ирина Кузема (300 баллов, горные лыжи 50+)
Андрей Должников (180 баллов, горные лыжи 50+)
Дарья Андриянова (280 баллов, горные лыжи PRO)
Кирилл Бугаев (300 баллов, горные лыжи PRO)
Анастасия Каплунова (250 баллов, горные лыжи)
Дмитрий Кудин (260 баллов, горные лыжи)
Марина Жидкова (280 баллов, сноуборд PRO)
Роман Морозов (200 баллов, сноуборд PRO)
Марина Жидкова (280 баллов, сноуборд)
Дмитрий Миханошин (200 баллов, сноуборд)
Лидеры сезона получили заслуженные победные кубки и подарочные абонементы на будущий горнолыжный сезон 2022*23 — всех поздравляем! Очень рады видеть новые лица на пьедестале!
фотоальбом смотрите в нашей группе в VK: https://vk.
Читать больше ➔
25 марта Финалы Кубка России по волейболу на снегу, не пропустите!
25 марта состоятся финалы Кубка России по волейболу на снегу! И это уникальный шанс увидеть настоящий снежный волейбол в нашем городе!
В своем telegram-канале глава города Владислав Логинов отметил:
«Таких соревнований в Красноярске еще не проводили! Удобную снежную площадку специалисты подготовили в Фанпарке «Бобровый лог». К нам в Красноярск приехали 12 профессиональных команд со всей России».
Для участия в Красноярск приехали сильнейшие спортсмены страны из Москвы, Нового Уренгоя, Московской области, Брянска, Татарстана, Санкт-Петербурга – в том числе, первые чемпионы Европы по данному виду спорта. Участвуют и хозяева турнира – красноярцы, которые уже смогли произвести настоящую сенсацию: команда «Флайбол», впервые принимающая участие в соревнованиях, сумела обыграть опытных соперников из Санкт-Петербурга и Татарстана и пробиться в полуфинал.
 д.)
· Театр оперы и балета (отправление через 20 минут после старта движения от ТЦ Авиатор – в 10:20, 12:20 и т.д.)
подробное расписание шаттлов размещено здесь
д.)
· Театр оперы и балета (отправление через 20 минут после старта движения от ТЦ Авиатор – в 10:20, 12:20 и т.д.)
подробное расписание шаттлов размещено здесь
Читать больше ➔
Сдать анализы в Сухом Логу, ул. Фучика, д. 16 – перечень анализов, график работы
+7 (343) 734-47-87
Список услуг:
Для вашей безопасности мы разделили потоки пациентов.В часы приема биоматериала на COVID-19 сдать остальные исследования можно только при условии сдачи биоматериала на COVID-19.
- Анализы для детей (мочи, кала)
- Анализы крови, мочи, кала
- Гинекологические анализы
- Урологические анализы
- Врач-косметолог
Дополнительные услуги
Врач-косметолог
Записаться
Как нас найти
показать на карте
панорама
График работы в отделениях
Цены на популярные анализы
Код исследования
Наименование
Цена, руб
11-10-001
Общий анализ крови (CBC/Diff — 5 фракций лейкоцитов)
255 р.
85-85-001
Общий анализ мочи
261 р.
61-00-176
Выявление РНК коронавируса COVID-19 (SARS-CoV-2), соскоб из ротоглотки и носоглотки
1100 р.
31-20-001
ТТГ чувствительный (тиреотропный гормон)
279 р.
23-12-001
Глюкоза
144 р.
Ограничение
на взятие биоматериала
Подробнее
Правила
подготовки
Подробнее
Работа без выходных
Оплата банковскими картами
Сведения о юридическом лице
Наименование:
ООО «Профис-Мед»
Юридический адрес:
624800, Свердловская область, г. Сухой Лог, ул. Фучика, д.16, пом. 74
Сухой Лог, ул. Фучика, д.16, пом. 74
Фактический адрес:
624800, Свердловская область, г. Сухой Лог, ул. Фучика, д.16, пом. 74
Лицензия:
ЛО-66-01-003536 от 20.08.2015 Министерство здравоохранения Свердловской обл.
на осуществление медицинской деятельности
Перезвоните мне
ПодпискиКак построить график логарифмической функции?
ПримерыБольше примеров
Purplemath
Логарифмы — это уничтожение экспонент. Например, поскольку 3 4 = 81, то log 3 (81) = 4.
журналы.
Содержимое продолжается ниже
MathHelp.
 com
comОднако это не означает, что графическое отображение журналов является «трудным»; просто это требует немного дополнительной осторожности.
По природе логарифма большинство логарифмических графиков имеют тенденцию иметь одинаковую форму, выглядя (на первый взгляд) как графики квадратного корня:
слева не дальше x = 0. Квадратный корень из нуля, конечно, равен нулю, поэтому график квадратного корня начинается с точки ( x , y ) = (0, 0). Затем он изгибается вправо и растет вбок быстрее, чем вверх.
В отличие от графика квадратного корня, график логарифма проходит через точку (1, 0). С этого момента график уходит вправо, как и в случае функции извлечения квадратного корня, расширяясь в стороны быстрее, чем вверх.
Однако слева от точки (1, 0) график логарифмической функции совсем другой. Вместо того, чтобы просто заканчиваться в точке (1, 0), график пересекает горизонтальную ось и скользит вниз по положительной стороне оси y .
Помня, что логарифмы являются инверсиями экспоненты, эта форма логарифмического графика имеет смысл: логарифмический график, являющийся обратным экспоненциальному, будет просто «переворотом» графика экспоненты:
Как на приведенных выше изображениях выделены экспоненциальные графики, снующие вдоль горизонтальной оси, едва выше оси, пока не пересекают вертикальную ось, обычно в точке (0, 1), в которой график очень быстро растет, увеличивая масштаб вверх намного быстрее, чем он движется. боком.
Логарифмические графики, обратные экспоненциальным графикам (т. е. являющиеся результатом переворота вокруг линии y = x ), ведут себя в обратном направлении от этого. Они бегут *вверх* по вертикальной оси, чуть правее оси, пока она не пересекает горизонтальную ось, обычно в точке (1, 0), после чего график очень медленно растет, приближаясь вбок быстрее, чем вверх.
Начертить экспоненту довольно просто. Например, на графике y = 2 x , вам нужно просто подставить некоторые значения для x , вычислить соответствующие значения y и нанести точки. Конечно, значения y растут очень быстро, поэтому у вас, как правило, получается высокий тонкий график, и вы быстро прекращаете рисовать точки.
Конечно, значения y растут очень быстро, поэтому у вас, как правило, получается высокий тонкий график, и вы быстро прекращаете рисовать точки.
Но как составить график журналов? Есть два варианта. Вот первый:
Как построить график логарифмической функции шаг за шагом?
Для построения графика логарифмической функции:
- Всегда помните, что журналы обратны экспоненциалам; это напомнит вам о форме, которую вы должны ожидать от графика.
- Выберите входные значения (то есть x -значения), которые являются степенями основания; например, если основание журнала равно 5, тогда выберите значения x , такие как 5 2 и 5 −1 .
- Список соответствующих y -значений; например, лог 5 (5 2 ) = 2 = y и log 5 (5 −1 ) = −1 = y
- Нанесите точки, следя за тем, чтобы график не пересекал вертикальную асимптоту.

- Эскиз линии для графика.
Вот как процесс выглядит при использовании:
- График y = log 2 ( x ).
Чтобы изобразить это на графике, используя свое понимание (а не считывая информацию с экрана калькулятора), мне нужно сначала помнить, что журналы не определены для отрицательных x или для x = 0. Из-за этого ограничения на домен (то есть на входные значения) журнала я даже не буду пытаться найти y -значения, скажем, для x = −3 или x = 0. На самом деле вертикальная линия x = 0 на самом деле является вертикальной асимптотой, которую я не могу пересечь.
Вместо этого я начну с x = 1 и буду работать оттуда, используя определение журнала.
- Так как 2 0 = 1, то запишите 2 (1) = 0, а (1, 0) находится на графике.
- Так как 2 1 = 2, то log 2 (2) = 1, и (2, 1) находится на графике.

- Поскольку 3 не является степенью числа 2, то log 2 (3) будет каким-то беспорядочным значением. Поэтому я не буду строить графики x = 3, .
- Так как 2 2 = 4, то log 2 (4) = 2, и (4, 2) находится на графике.
- Поскольку 5, 6 и 7 также не являются степенями двойки, я пропущу их и перейду к x = 8.
- Так как 2 3 = 8, то log 2 (8) = 3, поэтому (8, 3) находится на графике.
- Следующая степень числа 2 равна 16: поскольку 2 4 = 16, то log 2 (16) = 4, и (16, 4) находится на графике.
- Следующая степень числа 2, равная x = 32, на мой вкус слишком велика; Мне не хочется рисовать такой широкий график, поэтому я закончу на 9.0023 x = 16,
Приведенное выше дает мне точку (1, 0) и несколько точек вправо, но что мне делать со значениями x от 0 до 1?
Для этого интервала мне нужно мыслить в терминах отрицательных степеней и обратных величин. Подобно тому, как левая половина экспоненциальной функции имеет мало графически отображаемых точек (поскольку остальные из них просто слишком близки к оси x , чтобы их можно было различить), так и нижняя половина логарифмической функции имеет мало графически отображаемых точек. , остальные слишком близки к y — ось должна быть различима. Но я могу найти несколько точек на графике:
Подобно тому, как левая половина экспоненциальной функции имеет мало графически отображаемых точек (поскольку остальные из них просто слишком близки к оси x , чтобы их можно было различить), так и нижняя половина логарифмической функции имеет мало графически отображаемых точек. , остальные слишком близки к y — ось должна быть различима. Но я могу найти несколько точек на графике:
- Поскольку 2 −1 = ½ = 0,5, то log 2 (0,5) = -1, и (0,5, -1) находится на графике.
- Поскольку 2 −2 = ¼ = 0,25, то log 2 (0,25) = –2, и (0,25, –2) находится на графике.
- Так как 2 −3 = 1 / 8 = 0,125, то log 2 (0,125) = -3, а (0,125, -3) находится на графике.
- Следующая степень числа 2 (поскольку x медленно сползает влево) равна 1 / 16 = 2 −4 , но значение x для точки (0,0625, −4) кажется слишком маленьким, чтобы возиться с (это слишком близко к оси y , чтобы ее можно было различить), поэтому я уйду с точками, которые я уже нашел.

Перечисляя эти точки, я получаю Т-диаграмму:
Рисую точки, а затем рисую линию (вспоминая , а не , чтобы перейти влево от оси y !), я получаю этот график:
Будьте в курсе и смиритесь с тем, как работают силы, и графические журналы не должны вызывать особых проблем.
URL: https://www.purplemath.com/modules/graphlog.htm
Стр. 2 Стр. 3
Вычисление и построение логарифмических функций — Промежуточная алгебра
Экспоненциальные и логарифмические функции
0 0Цели обучения
К концу этого раздела вы сможете:
- Преобразование экспоненциальной формы в логарифмическую
- Вычисление логарифмических функций
- График Логарифмические функции
- Решение логарифмических уравнений
- Использование логарифмических моделей в приложениях
Прежде чем начать, пройдите этот тест на готовность.
- Решить:
Если вы пропустили эту проблему, просмотрите (рисунок).
- Оценка:
Если вы пропустили эту проблему, просмотрите (рисунок).
- Решить:
Если вы пропустили эту проблему, просмотрите (рисунок).
Мы потратили некоторое время на поиск обратной функции. Хорошо работает «отмена» операции другой операцией. Вычитание «отменяет» сложение, умножение «отменяет» деление, извлечение квадратного корня «отменяет» возведение в квадрат.
Изучая экспоненциальную функцию, мы увидели, что она взаимно однозначна, поскольку ее графики проходят тест горизонтальной линии. Это означает, что экспоненциальная функция имеет обратную. Если мы попробуем наш алгебраический метод найти обратную, мы столкнемся с проблемой.
Чтобы справиться с этим, мы определяем логарифмическую функцию с основанием a как обратную экспоненциальной функции. Мы используем обозначение и говорим, что обратная функция экспоненциальной функции является логарифмической функцией.
Логарифмическая функция
Функция представляет собой логарифмическую функцию с основанием , где и
Преобразование между экспоненциальной и логарифмической формами
Поскольку уравнения и эквивалентны, мы можем перемещаться между ними вперед и назад. Этот метод часто используется для решения некоторых экспоненциальных и логарифмических уравнений. Чтобы помочь с преобразованием туда и обратно, давайте внимательно посмотрим на уравнения. См. (Рисунок). Обратите внимание на положение показателя степени и основания.
Если мы осознаем, что логарифм является показателем степени, это упрощает преобразование. Вы можете повторить: «От основания до степени дайте нам число».
Преобразование в логарифмическую форму: ⓐ ⓑ и ⓒ
Преобразование в логарифмическую форму: ⓐ ⓑ ⓒ
Преобразование в логарифмическую форму: ⓐ ⓑ ⓒ
В следующем примере мы делаем обратное — преобразуем формальную логарифмическую форму в экспоненциальную логарифмическую форму. {3} \ hfill \ \ \text{При одинаковом основании степени должны быть равны.}\hfill & & & \hfill x& =\hfill & 3\hfill & \text{Поэтому}\phantom{\rule{0.2em}{0ex} {\ text {log}} _ {\ frac {1} {2}} \ frac {1} {8} = 3 \ hfill \ end {массив}
*** Сообщение об ошибке:
Отсутствует # в преамбуле выравнивания.
начальный текст: $\begin{массив}{}
Вкладка «Дополнительное выравнивание» изменена на \cr.
начальный текст: $\begin{массив}{}\\ \\ &
Вкладка «Дополнительное выравнивание» изменена на \cr.
начальный текст: $\begin{array}{}\\ \\ & &
Вкладка «Дополнительное выравнивание» изменена на \cr.
начальный текст: $\begin{array}{}\\ \\ & & &
Отсутствует $ вставлен.
начальный текст: …fill \phantom{\rule{1em}{0ex}}{\text{log}}_
Отсутствует $ вставлен.
начальный текст: …0ex}}{\text{log}}_{\frac{1}{2}}\frac{1}{8}&
Вкладка «Дополнительное выравнивание» изменена на \cr.
начальный текст: …0ex}}{\text{log}}_{\frac{1}{2}}\frac{1}{8}&
Вкладка «Дополнительное выравнивание» изменена на \cr.
начальный текст: .
{3} \ hfill \ \ \text{При одинаковом основании степени должны быть равны.}\hfill & & & \hfill x& =\hfill & 3\hfill & \text{Поэтому}\phantom{\rule{0.2em}{0ex} {\ text {log}} _ {\ frac {1} {2}} \ frac {1} {8} = 3 \ hfill \ end {массив}
*** Сообщение об ошибке:
Отсутствует # в преамбуле выравнивания.
начальный текст: $\begin{массив}{}
Вкладка «Дополнительное выравнивание» изменена на \cr.
начальный текст: $\begin{массив}{}\\ \\ &
Вкладка «Дополнительное выравнивание» изменена на \cr.
начальный текст: $\begin{array}{}\\ \\ & &
Вкладка «Дополнительное выравнивание» изменена на \cr.
начальный текст: $\begin{array}{}\\ \\ & & &
Отсутствует $ вставлен.
начальный текст: …fill \phantom{\rule{1em}{0ex}}{\text{log}}_
Отсутствует $ вставлен.
начальный текст: …0ex}}{\text{log}}_{\frac{1}{2}}\frac{1}{8}&
Вкладка «Дополнительное выравнивание» изменена на \cr.
начальный текст: …0ex}}{\text{log}}_{\frac{1}{2}}\frac{1}{8}&
Вкладка «Дополнительное выравнивание» изменена на \cr.
начальный текст: . ..t{log}}_{\frac{1}{2}}\frac{1}{8}& =\hfill &
Вкладка «Дополнительное выравнивание» изменена на \cr.
начальный текст: …\text{Преобразовать в экспоненциальную форму.}\hfill &
..t{log}}_{\frac{1}{2}}\frac{1}{8}& =\hfill &
Вкладка «Дополнительное выравнивание» изменена на \cr.
начальный текст: …\text{Преобразовать в экспоненциальную форму.}\hfill &
Найдите значение ⓐ ⓑ ⓒ
Найдите значение ⓐ ⓑ ⓒ
Когда мы встречаем такое выражение, мы можем найти его точное значение двумя способами. При осмотре мы понимаем, что это означает, какой мощности будет, поскольку мы знаем. Альтернативный способ — установить выражение равным, а затем преобразовать его в показательное уравнение.
Найдите точное значение каждого логарифма без использования калькулятора:
ⓐ
ⓑ и ⓒ
Найдите точное значение каждого логарифма без использования калькулятора:
ⓐ
ⓑ
ⓒ
ⓐ
2.
Графики логарифмических функций
Чтобы построить график логарифмической функции, проще всего преобразовать уравнение в его экспоненциальную форму. Как правило, когда мы ищем упорядоченные пары для графика функции, мы обычно выбираем значение x , а затем определяем соответствующий и -значение.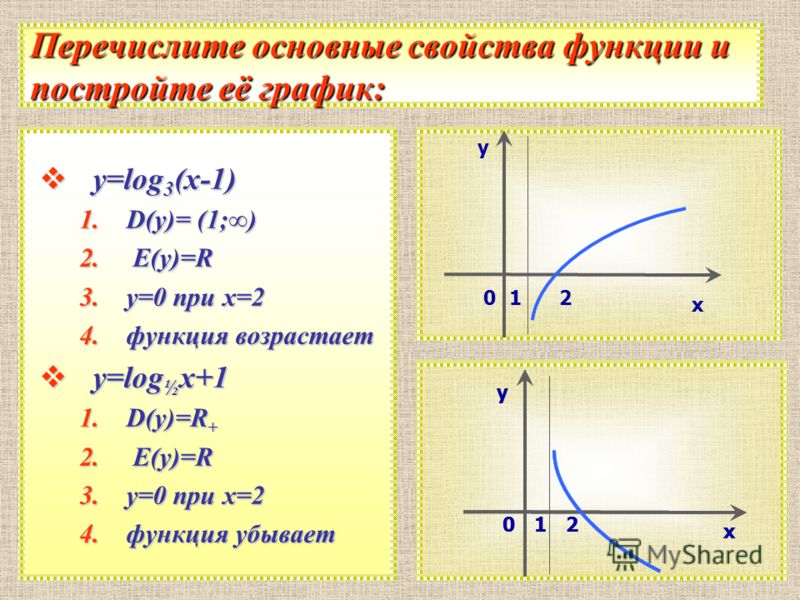 В этом случае вам может быть проще выбрать значения y , а затем определить соответствующее значение x .
В этом случае вам может быть проще выбрать значения y , а затем определить соответствующее значение x .
График
Чтобы построить график функции, мы сначала перепишем логарифмическое уравнение в экспоненциальной форме,
Мы будем использовать точечный график для построения графика функции. Будет проще начать со значений y , а затем получить x .
In the third column below (x, y) we have (1 over 4, 2), (1 over 2, negative 1), (1, 0), (2, 1), (4, 2), and (8, 3).» data-label=»»>| 0 | ||
| 1 | ||
| 2 | ||
| 3 |
График:
График:
Графики и имеют форму, которую мы ожидаем от логарифмической функции, где
Заметим, что для каждой функции график содержит точку Это имеет смысл, потому что означает, что верно для любого a .
График каждой функции также содержит точку Это имеет смысл как среднее значение, верное для любого a .
Заметьте также, что график каждой функции также содержит точку Это имеет смысл как среднее значение, верное для любого a .
Посмотрите еще раз на каждый график. Теперь мы увидим, что многие характеристики логарифмической функции являются просто «зеркальными отражениями» характеристик соответствующей экспоненциальной функции.
Какова область применения функции? График никогда не достигает оси y . Домен состоит из всех положительных чисел. Мы запишем домен в интервальной нотации как
Каков диапазон для каждой функции? Из графиков видно, что диапазон представляет собой множество всех действительных чисел. Ограничений по ассортименту нет. Мы запишем диапазон в интервальных обозначениях как
. Когда график приближается к оси y так близко, но никогда не пересекает ее, мы называем линию y — ось, вертикальная асимптота.
Свойства графика времени
| Домен | |
| Диапазон | |
| Нет | |
| Содержит | |
| Асимптота |
Наш следующий пример смотрит на график когда
График
Чтобы построить график функции, мы сначала перепишем логарифмическое уравнение в экспоненциальной форме,
Мы будем использовать точечный график для построения графика функции.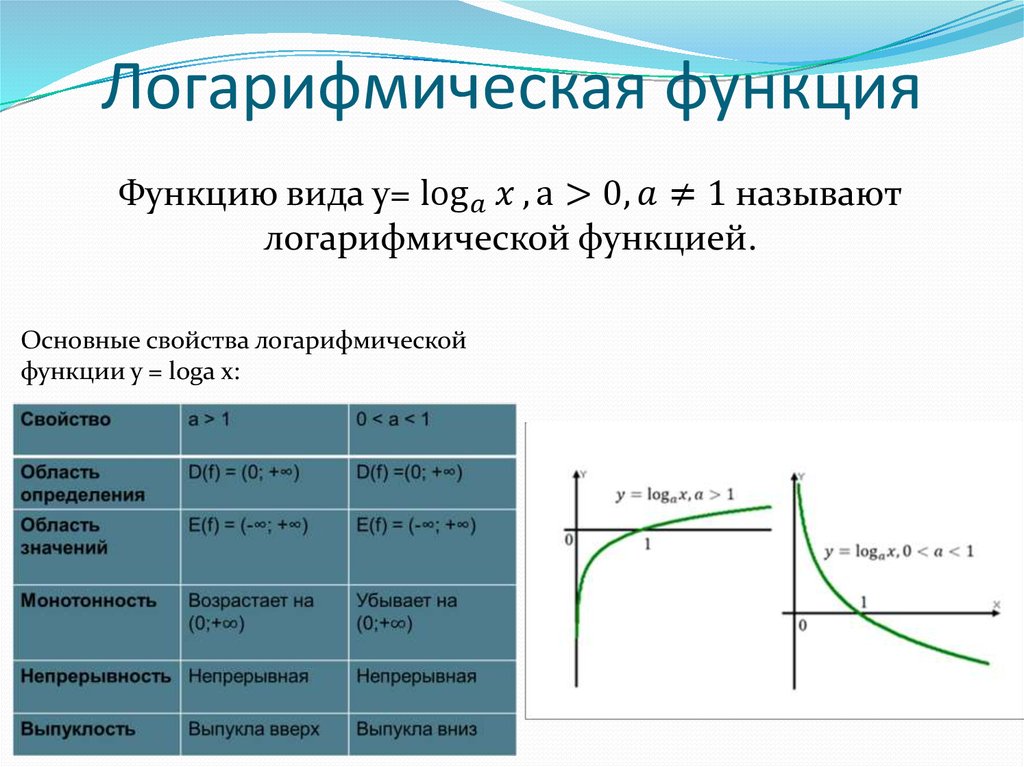 Будет проще начать со значений y , а затем получить x .
Будет проще начать со значений y , а затем получить x .
| 0 | ||
| 1 | ||
| 2 | ||
| 3 |
График:
График:
Теперь давайте посмотрим на графики и , чтобы мы могли определить некоторые свойства логарифмических функций, где
3 имеют одинаковую форму. . Хотя это форма, которую мы ожидаем от логарифмической функции, где
. Хотя это форма, которую мы ожидаем от логарифмической функции, где
Мы снова замечаем, что для каждой функции график содержит точки. Это имеет смысл по тем же причинам, о которых мы говорили выше.
Мы замечаем, что домен и диапазон также совпадают — домен и диапазон равны Ось — снова является вертикальной асимптотой.
Мы суммируем эти свойства в таблице ниже. Которые также включают, когда
Свойства графика
» data-label=»»>| , когда | когда | ||
|---|---|---|---|
| Домен | Домен | ||
| Диапазон | Диапазон | ||
| -перехват | -перехват | ||
| -перехват | нет | -перехват | Нет |
| Содержит | Содержит | ||
| Асимптота | -ось | Асимптота | -ось |
| Основная форма | увеличение | Основная форма | По убыванию |
Ранее мы говорили о том, что логарифмическая функция является обратной экспоненциальной функции Графики на (рисунке) показывают экспоненциальную (синий) и логарифмический (красный) функции на одном графике для обоих и
Примечание как графики являются отражением друг друга через линию Мы знаем, что это верно для обратных функций.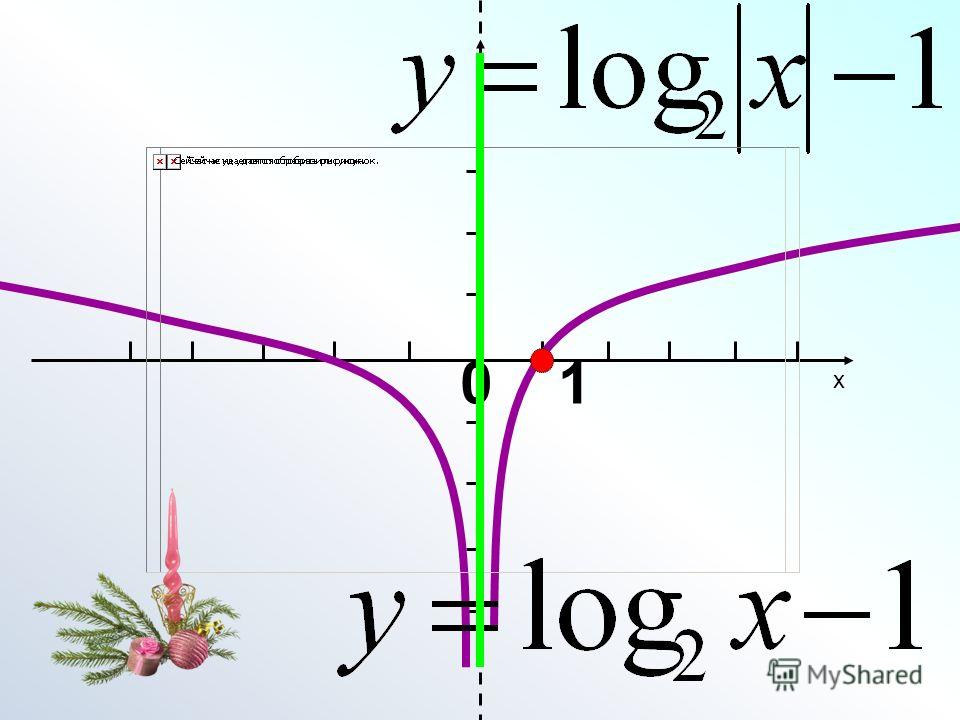 Визуальное представление этих графиков поможет вам запомнить домен и диапазон каждой функции. Обратите внимание на 9Ось 0291 x представляет собой горизонтальную асимптоту экспоненциальной функции, а ось y представляет собой вертикальную асимптоту логарифмической функции.
Визуальное представление этих графиков поможет вам запомнить домен и диапазон каждой функции. Обратите внимание на 9Ось 0291 x представляет собой горизонтальную асимптоту экспоненциальной функции, а ось y представляет собой вертикальную асимптоту логарифмической функции.
Решение логарифмических уравнений
Когда мы говорили об экспоненциальных функциях, мы ввели число e . Точно так же, как и были основанием для экспоненциальной функции, оно также может быть использовано в качестве основания для логарифмических функций. Логарифмическая функция с основанием e называется натуральной логарифмической функцией. Функция обычно записывается, и мы читаем ее как «el en of
Натуральная логарифмическая функция
Функция представляет собой натурально-логарифмическую функцию с основанием, где
Когда основание логарифмической функции равно 10, мы называем ее десятичной логарифмической функцией, и основание не показано. Если основание a логарифма не показано, мы предполагаем, что оно равно 10. состоит в том, чтобы преобразовать уравнение в экспоненциальную форму, а затем решить показательное уравнение, как мы делали раньше. При решении логарифмических уравнений нам нужно помнить, что для основания a , а также область. Как и в случае с радикальными уравнениями, мы должны проверять наши решения, чтобы исключить любые посторонние решения.
Если основание a логарифма не показано, мы предполагаем, что оно равно 10. состоит в том, чтобы преобразовать уравнение в экспоненциальную форму, а затем решить показательное уравнение, как мы делали раньше. При решении логарифмических уравнений нам нужно помнить, что для основания a , а также область. Как и в случае с радикальными уравнениями, мы должны проверять наши решения, чтобы исключить любые посторонние решения.
Solve: ⓐ and ⓑ
ⓐ
ⓑ
Solve: ⓐ ⓑ
ⓐ
ⓑ
Solve: ⓐ ⓑ
ⓐ
ⓑ
Solve: ⓐ и ⓑ
ⓐ
ⓑ
Решить: ⓐ ⓑ
ⓐ
ⓑ
Решить: ⓐ ⓑ
ⓐ
ⓑ
Использование логарифмических моделей в приложениях
Многие приложения моделируются логарифмическими уравнениями. Сначала мы рассмотрим логарифмическое уравнение, которое определяет уровень звука в децибелах (дБ).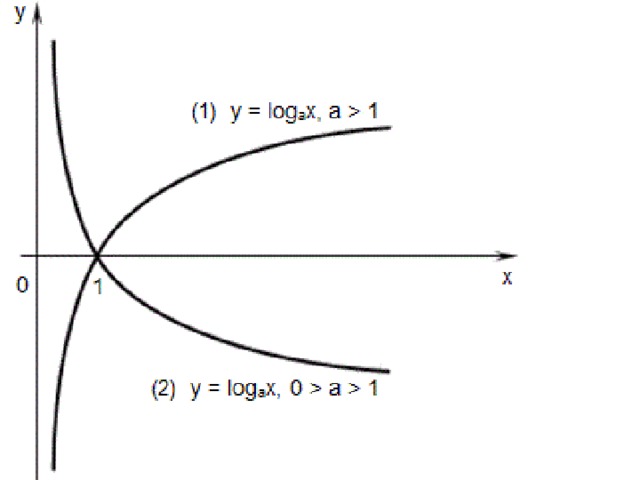 Децибелы варьируются от 0, что едва слышно, до 160, что может привести к разрыву барабанной перепонки. В формуле представляет собой интенсивность звука, который едва слышен.
Децибелы варьируются от 0, что едва слышно, до 160, что может привести к разрыву барабанной перепонки. В формуле представляет собой интенсивность звука, который едва слышен.
Децибел Уровень звука
Уровень громкости, D , измеренный в децибелах, звука силой I , измеренный в ваттах на квадратный дюйм, равен
Продолжительное воздействие шума силой 85 дБ может вызвать необратимое повреждение внутреннего уха, которое приведет к потере слуха. Каков уровень децибел музыки, проходящей через наушники с интенсивностью ватт на квадратный дюйм?
Multiplying gives that D equals 100. Hence, the decibel level of music coming through earphones is 100 dB.» data-label=»»>| Замена уровня интенсивности, I. | |
| Упрощение. | |
| С | |
| Умножение. | |
| Уровень децибел музыки, воспроизводимой через наушники, составляет 100 дБ. |
Какой уровень шума в децибелах у одной из новых бесшумных посудомоечных машин с интенсивностью ватт на квадратный дюйм?
Бесшумные посудомоечные машины имеют уровень шума 50 дБ.
Какой уровень шума в децибелах при интенсивном городском движении с интенсивностью ватт на квадратный дюйм?
Уровень децибел интенсивного трафика составляет 90 дБ.
Магнитуда землетрясения измеряется по логарифмической шкале, называемой шкалой Рихтера. Модель где — интенсивность ударной волны. Эта модель обеспечивает способ измерения интенсивности землетрясений.
Интенсивность землетрясения
Магнитуда R землетрясения измеряется как где I — интенсивность ударной волны.
В 1906 году в Сан-Франциско произошло сильное землетрясение силой 7,8 балла по шкале Рихтера. В результате пожаров было уничтожено более 80% города. В 2014 году в Лос-Анджелесе произошло умеренное землетрясение силой 5,1 балла по шкале Рихтера, причинившее ущерб в размере 108 миллионов фунтов стерлингов. Сравните силы двух землетрясений.
Чтобы сравнить интенсивности, нам сначала нужно преобразовать величины в интенсивности, используя логарифмическую формулу. Затем мы установим коэффициент для сравнения интенсивностей.
Затем мы установим коэффициент для сравнения интенсивностей.
В 1906 году в Сан-Франциско произошло сильное землетрясение силой 7,8 балла по шкале Рихтера. В 1989 году землетрясение в Лома-Приета также затронуло район Сан-Франциско и имело силу 6,9 балла по шкале Рихтера. Сравните силы двух землетрясений.
Интенсивность 19Землетрясение 06 было примерно в 8 раз сильнее землетрясения 1989 года.
В 2014 году в Чили произошло сильное землетрясение магнитудой 8,2 балла по шкале Рихтера. В 2014 году в Лос-Анджелесе также произошло землетрясение силой 5,1 балла по шкале Рихтера. Сравните силы двух землетрясений.
Сила землетрясения в Чили примерно в 1259 раз превышала силу землетрясения в Лос-Анджелесе.
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практических занятий по оценке и построению графиков логарифмических функций.
- Переписывание логарифмических уравнений в экспоненциальной форме
- Упрощение логарифмических выражений
- Графики логарифмических функций
- Использование логарифмов для расчета уровней децибел
Ключевые понятия
- Свойства графика It shows that when a is greater than 1, the domain is 0 to infinity, the range is negative infinity to infinity, the x-intercept is 1, 0, there is no y intercept, the function contains a, 1 and , 1 over a, negative 1, the asymptote is the y axis 0, and the basic shape is increasing. It shows that when a is greater than 0 and less than 1, the domain is 0 to infinity, the range is negative infinity to infinity, the x-intercept is 1, 0, there is no y intercept, the function contains a, 1 and 1 over a, negative 1, the asymptote is the y axis, and the basic shape is decreasing.» data-label=»»>
когда когда Домен Домен Диапазон Диапазон x — перехват x — перехват у — перехват нет y -перехват нет Содержит Содержит Асимптота у -ось Асимптота у -ось Основная форма увеличение Основная форма уменьшение - Децибел Уровень звука: Уровень громкости звука интенсивностью , измеренный в децибелах, , измеренный в ваттах на квадратный дюйм, равен .
- Интенсивность землетрясения: Магнитуда землетрясения измеряется где — интенсивность его ударной волны.

Практика ведет к совершенству
Преобразование экспоненциальной формы в логарифмическую
В следующих упражнениях преобразуйте экспоненциальную форму в логарифмическую.
В следующих упражнениях преобразуйте каждое логарифмическое уравнение в показательную форму.
Evaluate Logarithmic Functions
In the following exercises, найти значение в каждом логарифмическом уравнении.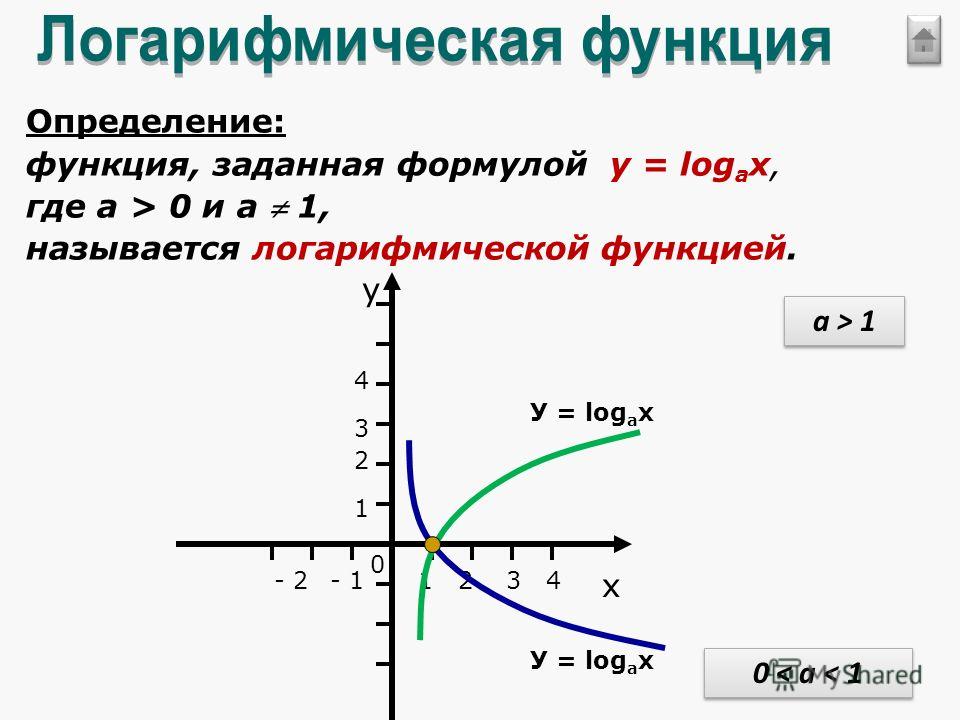
In the following exercises, find the exact value of each logarithm без использования калькулятора.
2
0
График логарифмические функции
В следующих упражнениях, график график.
Solve Logarithmic Уравнения
В следующих упражнениях есть каждая.
Использование логарифмических моделей в приложениях
В следующих упражнениях для решения используйте логарифмическую модель.
Какой уровень громкости в децибелах при обычном разговоре с интенсивностью ватт на квадратный дюйм?
Каков уровень децибел шепота с интенсивностью ватт на квадратный дюйм?
Уровень шума шепота составляет 20 дБ.
Какой уровень шума от мотоцикла в децибелах с интенсивностью ватт на квадратный дюйм?
Каков уровень шума мусоропровода в децибелах с интенсивностью ватт на квадратный дюйм?
Звук мусоропровода имеет уровень децибел 100 дБ.
В 2014 году в Чили произошло сильное землетрясение магнитудой по шкале Рихтера. В 2010 году на Гаити также произошло сильное землетрясение по шкале Рихтера. Сравните силы двух землетрясений.
В районе Лос-Анджелеса часто происходят землетрясения. В 1994 году землетрясение в Нортридже имело магнитуду по шкале Рихтера. В 2014 году в Лос-Анджелесе также произошло землетрясение по шкале Рихтера. Сравните силы двух землетрясений.
Сила землетрясения в Нортридже 1994 года в районе Лос-Анджелеса была примерно в 40 раз выше силы землетрясения 2014 года.



