График натурального логарифма: Натуральные логарифмы. Функция у = lп х, её свойства, график, дифференцирование — урок. Алгебра, 11 класс.

2

Значит ln. Логарифм произведения и логарифм частного

Урок и презентация на темы: «Натуральные логарифмы. Основание натурального логарифма. Логарифм натурального числа»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 11 класса
Интерактивное пособие для 9–11 классов «Тригонометрия»
Интерактивное пособие для 10–11 классов «Логарифмы»

Что такое натуральный логарифм

Ребята, на прошлом уроке мы с вами узнали новое, особенное число – е. Сегодня мы продолжим работать с этим числом.
Мы с вами изучили логарифмы и знаем, что в основании логарифма может стоять множество чисел, которые больше 0. Сегодня мы также рассмотрим логарифм, в основании которого стоит число е. Такой логарифм принято называть натуральным логарифмом. x$ в точке (0;1) равен 45&deg. Тогда угол наклона касательной к графику натурального логарифма в точке (1;0) также будет равен 45&deg. Обе эти касательные будут параллельны прямой $y=x$. Давайте схематично изобразим касательные:

Свойства функции $y=\ln{x}$

1. $D(f)=(0;+∞)$.
2. Не является ни четной, ни нечетной.
3. Возрастает на всей области определения.
4. Не ограничена сверху, не ограничена снизу.
5. Наибольшего значения нет, наименьшего значения нет.
6. Непрерывна.
7. $E(f)=(-∞; +∞)$.
8. Выпукла вверх.
9. Дифференцируема всюду.

В курсе высшей математики доказано, что производная обратной функции есть величина, обратная производной данной функции .
Углубляться в доказательство не имеет большого смысла, давайте просто запишем формулу: $y»=(\ln{x})»=\frac{1}{x}$.

Пример.
Вычислить значение производной функции: $y=\ln(2x-7)$ в точке $х=4$.
Решение.
В общем виде наша функция представляют функцию $y=f(kx+m)$, производные таких функций мы умеем вычислять.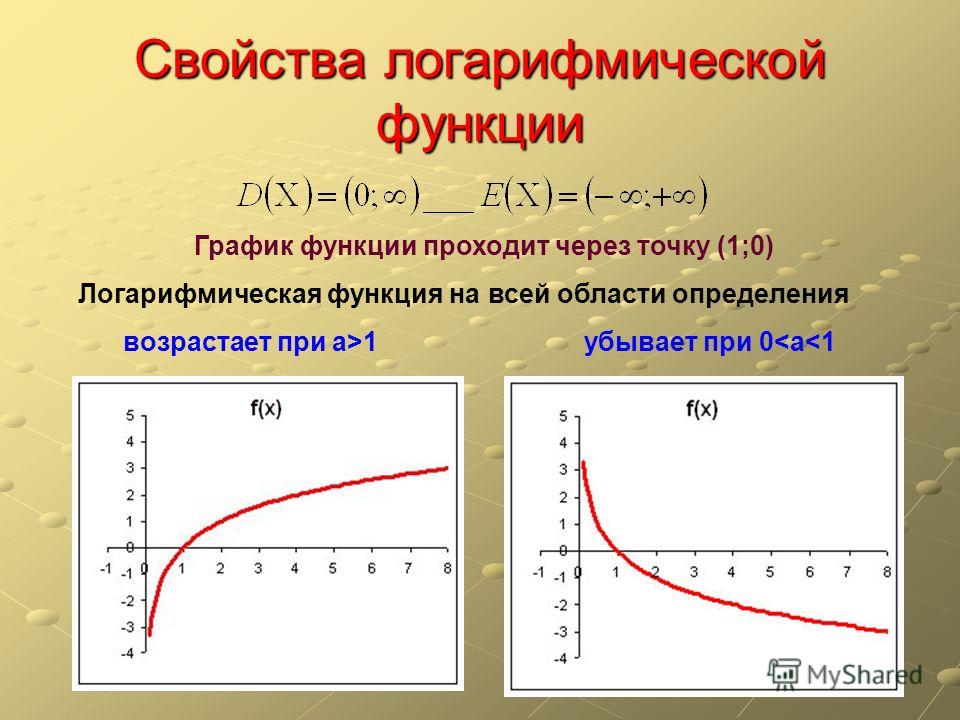

6=1$.
$x=±1$.
Точка $х=-1$ не принадлежит области определения. Тогда имеем одну стационарную точку $х=1$. Найдем промежутки возрастания и убывания:

Точка $х=1$ – точка минимума, тогда $y_min=1-6*\ln{1}=1$.
Ответ: Функция убывает на отрезке (0;1], функция возрастает на луче $}

Справочник по логарифмической функции

Справочник по логарифмической функции

Дополнительно

Показать рекламу

Скрыть рекламу
О рекламе

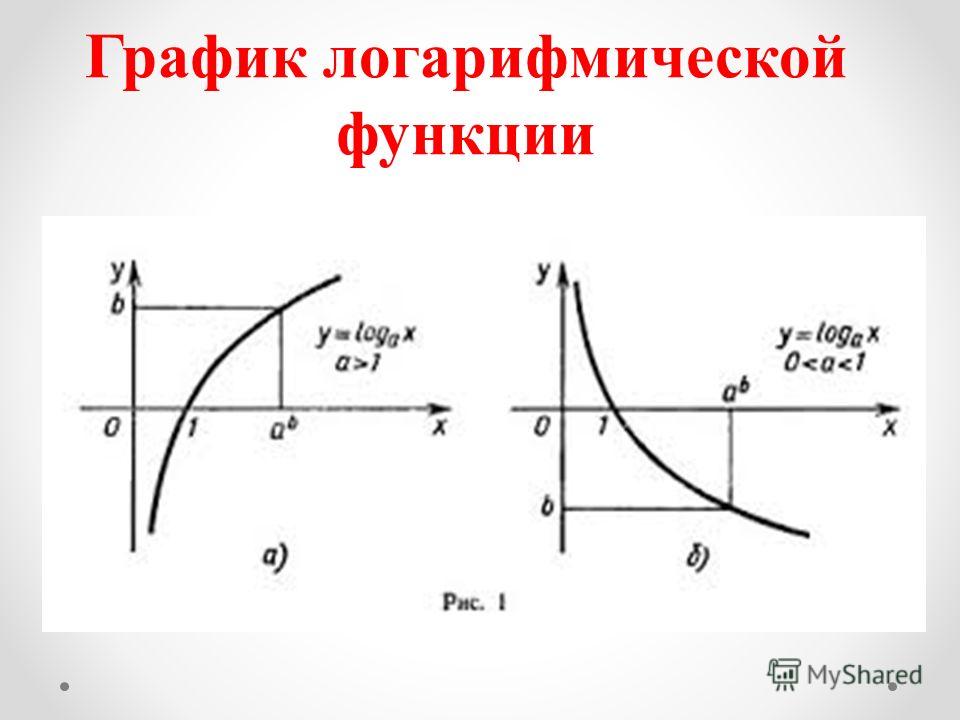
Это логарифмическая функция:

f(x) = log _a (x)

a любое значение больше 0, кроме 1

Свойства зависят от значения «a»

a=1 , график не определен

Кроме того, есть два случая, на которые стоит обратить внимание:

a от 0 до 1		и выше 1
Пример: f(x) = log ½ (x)		Пример: f(x) = log 2 (x)
Для a от 0 до 1 Когда x приближается к 0, оно достигает бесконечности При увеличении x оно достигает — бесконечность Это строго убывающая функция Имеет вертикальную асимптоту вдоль оси Y (x=0).		Для и выше 1: Когда x приближается к 0, оно достигает — бесконечность При увеличении x оно достигает бесконечности это строго возрастающая функция Имеет вертикальную асимптоту вдоль оси Y (x=0).

Постройте график здесь (используйте ползунок «a»)

В общем, логарифмическая функция:

• всегда находится на положительной стороне (и никогда не пересекает) оси Y
• всегда пересекает ось x в точке x=1 … другими словами, она проходит через (1,0)
• равно 1 , когда x=a , другими словами, оно проходит через (a,1)
• — инъективная (однозначная) функция
.

Его областью определения являются положительные действительные числа: (0, +∞)

Его диапазоном являются действительные числа:

Обратное

log _a (x)  является обратной функцией a ^x (экспоненциальная функция)

Таким образом, логарифмическая функция может быть «обращена» экспоненциальной функцией.

Функция натурального логарифма

Это «Натуральный» Функция логарифма:

f(x) = log _e (x)

Где e равно «числу Эйлера» 18…7818 9,018 и т.д.

Но чаще записывают так:

f(x) = ln(x)

«ln» означает «логарифм, натуральный»

Итак, когда вы видите ln(x), просто помните, что это логарифмическая функция с основанием e : log _e (x).

 

График f(x) = ln(x)

В точке (e,1) наклон линии равен 1/e , и линия касается кривой.

 

Copyright © 2017 MathsIsFun.com

Документ без названия

Документ без названия

	Математика 121 — Математика для биологии I Осенний семестр 2003 г. Аллометрическое моделирование — рабочие примеры
	© 1999, Все права защищены, SDSU и Джозеф М. Махаффи Государственный университет Сан-Диего — Последнее обновление этой страницы: 02 октября 2003 г.

Аллометрическое моделирование — Работал Примеры

1. Экспоненциальные и логарифмические функции
2. Экспоненциальное и логарифмическое построение графиков Функции
3. Аллометрические модели

Ниже представлен набор рабочих примеров, в которых используется экспоненциальная функция e и натуральный логарифм ln. А еще есть слово задача о биоразнообразии, чтобы показать приложение к аллометрическим моделирование.

Примеры экспоненциального и логарифмического Функции

Пример 1: Решите уравнение

e ^{x -2} = 3.

Решение:

Натуральный логарифм обеих частей дает

х — 2 = ln(3),

так

х = ln(3) + 2.

Пример 2: Решите уравнение

ln(2 х + 1) = 4.

Решение:

Возводя в степень обе части, находим

2 х + 1 = е ⁴ ,

так

х = ( е ⁴ — 1)/2.

График экспоненциальный и логарифмический Функции

 

Пример 3: Нарисуйте уравнение

ф ( х ) = 4 — е ^{— 2 х} .

Определите все точки пересечения и любые горизонтальные асимптоты.

Решение:

Начнем с поиска перехватов. Когда х = 0, ф (0) = 4 — е ⁰ = 4 — 1 = 3.

Таким образом, точка пересечения y равна (0,3).

Решение 4 — е ^{— 2 х} = 0, дает e ^-2x = 4 или e ^{2 x} = 1/4.

Таким образом, 2 х = ln(1/4) = пер(2 ^-2 ) = -2ln(2) или x = -ln(2) = -0,6931.

Следовательно, точка пересечения x равна (-0,693,0).

Для больших значений x , e ^{— 2 x} очень близко к нулю, поэтому есть горизонтальная асимптота для большого положительного x с f ( x ) стремится к 4.

График показан ниже.

Пример 4: Нарисуйте уравнение

ф ( х ) = ln( х + 2).

Определите все точки пересечения и любые вертикальные асимптоты.

Решение:

Домен f ( x ) равен x > -2. Мы начните с поиска перехватов. Когда х = 0, ф (0) = ln(2) = 0,6931. Таким образом, точка пересечения y равна (0,0,693).

Решение ln( x + 2) = 0, дает х + 2 = 1 или х = -1. Таким образом, точка пересечения x равна (-1, 0).

На краю области имеется вертикальная асимптота, где х = -2.

График показан ниже.

 

Аллометрическое моделирование

Пример 5: Три острова в Тихом океане цепь. Остров А находится в 15 км

2 , Остров B составляет 110 км ² , и Остров С находится в 74 км ² . обширный биологическое исследование обнаружило 5 видов птиц на острове А и 9 видов птиц на острове Б.

а. Предположим, что между числом видов существует степенная зависимость ( N ) на каждом из этих островов и их площадь ( А ) формы

Н = кА ^x .

Использовать данные с островов A и B для определения констант k и ^x . Используйте это выражение, чтобы предсказать количество видов на острове. С.

б. Какой размер острова потребуется для поддержки 20 видов птиц возле этой цепи островов?

Решение:

а. Натуральный логарифм обеих частей данного степенного закона отношение, а затем решение для наклона

x , получаем

ln( N ) = ln( k ) + x ln( A )

Мы можем использовать этот наклон с любой из точек ( A, N ), чтобы найти ln( k )

ln(5) = ln( к ) + 0,295 Ин(15)

ln( k ) = ln(5) — 0,295 ln(15) = 0,811

к = 2,25

Таким образом, отношение степенного закона определяется выражением

.