20 баллов , Ребят помогите пожалуйста. Заранее спасибо. Даю 20 баллов…
Знайдіть sin a якщо ctg a=√3 і п <а< 3п\2…
Помогите пожалуйста
2sin240+tg120-cos540=…
Упростите выражение 36b-4b+13b…
Xy во 2 степени -13xy во 2 степени +5xy во 2 степени…
Математика
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий языкМХК
ОБЖ
Психология
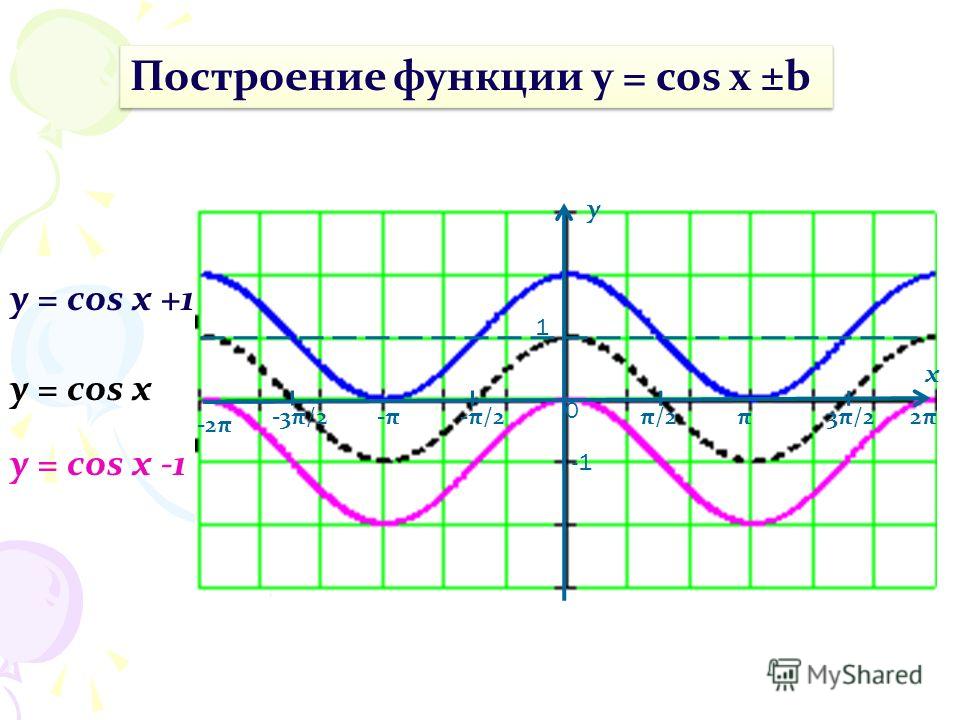
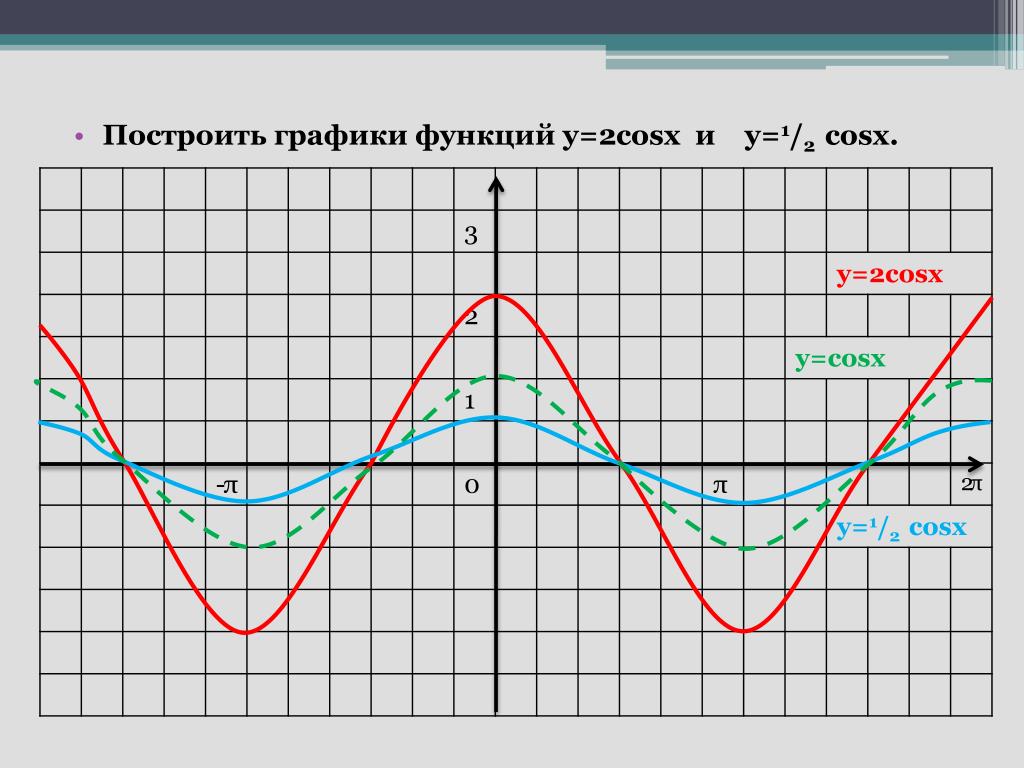
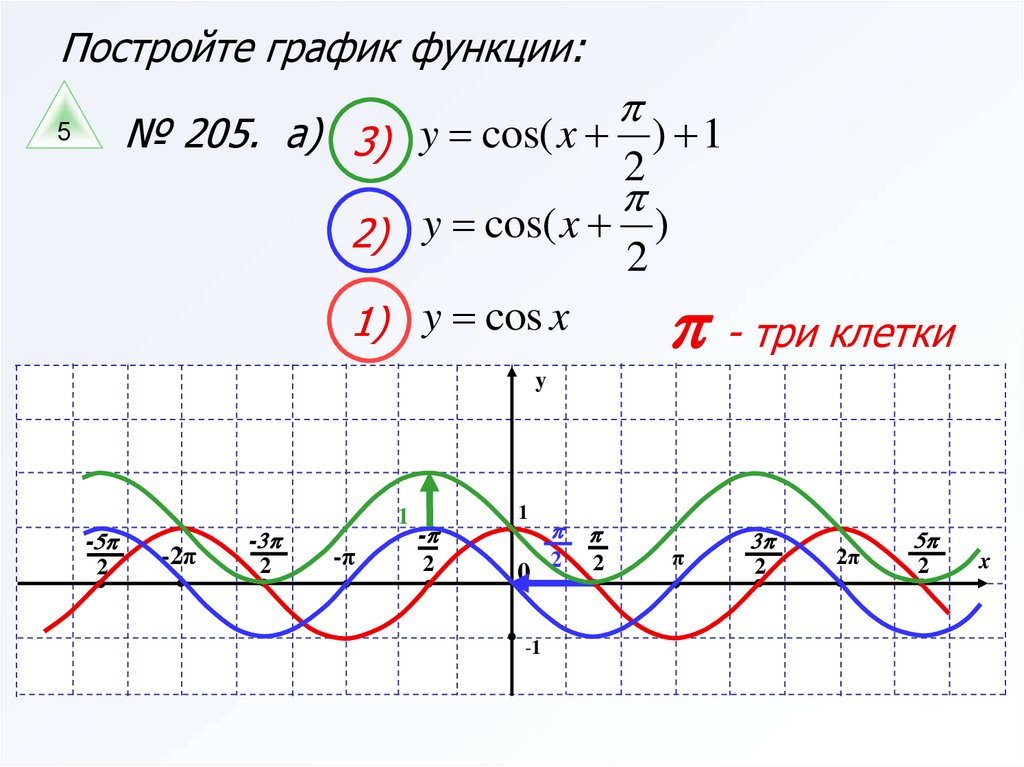
Постройте график функции cos п 2 x.
 Графики тригонометрических функций кратных углов
Графики тригонометрических функций кратных угловДополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
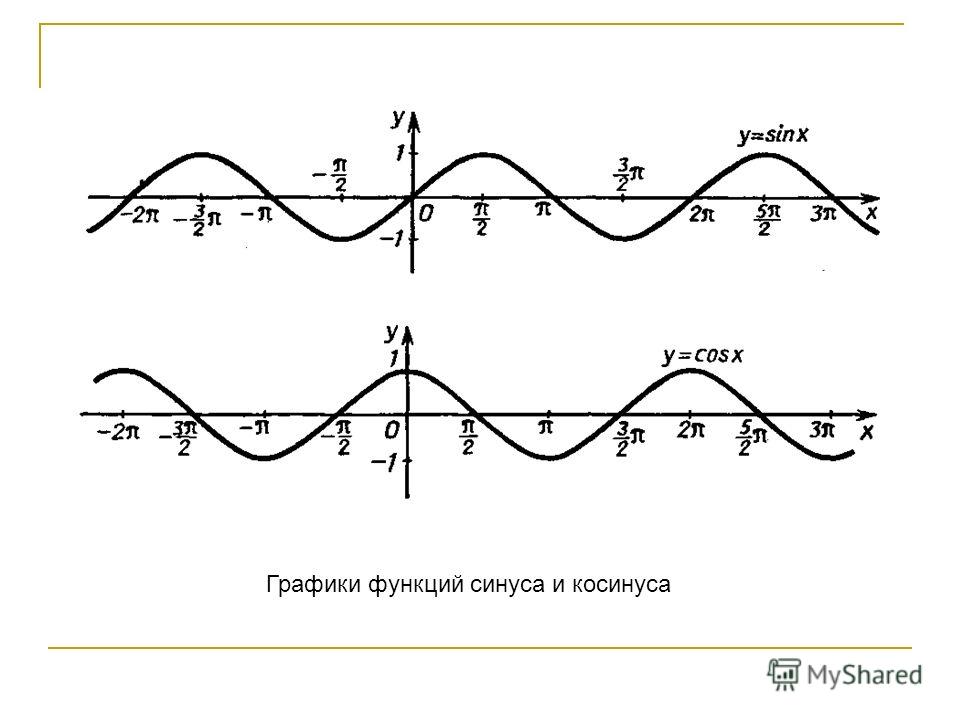
Определение функции косинуса у=cos(x)
Ребята, мы уже познакомились с функцией Y=sin(X).
Давайте вспомним одну из формул привидения : sin(X + π/2) = cos(X).
Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.
График функции sin(X + π/2) получается из графика функции sin(X) параллельным переносом на π/2 единиц влево. Это и будет график функции Y=cos(X).
График функции Y=cos(X) так же называют синусоидой.
Свойства функции cos(x)
- Запишем свойства нашей функции:
- Область определения – множество действительных чисел.
- Функция четная. Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
- Функция Y=cos(X) убывает на отрезке и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
- Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1 - Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
- Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
- Область значений отрезок [- 1; 1]. Это также хорошо видно из графика.

- Функция Y=cos(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Примеры с функцией cos(x)
1. Решить уравнение cos(X)=(x — 2π) 2 + 1
Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π) 2 + 1 (см. рисунок).
y=(x — 2π) 2 + 1 — это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.
2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0
Решение: Чтобы построить требуемый график, давайте построим два графика функции по «кусочкам». Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
при x ≥ 0. Изобразим оба «кусочка» на одном
графике.
3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.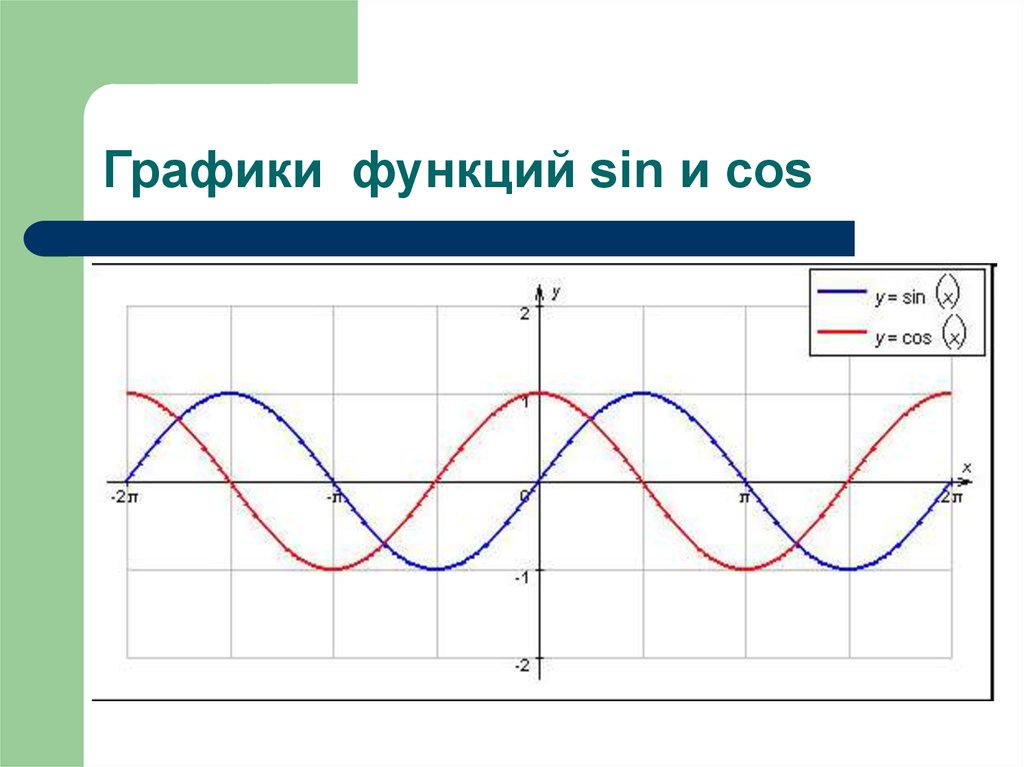
Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.
4. Построить график функции y=cos(π/3 — x) + 1
Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.
Задачи для самостоятельного решения
1)Решить уравнение: cos(x)= x – π/2.
2) Решить уравнение: cos(x)= — (x – π) 2 — 1.
3) Построить график функции y=cos(π/4 + x) — 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке .
6) Найти наибольшее и наименьшее значение функции
y=cos(x) на отрезке [- π/6; 5π/4].
Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.
Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
у 0 = sin x 0 .
Преобразуем это соотношение следующим образом:
Следовательно, функция у = sin ωx при х = x 0 / ω принимает то же самое значение у 0 , что и функция у = sin х при х = x 0 . А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у = sin x . Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.
Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.
График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.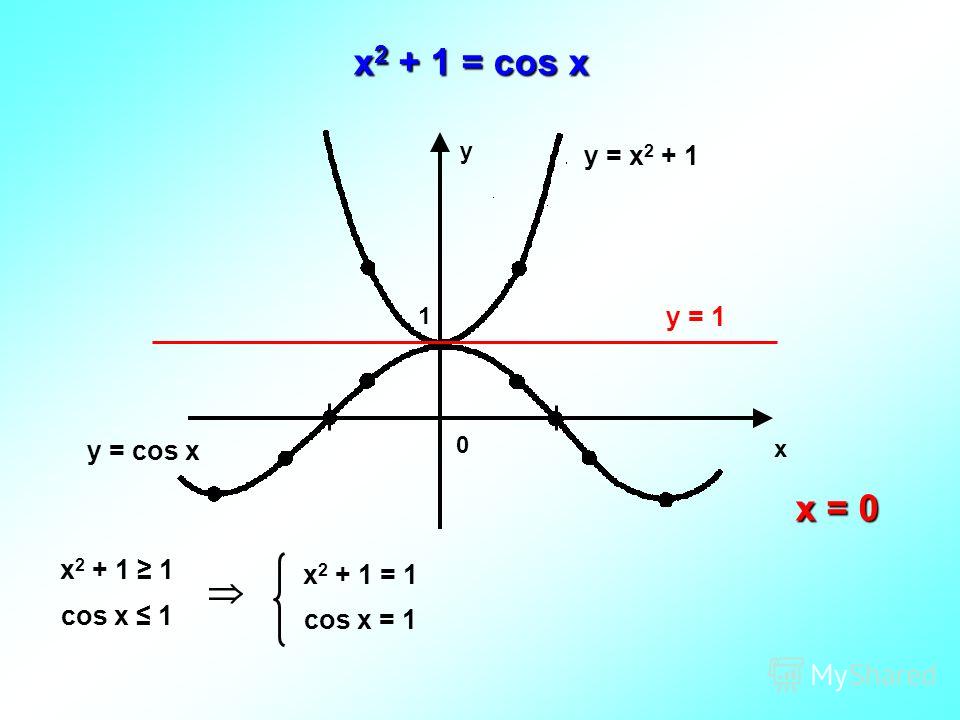
Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π
/ x / 2 = 4π .
Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :
Аналогично строятся графики и других тригонометрических функций кратных углов. На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.
На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.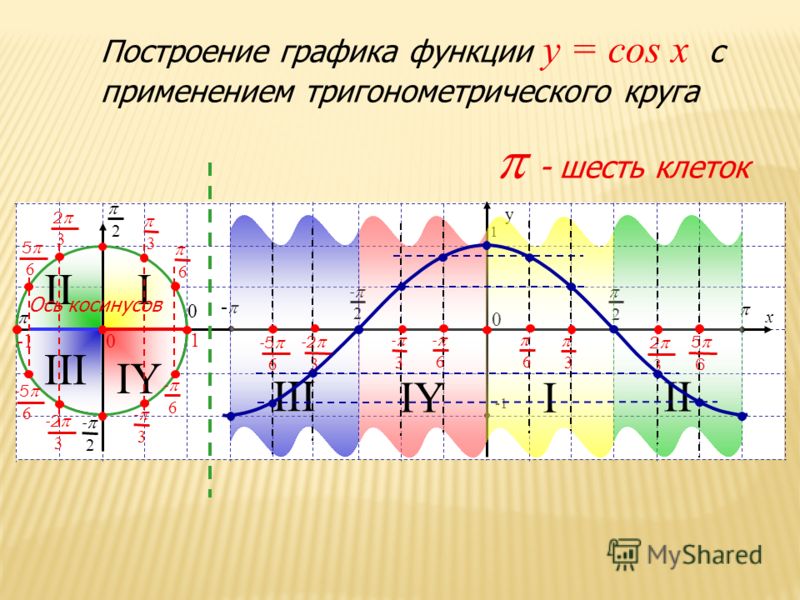
График функции у = tg x / 2 , полученный «растяжением» тангенсоиды у = tg x вдвое вдоль оси х.
И, наконец, анимация, выполненная программой Maple:
Упражнения
1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.
а). y = sin 4x / 3 г). y = tg
б). у= cos 5x / 3 д). у = ctg 5x / 3 з). у= ctg x / 3
в). y = tg 4x / 3 е). у = sin 2x / 3
2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).
3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.
4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .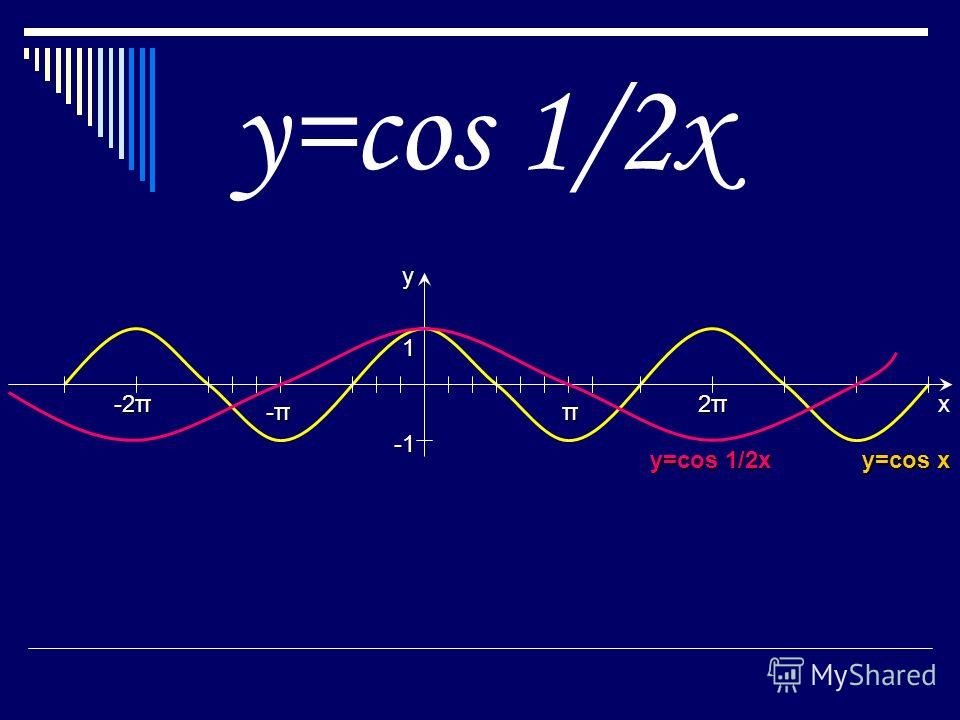
5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.
6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.
«Графики функций и их свойства» — y = ctg x. 4) Ограниченность функции. 3) Нечётная функция. (График функции симметричен относительно начала координат). y = tg x. 7) Функция непрерывна на любом интервале вида (?k; ? + ?k). Функция y = tg x непрерывна на любом интервале вида. 4) Функция убывает на любом интервале вида (?k; ? + ?k). График функции y = tg x называется тангенсоидой.
«График функции Y X» — Шаблон параболы у = х2. Чтобы увидеть графики, щелкни мышкой. Пример 2. Построим график функции y = x2 + 1, опираясь на график функции y=x2 (щелчок мышкой). Пример 3. Докажем, что графиком функции у = х2 + 6х + 8 является парабола, и построим график. График функции y=(x — m)2 является параболой с вершиной в точке (m; 0).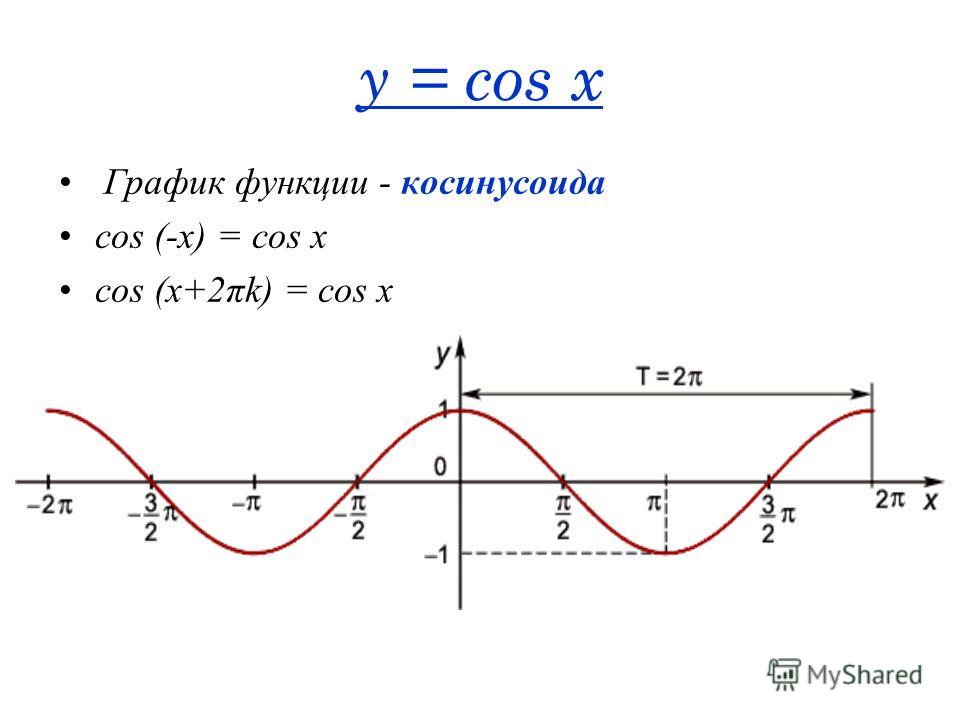
«Математика графики» — Как можно строить графики? Наиболее естественно функциональные зависимости отражаются с помощью графиков. Интересное применение: рисунки,… Зачем мы изучаем графики? Графики элементарных функций. Что вы можете нарисовать с помощью графиков? Рассматриваем применение графиков в учебных предметах: математике, физике,…
«Построение графиков с помощью производной» — Обобщение. Построить эскиз графика функции. Найти асимптоты графика функции. График производной функции. Дополнительное задание. Исследовать функцию. Назвать промежутки убывания функции. Самостоятельная работа учащихся. Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.
«Графики с модулем» — Отобрази «нижнюю» часть в верхнюю полуплоскость. Модуль действительного числа. Свойства функции y = |x|. |x|. Числа. Алгоритм построения графика функции. Алгоритм построения. Функция y= lхl. Свойства. Самостоятельная работа. Нули функции. Советы великих.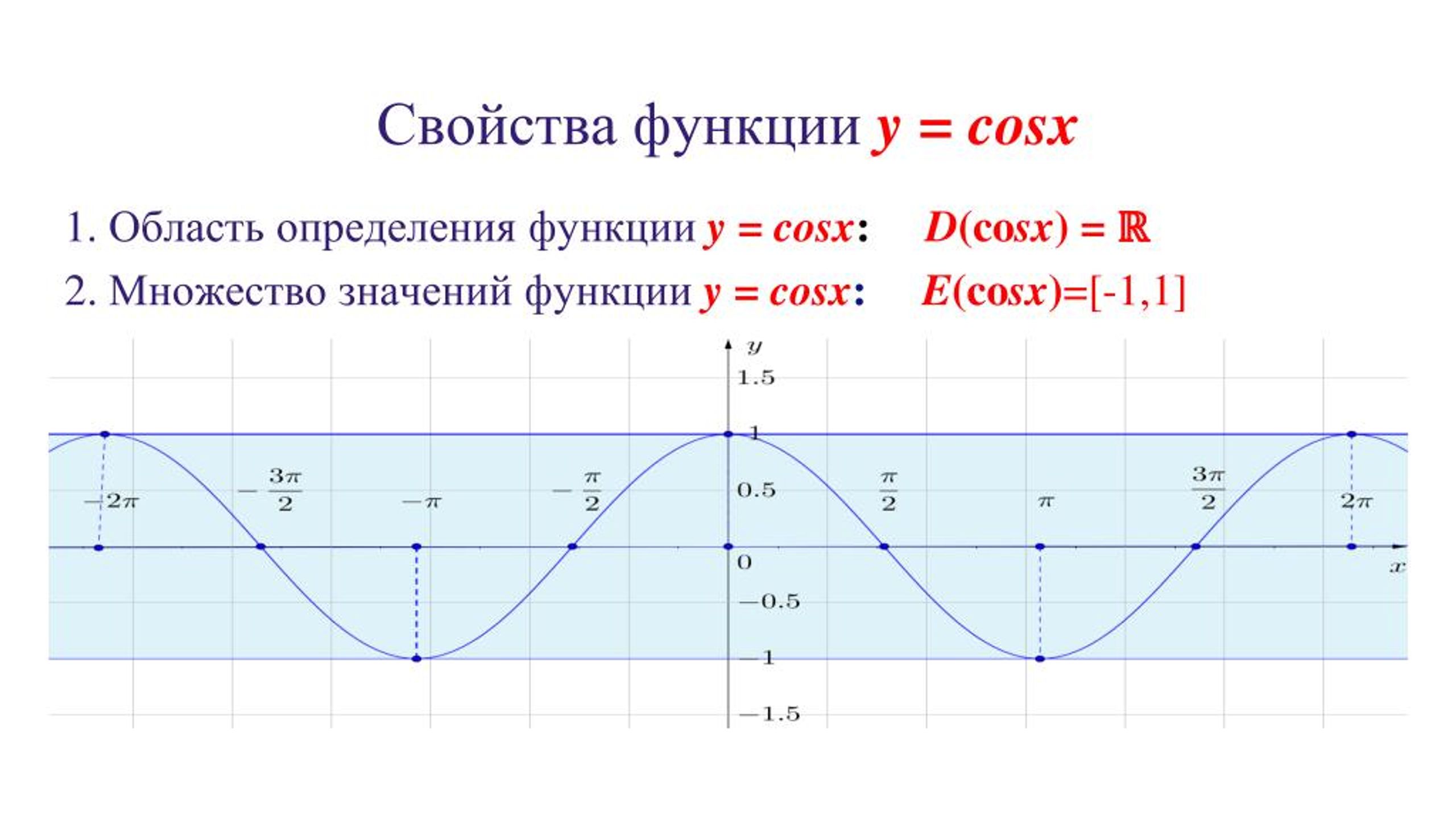 Решение самостоятельной работы.
Решение самостоятельной работы.
«Уравнение касательной» — Уравнение касательной. Уравнение нормали. Если,то и кривые пересекаются под прямым углом. Условия параллельности и перпендикулярности двух прямых. Угол между графиками функций. Уравнение касательной к графику функции в точке. Пусть функция дифференцируема в точке. Пусть прямые заданы уравнениями и.
Всего в теме 25 презентаций
Графики функции синуса и косинуса
Результаты обучения
- Определите амплитуду, период, фазовый сдвиг и вертикальный сдвиг графика синуса или косинуса из его уравнения.
- График вариантов y=cos x и y=sinx .
- Определите формулу функции, которая будет иметь заданный синусоидальный график.
- Определите функции, моделирующие круговое и периодическое движение.
Графические вариации y=sin(x) и y=cos(x)
Напомним, что функции синуса и косинуса связывают действительные числа с x – и y – координаты точки на единичной окружности. Так как же они выглядят на графике в координатной плоскости? Начнем с функции синуса . Мы можем создать таблицу значений и использовать их для построения графика. В таблице ниже перечислены некоторые значения функции синуса на единичном круге.
Так как же они выглядят на графике в координатной плоскости? Начнем с функции синуса . Мы можем создать таблицу значений и использовать их для построения графика. В таблице ниже перечислены некоторые значения функции синуса на единичном круге.
| х | 0 | [латекс]\frac{\pi}{6}[/латекс] | [латекс]\frac{\pi}{4}[/латекс] | [латекс]\frac{\pi}{3}[/латекс] | [латекс]\frac{\pi}{2}[/латекс] | [латекс]\frac{2\pi}{3}[/латекс] | [латекс]\frac{3\pi}{4}[/латекс] | [латекс]\frac{5\pi}{6}[/латекс] | [латекс]\pi[/латекс] |
| [латекс]\sin(x)[/латекс] | 0 | [латекс]\фракция{1}{2}[/латекс] | [латекс]\frac{\sqrt{2}}{2}[/латекс] | [латекс]\frac{\sqrt{3}}{2}[/латекс] | 1 | [латекс]\frac{\sqrt{3}}{2}[/латекс] | [латекс]\frac{\sqrt{2}}{2}[/латекс] | [латекс]\фракция{1}{2}[/латекс] | 0 |
Нанесение точек из таблицы и продолжение вдоль оси x дает форму функции синуса.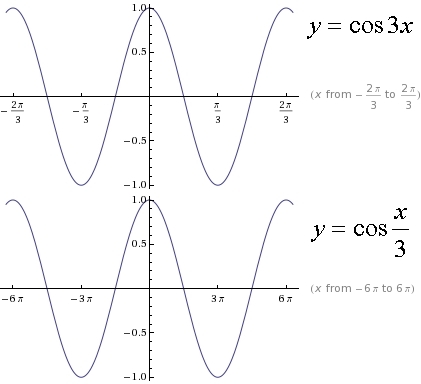 См. рис. 2.
См. рис. 2.
Рис. 2. Синусоидальная функция
Обратите внимание, что значения синуса положительны между 0 и π, которые соответствуют значениям функции синуса в квадрантах I и II на единичной окружности, а значения синуса отрицательны между π и 2π, которые соответствуют значениям функция синуса в квадрантах III и IV на единичной окружности. См. рис. 3.
Рисунок 3. График значений функции синуса
Теперь давайте аналогично рассмотрим косинусную функцию . Опять же, мы можем создать таблицу значений и использовать их для построения графика. В таблице ниже перечислены некоторые значения функции косинуса на единичном круге.
| х | 0 | [латекс]\frac{\pi}{6}[/латекс] | [латекс]\frac{\pi}{4}[/латекс] | [латекс]\frac{\pi}{3}[/латекс] | [латекс]\frac{\pi}{2}[/латекс] | [латекс]\frac{2\pi}{3}[/латекс] | [латекс]\frac{3\pi}{4}[/латекс] | [латекс]\frac{5\pi}{6}[/латекс] | [латекс]\pi[/латекс] |
| [латекс]\cos(x)[/латекс] | 1 | [латекс]\frac{\sqrt{3}}{2}[/латекс] | [латекс]\frac{\sqrt{2}}{2}[/латекс] | [латекс]\фракция{1}{2}[/латекс] | 0 | [латекс]-\frac{1}{2}[/латекс] | [латекс]-\frac{\sqrt{2}}{2}[/латекс] | [латекс]-\frac{\sqrt{3}}{2}[/латекс] | −1 |
Как и в случае функции синуса, мы можем нанести точки на график функции косинуса, как показано на рисунке 4.
Рисунок 4. Функция косинуса
Поскольку мы можем вычислить синус и косинус любого действительного числа, обе эти функции определены для всех действительных чисел. Думая о значениях синуса и косинуса как о координатах точек на единичной окружности, становится ясно, что диапазон обеих функций должен быть интервалом [−1,1].
На обоих графиках форма графика повторяется после 2π, что означает периодичность функций с периодом [latex]2π[/latex]. Периодическая функция — это функция, для которой конкретное горизонтальное смещение , P дает функцию, равную исходной функции: [латекс]f (x + P) = f(x)[/латекс] для все значения x в домене f . Когда это происходит, мы называем наименьшее такое горизонтальное смещение с [латекс]P > 0[/латекс] период функции. На рис. 5 показаны несколько периодов функций синуса и косинуса.
Рисунок 5
Повторный взгляд на функции синуса и косинуса в области с центром на оси y помогает обнаружить симметрию. Как мы видим на рисунке 6, синусоидальная функция симметрична относительно начала координат. Вспомним из книги «Другие тригонометрические функции», что мы определили по единичному кругу, что синусоидальная функция является нечетной функцией, потому что [латекс]\sin(-x)=-\sin x[/латекс]. Теперь мы можем ясно увидеть это свойство на графике.
Как мы видим на рисунке 6, синусоидальная функция симметрична относительно начала координат. Вспомним из книги «Другие тригонометрические функции», что мы определили по единичному кругу, что синусоидальная функция является нечетной функцией, потому что [латекс]\sin(-x)=-\sin x[/латекс]. Теперь мы можем ясно увидеть это свойство на графике.
Рис. 6. Нечетная симметрия синуса
На рисунке 7 показано, что функция косинуса симметрична относительно оси y . Опять же, мы определили, что функция косинуса является четной функцией. Теперь из графика видно, что [латекс]\cos(−x)=\cos x[/латекс].
Рис. 7. Четная симметрия функции косинуса
Общее примечание: Характеристики функций синуса и косинуса
Функции синуса и косинуса имеют несколько отличительных характеристик:
- Это периодические функции с периодом 2π.
- Домен каждой функции [латекс]\влево(-\infty,\infty\right)[/латекс], а диапазон – [латекс]\влево[−1,1\вправо][/латекс].

- График [latex]y=\sin x[/latex] симметричен относительно начала координат, потому что это нечетная функция.
- График [latex]y=\cos x[/latex] симметричен относительно оси y , потому что это четная функция.
Исследование синусоидальных функций
Как мы видим, функции синуса и косинуса имеют регулярный период и диапазон. Если мы понаблюдаем за океанскими волнами или рябью на пруду, мы увидим, что они напоминают функции синуса или косинуса. Однако они не обязательно идентичны. Некоторые выше или длиннее других. Функция, которая имеет ту же общую форму, что и функция синуса или косинуса , известна как синусоидальная функция . Общие формы синусоидальных функций:
[латекс]у = А\sin (Вх-С) + D[/латекс]
и
[латекс]y = A\cos (Bx−C) + D[/латекс]
Определение периода синусоидальных функций функции синуса и косинуса. Мы можем использовать то, что мы знаем о преобразованиях, для определения периода.
В общей формуле B связано с периодом соотношением [latex]P=\frac{2π}{|B|}[/latex]. Если [латекс]|B| > 1[/latex], то период меньше [latex]2π[/latex] и функция подвергается горизонтальному сжатию, а если [latex]|B| < 1[/latex], то период больше, чем [latex]2π[/latex], и функция подвергается горизонтальному растяжению. Например, [латекс]f(x) = \sin(x), B= 1[/латекс], поэтому период равен [латекс]2π[/латекс], что мы знали. Если [латекс]f(x) =\sin (2x)[/латекс], то [латекс]B= 2[/латекс], поэтому период равен [латекс]π[/латекс], а граф сжат. Если [латекс]f(x) = \sin\left(\frac{x}{2} \right)[/latex], то [latex]B=\frac{1}{2}[/latex], поэтому период равен [латекс]4π[/латекс], а график растянут. Обратите внимание на рис. 8, как период косвенно связан с [латекс]|В|[/латекс].
Рисунок 8
Общее примечание: период синусоидальных функций
Если принять C = 0 и D = 0 в уравнениях синуса и косинуса общего вида, мы получим формы
[латекс]у=А\ sin\left(Bx\right)[/latex]
[latex]y=A\cos\left(Bx\right)[/latex]
Период равен [latex]\frac{2π}{|B| }[/латекс].
Пример 1. Определение периода функции синуса или косинуса
Определение периода функции [latex]f(x) = \sin\left(\frac{π}{6}x\right)[/latex ].
Показать решение
Попробуйте
Определите период функции [latex]g(x)=\cos\left(\frac{x}{3}\right)[/latex].
Показать решение
Определение амплитуды
Возвращаясь к общей формуле для синусоидальной функции, мы проанализировали, как переменная B относится к периоду. Теперь давайте обратимся к переменной A , чтобы мы могли проанализировать, как она связана с амплитудой или максимальным расстоянием от покоя. представляет коэффициент вертикального растяжения, а его абсолютное значение | А | это амплитуда. Локальные максимумы будут на расстоянии | А | над вертикальной средней линией графика, которая представляет собой линию x = D ; поскольку в этом случае D = 0, средней линией является ось x . Локальные минимумы будут на таком же расстоянии ниже средней линии. Если | А | > 1, функция растянута. Например, амплитуда [латекс]f(x)=4\sin\left(x\right)[/latex] вдвое больше амплитуды
Локальные минимумы будут на таком же расстоянии ниже средней линии. Если | А | > 1, функция растянута. Например, амплитуда [латекс]f(x)=4\sin\left(x\right)[/latex] вдвое больше амплитуды
[латекс]f(x)=2\sin\left(x\right)[/latex]
If [латекс]| А | < 1[/latex], функция сжата. На рис. 9 сравниваются несколько синусоидальных функций с разными амплитудами.
Рисунок 9
Общее примечание: Амплитуда синусоидальных функций
Если принять C = 0 и D = 0 в уравнениях синуса и косинуса общего вида, мы получим формы
[латекс]у=А\ sin(Bx)[/latex] и [latex]y=A\cos(Bx)[/latex]
Амплитуда равна A, а высота по вертикали от средней линии равна |A|. Кроме того, обратите внимание, что в примере
[латекс]|A|=\text{амплитуда}=\frac{1}{2}|\text{максимум}−\text{минимум}|[/latex]
Пример 2. Определение амплитуды функции синуса или косинуса
Какова амплитуда синусоидальной функции [latex]f(x)=−4\sin(x)[/latex]? Растянута или сжата функция по вертикали?
Показать решение
Попробуйте
Какова амплитуда синусоидальной функции [latex]f(x)=12\sin (x)[/latex]? Растянута или сжата функция по вертикали?
Показать решение
Анализ графиков вариаций
y = sin x и y = cos x Теперь, когда мы понимаем, как A и B соотносятся с уравнениями формы косинуса и косинуса , мы исследуем переменные C и Д . Напомним общую форму:
Напомним общую форму:
[латекс]у = А \sin(Bx-C)+D[/латекс] и [латекс]у=А\cos(Вх-С)+D[/латекс]
или
[латекс]y=A\sin(B(x−\frac{C}{B}))+D[/latex] и [latex]y=A\cos(B(x−\frac{C}{) B}))+D[/latex]
Значение [latex]\frac{C}{B}[/latex] для синусоидальной функции называется фазовым сдвигом , или горизонтальным смещением основного синуса или функция косинуса . Если C > 0, график сдвигается вправо. Если C < 0, график сдвинется влево. Чем больше значение | C |, тем больше сдвигается график. На рисунке 11 показано, что график [latex]f(x)=\sin(x−π)[/latex] смещается вправо на π единиц, что больше, чем мы видим на графике [latex]f(x) )=\sin(x−\frac{π}{4})[/latex], что сдвигается вправо на [latex]\frac{π}{4}[/latex]единиц.
Рисунок 11
В то время как C относится к сдвигу по горизонтали, D указывает сдвиг по вертикали от средней линии в общей формуле для синусоидальной функции. Средняя линия функции [latex]y=\cos(x)+D[/latex] проходит через [latex]y=D[/latex].
Средняя линия функции [latex]y=\cos(x)+D[/latex] проходит через [latex]y=D[/latex].
Рисунок 12
Любое значение D , отличное от нуля, сдвигает график вверх или вниз. На рисунке 13 сравнивается [latex]f(x)=\sin x[/latex] с [latex]f(x)=\sin (x)+2[/latex], сдвинутым на 2 единицы вверх на графике.
Рисунок 13
Общее примечание: вариации функций синуса и косинуса A\cos(Bx−C)+D[/latex], [latex]\frac{C}{B}[/latex] это
фазовый сдвиг и D — это вертикальный сдвиг .Пример 3. Определение фазового сдвига функции
Определите направление и величину фазового сдвига для [latex]f(x)=\sin(x+\frac{π}{6})−2[/latex ].
Показать решение
Попробуйте
Определите направление и величину фазового сдвига для [латекса]f(x)=3\cos(x−\frac{\pi}{2})[/latex].
Показать решение
Пример 4.
 Определение вертикального смещения функции
Определение вертикального смещения функцииОпределите направление и величину вертикального смещения для [латекс]f(x)=\cos(x)−3[/латекс].
Показать решение
Попробуйте
Определите направление и величину вертикального смещения для [латекс]f(x)=3\sin(x)+2[/латекс].
Показать решение
Как сделать: Имея синусоидальную функцию в форме [латекс]f(x)=A\sin(Bx−C)+D[/латекс], определите срединную линию, амплитуду, период и фазовый сдвиг.
- Определите амплитуду как |A|.
- Определить период как [latex]P=\frac{2π}{|B|}[/latex].
- Определите фазовый сдвиг как [латекс]\frac{C}{B}[/latex].
- Определить среднюю линию как y = D.
Пример 5. Идентификация вариаций синусоидальной функции из уравнения
Определите среднюю линию, амплитуду, период и фазовый сдвиг функции [latex]y=3\sin(2x)+1[/latex].
Показать решение
Попробуйте
Определите среднюю линию, амплитуду, период и фазовый сдвиг функции [latex]y=\frac{1}{2}\cos(\frac{x}{3}−\frac{π} {3})[/латекс].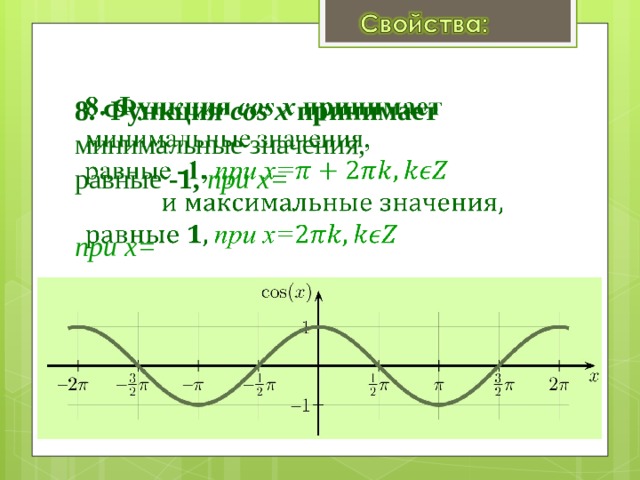
Показать решение
Попробуйте
Пример 6. Определение уравнения синусоидальной функции на графике
Определите формулу косинуса на рисунке 15.
Рисунок 15
Показать решение
Попробуйте
Определите формулу для функции синуса на рисунке 16.
Рисунок 16
Показать решение
Попробуйте
Пример 7. Определение уравнения синусоидальной функции на графике
Определите уравнение для синусоидальной функции на рисунке 17.
Рисунок 17
Показать решение
Попробуйте
Напишите формулу функции, изображенной на рисунке 18.
Рисунок 18
Показать решение
Попробуйте
Графические варианты
y = sin x и y = cos x В этом разделе мы узнали о типах вариаций синуса и косинуса и использовали эту информацию для записи функций уравнения из графиков.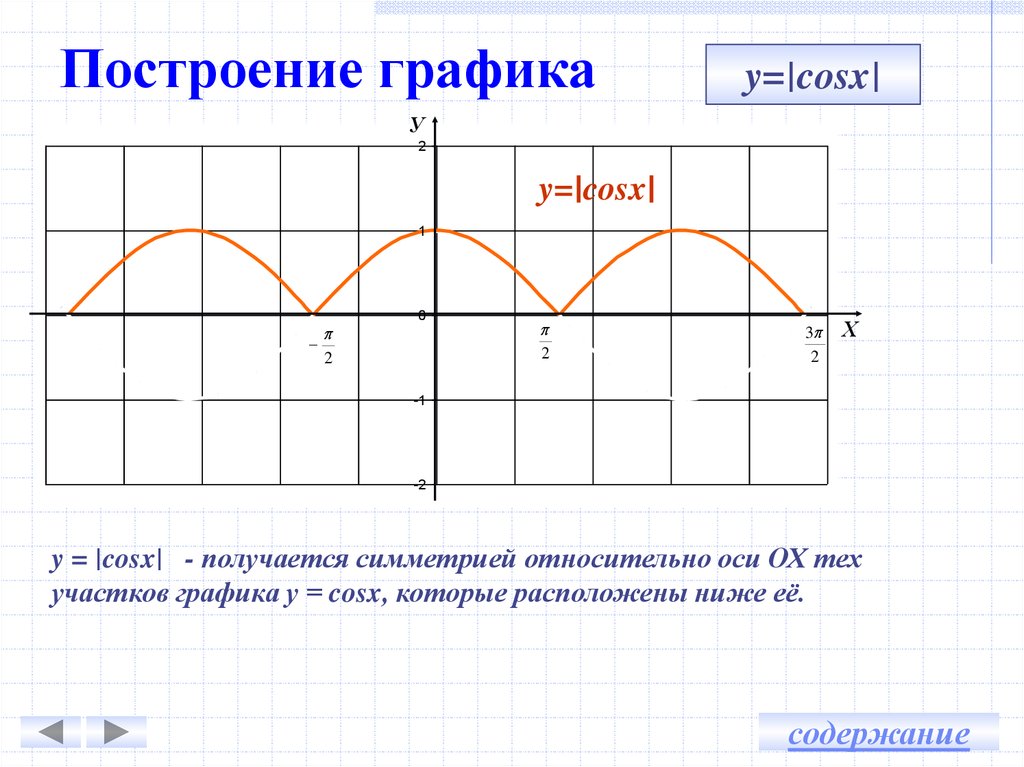 Теперь мы можем использовать ту же информацию для создания графиков из уравнений.
Теперь мы можем использовать ту же информацию для создания графиков из уравнений.
Вместо того, чтобы сосредоточиться на уравнениях общей формы
[латекс]y=A\sin(Bx−C)+D[/латекс] и [латекс]y=A\cos(Bx−C)+D[/латекс ],
мы примем C = 0 и D = 0 и будем работать с упрощенной формой уравнений в следующих примерах.
Как: Имея функцию [latex]y=Asin(Bx)[/latex], нарисуйте ее график.
- Определите амплитуду | А |.
- Определите период, [latex]P=\frac{2π}{|B|}[/latex].
- Начните с исходной точки, при этом функция увеличивается вправо, если A положительна, или уменьшается, если A отрицательна.
- При [latex]x=\frac{π}{2|B|}[/latex] имеется локальный максимум для A > 0 или минимум для A < 0, при этом y = A .
- Кривая возвращается к оси x в точке [latex]x=\frac{π}{|B|}[/latex].
- Существует локальный минимум для A > 0 (максимум для A < 0) at [latex]x=\frac{3π}{2|B|}[/latex] с y = – A .

- Кривая снова возвращается к оси x в точке [latex]x=\frac{π}{2|B|}[/latex].
Пример 8: построение графика функции и определение амплитуды и периода
Нарисуйте график [latex]f(x)=−2\sin(\frac{πx}{2})[/latex].
Показать решение
Попробуйте
Нарисуйте график [латекс]g(x)=−0,8\cos(2x)[/латекс]. Определите среднюю линию, амплитуду, период и фазовый сдвиг.
Показать решение
Как: Дана синусоидальная функция с фазовым и вертикальным сдвигом, нарисуйте ее график.
- Выразите функцию в общем виде [латекс]y=A\sin(Bx-C)+D[/латекс] или [латекс]y=A\cos(Bx-C)+D[/латекс].
- Определите амплитуду, | А |.

- Определите период, [латекс]P=2π|B|[/латекс].
- Определить фазовый сдвиг, [латекс]\фракция{С}{В}[/латекс].
- Нарисуйте график [latex]f(x)=A\sin(Bx)[/latex], сдвинутый вправо или влево на [latex]\frac{C}{B}[/latex] и вверх или вниз на Д .
Пример 9: построение преобразованной синусоиды
Нарисуйте график [латекс]f(x)=3\sin\left(\frac{π}{4}x−\frac{π}{4}\right) [/латекс].
Показать решение
Попробуйте
Нарисуйте график [латекс]g(x)=−2\cos(\frac{\pi}{3}x+\frac{\pi}{6})[/latex]. Определите среднюю линию, амплитуду, период и фазовый сдвиг.
Показать решение
Попробуйте
Пример 10. Определение свойств синусоидальной функции
Учитывая [латекс]y=-2\cos\left(\frac{\pi}{2}x+\pi\right)+3[/latex], определите амплитуду, период, фазовый сдвиг и сдвиг по горизонтали. Затем постройте график функции.
Показать решение
youtube.com/embed/QNQAkUUHNxo?feature=oembed&rel=0″ frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Использование преобразований функций синуса и косинуса
Мы можем использовать преобразования функций синуса и косинуса во многих приложениях. Как упоминалось в начале главы, круговое движение может быть смоделировано с помощью функции синуса или косинуса .
Пример 11. Нахождение вертикальной составляющей кругового движения
Точка вращается вокруг окружности радиусом 3 с центром в начале координат. Нарисуйте график зависимости координаты y точки от угла поворота.
Показать решение
Попробуйте
Какова амплитуда функции [латекс]f(x)=7\cos(x)[/латекс]? Нарисуйте график этой функции.
Показать решение
Пример 12.
 Нахождение вертикальной составляющей кругового движения
Нахождение вертикальной составляющей кругового движенияКруг радиусом 3 фута установлен так, что его центр находится на расстоянии 4 фута от земли. Ближайшая к земле точка обозначена P , как показано на рисунке 23. Нарисуйте график высоты над землей точки P при вращении круга; затем найдите функцию, которая дает высоту через угол поворота.
Рисунок 23
Показать решение
Попробуйте
Груз прикреплен к пружине, которую затем подвешивают к доске, как показано на рис. 25. Когда пружина колеблется вверх и вниз, положение y веса относительно доски колеблется от –1 дюйма (в момент времени x = 0) до –7 дюймов. (в момент времени x = π) под доской. Предположим, что положение y задано как синусоидальная функция x . Нарисуйте график функции, а затем найдите функцию косинуса, которая дает положение y через x.
Рисунок 25
Показать решение
Пример 13.
 Определение роста всадника на колесе обозрения
Определение роста всадника на колесе обозренияЛондонский глаз — это огромное колесо обозрения диаметром 135 метров (443 фута). Он совершает один оборот каждые 30 минут. Всадники садятся с платформы на высоте 2 метра над землей. Выразите высоту всадника над землей как функцию времени в минутах.
Показать решение
Попробуйте
Ключевые уравнения
| Синусоидальные функции | [латекс]f(x)=A\sin(Bx−C)+D[/латекс] |
| [латекс]f(x)=A\cos(Bx−C)+D[/латекс] |
- Периодические функции повторяются после заданного значения. Наименьшей такой величиной является период. Основные функции синуса и косинуса имеют период 2π.
- Функция sin x нечетна, поэтому ее график симметричен относительно начала координат. Функция cos x четная, поэтому ее график симметричен относительно оси y .
- График синусоидальной функции имеет ту же общую форму, что и синусоидальная или косинусоидальная функция.

- В общей формуле синусоидальной функции период равен [latex]\text{P}=\frac{2\pi}{|B|}[/latex].
- В общей формуле синусоидальной функции | A |представляет собой амплитуду. Если | А | > 1 функция растягивается, а если | А | < 1 функция сжимается.
- Значение [latex]\frac{C}{B}[/latex] в общей формуле для синусоидальной функции указывает на фазовый сдвиг.
- Значение D в общей формуле синусоидальной функции указывает на сдвиг по вертикали от средней линии.
- Комбинации вариаций синусоидальных функций могут быть обнаружены из уравнения.
- Уравнение синусоидальной функции можно определить по графику.
- Функцию можно изобразить в виде графика, указав ее амплитуду и период.
- Функцию также можно изобразить в виде графика, указав ее амплитуду, период, фазовый сдвиг и сдвиг по горизонтали.
- Синусоидальные функции могут использоваться для решения реальных задач.
Глоссарий
- амплитуда
- вертикальная высота функции; константа A , фигурирующая в определении синусоидальной функции
- средняя линия
- горизонтальная линия y = D , где D появляется в общем виде синусоидальной функции
- периодическая функция
- функция f ( x ), которая удовлетворяет [latex]f(x+P)=f(x)[/latex] для конкретной константы P и любого значения x
- фазовый сдвиг
- горизонтальное смещение основной функции синуса или косинуса; константа [латекс]\frac{C}{B}[/latex]
- синусоидальная функция
- любая функция, которая может быть выражена в виде [латекс]f(x)=A\sin(Bx−C)+D[/latex] или [латекс]f(x)=A\cos(Bx−C)+ Д[/латекс]
Python: как построить график y=cosh(x) *cos(5x)
спросил
Изменено 1 год, 5 месяцев назад
Просмотрено 585 раз
с использованием Python Я хотел бы построить кривую для функции y=cosh(x)*cos(5x) в своем блокноте Jupyter.
Другими словами: (гиперболический косинус х) умножить на (косинус 5х)
Как мне это сделать? Что мне нужно для импорта? Заранее большое спасибо.
Привет
- питон
- график
- тригонометрия
- кривая
- гиперболическая функция
2
Укажите необходимый диапазон значений x. Вы можете использовать Seaborn поверх Matplotlib, чтобы сделать его красивее, но это необязательно:
импортировать seaborn как sns импортировать matplotlib.pyplot как plt импортировать numpy как np x = np.arange(-5,5,0.1) # старт, стоп, шаг y = (np.cos(x))*(np.cos(5*x)) # установить серый фон (используйте sns.set_theme(), если версия Seaborn 0.11.0 или выше) sns.set (стиль = "темная сетка") plt.plot(x,y) plt.show()
0
Вам потребуется импортировать библиотеку графиков и математическую библиотеку. Наиболее часто используемая библиотека для построения графиков —
Наиболее часто используемая библиотека для построения графиков — matplotlib , а для математики — numpy . Для построения графиков bokeh является альтернативой matplotlib , и я считаю, что это здорово, потому что графики по умолчанию интерактивны. Недостатком является то, что, поскольку он не так широко используется, как matplotlib , вы с меньшей вероятностью найдете по нему помощь с точки зрения ответов и руководств StackOverflow.
В любом случае, на код:
# Импортируем необходимые пакеты и модули импортировать matplotlib.pyplot как plt импортировать numpy как np # Установите свой x-диапазон и рассчитайте y хмин = -2,5 хмакс = 2,5 количество точек = 100 x = np.linspace (xmin, xmax, число точек) у = np.cos(x)*np.cos(5*x) # Сюжет -- это действительно может быть так просто [1] plt.plot(x,y)
Обе приведенные выше графические библиотеки предоставляют гибкие возможности размещения осей, легенд, заголовков и т.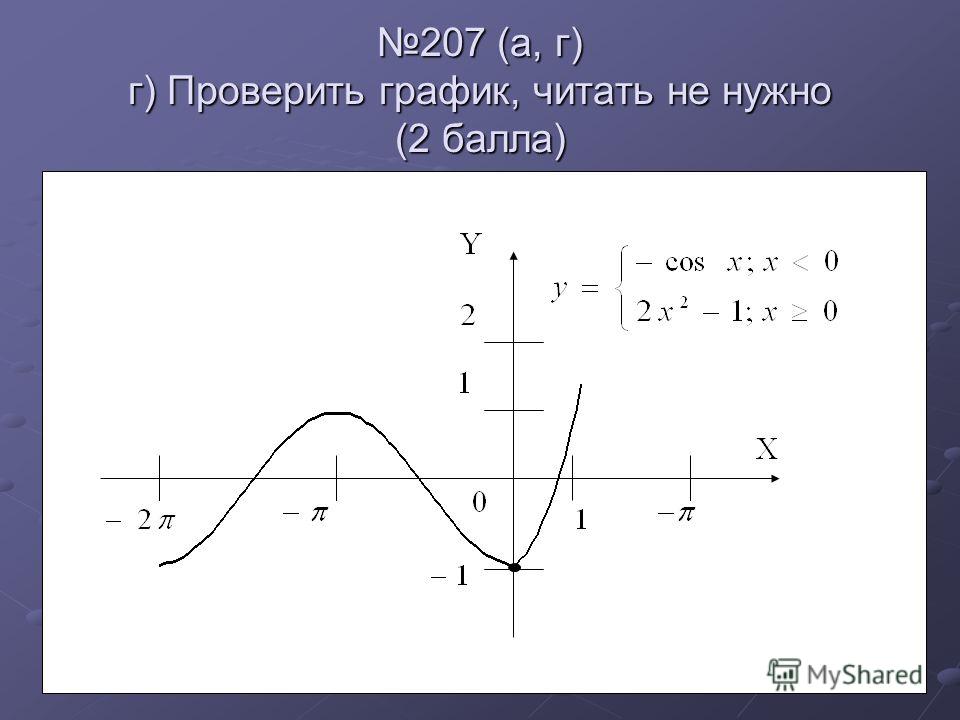


_5.jpg)