График натурального логарифма x: Натуральные логарифмы. Функция у = lп х, её свойства, график, дифференцирование — урок. Алгебра, 11 класс.

2

Натуральный логарифм 0 равен. Логарифм

Что такое логарифм?

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Что такое логарифм? Как решать логарифмы? Эти вопросы многих выпускников вводят в ступор. Традиционно тема логарифмов считается сложной, непонятной и страшной. Особенно — уравнения с логарифмами.

Это абсолютно не так. Абсолютно! Не верите? Хорошо. Сейчас, за какие-то 10 — 20 минут вы:

1. Поймете, что такое логарифм .

2. Научитесь решать целый класс показательных уравнений. Даже если ничего о них не слышали.

3. Научитесь вычислять простые логарифмы.

Причём для этого вам нужно будет знать только таблицу умножения, да как возводится число в степень…

Чувствую, сомневаетесь вы… Ну ладно, засекайте время! Поехали!

Для начала решите в уме вот такое уравнение:

Если Вам нравится этот сайт. ..

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Логарифмом числа b по основанию а называется показатель степени, в который нужно возвести число а чтобы получить число b.

Если , то .

Логарифм — крайне важная математическая величина , поскольку логарифмическое исчисление позволяет не только решать показательные уравнения, но и оперировать с показателями, дифференцировать показательные и логарифмические функции, интегрировать их и приводить к более приемлемому виду, подлежащему расчету.

Вконтакте

Все свойства логарифмов связаны напрямую со свойствами показательных функций. Например, тот факт, что означает, что:

Следует заметить, что при решении конкретных задач, свойства логарифмов могут оказаться более важными и полезными, чем правила работы со степенями.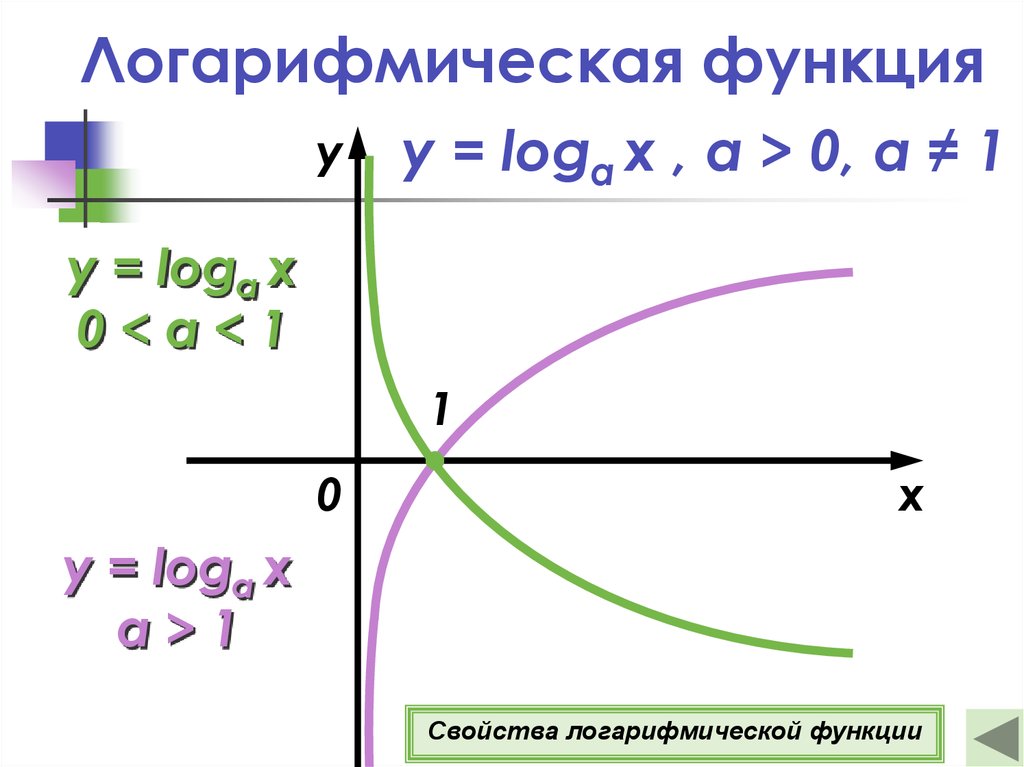

Приведем некоторые тождества:

Приведем основные алгебраические выражения:

;

.

Внимание! может существовать только при x>0, x≠1, y>0.

Постараемся разобраться с вопросом, что такое натуральные логарифмы. Отдельный интерес в математике представляют два вида — первый имеет в основании число «10», и носит название «десятичный логарифм». Второй называется натуральным. Основание натурального логарифма — число «е». Именно о нем мы и будем детально говорить в этой статье.

Обозначения:

• lg x — десятичный;
• ln x — натуральный.

Используя тождество можно увидеть, что ln e = 1, как и то, что lg 10=1.

График натурального логарифма

Построим график натурального логарифма стандартным классическим способом по точкам. При желании, проверить правильно ли мы строим функцию, можно при помощи исследования функции. Однако, есть смысл научится строить его «вручную», чтобы знать, как правильно посчитать логарифм.

Функция: y = ln x. Запишем таблицу точек, через которые пройдет график:

Поясним, почему мы выбрали именно такие значения аргумента х. Всё дело в тождестве: . Для натурального логарифма это тождество будет выглядеть таким образом:

Для удобства мы можем взять пять опорных точек:

;

;

.

;

.

Таким образом, подсчет натуральных логарифмов — довольно несложное занятие, более того, он упрощает подсчеты операций со степенями, превращая их в обычное умножение.

Построив по точкам график, получаем приблизительный график:

Область определения натурального логарифма (т.е. все допустимые значения аргумента Х) — все числа больше нуля.

Внимание! В область определения натурального логарифма входят только положительные числа! В область определения не входит х=0. Это невозможно исходя из условий существования логарифма .

Область значений (т.е. все допустимые значения функции y = ln x) — все числа в интервале .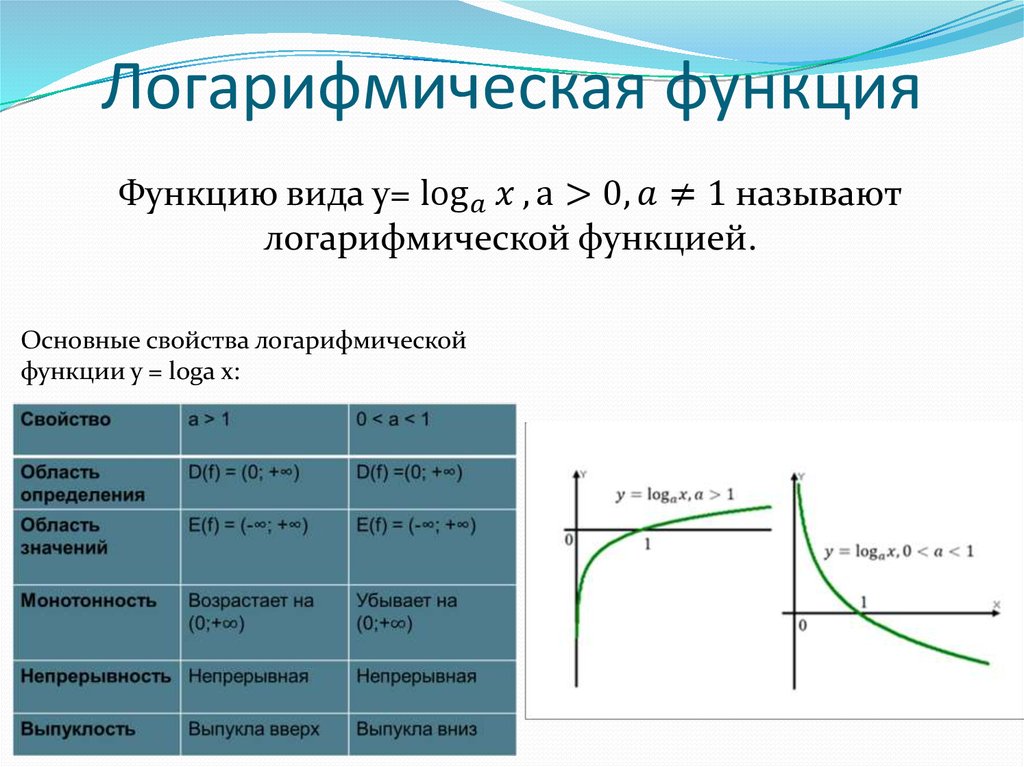

Предел натурального log

Изучая график, возникает вопрос — как ведет себя функция при y

Очевидно, что график функции стремится пересечь ось у, но не сможет этого сделать, поскольку натуральный логарифм при х

Предел натурального log можно записать таким образом:

Формула замены основания логарифма

Иметь дело с натуральным логарифмом намного проще, чем с логарифмом, имеющим произвольное основание. Именно поэтому попробуем научиться приводить любой логарифм к натуральному, либо выражать его по произвольному основанию через натуральные логарифмы.

Начнем с логарифмического тождества:

Тогда любое число, либо переменную у можно представить в виде:

где х — любое число (положительное согласно свойствам логарифма).

Данное выражение можно прологарифмировать с обеих сторон. Произведем это при помощи произвольного основания z:

Воспользуемся свойством (только вместо «с» у нас выражение):

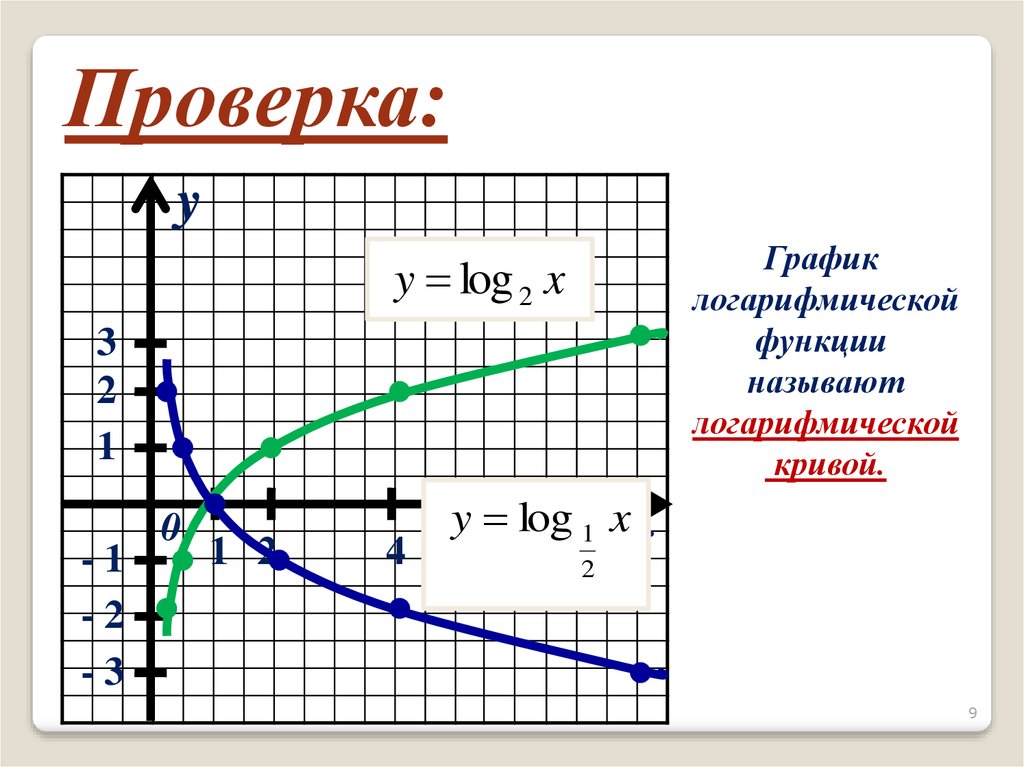
Отсюда получаем универсальную формулу:

.

В частности, если z=e, то тогда:

.

Нам удалось представить логарифм по произвольному основанию через отношение двух натуральных логарифмов.

Решаем задачи

Для того чтобы лучше ориентироваться в натуральных логарифмах, рассмотрим примеры нескольких задач.

Задача 1 . Необходимо решить уравнение ln x = 3.

Решение: Используя определение логарифма: если , то , получаем:

Задача 2 . Решите уравнение (5 + 3 * ln (x — 3)) = 3.

Решение: Используя определение логарифма: если , то , получаем:

.

Еще раз применим определение логарифма:

.

Таким образом:

.

Можно приближенно вычислить ответ, а можно оставить его и в таком виде.

Задача 3. Решите уравнение .

Решение: Произведем подстановку: t = ln x. Тогда уравнение примет следующий вид:

.

Перед нами квадратное уравнение. Найдем его дискриминант:

Первый корень уравнения:

.

Второй корень уравнения:

.

Вспоминая о том, что мы производили подстановку t = ln x, получаем:

В статистике и теории вероятности логарифмические величины встречаются очень часто. Это неудивительно, ведь число е — зачастую отражает темп роста экспоненциальных величин.

В информатике, программировании и теории вычислительных машин, логарифмы встречаются довольно часто, например для того чтобы сохранить в памяти N понадобится битов.

В теориях фракталов и размерностях логарифмы используются постоянно, поскольку размерности фракталов определяются только с их помощью.

В механике и физике нет такого раздела, где не использовались логарифмы. Барометрическое распределение, все принципы статистической термодинамики, уравнение Циолковского и прочее — процессы, которые математически можно описать только при помощи логарифмирования.

В химии логарифмирование используют в уравнениях Нернста, описаниях окислительно-восстановительных процессов.

Поразительно, но даже в музыке, с целью узнать количество частей октавы, используют логарифмы.

Натуральный логарифм Функция y=ln x ее свойства

Доказательство основного свойства натурального логарифма

нередко берут цифру е = 2,718281828 . Логарифмы по данному основанию именуют натуральным . При проведении вычислений с натуральными логарифмами общепринято оперировать знаком l n , а не log ; при этом число 2,718281828 , определяющие основание, не указывают.

Другими словами формулировка будет иметь вид: натуральный логарифм числа х — это показатель степени , в которую нужно возвести число e , чтобы получить x .

Так, ln(7,389…) = 2, так как e 2 =7,389… . Натуральный логарифм самого числа e = 1, потому что e 1 =e , а натуральный логарифм единицы равен нулю, так как e 0 = 1.

Само число е определяет предел монотонной ограниченной последовательности

вычислено, что е

= 2,7182818284… .

Весьма часто для фиксации в памяти какого либо числа, цифры необходимого числа ассоциируют с какой-нибудь выдающейся датой. Скорость запоминания первых девяти знаков числа е после запятой возрастет, если заметить, что 1828 — это год рождения Льва Толстого!

На сегодняшний день существуют достаточно полные таблицы натуральных логарифмов.

График натурального логарифма (функции y = ln x ) является следствием графика экспоненты зеркальным отражением относительно прямой у = х и имеет вид:

Натуральный логарифм может быть найден для каждого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a .

Элементарность этой формулировку, которая состыковывается со многими другими формулами, в которых задействован натуральный логарифм, явилось причиной образования названия «натуральный».

Если анализировать натуральный логарифм , как вещественную функцию действительной переменной, то она выступает обратной функцией к экспоненциальной функции, что сводится к тождествам:

e ln(a) =a (a>0)

ln(e a) =a

По аналогии со всеми логарифмами, натуральный логарифм преобразует умножение в сложение, деление в вычитание:

ln (xy ) = ln (x ) + ln (y )

ln (х/у)= lnx — lny

Логарифм может быть найден для каждого положительного основания, которое не равно единице, а не только для e , но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, обычно, определяются в терминах натурального логарифма.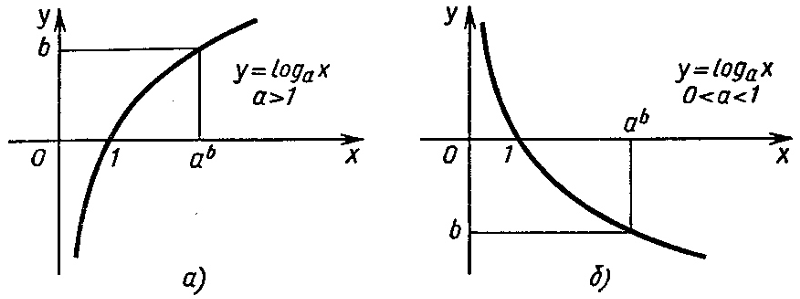

Проанализировав график натурального логарифма,

получаем, что он существует при положительных значениях переменной x . Он монотонно возрастает на своей области определения.

При x → 0 пределом натурального логарифма выступает минус бесконечность ( -∞ ).При x → +∞ пределом натурального логарифма выступает плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a возрастает быстрее логарифма. Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумы у него отсутствуют.

Использование натуральных логарифмов весьма рационально при прохождении высшей математики. Так, использование логарифма удобно для нахождения ответа уравнений, в которых неизвестные фигурируют в качестве показателя степени. Применение в расчетах натуральных логарифмом дает возможность изрядно облегчить большое количество математических формул. Логарифмы по основанию е присутствуют при решении значительного числа физических задач и естественным образом входят в математическое описание отдельных химических, биологических и прочих процессов. Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.

Урок и презентация на темы: «Натуральные логарифмы. Основание натурального логарифма. Логарифм натурального числа»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 11 класса
Интерактивное пособие для 9–11 классов «Тригонометрия»
Интерактивное пособие для 10–11 классов «Логарифмы»

Что такое натуральный логарифм

Ребята, на прошлом уроке мы с вами узнали новое, особенное число – е.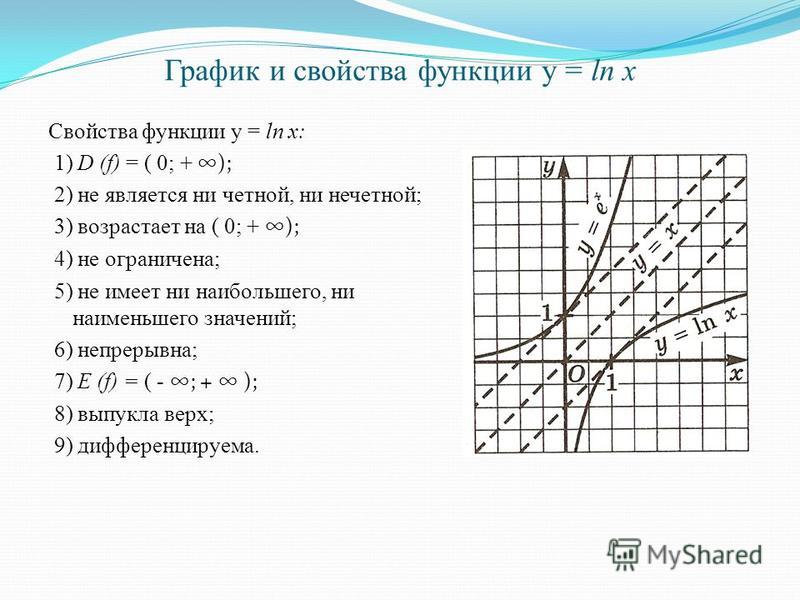 x$ в точке (0;1) равен 45&deg. Тогда угол наклона касательной к графику натурального логарифма в точке (1;0) также будет равен 45&deg. Обе эти касательные будут параллельны прямой $y=x$. Давайте схематично изобразим касательные:

Свойства функции $y=\ln{x}$

1. $D(f)=(0;+∞)$.
2. Не является ни четной, ни нечетной.
3. Возрастает на всей области определения.
4. Не ограничена сверху, не ограничена снизу.
5. Наибольшего значения нет, наименьшего значения нет.
6. Непрерывна.
7. $E(f)=(-∞; +∞)$.
8. Выпукла вверх.
9. Дифференцируема всюду.

В курсе высшей математики доказано, что производная обратной функции есть величина, обратная производной данной функции .
Углубляться в доказательство не имеет большого смысла, давайте просто запишем формулу: $y»=(\ln{x})»=\frac{1}{x}$.

Пример.
Вычислить значение производной функции: $y=\ln(2x-7)$ в точке $х=4$.
Решение.
В общем виде наша функция представляют функцию $y=f(kx+m)$, производные таких функций мы умеем вычислять. 6=1$.
$x=±1$.
Точка $х=-1$ не принадлежит области определения. Тогда имеем одну стационарную точку $х=1$. Найдем промежутки возрастания и убывания:

Точка $х=1$ – точка минимума, тогда $y_min=1-6*\ln{1}=1$.
Ответ: Функция убывает на отрезке (0;1], функция возрастает на луче $}

Логарифмические функции

Логарифмические функции

Графер Калькулятор Возврат Справка Точечная диаграмма

---

Содержание: Эта страница соответствует § 4.2 (стр. 330) текста.

Предлагаемые проблемы из текста:

р. 337 #1, 3, 6, 12, 13, 17, 19, 21, 27, 29, 37, 41, 47, 59, 65, 73, 78

Определение

Графики

Натуральный логарифм

---

Определение

Если a — любое положительное число, отличное от 1, то f(x) = a ^x , экспоненциальная функция с основанием a, равна взаимно однозначно и, следовательно, имеет обратное .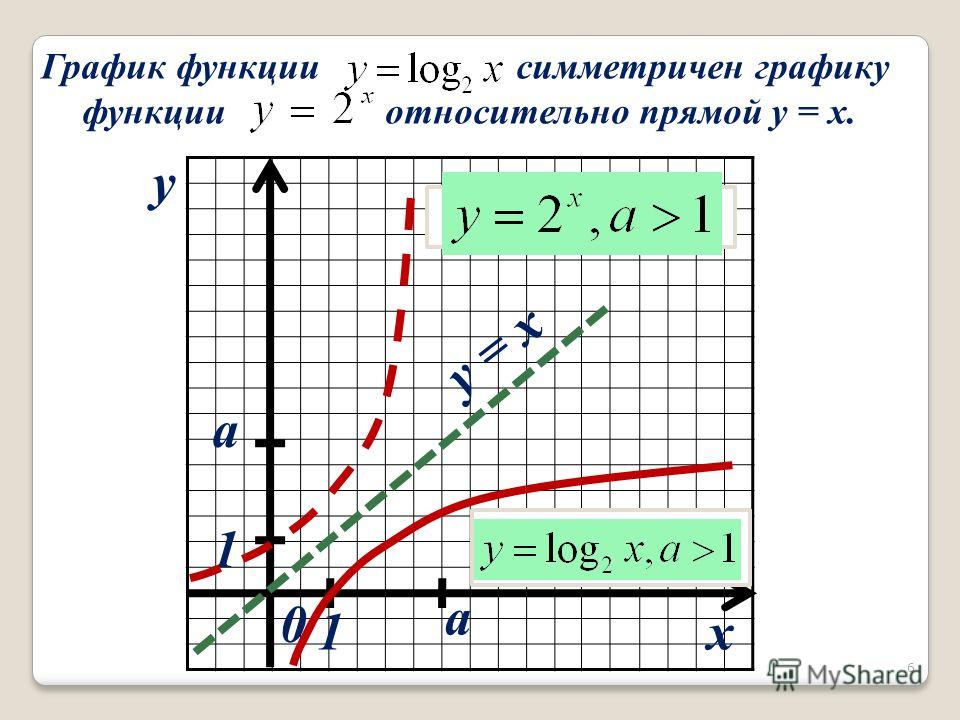 Обзор этих концепций см. в разделе об обратном функции. Мы можем видеть, что f имеет обратную сторону, посмотрев на ее график и заметив, что она проходит через горизонтальную линейный тест. Другими словами, никакая горизонтальная линия не пересекается с графиком функции f более чем в одной точке. Взгляните еще раз на апплет из предыдущего раздела, показывающий графики экспоненциальных функций.

Перетащите точку, которая изначально находилась в (1,2), чтобы увидеть графики других экспоненциальных функций.

Во всех случаях, за исключением случаев, когда основание равно 1, график проходит тест горизонтальной линии.

Определение

Логарифмическая функция с основанием a , записанная log _a (x), является обратной экспоненциальной функции ^х .

Напомним, что обращение функции просто отменяет то, что сделали функции, и эту идею можно выразить через функциональный состав. Тот факт, что журнал _a (x) является инверсией ^x , может быть выражено с помощью следуя двум тождествам.

логарифмическая идентичность 1
логарифмическая идентичность 2

Пример 1 .

журнал ₂ 16 = журнал ₂ 2 ⁴ = 4, тождеством 1.

log ₅ (1/25) = log ₅ 5 ^-2 = -2, по тождеству 1.

Упражнение 1 :

Оцените следующее:

(а) бревно ₄ 16

(б) бревно ₃ (1/27)

(c) log ₄ 2 (Подсказка: запишите 2 как степень числа 4.)

Ответы

Вернуться к содержанию

Графики

В предыдущем разделе мы видели, что графики экспоненциальных функций легко рисовать, поскольку все они проходят через точки (0,1) и везде возрастают, если основание больше 1, и везде убывают, если основание находится между 0 и 1.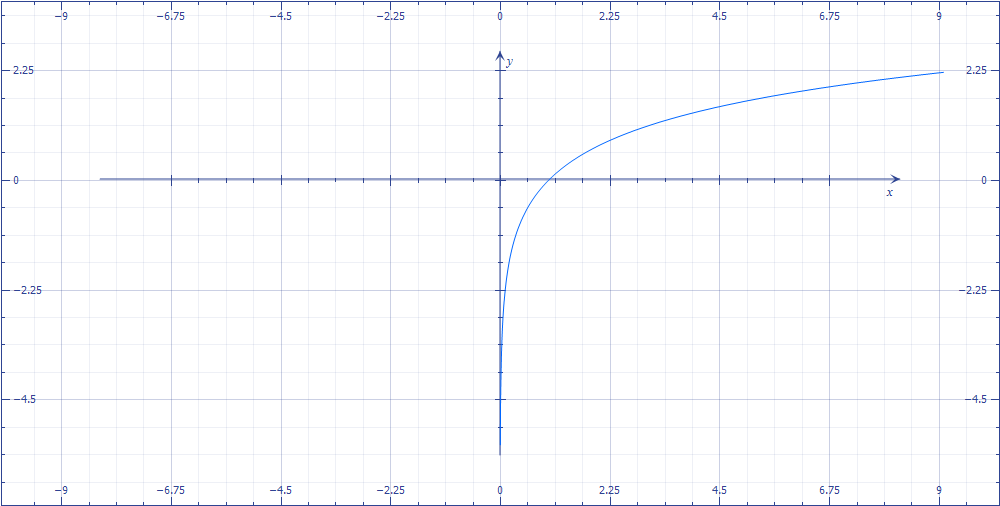 Кроме того, как мы видели в разделе об инверсиях, функция и ее обратная имеют графики, которые являются отражением друг друга через линию y = x. Апплет ниже показывает график экспоненциальной функции, линию y = x и график функции логарифма, обратной к экспоненциальный. Поскольку экспоненциальная функция изначально равна 2 ^x , логарифмическая функция изначально журнал ₂ . Если вы перетащите точку, которая изначально находилась в (1,2), то экспоненциальный и логарифмический графики обновляются.

Основание экспоненциальной и логарифмической функций a.

Есть несколько свойств логарифмических функций, которые легко следуют из определения и очевидны. из графиков в апплете выше.

• Область определения каждой логарифмической функции (0, inf). Другими словами, журнал _a x определяется только для x > 0. Это связано с тем, что диапазон каждой экспоненциальной функции равен (0, inf), а логарифмические функции являются обратными показательных функций.
• Поскольку графики всех показательных функций содержат точку (0,1), графики всех логарифмических функций содержат точку (1,0), отражение (0,1) на прямой y = x. Другими словами, log _a 1 = 0 для всех а.
• Если основание а больше 1, журнал функции _и увеличивается везде. Если основание a находится между 0 и 1, то журнал функции _a увеличивается везде.
• Поскольку a ¹ = a, логарифмическое тождество 1 выше подразумевает log _a a = 1.

Упражнение 2 :

(a) Нарисуйте графики 3 ^x и log ₃ x и линию y = x в одной и той же координатной плоскости.

(b) Нарисуйте графики 1,5 ^x и log _1,5 x и линия y = x в одной координатной плоскости.

(c) Нарисуйте графики 0,5 ^x и log _0,5 x и линию y = x в одной и той же координатной плоскости.

Используйте апплет выше, чтобы проверить свои ответы, перетащив точку, пока не отобразится правильная экспоненциальная функция.

Вернуться к содержанию

Натуральный логарифм

В предыдущем разделе мы описали число e и отметили, что e ^x — самая важная экспоненциальная функция. Она настолько важна, что ее часто называют экспоненциальной функцией . Отсюда следует, что его обратное, логарифм с основанием e является наиболее важной из логарифмических функций. Логарифм по основанию e называется натуральный логарифм, и он обозначается ln.

Натуральный логарифм x = ln x = log _e x

Многие научные калькуляторы имеют кнопки, предназначенные для натурального логарифма и логарифма по основанию 10, который также называется десятичный логарифм .

Когда мы пишем log x без нижнего индекса, то имеем в виду десятичный логарифм, log ₁₀ x.

Производители многих калькуляторов следуют этому соглашению. Например, у TI-82 есть кнопка LN для естественного логарифм и кнопку LOG для десятичного логарифма. Калькулятор Java использует функции ln() и log() для естественного логарифм и десятичный логарифм соответственно.

Упражнение 3 :

Используйте ваш любимый калькулятор, чтобы убедиться, что ln(e) = 1 и log(10) = 1. Это частные случаи оператора логарифм _а а = 1.

Вернуться к содержанию

---

Графер Калькулятор Возврат Справка Точечная диаграмма

Логарифмические функции и их графики

4.2 — Логарифмические функции и их графики

Обратная экспоненциальная функция

В разделе об экспоненциальных функциях мы заявили, что экспоненциальные функции были взаимно однозначными.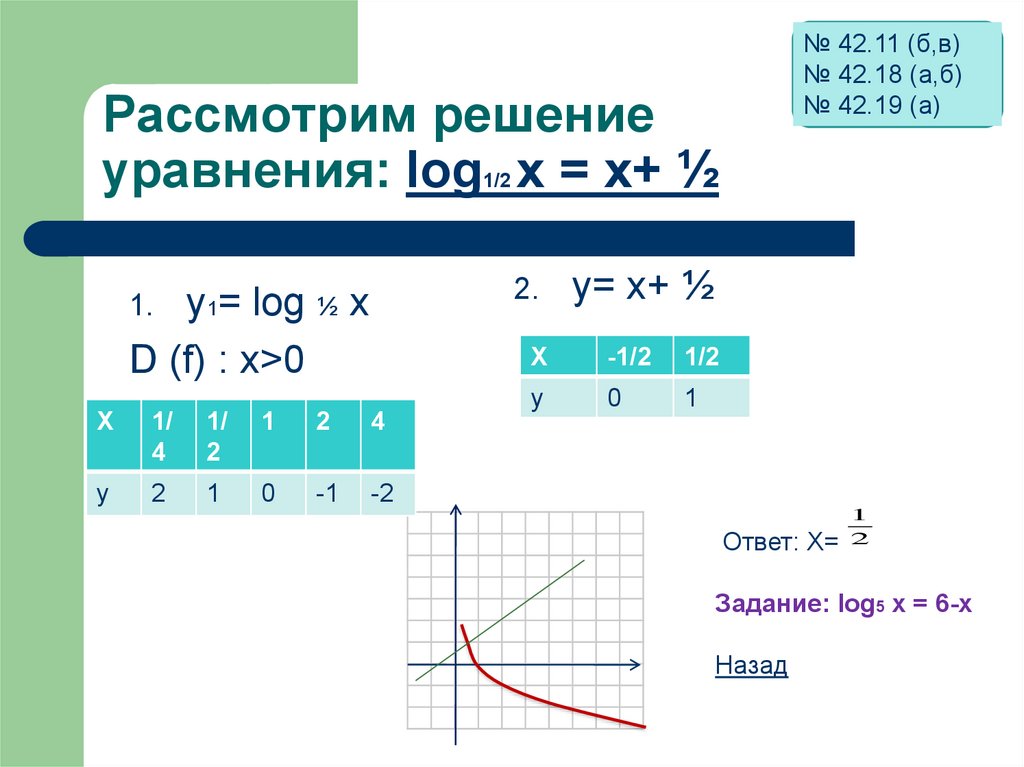 Один к одному функции обладали тем особым свойством, что они имеют обратные это тоже функции. И, как многие из вас говорили в классе, и я так рад, что вы помните, функции один-к-одному могут применяться к обеим частям уравнения. Они также проходят тест горизонтальной линии.

Этот раздел посвящен обратной экспоненциальной функция. Обратной экспоненциальной функцией является логарифмическая функция. Помните, что инверсия функция получается путем переключения координат x и y. Это отражает график относительно прямой y=x. Как видно из графика справа, логарифмическая кривая является отражением экспоненциальной кривой.

В таблице ниже показано, как значения x и y точек на экспоненциальной кривую можно переключать, чтобы найти координаты точек на логарифмической изгиб.

Точка на экспоненциальной кривой	Соответствующая точка на логарифмической кривой
(-3, 1/8)	(1/8, -3)
(-2, 1/4)	(1/4, -2)
(-1, 1/2)	(1/2, -1)
(0, 1)	(1, 0)
(1, 2)	(2, 1)
(2, 4)	(4, 2)
(3, 8)	(8, 3)

Сравнение экспоненциальной и логарифмической функций

Давайте посмотрим на некоторые свойства из двух функций.

Стандартная форма логарифмической функции: y = log _a x

Обратите внимание, если «a» в приведенном выше выражении не является нижним индексом (ниже, чем «лог»), тогда вам нужно обновить свой веб-браузер.

	Экспоненциальный	Логарифмический
Функция	у=а х , а>0, а≠1	у=log а х, а>0, а≠1
Домен	все реалы	х > 0
Диапазон	г > 0	все реалы
перехват	г = 1	х = 1
увеличение	при > 1	при > 1
уменьшение	, когда 0 < а < 1	, когда 0 < а < 1
асимптота	ось x (y=0)	ось Y (x=0)
непрерывный	да	да
гладкая	да	да

Рабочее определение логарифма

В экспоненциальной функции x был показателем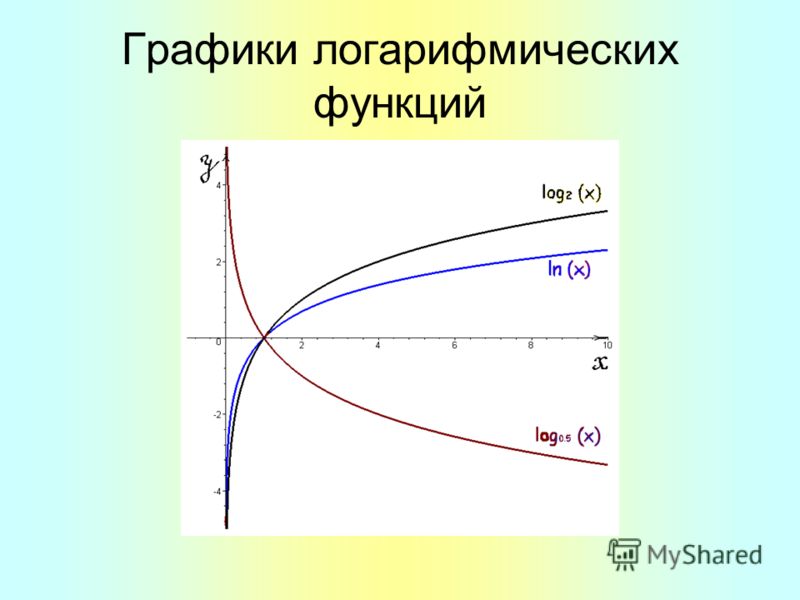 степени. Цель обратной функции чтобы сообщить вам, какое значение x было использовано, когда вы уже знаете значение y. Итак, целью логарифм, чтобы сказать вам показатель степени.

Таким образом, наше простое определение логарифма состоит в том, что он является показателем степени.

Другой способ взглянуть на выражение «log _a x» — это «в какую степень (показатель степени) нужно возвести а получить х?»

Эквивалентные формы

Логарифмическая форма уравнения y=log _a x эквивалентна экспоненциальной форме x=a ^y .

Чтобы переписать одну форму в другую, оставьте основу прежней и поменяйте местами две другие стороны. ценности.

Свойства логарифмов

журнал _a 1 = 0, потому что a ⁰ = 1

Независимо от базы, если она разрешена, логарифм 1 всегда равен 0. Это потому что логарифмические кривые всегда проходят через (1,0) 905:00

log _a a = 1, потому что a ¹ = a

Любое значение, возведенное в первую степень, такое же значение.

log _a a ^x = x

Основание логарифма x и a в степени x являются обратными функциями. Всякий раз, когда инверсия функции применяются друг к другу, они инвертируются, и у вас остается в аргумент, в данном случае x.

log _a x = log _a y означает, что x = y

Если два бревна с одинаковым основанием равны, то аргументы должны быть равны.

log _a x = log _b x означает, что a = b

Если два логарифма с одним и тем же аргументом равны, то основания должны быть равны.

Обычные бревна и натуральные бревна

На вашем калькуляторе есть две кнопки логарифмирования. Один помечен как «журнал» и другой отмечен «лн». Ни в одном из них не записана база. База может быть определена, однако, взглянув на обратную функцию, которая написана над ключом и доступ по 2 ^{-й ключ} .

Десятичный логарифм (основание 10)

Когда вы видите написанное «журнал» без основания, примите, что основание равно 10.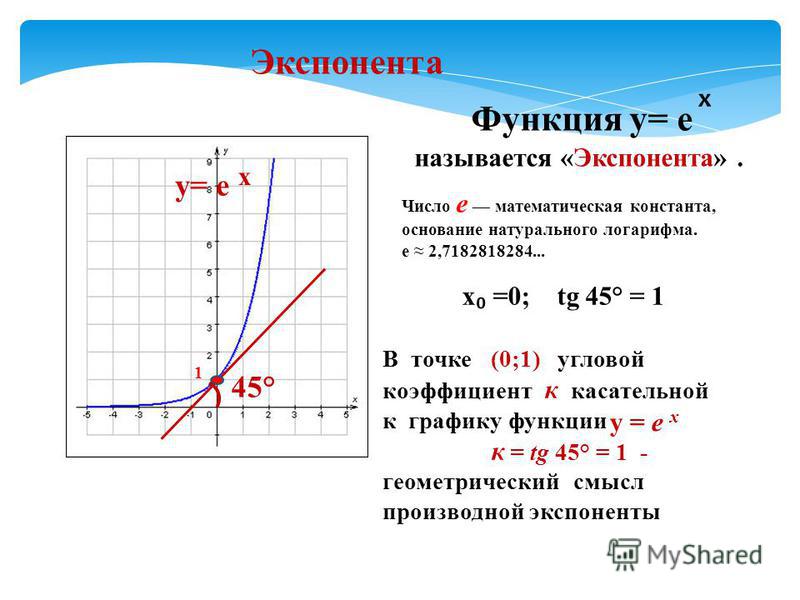
То есть: log x = log ₁₀ x.

Некоторые приложения, использующие десятичные логарифмы, относятся к pH (для измерения кислотности), децибелам. (сила звука), шкала Рихтера (землетрясения).

Интересное (возможно) примечание о рН. «Глава 50: Канализация» деревни Кодекса Форсайта требует запрещает сброс отходов с рН менее 5,5 или выше 10,5 (раздел 50.07).

Обычные журналы служат и для другой цели. Каждое увеличение десятичного логарифма на 1 является результатом 10-кратного аргумента. То есть землетрясение силой 6,3 имеет 10 раз превышает величину землетрясение силой 5,3 балла. Уровень децибел громкой рок-музыки или бензопилы (115 децибел = 11,5 бел) в 10 раз громче, чем куры внутри здания (105 децибел = 10,5 бел)

Натуральные логарифмы (основание e)

Помните тот номер e , который у нас был из предыдущего раздела? Знаешь, тот, который был примерно 2,718281828 (но не повторяется и не заканчивается). Это основа естественного логарифм.

Когда вы видите написанное «ln», основание равно e .
То есть: ln x = log _e x

Модели экспоненциального роста и затухания являются одним из приложений, использующих натуральные логарифмы. Этот включает непрерывное накопление, радиоактивный распад (период полураспада), рост населения. Обычно приложения, в которых постоянно происходит процесс. Теперь эти приложения были первыми упоминается в экспоненциальном разделе, но вы сможете решить для других переменных участие (после раздела 4) с использованием логарифмов.

В высшей математике натуральный логарифм является предпочтительным логарифмом. Есть несколько особые свойства функции натурального логарифма и ее обратной функции, которые делают жизнь намного интереснее. проще в расчетах.

Поскольку «ln x» и « e ^x » являются обратными функциями друг друга, всегда, когда «ln» и «e» появляются правильно рядом друг с другом, между которыми абсолютно ничего нет (то есть, когда они составлены друг с другом), затем они инвертируются, и у вас остается Аргумент.