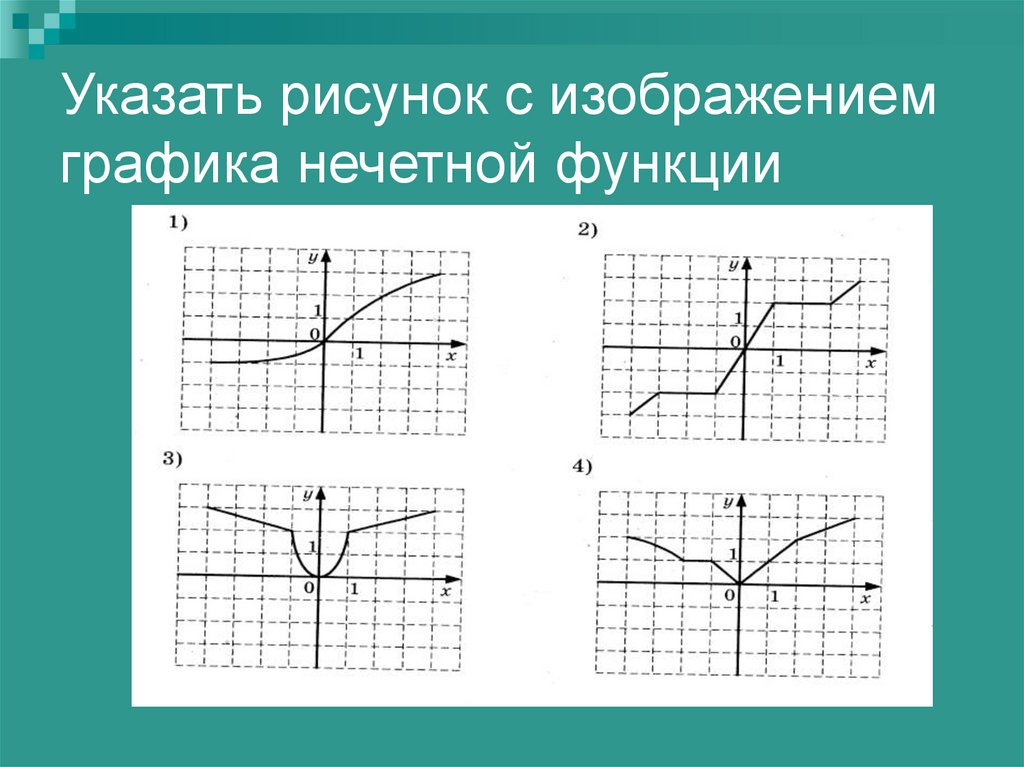
2.3.Построение графиков чётной и нечётной функций
Как уже отмечалось, для чётной функции y=f(x) во всей области изменения её аргумента справедливо соотношение f(x)=f(- x). Следовательно, функция такого рода принимает одинаковые значения при всех значениях аргумента, равных по абсолютной величине, но противоположных по знаку. График чётной функции симметричен относительно оси ординат.
Для построения графика чётной функции y=f(x) следует построить ветвь графика этой функции только в области положительных значений аргумента x. График функции y=f(x) в области отрицательных значений аргумента симметричен построенной ветви относительно оси ординат и получается отражением её относительно этой оси.
Пример 8. Построить график функции y=.
Р
е ш е н и е: Данная функция – чётная,
поэтому достаточно построить её график
лишь в области положительных значений
x
(точка x=0
не входит в область определения функции).
Рис.11
Рис.12
Рис.13.
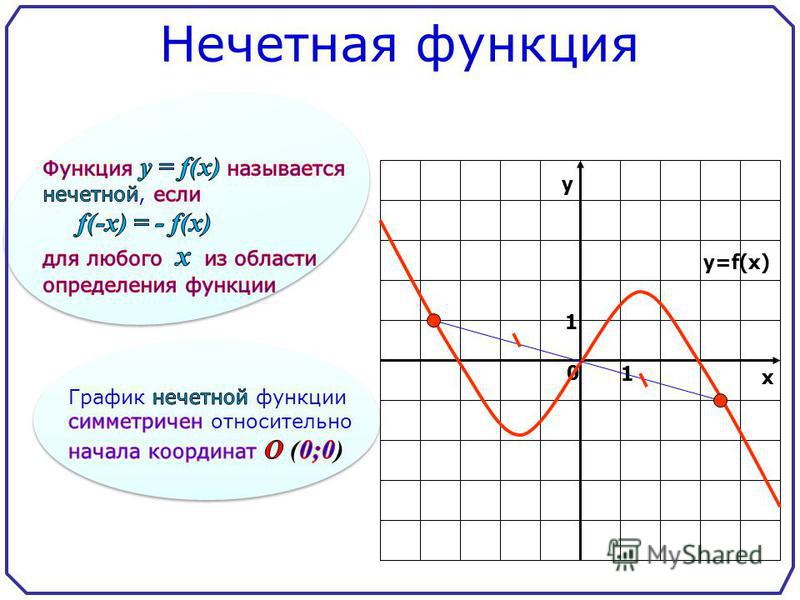
Для нечётной функции y=f(x) в области всех значений аргумента справедливо равенство f(-x)= -f(x). Таким образом, в области отрицательных значений аргумента ординаты графика нечётной функции равны по величине, но противоположны по знаку ординатам графика той же функции при соответствующих положительных значениях x. График нечётной функции симметричен относительно начала координат.
Для построения графика нечётной функции y=f(x) следует строить ветвь графика этой функции только в области положительных значений аргумента (x).
График
функции y=f(x)
в области отрицательных значений
аргумента симметричен построенной
ветви относительно начала координат и
может быть получен отражением этой
ветви относительно оси ординат с
последующим отражением в области
отрицательных значений x
относительно оси абсцисс.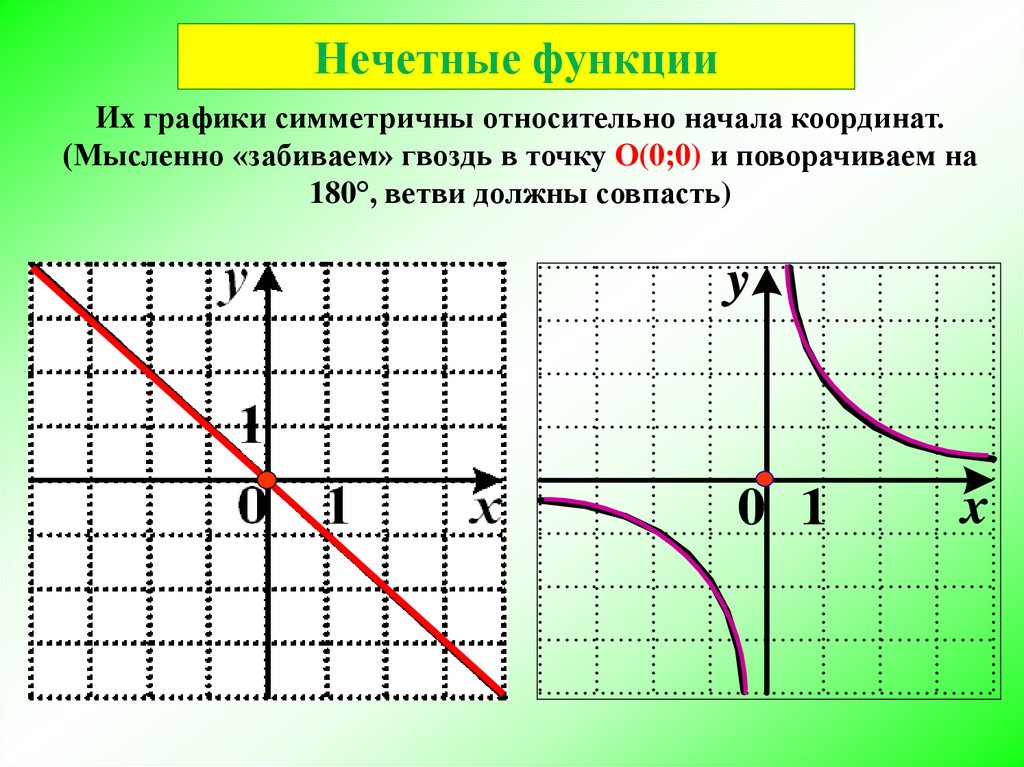
Пример 9. Построить график функции y=x.
Р е ш е н и е: Исходная функция является нечётной, поэтому строим её в области положительных значений аргумента (x), где она имеет вид y=x2. График функции y=x в области отрицательных значений аргумента получаем отражением построенной ветви относительно начала координат (рис.12).
Пример 10. Построить график функции y= .
Р е ш е н и е: Данная функция является нечётной, поэтому строим её график лишь в области x>0 (точка x=0 не входит в область определения функции), где она имеет вид y=1. Ветвь графика данной функции при x<0 получаем отражением относительно начала координат построенной ветви кривой (рис.13). Стрелки означают, что точки (0,1) и (0,-1) не принадлежат графику.
Прямая
и обратная функции выражают одну и ту
же зависимость между переменными x
и y,
с тем только отличием, что в обратной
функции эти переменные поменялись
ролями, что равносильно изменению
обозначений осей координат. Поэтому
график обратной функции симметричен
графику прямой функции относительно
биссектрисы
I
и III
координатных углов, т.е. относительно
прямой y=x.
Таким образом, получаем следующее
правило.
Поэтому
график обратной функции симметричен
графику прямой функции относительно
биссектрисы
I
и III
координатных углов, т.е. относительно
прямой y=x.
Таким образом, получаем следующее
правило.
Для построения графика функции y=, обратной по отношению к функцииy=f(x), следует построить график y=f(x) и отразить его относительно прямой y=x.
Пример 11. Построить график функции y=.
Р е ш е н и е: Чтобы построить график данной функции, рассмотрим график параболыy=x 2 (рис.14 – пунктирная кривая) и график обратной к ней функции y=, получаемый отражением параболы относительно прямой y=x. Обратная функция является двузначной. В силу того, что исходная функция y=однозначна и область её изменения есть полуинтервал 0y<, графиком функцииy=является верхняя ветвь отражённой параболы (сплошная кривая). Нижняя же ветвь (штрих-пунктир) представляет собой график функцииy= -.
Рис.15
Пример
12.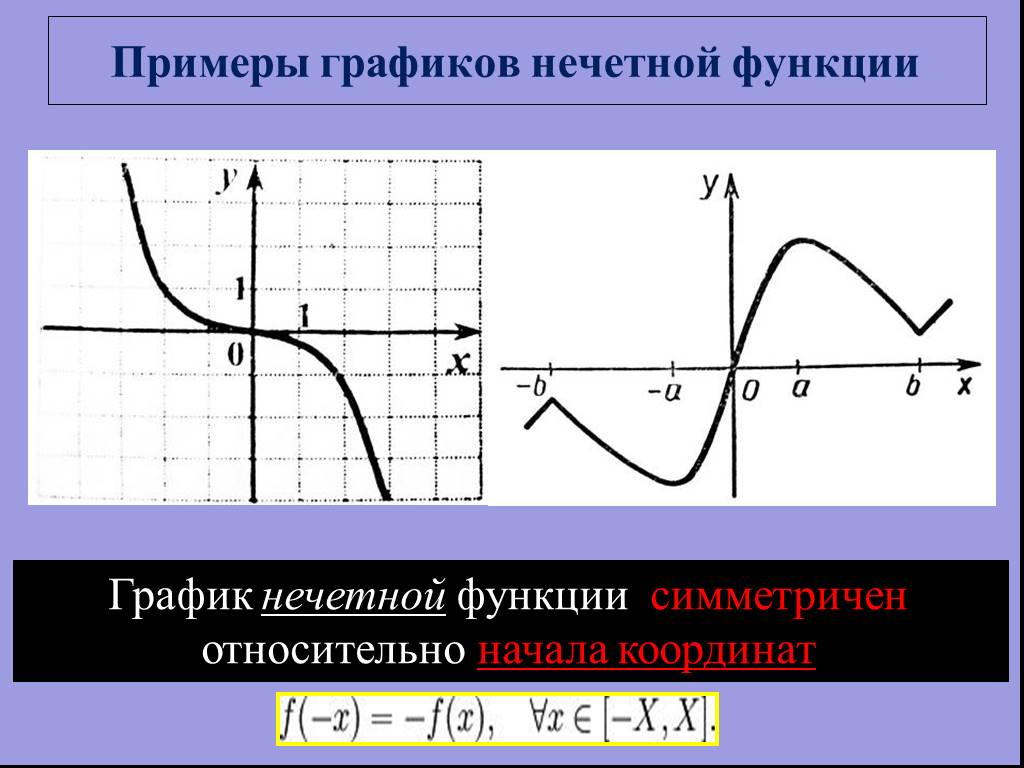 Построить
график функции y=
.
Построить
график функции y=
.
Р е ш е н и е: Данная функция является обратной по отношению к функции y=x, поэтому строим график функции y=x и отражаем его относительно прямой y=x (рис.15).
Нечётная функция | это… Что такое Нечётная функция?
ТолкованиеПеревод
- Нечётная функция
f(x) = x — пример нечётной функции.
f(x) = x2 — пример чётной функции.
f(x) = x3, нечётная
f(x) = x3 + 1 ни чётная, ни нечётная
Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.
Или по-другому
Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.

Содержание
- 1 Определения
- 2 Свойства
- 3 Примеры
- 3.1 Нечётные функции
- 3.2 Чётные функции
- 4 Вариации и обобщения
Определения
- Функция называется нечётной, если справедливо равенство
- Функция f называется чётной, если справедливо равенство
- Если не выполняется ни одно из этих равенств, то функция называется функцией общего вида.
Свойства
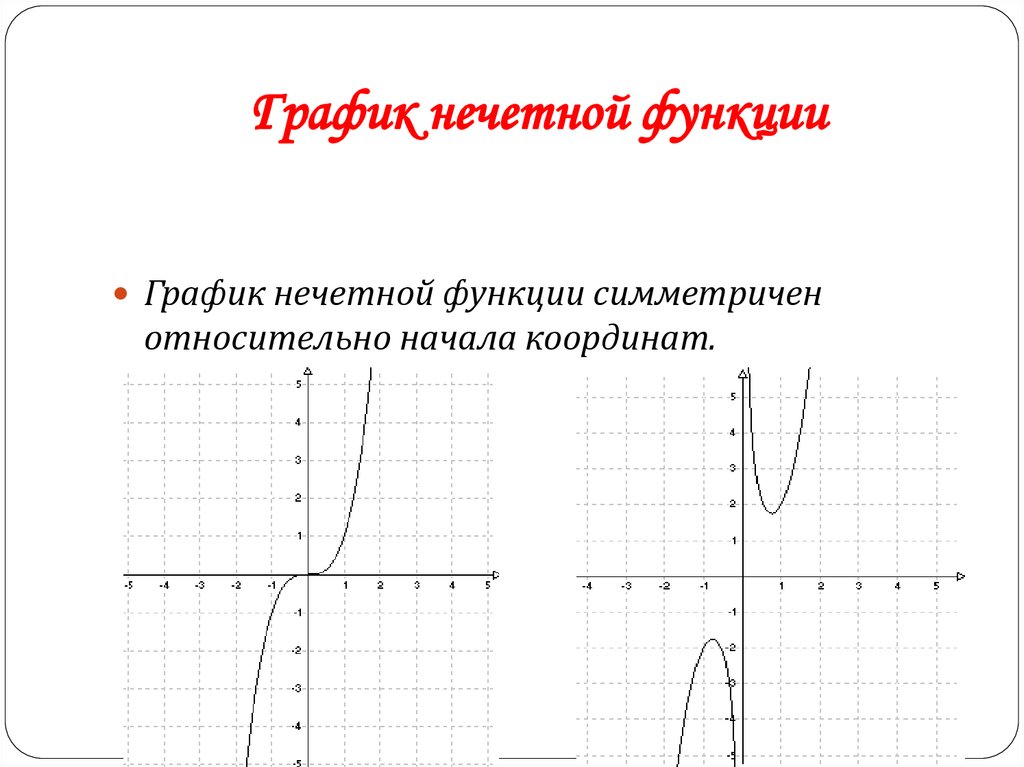
- График нечётной функции симметричен относительно начала координат O.
- График чётной функции симметричен относительно оси ординат Oy.
- Произвольная функция может быть представлена в виде суммы нечётной и чётной функций:
- f(x) = g(x) + h(x),
где
- Функция — единственная функция, одновременно являющаяся нечётной и чётной.

- Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.
- Произведение или дробь двух нечётных функций чётно.
- Произведение или дробь двух чётных функций чётно.
- Произведение или дробь нечётной и чётной функций нечётно.
- Композиция двух нечётных функция нечётна.
- Композиция двух чётных функций чётна.
- Композиция чётной функции с нечётной чётна.
- Композиция любой функции с чётной чётна (но не наоборот).
- Функция, обратная чётной, чётна, а нечётной — нечётна.
- Производная чётной функции нечётна, а нечётной — чётна.
- То же верно про производную третьего, пятого и вообще любого нечётного порядка.
- Производная чётного порядка сохраняет чётность.
Примеры
Нечётные функции
- Нечётная степень где — произвольное целое число.
- Синус .
- Тангенс .
Чётные функции
- Чётная степень где — произвольное целое число.

- Косинус .
Вариации и обобщения
- Понятие чётности и нечётности функций естественно обобщаются на случай отображений между векторными пространствами.
Wikimedia Foundation. 2010.
Игры ⚽ Нужен реферат?
- Нечётное
- Нечётное число
Полезное
{3}f(x)=x3
или
f(x)=1xf\left(x\right)=\frac{1}{x}f(x)=x1
были отражены по обоим осей, результатом будет исходный график.
Рис. 12. (a) Кубическая функция набора инструментов (b) Горизонтальное отражение кубической функции набора инструментов (c) Горизонтальные и вертикальные отражения воспроизводят исходную кубическую функцию.
Мы говорим, что эти графы симметричны относительно начала координат. Функция с графиком, симметричным относительно начала координат, называется 9{x}f(x)=2x
не является ни четным, ни нечетным.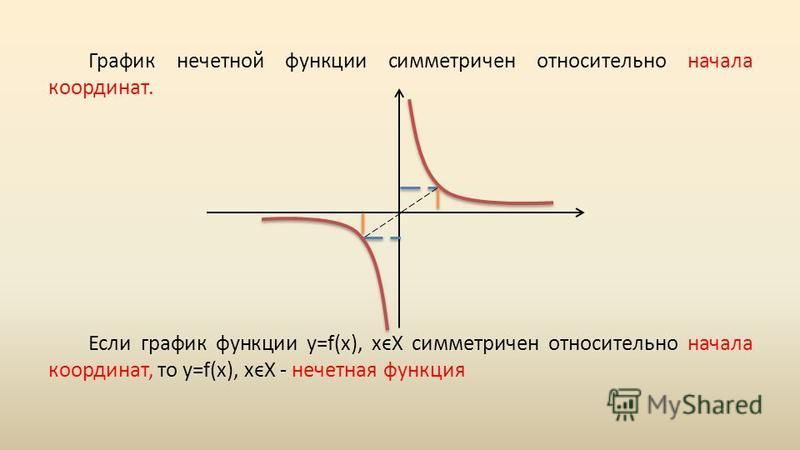 Кроме того, единственная функция, которая одновременно является четной и нечетной, — это функция-константа
Кроме того, единственная функция, которая одновременно является четной и нечетной, — это функция-константа
f(x)=0f\left(x\right)=0f(x)=0
.
Общее примечание: четные и нечетные функции \left(-x\right)f(x)=f(−x)
График четной функции симметричен относительно
y-y\text{-}y-
ось.
Функция называется нечетной, если для каждого входа
xxx
f(x)=−f(−x)f\left(x\right)=-f\left(-x\right)f( x)=−f(−x)
График нечетной функции симметричен относительно начала координат.
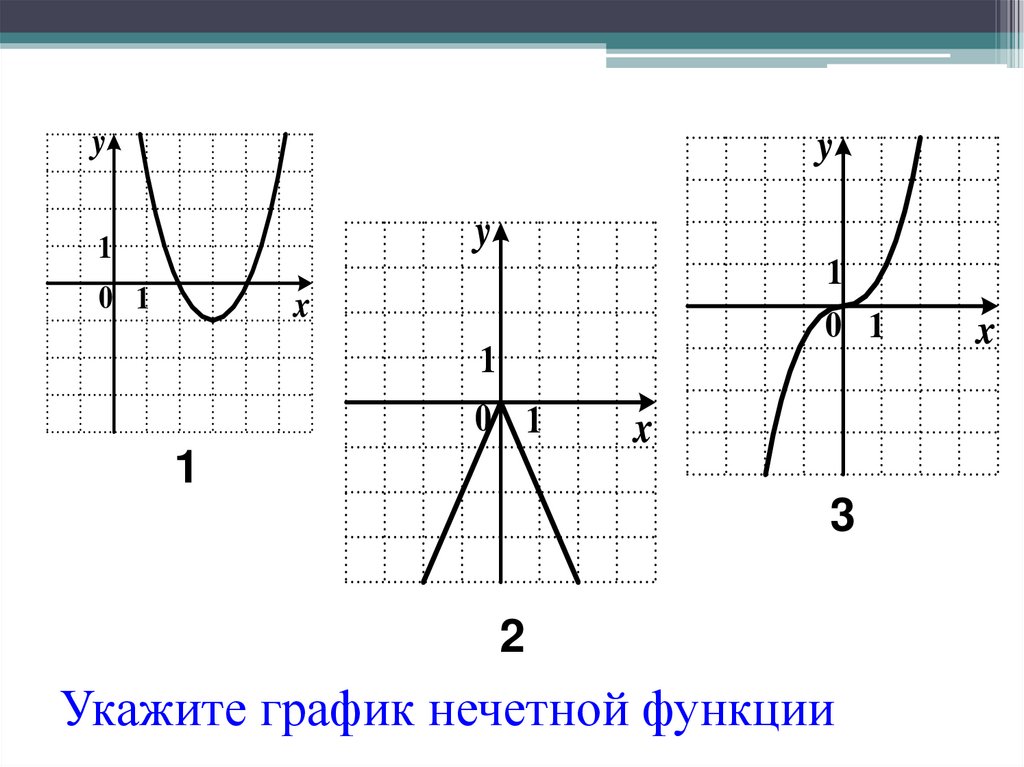
Как: Имея формулу функции, определить, является ли функция четной, нечетной или ни одной из них.
- Определите, удовлетворяет ли функция
f(x)=f(−x)f\left(x\right)=f\left(-x\right)f(x)=f(−x)
. Если да, то даже. 9{2}+7f(s)=s4+3s2+7
9{2}+7f(s)=s4+3s2+7четное, нечетное или ни то, ни другое? Решение
Лицензии и атрибуты
Лицензионный контент CC, совместно используемый ранее
- Precalculus. Автор : Джей Абрамсон и др. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/precalculus/pages/1-introduction-to-functions. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу: http://cnx.org/contents/[email protected]
Все права защищены. Содержание
- Знакомство с нечетными и четными функциями. Автор : Mathispower4u. Лицензия : Все права защищены . Условия лицензии : Стандартная лицензия YouTube
BioMath: Функции
В этом разделе будет представлено несколько терминов для квалификации функции.
 Понимание этих свойств пригодится, когда вы рисуете графики функций или смотрите, что происходит, когда заданная величина максимизируется или минимизируется.
Понимание этих свойств пригодится, когда вы рисуете графики функций или смотрите, что происходит, когда заданная величина максимизируется или минимизируется.Функции возрастания и убывания
Представьте, что вы наблюдаете, как со временем меняется определенное свойство биологической системы. Математически вы бы смотрели на то, увеличивается или уменьшается функция, моделирующая свойство.
Чтобы определить, является ли функция возрастающей или убывающей, мы должны «прочитать» график функции слева направо. Вы можете думать об увеличении функционировать как тот, который поднимается на слева направо, а убывающая функция как на падает на слева направо.
Большинство функций не увеличиваются/уменьшаются для всех x в домене, а увеличиваются на на одних интервалах и уменьшаться на других. Мы говорим, что f возрастает на некотором интервале, I , если для x 1 и x 2 в I ,
С другой стороны, мы говорим, что f убывает на I , если для x 1 и x 2 в I ,
Чтобы определить, увеличивается или уменьшается график функции в течение заданного интервале, читаем график слева направо и определяем, имеет ли он восходящий или нисходящий тренд, как показано на рисунке ниже,
Если представить, что по графику катится мяч, то на графике он будет катиться вниз по склону.
 части графика, которые уменьшаются, и он будет катиться вверх по частям
график, который увеличивается.
части графика, которые уменьшаются, и он будет катиться вверх по частям
график, который увеличивается.Нечетные и четные функции
Некоторые функции обладают особым свойством быть нечетными или четными. Нечетные и четные функции имеют особые графические симметрии.
Определение
Функция f ( x ) вызывается нечетным если,
для всех x в домене f .
Как узнать, является ли функция нечетной? Пример нечетной функции: f ( x ) = x . Мы можем продемонстрировать, что f ( x ) = x нечетно, показав, что f (− x ) = — f (x), заменив — x вместо x 9,
ж (- х ) = — х = — ф ( х ).

Если функция не нечетная, она может (но не обязательно) быть четной.
Определение
Функция f ( x ) вызывается даже если,
е (- х ) = е ( х ),
для всех х в домене ф .
Пример четной функции: f ( x ) = x 2 . Мы можно продемонстрировать, что f ( x ) = x 2 четно, показав, что f (- x ) = f ( x ) 03 как,
е (- х ) = (- х 2 ) = (−1) 2 x 2 = x 2 = f ( x ).

Как сказано выше, графики нечетных и четных функций имеют особые симметрии.
График нечетной функции симметричен относительно начала координат. Граф симметричен относительно начала координат, если точка (- x , — y ) лежит на графе всякий раз, когда ( x , y ) лежит на нем. С другой стороны, график четной функции симметричен относительно у -ось. График симметричен относительно оси y , если точка ( -x , y ) лежит на график всякий раз, когда ( x , y ) это делает.
Не все функции классифицируются как нечетные или четные; функция, которая не является четной или нечетное не называется и .
Примером функции, которая не является ни четной, ни нечетной, является число 9.0132 f
( x ) = x + 1. Мы можем продемонстрировать это, найдя f (− x ) какf (- х ) = — х + 1,
Обратите внимание, что f (- x ) не равно — f ( x ), потому что
— f ( х ) = -( х + 1) = — х -1;
и f (− x ) не равно f ( x ), потому что
ф ( х ) = х + 1.

Тот факт, что четные и нечетные функции имеют определенные графические симметрии, полезен знать. В частности, если вы знаете, что некоторая функция f ( x ) является нечетной (четной) и знаете значение f ( a ), то вы также знаете, что значение f (- a ) равно — f ( а ) (е(а)). Точно так же, если вы знаете, что некоторая функция f ( x ) является четной, и знаете значение f ( a ), то вы также знаете, что значение f (− a ) равно — ф ( а ). Это становится важным, когда вы изучаете интегральное исчисление, потому что интеграл нечетной или четной функции на симметричном интервале можно значительно упростить.
Максимумы и минимумы функций
Функция может достигать значений, которые можно классифицировать как максимальные и/или минимальные.
 В совокупности максимумы и минимумы называются экстремумами.
В совокупности максимумы и минимумы называются экстремумами.Графически вы можете думать о максимумах и минимумах как о функциональных значениях вершины и долины. Экстремумы могут быть классифицированы как глобальные или локальные. Как следует из названий, глобальный максимум — это максимальное значение функции достигается, а глобальный минимум — это минимальное значение, которого достигает функция. Если функция ограничен и имеет область определения, состоящую из всей прямой, глобальный максимум равен самый высокий пик и глобальный минимум — это самая низкая долина.
И максимум, и минимум функции должны быть конечными числами. Следовательно, если функция возрастает без ограничена, эта функция не имеет глобального максимума. Точно так же, если функция неограниченно убывает, глобального минимума нет. Однако эти неограниченные функции могут иметь локальные максимумы и минимумы, как показано на рисунке ниже,
Экстремумы, изображенные на приведенном выше графике, являются локальными, поскольку функция возрастает и неограниченно уменьшается, как показано стрелками на графике.



 9{2}+7f(s)=s4+3s2+7
9{2}+7f(s)=s4+3s2+7 Понимание этих свойств пригодится, когда вы рисуете графики функций или смотрите, что происходит, когда заданная величина максимизируется или минимизируется.
Понимание этих свойств пригодится, когда вы рисуете графики функций или смотрите, что происходит, когда заданная величина максимизируется или минимизируется.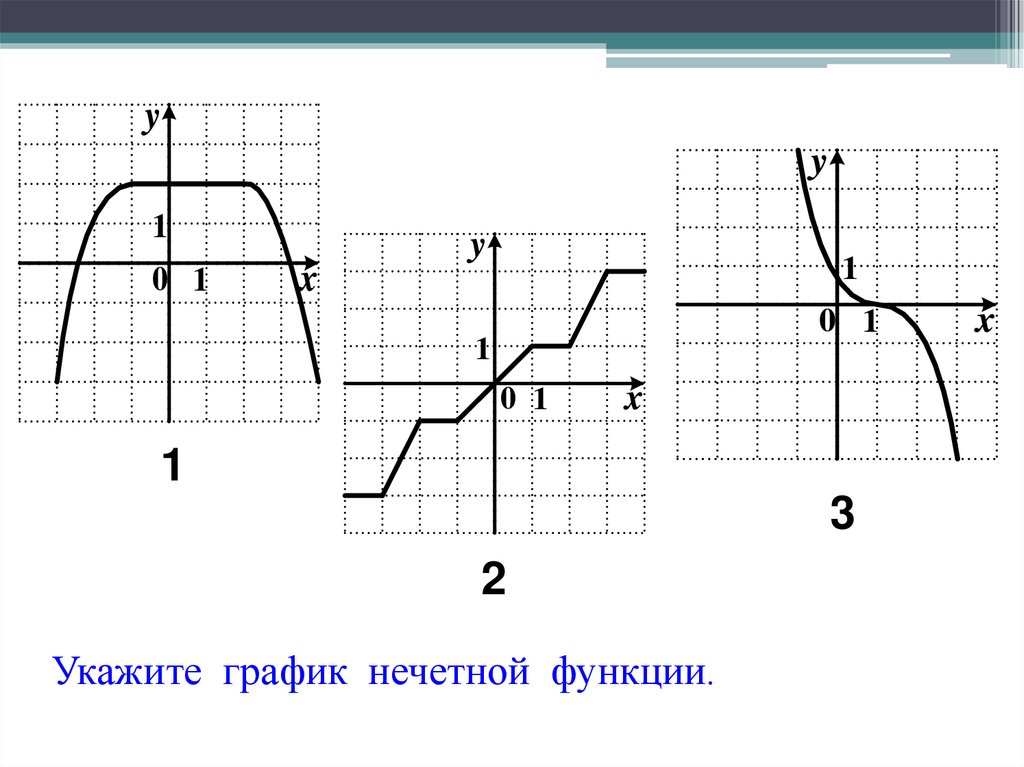 части графика, которые уменьшаются, и он будет катиться вверх по частям
график, который увеличивается.
части графика, которые уменьшаются, и он будет катиться вверх по частям
график, который увеличивается.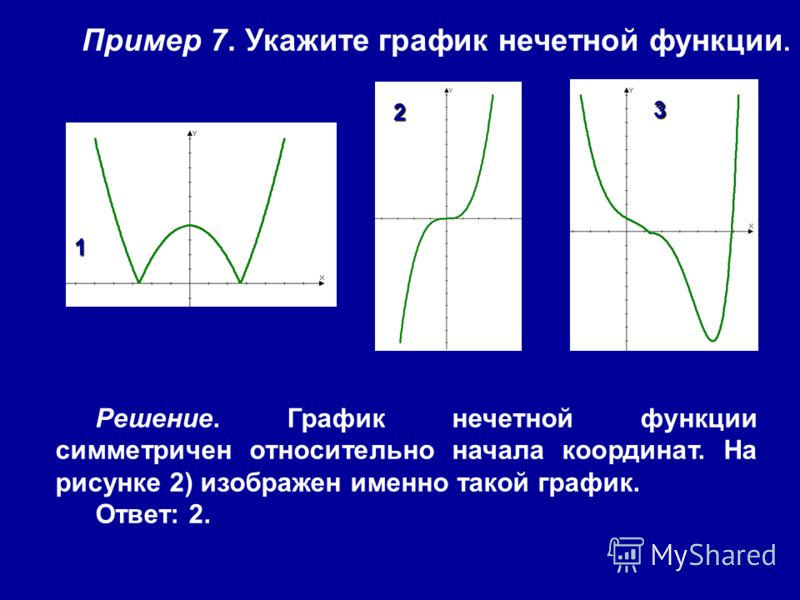
 В совокупности максимумы и минимумы называются экстремумами.
В совокупности максимумы и минимумы называются экстремумами.