Шутить изволите, Dimoniada . Конечно написал чушь собачью — невнимательно прочитал условие. Но ведь в главном я, все-таки, прав – ответ-то у меня верный! Вот «нормальное» решение. Кратко: Подробно: 2. Следствие: Пусть одна из вершин четырехугольника фиксирована на стороне прямоугольника. Тогда выбор трех остальных вершин (лежащих на трех других сторонах прямоугольника) таким образом, чтобы получился четырехугольник минимального периметра, равносилен выполнению условия «угол падения равен углу отражения» в каждой из четырех вершин четырехугольника по отношению к соответствующей стороне прямоугольника. Физическая аналогия: Траектория луча света (или бильярдного шара), запускаемого из любой точки на стороне прямоугольника, после трех отражений от других сторон прямоугольника и вернувшегося в исходную точку. Нетрудно видеть, что эта траектория будет периодической. 3. Другими словами, четырехугольник, обладающий минимальным периметром – вписанный параллелограмм. Ну а полупериметр вписанного в прямоугольник параллелограмма равен диагонали прямоугольника.  Все остальные вписанные четырехугольники, отличающиеся от параллелограммов, имеют, естественно, больший полупериметр. (Периметр произвольного, вписанного в прямоугольник параллелограмма можно найти как несложным тригонометрическим расчетом, так и на основе чисто геометрических соображений).Обсуждение.  А периметр вписанного параллелограмма улучить оказалось невозможным, откуда и был сделан вывод о минимуме его периметра. Эта аргументация предполагает с самого начала существование (хотя бы одного) вписанного четырехугольника минимального периметра (на самом деле, мы утверждаем, что их оказалось бесконечно много). Строгое доказательство существования опирается здесь на теорему Кантора (Вейерштрасса) о достижении экстремума непрерывной функции [в данном случае – периметра] на компактном множестве [в данном случае – на замкнутом, ограниченном множестве вершин вписанных четырехугольников в четырехмерном пространстве]. Для замкнутости этого множества и требуется включение в него вырожденных ситуаций, а ограниченность множества очевидна, т.к. вершины четырехугольника находятся на сторонах (ограниченного) прямоугольника. ============== |
Круг этих вопросов обсуждается, например, в книге Тихомирова из библиотечки Кванта «Рассказы о максимумах и минимумах».Вопросы к зачёту по геометрии за 1 полугодие. 8 класс.
Вопросы к зачёту по геометрии
Часть 1
1. Определение многоугольника. Что такое вершины, стороны, диагонали и периметр многоугольника?
Многоугольник – это геометрическая фигура, у которой смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек.
Вершина многоугольника – это точка пересечения двух соседних сторон многоугольника.
Сторона многоугольника – это отрезок соединяющий две соседние вершины многоугольника.
Диагональ многоугольника – это отрезок, соединяющий две любые не соседние вершины многоугольника.
Периметр многоугольника – это сумма длин всех сторон многоугольника.
2. Определение выпуклого многоугольника.
Запишите
формулу для вычисления суммы углов выпуклого многоугольника.
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Сумма углов выпуклого n-угольника равна (n-2)∙ 180 ̊
3. Начертите четырехугольник и укажите его диагонали, противоположные вершины, противоположные и смежные стороны. Запишите формулу для вычисления суммы углов выпуклого многоугольника, в частности, сумму углов выпуклого четырехугольника.
Сумма углов выпуклого n-угольника равна (n-2)∙ 180 ̊.
Сумма углов выпуклого четырехугольника равна 360 ̊.
4. Определение параллелограмма. Сформулируйте признаки параллелограмма.
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
Признаки параллелограмма:
1)Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
2)Если в
четырехугольнике противоположные стороны попарно равны, то этот четырехугольник
– параллелограмм.
3)Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм.
5. Определение параллелограмма. Сформулируйте свойства параллелограмма.
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмм:
1)В параллелограмме противоположные стороны равны и противоположные углы равны.
2)Диагонали параллелограмма точкой пересечения делятся пополам.
6. Сформулируйте теорему Фалеса.
Теорема (Фалеса). Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямы, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
7. Дайте определение средней линии треугольника. Сформулируйте ее свойства.
Средней линией
треугольника называют отрезок, соединяющий середины двух сторон треугольника.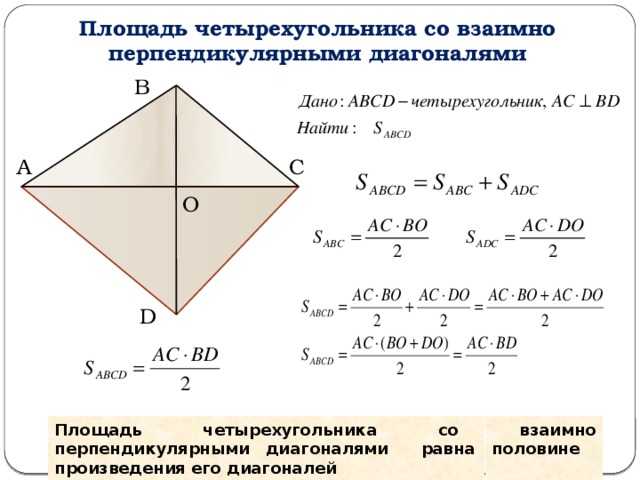
Свойства средней линии треугольника:
1)Средняя линия треугольника параллельна третьей стороне треугольника.
2)Средняя линия треугольника равна половине основания.
8. Сформулируйте теорему Вариньона.
Теорема (Вариньона). Середины сторон произвольного четырехугольника являются вершинами параллелограмма.
9. Дайте определение трапеции. Как называются стороны трапеции? Какая трапеция называется равнобедренной, прямоугольной?
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Параллельные стороны трапеции называются ее основаниями.
Не параллельные стороны трапеции называются ее боковыми сторонами.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Трапеция, один из углов которой прямой, называется прямоугольной.
10. Дайте определение равнобедренной трапеции. Сформулируйте признаки и свойства
равнобедренной трапеции.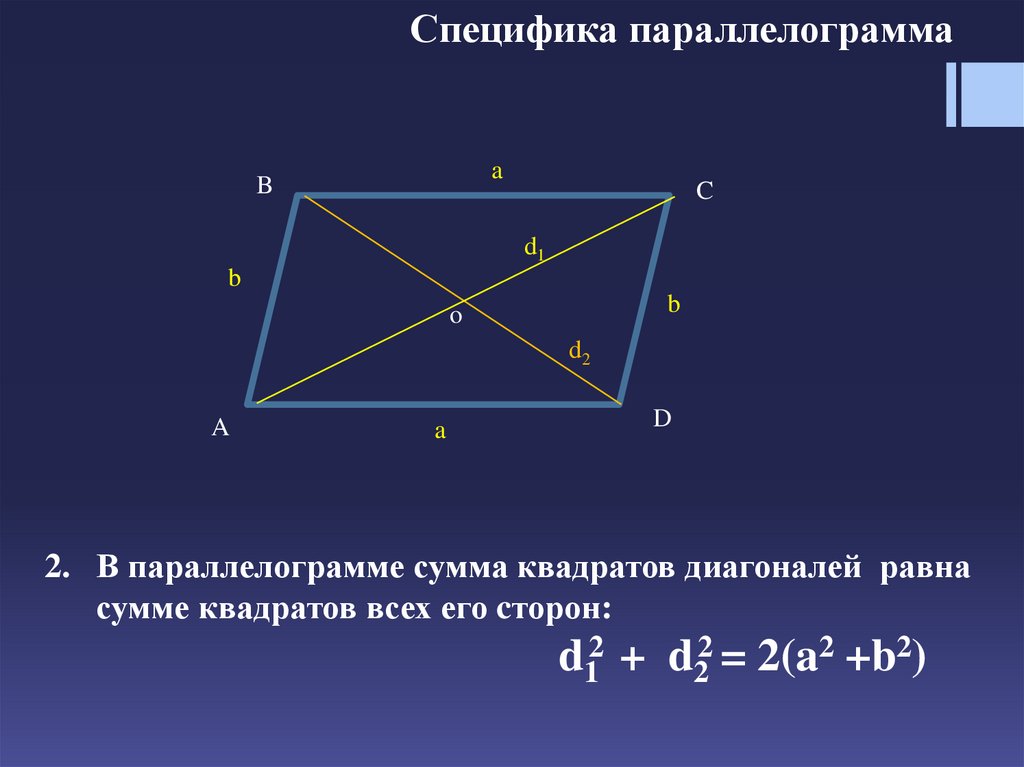
Трапеция называется равнобедренно, если ее боковые стороны равны.
Свойства равнобедренной трапеции:
1)В равнобедренной трапеции углы при основании равны.
2)В равнобедренной трапеции диагонали равны.
Признаки равнобедренной трапеции:
1)Если у трапеции углы при основании равны, то она равнобедренная.
1)Если у трапеции диагонали равны, то она равнобедренная.
11. Дайте определение средней линии трапеции. Сформулируйте ее свойства. Напишите формулу для вычисления площади трапеции.
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон.
Свойства средней линии трапеции:
1)Средняя линия трапеции параллельна основаниям трапеции.
2)Средняя линия равна полусумме оснований трапеции.
12. Какой четырехугольник называется прямоугольником? Сформулируйте характеристическое свойство прямоугольника. Чему равна площадь прямоугольника?
Прямоугольником
называется параллелограмм, у которого все углы прямые.
Диагонали прямоугольника равны.
Площадь прямоугольника вычисляется по формуле S=a∙b
13. Какой четырехугольник называется ромбом? Сформулируйте характеристические свойства ромба. Как можно вычислить площадь ромба?
Ромбом называется параллелограмм, у которого все стороны равны.
Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Площадь ромба вычисляется по формуле S=a∙h=½d₁d₂
14. Какой четырехугольник называется квадратом? Сформулируйте основные свойства квадрата. Как можно вычислить площадь квадрата?
Квадратом называется прямоугольник, у которого все стороны равны.
Основные свойства квадрата:
1)Все углы квадрата прямые.
2)Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
15. По каким формулам можно вычислить площадь треугольника? Перечислите следствия теоремы о площади треугольника.
Площадь
треугольника равна половине произведения его основания на высоту.
Следствие 1.Площадь прямоугольного треугольника равна половине произведения его катетов.
Следствие 2.Если высоты двух треугольников равны, то их площади относятся как основания.
16. Сформулируйте теоремы об отношение площадей треугольников с равными: высотами, основаниями, углами.
Если высоты двух треугольников равны, то их площади относятся как основания.
Если основания двух треугольников равны, то их площади относятся как высоты.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся произведения сторон, заключающих равные углы.
Медианы треугольника и равновеликость.
Медиана разбивает треугольник на два равновеликих треугольника.
17. Какие две точки называются симметричными относительно данной прямой? Какая фигура называется симметричной относительно данной прямой?
Две точки А и А’
плоскости называются симметричными относительно прямой с, если эта прямая
проходит через середину отрезка АА’ и перпендикулярна к нему.
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
18. Какие две точки называются симметричными относительно данной точки? Какая фигура называется симметричной относительно данной точки?
Две точки А и В называются симметричными относительно точки О, еслиточка О является серединой отрезка АВ.
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
19. Сформулируйте основные свойства площади многоугольников. Сформулируйте теорему о площади параллелограмма.
Основные свойства площади многоугольников:
1)Равные многоугольники имеют равную площадь.
2)Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих треугольников.
3)Площадь квадрата равна квадрату его стороны.
Площадь
параллелограмма равна произведению его основания на высоту.
20. Сформулируйте прямую и обратную теорему Пифагора.
Теорема (Пифагора).В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема, обратная теореме Пифагора. Если квадрат одной стороны равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Часть 2
1. Определение параллелограмма. Сформулируйте свойства параллелограмма. Докажите свойство противоположных сторон и противоположных углов параллелограмма.
2. Определение параллелограмма. Сформулируйте свойства параллелограмма. Докажите свойство диагоналей параллелограмма.
3. Определение параллелограмма. Сформулируйте признаки параллелограмма. Докажите признаки по противоположным сторонам и противоположным углам четырехугольника.
4. Определение параллелограмма. Сформулируйте
признаки параллелограмма. Докажите признак по диагоналям и признак по двум
сторонам четырехугольника.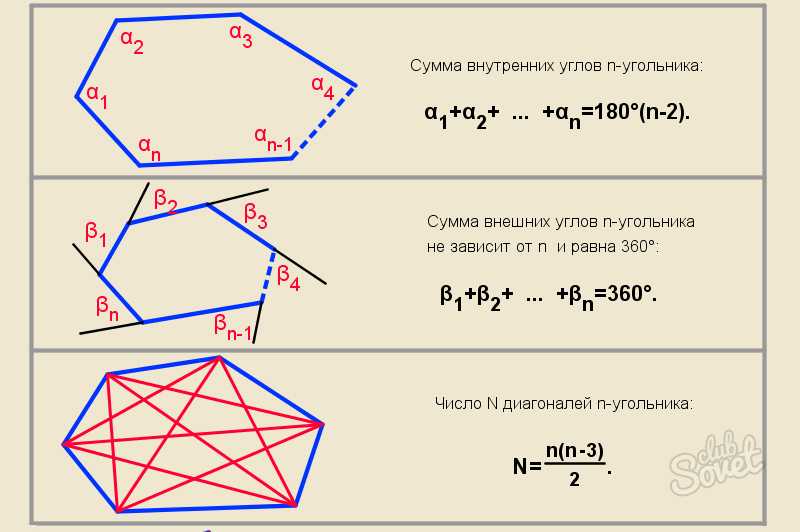
5. Сформулируйте и докажите теорему Фалеса.
6. Определение средней линии треугольника. Докажите теорему о средней линии треугольника.
7. Определение средней линии треугольника. Сформулируйте теорему о средней линии треугольника. Сформулируйте и докажите теорему Вариньона.
8. Дайте определение равнобедренной трапеции. Сформулируйте свойства и признаки равнобедренной трапеции. Докажите их для углов.
9. Дайте определение равнобедренной трапеции. Сформулируйте свойства и признаки равнобедренной трапеции. Докажите их для диагоналей.
10. Дайте определение средней линии трапеции. Сформулируйте и докажите теорему о средней линии трапеции.
11. Дайте определение прямоугольника. Сформулируйте и докажите характеристическое свойство прямоугольника.
12. Дайте определение ромба. Сформулируйте и докажите характеристические свойства ромба.
13. Сформулируйте
свойства площадей многоугольников.
Сформулируйте и докажите теорему о площади
прямоугольника.
14. Сформулируйте и докажите теоремы о площади треугольника и площади параллелограмма.
15. Сформулируйте и докажите теорему об отношении площадей двух треугольников, имеющих по равному углу.
16. Сформулируйте и докажите теоремы об отношении площадей двух треугольников, имеющих по равному основанию; равной высоте.
17. Сформулируйте и докажите теорему о вычислении площади трапеции.
18. Сформулируйте и докажите теорему Пифагора. Сформулируйте обратную теорему Пифагора.
19. Сформулируйте теорему Пифагора. Сформулируйте и докажите обратную теорему Пифагора.
геометрия — Максимальная площадь: Четырехугольник с фиксированным периметром и внутренним углом
спросил
Изменено 4 года, 9 месяцев назад
Просмотрено 1к раз
$\begingroup$
Редактировать (1 мая 2018 г.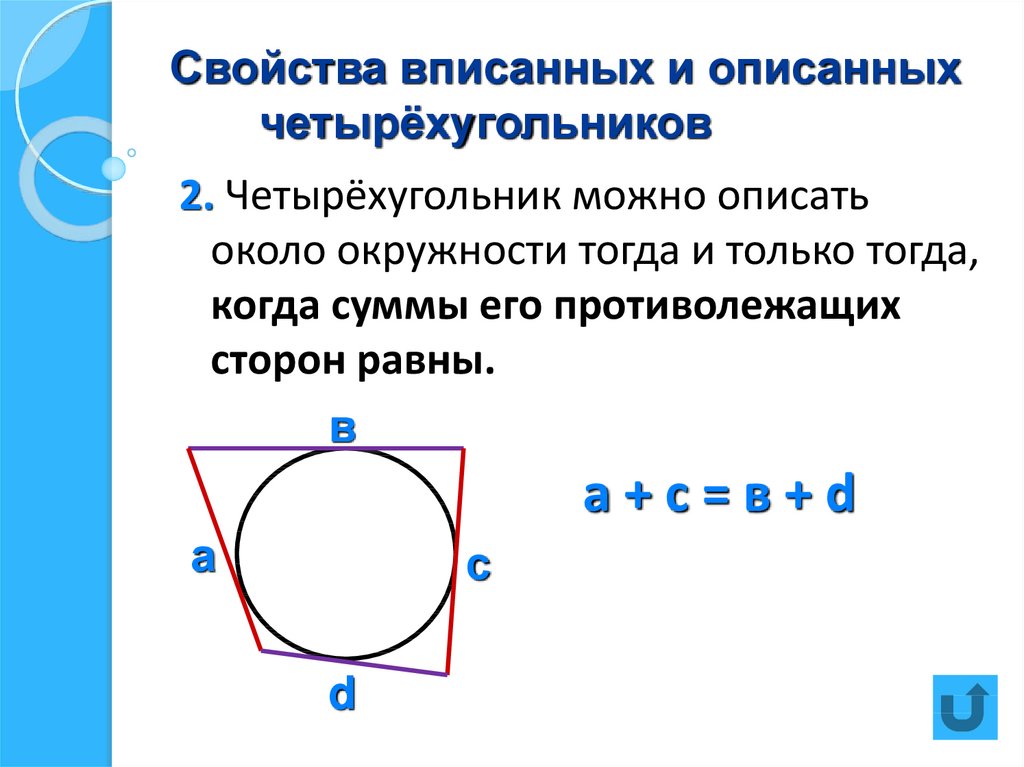
{\circ}$. Какова максимально возможная площадь? 92/16$.)
- геометрия
- тригонометрия
- ссылка-запрос
- оптимизация
- выпуклая оптимизация
$\endgroup$
4
$\begingroup$
Вот обзор того, что я собираюсь сделать.
- Докажите, что четырехугольник должен быть выпуклым.
- Докажите, что $\треугольник BCD$ должен быть равнобедренным. 9\circ — \theta$ сохраняет периметр, но увеличивает площадь.
- Пусть $n$ — любое целое число $\ge 3$ и $[n] = \{ 0, 1, \ldots, n — 1 \}$.
- Пусть $v_0, v_1, \ldots, v_{n-1}$ — вершины любого простого $n$-угольника с периметром $p$ и площадью $\mathcal{A}$.
- Расширение определения $v_k$ по периодичности. Для любого $k = qn+r$, где $r \in [n]$, $v_k$ является псевдонимом $v_r$.
2}$ максимизируется?Ребра $v_{k-1}v_k$ $n$-угольника можно разделить на две группы, свободные (т.е. и $\alpha_k$, и $\alpha_{k-1}$ не являются исправлено), а те нет.
Для любого свободного ребра $v_{k-1}v_k$ рассмотрим следующие возмущения $n$-угольника, сдвигающие $v_k$ вдоль прямой $v_{k+1}v_k$ на малое расстояние $\epsilon $.
$$v_j \rightarrow v_j(\epsilon) = \begin{cases} v_{k} + \frac{\epsilon}{\ell_{k+1}}(v_k — v_{k+1}), & j = k\\v_j, & j \ne k\end{cases}$$ 92}\право|_{\эпсилон=0} = 0 \quad\подразумевается\quad \frac{\ell_k\sin\alpha_k}{2\mathcal{A}} = \frac{2(1+\cos\alpha_k)}{p} \quad\iff\quad \frac{p\ell_k}{4\mathcal{A}} = \cot\frac{\alpha_k}{2}\tag{*1a} $$ Аналогично, если мы потревожим многоугольник, сдвинув $v_{k-1}$ вдоль линии $v_{k-2}v_{k-1}$ для малого расстояния $\epsilon$:
$$v_j \rightarrow v_j(\epsilon) = \begin{cases} v_{k-1} + \frac{ \epsilon}{\ell_{k-1}}(v_{k-1} — v_{k-2}), & j = k-1\\v_j, & j \ne k-1\end{case} $$
Получаем следующее соотношение $$\frac{p\ell_k}{4\mathcal{A}} = \cot\frac{\alpha_{k-1}}{2}\tag{*1b}$$ 92}$, нам нужно, чтобы все оставшиеся углы были равны друг другу.
Когда ребро $v_{k-1}v_k$ несвободно, вышеперечисленные возмущения становятся недопустимыми, так как меняют углы $\alpha_{k-1}$ и $\alpha_k$. Вместо этого мы можем провести параллель сдвинем ребро $v_{k-1}v_k$ наружу на расстояние $\epsilon$, не изменяя остальные ребра. Если мы это сделаем, мы получим следующее соотношение, справедливое для всех ребер.
$$\frac{p\ell_k}{4\mathcal{A}} = \frac12\left(\cot\frac{a_k}{2} + \cot\frac{a_{k-1}}{2 }\справа)\тег{*1c}$$ Суммируя по $k$, находим, что максимальное значение $\mathcal{A}$ удовлетворяет: 9{-1}\\ &\ приблизительно 154.3031702366152 \end{выравнивание} $$
$\endgroup$
2
$\begingroup$
Рассмотрим четырехугольник $Q$ на изображении ниже:
Площадь $Q$ определяется выражением $$ f(a,b,c,d,A,C) = \frac{a d \sin A+bc \sin C}{2} $$
Итак, здесь мы хотим максимизировать $f(a,b,c,d,A,C)$ при условии: \начать{выравнивать*} А &= \альфа\\ а+b+с+d &= Н \\ a^2 + d^2 — 2ad \cos A &= b^2 + c^2 — 2bc \cos C \end{выравнивание*} 9{°}\\ d &= N-a-b-c \ приблизительно 22,79705048 \end{выравнивание*}
$\endgroup$
3
геометрия.
Почему если задан многоугольник с n сторонами, правильный (т. е. все стороны равны) заключает в себе наибольшую площадь при постоянном периметре?Вот элегантное доказательство, но оно основано на реальном анализе, а не только на евклидовой геометрии. Я предполагаю, что вас интересуют только несамопересекающиеся многоугольники, поскольку неясно, что следует определять как площадь самопересекающегося многоугольника. 9n$, которые описывают углы, образуемые сторонами несамопересекающегося вписанного многоугольника (который может иметь стороны длины $0$).
Тогда очевидно, что $D$ — замкнутое ограниченное множество, а значит, компактное.
Пусть $f(v)$ — площадь многоугольника $P$, описываемого вектором $v$.
Тогда $f$ непрерывна на $D$.
Следовательно, $f$ достигает максимума на $D$.
Пусть $a \in D$ такое, что $f(a) = \max_{v \in D} f(v)$, и пусть R — многоугольник, описываемый $a$.
Если $R$ не является правильным:
$R$ имеет две стороны $AB,BC$ неравной длины.
n$, описывающих вершины ориентированного многоугольника с периметром $p$ (который может иметь стороны длины $0$ и самопересечения) такие, что одна вершина равна $(0,0)$.Тогда $D$ является замкнутым (поскольку его можно выразить в виде нестрогих неравенств) ограниченным множеством и, следовательно, компактным.
Пусть $f(v)$ — площадь со знаком многоугольника $P$, описываемого вектором $v$.
Тогда $f$ непрерывна на $D$.
Следовательно, $f$ достигает максимума на $D$.
Пусть $a \in D$ такое, что $f(a) = \max_{v \in D} f(v)$, и пусть R — многоугольник, описываемый $a$.
Если $R$ имеет две стороны $AB,BC$ такие, что $|AB| \ne |BC|$ или $Area(\треугольник ABC) < 0$: 9\circ$.
Если $R$ не является циклическим:
Пусть $X,Y,Z,W$ — четыре вершины $R$ по порядку, не лежащие на окружности.
Эти четыре вершины делят стороны $R$ на четыре части.
Жестко переместите эти четыре секции так, чтобы $R$ остался многоугольником, а $XYZW$ стал циклическим.
РЕДАКТИРОВАТЬ: работает только с углом $\angle BCD$. Я считаю, что проблема плохо определена, если четырехугольник не является выпуклым, например, я не верю, что существует максимум (в настоящее время у меня нет подходящей комнаты или времени, чтобы доказать это).
Рассмотрим эллипс $\mathcal{E}$ с фокусами $B, D$, содержащими $C$.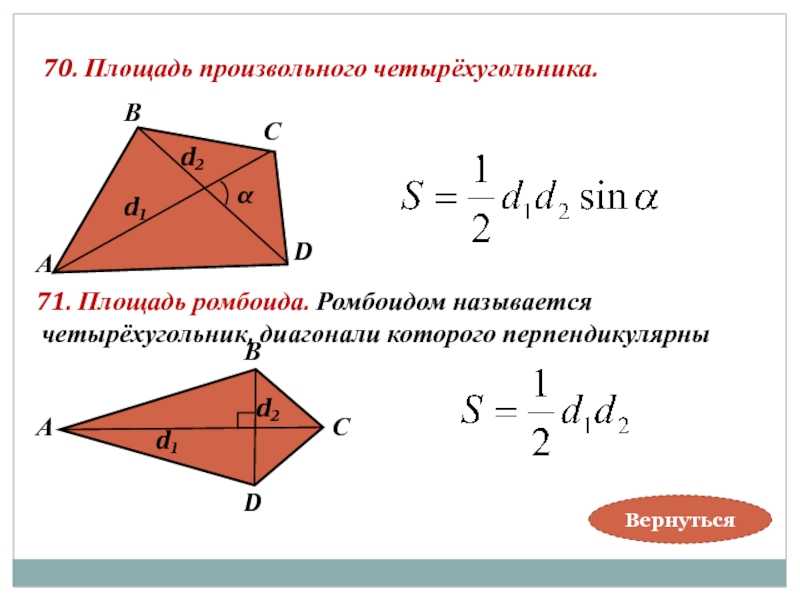
Перемещая $C$ вдоль $E$, видим, что периметр $ABCD$ не изменился. Площадь $ABCD$ равна $[BAD] + [BCD]$, и $[BAD]$ также остается неизменной. Площадь $\треугольника BCD$ меняется, это
$$[BCD] = \frac{1}{2} \cdot BD \cdot CC’$$
где $C’$ — основание высоты от $C$. Ясно, что $BD$ инвариантна, а $CC’$ — единственная изменяющаяся величина. Он получает максимум , когда она становится полуосью $\mathcal{E}$. При этом $\треугольник BCD$ равнобедренный.
Предположим, что $AD > AB$. Пусть $E$ лежит на отрезке $\overline{AD}$ так, что $AE = AB$. Кроме того, пусть $D’$ — середина $\overline{ED}$, а $B’$ — точка на луче $\overrightarrow{AB}$ такая, что $AB’ = AD’$. Таким образом, периметры $\треугольника ABD$ и $\треугольника AB’D’$ равны. Кроме того, $EBB’D’$ — равнобедренная трапеция, пусть высота равна $h$. Тогда $[BB’D’] = h\cdot D’B’$ и $[BED’] = h \cdot EB$, поэтому $[BB’D’] > [BED’]$. Кроме того, $ED’ = D’D$, и, используя высоту от $B$ до линии $\overline{AD}$, получаем $[BED’] = [BD’D]$.
В следствии,
$$[BB’D’] > [BD’D] \подразумевает [ABD’] + [BB’D’] > [ABD’] + [BD’D] \подразумевает [B’AD’] > [BAD] $$
Обратите внимание, что $B’AD’$ был равнобедренным. Таким образом, периметр $ABCD$ остается постоянным, а площадь $\треугольника BAD$ максимальна. Это происходит, когда $\треугольник BAD$ равнобедренный. 92} \примерно 154,3$$
$\endgroup$
3
$\begingroup$
Нет требования, чтобы четырехугольник был выпуклым. Люди предполагают, что результат должен быть выпуклым, но это неверно. Если четырехугольник вогнут в точке $D$, его нельзя превратить в выпуклый четырехугольник, не нарушая ограничения, состоящего в том, что угол $A$ равен $30$ градусам.
9{\circ}$ угол сохраняется, но результат намного выше заявленного ранее максимума для выпуклых фигур.$\endgroup$
0
$\begingroup$
Напишите выражение для площади четырехугольника как суммы площадей двух равнобедренных треугольников, $ADB$ и $DCB$, как частный случай, такой что $AD + DC = AB + BC = 30$.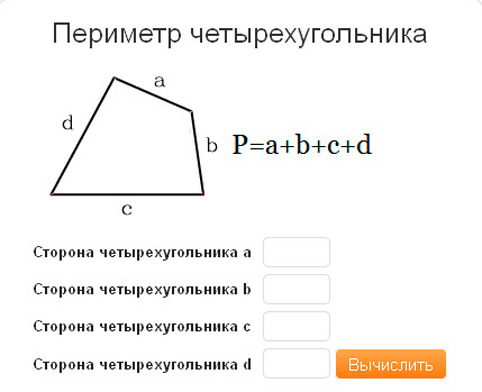
2-(2x(40-x)cos(30))}}))$$
Где $0 \le x \le 20$
Примечание: в ограниченном домене учитываются все комбинации длин двух соседних сторон.
Установка производной $dA/dx = 0$ и решение для x дает:
$$x = 20\ldots, \text{ отсюда } A_{max} = 100$$
Таким образом, равнобедренный треугольник оптимальна, и отсюда следует, что равнобедренные треугольники вплотную друг к другу оптимальны для общего случая.
$\endgroup$
2
9\circ$.Чтобы решить эту проблему, мы немного обобщим ее и найдем условия для достижения оптимальности.
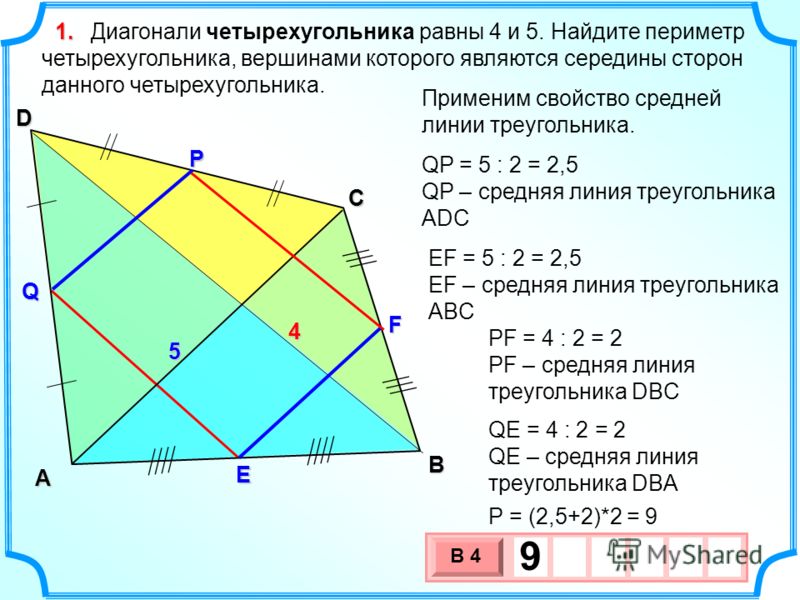2}$ максимизируется?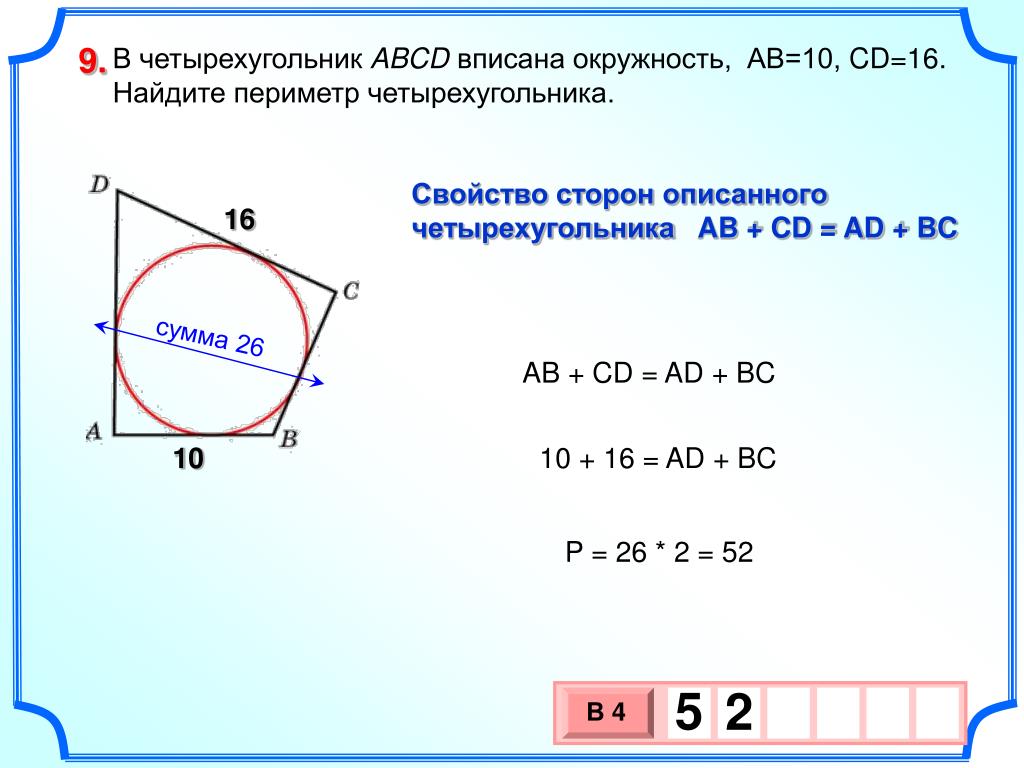
Почему если задан многоугольник с n сторонами, правильный (т. е. все стороны равны) заключает в себе наибольшую площадь при постоянном периметре?
n$, описывающих вершины ориентированного многоугольника с периметром $p$ (который может иметь стороны длины $0$ и самопересечения) такие, что одна вершина равна $(0,0)$.