Основы программирования в R
Распределение количественных показателей и проверка распределения на нормальность
Иногда в процессе анализа данных мы сталкиваемся с необходимостью определить тип распределения данных. Решить эту задачу непросто: нет такого универсального статистического теста, который позволил бы однозначно определить тип распределения, за исключением случаев, когда оно является нормальным. Но распределение данных можно сравнить с нормальным распределением. Требование нормальности распределения данных лежит в основе некоторых статистических тестов и моделей; плюс, при визуальном сравнении с нормальным распределением удобно отмечать всякие особенности распределения (скошенность, наличие «длинных хвостов» и прочее).
Начнем с визуального анализа. Например, наложим на гистограмму, построенную для показателя, график плотности нормального распределения с соответствующими параметрами.
Напоминание 1. О графике плотности распределения можно думать как о «сглаженной» гистограмме с большим числов столбцов.
Напоминание 2.
Для примера — графики плотности нормального распределения с разными параметрами.
# add = TRUE - чтобы добавлять графики к уже нарисованным curve(dnorm(x, mean = 2, sd = 1), xlim = c(-10, 10), col = "green" ) curve(dnorm(x, mean = -1, sd = 1), xlim = c(-10, 10), col = "blue", add = TRUE) curve(dnorm(x, mean = 2, sd = 3), xlim = c(-10, 10), col = "red", add = TRUE)
Теперь попробуем совместить на графике гистограмму и график плотности нормального распределения с соответствующими параметрами. Загрузим датафрейм с данными проекта Comparative Political Data Set, с которым мы уже работали.
df <- read.csv("http://math-info.hse.ru/f/2018-19/pep/hw/CPDS.csv", dec = ",") df <- subset(df, df$year >= 2014) # выберем данные
Построим гистограмму для показателя vturn (явка на выборы) и наложим на неё график плотности нормального распределения с соответствующими параметрами. Какие параметры считать соответствующими? Среднее значение, равное среднему значению показателя vturn, и стандартное отклонение, равное стандартному отклонению vturn.
# freq = FALSE - обязательно, так как нужны не абсолютные частоты, а нормализованные
hist(df$vturn, main = "Histogram of turnout", col = "tomato", freq = FALSE)
# na.rm = TRUE - не учитываем пропуски (NA)
# lwd - line width, толщина линии
curve(dnorm(x, mean = mean(df$vturn, na.rm = TRUE),
sd = sd(df$vturn, na.rm = TRUE)),
col = "blue", lwd = 2, add = TRUE)Пока кажется, что распределение явки не очень похоже на нормальное из-за высокого, сильно выделяющегося столбца на участке от 50 до 60.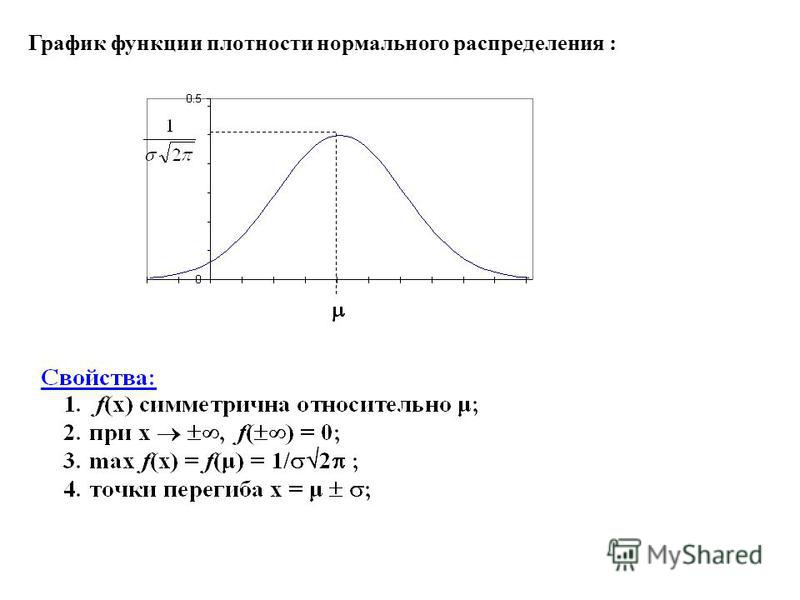 А теперь проверим формально.
А теперь проверим формально.
Один из статистических критериев, позволяющих проверить нормальность распределения данных, это критерий Шапиро-Уилка. С помощью этого критерия проверяется нулевая гипотеза, которая состоит в том, что данные распределены нормально.
shapiro.test(df$vturn)
## ## Shapiro-Wilk normality test ## ## data: df$vturn ## W = 0.96857, p-value = 0.01167
P-value < 0.05, следовательно, «жизнеспособность» нулевой гипотезы, оценённая на основе имеющихся данных, мала. На имеющихся данных на уровне значимости 5% (0.05) есть основания отвергнуть нулевую гипотезу о том, что данные распределены нормально. Показатель явки не распределён нормально.
Связь между качественными переменными: таблицы сопряженности и критерий хи-квадрат
С таблицами частот мы уже знакомы. Познакомимся с таблицами сопряжённости (contingency tables) — таблицами, которые иллюстрируют совместное распределение переменных. Построим таблицу сопряженности для двух признаков:
Построим таблицу сопряженности для двух признаков: poco (принадлежность к пост-коммунистическим странам) и gov_party (тип партийной системы).
ctab <- table(df$poco, df$gov_party) # View(ctab)
По полученной таблице сопряжённости можно определить, например, что число пост-коммунистических стран с гегемонией правых/центристских партий равно 4.
Связь между качественными переменными можно визуализировать с помощью мозаичного графика (mosaic plot). Подробнее о мозаичном графике см. здесь и здесь. Для этого потребуется библиотека vcd (от visualising categorical data).
install.packages("vcd")library(vcd) mosaic(data = df, poco ~ gov_party)
С помощью мозаичного графика мы можем визуализировать таблицу сопряжённости. Тёмно-серый цвет соответствует пост-коммунистическим странам, светло-серый — всем остальным. Разбивка на пять блоков по горизонтали — разбивка по значениям переменной gov_party (гегемония правых/центристских партий, доминирование левых партий и прочие).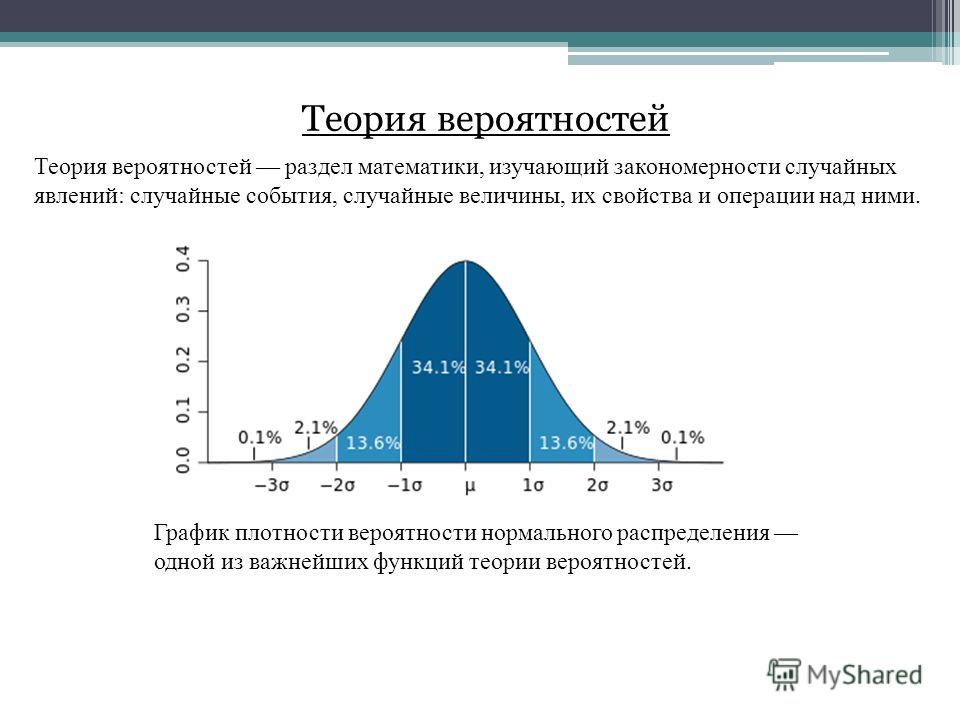
Чтобы всё совсем стало понятно, поправим подписи по осям. Создадим список (list) с поименованными векторами, один для подписей к poco, другой — к gov_party.
args <- list(poco = c("No", "Yes"),
gov_party = c("Hegemony R", "Dominance R/C", "Balance R/L", "Dominance L", "Hegemony L"))А теперь добавим полученные подписи — запишем их в аргумент set_labels:
mosaic(data = df, poco ~ gov_party, set_labels = args)
Проблему длинных подписей, которые накладываются друг на друга, можно решать по-разному. Мы пока на время воспользуемся простым, но не самым красивым: повернём подписи и сделаем их горизонтальными.
mosaic(data = df, poco ~ gov_party, set_labels = args, rot_labels = 0)
Можем сократить подписи до аббревиатур, используя функцию abbreviate(). Заодно повернём подписи на 45 градусов и уберём подписи самих осей:
args <- list(poco = c("No", "Yes"),
gov_party = abbreviate(c("Hegemony R", "Dominance R/C", "Balance R/L", "Dominance L", "Hegemony L")))
axis_labs <- list(set_varnames = c(poco = "", gov_party = "")) # убираем подписи
mosaic(data = df, poco ~ gov_party,
set_labels = args,
rot_labels = 45,
labeling_args = axis_labs)А теперь проверим формально, есть ли связь между этими признаками (принадлежность к пост-коммунистическим странам и тип партийной системы).
\[ H_0: \text{признаки независимы (не связаны)} \] \[ H_1: \text{признаки не независимы (связаны)} \]
chisq.test(table(df$poco, df$gov_party))
## Warning in chisq.test(table(df$poco, df$gov_party)): Chi-squared ## approximation may be incorrect
## ## Pearson's Chi-squared test ## ## data: table(df$poco, df$gov_party) ## X-squared = 8.3005, df = 4, p-value = 0.08117
P-value > 0.05, следовательно, вероятность того, что мы получим результаты такие, какие получили и выше, при условии, что нулевая гипотеза верна, не мала. На имеющихся данных на уровне значимости 5% (0.05) нет оснований отвергнуть нулевую гипотезу о том, что признаки независимы. Тип партийной системы и принадлежность к пост-коммунистическим странам не связаны.
Замечание. R выдал предупреждение Chi-squared approximation may be incorrect. (Пояснение, возможно, будет понятно не всем, но его можно смело пропустить и посмотреть, как решается эта проблема).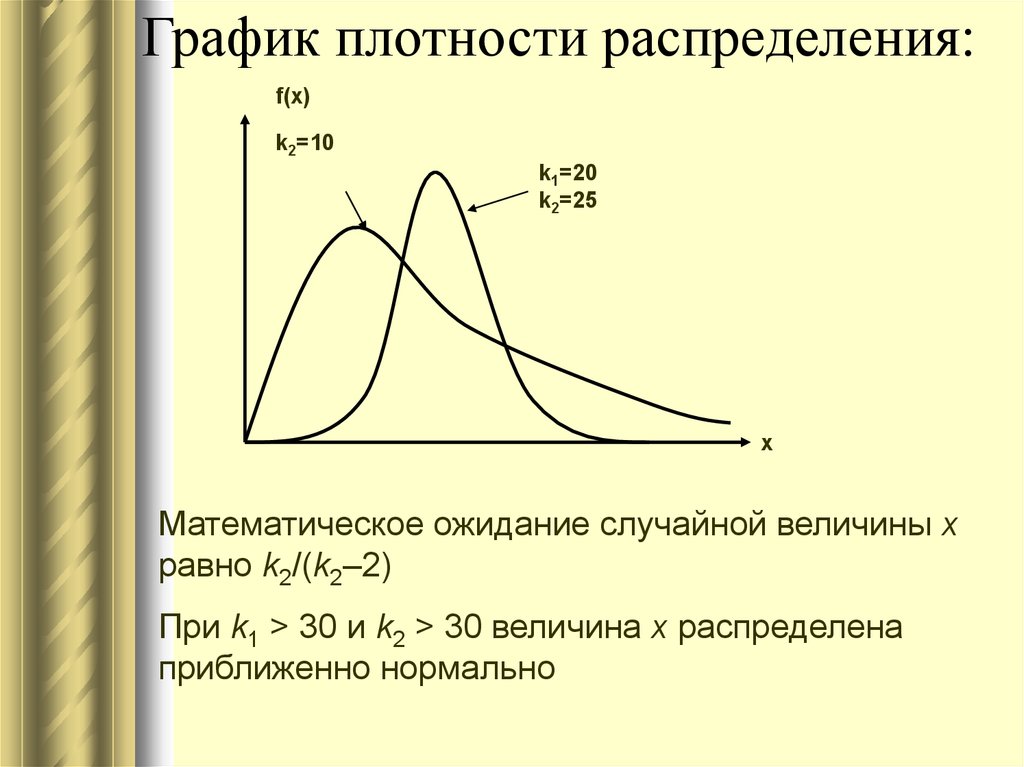
fisher.test(table(df$poco, df$gov_party))
## ## Fisher's Exact Test for Count Data ## ## data: table(df$poco, df$gov_party) ## p-value = 0.07206 ## alternative hypothesis: two.sided
Логика проверки гипотезы и выводы — те же самые, что и в критерии хи-квадрат.
Связь между количественными переменными: диаграммы рассеяния и коэффициенты корреляции
Напоминание про корреляции. Коэффициент корреляции К.Пирсона — показатель линейной связи между двумя переменными, измеренными в количественной шкале. Коэффициент корреляции принимает значения от \(-1\) до \(1\).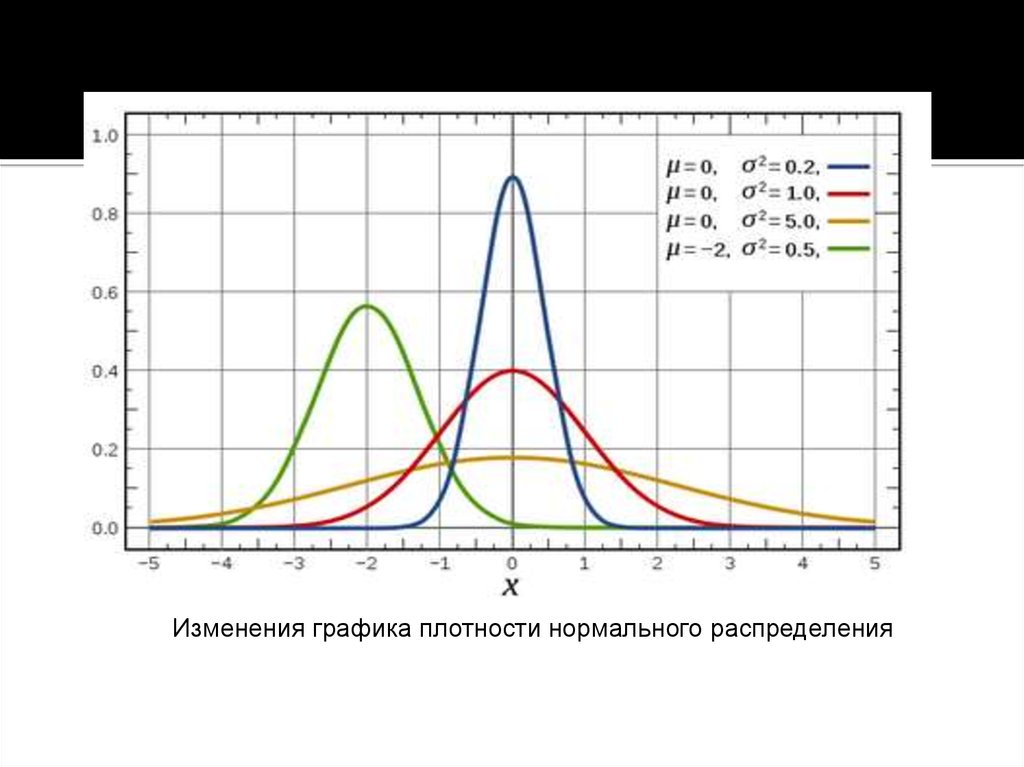 Отрицательные значения коэффициента корреляции свидетельствуют об обратной связи между переменными (с ростом значений одной переменной значения другой переменной уменьшаются), положительные значения коэффициента корреляции — о прямой связи между переменными (с ростом значений одной переменной значения другой переменной увеличиваются). Если коэффициент корреляции Пирсона между переменными равен 0, это не всегда означает, что связи между ними нет — связь между ними может просто быть нелинейной (например, квадратичной). Коэффициент корреляции показывает только связь между переменными, а не зависимость (
Отрицательные значения коэффициента корреляции свидетельствуют об обратной связи между переменными (с ростом значений одной переменной значения другой переменной уменьшаются), положительные значения коэффициента корреляции — о прямой связи между переменными (с ростом значений одной переменной значения другой переменной увеличиваются). Если коэффициент корреляции Пирсона между переменными равен 0, это не всегда означает, что связи между ними нет — связь между ними может просто быть нелинейной (например, квадратичной). Коэффициент корреляции показывает только связь между переменными, а не зависимость (Y зависит от X) и не влияние (X влияет на Y) и, конечно, ничего не сообщает о причинно-следственной связи.
Коэффициент корреляции Ч.Спирмена также используется для измерения связи между двумя переменными, измеренными в количественной шкале, преимущественно в порядковой (ординальной). Коэффициент корреляции Спирмена, в отличие от коэффициента Пирсона, является устойчивым к наличию нетипичных значений.
Связи между количественными переменными можно представить в виде корреляционной матрицы. Корреляционная матрица всегда симметрична (коэффициент корреляции между переменными X и Y равен коэффициенту корреляции между переменными Y и X), и на главной диагонали такой матрицы стоят 1 (корреляция переменной самой с собой равна 1).
Диаграммы рассеяния (scatterplots)
Допустим, мы хотим посмотреть на связь между переменными gov_right1. Построим диаграмму рассеяния (scatterplot).
plot(df$gov_left1, df$gov_right1)
По диаграмме рассеяния видно, что связь между переменными обратная (чем больше x, тем меньше y) и, скорее всего, сильная.
Как можно заметить, особой красотой этот график не отличается. График скучный. Что мы можем сделать? Во-первых, подписать оси и изменить тип маркера для точек.
Все типы маркеров мы можем посмотреть, запросив help по аргументу pch, он как раз отвечает за тип точек (pch — от point character).
?pch
plot(df$gov_left1, df$gov_right1,
xlab = "Left parties (% of total)",
ylab = "Right parties (% of total)",
pch = 19) Во-вторых, мы можем добавить цвета, причем вполне содержательно. Допустим, мы хотим разделить страны на пост-коммунистические и не пост-коммунистические и отразить это на графике. То есть, точки, соответствующие пост-коммунистическим странам и точки, соответствующие всем остальным странам будут отличаться по цвету.
str(df$poco) # проверим, какие значения принимает poco
## int [1:108] 0 0 0 0 0 0 0 0 0 1 ...
Показатель poco числовой, но по смыслу он качественный, то есть факторный. Поправим тип:
df$poco <- factor(df$poco)
colors <- c("blue", "red")[df$poco] # устанавливаем цвета по группирующей переменной
plot(df$gov_left1, df$gov_right1,
xlab = "Left parties (% of total)",
ylab = "Right parties (% of total)",
pch = 19,
col = colors)Матрица диаграмм рассеяния (scatterplot matrix)
Иногда в ходе предварительного анализа бывает нужно посмотреть на связь «всего со всем».
Построим диаграммы рассеяния для процентов голосов за разные партии.
pairs(df[10:12], col = colors) # выбираем столбцы 10-12
На пересечении названий переменных находятся диаграммы рассеяния, соответствующие парам показателей.
А теперь проиллюстрируем то же самое, но более красочно. Для этого потребуется библиотека car.
install.packages("car")library(car) scatterplotMatrix(df[10:12])
На диагонали этой матрицы диаграмм рассеяния добавляются графики плотности распределения («сглаженные» гистограммы). На сами диаграммы рассеяния добавляется регрессионная прямая (прямая вида \(y = kx+b\), при \(k < 0\) наклон прямой отрицательный, связь между \(x\) и \(y\) обратная, при \(k > 0\) наклон прямой положительный, связь между \(x\) и \(y\) прямая). Можно также добавить кривую взвешенной регрессии (loess regression от locally weigthed regression). Логика её построения (в очень упрощённом виде) такая:
Логика её построения (в очень упрощённом виде) такая:
- все значения \(x\) разбиваем на много маленьких интервалов;
- на каждом интервале строим регрессионную прямую;
- «сглаживаем» получившуюся ломаную линию, чтобы получить гладкую кривую;
Чтобы добавить линию взвешенной регресии, нужно убрать обычную регрессионную прямую (reg.line = FALSE) и добавить новую сглаженную (smooth = TRUE):
scatterplotMatrix(df[10:12], regLine = FALSE, smooth = TRUE)
Наведем красоту на графике выше, создадим вектор с названиями переменных в более внятном виде и чуть-чуть увеличим шрифт у подписей на диагонали:
labs <- c("Right", "Center", "Left")
# var.labels - названия переменных на диагонали
# cex.labels - размер шрифта для labels
# main - название графика
scatterplotMatrix(df[10:12], regLine = FALSE, smooth = TRUE,
var.labels = labs,
cex.labels = 1.3,
main = "Correlations of parties' share")А теперь поменяем графики плотности на диагонали на гистограммы (при желании можно поменять на ящики с усами, вписав "boxplot"):
# diagonal=list()
scatterplotMatrix(df[10:12], regLine = FALSE, smooth = TRUE,
var. labels = labs,
cex.labels = 1.3,
main = "Correlations of parties' share",
diagonal = list(method = "histogram"))
labels = labs,
cex.labels = 1.3,
main = "Correlations of parties' share",
diagonal = list(method = "histogram"))Ещё один вариант симпатичного графика для корреляций — разноцветный график, созданный с помощью пакета gclus.
library(gclus)
## Warning: package 'gclus' was built under R version 3.5.2
# получим вектор коэффициентов корреляции (по модулю)
coeffs <- abs(cor(df[10:12]))
# зададим цвета (автоматическое разбиение по вектору коэффициентов)
colors <- dmat.color(coeffs)
# отсортируем так, чтобы графики, где связь переменных наибольшая,
# были ближе к диагонали
order <- order.single(coeffs)
# строим сам график
# gap - расстояние между графиками в матрице
cpairs(df[10:12], order, panel.colors = colors, gap = .5,
main = "Correlations of parties' shares" )Корреляционный анализ
Для начала посмотрим на коэффициент корреляции между какими-нибудь двумя переменными:
cor(df$gov_left1, df$gov_right1)
## [1] -0.6594741
Если бы в одной из переменных были пропущенные значения (NA), коэффициент корреляции бы не рассчитался. Тут можно действовать по аналогии с расчетом среднего значения:
# использовать всё, кроме NA (complete observations) cor(df$gov_left1, df$gov_right1, use = "complete.obs")
## [1] -0.6594741
Как известно, существуют разные коэффициенты корреляции. Самые распространенные — линейный коэффициент корреляции Пирсона, коэффициент ранговой корреляции Спирмена и коэффициент ранговой корреляции Кендалла. По умолчанию считается коэффициент Пирсона, остальные можно получить, прописав дополнительный аргумент:
cor(df$gov_left1, df$gov_right1, method = "spearman") # коэфф. Спирмена
## [1] -0.6544615
Проверить значимость коэффициента корреляции — проверить нулевую гипотезу о том, что истинный коэффициент корреляции равен 0.
\[ H_0: r = 0 \text{ (связи нет)} \]
\[ H_1: r \ne 0 \text{ (связь есть)} \]
corr <- cor.test(df$gov_left1, df$gov_right1) corr
## ## Pearson's product-moment correlation ## ## data: df$gov_left1 and df$gov_right1 ## t = -9.0321, df = 106, p-value = 8.441e-15 ## alternative hypothesis: true correlation is not equal to 0 ## 95 percent confidence interval: ## -0.7544286 -0.5374832 ## sample estimates: ## cor ## -0.6594741
В выдаче R мы видим две важные вещи: значение коэффициента корреляции (sample estimates) и pvalue. В нашем случае p-value < 0.05, следовательно, на 5% уровне значимости есть основания отвергнуть нулевую гипотезу о равенстве коэффициента корреляции нулю. Раз эту гипотезу отвергаем, считаем, что коэффициент корреляции не 0, а следовательно, связь между процентом левых и правых партий действительно есть.
Выдача R представляет собой список (list):
str(corr)
## List of 9 ## $ statistic : Named num -9.03 ## ..- attr(*, "names")= chr "t" ## $ parameter : Named int 106 ## ..- attr(*, "names")= chr "df" ## $ p.value : num 8.44e-15 ## $ estimate : Named num -0.659 ## ..- attr(*, "names")= chr "cor" ## $ null.value : Named num 0 ## ..- attr(*, "names")= chr "correlation" ## $ alternative: chr "two.sided" ## $ method : chr "Pearson's product-moment correlation" ## $ data.name : chr "df$gov_left1 and df$gov_right1" ## $ conf.int : num [1:2] -0.754 -0.537 ## ..- attr(*, "conf.level")= num 0.95 ## - attr(*, "class")= chr "htest"
А значит, из него можно вызывать отдельные элементы.
coeff <- corr$estimate # коэффициент pvalue <- corr$p.value # p-value coeff; pvalue
## cor ## -0.6594741
## [1] 8.440678e-15
Если хотим посмотреть на корреляцию «всего со всем», можем указать столбцы в базе (переменные) и получить корреляционную матрицу:
cor(df[10:12])
## gov_right1 gov_cent1 gov_left1 ## gov_right1 1.0000000 -0.4397581 -0.6594741 ## gov_cent1 -0.4397581 1.0000000 -0.2777804 ## gov_left1 -0.6594741 -0.2777804 1.0000000
Для того, чтобы получить корреляционную матрицу и значимость коэффициентов в ней, нужно постараться. Загрузим библиотеку Hmisc.
# install.packages("Hmisc")
library(Hmisc)
# Внимание: функция привередничает - требует матрицу, а не просто столбцы из базы
rcorr(as.matrix(df[10:12])) ## gov_right1 gov_cent1 gov_left1 ## gov_right1 1.00 -0.44 -0.66 ## gov_cent1 -0.44 1.00 -0.28 ## gov_left1 -0.66 -0.28 1.00 ## ## n= 108 ## ## ## P ## gov_right1 gov_cent1 gov_left1 ## gov_right1 0.0000 0.0000 ## gov_cent1 0.0000 0.0036 ## gov_left1 0.0000 0.0036
Но то, что мы увидели, немного не похоже на то, что хотелось бы показать другим. Единой таблички с коэффициентами и значимостью нет. Действительно, в R есть некоторые проблемы с корреляционными матрицами.
Воспользуемся уже написанной функцией, доступной по ссылке, и немного модифицируем её. Чтобы воспользоваться этой функцией, помимо уже установленного нами пакета
Чтобы воспользоваться этой функцией, помимо уже установленного нами пакета Hmisc потребуется библиотека xtable. Как и stargazer, она используется для выгрузки выдач R в html или LaTeX.
install.packages("xtable")Скопируем код для функции с сайта в R-файл (New RScript) и назовем его correlation.R. Модифицируем код: в качестве аргумента функции corstars добавим file (про написание собственных функций поговорим позже).
corstars <-function(x, method=c("pearson", "spearman"), removeTriangle=c("upper", "lower"),
result=c("none", "html", "latex"), file)А также допишем в строки 46 и 47 file = file:
if(result[1]=="html") print(xtable(Rnew), type = "html", file = file)
else print(xtable(Rnew), type="latex", file = file)Это нужно для того, чтобы R не просто выводил результат в консоль, но и сохранял код для таблички в отдельный файл.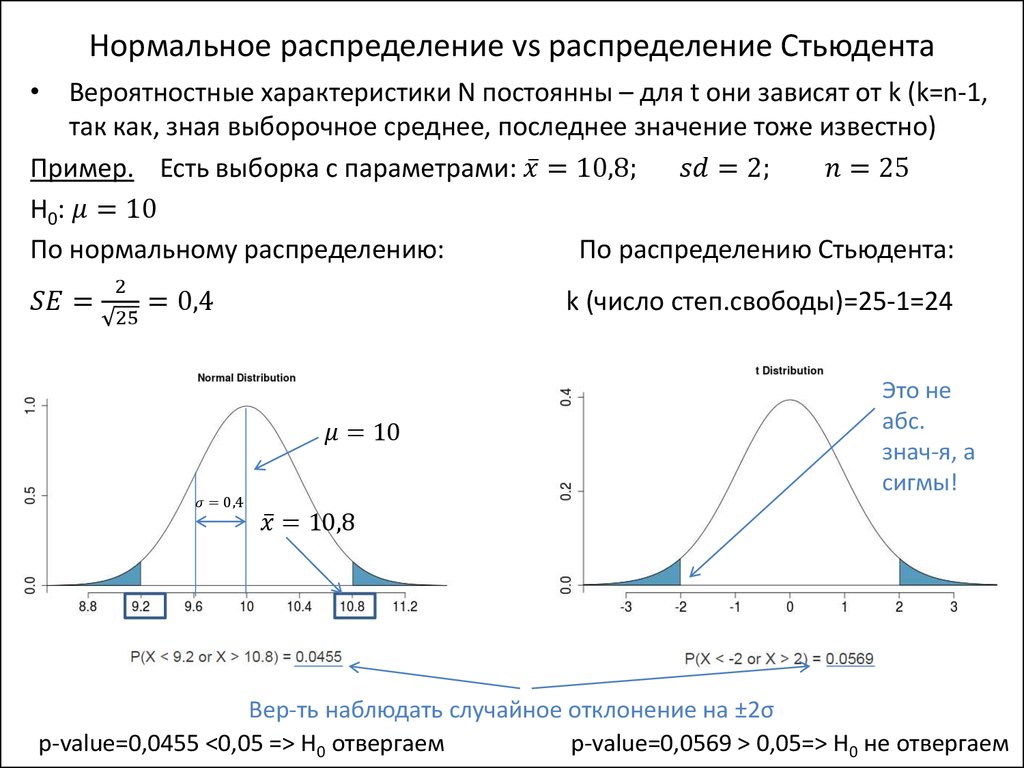
Добавим также строку require(xtable), например, после require(Hmisc), иначе R не поймет, откуда брать функцию xtable. Теперь сохраним все изменения в файле correlation.R и загрузим его сюда:
source("correlation.R")Теперь R знает, что из этого файла можно брать функции, и не будет ругаться, если встретит незнакомое (не встроенное в базовые библиотеки) название.
Финальный аккорд:
# сохраняем результат в файл corrtable.htm - можем открыть через браузер иди Word
corstars(x = df[10:12], method = "pearson", removeTriangle = "upper",
result = "html", file = "corrtable.htm")А вот и итоговая таблица со звёздочками:
| gov_right1 | gov_cent1 | |
|---|---|---|
| gov_right1 | ||
| gov_cent1 | -0.44*** | |
| gov_left1 | -0.71**** | -0.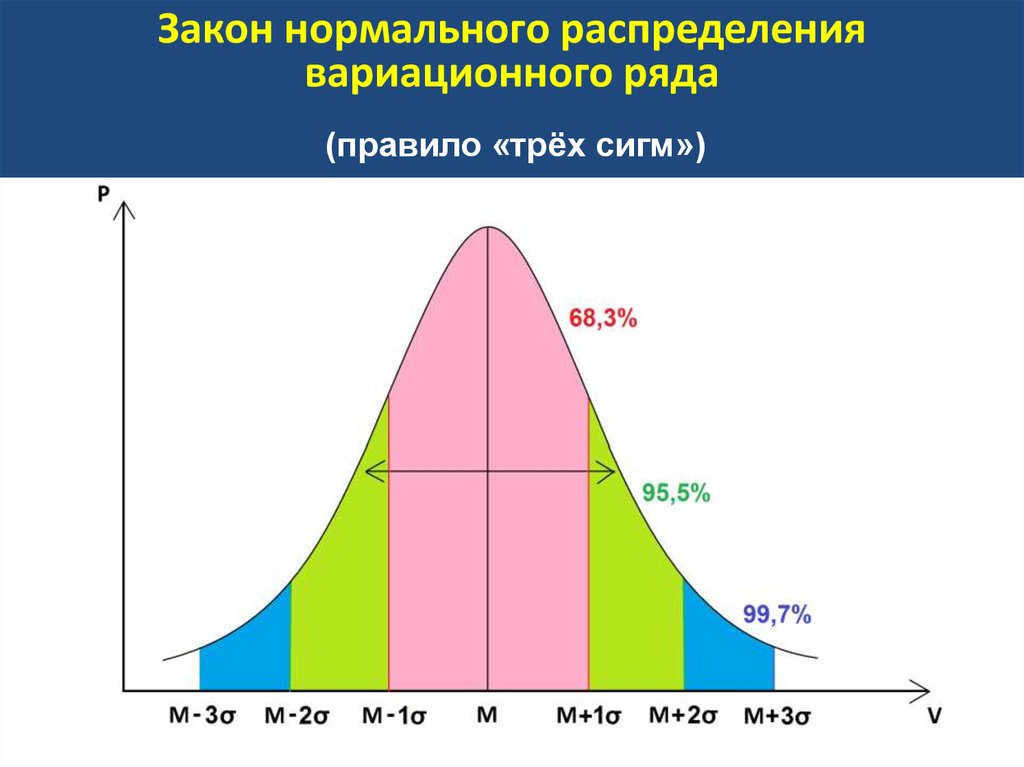 24* 24* |
На этом всё.
Error
Sorry, the requested file could not be found
More information about this error
Jump to…
Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.Задачи для самостоятельной работыРешения задачТест 1.1.3. Предел функции в точкеВидеолекция. Непрерывность функции в точкеLecture 1. Сontinuity of a function at a pointПрактическое занятие. Исследование функций на непрерывность. Классификации точек разрываPractical lesson. The study of function continuity and classification of discontinuity pointsЗадачи для самостоятельной работыРешения задачТест 1.
Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.Задачи для самостоятельной работыРешения задачТест 1.1.3. Предел функции в точкеВидеолекция. Непрерывность функции в точкеLecture 1. Сontinuity of a function at a pointПрактическое занятие. Исследование функций на непрерывность. Классификации точек разрываPractical lesson. The study of function continuity and classification of discontinuity pointsЗадачи для самостоятельной работыРешения задачТест 1. 1.4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.
1.4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1. 1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.7 (часть 1). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 1)Тест 1.1.7 (Часть 2). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 2)Теоретический материал (Часть 1)Задачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Теоретический материал (Часть 2)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.
1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.7 (часть 1). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 1)Тест 1.1.7 (Часть 2). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 2)Теоретический материал (Часть 1)Задачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Теоретический материал (Часть 2)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1. 1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2.
1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2. Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1.2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1.
Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1.2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1. 3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3.
3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.
Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1. 3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3).
3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1.
The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.
Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2. 1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов.
1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson.
Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1.
Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.
Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3. 1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesРешения задач (лабораторная работа)Теоретический материалТест 3.
1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesРешения задач (лабораторная работа)Теоретический материалТест 3. 2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.
2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3. 4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2.
4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2.
Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2).
Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)
Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)
Кривая нормальной плотности
Кривая нормальной плотностиСтатистические апплеты
Апплет вычисляет площадь, заштрихованную темно-желтым цветом под кривой. Чтобы найти долю значений меньше заданного значения, перетащите левый флажок на это значение. Точно так же, чтобы найти долю значений, превышающих заданное значение, перетащите правый флажок на это значение. Чтобы определить пропорцию между двумя значениями, перетащите правый флажок к меньшему значению, а левый — к большему.
Нажмите кнопку «Проверить меня», чтобы завершить задание.
Среднее значение и стандартное отклонение (стандартное отклонение) характеризуют кривую нормальной плотности. Среднее значение является центральной точкой кривой плотности. В приведенном ниже апплете четыре станд. разв. слева и справа от среднего значения отмечены на оси графика. Чтобы изменить эти параметры, введите желаемое значение (значения) и нажмите кнопку ОБНОВИТЬ. По умолчанию среднее значение установлено равным 0, а станд. разв. устанавливается равным 1 (т. е. «Стандартная нормальная плотность»).
Хвост кривой ограничен двумя вертикальными зелеными флажками. Значения хвоста можно установить, щелкнув флажок и перетащив его. Обратите внимание, что значение флага отображается в верхней части каждого флага. Если установлен флажок 2-хвостый, хвосты блокируются симметрично относительно среднего значения.
Вопрос 1.1
UFrLAoMOXlCXUEet1pXH/H/trjlGtOfsQh28RLJLS9bMJFKyaZGLM0lRbT/8uLZoIkLs83i6l6tbUukhOynU9RbZwEJrK4QtTcgSgYmJXi6NTh86hNLEfn8NOv+Qf3r5uMZ6xBDhNW/flH756Nfg+nD5PUj435W3RVvGrSQ/EkUV2+JyHQCDeFdar9IpkVxq0uYoKzQc3dM2CRK7o7vL8tBtcODL/vZQcu7wMIFTI0gy8NkrMO958fuqpnCsQgKh20mpn/kC/ycn797ZINwSowPLU3ZtFyR+X0ad4K7jIzD/tQg/GoTdJKqYzwBDBf77ZbQqzqQ+MtsjLNUVF56lHR0s9aIqxWsg2nr6XUGug0J++LW6GZq7VxL+wiw=
3
Правильно.
Попробуйте еще раз.
Неверно.
Вопрос 1,2
Q6cNePF9dbrpQqJy0g+azI4CQCpRD/wq4Rcpv2yG3Vm+PF4CGrF7PUbbEh4RFf5Ez36YqyBzSQEP3hhplj8LodIsuo/UtXH8V2Yt6w/gPUpBuBgt7aU8ZZtDL4lu4jR1MOMjyAPT8y815qXTKjzxCAgK7a8lYEEWF7iqFA31zM/v5Mt1Kk8MXOPnLkd98G9qybF2m208cILQjc4bJO3BUFysn/UHCqN/Jp1lvjInaZrmNHqzdv1EOGJem+Cl8ZP0wwtKcexCoUc09nU3mkUUCgVaO/8CnBD64cHHgKZmwgXo0h2jEby026FhoedjipZXhfBqzPm5lzTo/HBn58gMGLlizdl3xow17AyrSlFiaucWxdhB6qg3addUrb80z2A2cHWE64HBIcaKvsdaj9CAQlTVPArUjjRHaBZbFUQ1SeieKXt0PwwUgSIMUZTmIIJJIF5AajhJbMsL7MO8VnOI2UFgZRfTL380goPFHhUVlSY=
3
Правильно.
Попробуйте еще раз.
Неверно.
Вопрос 1,3
Предположим, вы знаете, что время, необходимое вашей подруге Сьюзен, чтобы добраться от дома до класса, составляет в среднем 50 минут при стандартном отклонении 5 минут. Используйте апплет, чтобы ответить на приведенные ниже вопросы.
- Какая часть походов Сьюзен на занятия занимает более 50 минут? (Подсказка: вам не нужно использовать апплет, чтобы узнать это значение) uJISCg90RZk=
- Какая часть поездок Сьюзан в класс будет длиться менее 40 минут? pm8f93oFmjs=
- Какая доля поездок Сьюзан в класс займет более 50 минут или менее 40 минут? 4Dm6tl/E7rY=
(Ваши ответы должны быть точными с точностью до 2 знаков после запятой. )
)
3
Попробуйте еще раз.
Неверно. Смотрите выше правильные ответы.
Отличная работа.
Различные расчеты с использованием апплета
Вопрос 1,4
LSUE6AxOUrLEs3oFVOjlCq9qsII9LVfBAppTTUbL1PmTogQCgh/2dw1xyyx4mZROztYiZ4cts9RY1F9KTlMab74dyitGgbYUSSbj4MnZ0i3Khv9Gp7xXMYcPf7ud2fl9JYDjfoBrxr2minXKgQFkwEOU7EhBFaMFrP7TPebyB2IEI1TfFqRqMFmCUeMf90XcE9otisnNbst6o/sHy3kOs6iNQp0arlkrfu8aAJdVO7cOw5X0znu30+zOApmenPM4vI7de8WBdjbLuDGY5NhP0e1GBtwWePIBaSytcVX6sytlOr7jfr0nfLTzXXQ+A3sSRjI2yzvD0HKkLtOOx26eeWJ/doRrvdcpAnP9b1H9fT33IFzRgJbEPw==
3
Правильно.
Попробуйте еще раз.
Неверно.
Вопрос 1,5
BeiJJFZ3E1pjfM3viVbY4qJ0R7WgSzSysSc0txgovqIB1Yn/D33cYoV9JXXNWa1TILzlWil1Bvg6xZLlaCoenfj9rcatEAuElMmBgwwtJsAJ/rKHsoyDXj1piIdOFy1DlLgedYX8t79PD/TluUykAo/rnI/WxCn6I+dty+k2oLIzG+nwqbUvrsj5RgaKdmR6stR2VIeGfWuG1UMr7dzfxJcMrI4iOwLljc1tuIueqeoLVVGTv4EHbOaDl1kYCD3p7jQ9Ym++1ZJDOLQ0gjhU6vtJf5o5sORqqAWGeaOSU5RoXYdaMaMO/PBw0K6SziD50nR+03qFCdJIdK9c4K6bqwLg/EZzXsCj/WD/Y2/O8xU6+DP+AU17sNQ6l6aVrFIq6zpodOPAKPyq9YwpeW8Boea8UA9pw7Kv31Wc0BDDYAoLr8jJJAaNtjtFD+uWdTcPzfKzYoxBP/Q=
3
Правильно.
Попробуйте еще раз.
Неверно.
Вопрос 1,6
u03JWmyi5xc8GoLK+GWAun2UjwKX2ED4Wy0idfY9WYn3uDIfO02RW6RnwYbm7kguKuZ67PbwNlIMloa/gjQhYQVDLBjChKocpkGwUr8p8upt6G2Mp2cj443/7/tG8R6KZcW+pA==
Независимо от среднего значения и стандартного отклонения, если распределение является нормальным, 0,023 площади под кривой упадет ниже значения, которое на два стандартных отклонения ниже среднего. -10,0 соответствует двум стандартным отклонениям ниже среднего в первом вопросе, а 0,0 соответствует двум стандартным отклонениям ниже среднего во втором вопросе; следовательно, оба ответа были идентичными.
Оверловый График нормальной плотности — Stat_Overlay_Normal_Density • GGPUBR
Источник: R/Stat_Overlay_Normal_Density.R
STAT_OVERLAI_NORMAL.
распределение плотности 'x'. Это полезно для визуального осмотра
степень отклонения от нормы.
stat_overlay_normal_density( отображение = NULL, данные = NULL, геометрия = "линия", позиция = "личность", на.рм = ЛОЖЬ, show.legend = нет данных, inherit.aes = ИСТИНА, ... )
Аргументы
- отображение
Набор эстетических отображений, созданных с помощью
aes(). Если указано иinherit.aes = TRUE(по умолчанию), он сочетается с сопоставлением по умолчанию на верхнем уровне сюжета. Вы должны предоставитьотображение, если нет участка отображение.- данные
Данные для отображения в этом слое. Есть три опции:
Если
NULL, по умолчанию данные наследуются от графика данные, как указано в вызовеggplot().data.frameили другой объект переопределит график данные. Все объекты будут укреплены для создания фрейма данных. Видетьfortify()для которых будут созданы переменные.Функция
 Возвращаемое значение должно быть
Возвращаемое значение должно быть data.frameи будут использоваться в качестве данных слоя. Функция~ голова (.x, 10)).- геом
Геометрический объект для отображения данных либо в виде
ggprotoGeomподкласс или как строка, именующая geom, лишеннаяпрефикс geom_(например,"точка"вместо"geom_point")- позиция
Регулировка положения, либо в виде строки с названием регулировки (например,
"jitter"для использованияposition_jitter), или результат вызова функция регулировки положения. Используйте последний, если вам нужно изменить настройки регулировки.- н/д
Если FALSE (по умолчанию), удаляет отсутствующие значения с предупреждением. Если TRUE, автоматически удаляет отсутствующие значения.
- шоу.


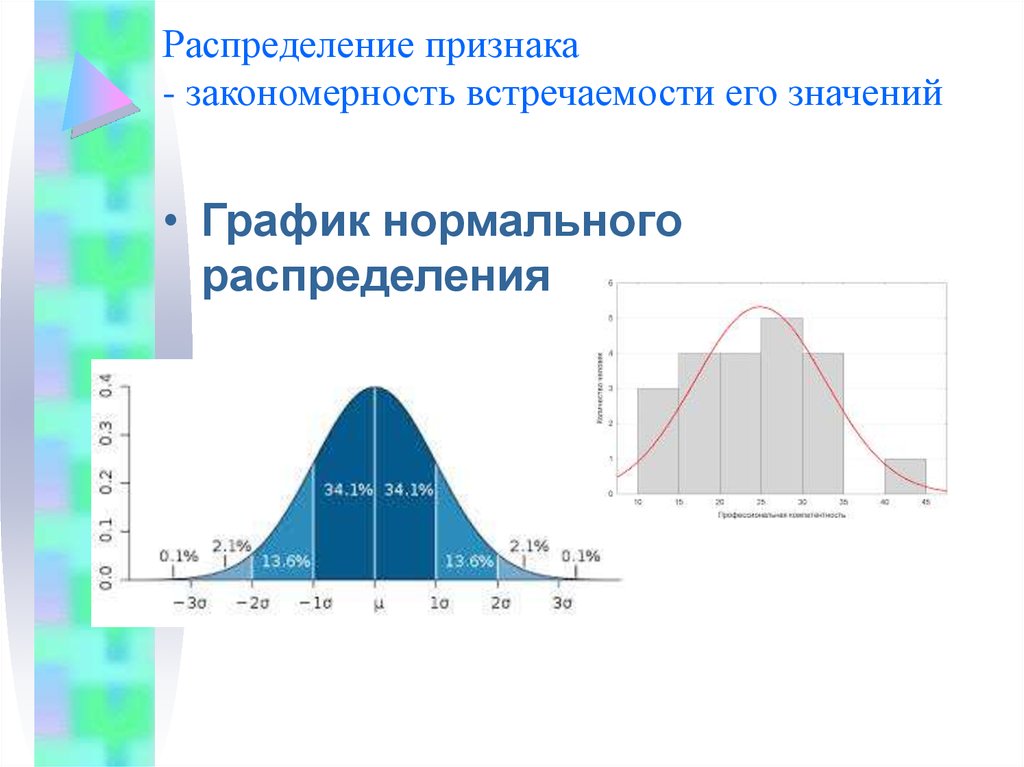 csv("http://math-info.hse.ru/f/2018-19/pep/hw/CPDS.csv", dec = ",")
df <- subset(df, df$year >= 2014) # выберем данные
csv("http://math-info.hse.ru/f/2018-19/pep/hw/CPDS.csv", dec = ",")
df <- subset(df, df$year >= 2014) # выберем данные 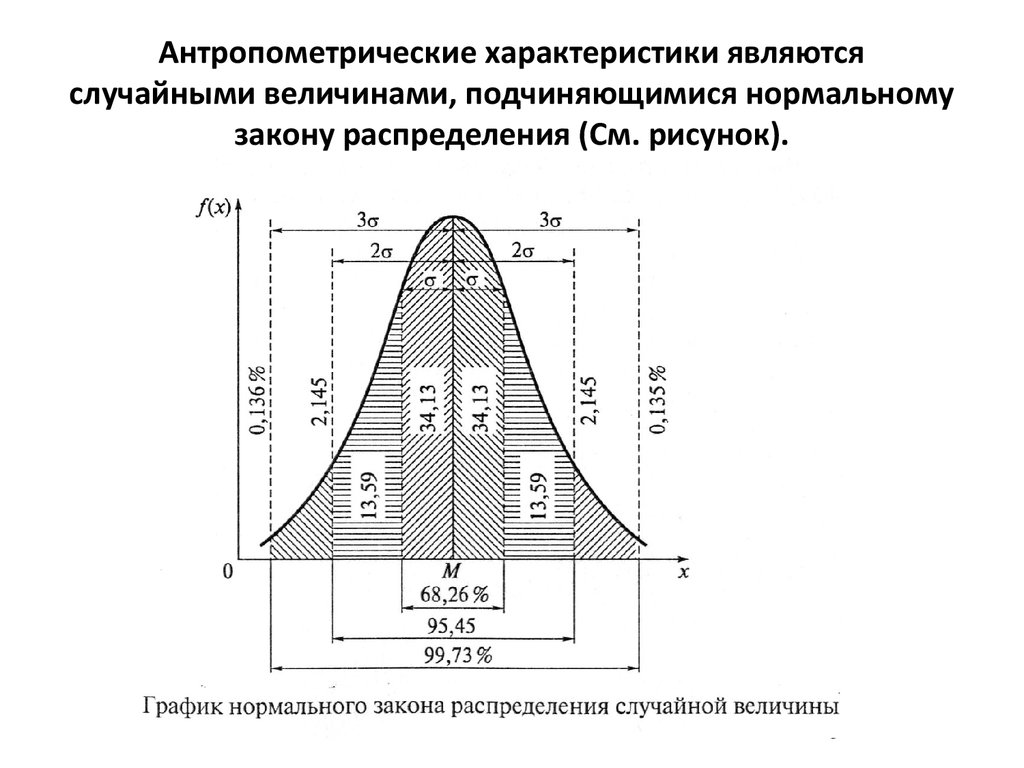 labels = labs,
cex.labels = 1.3,
main = "Correlations of parties' share",
diagonal = list(method = "histogram"))
labels = labs,
cex.labels = 1.3,
main = "Correlations of parties' share",
diagonal = list(method = "histogram"))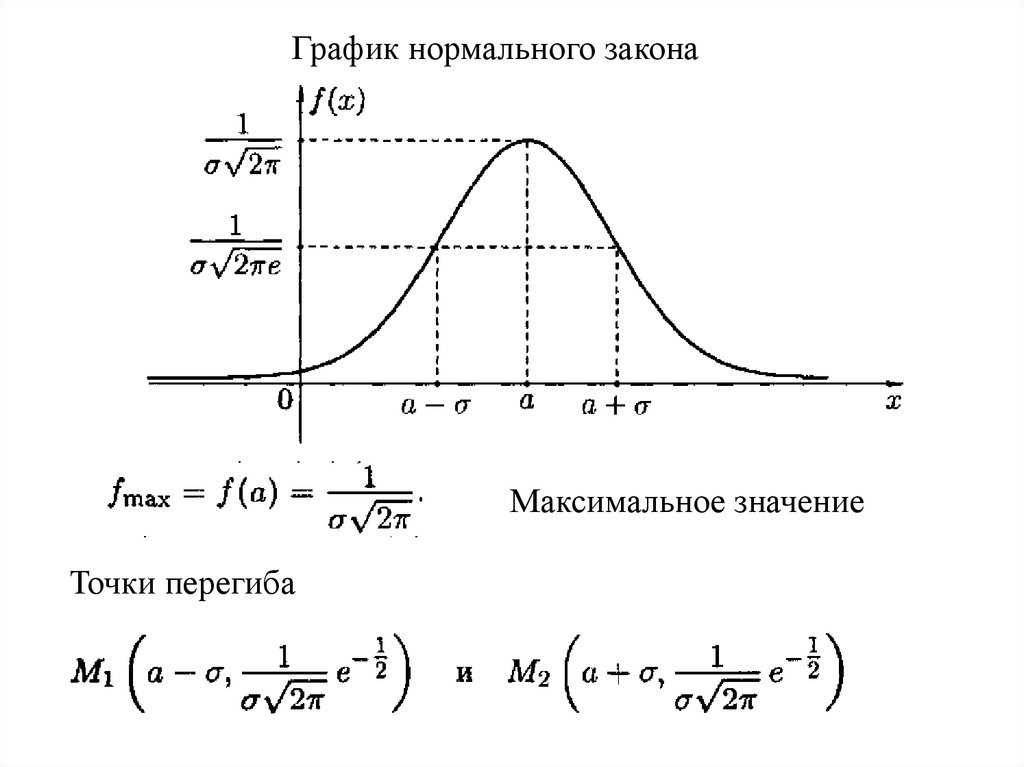 6594741
6594741 test(df$gov_left1, df$gov_right1)
corr
test(df$gov_left1, df$gov_right1)
corr .- attr(*, "names")= chr "df"
## $ p.value : num 8.44e-15
## $ estimate : Named num -0.659
## ..- attr(*, "names")= chr "cor"
## $ null.value : Named num 0
## ..- attr(*, "names")= chr "correlation"
## $ alternative: chr "two.sided"
## $ method : chr "Pearson's product-moment correlation"
## $ data.name : chr "df$gov_left1 and df$gov_right1"
## $ conf.int : num [1:2] -0.754 -0.537
## ..- attr(*, "conf.level")= num 0.95
## - attr(*, "class")= chr "htest"
.- attr(*, "names")= chr "df"
## $ p.value : num 8.44e-15
## $ estimate : Named num -0.659
## ..- attr(*, "names")= chr "cor"
## $ null.value : Named num 0
## ..- attr(*, "names")= chr "correlation"
## $ alternative: chr "two.sided"
## $ method : chr "Pearson's product-moment correlation"
## $ data.name : chr "df$gov_left1 and df$gov_right1"
## $ conf.int : num [1:2] -0.754 -0.537
## ..- attr(*, "conf.level")= num 0.95
## - attr(*, "class")= chr "htest" 0000000 -0.2777804
## gov_left1 -0.6594741 -0.2777804 1.0000000
0000000 -0.2777804
## gov_left1 -0.6594741 -0.2777804 1.0000000 Возвращаемое значение должно быть
Возвращаемое значение должно быть 