3. Интегрирование тригонометрических функций.
1.Первообра́зная. Функция F(x) называется первообразной для функции ƒ(x) на некотором отрезке [a,b], если для всех из этого отрезка выполняется равенство:
F'(x)= ƒ(x).
Неопределенный интеграл и его свойства. Неопределённый интегра́л для функции — это совокупность всех первообразных данной функции.
Свойства неопределенного интеграла:
1.
2.
3.
4. где u, v, w – некоторые функции от х.
6.
1. ∫ xαdx = xα+1/ (α+1) + C α ≠-1 | 10. = ln | x + | + C |
2. = ln |x| + C | 11. = arctg( )+C |
3. | 12. = ln | | + C |
4. ∫ ax dx = ax/lna + C | 13 = ln | | + C |
5. ∫ sin(x)dx = — cos(x) + C | 14. = ln |tg( )| + C |
6. ∫ cos(x)dx = sin(x) + C | 15. = ln |tg( )| + C |
7. = tg(x) + C | 16.∫ tg(x) dx = – ln |cos(x)| + C |
8. = -ctg(x) + C | 17.∫ ctg(x) dx = ln |sin(x)| + C |
9. = arcsin ( )+ C |
2. Понятие об основных методах интегрирования
а).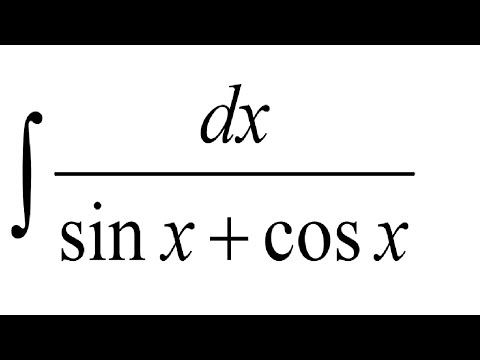 Метод разложения.
Метод разложения.
Пусть f(x) = f1(x) + f2(x). Тогда на основании свойства 4
.
f1, f2 стараемся подобрать так, чтобы интегралы брались непосредственно.
б). Метод подстановки (введение новой переменной)
Так как неопределенный интеграл не зависит от выбора аргумента и, учитывая, что
dx = j/(t)dt,
получаем формулу замены переменной в неопределенном интеграле
.
То есть интеграл, стоящий в правой части, может оказаться проще интеграла в левой части.
в) Метод интегрирования по частям
Пусть u и v — непрерывно дифференцируемые функции от х.
d(u×v) = udv + vdu.
Интегрируя обе части этого уравнения, получим
.
Интегрирование
рациональных дробей.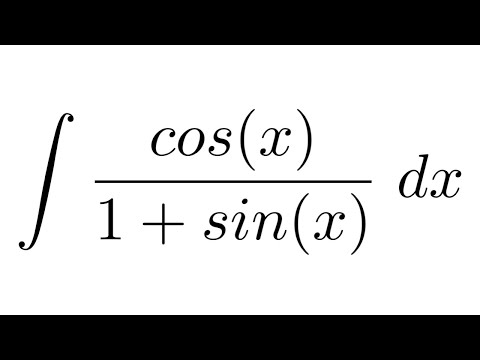
Нужно вычислить интеграл вида
, где Р(х) — целый многочлен; а,b,c — const, a ¹ 0.
Разделив Р(х) на знаменатель, получаем
.
Теперь все сводится к вычислению
.
Интегрирование тригонометрических функций.
I. Интеграл вида ∫R(sinx;cosx)dx, где R(sin(x), cos(x)) – это рациональная функция относительно sin(x) и cos(x) подстановкой tg(x/2) = t сводится к интегралу от рациональной функции относительно t.
Такая подстановка называется универсальной, т.е. она пригодна для вычислений интеграла sin(x) и cos(x).
II. Интеграл вида ∫(sinmx)*(cosnx)dx I случай. m и n – положительные, одно из них нечетное.
Пусть m=2p+1 , тогда ∫sin2p(x)cosn(x) sin(x)dx = – ∫(sin2x) p cosn(x) d(cos(x)) =
=
– ∫(1 –cos2x) p cosn(x)
d(cos(x)).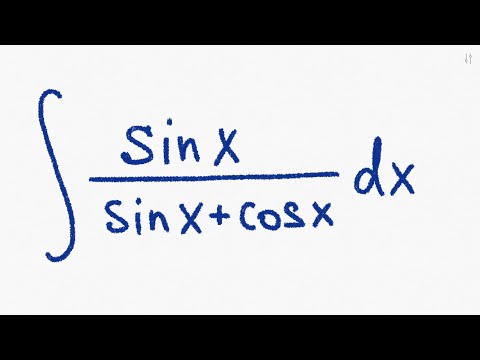
II.случай. m и n – целые, положительные, четные.
Пусть m=2p, n=2q, тогда
∫sinm(x)cosn(x)dx = ∫sin2p(x)cos2q(x)dx = ∫(sin2x) p(cos2x) qdx =((1-cos2x)/2)p*((1+cos2x)/2)q;
Возводя скобки в соответствующие степени и разбивая интеграл на сумму интегралов, в результате получаем интегралы либо типа а), либо типа б).
III.случай. m + n = –2k; tg(x)=t; ctg(x)=t;
Интегрирование иррациональных функций.
I. Интеграл вида R(X,((ax+b)/(cx+d))(1/n)), где R(X,((ax+b)/(cx+d))(1/n)) — рациональная функция относительно x и ((ax+b)/(cx+d))(1/n) , подстановкой (ax+b)/(cx+d)=tn сводится к интегралу от рациональной функции относительно t.
II. Интегралы
от дифференцированных биномов
(биномиальный дифференциал).
Определение : xm(a + bxn)P dx – называется дифференциальным биномом.
Академик Чебышев доказал, что ∫ xm(a + bxn)P dx выражается через элементарные функции в трех случаях:
1) если P-целое, то следует сделать подстановку
(x)λ=t, где λ – общий знаменатель чисел m и n.
2)P – не целое, (m+1)/n — целое, тогда вводим a+bxn=ts, где s – знаменатель P.
3) P+(m+1)/n- целое, тогда замена такая:
ax–n + b = tS , где s – знаменатель P.
В остальных случаях интеграл не берется.
III. Тригонометрические подстановки.
R(X,(a2-x2)(1/2) ))
а) Интеграл вида ∫R(X,(a2-x2)(1/2) )dx
подстановкой
x
= a∙sin(t)
сводится к интегралу от рациональной
функции относительно sin(t)
и cos(t).
б) интеграл вида ∫R(X,(a2-x2)(1/2) )dx подстановкой x= a∙ sec(t) сводится к интегралу от рациональной функции относительно sin(t) и cos(t).
в) интеграл вида ∫R(X,(a2-x2
4. Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Определенный интеграл от функции f (x) в пределах от a до b вводится как предел суммы бесконечно большого числа слагаемых, каждое из которыхстремится к нулю: Где Формула Ньютона-Лейбница Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) — первообразная функции f (x) на [a, b], то
Замена переменной в определенном интеграле
Определенный интеграл по переменной x можно преобразовать в определенный интеграл относительно переменной t с помощью подстановки x = g (t):
Новые пределы интегрирования по переменной t определяются выражениями
где
g -1 — обратная функция к g, т. е. t = g -1(x).
е. t = g -1(x).
Интегрирование по частям для определенного интеграла
В этом случае формула интегрирования по частям имеет вид:
где означает разность значений произведения функций uv при x = b и x = a.
Исчисление— Как найти неопределенный интеграл от sin(sin(x))dx?
спросил
Изменено 2 месяца назад
Просмотрено 7к раз
$\begingroup$
(Я получил эту функцию по ошибке, когда я неправильно написал другую функцию. Теперь мне любопытно, как найти первообразную того, что я неправильно написал)
Я понятия не имею, как его рассчитать, равно как и Wolfram Alpha или любой другой сайт, который я пробовал. Формулы триггеров из школьного курса тоже не кажутся полезными.
- исчисление
- неопределенные интегралы
$\endgroup$
3
$\begingroup$
Из этого ответа https://math.stackexchange.com/a/877417/65203 и https://en.wikipedia.org/wiki/Jacobi%E2%80%9{2k+1}x}{(2n+1)!k!(n-k)!(2k+1)}+C$
$\endgroup$
Интеграл синкса: формула, доказательство, примеры, решение
Интеграл синкса вместе с его формулой и доказательством с примерами. Также узнайте, как рассчитать интеграцию sinx с пошаговыми примерами.
от Алана Уокера — Опубликовано на 27 февраля 2023 г.
Введение в интеграл от sin x
В исчислении интеграл — это фундаментальное понятие, которое присваивает числа функциям для определения смещения, площади, объема и всех тех функций, которые содержат комбинацию крошечных элементов. Он подразделяется на две части: определенный интеграл и неопределенный интеграл. Процесс интегрирования вычисляет интегралы. Этот процесс определяется как нахождение первообразной функции.
Он подразделяется на две части: определенный интеграл и неопределенный интеграл. Процесс интегрирования вычисляет интегралы. Этот процесс определяется как нахождение первообразной функции.
Интегралы могут обрабатывать почти все функции, такие как тригонометрические, алгебраические, экспоненциальные, логарифмические и т. д. Эта статья научит вас тому, что представляет собой интеграл тригонометрической функции синуса. Вы также поймете, как вычислить интеграл греха, используя различные методы интегрирования.
Что такое интеграл греха?
Интеграл от sin x является первообразной функции синуса, которая равна –cos x. Это также известно как обратная производная функции синуса, которая является тригонометрической идентичностью.
Функция синуса представляет собой отношение противоположной стороны к гипотенузе треугольника, которое записывается как:
Sin = противолежащая сторона / гипотенуза
Интеграл формулы sinx
Формула интеграла sinx содержит знак интеграла, интегрирование и функция как синус. Он обозначается ∫(sin x)dx. В математической форме интеграл от sin x имеет вид:
Он обозначается ∫(sin x)dx. В математической форме интеграл от sin x имеет вид:
∫(sin x)dx = -cos x + c
Где c — любая вовлеченная константа, dx — коэффициент интегрирования, а ∫ — символ интеграла.
Как вычислить интеграл от sin(x)?
Интеграл от sin x — это его первообразная, которую можно вычислить, используя различные методы интегрирования. В этой статье мы обсудим, как вычислить интеграл синуса, используя:
- Производные
- Метод замены
- Определенный интеграл
Интеграл sinx с использованием производных
Производная функции вычисляет скорость изменения, а интегрирование — это процесс нахождения первообразной функции. Следовательно, мы можем использовать производную для вычисления интеграла функции. Давайте обсудим вычисление интеграла от sin x с использованием производных.
Доказательство интеграла от sin x с использованием производных
Поскольку мы знаем, что интегрирование является обратной производной. Следовательно, мы можем вычислить интеграл от sin x, используя его производную. Для этого нам нужно найти какие-то формулы производных или формулу, которая дает sin x как производную любой функции.
Следовательно, мы можем вычислить интеграл от sin x, используя его производную. Для этого нам нужно найти какие-то формулы производных или формулу, которая дает sin x как производную любой функции.
В производной мы знаем, что
d/dx (cos x) = -sin x
Это означает, что производная cos x дает нам sin x. Но он имеет отрицательный знак. Следовательно, чтобы получить интеграл от синуса, мы должны умножить приведенное выше уравнение на знак минус, то есть:
-d/dx (cos x) = sin x
Следовательно, интеграл от sin x равен минусу cos x. Он записывается как:
∫(sin x)dx = -cos x + c
Интеграл от sin x методом подстановки
Метод подстановки включает множество тригонометрических формул. Мы можем использовать эти формулы для проверки интегралов различных тригонометрических функций, таких как синус, косинус, тангенс и т. д. Давайте разберемся, как доказать интеграл от греха с помощью метода подстановки.
Доказательство интеграла от sin x методом подстановки
Чтобы доказать интеграл от sin x методом подстановки, предположим, что:
y = sin x
Дифференцирование по x,
dy/dx = cos x
Чтобы вычислить интеграл, мы можем написать приведенное выше уравнение как:
dy = cos x dx
Из тригонометрических тождеств мы знаем, что cos x = √1 — sin²x. Тогда приведенное выше уравнение принимает вид
Тогда приведенное выше уравнение принимает вид
dy = √1 — sin²x. дх
Теперь подставим значение sin2 x, например:
dy = √1 – y2. Dx
Умножение обеих сторон на sin x,
(sin x dy) / √1 — y² = sin x dx
Снова подставьте sin x = y в левой части.
(y dy) / √1 — y² = sin x dx
Интегрирование с обеих сторон путем применения интеграла,
∫ (y dy) / √1 — y² = ∫ sin x dx
Пусть 1 — y² = u . Тогда -2y dy = du (или) y dy = -1/2 du.
Тогда приведенный выше левый интеграл принимает вид
(-1/2) ∫ 1/√u du = ∫ sin x dx
(-1/2) ∫ u-1/2 du = ∫ sin x dx
Поскольку степенное правило интегрирования равно ∫ xn dx = (xn+1)/(n+1) + C. Следовательно, используя эту формулу, мы получаем
(-1/2) (u1/2 / (1/2)) + C = ∫ sin x dx
-u1/2 + C = ∫ sin x dx
Снова подставив u = 1 — y², получим
-(1 — y²)1/2 + C = ∫ sin x dx
И снова подставим y = sin x здесь,
-(1 — sin²x)1/2 + C = ∫ sin x dx
-(cos²x)1/2 + C = ∫ sin x dx
-cos x + C = ∫ sin x dx
Следовательно, интеграл от sin x равен –cos x.
Интеграл от sin x с использованием определенного интеграла
Определенный интеграл — это тип интеграла, который вычисляет площадь кривой с использованием бесконечно малых элементов площади между двумя точками. Определенный интеграл можно записать как:
∫abf(x) dx = F(b) – F(a)
Давайте разберемся с проверкой интеграла от sin x с помощью неопределенного интеграла.
Доказательство интеграла от sin x с использованием определенного интеграла
Чтобы вычислить интеграл от sin x с помощью определенного интеграла, мы можем использовать интервал от 0 до π или от 0 до π/2. Давайте вычислим интеграл от sin x от 0 до π. Для этого мы можем записать интеграл в виде:
∫0πsin x dx = -cos x|0π
Теперь подставим предел в заданную функцию.
∫0πsin x dx = -cos (π) + cos (0)
Так как cos 0 равен 1, а cos π равно -1, то
∫0πsin x dx = -1 -1= — 2
Это вычисление определенного интеграла от sin x. Теперь, чтобы вычислить интеграл от sin x между интервалами от 0 до π/2, нам просто нужно заменить π на π/2.