Пошаговое руководство построение графика квадратичной функции
Для того, чтобы начертить график функции в Прямоугольной системе координат, нам необходимы две перпендикулярные прямые xOy (где O это точка пресечения x и y), которые называются «координатными осями», и нужна единица измерения.
У точки в этой системе есть две координаты.
M(x, y): M это название точки, x это абсцисса и она измеряется по Ox, а y это ордината и мерится по Oy.
Две координаты отображают расстояние от точки до двух осей.
Если мы рассмотрим функцию f: A -> B (где A — область определения, B — область значений функции), тогда точку на графике данной функции можно представить в форме P(x, f(x)).
Пример
f:A -> B, f(x) = 3x — 1
If x = 2 => f(2) = 3×2 — 1 = 5 => P(2, 5) ∈ Gf (где Gf это график данной функции).
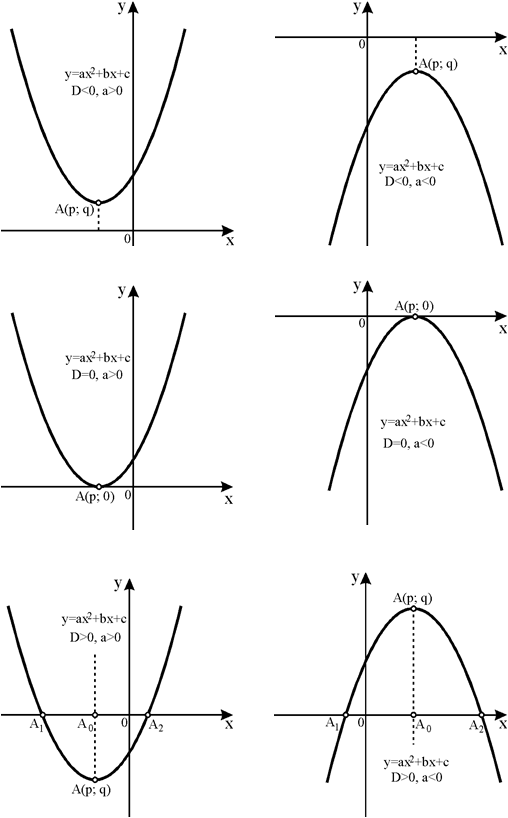
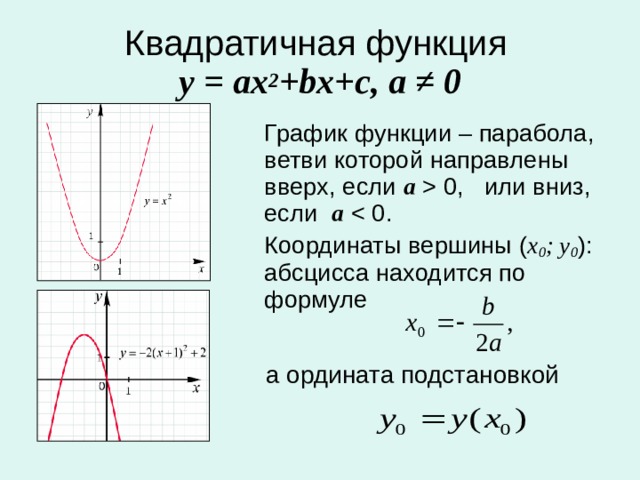
Квадратичная функция
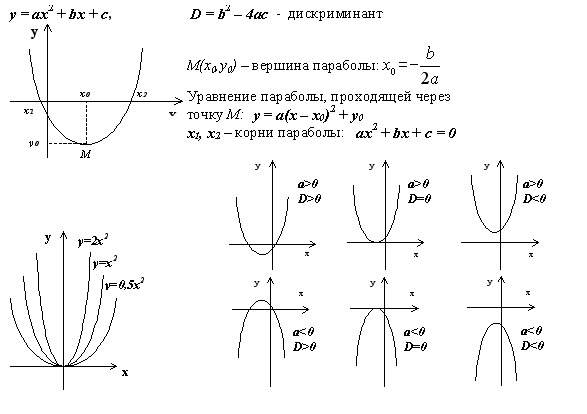
Стандартная форма: f(x) = ax2 + bx + c
Вершинная форма: $f(x)=(a+\frac{b}{2a})^2-\frac{\Delta}{4a}$
где Δ = b2 — 4ac
Если a > 0, то минимальным значением f(x) будет $-\frac{\Delta}{4a}$ , которое получается, если $x=-\frac{b}{2a}$. Графиком будет выпуклая парабола, вершина которой (точка, в которой она меняет направление) это $V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
Графиком будет выпуклая парабола, вершина которой (точка, в которой она меняет направление) это $V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
Если a < 0, то минимальное значение f(x) будет $-\frac{\Delta}{4a}$ , которое получается, если $x=-\frac{b}{2a}$. Графиком будет вогнутая парабола, вершина которой это$V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
Парабола симметрична относительно прямой, которую она пересекает $x=-\frac{b}{2a}$ и которая называется «осью симметрии».
Именно поэтому, когда мы присваиваем знаячения x, то вибираем их симметричными относительно $-\frac{b}{2a}$.
При построении графика, точки пересечения с осями координат очень важны.
|. Точка, расположенная на оси 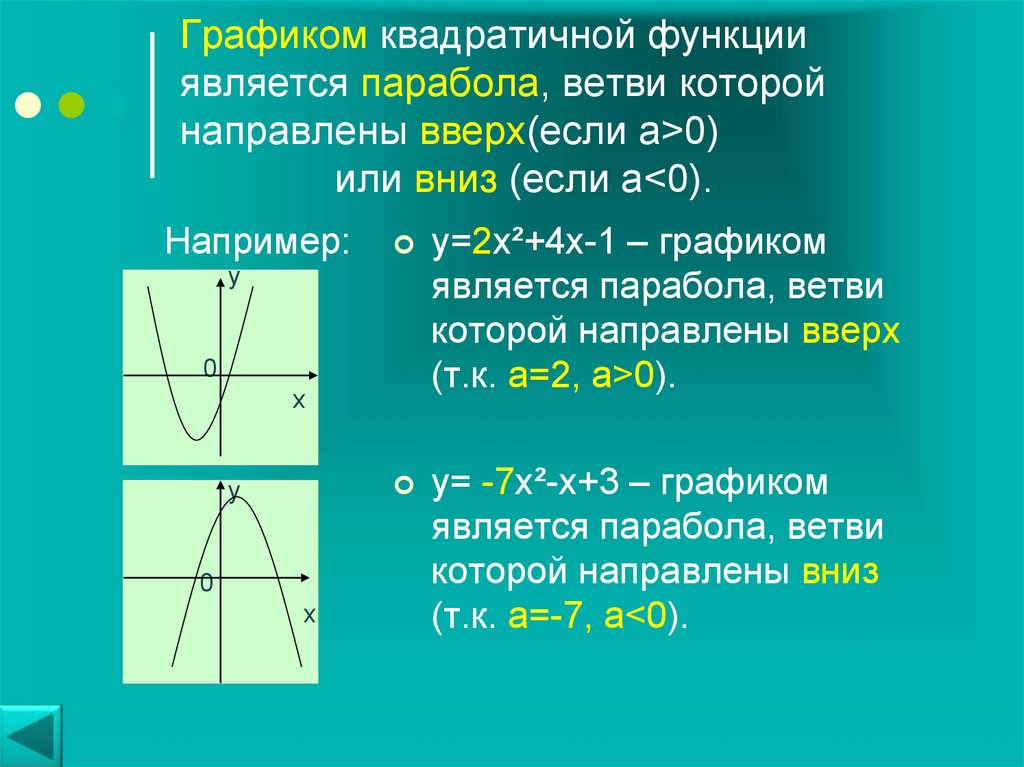
Таким образом, для того чтобы найти координаты точки пересечения с осью Ox, мы должны решить уравнение f(x)=0. Мы получаем уравнение a2 + bx + c = 0.
Решение уравнения зависит от знака Δ = b2 — 4ac.
Иммем следующие варианты:
1) Δ < 0,
тогда у уравнения нет решений в R (множестве действительных чисел) и график не пересекает Ox. Форма графика будет:
или
2) Δ = 0,
тогда у уравнения два решения $x_1=x_2=-\frac{b}{2a}$
График касается оси Ox в вершине параболы. Форма графика будет:
или
3) Δ > 0,
тогда у уравнения два разных решения.
$x_1=\frac{-b-\sqrt{\Delta}}{2a}$ и $x_2=\frac{-b+\sqrt{\Delta}}{2a}$
График функции будет пересекать ось Ox в точках M(x1 и Ox. Форма графика будет:
или
||. Точка, находящаяся на оси Oy имеет форму R(0, y), потому что расстояние от Oy равно 0. Если точка находиться и на Oy и на графике функции, то она также имеет форму R(x, f(x)) ⇒ x = 0 ⇒ R(0, f(0)).
Точка, находящаяся на оси Oy имеет форму R(0, y), потому что расстояние от Oy равно 0. Если точка находиться и на Oy и на графике функции, то она также имеет форму R(x, f(x)) ⇒ x = 0 ⇒ R(0, f(0)).
В случае квадратичной функции,
f(0) = a×02 + b×0 + c ⇒ R(0, c).
Необходимые шаги для построения графика квадратичной функции
f: R → R
f(x) = ax2 + bx + c
1. Составляем таблицу переменных, куда заносим некоторые важные значения
2. Вычисляем координаты вершины$V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
3. Также записываем 0 в таблицу и нулевые значения симметричные $-\frac{b}{2a}$.
или
4. Мы определяем точку пересечения с осью Ox,решая уравнение f(x)=0 и записываем корни x1 и x2 в таблице.
Δ > 0 ⇒
Δ < 0 ⇒ точек пересечения нет.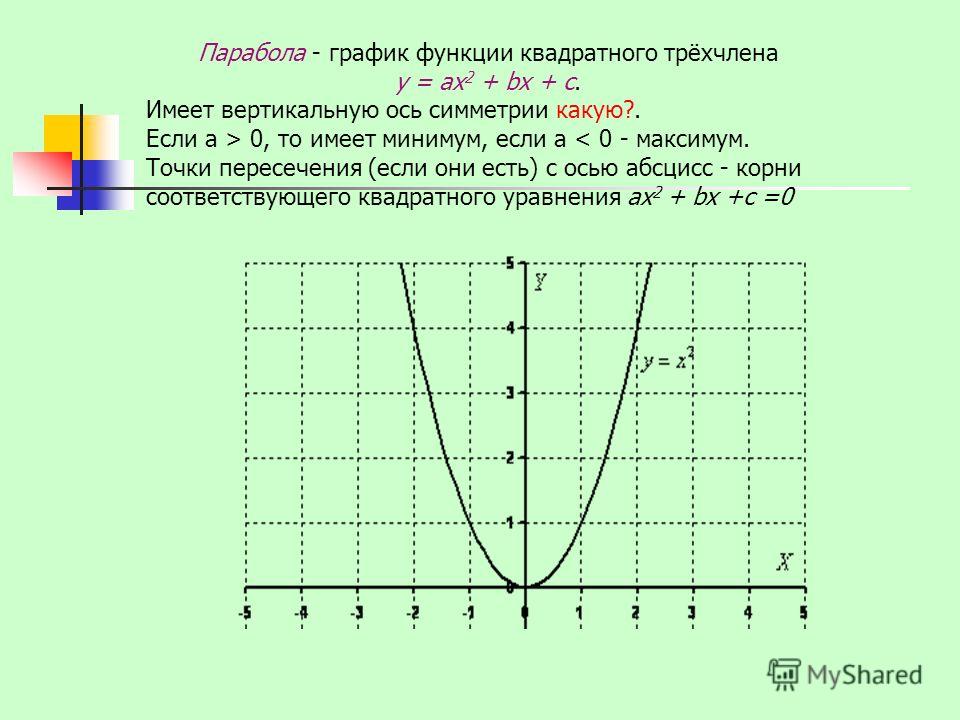 В этом случае мы выберем два удобных значения, которые симметричны $-\frac{b}{2a}$
В этом случае мы выберем два удобных значения, которые симметричны $-\frac{b}{2a}$
Δ = 0 ⇒ график касается Ox прямо в вершине параболы. Мы снова выберем два удобных значения, симметричных $-\frac{b}{2a}$. Для лучшего определения формы графика мы может выбрать другие пары значений для x, но они должны быть симметричны $-\frac{b}{2a}$.
5. Мы наносим эти значения на систему координат и строим график, соединяя эти точки.
Пример 1
f: R → R
f(x) = x2 — 2x — 3
a = 1, b = -2, c = -3
Δ = b2 — 4×a×c = (-2)2 — 4×1×(-3) = 16
$-\frac{b}{2a}=\frac{2}{2}=1$
⇒ V(1; -4)
1. $-\frac{\Delta}{4a}=-\frac{16}{4}=-4$
2. f(0) = -3
Симметричное 0 значение относительно 1 равно 2.
f(2) = -3
Δ = 16 > 0
$x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{2-4}{2}=-1$
$x_1=\frac{2+4}{2}=3$
Мы нашли точки:
A(-1; 0)
B(0; -3)
V(1; -4)
C(2; -3)
D(3; 0)
График будет иметь вид:
Пример 2
f: R → R
f(x) = -x2 — 2x + 8
a = -1, b = -2, c = 8
Δ = b2 — 4×a×c = (-2)2 — 4×(-1)×8 = 36
$-\frac{b}{2a}=\frac{2}{-2}=-1$
⇒ V(-1; 9)
1. $-\frac{\Delta}{4a}=-\frac{-36}{-4}=9$
$-\frac{\Delta}{4a}=-\frac{-36}{-4}=9$
2. f(0) = 8
f(-2) = 8 (симметричное 0 значение относительно -1 равно -2)
3. f(x) = 0 ⇒ -x2 — 2x + 8 = 0
Δ = 36
x1 = 2 и x2 = -4
A(-4; 0)
B(-2; 8)
V(-1; 9)
C(0; 8)
D(2; 0)
Пример 3
f: R → R
f(x) = x2 — 4x + 4
a = 1, b = -4, c = 4
Δ = b2 — 4×a×c = (-4)2 — 4×1×4 = 0
$-\frac{b}{2a}=\frac{4}{2}=2$
⇒ V(2; 0)
1. $-\frac{\Delta}{4a}=0$
2. f(0) = 4
f(4) = 4 (симметричное 0 значение относительно 2 равно 4)
3. f(x) = 0 ⇒ x2 — 4x + 4 = 0
Δ = 0
x1 = x2 = $-\frac{b}{2a}$ = 2
A(-2; 9)
B(0; 4)
V(2; 0)
C(4; 4)
D(5; 9)
Пример 4
f: R → R
f(x) = -x2 + 4x — 5
a = -1, b = 4, c = -5
Δ = b2 — 4×a×c = 42 — 4×(-1)×(-5) = 16 — 20 = -4
$-\frac{b}{2a}=\frac{-4}{-2}=2$
⇒ V(2; -1)
1. $-\frac{\Delta}{4a}=-\frac{-4}{-4}=-1$
$-\frac{\Delta}{4a}=-\frac{-4}{-4}=-1$
2. f(0) = -5
f(4) = -5 (симметричное 0 значение относительно 2 равно 4)
3. f(x) = 0 ⇒ -x2 + 4x — 5 = 0,
Δ < 0
У этого уравнения нет решений.
Мы выбрали симметричные значения вокруг 2
A(-1; -10)
B(0; 5)
V(2; -1)
C(4; -5)
D(5; -10)
Если область определения не R (множество действительных чисел), а какой-то интервал, то мы стираем часть графика, которая соответствует тем значениям x, которые не находятся в данном интервале. Необходимо записать конечные точки интервала в таблице.
Пример 5
f: [0; +∞) → R
f(x) = x2 — 2x — 3
a = 1, b = -2, c = -3
Δ = b2 — 4×a×c = (-2)2 — 4×1×(-3) = 16
$-\frac{b}{2a}=1$
⇒ V(1; -4)
1. $-\frac{\Delta}{4a}=-4$
2. f(0) = -3
f(2) = -3 симметричное 0 значение относительно 1 равно 2)
3. f(x) = 0 ⇒ x2 — 2x — 3 = 0,
Δ = 16
x1 = -1 ∉ [0; ∞)
x2 = 3
A(0; -3)
V(1; -4)
B(2; -3)
C(3; 0)
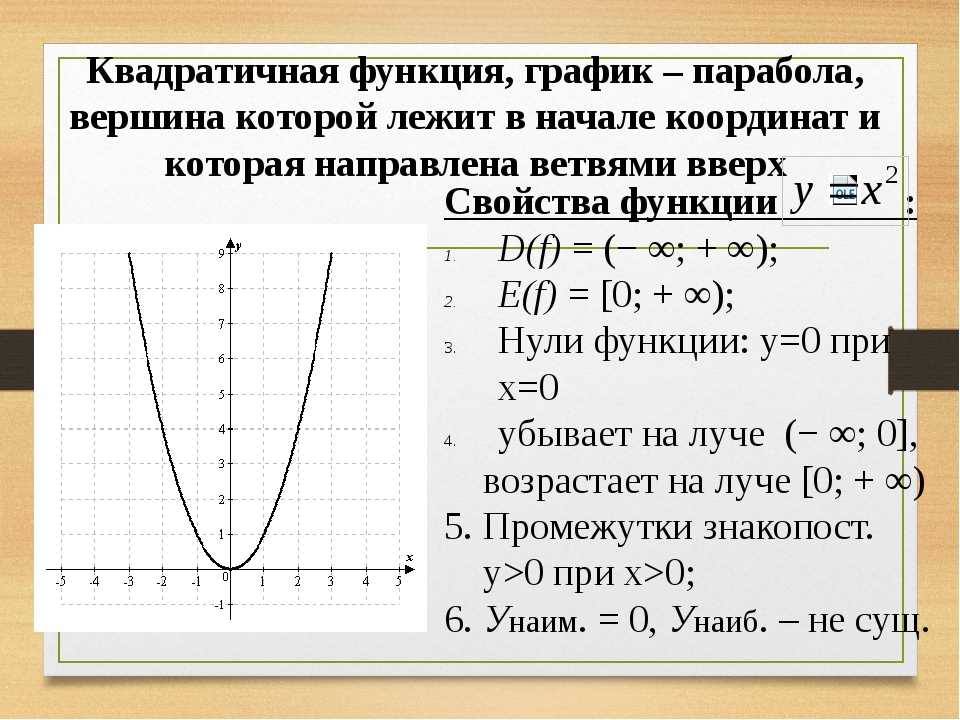
Квадратичная функция и её график
Вершина этой параболы находится в точке (0; 0).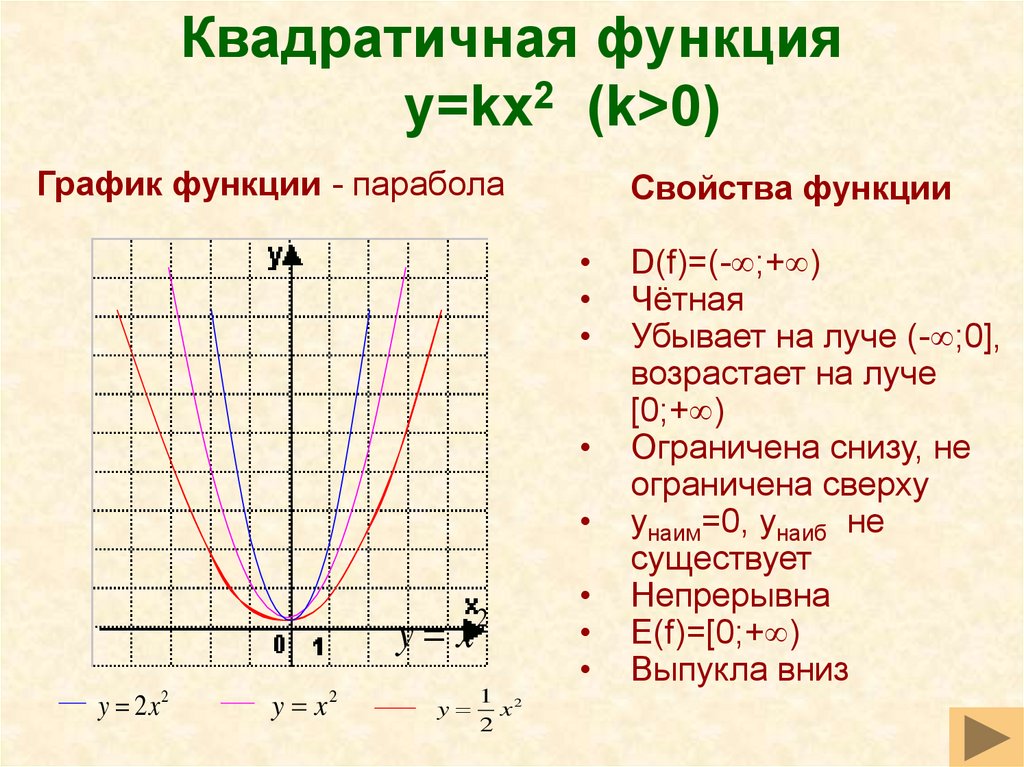 И не забудь про то, что ветви параболы бесконечно поднимаются ввысь и не ограничены точками с координатами (3; 9) и (3; -9).
И не забудь про то, что ветви параболы бесконечно поднимаются ввысь и не ограничены точками с координатами (3; 9) и (3; -9).
Еще одна стандартная парабола задается функцией y = —x2 (в этом случае а = -1). Для этого графика я тоже напишу табличку:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -9 | -4 | -1 | 0 | -1 | -4 | -9 |
Начало координат тоже является вершиной этой параболы, как и в предыдущем случае, но ветви уже будут направлены вниз:
Сразу напрашивается вывод: если перед х2 стоит положительное число, то ветви параболы направлены вверх, если отрицательное — то вниз.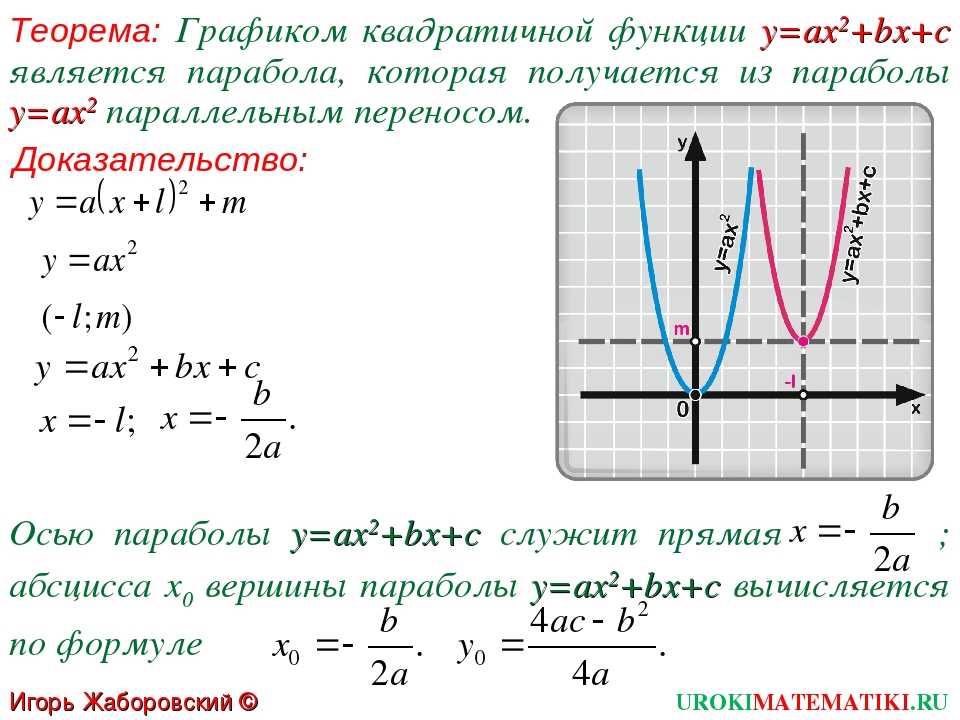
Если у тебя черный пояс по рисованию стандартных парабол, то следующий раздел пройдет у тебя «на ура».
Параболы со смещенной вершиной.
Зачем я начала статью со стандартной параболы? Ответ прост. Графиком любой квадратичной функции
Чтобы начертить подобные параболы нужно сначала узнать, где находится вершина.
Пусть вершиной параболы будет точка О с координатами (x1; y1). Тогда найти эти координаты можно по формулам:
Кстати, можно найти координаты вершины и другим способом.
Координату хО находим по той же формуле, а координату уО можно найти подстановкой координаты хО в функцию.
Без примера не обойтись)
Пример 1.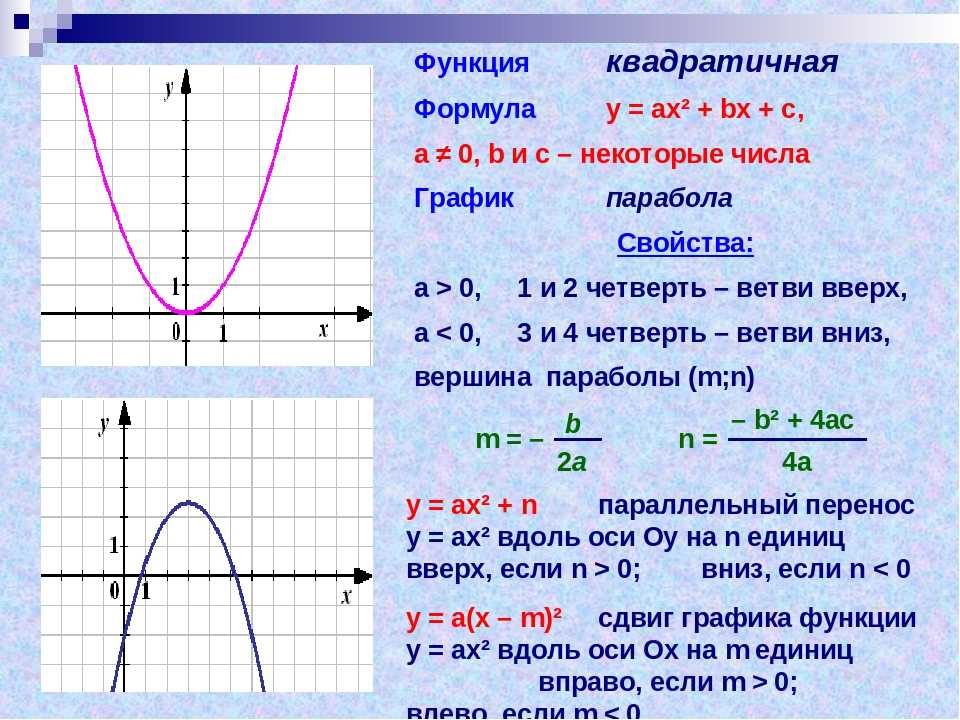
Дана функция y = x2 — 4x + 4. Найдите вершину параболы и постройте график.
Найдем сначала вершину параболы двумя способами, чтобы убедится, что оба способа рабочие.
1 способ: по формулам.
2 способ: подстановкой.
Одну координаты мы уже нашли по формуле. Подставляем ее в исходную функцию.
Итак, получили, что О(2; 0) — вершина параболы. Отмечаем ее на координатной плоскости.
Перед х2 стоит положительное число, значит ветви параболы направлены вверх. Наша задача: нарисовать стандартную параболу, представив, что точка О — начало координат. Если тебе это сложно сделать, то необходимо начертить таблицу значений и уже по ней рисовать параболу.
Параболы-стройняшки и параболы-пухляшки.
Удивительно, но числовой коэффициент перед х2 оказывается влияет на стройность и полноту парабол.
Если числовой коэффициент лежит в промежутке (-1; 0) ∪ (0; 1), то парабола будет более обширно смотреться на координатной плоскости.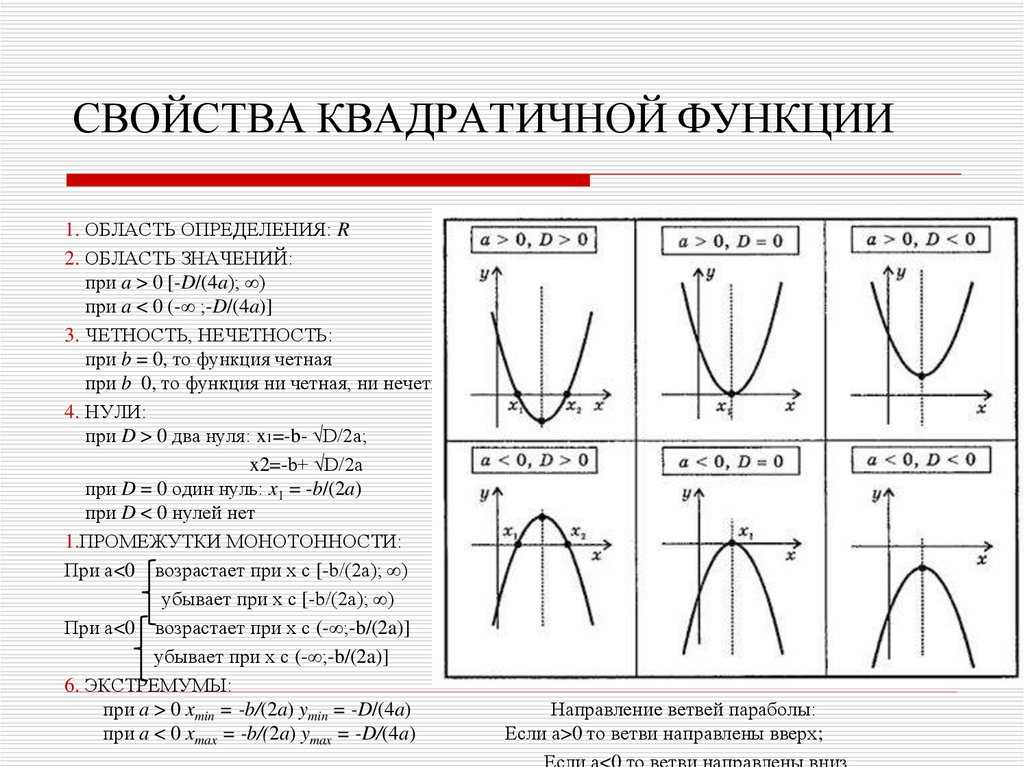
А если числовой коэффициент лежит в промежутке (-∞; -1) ∪ (1; +∞), то парабола будет прижиматься к оси Оу и занимать меньше места на плоскости.
Не веришь? Давай проверим! Для примера возьмем две функции:
К сожалению, здесь схитрить не получится: обе параболы нестандартные и для обеих необходимо создать таблицы значений. Но перед эти определимся с их вершинами.
Пусть вершиной первой параболы будет точка А(хА; уА), а вершиной второй параболы — точка B(хB; уB). Вершины буду находить по второму способу (см. выше).
Переходим к таблицам значений.
Голубая парабола.
| x | 0 | 2 | 4 | 6 | 8 |
| y | 3 | 6 | 7 | 6 | 3 |
Зеленая парабола.
| x | -1,5 | -1 | -0,25 | 0 | 1 |
| y | -3 | 1 | 4,5 | 3 | -3 |
Чертим обе параболы по получившимся координатам.
Вот о чем я и говорила) Перед тобой парабола-стройняшка и парабола-пухляшка во всей красе.
А ты заметил, что свободный член в уравнении функции — это точка пересечения графика с осью Оу? В обеих функциях свободный член равен 3 и графики пересекают ось Оу в точке с координатами (0; 3).
Практикум по параболам.
Теорию о параболах можно еще писать и дальше, но тебя, скорее всего, интересует практика по графикам.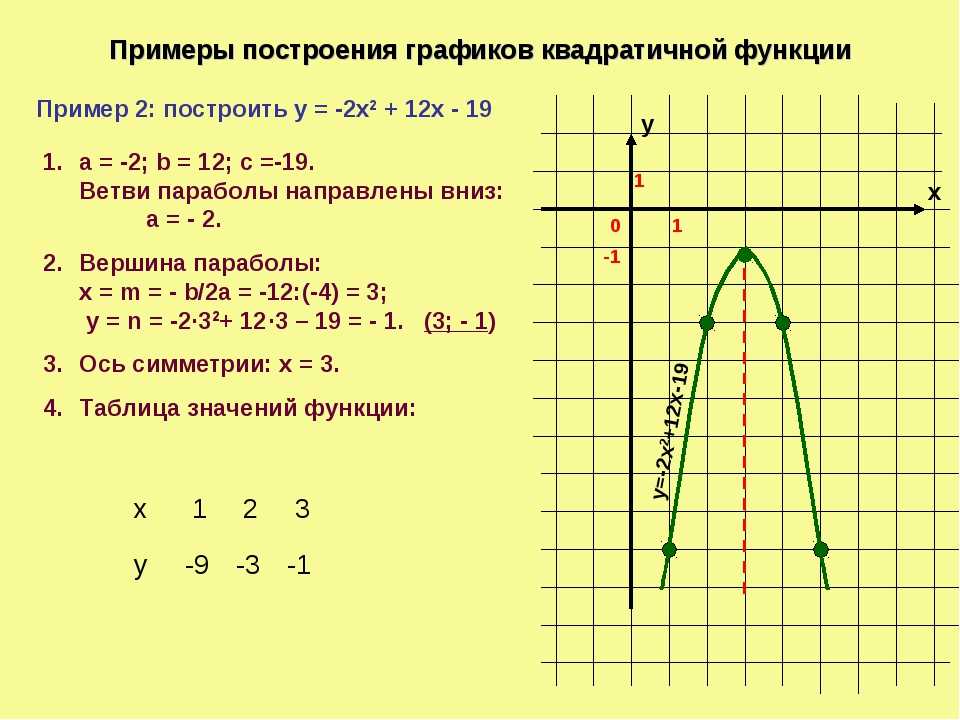
Поскольку речь идет о параболах, то с параболами мы и будем сейчас возиться.
Задание 1. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
Решение. Коэффициент а, стоящий перед х2, отвечает за направление ветвей параболы, а свободный член с — за пересечение графика с осью Оу.
А) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с отрицателен, то график пересекает ось Оу ниже нуля. Подходит график 1.
Б) Если коэффициент а отрицателен, то ветви направлены вниз; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 3.
В) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с положителен, то график пересекает ось Оу выше нуля.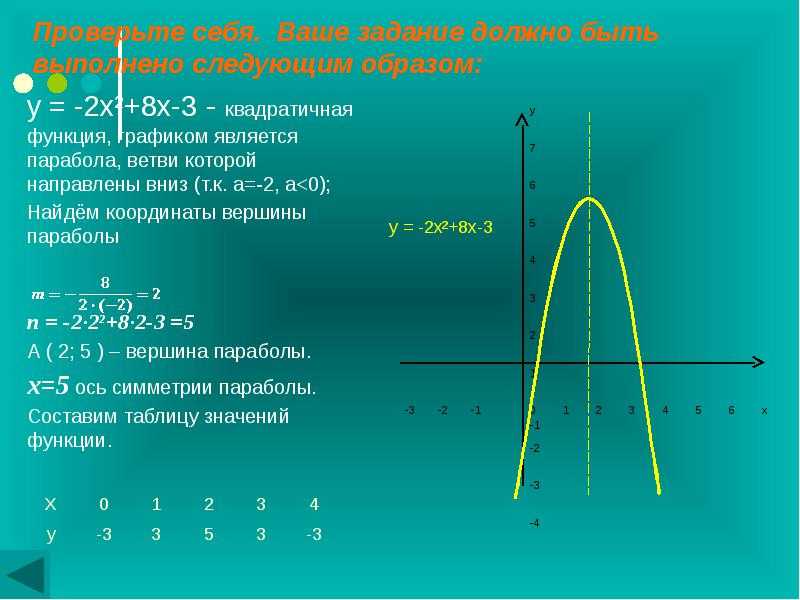 Подходит график 2.
Подходит график 2.
Задание 2 (наоборот). На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
А) Ветви направлены вверх, значит а > 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 3.
Б) Ветви направлены вверх, значит а > 0; график пересекает ось Оу ниже нуля, значит и с < 0. Подходит вариант под номером 1.
В) Ветви направлены вниз, значит а < 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 2.
Задание 3. Установите соответствие между графиками и их функциями.
График В отличается от остальных тем, что его ветви направлены вниз. За направление ветвей отвечает коэффициент перед х2 — он отрицательный. Отрицательный коэффициент только в функции под номером 3. Значит В-3.
Отрицательный коэффициент только в функции под номером 3. Значит В-3.
Дальше рекомендую отработанную годами технику. Она минимизирует твои ошибки, если ты, конечно, умеешь считать)
Итак, рассматриваем график А и выбираем на нем точку с красивыми координатами (красивые значит не дробные). Мне нравится тут вершина. Ее координаты (4; -3). Даже не спрашивайте почему не прорисованы оси; эти задания взяты с сайта ФИПИ)
Теперь эти координаты подставляем в оставшиеся функции: вместо у подставляем -3, а вместо х подставляем 4.
Подставляем в первую функцию: -3 = 2 · 42 — 16 · 4 + 29; -3 = -3 — верно. Значит, А-1.
И остается Б-2.
Задание 4 (наоборот, но принципе тот же). Установите соответствие между функциями и их графиками.
Очевидно, что В-2.
На графике 1 выбираем точку. Вершина снова четкая, но для разнообразия давайте возьмем другую точку, например, точку с координатами (-4; 1). Будь внимателен и смотри, чтобы точно такой же точки не было на третьем графике!
Подставляем в функцию А: 1 = (-4)2 + 4 · (-4) + 1; 1 = 1 — верно. Значит, А-1.
Значит, А-1.
Соответственно, Б-3.
Если ты считаешь, что чего-то не хватает или у тебя есть ещё задания из первой части, связанные с параболами, — напиши мне в VK)
OpenAlgebra.com: Графические параболы
На этом этапе нашего исследования мы должны быть в состоянии найти x и y пересечений и решить любое квадратное уравнение. Теперь мы изучим простой метод, используемый для их построения.
Плейлист графических парабол на YouTube
График квадратного уравнения называется параболой.
Одна из наших основных функций
можно изобразить, нанеся точки. Мы делаем это, выбирая около пяти x -значения и нахождение соответствующих им y -значений.
График :
Чем больше точек мы наносим, тем легче увидеть, что график имеет U-образную форму.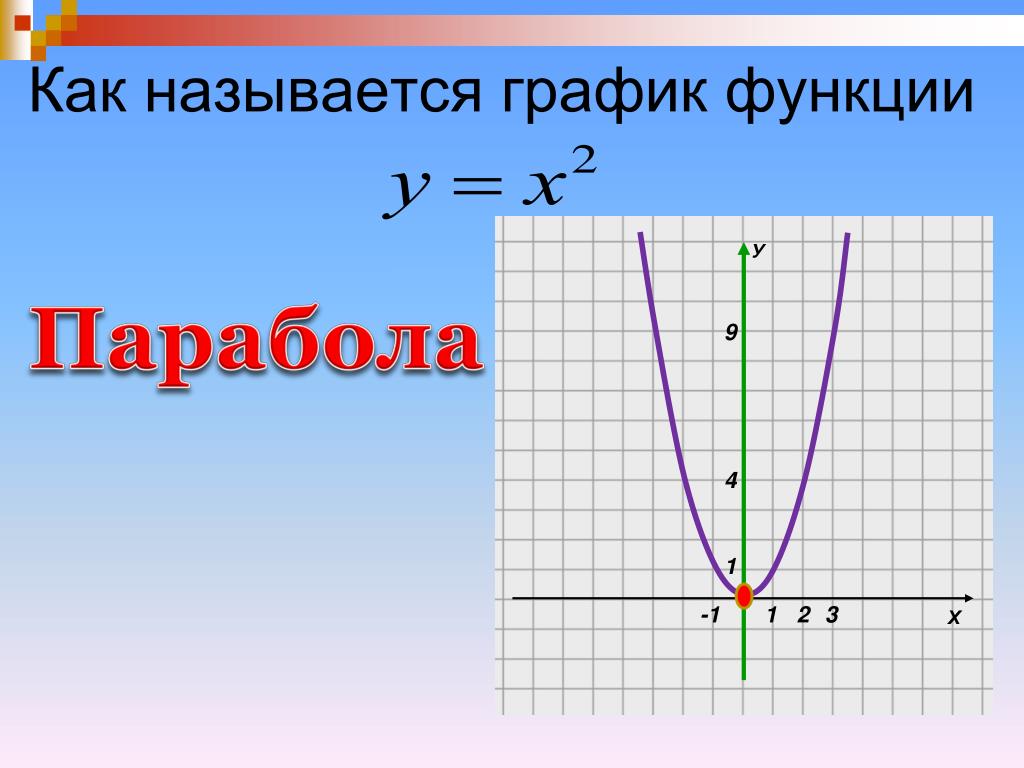 Вершина в данном случае является точкой изменения графика с убывающей на возрастающую, или точкой с наименьшим значением y . Здесь вершина (0, 0), которая также является точкой пересечения x и y . Линия х = 0, ось y является линией симметрии . Это линия, по которой мы могли бы согнуть нашу бумагу, чтобы увидеть, что две стороны графика совпадают.
Вершина в данном случае является точкой изменения графика с убывающей на возрастающую, или точкой с наименьшим значением y . Здесь вершина (0, 0), которая также является точкой пересечения x и y . Линия х = 0, ось y является линией симметрии . Это линия, по которой мы могли бы согнуть нашу бумагу, чтобы увидеть, что две стороны графика совпадают.
По заданному графику найдите точки пересечения x и y , вершину, 5-ю точку на графике и линию симметрии.
Линия симметрии: x = 1
Точки пересечения по оси x: (-2,0) и (4,0)
Точки пересечения с y: (0, -8)
Вершина: (1, — 9)
5-я точка: (2, -8)
Напомним, что две точки определяют прямую — для парабол это не так. Параболы требуют минимум 3 точки, но обычно мы хотим найти по крайней мере пять точек, чтобы построить хороший график.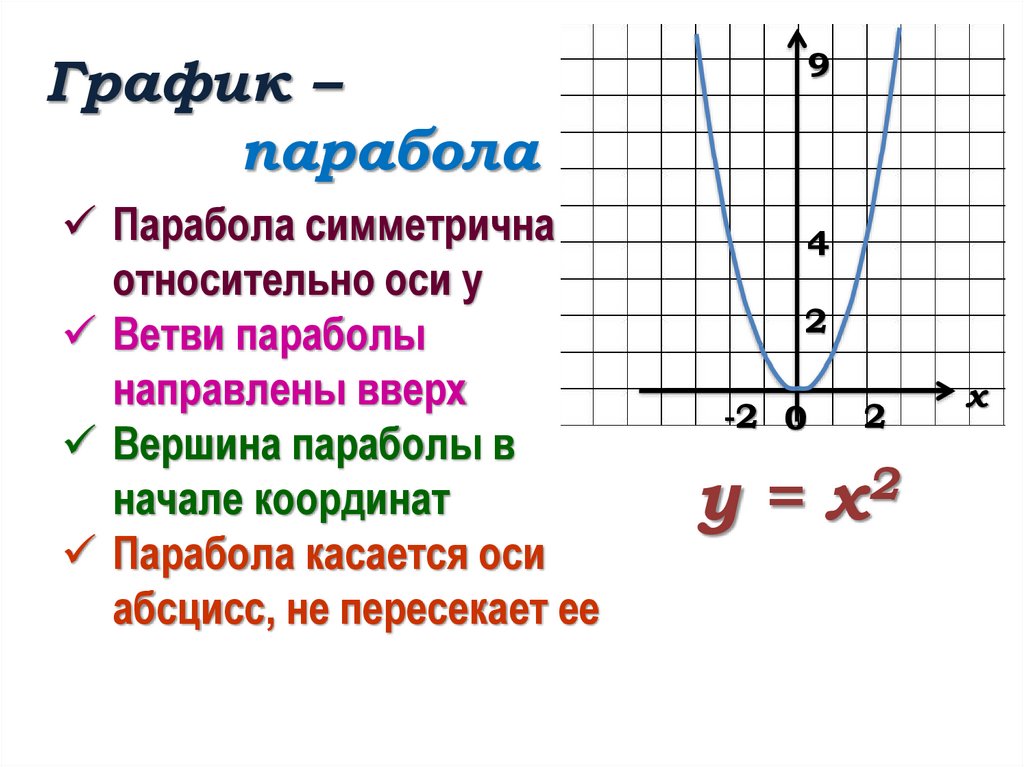 Найдите вершину, x — и y — точки пересечения, а также линию симметрии.
Найдите вершину, x — и y — точки пересечения, а также линию симметрии.
График:
Шаг 1 : Найдите точку пересечения и (0, c ).
Шаг 2 : Найдите x — перехватывает, устанавливая y = 0 и вычисляя x .
Шаг 3 : Найдите вершину. Вы можете найти значение x вершины, используя вершину x = -b/(2a).
Шаг 4 : Нанесите точки и определите ось симметрии.
Область и диапазон вышеуказанной функции можно определить по графику. В предыдущей задаче домен состоит из всех действительных чисел, а диапазон состоит из всех действительных чисел, больших или равных -1. Также полезно отметить, что у нас минимум y -значение -1, это будет важным фактом при работе над текстовыми задачами.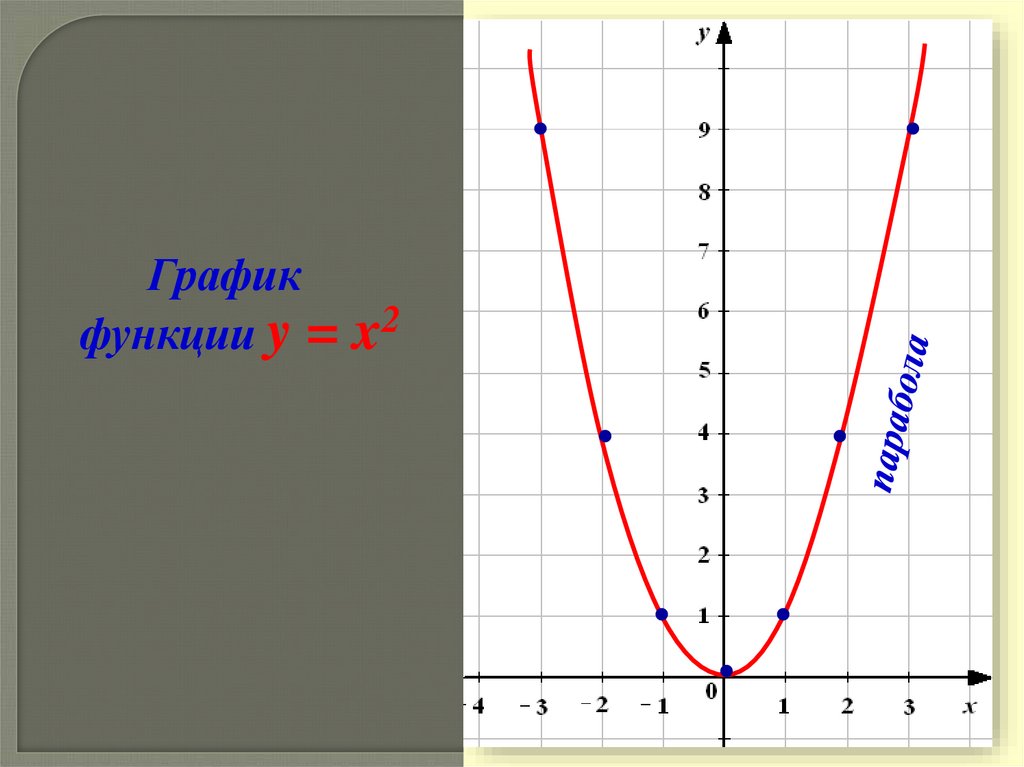
Совет : осью симметрии любой квадратичной функции будет вертикальная линия
При попытке найти точки пересечения x , где результирующее квадратное уравнение не учитывается, просто используйте квадратную формулу для его решения.
График:
Эта парабола выглядит немного по-другому, обратите внимание, что она открывается вниз, а также обратите внимание, что предыдущая парабола открылась. Есть простой тест, чтобы узнать, как он открывается, еще до того, как мы начнем.
Поэтому, когда вас попросят нарисовать параболу, вы можете получить две важные части информации, не выполняя никакой работы. При осмотре вы можете сказать, открывается ли он вверх или вниз, и вы можете определить и -перехват.
Нанесите на график и пометьте все важные точки :
Нанесите на график и пометьте все важные точки :
0 70 0 0 0 70
Областью предыдущей задачи являются все действительные числа, а диапазон состоит из всех действительных чисел, больших или равных -5.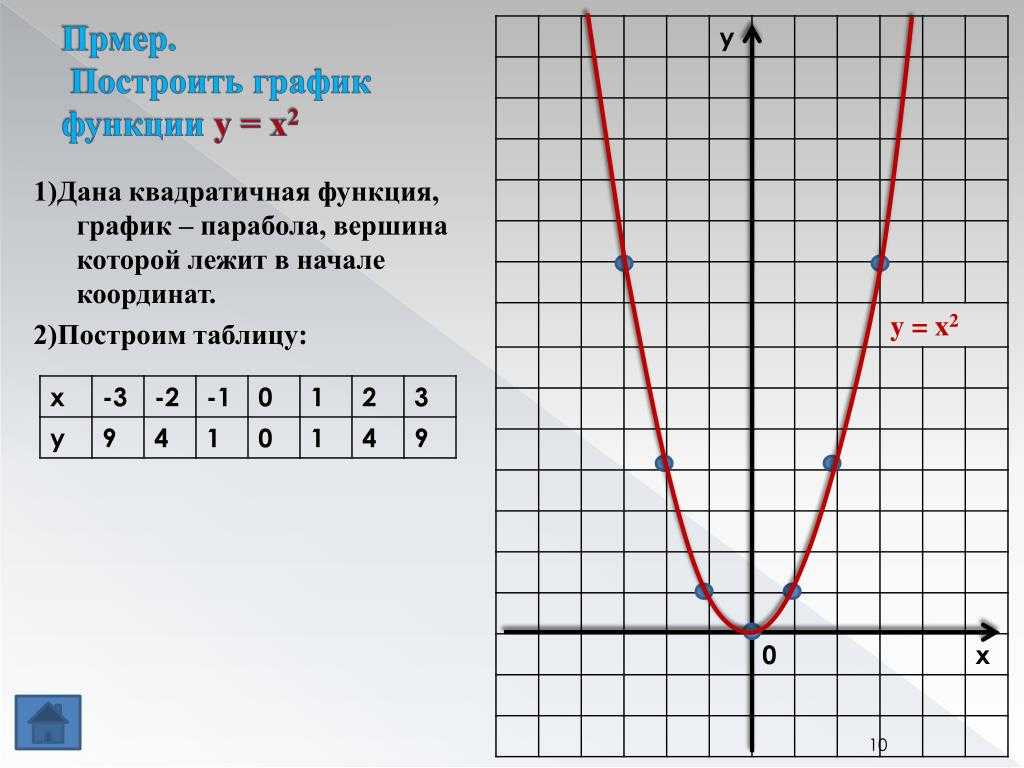 Также обратите внимание, что минимум г — значение равно -5. Оказывается, не все параболы имеют два пересечения x , как можно было бы ожидать. Иногда у них есть только один перехват x , а иногда и нет.
Также обратите внимание, что минимум г — значение равно -5. Оказывается, не все параболы имеют два пересечения x , как можно было бы ожидать. Иногда у них есть только один перехват x , а иногда и нет.
Пожалуйста, имейте в виду, что все квадратичные функции имеют вершину и точку пересечения и . Кроме того, мы все равно сможем найти другую точку, используя симметрию. Поэтому в некоторых случаях допустимо наносить и маркировать только три точки.
Отметьте и обозначьте все важные моменты:
Нанесите на график и обозначьте все важные точки:
Снаряд брошен в начальный объект 91002 Снаряд Проблема: 9002 скорость 44 метра в секунду. Сколько времени потребуется, чтобы достичь максимальной высоты? Какая максимальная высота?
Примеры видео на YouTube :
Как построить параболу за 3 простых шага — Mashup Math
Полное руководство по построению параболы на координатной плоскости Предварительный просмотр руководства: Как построить параболу.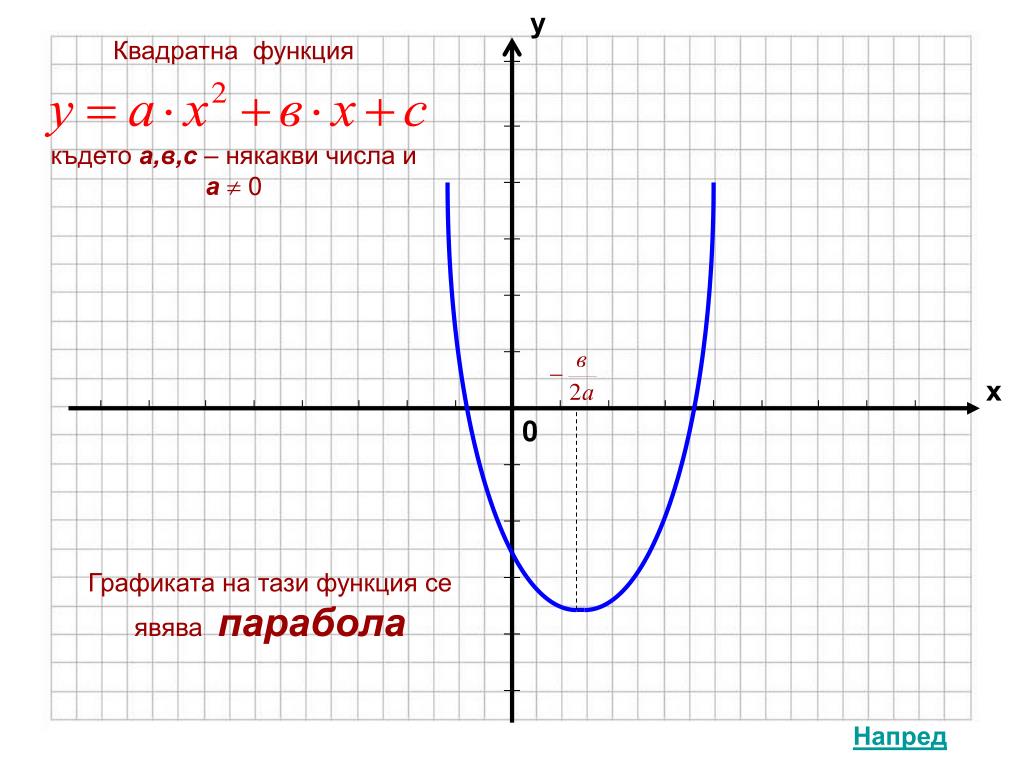
В алгебре важно понимать поведение квадратичных функций и их графики. В этом кратком руководстве рассматриваются следующие ключевые понятия (включая примеры):
Как построить параболу? 92+bx+c (обратите внимание, что в этом руководстве мы будем использовать f(x)= и y= взаимозаменяемо). Построение графика параболы на координатной плоскости с использованием ее формулы является важным навыком алгебры, и это руководство научит вас простому 3-этапному процессу, который вы можете использовать для построения графика параболы практически в любом сценарии.
Прежде чем вы научитесь строить параболы в стандартной форме, давайте рассмотрим некоторые ключевые понятия и словарный запас, связанные с квадратичными функциями и их графиками, прежде чем перейти к нескольким примерам построения графиков парабол. 92 -4x + 5, a=1, b=-4 и c=5
График функции представляет собой параболу — U-образную плоскую кривую, симметричную относительно линии симметрии, проходящей через вершинная точка.
 Парабола симметрична и образует зеркальное отражение самой себя по разные стороны от линии симметрии, проходящей через точку вершины.
Парабола симметрична и образует зеркальное отражение самой себя по разные стороны от линии симметрии, проходящей через точку вершины.На рисунке 01 ниже показаны примеры квадратичных функций в стандартной форме вместе с соответствующим графиком. Обратите внимание на U-образную параболу для каждого графика вместе с точкой вершины. Также обратите внимание, что парабола может открываться вверх (U-образная форма) или открываться вниз (перевернутая U-образная форма).
Рисунок 01: Как построить параболу: примеры построения параболы на координатной плоскости
Теперь, когда вы знаете, как выглядит график квадратичной функции в стандартной форме, давайте еще раз посмотрим, что такое вершина параболы.
Что такое вершина параболы?Вершина параболы — это координатная точка (x,y), в которой пересекаются парабола и ее ось симметрии.

В Рисунок 01 выше вершина параболы помечена, а осью симметрии является горизонтальная пунктирная линия, которая проходит через нее.
Проще говоря, что является вершиной параболы? Вершина — это точка в самом низу кривой для парабол, открывающихся вверх, или в самом верху кривой для парабол, открывающихся вниз.
Если вы можете найти вершину параболы, то вы можете легко научиться рисовать параболу на координатной плоскости, поэтому важно понять, что такое вершина параболы и как ее найти. К счастью, найти вершину параболы несложно, если выполнить два простых шага:2-4х+5 равно (2,1).
График этой функции, включая точку вершины, показан на координатной плоскости Рисунок 03 .
Теперь, когда вы знаете, как найти точку вершины параболы, вы готовы выполнить несколько пошаговых примеров того, как изобразить параболу на координатной плоскости, используя 3 простых шага (первый из которых определить, что является вершиной параболы).
Как построить параболу: Пример №1
92 + 6x + 5
Теперь вы готовы начать рисовать параболу на координатной плоскости, используя простой трехэтапный метод:
Шаг 1: Найдите координаты точки вершины
Шаг 2: Создайте таблицу функций и «постройте» две точки на каждой стороне вершины
Шаг 3: Нанесите точки и постройте кривую (параболу)
Теперь давайте продолжим и применим эти три шага к этому первому примеру: 92 + 6x + 5, мы будем использовать тот же процесс, что и в Рисунок 02 выше, следующим образом:
Поскольку b=6 и a=1, x=-b/2a → x= -6 / 2(1) → x = -6/2 → x = -3
Шаг B: Введите значение координаты x из шага A в функцию, чтобы найти значение координаты y.
Теперь, когда вы знаете, что значение координаты x для вершины равно x=-3, вы можете ввести x=-3 в функцию, чтобы найти значение координаты y следующим образом: 92 -6(-3) + 5 → f(2) = 4 — 8 + 5 = -4 → y=-4
Итак, координаты вершины парабола (-3,-4)
Как построить параболу: используйте таблицу функций.

Шаг 2: Создайте таблицу функций и «постройте» две точки на каждой стороне вершины
Как только вы определите координаты точки вершины, вы можете построить таблицу функций, как показано на рис. 9.0191 Рисунок 04 . Ваша таблица функций должна включать столбец с координатами x и столбец с координатами y, а также строки не менее чем для пяти точек на графике.
Поскольку вершина представляет собой «точку поворота» U-образной параболы, координаты вершины должны быть помещены в середину таблицы функций.
Затем пришло время «построить» точки по обе стороны от точки вершины, введя значения x, которые меньше -3 и больше 3, в исходную функцию и выводят значения.
Опять же, поскольку координата x точки вершины равна -3, мы выберем два значения x меньше -3 (-4 и -5 в этом примере) и два значения x больше — 3 (-2 и -1 в этом примере).
Затем возьмите каждое значение x и введите его в функцию, чтобы найти соответствующее значение y.
92+6(-5)+5 = 0, вы можете заключить, что когда x равно -5, y равно 0 (и что (-5,0) является точкой на параболе. Теперь повторите этот процесс чтобы найти f(-4), f(-2) и f(-1), чтобы заполнить таблицу функций, как показано на Рисунок 05 ниже. Например, чтобы найти значение координаты y при x=-5, просто оцените значение f(-5), как показано на Рисунок 04 ниже.
Например, чтобы найти значение координаты y при x=-5, просто оцените значение f(-5), как показано на Рисунок 04 ниже.Рисунок 05: Заполненная таблица функций
Шаг 3: Нанесите точки и постройте кривую (параболу)
Третий и последний шаг — нанесение всех пяти точек таблицы функций на координатную плоскость. Вы должны заметить, что точки следуют симметричной U-образной форме с точкой поворота вокруг точки вершины, которая в этом примере (-3,-4).
Обратите внимание, что точки в заполненной таблице функций: (-5,0), (-4,-3), (-3,-4), (-2,-3) и (-1,0) .
 После нанесения этих пяти точек на координатную плоскость у вас должен получиться график, похожий на Рисунок 06 ниже.
После нанесения этих пяти точек на координатную плоскость у вас должен получиться график, похожий на Рисунок 06 ниже.Рисунок 06: Как построить параболу: начертите все точки из таблицы функций.
После того, как ваши точки были нанесены, вы готовы построить свою параболу, нарисовав U-образную кривую, которая проходит через все пять точек, как показано на рисунке 9.2 -2(1) -6 → f(1) = 1- 2 -6 = -7 → y=-7
Итак, координаты вершины параболы равны (1,-7)
Шаг 2: Создайте таблицу функций и «постройте» две точки с каждой стороны вершины
Теперь, когда вы знаете координаты точки вершины (1,-7), вы можно начать построение точек по обе стороны от вершины, вводя значения x, которые меньше 1 (0 и -1 в этом примере) и больше 1 (2 и 3 в этом примере) в исходную функцию и выводят значения координаты y.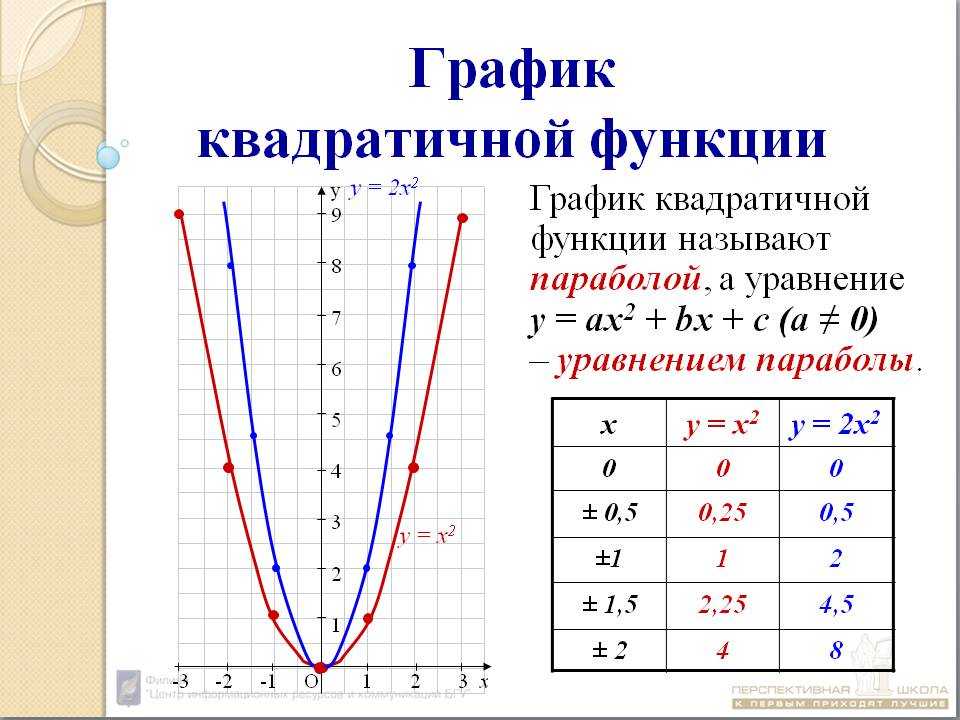 92-2(0)-6 = 0-0-6 = -6
92-2(0)-6 = 0-0-6 = -6
Итак, вы можете заключить, что, когда x равно 0, y равно -6 (и что (-6,0) является точкой на параболе На рисунке 08 ниже показано, как вычислить f(0), а также все другие точки в таблице данных.
Рисунок 08: Заполненная таблица данных
Шаг 3: Нанесите точки и постройте кривую (параболу)
После заполнения таблицы данных вы готовы нанести на координатную плоскость все пять следующих точек: (-1,-3), (0,-6), (1,-7), (2,-6) и (3,-3). 92 +8(4) -12 → f(4) = -16 + 32 — 12 → y=4
Итак, координаты вершины параболы равны (4,4)
Шаг 2: Создайте таблицу функций и «постройте» две точки на каждой стороне вершины
Затем используйте точку вершины (4,4) для построения точек на каждой стороне вершины путем ввода значений x, которые оба меньше 4 (3 и 2 в этом примере) и больше 4 (5 и 6 в этом примере) в исходную функцию и выводят значения координаты y.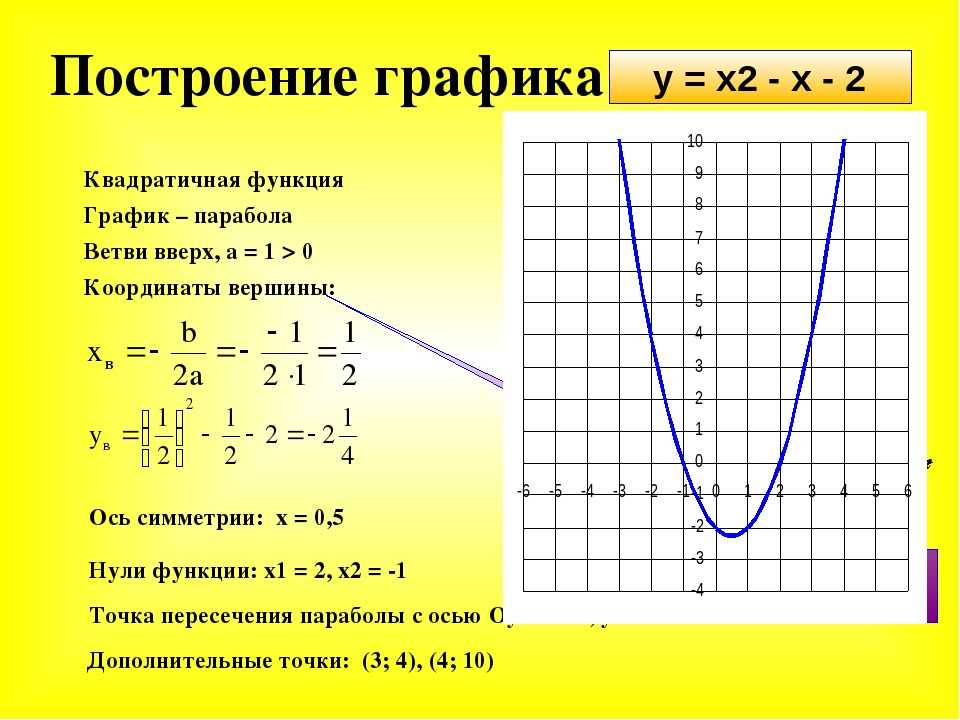 92+8(5)-12 = -25 + 40 — 12 = 3
92+8(5)-12 = -25 + 40 — 12 = 3
Итак, вы можете заключить, что когда x равно 5, y равно 3 (и что (5,3) является точкой на параболе. На рисунке 11 ниже показано, как вычислить f(5), а также все другие точки в таблице данных.
Рисунок 11: Завершенная функциональная схема
Шаг 3: Нанесите точки и постройте кривую (параболу)
Теперь вы готовы нанести точки (2,0), (3,3), (4,4), (5,3), и (6,0) на координатной плоскости, как показано на Рисунок 12 внизу:
Рисунок 12
Обратите внимание, что парабола в примере №3 раскрывается вниз (в то время как параболы в примерах 1 и 2 раскрываются вверх). Это совершенно нормально, так как параболы могут раскрываться вверх или вниз.
Последним шагом будет начертить кривую, проходящую через точки, чтобы завершить построение параболы, как показано на .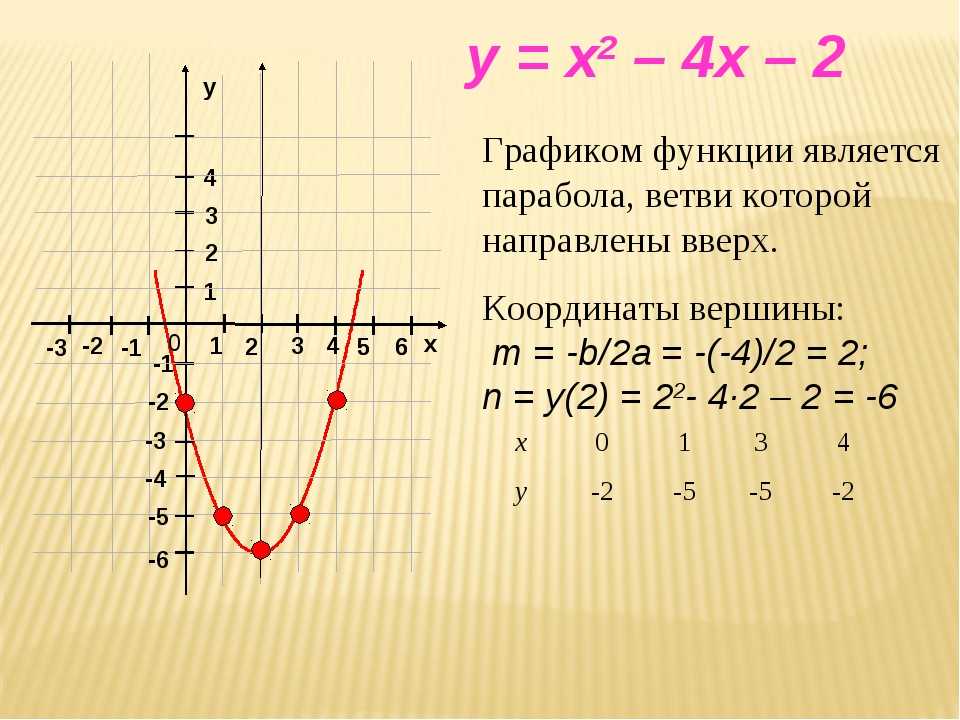

 Парабола симметрична и образует зеркальное отражение самой себя по разные стороны от линии симметрии, проходящей через точку вершины.
Парабола симметрична и образует зеркальное отражение самой себя по разные стороны от линии симметрии, проходящей через точку вершины.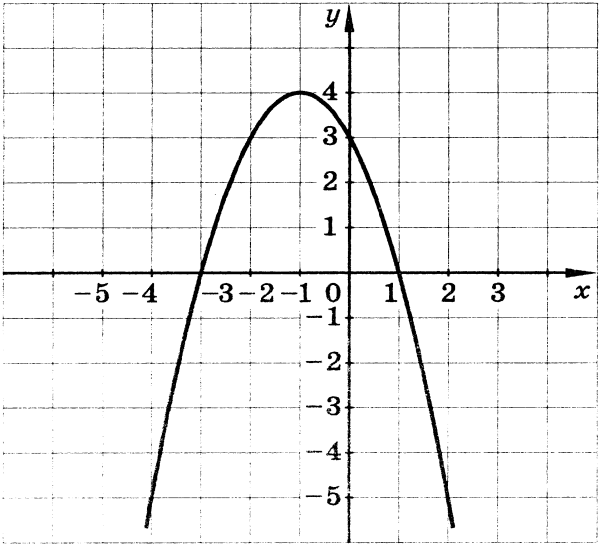

 Например, чтобы найти значение координаты y при x=-5, просто оцените значение f(-5), как показано на Рисунок 04 ниже.
Например, чтобы найти значение координаты y при x=-5, просто оцените значение f(-5), как показано на Рисунок 04 ниже. После нанесения этих пяти точек на координатную плоскость у вас должен получиться график, похожий на Рисунок 06 ниже.
После нанесения этих пяти точек на координатную плоскость у вас должен получиться график, похожий на Рисунок 06 ниже.