Функция ФИ и плотность стандартного нормального распределения в Excel
Функция ФИ в Excel предназначена для определения значения плотности вероятности величины, описанной законом стандартного нормального распределения, и возвращает соответствующее число.
Значения функции плотности стандартного нормального распределения в Excel
Если случайная величина распределена непрерывно, она может иметь любое значение, взятое из интервала, в котором она определена. Такое число значений стремится к бесконечности, следовательно, вероятность попадания в какую-либо определенную точку из данного интервала стремится к нулю (сумма вероятностей должна соответствовать числу 1). Поэтому, является возможным только определение вероятности нахождения некоторой величины в заданном интервале значений. С этой целью было введено понятие плотности вероятности – производная функции распределения. Для вычисления вероятности определяют площадь, образованную кривой графика, осью абсцисс и двумя вертикальными линиями, проведенными от точек, соответствующих граничным значениям исследуемого интервала.
Рассматриваемая функции вычисляет то же значение, которое возвращает функция НОРМ.СТ.РАСП, у которой второй аргумент принимает значение ЛОЖЬ.
Пример 1. Построить график плотности вероятности для известных значений x, которые внесены в таблицу Excel.
Вид таблицы данных:
Для построения графика определим значения плотности для известных значений x. Используем формулу, предварительно выделив ячейки в диапазоне B2:B22:
=ФИ(A2)
Полученные значения:
Используем полученные данные для построения графика:
Значение плотности вероятности имеет смысл при определении вероятности нахождения величины в некотором диапазоне. Ее используют для вычисления интеграла с указанными граничными значениями некоторой величины, в результате чего получают вероятность нахождения некоторого значения в диапазоне, заданного этими граничными значениями.
В Excel функция плотности используется преимущественно для построения графиков. Вероятность определяется функцией НОРМ.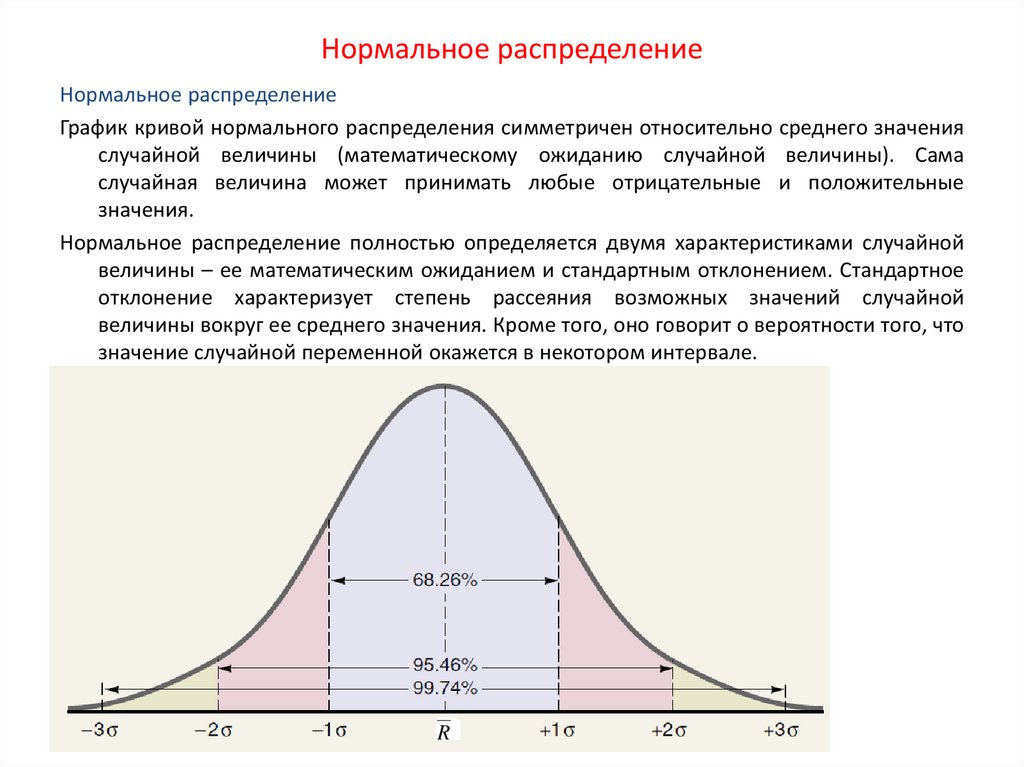 СТ.РАСП (для стандартного нормального распределение) с последним аргументом, принимающим значение ИСТИНА.
СТ.РАСП (для стандартного нормального распределение) с последним аргументом, принимающим значение ИСТИНА.
Пример расчета плотности стандартного нормального распределения в Excel
Пример 2. Определить максимальное значение плотности вероятности для ряда значений двумя различными способами.
Вид таблицы данных:
Максимальное значение плотности вероятности для некоторой величины, распределенной по стандартному нормальному закону, можно определить с помощью функции МАКС, исследуя массив значений, возвращаемых функцией ФИ в формуле массива CTRL+SHIFT+Enter:
=МАКС(ФИ(A2:A9))
Полученный результат:
Другой способ – нахождение значения плотности для среднего значения известных величин. Однако, для начала необходимо стандартизировать имеющийся ряд значений с помощью функции НОРМАЛИЗАЦИЯ. Для нахождения используем формулу (вводить как формулу массива CTRL+SHIFT+Enter):
Полученное значение:
Небольшая разница в полученных значениях свидетельствует о том, что исследуемый ряд значений можно рассматривать как нормальное стандартное распределение некоторой величины.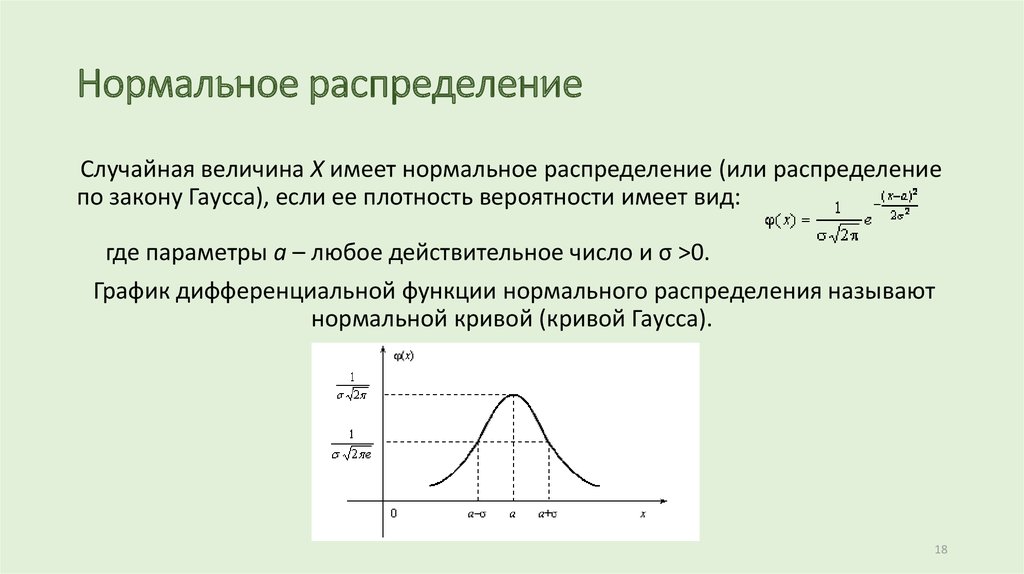
Правила использования функции ФИ в Excel
Функция ФИ имеет следующую синтаксическую запись:
=ФИ(x)
- x – обязательный, принимает число для некоторой величины, распределенной по стандартному нормальному закону, для которой необходимо определить значение плотности распределения.
Примечания:
- В качестве аргумента функции можно передавать ссылку на ячейку с числовыми данными или само число. Функция ФИ автоматические преобразует логические значения и текстовые строки, содержащие числа, к числовым значениям.
- Если аргумент функции принимает данные, не преобразуемые к числовым значениям, результатом выполнения ФИ будет код ошибки #ЗНАЧ!
- Для больших значений, значение плотности вероятности которых стремится к нулю, функция возвращает число 0. Например, =ФИ(100) вернет число 0.
Нормальное распределение (Распределения Гаусса)
Нормальное распределение (Распределения Гаусса)Из курса А.А.Авдеева, читавшегося в Страсбургском университете в 2003-2005 годах (перевод на русский и адаптация к традиции русской терминологии еще не закончены)
|
|
||||||||||||
|
[Объяснение] [Распределение Z]
Нормальное распределение, или распределение Гаусса (Gauss)
используестя для проверки различных гипотез, включая гипотезу о
равенстве двух средних.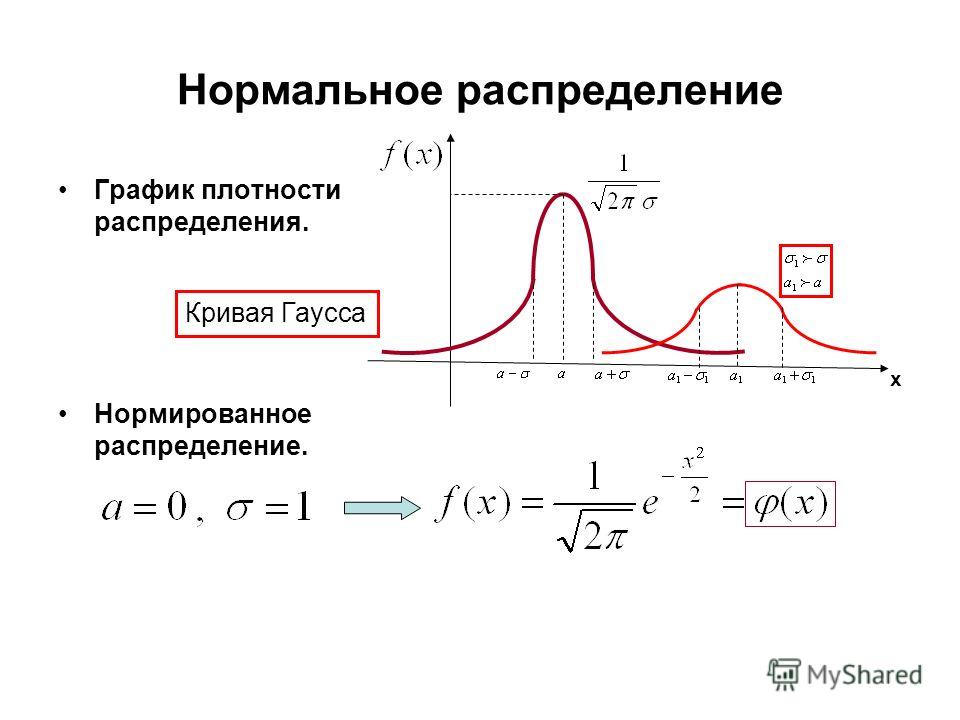 Это распределение имеет среднюю арифметическую равную 0
и дисперсию равную 1. На графике слева представлена
плотность распределения и вероятность (p)
соответствующая различным (как говорят «критическим») значениям
Z.
Это распределение имеет среднюю арифметическую равную 0
и дисперсию равную 1. На графике слева представлена
плотность распределения и вероятность (p)
соответствующая различным (как говорят «критическим») значениям
Z.
Значения в таблице представляют
собой площадь, находящуюся под частью кривой, которую описывает
стандартизированноя нормальная функция (Gausse)в
интервале значений от 0 до Z. Например, площадь,
ограниченная значениями 0 и 2,36, находится на
пересечении линии 2,30 и колонки 0,06. Она равна 0,4909.
Если значение Z является отрицательным,
то, учитывая симмертичность функции относительно средней, искомая вероятность
(площадь) будет находится на пересечении линии и колонки, соответсвующих
абсолютному значению Z ( |Z| ). Например, площадь между
0 и -1.3 равна площади между
0 et 1.3; то есть она находится на пересечении
линии 1.3 и колоники 0 и равна
0,4032.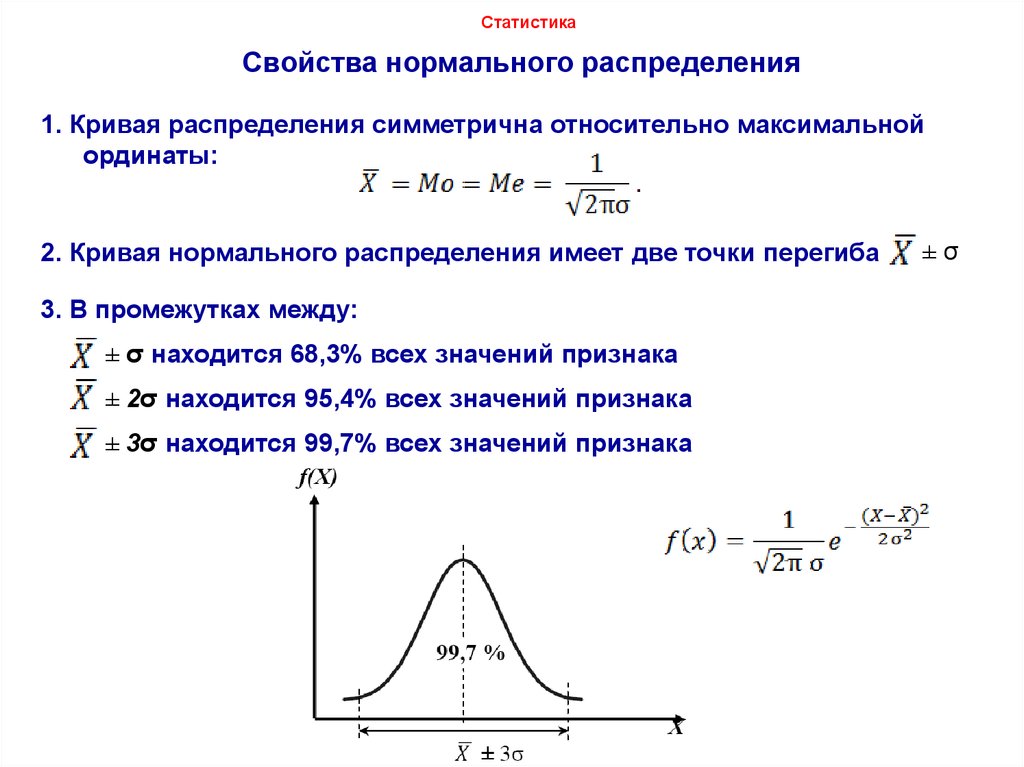
Чтобы лучше разобраться в том, как расчитывается вероятность гипотез с помощью таблицы значений нормального распределения, попробуйте самостоятельно построить в Экселе соответствующую таблицу (как ту, что вы видите ниже), используя встроенные функции данного таблятора.
|
Нормальное распределение
|
Интеграл от 0 до z
|
Плотность Durves и нормальное распределение
Плотность Durves и нормальное распределение Статистика в руках
инженер как фонарный столб для пьяного
они используются больше для поддержки, чем для освещения.
А. Э. Хаусман
Глава 2
Раздел 2.1
В главе 1 мы узнали, что исследование одного
количественная переменная требует нанесения данных на график, обычно
гистограмма или стеблевой график. Мы должны искать общую закономерность,
обсуждая форму, центр и распространение и отмечая любые выбросы. Тогда мы можем
вычислить числовую сводку для описания центра и разброса.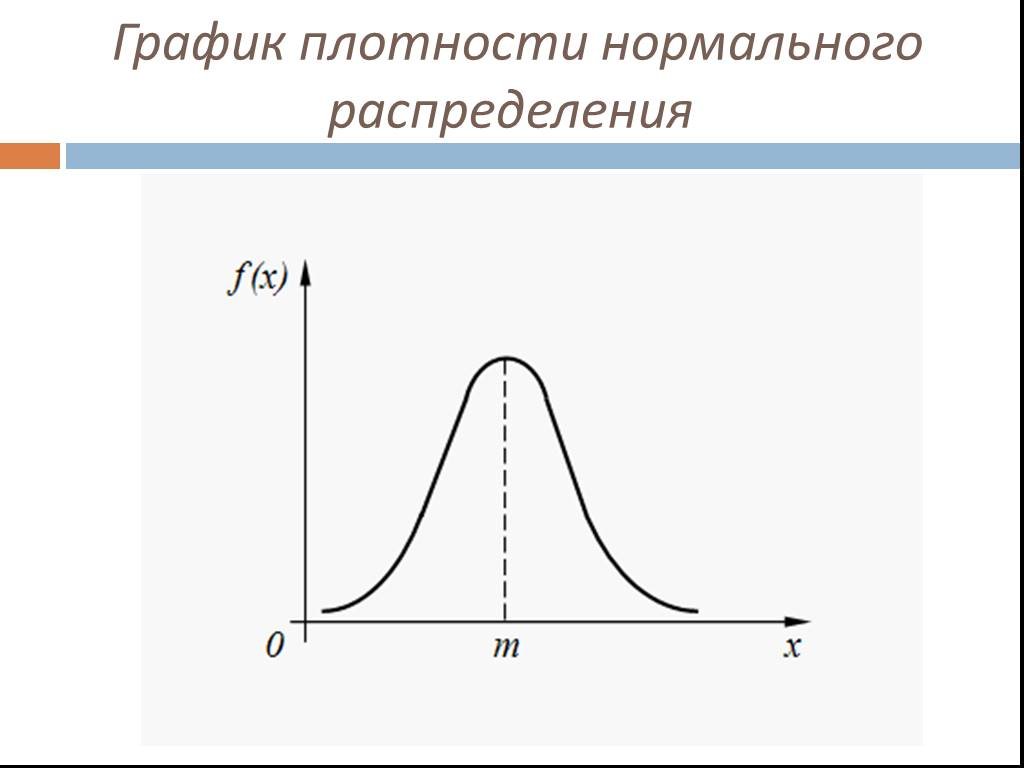 .. среднего и
стандартное отклонение для симметричных распределений и сводка по 5 числам для асимметричных
дистрибутивы.
.. среднего и
стандартное отклонение для симметричных распределений и сводка по 5 числам для асимметричных
дистрибутивы.
ТЕПЕРЬ добавим еще один шаг…
Иногда общая картина очень большого количества наблюдений ТАК
РЕГУЛЯРНОЕ, что мы можем описать его гладкой кривой. Эта кривая представляет собой математическая модель для распределения, т.е. идеализированное описание .
Он дает быстрое представление об общей картине, но игнорирует мелкие неровности.
а также выбросы. С плавной кривой работать легче, чем с
гистограммы, потому что гистограмма зависит от выбора классов, в то время как
кривая не зависит ни от какого выбора, сделанного нами.
Обоснование… столбцы гистограммы предполагают
площади… эти площади представляют пропорций наблюдений.
общая площадь под плавной кривой, очерчивающей гистограмму, равна ровно 1
(представляющие ВСЕ наблюдения).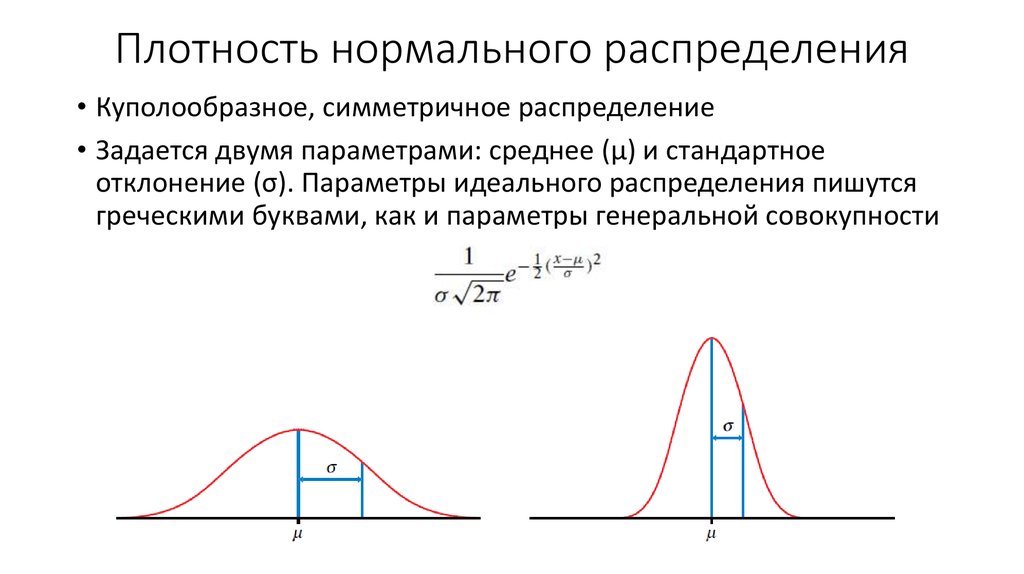 Кривая теперь представляет собой кривую плотности .
Кривая плотности — это кривая, которая всегда находится на горизонтальной оси или над ней, и
имеет площадь ровно 1 под ним. При рассмотрении конкретной точки данных
есть область слева и область справа. НОРМАЛЬНАЯ кривая – это одна
который имитирует симметричную гистограмму, а среднее значение и медиана РАВНЫ.
Другие кривые могут быть скошены, так как соответствующие им гистограммы со средним скошенным
в направлении хвоста.
Кривая теперь представляет собой кривую плотности .
Кривая плотности — это кривая, которая всегда находится на горизонтальной оси или над ней, и
имеет площадь ровно 1 под ним. При рассмотрении конкретной точки данных
есть область слева и область справа. НОРМАЛЬНАЯ кривая – это одна
который имитирует симметричную гистограмму, а среднее значение и медиана РАВНЫ.
Другие кривые могут быть скошены, так как соответствующие им гистограммы со средним скошенным
в направлении хвоста.
Графически МЕДИАНА кривой плотности
точка равной площади, точка с половиной площади под кривой слева от нее
а другая половина справа от него. Квартили делят площадь под
кривой на четверти. 1/4 площади слева от Q 1 и
3/4 площади находится слева от Q 3 . Вы можете примерно определить
медиана и квартили любой кривой плотности на глаз путем деления площади под
кривая на четыре равные части. СРЕДНЕЕ – это точка, в которой кривая
бы БАЛАНС , если он изготовлен из твердого материала.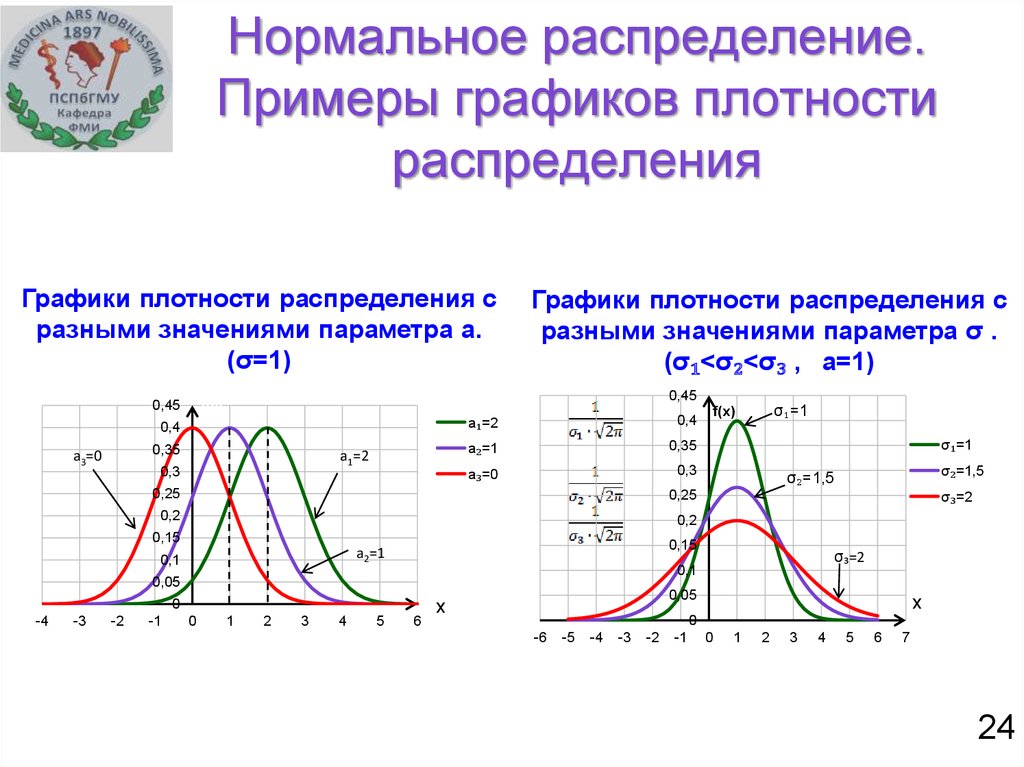
Новое обозначение… поскольку кривая плотности является идеализированное описание данных (не фактические данные), мы будем различать среднее значение и стандартное отклонение кривой и среднее значение (`x ) и эталон(ы) из фактических наблюдений. Обозначение среднего из этого идеализированного распределения есть m (греч. mu small «м»), а стандартное отклонение — с (греч. сигма маленькая «с»).
Результат нормального распределения с некоторыми исходами случайности, которые повторяются много-много раз. Случайные эксперименты могут быть выполняется на ТИ-83 с некоторым умением. Поскольку вы будете только делая вид, что проводит эксперимент, это называется «моделирование». См. стр. 85 в тексте для броска игральной кости.
Нормальные распределения симметричны,
одновершинные и колоколообразные. Их называют нормальными кривыми. Все
нормальные распределения имеют одинаковую общую форму. Точная кривая плотности
для конкретного нормального распределения описывается, давая его среднее значение
m и стандартное отклонение s.
Среднее значение находится в центре симметричной кривой и совпадает с
медиана. Изменение м без изменения
s перемещает нормальную кривую вдоль горизонтальной оси
БЕЗ изменения его распространения. Стандартное отклонение контролирует спред.
Кривая с большим стандартным отклонением более растянута.
Все
нормальные распределения имеют одинаковую общую форму. Точная кривая плотности
для конкретного нормального распределения описывается, давая его среднее значение
m и стандартное отклонение s.
Среднее значение находится в центре симметричной кривой и совпадает с
медиана. Изменение м без изменения
s перемещает нормальную кривую вдоль горизонтальной оси
БЕЗ изменения его распространения. Стандартное отклонение контролирует спред.
Кривая с большим стандартным отклонением более растянута.
Кривая плотности имеет точки, в которых «изменения» кривизны.., они называются «точками перегиба». Эти точки расположены по обе стороны от среднего на расстоянии s. Точки перегиба расположены на m + в качестве.
Нормальные распределения важны, потому что
они являются хорошим описанием многих реальных данных (например, результатов SAT и психологических
тесты), они являются хорошим приближением к результатам многих видов случайных
результаты (бросание монеты, бросание игральной кости), и они являются основой для статистических
процедуры вывода и хорошо работают для других примерно симметричных распределений.
Эмпирическое правило. .. В нормальном распределении со средним м и стандартное отклонение с
68% наблюдения будут находиться в пределах одного стандартного отклонения от среднего
95% наблюдений приходится на два стандартные отклонения среднего
99,7% наблюдений попадают в 3 стандартные отклонения среднего
Можно описать любое нормальное распределение с сокращенным обозначением…
Н(м,с)
Часто результаты тестов указываются в процентили , а не необработанные баллы. Если вы забьете как 94-й
процентиль, то 94% учащихся, сдавших тест, набрали меньше или равно
ты. Процентили используются, когда нужно изучить, где индивидуум
смотровые площадки относительно по отношению к другим лицам в распределении.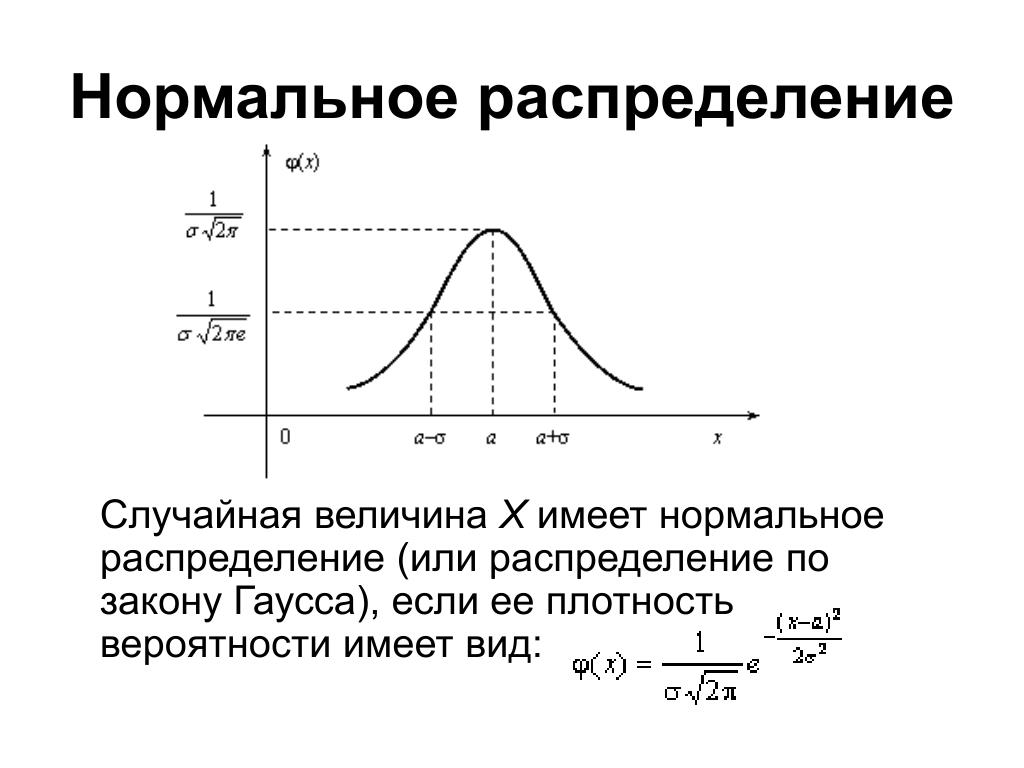 На нашем статистическом языке медиана — это 50-й процентиль и Q 1 .
занимает 25-е место, а Q 3 — 75-е. Хорошее объяснение содержится в упр. 2,6
и 2.7 на стр. 89.
На нашем статистическом языке медиана — это 50-й процентиль и Q 1 .
занимает 25-е место, а Q 3 — 75-е. Хорошее объяснение содержится в упр. 2,6
и 2.7 на стр. 89.
Индекс
Нормальное распределение | Определение, примеры, графики и факты
нормальное распределение
Просмотреть все СМИ
- Связанные темы:
- функция распределения стандартное нормальное распределение
Просмотреть весь связанный контент →
нормальное распределение , также называемое распределением Гаусса , наиболее распространенная функция распределения для независимых, случайно сгенерированных переменных. Его знакомая колоколообразная кривая повсеместно используется в статистических отчетах, от анализа опросов и контроля качества до распределения ресурсов.
График нормального распределения характеризуется двумя параметрами: средним, или средним значением, которое является максимумом графика и относительно которого график всегда симметричен; и стандартное отклонение, которое определяет степень отклонения от среднего значения.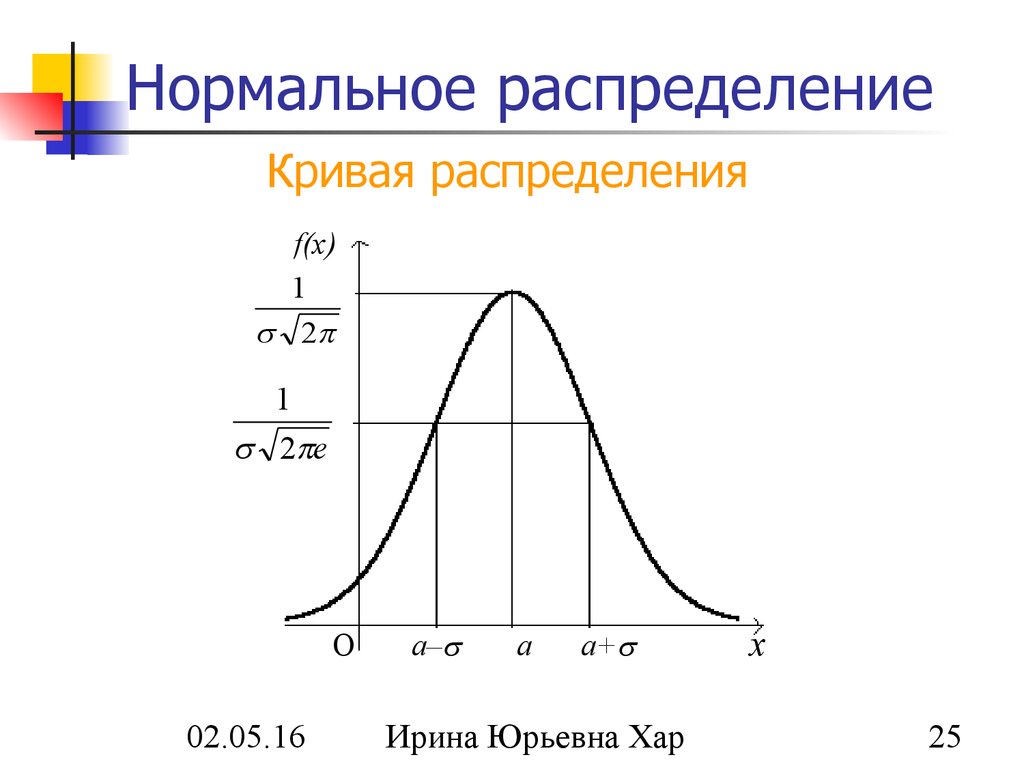 Небольшое стандартное отклонение (по сравнению со средним) дает крутой график, тогда как большое стандартное отклонение (опять же по сравнению со средним) дает плоский график. См. рисунок.
Небольшое стандартное отклонение (по сравнению со средним) дает крутой график, тогда как большое стандартное отклонение (опять же по сравнению со средним) дает плоский график. См. рисунок.
Нормальное распределение получается функцией нормальной плотности, p ( x ) = e − ( x — μ) 2 /2σ 2 /σКвадратный корень из √2π. В этой экспоненциальной функции e — это константа 2,71828…, это среднее значение, а σ — это стандартное отклонение. Вероятность попадания случайной величины в любой заданный диапазон значений равна доле площади, заключенной под графиком функции между заданными значениями и над осью х . Поскольку знаменатель (σквадратный корень из √2π), известный как нормирующий коэффициент, приводит к тому, что общая площадь, заключенная в графике, точно равна единице, вероятности могут быть получены непосредственно из соответствующей площади, т. е. площадь 0,5 соответствует вероятность 0,5.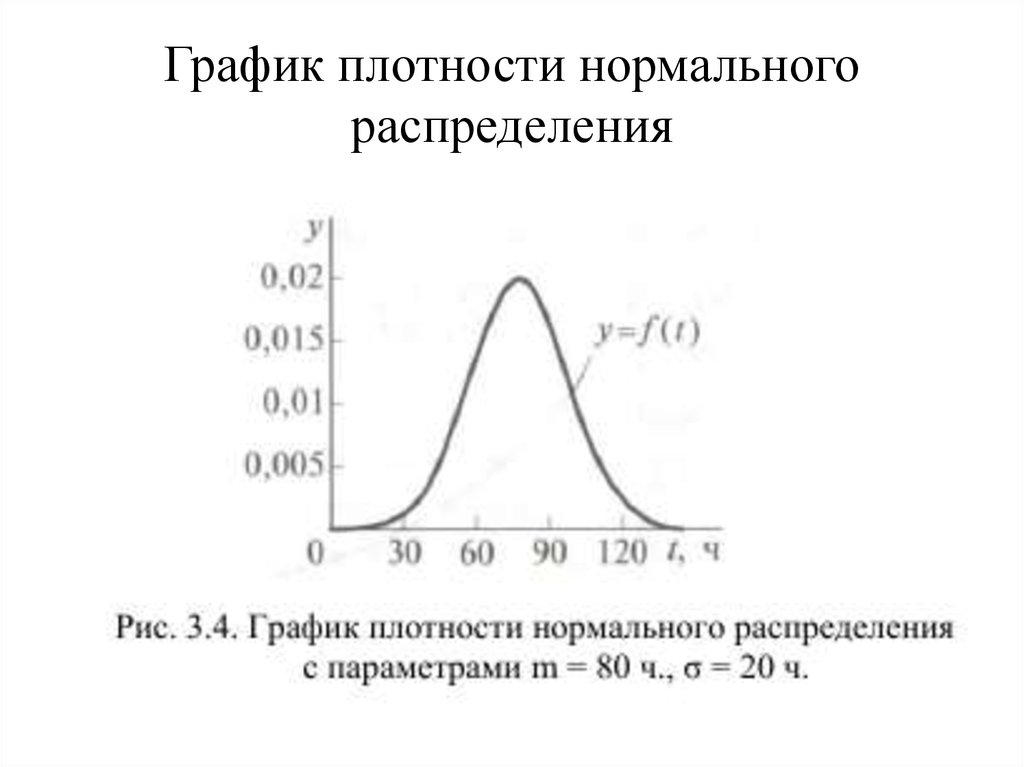 Хотя эти площади можно определить с помощью вычислений, таблицы были созданы в 19 веке.го века для особого случая = 0 и σ = 1, известного как стандартное нормальное распределение, и эти таблицы можно использовать для любого нормального распределения после соответствующего масштабирования переменных путем вычитания их среднего значения и деления на их стандартное отклонение, ( x − μ)/σ. Калькуляторы почти исключили использование таких таблиц. Для получения дополнительной информации см. теория вероятностей.
Хотя эти площади можно определить с помощью вычислений, таблицы были созданы в 19 веке.го века для особого случая = 0 и σ = 1, известного как стандартное нормальное распределение, и эти таблицы можно использовать для любого нормального распределения после соответствующего масштабирования переменных путем вычитания их среднего значения и деления на их стандартное отклонение, ( x − μ)/σ. Калькуляторы почти исключили использование таких таблиц. Для получения дополнительной информации см. теория вероятностей.
Термин «распределение Гаусса» относится к немецкому математику Карлу Фридриху Гауссу, который впервые разработал двухпараметрическую экспоненциальную функцию в 1809 году.в связи с исследованиями ошибок астрономических наблюдений. Это исследование привело Гаусса к формулировке закона ошибки наблюдения и развитию теории приближения методом наименьших квадратов. Другое известное раннее применение нормального распределения было сделано британским физиком Джеймсом Клерком Максвеллом, который в 1859 году сформулировал свой закон распределения молекулярных скоростей, позже обобщенный как закон распределения Максвелла-Больцмана.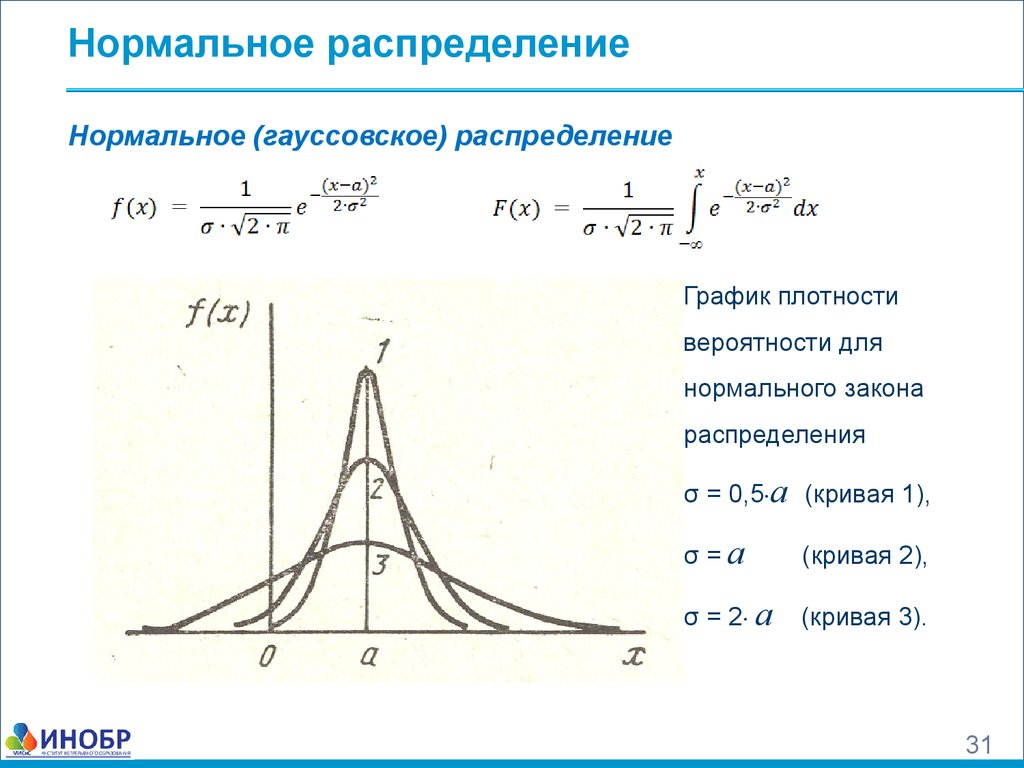

 0239
0239 1664
1664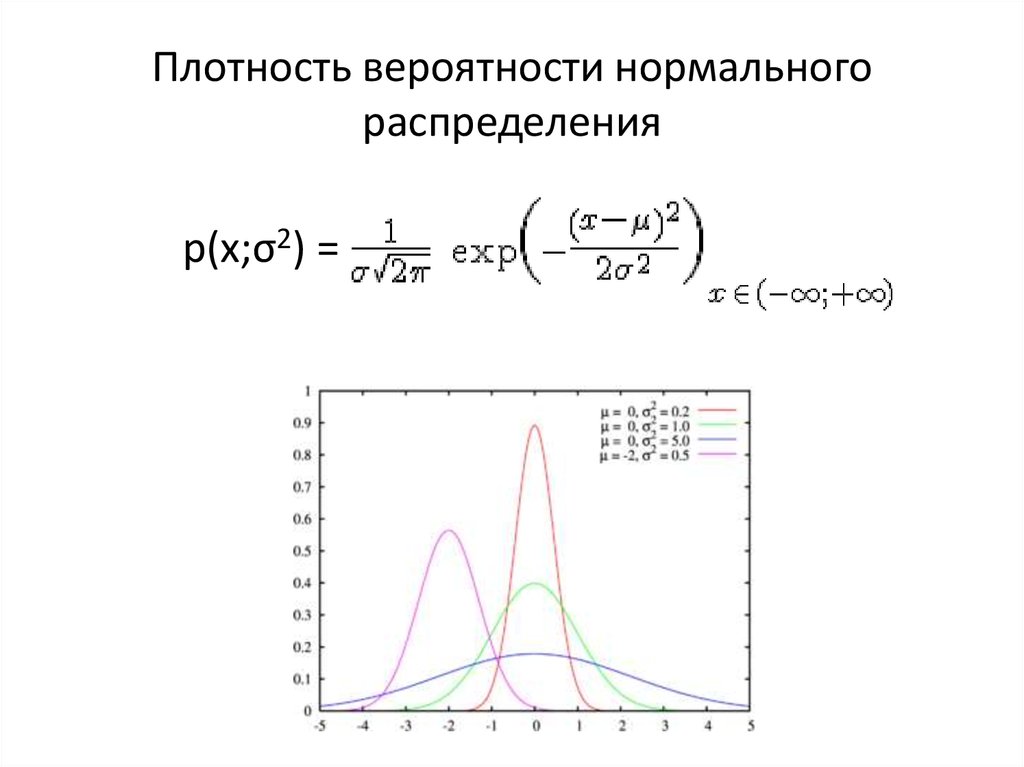 2881
2881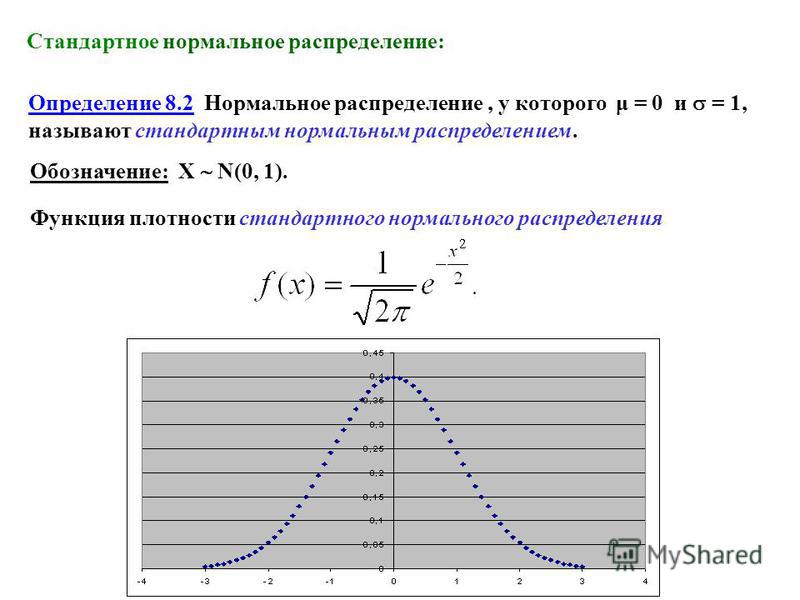 3810
3810 4394
4394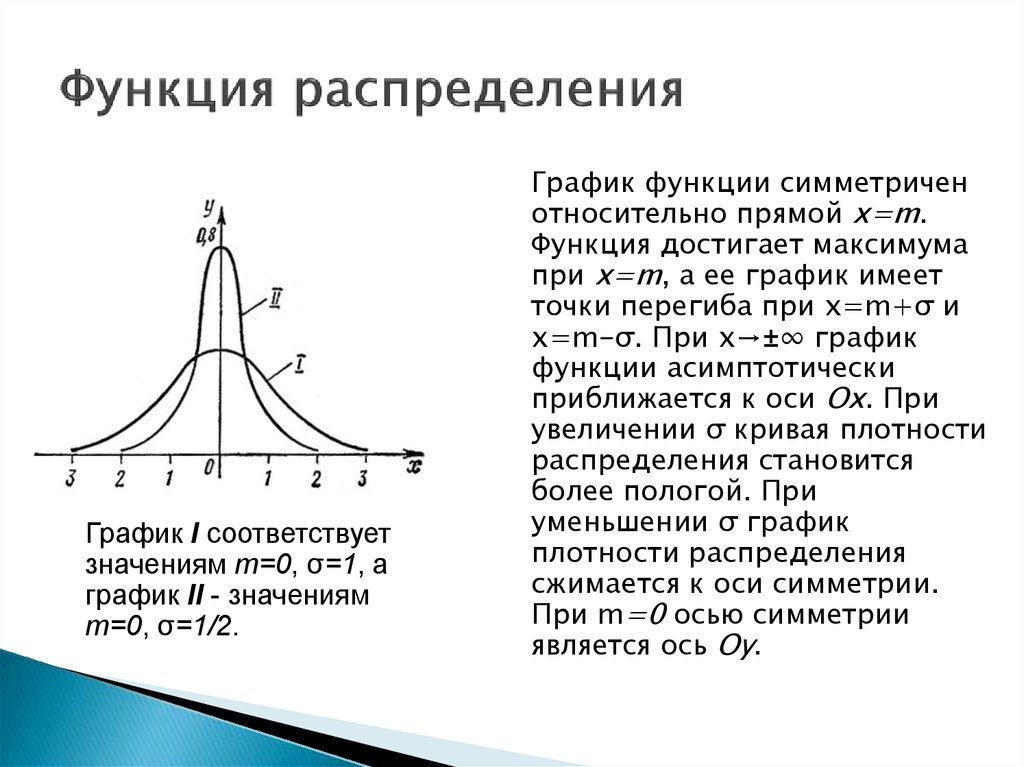 4726
4726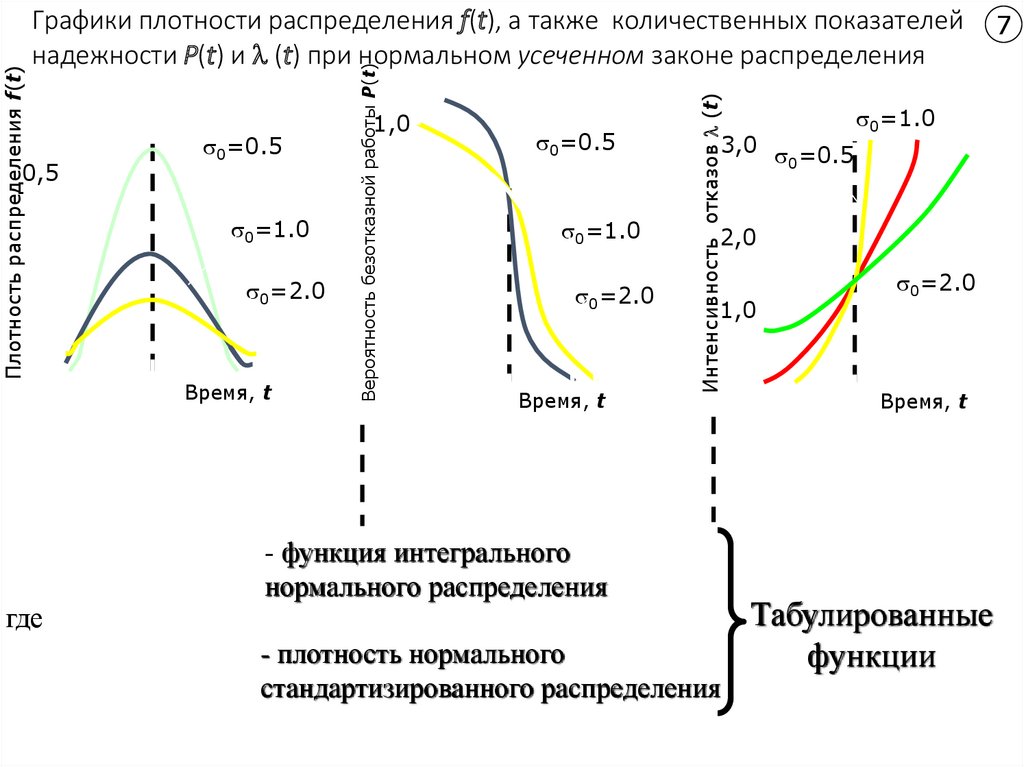 3
3 4962
4962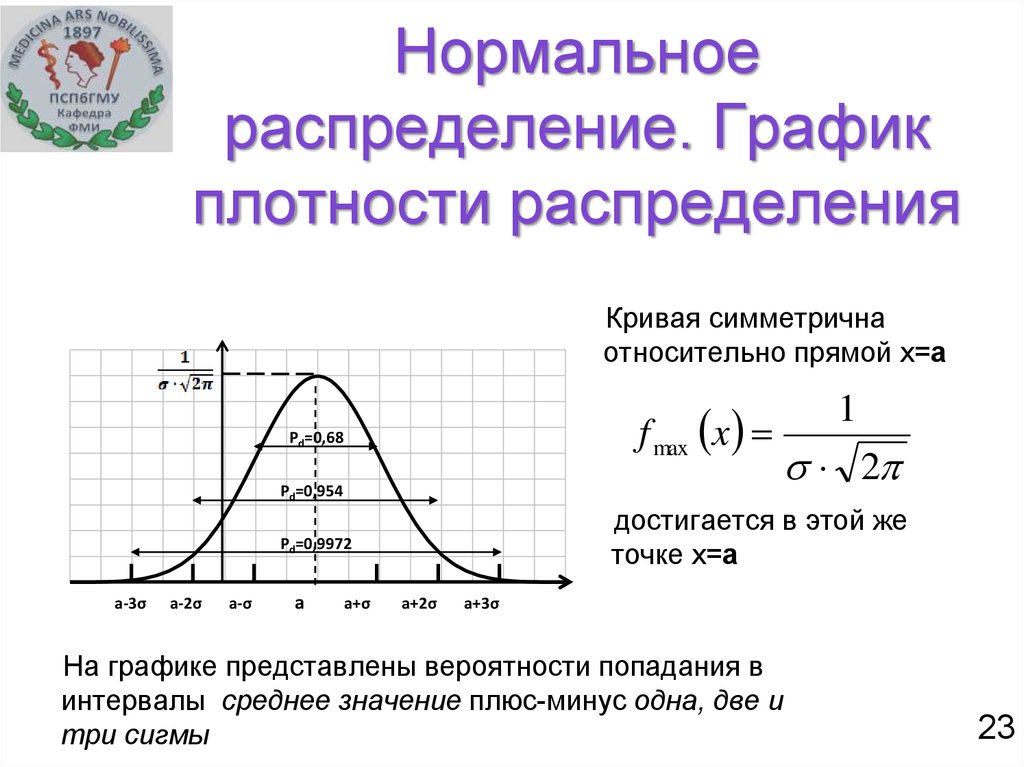 4988
4988