Как видим, Wolfram|Alpha не только вычисляет определенный интеграл, но и выводит его геометрическую интерпретацию.
Обратите внимание, что при вычислении интеграла в Wolfram|Alpha не обязательно указывать дифференциал переменной интегрирования (dx). Как это было сделано в первом примере. Wolfram|Alpha и без этого прекрасно понимает, что имеется в виду, когда получает запрос integrate. Однако, при вычислении интегралов «вручную», отсутствие dx в подинтегральном выражении считается грубой ошибкой. Поэтому, правильнее будет все же использовать dx. Особенно, если подинтегральная функция содержит другие буквы, кроме «x».
- integrate sinx dx, x=0..pi
Но все же для Wolfram|Alpha указание dx в подинтегральном выражении не обязательно, если только вы явно указываете для какой переменной устанавливаются пределы интегрирования. Сравните, например, два таких интеграла:
- integrate t/x, x=1..e
- integrate t/x, t=1.
Wolfram|Alpha легко вычисляет определенные интегралы, которые интегрируются «по частям»:
- integrate xcosx dx, x=0..pi/3
Не составляют проблемы и более сложные интегралы от тригонометрических функций:
Начнем с построения простого 2-мерного графика: plot sin(sqrt(7)x)+19cos(x) для x от -20 до 20
Если заменить 7 на (-7), то получим графики действительной и мнимой частей функции: plot sin(sqrt(-7)x)+19cos(x) для x от -5 до 5
В двух предыдущих примерах мы задавали область значений аргумента х. А что будет, если не задавать область значений х?
Одной из уникальных особенностей Wolfram | Alpha является автоматический выбор подходящего диапазона х для построения графиков функций одной и двух переменных, например, как при построении графика этой функции, содержащей функции Бесселя:
Обращаясь к Wolfram | Alpha, чтобы построить график функции, мы всегда используем префикс plot. Если же мы введем какое-либо одномерное выражение без префикса plot, то получим кроме графика функции в прямоугольных декартовых координатах, еще и много других сведений об этой функции.
Во всех рассмотренных выше примерах Wolfram | Alpha строил также и контурные графики (линии уровня) в дополнение к трехмерным графикам (поверхностям). Чтобы увидеть связь между трехмерными и контурными графиками, нужно нажать кнопку «Show contour lines”. Отметим, что и трехмерные и контурные графики используют один и тот же диапазон аргументов.
Все трехмерные графики строятся с помощью функции plot3d системы Mathematica. Контурные графики были сделаны с помощью ContourPlot. В обоих случаях, чтобы увидеть код системы Mathematica для генерации изображения нужно нажать ссылку Copyable planetext в левом нижнем углу нужного изображения.
Свойство | Вольфрам |
Атомный номер | |
Атомная масса | 183,85 |
Группа | |
Период | |
Электронное строение | 4f14 5d4 6s2 |
Электроотрицательность | 2,36 |
Плотность при 20°С, г/cм3 | 19,3 |
Температура плавления, °С | |
Температура кипения, °С | |
Характерные степени окисления | +6 |
Цвет элемента | Серо-белый бл. |
Вольфрам — химический элемент VI группы периодической системы, атомный номер 74, атомная масса 183,85. В буквальном переводе название «вольфрам» означает «волчья пена». Происхождение названия связано со следующим явлением: если в оловянной руде находятся соединения, содержащие вольфрам, количество получаемого олова значительно уменьшается, вольфрам «съедает» олово, как волк овцу. Минералы, содержащие вольфрам, имеют большой вес. По этой причине один из таких минералов получил название «тунгстен» — «тяжелый камень». Во Франции и Англии этим названием обозначается и сам вольфрам.
Историческая справка.
Вольфрам является одним из наиболее популярных цветных металлов. Вольфрам — довольно редкий химический элемент — его содержание в земной коре оценивается в 0,0055%, тугоплавкий металл светло-серого цвета, применяемый в различных сплавах. Минералы этого элемента были открыты задолго до самого вольфрама. В XVII столетии вольфрамом или тунгстеном называли наиболее распространенные минералы этого элемента, которые в будущем получили название вольфрамита и шеелита.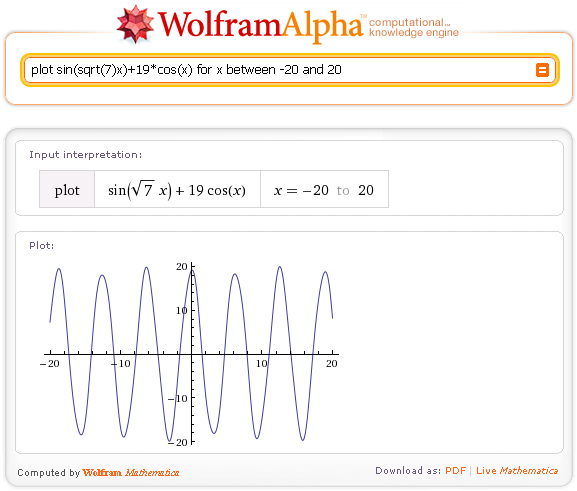
Вольфрам был открыт знаменитым шведским химиком Карлом Шееле. Аптекарь по профессии, Шееле в своей маленькой лаборатории провел много замечательных исследований. Он открыл кислород, хлор, барий, марганец. Незадолго до смерти, в 1781 году, Шееле — к этому времени уже член Стокгольмской Академии наук — обнаружил, что минерал тунгстен (впоследствии названный шеелитом) представляет собой соль неизвестной тогда кислоты. Вольфрам был открыт и выделен им в виде вольфрамового ангидрида позднее названного шеелитом WO3 в 1781. Спустя два года в 1783 году испанские химики братья д’Элуяр, работавшие ранее под руководством Шееле, выделили WO3 из минерала вольфрамита и, восстановив WO3 углеродом, впервые получили сам металл, названный ими Вольфрамом — которому суждено было произвести переворот в промышленности. Однако это произошло через целое столетие. Минерал же вольфрамит был известен еще Агриколе (16 в.) и называется у него «Spuma lupi» — волчья пена.
После своего открытия, вольфрам получил широкое практическое применение в виде легирующей добавки.
На всемирной металлургической выставке в Париже в 1900 году были впервые продемонстрированы новые экземпляры быстрорежущей стали (сплава с вольфрамом). После этого вольфрам стал широко использоваться в металлургической промышленности всех развитых стран. Однако существует интересный факт: вольфрамовая сталь была впервые изобретена именно в России – в 1865 году на уральском Мотовилихском заводе.
В начале XX в. вольфрамовую нить стали применять в электрических лампочках: она позволяет доводить накал до 2200°C и обладает большой светоотдачей. И в этом качестве вольфрам незаменим до наших дней.
10.02.2012, Пт, 15:02, Мск , Текст: Сергей Попсулин Сервис машинного знания Wolfram Alpha обзавелся платными аккаунтами. Их владельцам будет предоставлено множество дополнительных инструментов, включая возможность анализа файлов и изображений.
Создатель Wolfram Alpha британский ученый-математик Стивен Вольфрам (Stephen Wolfram) объявил о запуске версии Pro своего сервиса, который он называет машинной базой знаний.
Открытый в мае 2009 г. веб-сервис Wolfram Alpha представляет собой подобие поисковой системы, однако принцип его работы несколько иной. Он выдает не ссылки на релевантные сайты, которые содержат необходимую информацию, а непосредственно ответы.
Вопросы при этом могут касаться самых разных областей, причем как сфер жизни, так и научных дисциплин. На официальном сайте Wolfram Alpha в примерах указано 30 разделов, по которым пользователь может задавать вопросы, включая людей, историю, географию, физику, химию, материаловедение, фондовые рынки, музыку, спорт, финансы и т.д.
Также возможны вопросы на сравнение. Например, пользователь может попросить сравнить личный капитал Билла Гейтса и Уоррена Баффета. В этом случае достаточно ввести в поисковую строку «net worth bill gates vs warren buffet». В дополнение к текущим значениям система представит графики изменения накоплений с течением времени.
Кроме текстовых запросов, пользователь может вводить математические выражения, и Wolfram Alpha будет их вычислять.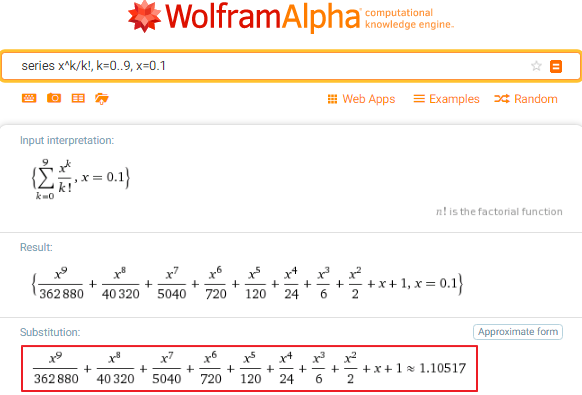
База знаний системы достаточно широкая, особенно в научной сфере. Например, ее можно спрашивать о каких-то редких растениях и животных.
Суть нововведения — Wolfram Alpha Pro — заключается в появлении новых способов ввода и вывода данных.
Функция анализа изображения, реализованная Wolfram Alpha
В дополнение к текстовым запросам и математическим выражениям версия Pro позволяет загружать для анализа различные документы с компьютера (в том числе созданные в специализированных программах), изображения и звуковые файлы. Также появилась возможность более широкого анализа данных. Например, пользователь может спросить о стоимости определенных строительных материалов в различных городах.
Функция анализа аудиофайла
Данные теперь могут выводиться в более сложном виде, включая 3D-графику, которой можно манипулировать.
Клавиатура со спецсимволами
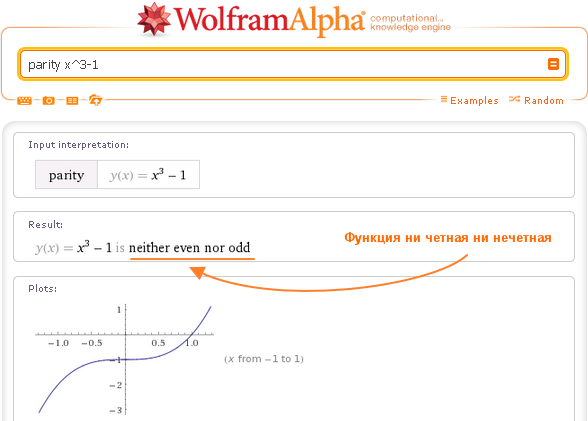
В дополнение к новым способам ввода и вывода данных Wolfram Alpha Pro запоминает историю запросов пользователя и позволяет настроить систему под себя, например, указать предпочитаемую систему измерения.
Также пользователю стали доступны новые инструменты: функция локального сохранения результатов в виде файла и экранная клавиатура со спецсимволами. Наконец, владельцу платного аккаунта предоставляется дополнительное машинное время, которое уходит на поиск ответов.
Стоимость версии Pro составляет $4,99 в месяц или $2,99 для учащихся. Также доступна возможность бесплатного ознакомления со всеми возможностями системы в течение определенного срока.
Создатель веб-сервиса Стивен Вольфрам называет сегодняшние изменения самыми масштабными нововведениями в истории движка. По его словам, целью проекта является предоставление справочной и аналитической информации, и в конечном счете система должна давать точный ответ практически на любой вопрос.
Добавим, что сервисом Wolfram Alpha пользуется функция голосового управления Siri на iPhone 4S. По информации The New York Times, четверть всех запросов, которые обрабатывает система, поступают от владельцев «яблочных» смартфонов.
Wolfram mathematica как пользоваться, вольфрам альфа построить график онлайн.
Wolfram mathematica как пользоваться, вольфрам альфа построить график онлайн Решение систем уравненийИнтеллектуальный «движек вычисления знаний». В отличие от традиционных поисковиков, которые выдают ссылки на различные сайты, сервис Wolfram Alpha самостоятельно анализирует запросы пользователя и представляет ему релевантную информацию.
Wolfram Alpha ответит на все вопросы
Например, если в качестве поискового запроса ввести название какого-либо населенного пункта, то пользователю будет показано количество его жителей, расположение на карте, погода, местное время, названия близлежащих крупных городов и т.д. Все эти данные можно закачать на ПК в виде PDF-документа.
Также Wolfram Alpha предназначен для использования в научных целях. Введя название какого-либо вида животного или растительного мира, можно получить множество различных научных данных о нем. Кроме того, сервис можно использовать для анализа различных трендов и множества других целей.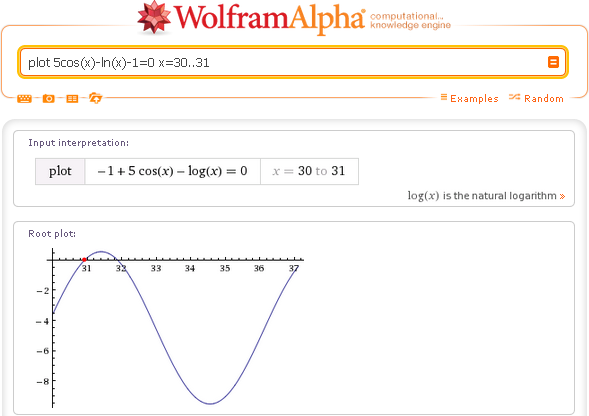
В принципе, Wolfram Alpha можно назвать поисковиком. Ведь он действительно ищет информацию, обрабатывая пользовательский запрос. Однако результаты поиска у Wolfram Alpha и, например, Google отличаются как небо и земля, не смотря на Альфа версию сервиса и относительно малую базу, которой обладает Wolfram Alpha , сервис может заинтересовать пользователя некоторыми фишками которые он предоставляет в результате запроса к нему.
И естественно поисковая выдача Wolfram Alpha сильно отличается от привычных нам поисковиков (Google, Яндекс и т.
д.) в ней нет всем привычных ссылок. Система обрабатывает поступившие данные и, используя миллионы алгоритмов, формулирует свой собственный ответ на поставленный вопрос. В итоге пользователь видит этот самый ответ, который, возможно, состоит всего лишь из пары слов или цифр – как раз то, что нам порой требуется.
Например, можно спросить: “Сколько певице Мадонне?”. Я написал просто
В ответ система сообщаетт возраст с точностью до дня.
увы Wolfram Alpha не знает всех знаменитостей, но надеюсь что узнает.
Функционал Wolfram Alpha не ограничивается лишь поиском ответов на поставленные вопросы. С помощью этой системы можно, например, строить графики и сопоставлять различные данные, что намного наглядней и лучше воспринимается, чем просто текст. Кроме того, с помощью Wolfram Alpha можно производить математические операции, как элементарные (которые без проблем выполняет и Google), так и решать уравнения различной сложности. Также Wolfram Alpha умеет строить графики функций, вычислять значения синуса или косинуса и так далее.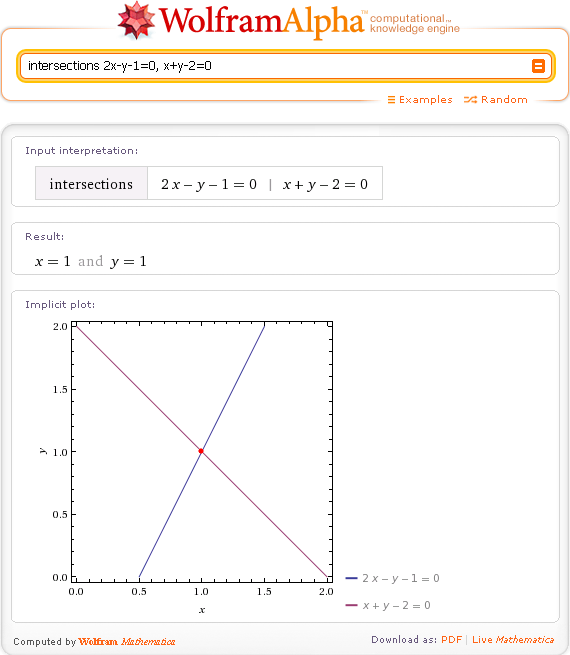
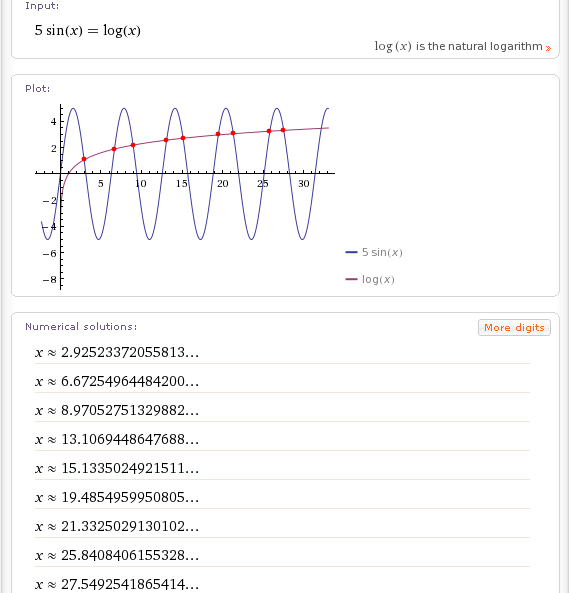
Например можно решить вот такое уровнение:
а вот например можно узнать какое растояние между Москвой и Тель-Авивом, я ввёл в поле
Moscow to Tel Aviv
И вот вам результат:
Один из минусов сервиса Wolfram Alpha – это его англоязычность…так что если хотите задать вопрос системе придется писать его на английском языке. Даже неизвестно, появится ли русскоязычная версия этой поисково-вычислительной системы.
В июле 2020 года NASA запускает экспедицию на Марс. Космический аппарат доставит на Марс электронный носитель с именами всех зарегистрированных участников экспедиции.
Регистрация участников открыта. Получите свой билет на Марс по этой ссылке .
Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.
Один из этих вариантов кода нужно скопировать и вставить в код вашей веб-станицы, желательно между тегами
и или же сразу после тега .
Подключить MathJax проще всего в Blogger или WordPress: в панели управления сайтом добавьте виджет, предназначенный для вставки стороннего кода JavaScript, скопируйте в него первый или второй вариант кода загрузки, представленного выше, и разместите виджет поближе к началу шаблона (кстати, это вовсе не обязательно, поскольку скрипт MathJax загружается асинхронно). Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.
Очередной канун Нового Года… морозная погода и снежинки на оконном стекле… Все это побудило меня вновь написать о.
.. фракталах, и о том, что знает об этом Вольфрам Альфа. По этому поводу есть интересная статья , в которой имеются примеры двумерных фрактальных структур. Здесь же мы рассмотрим более сложные примеры трехмерных фракталов.
Фрактал можно наглядно представить (описать), как геометрическую фигуру или тело (имея ввиду, что и то и другое есть множество, в данном случае, множество точек), детали которой имеют такую же форму, как и сама исходная фигура. То есть, это самоподобная структура, рассматривая детали которой при увеличении, мы будем видеть ту же самую форму, что и без увеличения. Тогда как в случае обычной геометрической фигуры (не фрактала), при увеличении мы увидим детали, которые имеют более простую форму, чем сама исходная фигура. Например, при достаточно большом увеличении часть эллипса выглядит, как отрезок прямой. С фракталами такого не происходит: при любом их увеличении мы снова увидим ту же самую сложную форму, которая с каждым увеличением будет повторяться снова и снова.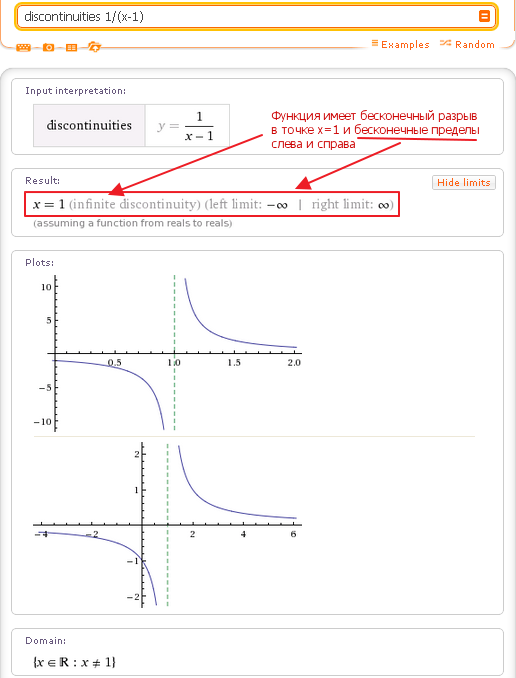
Бенуа Мандельброт (Benoit Mandelbrot), основоположник науки о фракталах, в своей статье Фракталы и искусство во имя науки написал: «Фракталы — это геометрические формы, которые в равной степени сложны в своих деталях, как и в своей общей форме. То есть, если часть фрактала будет увеличена до размера целого, она будет выглядеть, как целое, или в точности, или, возможно, с небольшой деформацией».
Integration is an important tool in calculus that can give an antiderivative or represent area under a curve.
The indefinite integral of `f(x)`
, denoted `int f(x)\ dx`
, is defined to be the antiderivative of `f(x)`
. In other words, the derivative of `int f(x)\ dx`
is `f(x)`
. Since the derivative of a constant is zero, indefinite integrals are defined only up to an arbitrary constant. For example, `int sin(x)\ dx = -cos(x) + «constant»`
, since the derivative of `-cos(x) + «constant»`
is `sin(x)`
. The definite integral of `f(x)`
from `x = a`
to `x = b`
, denoted `int_(a)^(b) f(x)\ dx`
, is defined to be the signed area between `f(x)`
and the `x` axis
, from `x = a`
and `x = b`
.
(pi) sin(x)\ dx = (-cos(pi))-(-cos(0)) = 2`
. Sometimes an approximation to a definite integral is desired. A common way to do so is to place thin rectangles under the curve and add the signed areas together. Wolfram|Alpha can solve a broad range of integrals.
How Wolfram|Alpha calculates integrals
Wolfram|Alpha computes integrals differently than people. It calls Mathematica»s Integrate function, which represents a huge amount of mathematical and computational research. Integrate doesn»t do integrals the way people do. Instead, it uses powerful, general algorithms that often involve very sophisticated math. There are a couple of approaches that it most commonly takes. One involves working out the general form for an integral, then differentiating this form and solving equations to match undetermined symbolic parameters. Even for quite simple integrands, the equations generated in this way can be highly complex and require Mathematica»s strong algebraic computation capabilities to solve.
Another approach that Mathematica uses in working out integrals is to convert them to generalized hypergeometric functions, then use collections of relations about these highly general mathematical functions.
While these powerful algorithms give Wolfram|Alpha the ability to compute integrals very quickly and handle a wide array of special functions, understanding how a human would integrate is important too. As a result, Wolfram|Alpha also has algorithms to perform integrations step by step. These use completely different integration techniques that mimic the way humans would approach an integral. This includes integration by substitution, integration by parts, trigonometric substitution, and integration by partial fractions.
| + | сложение | ||||||||||||||||||||||||||||||||||||
| — | вычитание | ||||||||||||||||||||||||||||||||||||
| * | умножение | ||||||||||||||||||||||||||||||||||||
| / | деление | ||||||||||||||||||||||||||||||||||||
| ^ | возведение в степень | ||||||||||||||||||||||||||||||||||||
| solve | решение уравнений, неравенств, систем уравнений и неравенств | ||||||||||||||||||||||||||||||||||||
| expand | раскрытие скобок | ||||||||||||||||||||||||||||||||||||
| factor | разложение на множители | ||||||||||||||||||||||||||||||||||||
| sum | вычисление суммы членов последовательности | ||||||||||||||||||||||||||||||||||||
| derivative | дифференцирование (производная) | ||||||||||||||||||||||||||||||||||||
| integrate | интеграл | ||||||||||||||||||||||||||||||||||||
| lim | предел | ||||||||||||||||||||||||||||||||||||
| inf | бесконечность | ||||||||||||||||||||||||||||||||||||
| plot | построить график функции | ||||||||||||||||||||||||||||||||||||
| log (a , b ) | логарифм по основанию a числа b | ||||||||||||||||||||||||||||||||||||
| sin, cos, tg, ctg | синус, косинус, тангенс, котангенс | ||||||||||||||||||||||||||||||||||||
| sqrt | корень квадратный | ||||||||||||||||||||||||||||||||||||
| pi | число «пи» (3,1415926535. 2), {x, 0.5, 2} В июле 2020 года NASA запускает экспедицию на Марс. Космический аппарат доставит на Марс электронный носитель с именами всех зарегистрированных участников экспедиции. Регистрация участников открыта. Получите свой билет на Марс по этой ссылке . Один из этих вариантов кода нужно скопировать и вставить в код вашей веб-станицы, желательно между тегами и или же сразу после тега . По первому варианту MathJax подгружается быстрее и меньше тормозит страницу. Зато второй вариант автоматически отслеживает и подгружает свежие версии MathJax. Если вставить первый код, то его нужно будет периодически обновлять. Если вставить второй код, то страницы будут загружаться медленнее, зато вам не нужно будет постоянно следить за обновлениями MathJax. Подключить MathJax проще всего в Blogger или WordPress: в панели управления сайтом добавьте виджет, предназначенный для вставки стороннего кода JavaScript, скопируйте в него первый или второй вариант кода загрузки, представленного выше, и разместите виджет поближе к началу шаблона (кстати, это вовсе не обязательно, поскольку скрипт MathJax загружается асинхронно). Очередной канун Нового Года… морозная погода и снежинки на оконном стекле… Все это побудило меня вновь написать о… фракталах, и о том, что знает об этом Вольфрам Альфа. По этому поводу есть интересная статья , в которой имеются примеры двумерных фрактальных структур. Здесь же мы рассмотрим более сложные примеры трехмерных фракталов. Фрактал можно наглядно представить (описать), как геометрическую фигуру или тело (имея ввиду, что и то и другое есть множество, в данном случае, множество точек), детали которой имеют такую же форму, как и сама исходная фигура. То есть, это самоподобная структура, рассматривая детали которой при увеличении, мы будем видеть ту же самую форму, что и без увеличения. Тогда как в случае обычной геометрической фигуры (не фрактала), при увеличении мы увидим детали, которые имеют более простую форму, чем сама исходная фигура. Бенуа Мандельброт (Benoit Mandelbrot), основоположник науки о фракталах, в своей статье Фракталы и искусство во имя науки написал: «Фракталы — это геометрические формы, которые в равной степени сложны в своих деталях, как и в своей общей форме. То есть, если часть фрактала будет увеличена до размера целого, она будет выглядеть, как целое, или в точности, или, возможно, с небольшой деформацией». Wolfram alpha синтаксис. Wolfram mathematica как пользоваться, вольфрам альфа построить график онлайн. Вычисление определенного интегралаПосле непосредственного проведения КР эксперимента необходимо извлечь информацию из полученных данных не только качественно, но также и количественно. Для этого обычно применяются такие программные пакеты как PeakFit, Origin и другие. Преимущество этого программного пакета заключается в именно пакетной обработке данных, то есть в возможности обрабатывать последовательно, с помощью одного заданного начального условия, сразу большое количество файлов с данными эксперимента при разных внешних параметрах (температуре, давлении). Для удобства и точности подгонки, полученные подогнанные данные одного спектра одновременно являются начальными для следующего. Для удобства и исключения каких либо неясностей при пакетной обработке спектров, в программе из имени файла считывается внешний параметр (температура, давление). Оно должно быть специфично — содержать в себе температуру в кельвинах, при которой был проведен данный эксперимент. Само имя файла следует разбить на несколько частей, например с помощью символа «_». Пример текста программы, написанной в Wolfram Mathematica, для обработки данных КР: При обработке спектров важную роль играет выбор модели для подгонки контуров. *При использовании в вычислениях физических констант нет необходимости вводить их численное значение. Достаточно в начале программы подключить пакет Physical Constants используя следующую запись: Самой распространенной и используемой во многих работах, ввиду универсальности, является модель Лоренца. Однако при описании низкочастотного диапазона спектра рекомендуется пользоваться функцией подгонки Harmonic (функция затухающего гармонического осциллятора). Кроме того, при работе с функцией Harmonic нет необходимости отдельно учитывать температурный фактор Бозе – Эйнштейна, ввиду того, что он является одним из составляющих этой функции. Ниже мы опишем два примера программы с использованием моделей для подгонки Harmonic и Lorentz: 1. Пример текста программы с использованием модели подгонки спектров Harmonic: Полный текст программы: Описание работы программы по шагам: Задаем (MyPath) и выбираем(SetDirectory) директорию, в которой хранится папка с нужными нам файлами с экспериментальными данными Выбираем тип и расширение файлов (*. Формируем форму вывода в файл Здесь задаем модель для подгонки. Условие If присутствует вследствие того, что для функции Harmonic существует два варианта (для стоксовой и антистоксовой компоненты) Задаем начальные данные для подгонки первого спектра i1, v1,w1 – интенсивность, частота и ширина первой линии соответственно i2, v2,w2 – интенсивность, частота и ширина второй линии соответственно c, b – параметры базовой линии (наклон и уровень по оси Oy). Значения Sfrom, Sto, Szero определяют Sfrom и Sto – вырезают частотный интервал для подгонки (в данном случае это 0 – 130 cm -1) Szero – значение на оси ординат, на котором закреплена ось абсцисс. ……- начало цикла — окончание цикла В данном случае в цикле участвуют файлы с 1 по 100. В этой строке происходит разбор имени файла на элементы (с помощью двух функций ToExpression и StringSplit) и считывание значения переменной T (температура, давление) из имени файла (iName). Вывод значения T. Считывание данных из выбранного файла с помощью функции ReadList и присвоение им имени FullData. Выбираем нужный нам диапазон данных с помощью функции Select и присваиваем ему имя Data. Функция FindFit является базовой функцией подгонки в Wolfram Mathematica. Максимальное число итераций – 5000. Вывод на экран исходных данных (Epilog-> Point ) функцией Plot, полученных линий в отдельности (условие If), подогнанного спектра (model/.fit) AxesOrigin – интервал значений по оси Ox PlotRange – интервал значений по оси Oy PlotStyle – совокупность параметров графика Axes->True – видимость осей Thickness – толщина линий AxesLabel – подписи по осям. Выделение подогнанных значений по точкам (функция Evaluate), соответственно данным из файла (iName). Вычисляем разницу между подогнанными значениями и экспериментальными данными. Вывод на экран значения Diff – погрешности подгонки (функция ListLinePlot) PlotRange – интервал значений по оси Ox AxesOrigin – точка пересечения осей FillingAxis – заполнение цветом области под графиком. Присвоение массиву подогнанных значений имени tmp. Дополнение массива ResultData массивом tmp на каждом шаге цикла (функция Append). Вывод на экран массива значений tmp. Окончание работы цикла. Вывод на экран полученных значений в табличной форме с помощью функции TableForm. 2. Пример текста программы с использованием модели подгонки спектров Lorentz: Программа, описанная в данном параграфе, по своей структуре практически полностью соответствует программе, описанной ранее, за исключением модели подгонки. Вследствие того, что при использовании модели подгонки Lorentz нужно отдельно учитывать температурный фактор Бозе — Эйнштейна, в тексте программы появился новый фрагмент. Задается массив чисел с именем BoseFactor. Он заполняется нулями, имеет два столбца и колличество строк такое же, как и у массива FullData. Задается массив элементов Eva1, который является фактором Бозе — Эйнштейна для стоксовой компоненты спектра (вычисляется для каждой точки массива FullData (массив экспериментальных данных)). Запись x-> FullData [] означает, что в выражении Eva1 переменная x принимает все значения первого столбца массива элементов FullData. Вычисляется массив с именем Diff1с помощью массива Eva1 (фактора Бозе — Эйнштейна). Данная запись означает, что второй столбец массива FullData поэлементно делится на массив факторов Бозе — Эйнштейна. — присвоение значений каждому столбцу массива BoseFactor. первый столбец равенпервому стобцу массива экспериментальных данных Fulldata. Второму столбцу присваивается значение Diff1. Diff1 имеет смысл интенсивности в каждой точке экспериментального спектра, домноженную на обратный температурный фактор Бозе — Эйнштейна. — выбор интересующего нас спектрального диапазона с помощью функции Select. Аналогичная строка присутствует и в тексте программы, представленной в П.1, но исходным массивом там служит массив экспериментальных данных FullData. Программа, описанная в данном разделе Wolfram AlphaWolfram Alpha – это система, предназначенная для хранения, обработки и выдачи пользователям структурированных данных по запросам на естественном английском языке. Wolfram Alpha не является поисковой системой. Это обусловлено тем, что она не предназначена для автоматической обработки неструктурированных текстов. Для ее работы необходимо предварительно вручную ввести фактографическую информацию в базу данных, а также разработать и реализовать алгоритмы ее обработки. Данные процедуры выполняются вручную сообществом разработчиков и экспертов системы Wolfram Alpha. Из анализа описания системы система Wolfram Alpha следует, что получения ответов система Wolfram Alpha должна: — уметь правильно разобрать запрос пользователя на естественном языке; — иметь соответствующую структурированную фактографическую информацию; — иметь алгоритмы обработки фактографической информации, обеспечивающие формирование ответа на запрос пользователя. Таким образом, система Wolfram Alpha автоматически способна обрабатывать только заранее структурированную вручную фактографическую информацию, хранящуюся в СУДБ. Для синтеза ответов могут использоваться детерминированные алгоритмы выборки дополнительной информации и проведения расчетов по фактографическим данным. По данным формальным признакам система Wolfram Alpha может быть отнесена к известному классу систем Business Intelligence. Системы данного класса являются узко специализированными, что обусловливает незначительный спектр вопросов, на которые можно получить ответы системы Wolfram Alpha. Данное ограничение является системным, так как заложено в концепцию ее функционирования. Таким образом, система Wolfram Alpha принципиально не позволяет пользователям искать ответы на любые интересующие их вопросы. Для этого предназначены вопросно-ответные поисковые системы. В отличие от системы Wolfram Alpha вопросно-ответные поисковые системы автоматически выявляют фактографическую информацию в обрабатываемых текстах и проводят ее индексацию без участия человека. 35 команд, которые наглядно покажут, в чем Wolfram Alpha круче GoogleМетодика сравнительного тестирования систем Wolfram Alpha и AskNet.ruДля проведения объективного тестирования системы Wolfram Alpha была взята коллекция вопросов дорожки вопросно-ответного поиска конференции TREC 2003 (http://trec. Результаты сравнительного тестирования систем Wolfram Alpha и AskNet.ruОбобщенные результаты сравнительного тестирования систем Wolfram Alpha и AskNet.ru представлены в таблице. Детальная информация по тестовым случаям приведена в приложении. Всего поведено тестовых случаев – 71. При анализе выдачи вопросно-ответной поисковой системы AskNet.ru проводился учет наличия и номера позиции правильного ответа. Среднее значение позиции правильного ответа на странице, если ответ был найден, составляет 1,63. Это означает, что в среднем правильный ответ находился в выдаче вопросно-ответной поисковой системы AskNet.ru на первом или на втором месте. Система Wolfram Alpha в 57 случаях не могла определить смысл запроса пользователя и выдавала сообщение «Wolfram Alpha isn’t sure what to do with your input». В трех тестовых случаях система Wolfram Alpha вывела диалог уточнения смыслового содержания введенного пользователем запроса. Сервис онлайн построения графиковЭтот сервис создан в помощь школьникам и студентам в изучении математики (алгебры и геометрии) и физики и предназначен для онлайн построения графиков функций (обычных и параметрических) и графиков по точкам (графиков по значениям), а также графиков функций в полярной системе координат. Просто введите формулу функции в поле «Графики:» и нажмите кнопку «Построить». WolframAlphaПочитайте в cправкe, как правильно вводить формулы функций. Загляните в раздел примеров, наверняка, там есть графики функций, похожие на то, что нужно Вам, останется только слегка откорректировать готовые формулы функций. Дополнительно на нашем сайте вы можете воспользоваться калькулятором матриц, с помощью которого можно производить различные преобразования и действия с матрицами онлайн. Список функций
Встроенные константыСкачать бесплатный Wolfram Mathematica 10. 0.2 для MS Windows 2000/XP/Vista/7/8Резонный вопрос — почему именно эта система? Потому, что принципы — это важно! Более чем 25-летнее развитие на основе смелых, инновационных дизайн-принципов, и как апофеоз — Wolfram Mathematica , мощнейшая вычислительная платформа. Автоматизация . Ключ ко всем продуктивным вычислениям. Принципиальное отличие Wolfram Mathematica — применение разумной автоматизации во всех без исключения частях, от выбора алгоритмов, до выведения графиков и построения пользовательских интерфейсов. Как итог — получение высококачественных итоговых результатов без необходимости алгоритмических знаний, плюс быстродействие даже при экспертном использовании. Интегрированная универсальная платформа . Специальные программы и добавочные тулбоксы мешают творческим разработкам новых идей и направлений, а их стоимость даже выше, чем их номинал. Для работы системы Wolfram Mathematica не нужно дополнительных пакетов, а значит и ненужных затрат. Гибридная символьно-численная методология . Wolfram AlphaОбычно символьные и численные вычисления считаются раздельными, а это — ущерб для пользователей. В системе Mathematica они оба тесно интегрированы, что позволяет делать построения гибридных методов для быстрого решения различных видов задач и при этом гарантирует результаты при сочетаний величин произвольных точностей. Мультипарадигмальный язык . Языков и стилей программирования много, однако ни один из них не подходит для всех задач идеально. Mathematica отличается от стандартных языков программирования одновременной поддержкой большого количества программных парадигм: процедурной, функциональной, основанной на правилах или шаблонах и многих других. Встроенная информация . Поиск различных данных в стандартных базах, а так же их постоянные обновления занимают массу времени и отвлекают от основной работы. Рабочий процесс с документацией . При обширных работах с электронной документацией возникает необходимость использования нескольких программ: для обработки, для визуализации, для интерактивного преподнесения… Система Mathematica включает в себя все элементы этого рабочего проекта, плюс интерактивные приложения — вместе, в уникально гибких документах. Математический процессор онлайн, процессор знаний, который по вашему запросу предоставляет данные об окружающем мире в числах. Работает все это с виду очень просто — вводишь свой запрос в поисковое поле, жмешь кнопку «=», получаешь результат: На самом деле, WolframAlpha предоставляет бесплатный и неограниченный доступ к своей базе знаний, которая включает огромное количество сведений о нашем мире в числовом измерении. Демография, экономика, история, лингвистика, физика, биология, химия. Для студентов, изучающих математику, WolframAlpha настоящая находка. Этот веб-сервис легко решает уравнения и системы, строит графики функций, вычисляет пределы, находит производные, берет интегралы… Похоже, трудно найти задачу, с которой WolframAlpha не сможет справиться. Надо только правильно сформулировать свой запрос. Кстати, хотя WolframAlpha использует специальный синтаксис, как и в других системах компьютерной математики, однако он неплохо понимает и обычные вопросы, заданные на обычном английском языке. Например, вы можете спросить у WolframAlpha: «How many students are in Russia now? » Вам интересно, что WolframAlpha ответит? Как пользоваться WolframAlpha? Краткое описание возможностей сервиса на русском языке можно . Чтобы детально познакомиться с WolframAlpha, и получше узнать, как использовать этот сервис для математических расчетов, стоит заглянуть на единственный веб-ресурс, где математические возможности WolframAlpha подробно, доступно и систематически описываются на русском языке — это блог Wolfram|Alpha по-русски . Поскольку математический движок WolframAlpha работает на основе алгоритмов известной системы компьютерной математики Mathametica, этим результатам можно полностью доверять. База знаний, из которой черпает свои способности WolframAlpha, постоянно пополняется актуальными материалами, фактическими и числовыми данными, алгоритмами — с каждым днем WolframAlpha становится «умнее»! Возможности этой системы лучше всего позволяют оценить многочисленные примеры ее использования из разных областей знания. Кроме всего прочего, WolframAlpha предлагает разнообразные математические продукты : здесь и бесплатные виджеты для сайтов, и недорогие мобильные математические приложения для установки на смартфоны студентов, надстройки и плагины для основных браузеров, инструменты для разработчиков и всякое такое. Например, для удобства использования вы можете вставить окно запроса Wolfram Alpha на свой сайт . Но если вы уже оценили возможности Wolfram Alpha, то наверняка захотите иметь этот инструмент всегда под рукой. С недавнего времени WolframAlpha начал использовать новый формат математических документов — CDF . Это формат, позволяющий создавать документы, содержащие интерактивные математические объекты. Например, в качестве таковых могут быть графики функций, дифференциальные уравнения и т.п. Параметры таких объектов пользователь может изменять при помощи встроенных в документ элементов управления, одновременно наблюдая происходящие изменения (похоже на Java-апплеты GeoGebra). На основе этого формата, а также виджетов Wolfram Alpha можно, например, создавать динамические иллюстрации математических правил и алгоритмов, проводить исследования, лабораторные занятия по математике. Познакомьтесь с Wolfram Alpha немедленно, если вы уже не сделаии этого ранее! В июле 2020 года NASA запускает экспедицию на Марс. Регистрация участников открыта. Получите свой билет на Марс по этой ссылке . Один из этих вариантов кода нужно скопировать и вставить в код вашей веб-станицы, желательно между тегами и или же сразу после тега . По первому варианту MathJax подгружается быстрее и меньше тормозит страницу. Зато второй вариант автоматически отслеживает и подгружает свежие версии MathJax. Если вставить первый код, то его нужно будет периодически обновлять. Если вставить второй код, то страницы будут загружаться медленнее, зато вам не нужно будет постоянно следить за обновлениями MathJax. Подключить MathJax проще всего в Blogger или WordPress: в панели управления сайтом добавьте виджет, предназначенный для вставки стороннего кода JavaScript, скопируйте в него первый или второй вариант кода загрузки, представленного выше, и разместите виджет поближе к началу шаблона (кстати, это вовсе не обязательно, поскольку скрипт MathJax загружается асинхронно). Очередной канун Нового Года… морозная погода и снежинки на оконном стекле… Все это побудило меня вновь написать о… фракталах, и о том, что знает об этом Вольфрам Альфа. По этому поводу есть интересная статья , в которой имеются примеры двумерных фрактальных структур. Здесь же мы рассмотрим более сложные примеры трехмерных фракталов. Фрактал можно наглядно представить (описать), как геометрическую фигуру или тело (имея ввиду, что и то и другое есть множество, в данном случае, множество точек), детали которой имеют такую же форму, как и сама исходная фигура. То есть, это самоподобная структура, рассматривая детали которой при увеличении, мы будем видеть ту же самую форму, что и без увеличения. Тогда как в случае обычной геометрической фигуры (не фрактала), при увеличении мы увидим детали, которые имеют более простую форму, чем сама исходная фигура. Бенуа Мандельброт (Benoit Mandelbrot), основоположник науки о фракталах, в своей статье Фракталы и искусство во имя науки написал: «Фракталы — это геометрические формы, которые в равной степени сложны в своих деталях, как и в своей общей форме. То есть, если часть фрактала будет увеличена до размера целого, она будет выглядеть, как целое, или в точности, или, возможно, с небольшой деформацией». Интеллектуальный «движек вычисления знаний». В отличие от традиционных поисковиков, которые выдают ссылки на различные сайты, сервис Wolfram Alpha самостоятельно анализирует запросы пользователя и представляет ему релевантную информацию. Wolfram Alpha ответит на все вопросы Также Wolfram Alpha предназначен для использования в научных целях. Введя название какого-либо вида животного или растительного мира, можно получить множество различных научных данных о нем. Кроме того, сервис можно использовать для анализа различных трендов и множества других целей. В принципе, Wolfram Alpha можно назвать поисковиком. Ведь он действительно ищет информацию, обрабатывая пользовательский запрос. Однако результаты поиска у Wolfram Alpha и, например, Google отличаются как небо и земля, не смотря на Альфа версию сервиса и относительно малую базу, которой обладает Wolfram Alpha , сервис может заинтересовать пользователя некоторыми фишками которые он предоставляет в результате запроса к нему. И естественно поисковая выдача Wolfram Alpha сильно отличается от привычных нам поисковиков (Google, Яндекс и т.д.) в ней нет всем привычных ссылок. Система обрабатывает поступившие данные и, используя миллионы алгоритмов, формулирует свой собственный ответ на поставленный вопрос. В итоге пользователь видит этот самый ответ, который, возможно, состоит всего лишь из пары слов или цифр – как раз то, что нам порой требуется. Например, можно спросить: “Сколько певице Мадонне?”. Я написал просто В ответ система сообщаетт возраст с точностью до дня. увы Wolfram Alpha не знает всех знаменитостей, но надеюсь что узнает. Функционал Wolfram Alpha не ограничивается лишь поиском ответов на поставленные вопросы. С помощью этой системы можно, например, строить графики и сопоставлять различные данные, что намного наглядней и лучше воспринимается, чем просто текст. Кроме того, с помощью Wolfram Alpha можно производить математические операции, как элементарные (которые без проблем выполняет и Google), так и решать уравнения различной сложности. Например можно решить вот такое уровнение: а вот например можно узнать какое растояние между Москвой и Тель-Авивом, я ввёл в поле Moscow to Tel Aviv И вот вам результат: Один из минусов сервиса Wolfram Alpha – это его англоязычность…так что если хотите задать вопрос системе придется писать его на английском языке. Даже неизвестно, появится ли русскоязычная версия этой поисково-вычислительной системы. С помощью Wolfram Alpha можно сравнивать практически всё, нужно только ввести вопрос в поисковую строку: книги, комиксы, сериалы, фильмы и даже вымышленных персонажей — любые продукты поп-культуры. Это делается по стандартному запросу вида х vs y . Например, результат запроса AC/DC vs ABBA можно видеть на скриншоте выше. Вычисление параметров для настройки фотокамерыТем, кто использует фотоаппараты с достаточным количеством настроек (в том числе это касается смартфонов), часто требуется рассчитать значения тех или иных параметров: ISO, контрастности, яркости, фокусного расстояния и прочих. Разъяснение терминов семейного родстваК сожалению, работает только для английского языка. Но как просто: не нужно ничего выдумывать, стоит просто ввести нужную последовательность терминов: сестра двоюродного брата дяди отца. А система не только расскажет, кем приходится столь дальний родственник, но и представит информацию в виде простой схемы. Вычисление уровня алкоголя в кровиКонечно, приблизительно, но как ещё можно это вычислить без приборов? Поисковый запрос в данном случае будет выглядеть до смешного просто: «вес рост количество in время». Вес указывается в фунтах, рост — в дюймах. Под количеством выпитого нужно указать объём алкоголя в виде drinks, shots, pints — Wolfram Alpha сама прикинет, что вы пили и какой в этом градус. А после сообщит, через какое время алкоголь будет полностью выведен из организма. Конвертация размеров обувиСистема Wolfram Alpha способна моментально перевести данные из одной системы в другую. Подсчёт калорийC этой задачей система справляется до безобразия просто. Вводим количество и название продукта и получаем подробный отчёт о содержании калорий, белков, жиров, углеводов и даже витаминов. Названия продуктов, к сожалению, должны быть на английском языке — фразу «15 тарелок гречки с мясом» Wolfram Alpha не распознает. Популярность имёнВыбираете кличку для собаки? Можете использовать поисковый запрос вида «имя name». Система выдаст подробную информацию о том, насколько это имя популярно, где наиболее распространено и в каких годах чаще всего использовалось. Курсы валютКонечно, это знает каждый поисковик. Но не каждый с ходу выдаёт результат, какова текущая стоимость определённой суммы валюты той или иной страны. Настройка музыкального инструментаБольше не нужны тюнеры и отдельные приложения для настройки инструментов. Wolfram Alpha позволяет просто ввести нужную ноту, например , и прослушать звук. При этом возможности математического поисковика приближаются к функциям профессиональных программ для настройки (вроде Guitar Pro). Очень удобная функция, которая работает на любой платформе, лишь бы был браузер. Как видите, математические вычисления способны немного упростить нашу жизнь. Может быть, вы знаете ещё какие-то удобные приёмы работы с Wolfram Alpha? Расскажите в комментариях. Wolfram|Alpha оживает с CDF — Стивен Вольфрам Письма Две недели назад мы сделали важное объявление: основываясь на технологии, которую мы разрабатывали более 20 лет, мы выпустили Computable Document Format (CDF). Есть много важных применений CDF, которые мы, без сомнения, увидим в ближайшие месяцы и годы. Но сегодня я рад объявить об экспериментальной версии от нас: Wolfram|Alpha с CDF. Начиная с сегодняшнего дня, как только у вас будет установлен бесплатный подключаемый модуль CDF (или если в вашей системе установлено Mathematica 8), вы можете перейти в верхний правый угол веб-сайта Wolfram|Alpha и установить CDF on, в результате чего Wolfram|Alpha будет генерировать не только статическую веб-страницу, но и полный вывод CDF, с которым вы можете напрямую взаимодействовать и выполнять вычисления. Есть некоторые немедленные последствия, такие как вращение 3D-графики, интерактивное считывание значений на графиках и изменение размера графики во время выполнения. Но где Wolfram|Alpha с CDF действительно начинает привлекать внимание, так это в том, что вы можете интерактивно манипулировать параметрами и фактически выполнять вычисления прямо в браузере. Иногда возможность динамического изменения параметров просто обогащает и без того довольно полный вывод. Но часто это то, что действительно делает результат значимым. Например, когда Wolfram|Alpha с CDF дает вам средства управления обработкой изображений, которые позволяют интерактивно выбирать различные функции изображения. Или когда Wolfram|Alpha с CDF динамически показывает вам поведение какой-либо смоделированной системы. Обычно Wolfram|Alpha с CDF начинается с демонстрации довольно простого набора элементов управления. Но часто есть +, который вы можете нажать, чтобы открыть гораздо более сложную «панель управления», которая позволяет вам изменять всевозможные функции и параметры в вычислениях. В частности, Wolfram|Alpha с CDF предоставляет расширенные интерактивные версии результатов, которые вы уже видели в некоторых версиях даже без CDF. Так как же работает Wolfram|Alpha с CDF? Происходит следующее: вместо того, чтобы серверы Wolfram|Alpha посылали вам HTML-код для обработки вашим веб-браузером, они отправляют CDF, который, по сути, содержит динамически сгенерированные программы, которые должны выполняться вашим подключаемым модулем CDF. Это интересный и мощный технологический стек, основанный на языке Mathematica . Ваш запрос поступает на серверы Wolfram|Alpha, где он обрабатывается с использованием множества Код Mathematica , который в конечном итоге генерирует результат, состоящий из фрагмента CDF. Затем этот CDF отправляется на ваш компьютер, где он запускается с использованием ядра Mathematica , но теперь под вашим контролем, локально внутри вашего плагина CDF. В результате вы получаете лучшее из обоих миров. У вас есть доступ как к крупномасштабным вычислительным мощностям, так и к знаниям, хранящимся на основных серверах Wolfram|Alpha, и вы получаете очень быстрое взаимодействие благодаря локальным вычислениям на вашем компьютере. И что делает это возможным, так это то, что, будучи основанным на языке Mathematica , CDF может описывать высокоуровневые алгоритмические процессы стандартным способом, который может быть легко доставлен на ваш компьютер. Если посмотреть на различные приложения CDF, некоторые из них, как правило, предполагают создание CDF человеком — скажем, для создания интерактивных демонстраций такого рода в проекте Wolfram Demonstrations Project. Но другие приложения включают автоматическую генерацию CDF, например, для создания интерактивных отчетов. И в каком-то смысле Wolfram|Alpha с CDF является началом окончательного вида автоматической генерации CDF. Вы начинаете с простой лингвистики в свободной форме, а Wolfram|Alpha автоматически генерирует CDF для всего, что вы описываете. Сейчас мы только на начальной стадии. Но то, что у нас есть, уже очень полезно — по крайней мере, для создания ядра того, что необходимо для конкретного интерактивного документа CDF. Я не хочу еще больше запутывать технологический стек, но есть пример Wolfram|Alpha с CDF, который в каком-то смысле даже более мощный: Wolfram|Alpha с CDF не в веб-браузере, а внутри Математика . В некотором смысле это расширение лингвистического программирования в свободной форме, которое мы представили в прошлом году с Mathematica 8. Но что нового, так это то, что теперь можно перейти непосредственно от лингвистики в свободной форме к полной интерактивной Программы Mathematica , включающие такие конструкции, как Manipulate. Для меня увлекательно и захватывающе видеть такого рода унификации в этих различных формах технологий, которые мы разрабатывали так долго. И каждый раз, когда мы делаем такое объединение, открываются всевозможные новые возможности, которые мы раньше едва могли себе представить. Но сегодняшний Wolfram|Alpha с CDF — это только начало. В течение следующих нескольких месяцев мы представим всевозможные улучшения. Например, на данный момент вы должны выбрать либо получение всего HTML-вывода из Wolfram|Alpha, либо весь CDF. Если вы выберете HTML, вы сможете использовать весь спектр оптимизаций в своем веб-браузере. Если вы выберете CDF, вы получите вычисляемый вывод CDF, с которым вы можете взаимодействовать. В будущем CDF будет автоматически перемежаться с HTML, так что вы сможете получить лучшее из обоих миров. В настоящее время существуют только определенные виды выходных данных Wolfram|Alpha, которые используют динамическую интерактивность с CDF. В будущем будет более широкий охват, так что абсолютно все, что может быть интерактивным, автоматически будет таковым. Но уже сегодня приятно видеть, как Wolfram|Alpha начинает оживать благодаря интерактивному выходу CDF. Дайте нам знать, что вы думаете об этом! Как построить график в Wolfram Alpha? – Пересмотр книгиСодержание Как построить график в Wolfram Alpha? Построение графика функций в декартовой плоскости с помощью Wolfram|Alpha — это такая простая задача: просто введите функцию, которую вы хотите построить, и через несколько секунд вы получите прекрасный результат. Как установить точки данных в системе Mathematica?Как | Построить график Как вы строите графики в Wolfram?Язык Wolfram Language предлагает обширную поддержку для построения графиков всех видов данных различными способами. Как построить набор данных в Mathematica? Вы также можете изменить размер точек на графике на , используя графические директивы PointSize или AbsolutePointSize с опцией PlotStyle. Как изменить размер точки в системе Mathematica?Язык Wolfram Language предлагает обширную поддержку для построения графиков всех видов данных различными способами. Как построить график в Wolfram?Построение графика функций в декартовой плоскости с помощью Wolfram|Alpha — это такая простая задача: просто введите функцию, которую вы хотите построить, и через несколько секунд вы получите прекрасный результат. Если вы чувствуете себя смелым, введите многомерную функцию, и результатом будет трехмерный декартов график. Как вы рисуете в Mathematica?Выполните следующие простые шаги:  04 марта 2022 Как построить набор данных в Mathematica?Создание графика из таблицы Как изменить размер графика в Mathematica?Чтобы сделать графику с явным размером стандартного размера, щелкните правой кнопкой мыши графику и выберите «Сделать стандартный размер». Как вы относитесь к Mathematica? Щелчок в любом месте + перетаскивание мыши увеличивает/уменьшает масштаб в точке, где был щелчок мышью. Как увеличить график в Mathematica?Чтобы изменить цвет точек на графике, используйте параметр PlotStyle. Здесь указан красный цвет: Копировать в буфер обмена. Любой из цветов, поддерживаемых языком Wolfram Language, можно использовать для окрашивания точек на графике. Как построить график в Mathematica?Как | Построить график Как построить график? Построение графика функций в декартовой плоскости с помощью Wolfram|Alpha — это очень простая задача: просто введите функцию, которую вы хотите построить, и через несколько секунд вы получите прекрасный результат. Как отображать данные в Wolfram Mathematica?Язык Wolfram Language предлагает обширную поддержку для построения графиков всех видов данных различными способами. Как построить точечный график в Mathematica?Выполните следующие простые шаги: 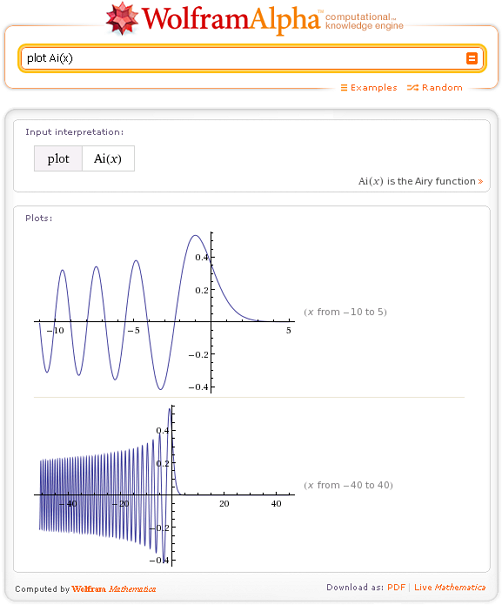 04 марта 2022 Как построить отрезок в Mathematica?Mathematica имеет встроенную команду для построения отрезка прямой между двумя точками P(a, b) и Q(c, d). Следующая 4-строчная процедура иллюстрирует ее использование. Выполните его с помощью , поместив курсор после последней строки и нажав клавишу Enter Какая польза от стиля построения в Mathematica?— это опция для построения графиков и связанных с ними функций, которая указывает стили, в которых объекты должны быть нарисованы. Что такое Mathematica ListPlot?ListPlot также известен как точечный график, если задан список высот yi. Получив список высот, ListPlot строит точки в том порядке, в котором они были заданы, показывая тенденцию данных. При наборе пар точки размещаются в заданных координатах. Как изменить размер графика в Mathematica?Изменение размера, обрезка и добавление полей к графике  Что такое Эпилог в системе Mathematica?Щелчок в любом месте + перетаскивание мыши увеличивает/уменьшает масштаб в точке, где был щелчок мышью. Ctrl + перетаскивание переключает масштабирование прямоугольника (от Szabolcs). Как изменить цвета графиков в Mathematica?Эпилог. Cell[BoxData[Эпилог], Input, CellTags -x26gt; Epilog_templates] — это параметр для графических функций, который дает список графических примитивов, которые должны быть отрисованы после того, как будет отрисована основная часть графики Как вы вписываете данные в функцию? Проверьте, насколько хорошо ваши данные моделируются линейной, квадратичной или экспоненциальной функцией. Как решить функцию в Mathematica?Чтобы сделать графику с явным размером стандартного размера, щелкните правой кнопкой мыши графику и выберите «Сделать стандартный размер». Как изменить размер точки в Mathematica?Чтобы сделать графику с явно заданным размером стандартным размером, щелкните правой кнопкой мыши графику и выберите «Сделать стандартный размер». Как обрезать график в Mathematica? Вы также можете изменить размер точек на графике на , используя графические директивы PointSize или AbsolutePointSize с опцией PlotStyle. Здесь PointSize используется с PlotStyle для установки размера точек на графике. 10 лучших приложений-калькуляторов для iPhone, которые стоит попробоватьЕсли есть большая потребность в наборе текста на компьютере на iPhone, попробуйте лучшие приложения-калькуляторы для iPhone, которые предлагает GhienCongList. Вычислительная мощность смартфонов и планшетов сделала карманные компьютеры устаревшими. Однако современные вычислительные приложения все еще развиваются. GhienCongListen познакомит вас с приложением калькулятор для iPhone лучше всего попробовать. Реклама Содержание PCC Lite PCalc Lite заслуживает места в этом списке. Это очень хорошее приложение для научного калькулятора, оно поддерживает базовые вычисления, такие как сложение, вычитание, умножение и деление, а также расширенные вычисления, такие как корень, степень, грех, косинус, тангенс, логарифм. Вы даже можете конвертировать единицы длины, веса, объема и скорости прямо в приложении. Реклама Преимущество PCalc в том, что это программное обеспечение поддерживает присоединение компьютерного виджета к центру уведомлений iOS, поэтому, когда вам это нужно срочно, вам просто нужно открыть Центр уведомлений, чтобы иметь возможность вводить данные, вычислять немедленно , Нет необходимости открывать приложение. >> Загрузите PCalc Lite здесь. Реклама CalzyCalzy имеет интересную функцию, которая сохраняет расчеты и может маркировать их. Приложение также включает в себя клавиатуру, поддержку 3D Touch, функции науки, истории и закладок, а также поддержку многозадачности. Это отличное приложение-калькулятор, и неудивительно, что Apple отметила его наградой за дизайн в 2018 году. >> Загрузите Calzy здесь. Calcularium Calcularium объединяет мощные инструменты для ввода и редактирования вычислений. Пользователи могут вводить числа, используя традиционную клавиатуру, голосовые или графические уравнения ввода, а затем маркировать каждое число и переменную для быстрого поиска и извлечения. >> Загрузите Calcularium здесь. SoulverSoulver отображает все ваши расчеты в прямой колонке, что позволяет быстро просмотреть предыдущие расчеты, а курсор редактирования позволяет менять строки, каждая ревизия автоматически обновляется, обновляется строка. Приложение включает поддержку пользовательских меток, конвертации единиц и валюты, и пользователи могут сохранять свои листы и делиться ими или работать с ними позже. >> Загрузите Soulver здесь. Numerical 2Numerical 2 — это приложение, в котором буквально нет знака равенства. Приложение ускоряет набор текста за счет удаления кнопки равенства, а также автоматического применения скобок. Numerical2 имеет полнофункциональную цифровую клавиатуру, клавишу дробей для быстрого вычисления дробей, возможность использовать числа пи и е в бесконечных позициях для получения точных результатов в любом уравнении. Приложение поддерживает ландшафтный режим, многозадачность с разделением экрана и включает пользовательскую клавиатуру для выполнения вычислений в другом приложении. Кроме того, Numerical также поставляется с несколькими темами. >> Загрузите Numerical 2 здесь. Desmos Graphing CalculatorDesmos Graphing Calculator — еще одно бесплатное приложение с полнофункциональным набором графических опций. Вы можете строить графики в полярных, декартовых и параметрических системах координат без ограничения количества выражений, которые вы можете отображать одновременно. Удобные ползунки позволяют корректировать значения на лету, чтобы вы могли видеть, как параметр влияет на график. >> Загрузите графический калькулятор Desmos здесь. Photomath PhotoMath решает математические задачи, десятичные дроби, линейные уравнения и тригонометрические функции, что упрощает и делает более удобным изучение математики учащимися на своих телефонах. Приложение обрабатывает все, от базовой алгебры до линейных, квадратных, уравнений и неравенств, систем уравнений, тригонометрии… >> Загрузите PhotoMath здесь. Wolfram AlphaWolfram Alpha предназначен для выполнения множества различных математических операций, таких как решение уравнений, преобразование единиц измерения, матрицы, тригонометрия… Кроме того, Wolfram Alpha также предоставляет большой объем знаний в различных областях. например, химия, астрономия, наука о жизни, музыка… >> Загрузите Wolfram Alpha здесь. MyScript Calculator 2MyScript Calculator 2 — это решение для преобразования рукописного текста в числовой текст, поэтому, если вы хотите выполнить деление в длинное число или найти квадратный корень из числа, просто напишите его пальцем и посмотрите результат. . Кроме того, вы можете выполнять множество математических функций, используя тригонометрию, базовую математику, проценты, обратные тригонометрические функции. |
Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.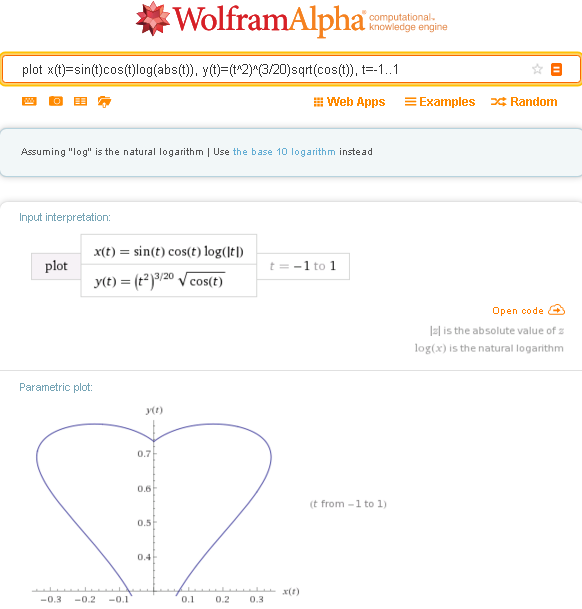
Например, при достаточно большом увеличении часть эллипса выглядит, как отрезок прямой. С фракталами такого не происходит: при любом их увеличении мы снова увидим ту же самую сложную форму, которая с каждым увеличением будет повторяться снова и снова.
Один из них Wolfram Mathematica.
Ниже представлен фрагмент программы, где описывается одиннадцать функций подгонки, и два коэффициента Бозе – Эйнштейна (nbes, nbeas — для стоксовой и антистоксовой компоненты):
txt)
Стоит отметить, что имя файла должно быть специфично — содержать в себе температуру в кельвинах, при которой был проведен данный эксперимент. Само имя файла следует разбить на несколько частей, например с помощью символа «_».
За счет этого достигается существенное повышение полноты поиска. Для обобщения, проведения логического вывода и синтеза ответов вопросно-ответные поисковые системы также используют правила обработки фактографической информации. Однако, в отличие от системы Wolfram Alpha, правила логической обработки при этом представляют из себя не отдельные алгоритмы, направленные на решение заранее определенных сравнительно простых задач, а логические правила, которые могут автоматически применяться в динамически формируемой последовательности, определяющей порядок обработки первичной фактографической информации и формирования ответа на вопрос пользователя. Для проверки данных положений проведем сравнительное тестирование систем Wolfram Alpha и AskNet.ru.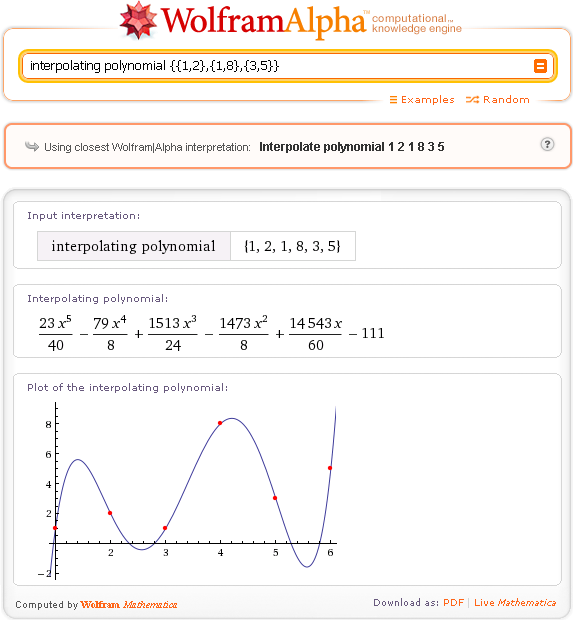
nist.gov/data/qa/2003_qadata/03QA.tasks/test.set.t12.txt). Это обусловлено тем, что данные тестовые вопросы имеют достаточно общий характер и могут быть использованы для тестирования систем вопросно-ответного поиска, работающих в интернете. В отличие от других тестовых дорожек вопросно-ответного поиска конференции TREC, используемые тестовые случаи конференции TREC 2003 не привязаны к тестовым коллекциям документов и не имеют группировки в тематически связанные последовательности вопросов. Тестовые коллекции семинара РОМИП не использовались ввиду того, что они предназначены для оценки качества поиска на русском языке, а система Wolfram Alpha не работает с русскоязычными запросами пользователей – «Wolfram Alpha сейчас не понимает русский язык». Тестирование проводилось путем последовательного поочередного ввода запросов из тестовой коллекции конференции TREC 2003. Тестирование систем было проведено по первым 71 тестовым случаям из 500, имеющихся в коллекции конференции TREC 2003. Это было обусловлено получением результатов тестирования, явно отражающих характеристики систем и позволяющих сформулировать достоверные выводы.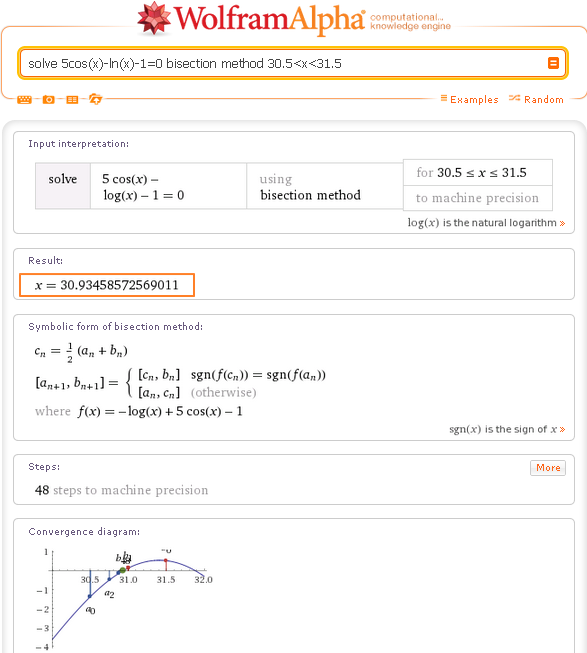
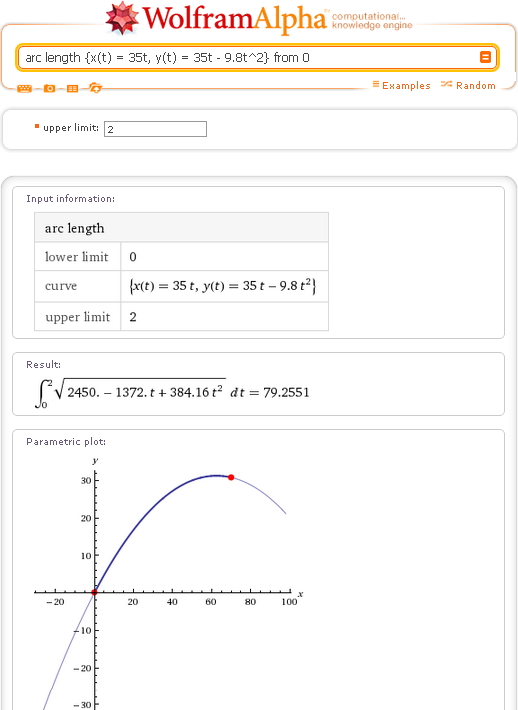В программу заложены специализированные функции многих технических направлений, таких как вычислительная биология, вейвлет — анализ и т.д.
Mathematica весьма выгодно отличается от других программ наличием огромной коллекции тщательно отобранных данных различного вида, которые периодически расширяются и обновляются.
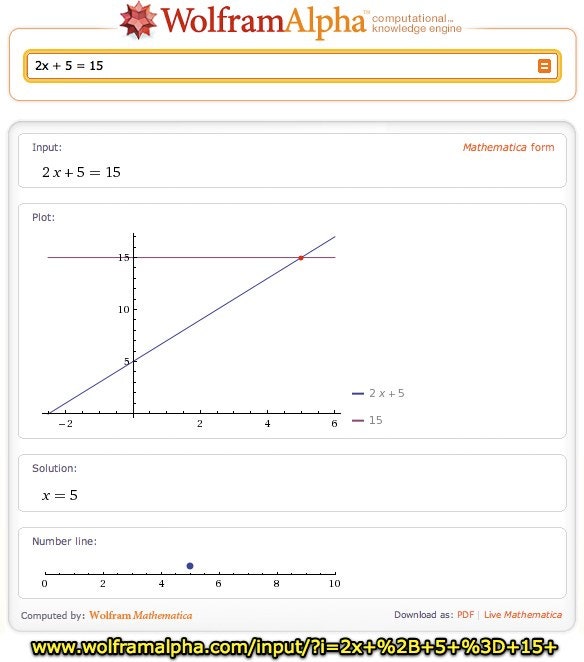
.., и конечно же МАТЕМАТИКА — математические правила, формулы, алгоритмы — здесь есть все это, и многое-многое другое.
2=6 :
Достаточно установить в ваш браузер подходящее расширение, тулбар или плагин из числа тех, которые предлагает официальный сайт Wolfram Alpha. С ними вы в любой момент сможете обратиться к Wolfram Alpha. Подробнее об этом .
Космический аппарат доставит на Марс электронный носитель с именами всех зарегистрированных участников экспедиции.
Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.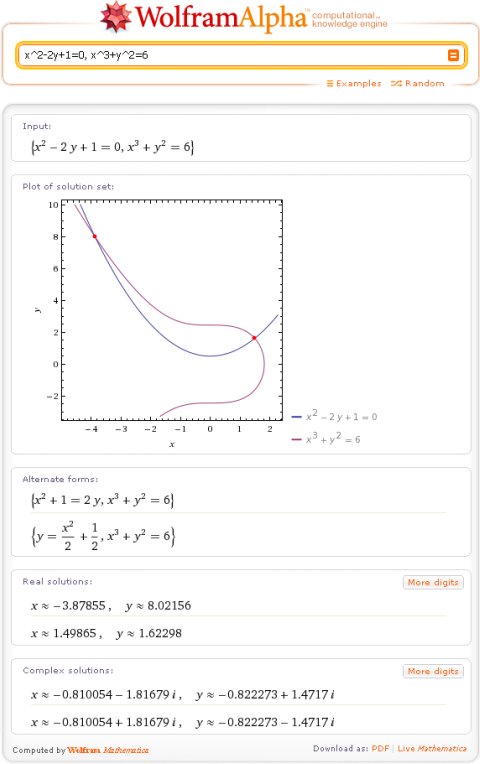
Например, при достаточно большом увеличении часть эллипса выглядит, как отрезок прямой. С фракталами такого не происходит: при любом их увеличении мы снова увидим ту же самую сложную форму, которая с каждым увеличением будет повторяться снова и снова.
д. Все эти данные можно закачать на ПК в виде PDF-документа.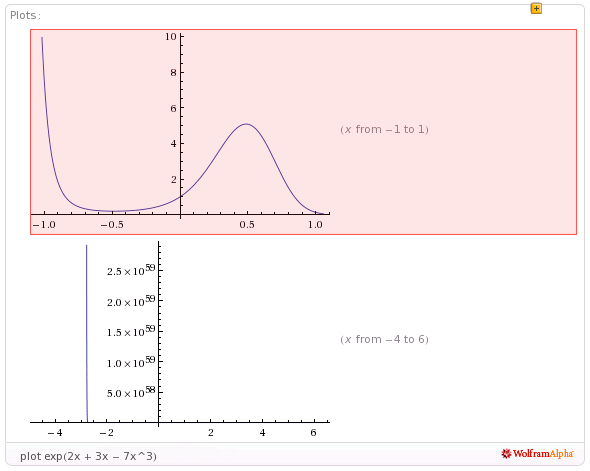
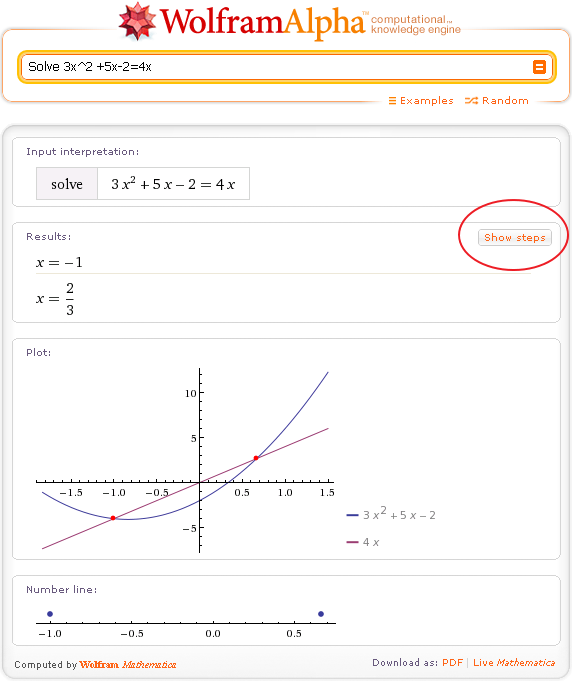Также Wolfram Alpha умеет строить графики функций, вычислять значения синуса или косинуса и так далее.
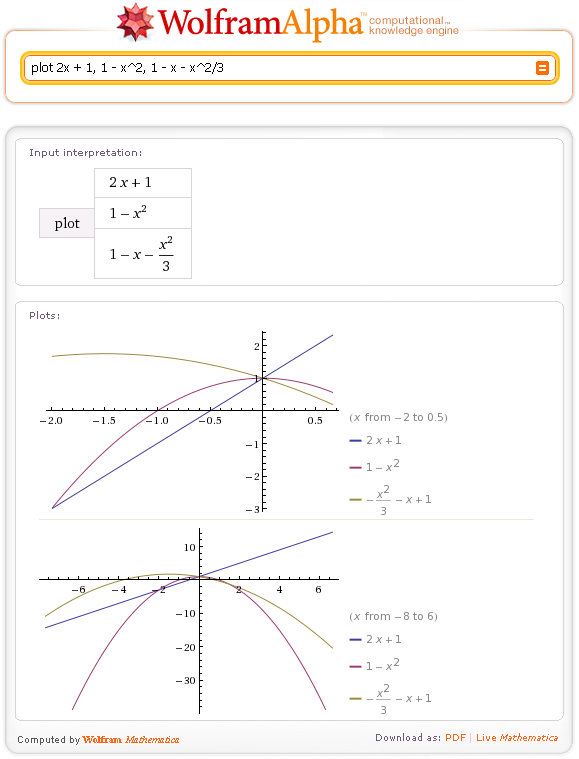Wolfram Alpha способна помочь в этом нелёгком деле.
Эта функция работает не только с инженерными и физическими единицами измерения, но и с размерной сеткой одежды или обуви. И не нужно вспоминать, где сохранена соответствующая табличка, если у вас есть смартфон и доступ к интернету. Пример запроса: US men’s size 8.5 shoe in france size .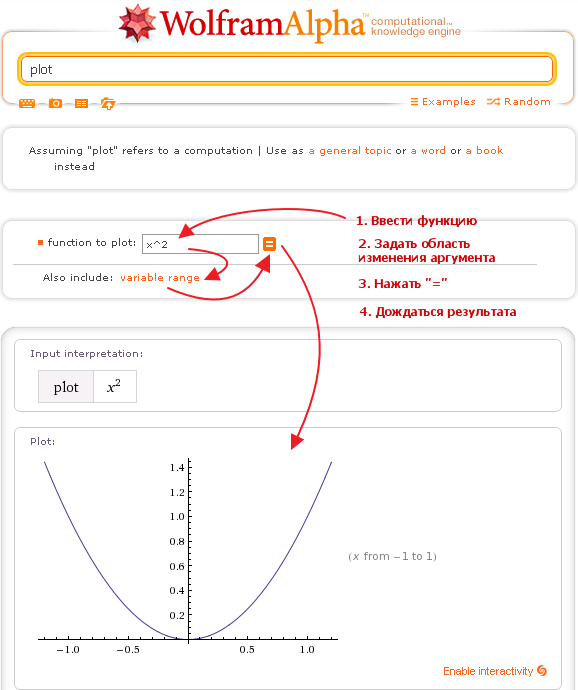
А Wolfram Alpha умеет это делать по запросу «страна, сумма, год» (под страной имеется в виду страна, валюта которой вас интересует). Лучший способ рассчитать реальную инфляцию.
Я думаю, что CDF сильно повлияет на то, как можно сообщать самые разные вещи. Потому что впервые это делает практичным включение живых вычислений в рутинную часть документа.
Wolfram|Alpha без CDF может дать вам только один конкретный график. Wolfram|Alpha с CDF автоматически создаст ползунки или другие элементы управления, которые позволят вам немедленно изменить параметры и постоянно обновлять график.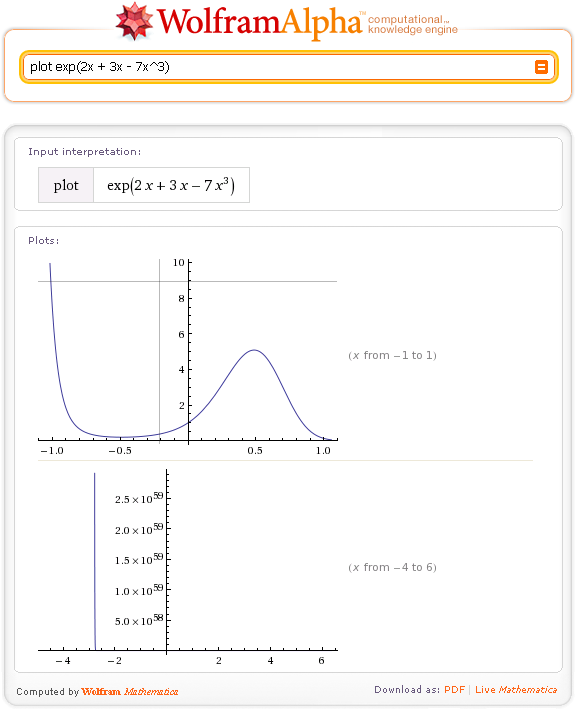
Но мы экспериментируем со всевозможными совершенно новыми видами результатов, которые существуют только в интерактивной форме CDF.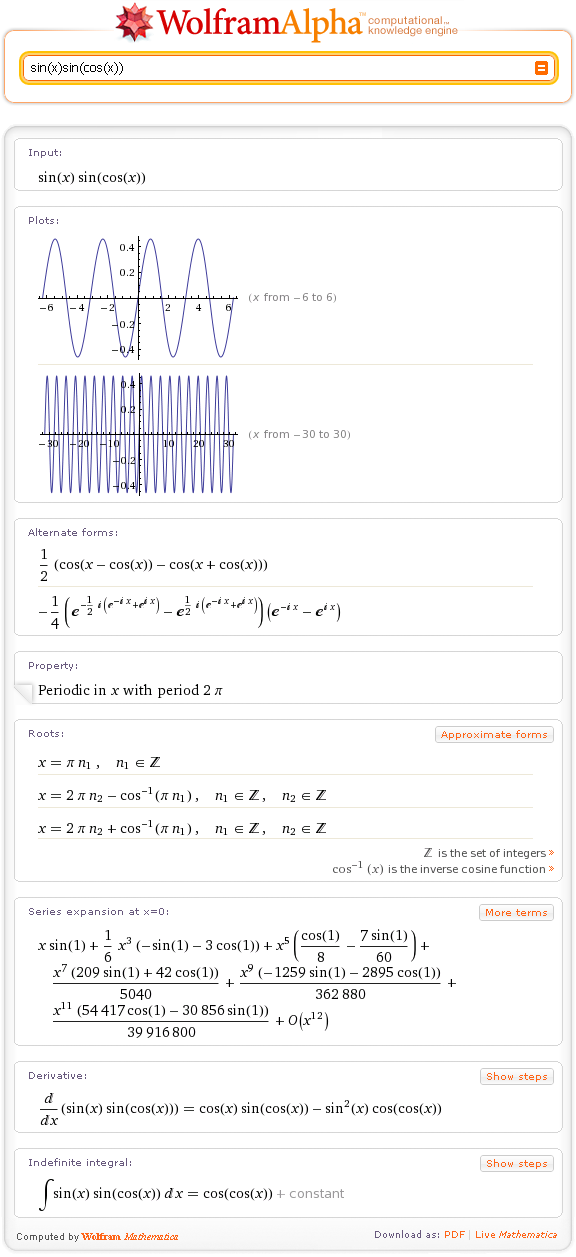
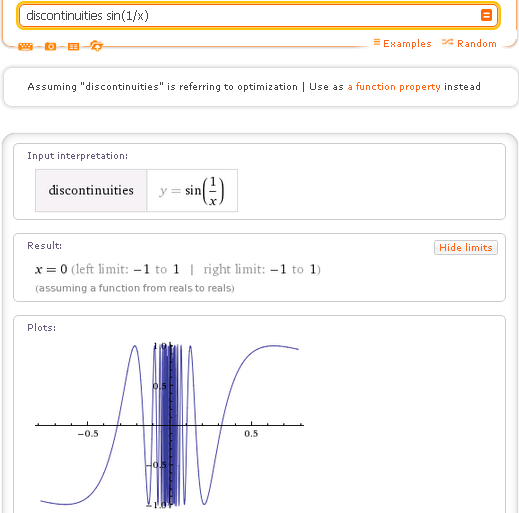
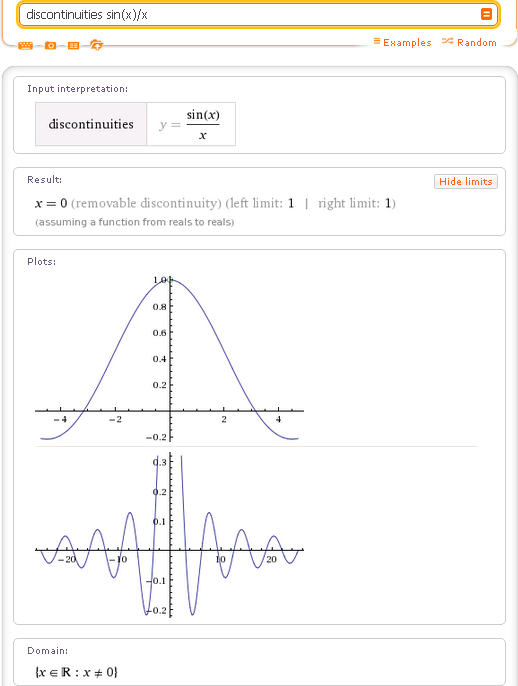
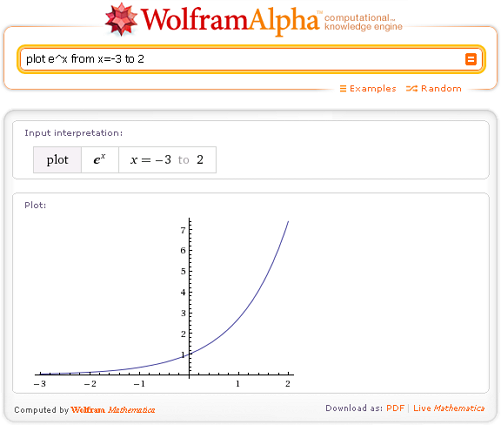
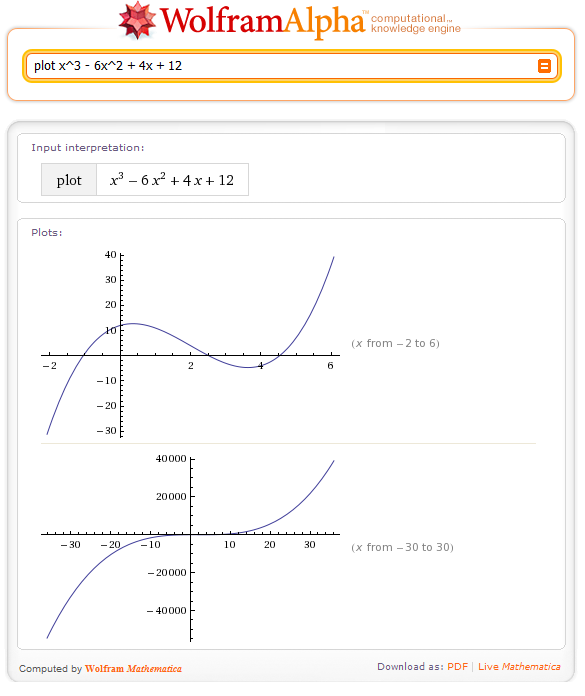
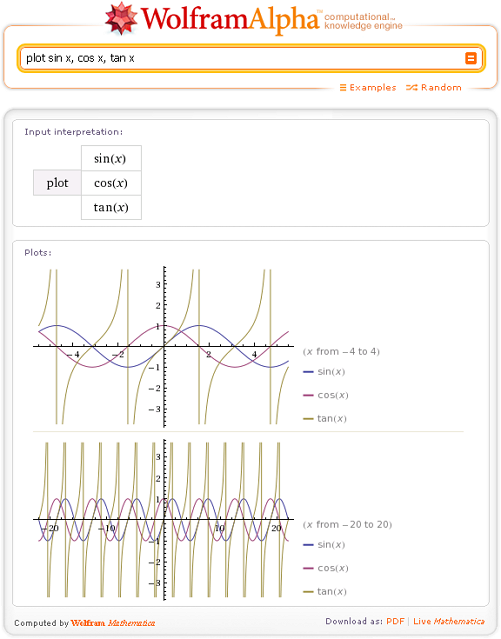Если вы чувствуете себя смелым, введите многомерную функцию, и результатом будет трехмерный декартов график. 
Здесь PointSize используется с PlotStyle для установки размера точек на графике.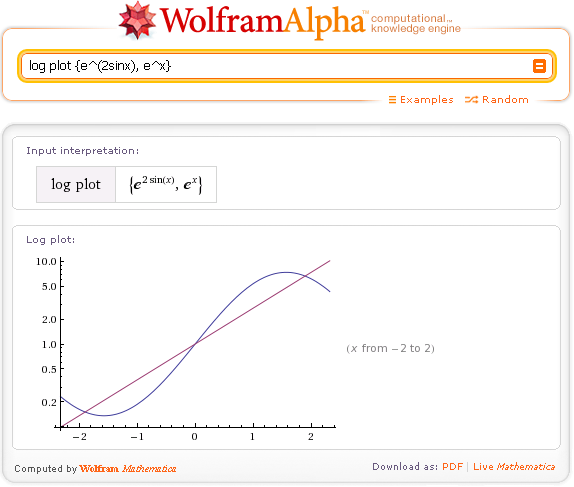 
Ctrl + перетаскивание переключает масштабирование прямоугольника (от Szabolcs). 
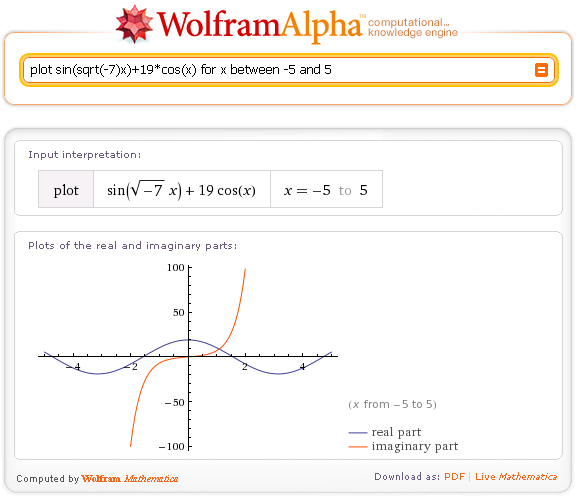Если вы чувствуете себя смелым, введите многомерную функцию, и результатом будет трехмерный декартов график. 
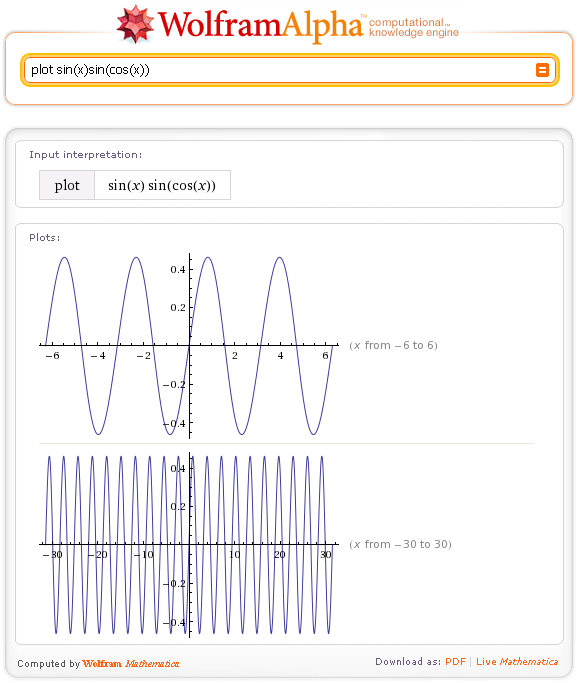
Элементы управления жестами позволяют переупорядочивать элементы каждого уравнения, а также сохранять формулы и переменные или разбивать отдельные переменные на подуравнения.
