Тесты по теме «Неравенства» онлайн
- Онлайн тесты
- Неравенства
-
Линейные неравенства с одной переменной.
23.05.2021 1515 0
Тематический тест, объединяющий две темы: «Линейные неравенства» и «Числовые промежутки» предназначен для учащихся 8 классов. Данный тест нацелен на определение уровня усвоения учебного материала по теме «Линейные уравнения» за основу взят учебник Макарычева — самый распространенный учебник по алгебре для 8 класса.
-
Тест по теме: «Решение неравенств методом интервалов», 10 класс
20.10.2020 74
Тест состоит из 8 вопросов по теме:»Решение неравенств методом интервалов», 10 класс, учебник Никольского С.
 М.
М. -
А8. «Решение неравенств и систем «
31.03.2020 426 0
Тест соответствует учебнику «Алгебра. 8 класс» под редакцией С.А. Теляковского.
-
Решение линейных неравенств
20.10.2021 376 0
Данный тест нацелен на определение уровня усвоения учебного материала по теме «Линейные неравенства» 9 класс учебник А.Г. Мерзляка, В.Б. Полонского и др.
-
Решите неравенство
12.
 11.2019
4083
11.2019
4083
Решение квадратных неравенств и неравенств высших степеней методом интервалов.
-
Алгебра. 8 класс. Решение неравенств первой степени.
05.05.2020 2729
Данный тест проверяет умение решать неравенства первой степени.
-
Иррациональные уравнения и неравенства
26.05.2020 2264 0
Тест предназначен для проверки умения решать простейшие иррациональные уравнения и неравенства.
-
Решение квадратных неравенств
22.
 12.2020
4321
0
12.2020
4321
0
Тест по теме «Решение квадратных неравенств» для 9 класса. Тест состоит из 10 вопросов с выбором одного правильного овета из предложенных четырех.Тест имеет ограничение по времени прохождения — 5 минут.
-
Решение неравенств методом интервалов
26.05.2020 3142 0
Тест предназначен для проверки умения решать неравенства методом интервалов, строить графическую интерпретацию .решения.
-
Неравенства, содержащие знак модуля №1
15.11.2020 173 0
Ребята! Тест нацелен на определение степени усвоения классной работы и содержит задания, аналогичные тем, что были разобраны в видео-уроке.

-
Числовые неравенства. Алгебра 8-9 класс.
18.08.2021 954 0
Тест для учащихся 8- 9 классов по теме «Числовые неравенства. Свойства числовых неравенств»
-
Итоговый тест по теме «Неравенства»
13.04.2020 3221 0
Тест предназначен для проверки усвоения знаний по теме «Неравенства с одной переменной и их системы» к учебнику алгебры 8 класс (авторы Ю.Н.Макарычева и др.). Содержит как задания базового уровня, так и задания повышенного уровня.
-
Квадратные неравенства
28.
 08.2020
2782
08.2020
2782
Тест создан к учебнику Алгебра 8 класс под редакцией А.Г.Мордковича по теме «Квадратные неравенства»
-
Тест по модулю 3
20.08.2020 4 0
Привет, ребята! Пришло время показать свои знания на практике.
-
Решение рациональных уравнений и неравенств
01.12.2020 380 0
Тест предназначен для проверки умения решать постейшие рациональные уравнения и неравенства и их системы
-
9 класс.
 Рациональные неравенства.
Рациональные неравенства.
06.12.2020 1162 0
Контрорльный тест по алгебре, 9 класс по теме «Рациональные неравенства». Содержит 8 заданий.
-
Неравенства, координатная прямая
17.12.2020 451 0
Тест содержит 12 заданий по теме «Координатная прямая», «Расстояние между точками координатной прямой». Критерии: «3» от 50 до 69%, «4» от 70 до 90%, «5» от 91 до 100%. Оценка выставляется сразу после прохождения теста.
-
Решение систем неравенств
08.01.2021 22 0
Тест предназначен для проверки знания методов решения систем неравенств, умения решать системы неравенств, изображать графически решение систем неравенств
-
Решение неравенств методом интервалов (ОГЭ, алгебра, 2 часть № 21)
19.
 03.2019
279
0
03.2019
279
0
Для проверки умения решать неравенства методом интервалов. Содержит теоретическую и практическую часть. Тест полезен при подготовке к экзаменам. Контактные данные не обязательны и нужны только если вы желаете получить комментарии после проверки (ссылка на страницу VK, электронная почта, WA.). В случае неудачного прохождения приглашаю https://vk.com/stairway5
-
Тест по алгебре
30.08.2019 1688
В данном тесте содержится 20 вопросов по алгебре за 8 класс. Тест содержит вопросы по следующим темам: — Квадратные уравнения — Неравенства
-
Квадратные уравнения
12.
 04.2020
50
0
04.2020
50
0
Тест по теме квадратный трехчлен проверяет умение решать квадратные уравнения и неравенства
-
Неравенства. Линейные неравенства. Квадратные неравенства
16.04.2020 2519 0
Тест по теме «Неравенства» предназначен для обучающихся 8-9 классов. Рекомендован при полготовке к ОГЭ
-
ОУД.03 Математика. Решение простейших неравенств.
07.06.2020 70 0
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Уравнения и неравенства».

-
Решение неравенств. Подготовка к ОГЭ 2021
10.10.2020 21 0
Тест для проверки знаний и умений по теме «Решение линейных неравенств и неравенеств высших степений (варианты фзяты из Базы ФИПИ)
Тригонометрические неравенства и методы их решения – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Тригонометрическими неравенствами называются неравенства, которые содержат переменную под знаком тригонометрической функции.
Методы решений неравенств:
- Решение тригонометрических неравенств с помощью единичной окружности.

- Графическое решение тригонометрических неравенств.
- Решение неравенств методом интервалов.
При решении более сложных тригонометрических неравенств пользуются двумя основными приемами:
I. Данное неравенство с помощью равносильных преобразований сводится к простейшим тригонометрическим неравенствам. При выполнении преобразований пользуются теми же приемами, что и при решении тригонометрических уравнений.
II. Применяется метод интервалов для определения числовых промежутков, в которых содержатся решения неравенства. Предварительно решается соответствующее тригонометрическое уравнение и устанавливаются интервалы знакопостоянства с учетом области определения неравенства.
Неравенство \(sinx>a\)
- При \(|a|≥1\) неравенство \(sinx>a\) не имеет решений: \(x\in \varnothing\).
- При \(a<−1\) решением неравенства \(sinx>a\) является любое действительное число: \(x\in \mathbb R\).

- При \(−1≤a<1\) решение неравенства \(sinx>a\) выражается в виде \(arcsin a + 2\pi n < x < \pi -arcsin a + 2\pi n,\;n \in \mathbb{Z}\).
Неравенство \(sinx≥a\)
- При \(|a|>1\) неравенство \(sinx\ge a\) не имеет решений: \(x\in \varnothing\).
- При \(a\le−1\) решением неравенства \(sinx\ge a\) является любое действительное число: \(x\in \mathbb R\).
- При \(-1<a<1\) решение неравенства \(sinx\ge a\) выражается в виде \(arcsin a + 2\pi n \le x \le \pi — arcsin a + 2\pi n,\;n \in \mathbb{Z}\).
- Случай \(a=1 \): \(x = \frac{\pi}2 +2\pi n,\;n \in \mathbb{Z}\).
Неравенство \(sinx<a\)
- При \(a>1\) решением неравенства \(sinx<a\) является любое действительное число: \(x\in \mathbb R\).\)
- При \(a≤−1\) у неравенства \(sinx<a\) решений нет: \(x\in \varnothing\).\)
- При \(-1<a\leq1\) решение неравенства \(sinx<a\) лежит в интервале \(-\pi — arcsin a + 2\pi n < x < arcsin a + 2\pi n,\;n \in \mathbb{Z}\).
 \)≤1\)
\)≤1\)
Неравенство \(sinx≤a\)
- При \(a≥1\) решением неравенства \(sinx≤a\) является любое действительное число: \(x\in \mathbb R\).
- При \(a<−1\) неравенство \(sinx≤a\) решений не имеет: \(x \in \varnothing\).
- При \(-1<a<1\) решение нестрогого неравенства \(sinx≤a\) находится в интервале \(-\pi — arcsin a + 2\pi n \le x \le arcsin a + 2\pi n,\;n \in \mathbb{Z}\).
- Случай \(a=−1\): \(x = -\frac{\pi}2 + 2\pi n,\;n \in \mathbb{Z}\).
Неравенство \(cosx>a\)
- При \(a≥1\) неравенство \(cosx>a\) не имеет решений: \(x\in \varnothing\).
- При \(a<−1\) решением неравенства \(cosx>a\) является любое действительное число: \(x\in \mathbb R\).
- При \(−1≤a<1\) решение неравенства \(cosx>a\) имеет вид \(-arccos a + 2\pi n < x < arccos a + 2\pi n,\;n \in \mathbb{Z}\).
Неравенство \(cosx≥a\)
- При \(a>1\) неравенство \(cosx≥a\) не имеет решений: \(x\in \varnothing\).

- При \( a≤−1\) решением неравенства \(cosx≥a\) является любое действительное число: \(x\in \mathbb R\).
- При \(-1<a<1\) решение неравенства \(cosx≥a\) имеет вид \(-arccos a + 2\pi n \le x \le arccos a + 2\pi n,\;n \in \mathbb{Z}\).
- Случай \(a=1\): \(x = 2\pi n,\;n \in \mathbb{Z}\).
Неравенство \(cosx<a\)\)
- При \(a>1\) неравенство \(cosx<a\) справедливо при любом действительном значении x: \(x\in \mathbb R\).\)
- При \(a≤−1\) неравенство \(cosx<a\) не имеет решений: \(x\in \varnothing\).\)
- При \(-1<a\leq1\) решение неравенства \(cosx<a\) записывается в виде \(arccos a + 2\pi n < x < 2\pi — arccos a + 2\pi n,\;n \in \mathbb{Z}\). \)≤1\)
Неравенство \(cosx≤a\)
- При \(a≥1\) решением неравенства \(cosx≤a\) является любое действительное число: \(x\in \mathbb R\).
- При \(a<−1\) неравенство \(cosx≤a\) не имеет решений: \(x\in \varnothing\).

- При \(-1<a<1\) решение нестрогого неравенства \(cosx≤a\) записывается как \(arccos a + 2\pi n \le x \le 2\pi — arccos a + 2\pi n,\;n \in \mathbb{Z}\).
- Случай \(a=−1\): \(x = \pi + 2\pi n,\;n \in \mathbb{Z}\).
Неравенство \(tgx>a\)
При любом действительном значении \(a\) решение строгого неравенства \(tgx>a\) имеет вид \(arctg a + \pi n < x < \frac{\pi}2 + \pi n,\;n \in \mathbb{Z}\).
Неравенство \(tgx≥a\)
Для любого значения \(a\) решение неравенства \(tgx≥a\) выражается в виде \(arctg a + \pi n \le x < \frac{\pi}2 + \pi n,\;n \in \mathbb{Z}\).
Неравенство \(tgx<a\)\)
Для любого значения \(a\) решение неравенства \(tgx<a\) записывается в виде \(-\frac{\pi}2 + \pi n < x < arctg a + \pi n,\;n \in \mathbb{Z}\).\)
Неравенство \(tgx≤a\)
При любом \(a\) неравенство \(tgx≤a\) имеет следующее решение: \(-\frac{\pi}2 + \pi n < x \le arctg a + \pi n,\;n \in \mathbb{Z}\).
Неравенство \(ctgx>a\)
При любом \(a\) решение неравенства \(ctgx>a\) имеет вид \(\pi n < x < arcctg a + \pi n,\;n \in \mathbb{Z}\).
Неравенство \(ctgx≥a \)
Нестрогое неравенство \(ctgx≥a\) имеет аналогичное решение \(\pi n < x \le arcctg a + \pi n,\;n \in \mathbb{Z}\).
Неравенство \(ctgx<a\)\)
Для любого значения \(a\) решение неравенства \(ctgx<a\) лежит в открытом интервале \(arcctg a + \pi n < x < \pi + \pi n,\;n \in \mathbb{Z}\).\)
Неравенство \(ctgx≤a\)
При любом \(a\) решение нестрогого неравенства \(ctgx≤a\) находится в полуоткрытом интервале \(arcctg a + \pi n \le x < \pi + \pi n,\;n \in \mathbb{Z}\).
Пример. Решите неравенство: \(cosx>\frac12\).
Решение: Данное неравенство можно решить двумя способами: графически и с помощью единичного круга. Рассмотрим каждый из способов.
Первый способ. Изобразим в одной системе координат функции, описывающие левую и правую части неравенства, то есть \(y=cosx \ и \ y=\frac12\). Выделим промежутки, на которых график функции косинус \(y=cosx\) расположен выше графика прямой \(y=\frac12\).
Изобразим в одной системе координат функции, описывающие левую и правую части неравенства, то есть \(y=cosx \ и \ y=\frac12\). Выделим промежутки, на которых график функции косинус \(y=cosx\) расположен выше графика прямой \(y=\frac12\).
Найдем абсциссы точек \(x_1\ и \ x_2\) – точек пересечения графиков функций \(y=cosx\ и\ y=\frac12\), которые являются концами одного из промежутков, на котором выполняется указанное неравенство: \(x_1=-arccos\frac12=-\frac{\pi}3; x_2=arccos\frac12=\frac{\pi}3\).
Учитывая, что косинус – функция периодическая, с периодом \(2\pi\), ответом будут значения x из промежутков \((-\frac{\pi}3+2\pi k;\frac{\pi}3+2\pi k), \ k\in Z\).
Второй способ. Построим единичную окружность и прямую \(x=\frac12\) (так как на единичной окружности косинусам отвечает ось абсцисс). Обозначим \(P_{x_1}\ и \ P_{x_2}\) – точки пересечения прямой и единичной окружности. Решением исходного уравнения будет множество точек абсциссы, которых меньше \(\frac12\). Найдем значение \(x_1 \ и \ x_2\), совершая обход против часовой стрелки так, чтобы \(x_1<x_2\): \)
Найдем значение \(x_1 \ и \ x_2\), совершая обход против часовой стрелки так, чтобы \(x_1<x_2\): \)
\(x_1=-arccos\frac12=-\frac{\pi}3; x_2=arccos\frac12=\frac{\pi}3\).
Учитывая периодичность косинуса, окончательно получим интервалы \((-\frac{\pi}3+2\pi k;\frac{\pi}3+2\pi k), \ k\in Z\).
Решение нестандартных уравнений и неравенств с помощью метода мажорант
12 Задание (2022) (C1)14 Задание (2022) (C3)ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВАТРИГОНОМЕТРИЯ
Решение нестандартных уравнений и неравенств с помощью метода мажорант
Метод мажорант применяется при решении нестандартных уравнений и неравенств, которые не получается решить с помощью стандартных приемов. При подготовке к ЕГЭ по математике, если вы хотите научиться решать задания группы С, с этим методом необходимо познакомиться.
В этой статье я показываю решение задачи С3 и задачи С1, которые решаются с использованием этого метода.
Название метода мажорант происходит от французских слов majorer — объявлять большим и minorer — объявлять меньшим.
Метод мажорант основан на том, что множество значений некоторых функций ограничено. При использовании метода мажорант мы выявляем точки ограниченности функции, то есть в каких пределах изменяется данная функция, а затем используем эту информацию для решения уравнения или неравенства.
Чтобы успешно пользоваться этим методом, нужно хорошо знать, какие функции имеют ограниченное множество значений.
Приведем примеры элементарных функций, которые имеют ограниченное множество значений:
1. или
2. или
3.
4.
5.
6.
7.
8.
9.
10.
Маркером того, что в данном уравнении нужно применить метод мажорант, является
a) наличие в уравнении функций, уравнения с которыми решаются принципиально разными способами. Например, если в одной части уравнения стоит многочлен, а в другой — тригонометрические функции.
Например, если в одной части уравнения стоит многочлен, а в другой — тригонометрические функции.
б) или если очевидно, что стандартными методами уравнение не решить.
При решении уравнения с помощью метода мажорант , мы, как правило:
- выясняем, что правая часть уравнения больше или равна какого-то числа, а левая — меньше или равна. Или наоборот.
- равенство возможно, если обе части уравнения равны этому числу
- приравниваем ту часть уравнения, которая проще, к этому числу и находим соответствующее значение х
- проверяем, что при этом значении х другая часть уравнения также равна этому числу.
Рассмотрим примеры уравнений такого рода:
1. Решите уравнение:
Очевидно, что мы не будем возводить двучлен в четвертую степень и трехчлен в десятую.
Заметим, что 4 и 10 — четные числа, следовательно,
при любом значении х
и при любом значении х.
Равенство возможно, если одновременно и
Корень первого уравнения ,
корни второго уравнения и . Число является корнем обоих уравнений, его мы и запишем в ответ.
Ответ: 3
2. Решите неравенство:
1. Упростим первый корень:
2. Не будем торопиться раскрывать модуль. Заметим, что оба слагаемых в левой части неравенства неотрицательны, следовательно, правая часть также должна быть неотрицательна, то есть
При этих значениях подмодульное выражение отрицательно, следовательно, раскрываем модуль с противоположным знаком:
В правой и левой частях неравенства стоит выражение . Вычтем его из обеих частей неравенства:
Так как квадратный корень — величина неотрицательная, следовательно, неравенство выполняется только если левая часть равна нулю.
3. Остается решить уравнение
а) Приведем второй логарифм к основанию 2:
б) Преобразуем первое слагаемое:
— мы раскрыли модуль с тем же знаком, так как по ОДЗ исходного неравенства.
в) Теперь мы можем ввести замену переменной: .
Получим уравнение:
Отсюда или
в) Вернемся к исходной переменной:
или
Отсюда или
Легко проверить что только число является решением исходного неравенства. Так как мы не находили ОДЗ, проверку сделать необходимо.
Ответ:
3. a) Решите уравнение:
б) Найдите все корни уравнения, на промежутке
1. Оценим, в каких пределах может принимать значения левая часть неравенства:
Так как все части неравенства положительны, прологарифмируем неравенство:
Итак, левая часть неравенства больше или равны единицы.
2. Оценим, в каких пределах может принимать значения правая часть неравенства:
Получили, что правая часть неравенства меньше или равна единицы.
Равенство возможно, только если обе части одновременно равны 1.
Найдем при каких значениях выполняется равенство
Итак, левая часть уравнения равна 1 при
Найдем при каких значениях х правая часть равна 1.
если
Итак, правая часть уравнения равна 1 при
Это решение должно совпадать с тем значением , при котором левая часть равна 1.
Выпишем значения из промежутка :
При
При
При
При
При — эта точка совпадет с первой точкой и цикл начнется снова.
Вспомним, что левая часть уравнения равна 1 при
Выпишем значения из промежутка
При
При
При
При — эта точка совпадает с первой точкой, и цикл начинается снова.
Мы видим, что при обе части уравнения равны 1.
Итак, решение уравнения
Ответим на вторую часть задания:
б) Найдите все корни уравнения на промежутке
Отметим на тригонометрическом круге полученное решение — эта точка изображена фиолетовым цветом. Она отстоит от на
Она отстоит от на
Мы начинаем движение по кругу из точки , и первое решение, которое нам встречается соответствует углу поворота на
Затем мы проходим по кругу точку 0, точку и следующее решение, которое принадлежит указанному промежутку
Ответ: а)
б) ,
4. Еще один пример, решение уравнения
посмотрите здесь
И.В. Фельдман, репетитор по математике.
Алгебра — полиномиальные неравенства
Существует довольно простой процесс их решения. Если вы сможете это запомнить, вы всегда сможете решить подобные неравенства.
Шаг 1 : Получить ноль на одной стороне неравенства. Однако неважно, на какой стороне ноль, мы будем учитывать его на следующем шаге, так что имейте это в виду, когда будете делать этот шаг. Убедитесь, что у вас есть что-то, что будет легко учитывать.
92} — 3x — 10 < 0\] Шаг 2 : Если возможно, разложите полином на множители. Обратите внимание, что это не всегда возможно учесть, но это ничего не изменит. Этот шаг действительно здесь, чтобы упростить процесс больше всего. Почти все проблемы, которые мы собираемся рассмотреть, будут факторизуемыми.
Обратите внимание, что это не всегда возможно учесть, но это ничего не изменит. Этот шаг действительно здесь, чтобы упростить процесс больше всего. Почти все проблемы, которые мы собираемся рассмотреть, будут факторизуемыми.
\[\влево( {х — 5} \вправо)\влево({х + 2} \вправо) < 0\]
Шаг 3 : Определите, где полином равен нулю. Обратите внимание, что эти точки не сделают неравенство верным (в данном случае), потому что \(0 < 0\) НЕ является истинным неравенством. Это не проблема. Эти точки позволят нам найти фактическое решение.
В нашем случае полином будет равен нулю при \(x = — 2\) и \(x = 5\).
Теперь, прежде чем перейти к следующему шагу, давайте разберемся, зачем нам нужны эти точки.
Мы еще не обсуждали построение графиков полиномов, однако графики полиномов представляют собой приятные гладкие функции, не имеющие разрывов. Это означает, что если мы движемся по числовой прямой (в любом направлении), если значение многочлена меняет знак (скажем, с положительного на отрицательный), то оно ДОЛЖНО перейти через ноль!
Это означает, что если мы движемся по числовой прямой (в любом направлении), если значение многочлена меняет знак (скажем, с положительного на отрицательный), то оно ДОЛЖНО перейти через ноль!
Итак, это означает, что эти два числа (\(x = 5\) и \(x = — 2\)) являются ЕДИНСТВЕННЫМИ местами, где многочлен может менять знак. Затем числовая линия делится на три области. В каждом регионе, если неравенство выполняется для одной точки из этого региона, то оно выполняется для ВСЕХ точек в этом регионе. Если это не так ( т.е. в одной точке области было положительно, а в другой отрицательно), то где-то в этой области тоже должно быть ноль, но этого не может быть, так как мы уже определили все места где многочлен может быть равен нулю! Точно так же, если неравенство не выполняется для какой-то точки в этом регионе, то оно не выполняется для ЛЮБОЙ точки в этом регионе.
Это подводит нас к следующему шагу.
Шаг 4 : Нанесите точки, в которых полином равен нулю (, т. е. точки из предыдущего шага), на числовую прямую и выберите контрольных точек из каждой области. Подставьте каждую из этих контрольных точек в полином и определите знак полинома в этой точке.
е. точки из предыдущего шага), на числовую прямую и выберите контрольных точек из каждой области. Подставьте каждую из этих контрольных точек в полином и определите знак полинома в этой точке.
Это этап процесса, на котором проделана вся работа, хотя он не так уж и плох. Вот числовой ряд для этой задачи.
Теперь поговорим об этом немного. Когда мы выбираем контрольные точки, убедитесь, что вы выбираете простые числа для работы. Поэтому не выбирайте большие числа или дроби, если только проблема не вынуждает вас к этому.
Кроме того, обратите внимание, что мы вставили контрольные точки в факторизованную форму полинома, и все, что нам действительно нужно, это определить, является ли полином положительным или отрицательным. Поэтому мы на самом деле не беспокоились о значениях полинома, а только о знаке, и мы можем получить его из показанного продукта. Произведение двух отрицательных значений равно положительному, и т.д. .
Теперь мы готовы к последнему этапу процесса.
Шаг 5 : Запишите ответ. Напомним, что ранее мы обсуждали, что если какая-либо точка из области удовлетворяет неравенству, то ВСЕ точки в этой области удовлетворяют неравенству, и аналогичным образом, если какая-либо точка из области не удовлетворяет неравенству, то НИ ОДНА из точек в этой области не будет удовлетворять неравенству.
Это означает, что все, что нам нужно сделать, это посмотреть на числовую строку выше. Если контрольная точка из области удовлетворяет неравенству, то эта область является частью решения. Если контрольная точка не удовлетворяет неравенству, то эта область не является частью решения.
Теперь также обратите внимание, что любое значение \(x\), удовлетворяющее исходному неравенству, будет также удовлетворять неравенству из шага 2, и аналогично, если \(x\) удовлетворяет неравенству из шага 2, то оно будет удовлетворять и неравенству из шага 2. исходное неравенство.
Итак, это означает, что все, что нам нужно сделать, это определить области, в которых полином из шага 2 отрицателен. Для этой задачи это только средняя область. Неравенство и обозначение интервала для решения этого неравенства:
Для этой задачи это только средняя область. Неравенство и обозначение интервала для решения этого неравенства:
\[ — 2 < x < 5\hspace{0.5in}\left( {- 2,5} \right)\]
Обратите внимание, что нам нужно исключить конечные точки, поскольку у нас есть строгое неравенство (< в данном случае) в неравенстве.
Линейные неравенства, вариация и решение График Определение линейного неравенства
Решение линейных неравенств Этапы решения неравенств
Пример Эскиз решения для 2x — у < 2 Раствор
Пример Эскиз решения для х + 3 года > 0 Раствор
Упражнения Зарисуйте решение следующего
Теперь попробуйте расположить на одной плоскости следующие неравенства.
Вариация Немного терминологии В текстовых задачах есть несколько фраз, которые встречаются достаточно часто, чтобы дать
им особое внимание.
Мы называем k константа соразмерность . k отражает систему единиц мы работаем с. Помните, что первый шаг после прочтения слова «проблема» — обозначить переменные. Примеры
Проблемы с начальным значением Иногда нам дают информацию о начальных условиях задачи
или какую-то другую информацию. Пример Население земного шара изменяется прямо в зависимости от прошедшего времени. с 1988. В 2002 г. население составляло 7 млрд. Что это будет быть в 2018 году? Решение Позволять п – население мира, t – количество лет, прошедших с 1988 год. п = кт Используя наши начальные условия (обратите внимание, что 2002 г. 14 лет после 1988 г.), 7 = к(14) к = 1/2 В 2018 г. t = 30, следовательно, Р = 1/2(30) = 15 миллиард. В этом году будет 15 миллиардов человек. 2018. Упражнения
Решение с помощью графика Если мы хотим решить систему уравнений, мы можем изобразить их и найти точка пересечения. Пример Решать х — 2 года = 3 2х — у знак равно 7 Мы просто наносим два уравнения на график и определяем точку пересечения. Точка пересечения имеет координаты примерно (3.
Назад на страницу квадратичных функций и линейных неравенств Назад на страницу «Основная алгебра, часть II» Назад к математике Домашняя страница отдела электронная почта Вопросы и предложения |
Рабочие листы по неравенствам
Благодаря достаточной практике наши рабочие листы по неравенствам, которые можно распечатать, содержат множество обучающих материалов, таких как выполнение утверждений о неравенстве, построение неравенств на числовой прямой, построение утверждений о неравенстве на основе графика, решение различных типов неравенств, построение графиков. решения с использованием соответствующих правил и многое другое для учащихся от 6 до старшей школы. Решения неравенств бесконечны и представлены в виде интервала. Начните практиковаться с нашими бесплатными таблицами неравенств!
Эксклюзивные рабочие листы по неравенству
»Перевод фраз неравенства
» Составные неравенства
»Один шаг неравенства
» Графическое линейное неравенство
». Неравенства
Неравенства
Заполнение утверждений о неравенстве
Решите эту партию распечатываемых рабочих листов о неравенствах, вставив каждый из четырех вариантов в утверждение о неравенстве. Учащиеся 6 класса обводят кружком все возможные значения, которые делают утверждение о неравенстве верным.
Графики неравенств на числовой прямой
Нарисуйте неравенство на числовой прямой, нарисовав круг над числом. Заполните его, если неравенство имеет ≥ или ≤, оставьте его незаполненным, если оно имеет > или <. Проведите линию вправо, если число решений больше числа, и влево, если их меньше.
Легкая
Средняя
Запись неравенств по числовым линиям
Изучите график и постройте неравенство, которое лучше всего его описывает. Учащиеся 7 класса ищут незамкнутые и замкнутые круги, следят за направлением линии и быстро строят инклюзивное или строгое большее или меньшее неравенство.
Легкая
Средняя
Идентификация графика решений
Если вы хотите отточить навыки решения и построения графиков неравенств, то эти распечатанные рабочие листы неравенств должны быть вашим очевидным выбором. Учащиеся выбирают график, который лучше всего описывает решение для каждого неравенства с одной переменной.
Выявление неравенств по числовым строкам
Внимательно рассмотрите график в этих PDF-файлах и постройте инклюзивное неравенство с закрытым кругом или строгое неравенство с открытым кругом. Учащиеся 7-го и 8-го классов используют знак <, если линия идет вправо, и >, если линия идет влево.
Идентификация решений в обозначениях интервалов
Сделайте логические выводы, является ли интервал со скобкой или круглыми скобками правильным решением неравенства. Задача в этих PDF-файлах для учащихся 8-х классов и старших классов состоит в том, чтобы выбрать правильную запись интервала, которая лучше всего описывает каждое неравенство.
Задача в этих PDF-файлах для учащихся 8-х классов и старших классов состоит в том, чтобы выбрать правильную запись интервала, которая лучше всего описывает каждое неравенство.
Рабочие листы «Перевод фраз о неравенстве»
Эти рабочие листы, предназначенные для печати, в первую очередь сосредоточены на чтении фраз и преобразовании их в алгебраические неравенства.
(12 листов)
Рабочие листы по одношаговым неравенствам
Вы ищете различные упражнения, чтобы представить или резюмировать одношаговые неравенства? Тогда будьте уверены, что вы находитесь в правильном месте. С множеством PDF-файлов для ваших учеников 6-го класса не будет недостатка в практических материалах.
(51 рабочий лист)
Рабочие листы по неравенствам в два шага
Совершенствуйте свои навыки решения и построения графиков неравенств за два простых шага. Учащиеся 7 класса разделяют одинаковые члены по обе стороны от неравенства. Используйте обратные операции, чтобы изолировать переменную, и решение неравенства станет утиным супом.
Используйте обратные операции, чтобы изолировать переменную, и решение неравенства станет утиным супом.
(51 рабочий лист)
Рабочие листы по многошаговым неравенствам
Методично работайте над решением и построением графиков многошаговых неравенств. Благодаря соответствующей практике, представленной в этих рабочих листах, поиск решений многошаговых неравенств больше не будет крепким орешком для ваших учащихся 8-го класса.
(45 рабочих листов)
Рабочие листы по составным неравенствам
Независимо от того, ищете ли вы неравенства, соединенные вместе союзом «и» или «или», эти рабочие листы по неравенствам расширят практику и подготовят учащихся старших классов к решению и построению графиков таких неравенств.
(51 рабочий лист)
Графики линейных неравенств. Рабочие листы
Визуализируйте неравенство на графике, проанализируйте свойства линии, наблюдайте за графиком и определите неравенство, зарисуйте график неравенства — вот несколько упражнений, представленных здесь, чтобы бросить вызов вашим старшеклассникам.

 М.
М. 11.2019
4083
11.2019
4083
 12.2020
4321
0
12.2020
4321
0

 08.2020
2782
08.2020
2782
 Рациональные неравенства.
Рациональные неравенства.
 03.2019
279
0
03.2019
279
0
 04.2020
50
0
04.2020
50
0



 \)≤1\)
\)≤1\)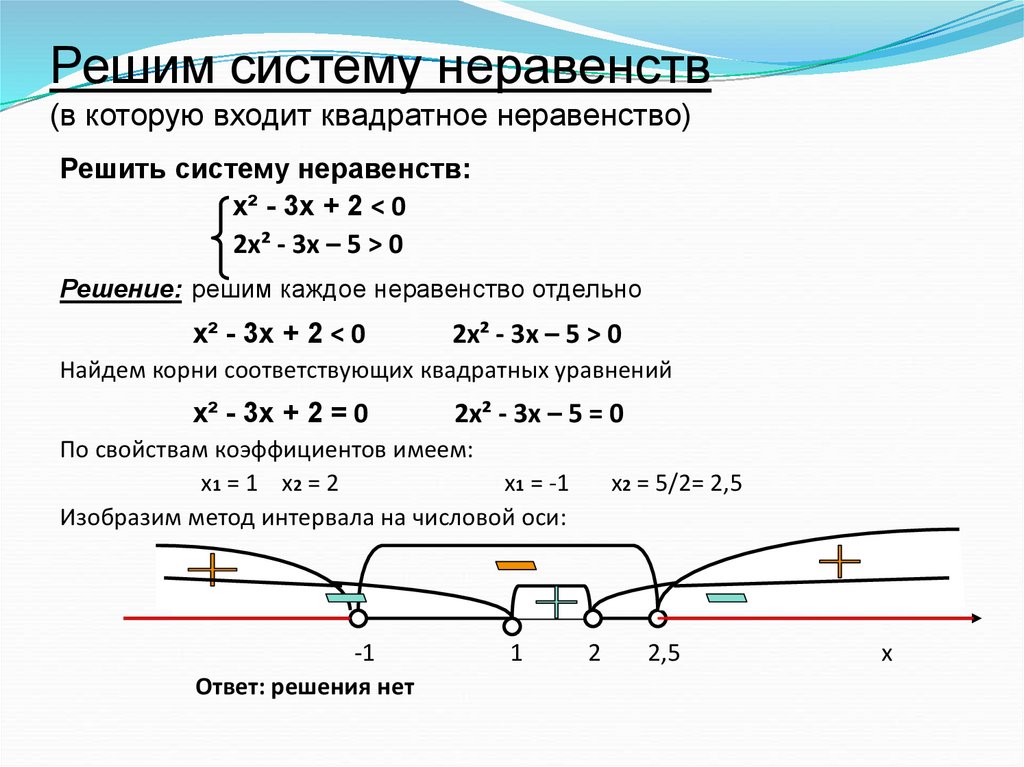

 Если уравнение дает (0,0) в виде точки, начертите другую удобную
точка, например, когда x = 1.
Если уравнение дает (0,0) в виде точки, начертите другую удобную
точка, например, когда x = 1.

 Вот словарь:
Вот словарь:
 Мы можем использовать эту информацию, чтобы найти k.
Найдя k, мы можем ответить на вопрос.
Мы можем использовать эту информацию, чтобы найти k.
Найдя k, мы можем ответить на вопрос. дюймов. Насколько большим он будет после
3 секунды?
дюймов. Насколько большим он будет после
3 секунды?  7,0.5).
Это только оценка. В следующем разделе мы покажем, как найти
точное решение
7,0.5).
Это только оценка. В следующем разделе мы покажем, как найти
точное решение