График y ln 1 x: Mathway | Популярные задачи

2

Полное исследование функции и построение графика : y= ln ((x+1)/(1-x)) — вопрос №2621047 — Учеба и наука

Ответы

Можно договорится по чату. 15.10.17

научу графикам в чате. 15.10.17

15. 10.17

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Решено

1) Постройте график функции y=x^2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…

Решено

вычислить скалярное произведение векторов m и n, если m=a + 2b — c, n=2a — b. /a/=2. /b/=3. угол между а и b равен 60 градусов. с перпендикулярно а, с перпендикулярно b

22 футболиста сыграли три тренировочных игры (разбиваясь каждый раз на два состава по 11 человек). Докажите, что какие-то два футболиста все три раза были соперниками.

Решено

Дан куб ABCDA1B1C1D1 Найдите угол между прямыми AD1 и BM, где М-середина ребра DD1

Решено

В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.

Пользуйтесь нашим приложением

y-1)ln(1-x)=0 [-2.5, 2.5, -1.25, 1.25]}

@a-s-adikesavan

Я включил свои комментарии в ответ, а не как комментарий из-за всех математика:

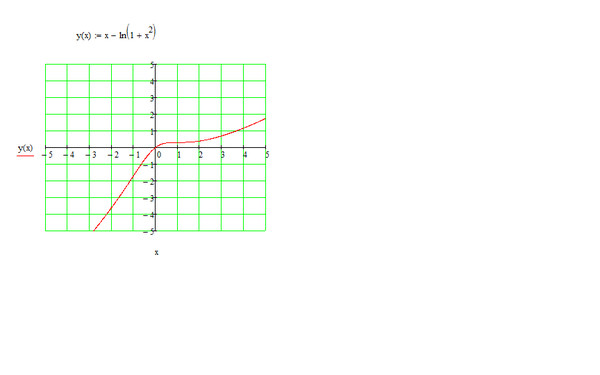
Для области определения функции:

Условие 1

#1-x>0#, так что #ln(1-x) в RR => color(red)(x<1)#
Это согласуется с вашим ответом

Условие 2
Я получаю другой результат для 2-го условия; следующим образом

#1+x/ln(1-x) > 0#, так что #ln(1+x/ln(1-x)) в RR#

При решении неравенства нужно быть осторожным со знаком знаменателя #ln(1-x)# и соответствующим образом изменить направление неравенства.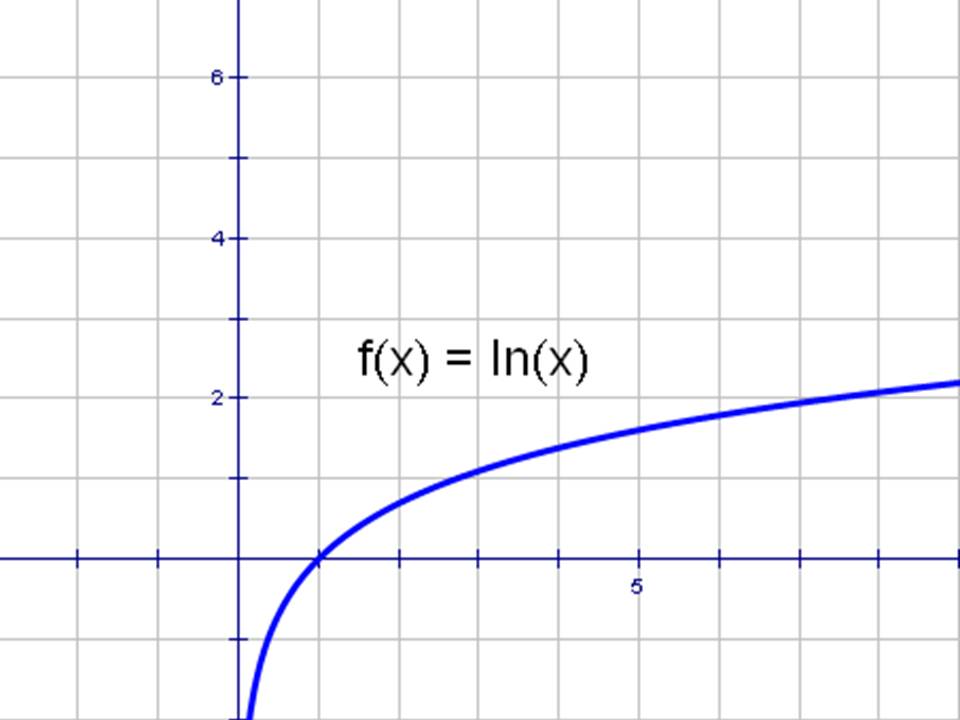

Используя тот факт, что для любого #A в RR#:

# ln A \ \ \ { (>0), (=0), (<0) :} \ \ iff {: (A>1), (A=1), (A<1) :}#

Давайте рассмотрим три случая:

Случай 1: #\ \ color(blue)(ln(1-x)>0)#

#ln(1-x)>0 =>1-x>1=>x<0 #
С учетом этого требования имеем:
#1+x/ln(1-x) > 0 #
# :. ln(1-x)+x>0 # (как #ln(1-x)>0#)
И это не имеет реальных решений:

Случай 2: #\ \ color(blue)(ln(1-x)=0)#

#ln(1-x)=0 =>1-x=1=>x=0 #
В этом случае #x/ln(1-x)# имеет неопределенную форму #0/0#, поэтому давайте воспользуемся правилом Лопиталя, чтобы найти предел:
#lim_(x rarr 0)(1+x/ln(1-x)) = 1+lim_(x rarr 0)(x/ln(1-x) )#
#» «= 1+lim_(x rarr 0)(1/(1/(1-x)(-1)))#
#» «= 1-1#
#» «= 0#
и как мы требуем #1+x/ln(1-x)>0# мы можем устранить это.

Случай 3: #\ \ color(blue)(ln(1-x)<0)#

#ln(1-x)<0 =>1-x<1=>x>0 #
С учетом этого требования имеем:
#1+x/ln(1-x) > 0 #
# :.

No related posts.