Разница между рациональными и иррациональными числами
- 2019
Математика — не что иное, как игра чисел. Число — это арифметическое значение, которое может быть цифрой, словом или символом, обозначающим количество, которое имеет много последствий, таких как подсчет, измерения, вычисления, маркировка и т. Д. Числа могут быть натуральными числами, целыми числами, целыми числами, действительными числами, сложными номера. Действительные числа далее делятся на рациональные числа и иррациональные числа. Рациональные числа
Как объединить кор…
Please enable JavaScript
Как объединить короткое красное платье
— это числа, которые являются целыми и дробными
С другой стороны, иррациональные числа — это числа, выражение которых в виде дроби невозможно. В этой статье мы собираемся обсудить различия между рациональными и иррациональными числами.
Сравнительная таблица
| Основа для сравнения | Рациональное число | Иррациональные числа |
|---|---|---|
| Имея в виду | Рациональные числа относятся к числу, которое может быть выражено в соотношении двух целых чисел. | Иррациональное число — это число, которое нельзя записать в виде отношения двух целых чисел. |
| Доля | Выражается в дроби, где знаменатель ≠ 0. | Не может быть выражено в долях. |
| Включает в себя | Совершенные квадраты | Surds |
| Десятичное расширение | Конечные или повторяющиеся десятичные дроби | Не конечные или не повторяющиеся десятичные дроби. |
Определение рациональных чисел
Термин «отношение» получен из слова «отношение», которое означает сравнение двух величин и выражается в простой дроби. Число называется рациональным, если оно может быть записано в виде дроби, такой как p / q, где и p (числитель), и q (знаменатель) являются целыми числами, а знаменатель — натуральное число (ненулевое число).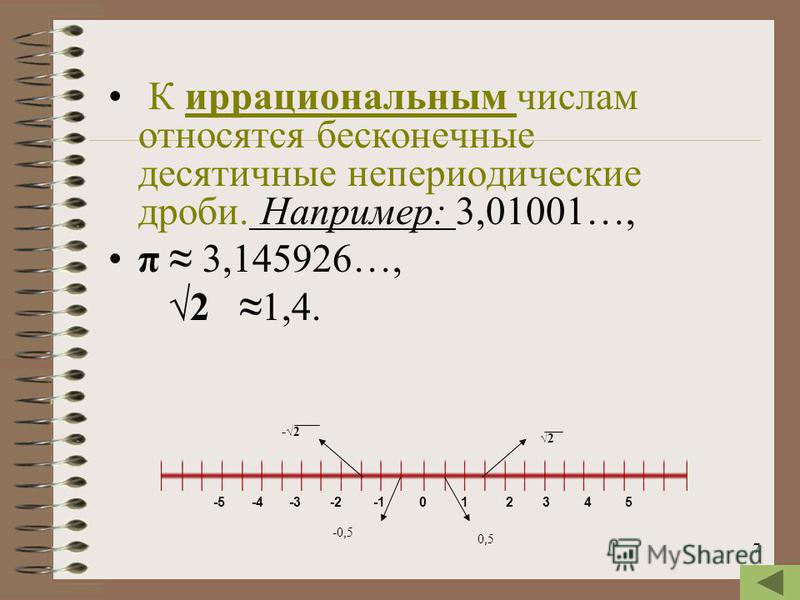
Целые числа, дроби, включая смешанную дробь, повторяющиеся десятичные дроби, конечные десятичные дроби и т. Д., Являются рациональными числами.
Примеры рационального числа
- 1/9 — числитель и знаменатель являются целыми числами.
- 7 — Можно выразить как 7/1, где 7 — это целое число 7 и 1.
- √16 — поскольку квадратный корень может быть упрощен до 4, что является частным дроби 4/1
- 0, 5 — Может быть записано как 5/10 или 1/2, и все заканчивающиеся десятичные дроби являются рациональными.
- 0.3333333333 — Все повторяющиеся десятичные дроби рациональны.
Определение иррациональных чисел
Число называется иррациональным, когда его нельзя упростить до какой-либо доли целого числа (x) и натурального числа (y). Это также может быть понято как число, которое нерационально. Десятичное разложение иррационального числа не является ни конечным, ни повторяющимся. Он включает в себя дополнительные числа и специальные числа, такие как π («пи» — наиболее распространенное иррациональное число) и e.
Surd — это несовершенный квадрат или куб, который нельзя уменьшить, чтобы удалить квадратный корень или кубический корень.
Примеры иррационального числа
- √2 — √2 не может быть упрощено, и поэтому оно нерационально.
- √7 / 5 — данное число является дробью, но это не единственный критерий, который следует называть рациональным числом. И числитель, и знаменатель должны быть целыми числами, а √7 не является целым числом. Следовательно, данное число нерационально.
- 3/0 — дробь с нулевым знаменателем, иррациональна.
- π — поскольку десятичное значение π никогда не заканчивается, никогда не повторяется и никогда не показывает какого-либо шаблона. Следовательно, значение pi не точно равно любой дроби. Число 22/7 является справедливым и приблизительным.
- 0.3131131113 — Десятичные дроби не заканчиваются и не повторяются. Поэтому его нельзя выразить как частное от дроби.
Различие между рациональными и иррациональными числами может быть ясно показано на следующих основаниях
- Рациональное число определяется как число, которое может быть записано в соотношении двух целых чисел.
Иррациональное число — это число, которое не может быть выражено в соотношении двух целых чисел. - В рациональных числах и числитель, и знаменатель являются целыми числами, где знаменатель не равен нулю. Пока иррациональное число нельзя записать дробью.
- Рациональное число включает числа, которые являются идеальными квадратами, такими как 9, 16, 25 и так далее. С другой стороны, иррациональное число включает в себя такие числа, как 2, 3, 5 и т. Д.
- Рациональное число включает только те десятичные дроби, которые являются конечными и повторяющимися. Наоборот, иррациональные числа включают те числа, десятичное разложение которых бесконечно, неповторяюще и не показывает паттерна.
Иррациональное число — это число, которое не может быть выражено в соотношении двух целых чисел.Заключение
Изучив вышеприведенные пункты, совершенно ясно, что выражение рациональных чисел может быть возможным как в дробной, так и в десятичной форме. Напротив, иррациональное число может быть представлено только в десятичной форме, но не в виде дроби. Все целые числа являются рациональными числами, но все нецелые числа не являются иррациональными числами.
Понятие о вещественных (действительных) числах, рациональные и иррациональные числа
| Справочник по математике | Арифметика | Рациональные и иррациональные числа |
Содержание
| Рациональные и иррациональные числа. Понятие о вещественных числах |
| Иррациональность числа |
| Десятичные приближения иррациональных чисел с недостатком и с избытком |
Рациональные и иррациональные числа. Понятие о вещественных числах
Целые числа и рациональные дроби (простые дроби и смешанные числа) составляют множество рациональных чисел, которое принято обозначать буквой Q .
Каждое из рациональных чисел можно представить в виде
,
где m – целое число, а n – натуральное число.
При обращении рациональных дробей в десятичные дроби получаются конечные и бесконечные периодические десятичные дроби.
Числа
и т.п. являются примерами иррациональных чисел.
Иррациональные числа нельзя представить в виде дроби, числитель которой является целым числом, а знаменатель натуральным числом.
При обращении иррациональных чисел в десятичные дроби получаются бесконечные непериодические десятичные дроби. Множество иррациональных чисел бесконечно.
Множество рациональных и иррациональных чисел составляют множество вещественных (действительных) чисел.
Множество вещественных чисел обозначают буквой R .
Иррациональность числа
Проведем доказательство иррациональности числа методом «от противного».
С этой целью предположим, что число является рациональным числом. Тогда существует дробь вида
,
удовлетворяющая равенству
и такая, у которой числитель и знаменатель являются натуральными числами, не имеющими простых общих делителей.
Используя данное равенство, получаем:
Отсюда вытекает, что число m2 является четным числом, а, значит, и число m является четным числом. Действительно, если мы предположим противное, т.е. предположим, что число m является нечетным числом, то найдется такое целое число k , которое удовлетворяет соотношению
m = 2k + 1 .
Следовательно,
m2 = (2k + 1)2 =
= 4k2 + 4k +1 ,
т.е. m является нечетным числом. Полученное противоречие доказывает, что число m является четным числом.
Значит, найдется такое целое число k , которое удовлетворяет соотношению
m = 2k .
Поэтому,
Отсюда вытекает, что число n2 является четным, а, значит, и число n является четным числом.
Итак, число m является четным, и число n является четным, значит, число 2 является общим делителем числителя и знаменателя дроби
.
Полученное противоречие доказывает, что несократимой дроби, удовлетворяющей соотношению
не существует. Следовательно, число является иррациональным числом, что и требовалось доказать.
Десятичные приближения иррациональных чисел с недостатком и с избытком
Разберем понятие десятичных приближений иррациональных чисел с недостатком и с избытком на конкретном примере.
Для этого рассмотрим иррациональное число
Это число, как и любое другое иррациональное число, изображается бесконечной непериодической десятичной дробью.
Последовательностью десятичных приближений числа с недостатком называют последовательность конечных десятичных дробей, которая получится, если у числа отбросить все десятичные знаки, начиная, сначала с первого десятичного знака, затем со второго десятичного знака, потом с третьего десятичного знака и т.д.
Если последний десятичный знак каждого десятичного приближения числа с недостатком увеличить на 1 , то получится десятичное приближение числа с избытком.
Само число располагается между каждым своим приближением с недостатком и соответствующим ему приближением с избытком.
Для числа возникающая бесконечная последовательность десятичных приближений с недостатком и с избытком, имеет следующий вид:
и т.
д.
Точно также можно построить последовательность десятичных приближений с недостатком и с избытком для любого иррационального числа.
Рациональные и иррациональные числа — математический обзор (видео и практика)
TranscriptFAQsPractice
Привет! Добро пожаловать в это видео о рациональных и иррациональных числах!
Рациональные и иррациональные числа составляют систему действительных чисел . Эта диаграмма Венна показывает визуальное представление того, как классифицируются действительные числа.
натуральных чисел составляют наименьшее подмножество, также известное как множество «счетных» чисел. Это все положительные недесятичные значения, начинающиеся с единицы. Целые числа — это натуральные числа плюс ноль. Набор целых чисел включает целые числа и все отрицательные недесятичные значения.
Рациональные числа включают наборы, показанные здесь, в дополнение к дробным значениям между ними.
Простой способ запомнить это — слово ratio в названии этой классификации. Все числа, входящие в набор рациональных чисел, можно записать в виде отношения целых чисел:
Если \(a\) и \(b\) целые числа: рациональные числа можно записать как \(\frac{a}{b}\), если \(b\neq 0\).
Ясно, что множество целых чисел можно записать в виде отношений, потому что любое целое число, деленное на 1, дает исходное целое число. Как показано здесь, целые числа могут быть выражены в виде дробей бесконечным числом способов.
Целое число 3 можно представить в виде дробей \(\frac{3}{1}\), \(\frac{6}{2}\), \(\frac{-24}{-8) }\)
Целое число -5 может быть представлено в виде следующих дробей \(\frac{-5}{1}\), \(\frac{5}{-1}\), \(\frac{-25}{5 }\)
Целое число 0 может быть представлено в виде дробей \(\frac{0}{3}\), \(\frac{0}{-2}\), \(\frac{0}{123} \)
В качестве примечания, это не единственные дроби, которые приводят к этим целым числам, это лишь некоторые из множества существующих примеров.
Дроби также могут быть записаны в виде десятичных дробей. Например:
.1 эквивалентно \(\frac{1}{10}\), потому что 1 находится в десятых десятичных разрядах
.13 эквивалентно \(\frac{13}{100}\) потому что 3 находится в сотых десятичных разрядах, а единица в десятых десятичных разрядах
.237 эквивалентно \(\frac{237 }{1,000}\), потому что 7 находится в тысячных десятичных разрядах, и так далее.
Эти десятичные числа можно записать в виде дробей, поэтому они считаются рациональными.
Другие десятичные числа имеют повторяющихся шаблонов. Они также считаются рациональными, поскольку могут быть выражены в виде дроби на основании следующего доказательства:
Повторяющаяся десятичная дробь \(2.\overline{17}\) представляет цифры \(2.1717171717\)…
Давайте попробуем это в качестве практической задачи.
Пусть \(x=2.
\overline{17}\). Повторяющаяся десятичная дробь состоит из двух цифр, что представляет сотые доли.
Итак, давайте умножим обе части уравнения на 100:
В результате получится \(100x=217,17171717\)…, что равно \(217,17\) повторения.
Мы перемещаем десятичную дробь на два знака, потому что мы умножили на 100. Теперь давайте вычтем исходное уравнение из этого:
| \(100x\) | \(=217,171717\)… | |
| \(–\)\(x\) | 9 \(=007\871 902,171 3||
| \( 99x\) | \(=215\) |
Обратите внимание, что повторяющаяся часть десятичной дроби теперь удалена.
Решение для \(x\) дает \(x=\frac{215}{99}\).
Итак, \(99x\) равно \(215\). Обратите внимание, что повторяющаяся часть десятичной дроби теперь удалена. Решение для \(x\) приводит к делению обеих частей на \(99\): \(x = \frac{215}{99}\).
Это дробное представление \(x=2.\overline{17}\).
Это доказательство показывает, что повторяющиеся десятичные числа также считаются рациональными, поскольку их можно записать в виде дроби целых чисел.
Если вы подключите это к своему калькулятору, вы получите что-то близкое, возможно, округленное, к 2,17 повторения.
Важно отметить, что не все десятичные дроби повторяются. Некоторые десятичные дроби имеют бесконечное число неповторяющихся цифр и, следовательно, не могут быть выражены в виде доли целых чисел. Эти типы действительных чисел классифицируются как иррациональный . Хотя в действительной системе счисления существует бесконечное количество иррациональных чисел, в математике чаще всего используются квадратные корни несовершенных квадратов, например, квадратный корень из 2, а также константы π и e. Обозначение иррациональных чисел позволяет повысить эффективность математических приложений.
Для геометрии вы можете вспомнить, что π = 3,14159… для бесконечности. Это получено из длины окружности любого круга и его диаметра. Поскольку десятичное значение неповторяющееся и бесконечное, мы используем приблизительное значение в математических приложениях. Бизнес-приложения, касающиеся непрерывного начисления процентов, используют иррациональное значение e, которое снова имеет приблизительное значение 2,718 для бесконечности.
Спасибо за просмотр и удачной учебы!
Часто задаваемые вопросы
Q
Все ли целые числа рациональные?
A
Да, рациональное число — это любое число, которое можно представить в виде дроби. Все целые числа подходят под это определение.
Q
Рациональны ли отрицательные числа?
A
Да, большинство отрицательных чисел рациональны. Рациональное число — это любое число, которое можно представить в виде дроби. К ним относятся целые числа, дроби, десятичные дроби, которые заканчиваются, и десятичные дроби, которые повторяются. Положительное и отрицательное не влияют на рациональность.
Q
Все ли рациональные числа являются целыми числами?
A
Нет, не все рациональные числа являются целыми числами. К рациональным числам относятся все числа, которые заканчиваются или повторяются. Целое число — это любое число без дробной части, которое больше или равно нулю.
пр. 2,7 — рациональное число, но не целое.
Q
В чем разница между рациональными и иррациональными числами?
A
Разница между рациональными и иррациональными числами заключается в том, что рациональное число можно представить в виде точной дроби, а иррациональное число — нет. Рациональное число включает в себя любое целое число, дробь или десятичное число, которое заканчивается или повторяется. Иррациональное число — это любое число, которое нельзя превратить в дробь, то есть любое число, не подпадающее под определение рационального числа.
Практические вопросы
Вопрос №1:
Рационально ли число π?
Да
Нет
Иногда
Невозможно определить
Показать ответ
Ответ:
Правильный ответ — нет.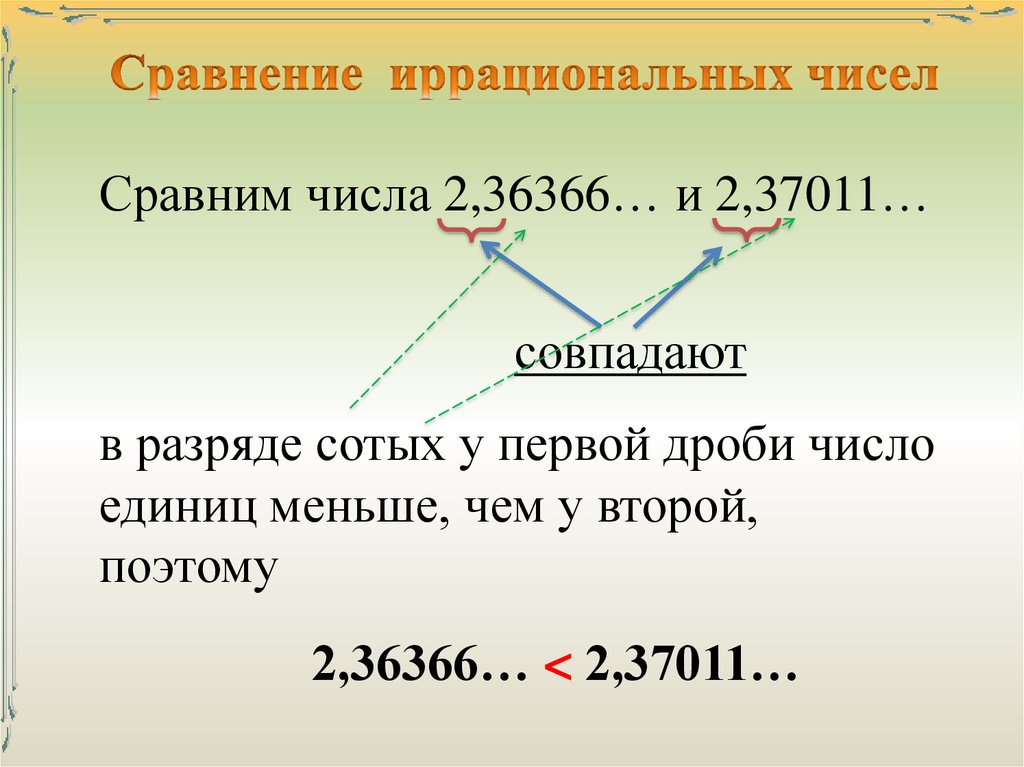
Пи (π) — иррациональное число, потому что это бесконечная десятичная дробь, которую нельзя упростить до точной дроби.
Скрыть ответ
Вопрос № 2:
Является ли \(1.\overline{3}\) рациональным числом?
Да
Нет
Иногда
Невозможно определить
Показать ответ
Ответ:
Правильный ответ — да. \(1.\overline{3}\) можно представить в виде дроби \(1\frac{1}{3}\), что означает, что оно рационально. Любое число, которое можно представить в виде дроби, считается рациональным.
Скрыть ответ
Вопрос № 3:
Какое из следующих чисел является примером рационального числа?
π
\(\sqrt{2}\)
4.17
\(4-\sqrt{7}\)
Показать ответ
Ответ: 7.
00403 90 Это единственное число из этого списка, которое можно превратить в дробь, \(4\frac{17}{100}\).
Скрыть ответ
Вопрос № 4:
Какое из следующих чисел является иррациональным?
\(\frac{17}{3}\)
13
\(2.\overline{97}\)
\(\sqrt{3}\)
Показать ответ
Ответ:
Правильный ответ: \(\sqrt{3}\). Квадратные корни несовершенных квадратов нерациональны, потому что они равны бесконечному десятичному числу, а это значит, что это число нельзя превратить в дробь.
Скрыть ответ
Вопрос № 5:
Является ли \(\frac{7}{9}\) рациональным?
Да
Нет
Иногда
Невозможно определить
Показать Ответ
Ответ:
Правильный ответ — да.
Рациональное число — это любое число, которое можно превратить в дробь, а \(\frac{7}{9}\) — это дробь. Скрыть ответ
Последнее обновление by Surbhi S
Математика — не что иное, как игра с числами. Число — это арифметическое значение, которое может быть цифрой, словом или символом, указывающим количество, которое имеет множество значений, таких как подсчет, измерения, расчеты, маркировка и т. д. Числа могут быть натуральными числами, целыми числами, целыми числами, действительными числами, комплексными числами. числа. Действительные числа далее делятся на рациональные числа и иррациональные числа.
На другом конце Иррациональные числа — это числа, выражение которых в виде дроби невозможно. В этой статье мы собираемся обсудить различия между рациональными и иррациональными числами. Взгляни.
Содержание: Рациональные и иррациональные числа
- Сравнительная таблица
- Определение
- Ключевые отличия
- Заключение
Сравнительная таблица
| Основание для сравнения | Рациональные числа | Иррациональные числа |
|---|---|---|
| Значение | Рациональные числа — это числа, которые могут быть выражены в виде отношения двух целых чисел. | Иррациональное число — это число, которое нельзя записать как отношение двух целых чисел. |
| Дробь | Выражается дробью, где знаменатель ≠ 0. | Не может быть выражен дробью. |
| Включает | Идеальные квадраты | Сурд |
| Десятичное расширение | Конечные или повторяющиеся десятичные дроби | Неконечные или неповторяющиеся десятичные дроби. |
Определение рациональных чисел
Термин «отношение» происходит от слова «отношение», которое означает сравнение двух величин, выраженное простой дробью. Число называется рациональным, если его можно записать в виде дроби, такой как p/q, где p (числитель) и q (знаменатель) являются целыми числами, а знаменатель — натуральным числом (ненулевым числом). Целые числа, дроби, включая смешанные дроби, повторяющиеся десятичные дроби, конечные десятичные дроби и т. д. — все это рациональные числа.
Примеры рационального числа
- 1/9 – И числитель, и знаменатель являются целыми числами.
- 7 — может быть выражено как 7/1, где 7 — это частное целых чисел 7 и 1.
- √16 — поскольку квадратный корень можно упростить до 4, что является частным от дроби 4/1
- 0,5 — может быть записано как 5/10 или 1/2, и все конечные десятичные дроби рациональны.
- 0.3333333333 – Все повторяющиеся десятичные дроби рациональны.
Определение иррациональных чисел
Число называется иррациональным, если его нельзя упростить до какой-либо доли целого числа (x) и натурального числа (y). Его также можно понимать как иррациональное число. Десятичное расширение иррационального числа не является ни конечным, ни повторяющимся. Он включает в себя surds и специальные числа, такие как π («пи» — наиболее распространенное иррациональное число) и e. Сурд — это несовершенный квадрат или куб, который нельзя уменьшить, чтобы удалить квадратный или кубический корень.
Примеры иррационального числа
- √2 – √2 не может быть упрощено и поэтому иррационально.
- √7/5 – Данное число является дробью, но это не единственный критерий, который можно назвать рациональным числом. И числитель, и знаменатель должны быть целыми числами, а √7 не является целым числом. Следовательно, данное число иррационально.
- 3/0 — Дробь со знаменателем ноль, иррациональна.
- π — поскольку десятичное значение π бесконечно, никогда не повторяется и никогда не показывает какой-либо закономерности. Следовательно, значение числа пи не равно какой-либо дроби. Число 22/7 просто и приблизительно.
- 0,3131131113 — Десятичные дроби не являются ни конечными, ни повторяющимися. Поэтому его нельзя выразить как частное дроби.
Основные различия между рациональными и иррациональными числами
Разницу между рациональными и иррациональными числами можно ясно увидеть на следующих основаниях
- Рациональное число определяется как число, которое можно записать в виде отношения двух целых чисел.
