Построение графиков, содержащих выражения под знаком модуля
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Построение графиков, содержащих выражения под знаком модуля
2. Цель работы:
построение графиков функций,содержащие выражения под знаком
модуля
3. Частный случай (под знаком модуля одно выражение и нет слагаемых без модуля)
1) построить график функции, опустив знакмодуля
2) отобразить симметрично оси Ох часть
графика, расположенного в области
отрицательных значений у.

4. Построить график функции:
у = |0,5х|у = |о,5х-3|
у
у
1
1
х
0 1
0
х
6
8
5. Построение графиков, содержащих выражения под знаком модуля
1) найти корни выражений, стоящих под знакоммодуля;
2) на числовой прямой проставить эти корни;
3) в каждом промежутке определить вид
функции;
4) построить график в каждом промежутке.
6. Построить график функции:
у =|3х+4|-2Решение: 3х+4=0
1
х = 1 3
Координатная плоскость
разбивается прямой х = 1 1
3
на две полуплоскости:
1
1) х< 1 3
у =-(3х+4)-2
х
у
у =-3х-6
-2
0
-3
3
1
2) х≥ 1 3
у=3х+4-2
х
у
у=3х+2
-1
-1
0
2
у
2
1
-2
1
3
1
0
-1
-2
х
7. Построить график функции:
у=|х-1| -|2 — х| + 2Решение: х=1
1) х<1
у=-х+1-2+х+2
у=1
2) -1 ≤ х≤ 2
у=х-1-2+х+2
у=2х-1
3) х>2
у =х-1+2-х+2
у=3
у
х=2
х
1
2
у
1
3
3
2
1
0
1 2
у=|х-1| — |2-х| +2
х
8.
 a) у=|х — 1|+|2 — х| +2Решение:
a) у=|х — 1|+|2 — х| +2Решение:у
у=|х-1|-|2-х|+2
3
2
1
0
1
2
х
х=1; х=2
1) х< 1
у=-х+1-2+х+2
у=1
2) 1≤х≤ 2
у=х-1-2+х+2
у=2х -1
3) х>2
у=х-1+2-х+2
у=3
х у
1 1
2 3
9. b) y=|3х|-3х; c) y=|х-3|+|1-х|+4;
b) y=|3х|-3х;Решение:
Решение:
0, х≥0
y=
-6х, х<0
y
6
1
-1 0
c) y=|х-3|+|1-х|+4;
y=│3x│-3
x
х=1, х=3
1) x≤1
y= -x+3+1-x-4
y=-2x
2) 1≤x≤3
y=-x+3-1+x-4
1
y=-2
0
3) x≥3
-2
y=x-3-1+x-4
y=2x-8
y
1
3
x
10. d) y=|5-х|-|2-х|-3; e) y=7-|х-1|+|х+5|;
Решение:1) х≤2
y=5-х-2+х-5
y=0
2) 2≤х≤5
y=5-х+2-х-3
y=-2х+4
0
3) x≥5
y=-5+х+2-х-3
y=-6
-6
y
1 2
5
x
y=│5-x│-│2-x│-3
Решение:
1) х≤-5
y=7+х-1-х-5
y=1
2) -5≤х≤1
y=7+х-1+х+5
y=2х+11
3) x≥1
y=7-х+1+х+5 -5
y=13
y
13
1
0
1
x
11.
 f) y=|х-5|-|5-х|; k) y= -|3-х|+|2-х|-3Решение:
f) y=|х-5|-|5-х|; k) y= -|3-х|+|2-х|-3Решение:x=5
1) х≤5
y=-х+5+5-х
y=-2х+10
x y
5 0
3 4
2) x≥5
y=x-5-5+x
y=2x-10
x y
5 0
3 -4
Решение:
1) х≤2
y=-4
2) 2≤х≤3
y=2х-8
y
x y
4
1
0
-4
y
3
2 -4
5 2
5
x
3) x≥3
y=-2
1
0
-2
-4
1 2
y=-│3-x│+│2-x│-3
3
x
12. l) y=| х-2|+|3+ х|-3
l)Решение:
2
1
y=|3 х-2|+|3+ 3
х|-3
x=6; х=-4,5
1)
х≤-4,5
1
2
y=- х+ 2-3 — х-3
3
2)
х
3
у
-4,5 0,5
y=-х-4
-4,5≤х≤6
y=- 1x+2+3+2 x-3
3
3
1
y= x+2
3
3)
y
x≥6
1
2
y= 3 x-2+3+ 3 x-3
y=x-2
-5 1
7
4
х
у
3
3
6
4
х
у
6
9
4
7
1
-4,5
0
-1
1
1
2
y=│ x-2│+│3+ x│-3
3
3
6
9
x
13. Вывод:
Решите уравнение: │х-3│+│1-х│=4(х=3; х=1)
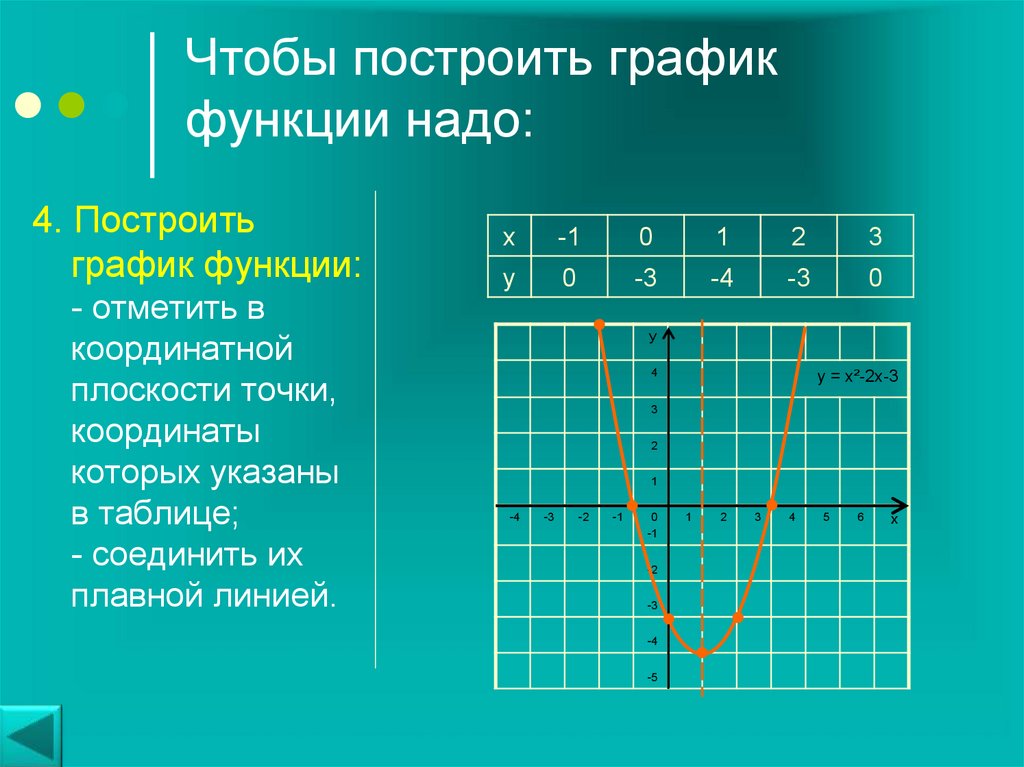
Постройте график функции: y= │х-3│+│1-х│- 4
Имея корни решенного уравнения и
рассматривая график построенной функции,
делаем вывод: корни данного уравнения – это
координаты точки пересечения графика с осями
координат.
Таким образом строим графики функций,
содержащие выражения под знаком модуля
опираясь на решение уравнения, содержащего
выражения под знаком модуля.
14. Занимательная графика
yПостроив графики нескольких
функций в одной прямоугольной
системе координат, получим
некое «произведение искусств».
6
. .
2
-1 0
1
3
4
6
7
х
English Русский Правила
Основные правила преобразования графиков функций 9 класс онлайн-подготовка на Ростелеком Лицей
Введение
Наверняка многие из вас могут быстро и правильно построить графики некоторых функций, не прибегая к вычислениям значений точек. Всем известно, что график функции – это прямая, а график функции – это парабола. Но как построить, например, график функции , не вычисляя значения точек? Для этого существуют правила преобразования графиков функций.
Преобразование симметрии относительно оси
Ox
Предположим, что у нас есть функция (график этой функции – это парабола) и необходимо построить график функции .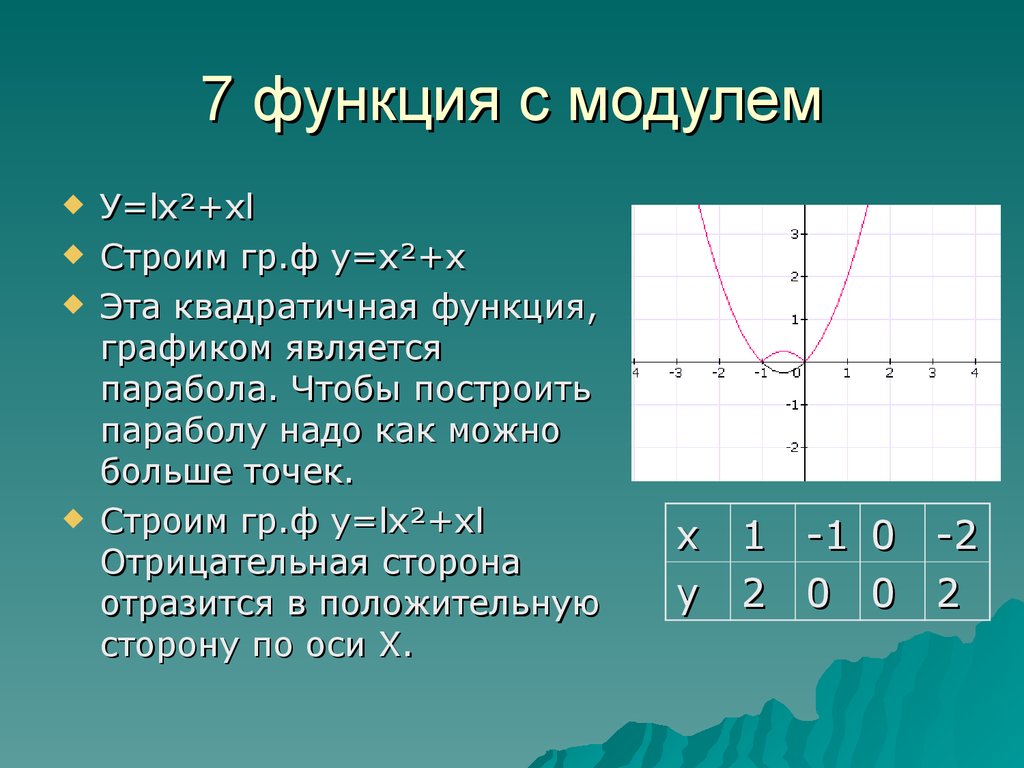 Вычислим значения некоторых точек для графиков этих функций.
Вычислим значения некоторых точек для графиков этих функций.
Из таблиц видно, что одним и тем же значениям аргумента соответствуют противоположные значения функций. Графически это означает, что графики расположены симметрично относительно оси абсцисс. То есть заданная парабола () зеркально отобразится относительно оси (см. Рис. 1).
Рис. 1. Графики функций и
Таким образом, если у нас есть произвольный график , то для построения графика необходимо график симметрично отразить относительно оси (см. Рис. 2). Такое преобразование называется преобразованием симметрии относительно оси .
Рис. 2. Преобразование симметрии относительно оси
Преобразование симметрии – зеркальное отражение относительно прямой.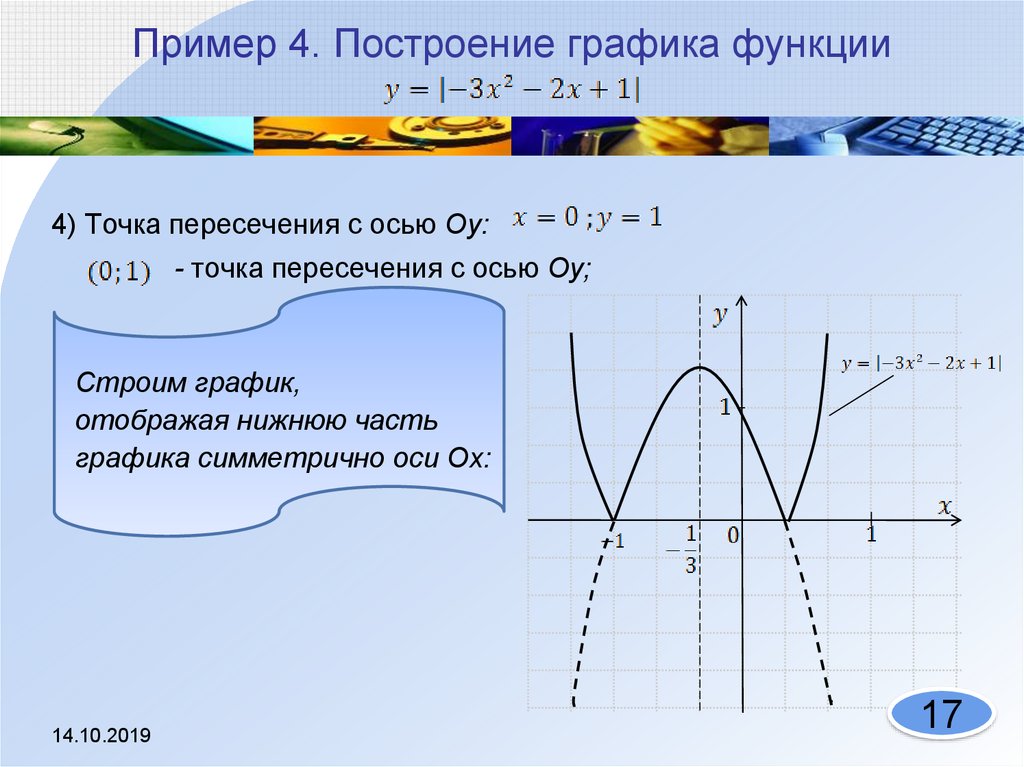 График получается из графика функции преобразованием симметрии относительно оси .
График получается из графика функции преобразованием симметрии относительно оси .
На рисунке 3 показаны примеры симметрии относительно оси .
Рис. 3. Симметрия относительно оси Ox
Параллельный перенос вдоль оси Oy
Предположим, что у нас есть функция (график этой функции – это парабола) и необходимо построить график функции . Вычислим значения некоторых точек для графиков этих функций.
Из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика больше на 3 единицы. Графически это означает, что график функции находится на 3 единицы выше, чем график функции (см. Рис. 4).
Рис. 4. Графики функций и
4. Графики функций и
График получается из графика функции параллельным переносом последнего вдоль оси ординат на единиц вверх, если , и на единиц вниз, если (см. Рис. 5, 6).
Рис. 5. Параллельный перенос вдоль оси (при )
Рис. 6. Параллельный перенос вдоль оси (при )
Растяжение от оси Ox и сжатие к оси Ox
Предположим, что у нас есть функция (график этой функции – это парабола) и необходимо построить график функции . Вычислим значения некоторых точек для графиков этих функций.
Из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика больше в 2 раза.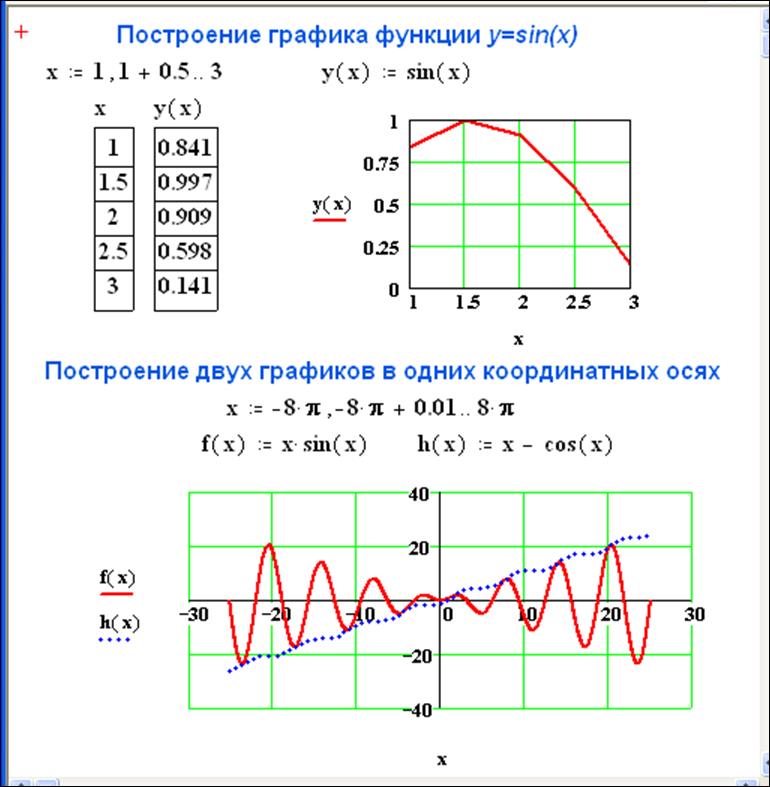 Графически это означает, что график функции сужается по сравнению с графиком функции (см. Рис. 7).
Графически это означает, что график функции сужается по сравнению с графиком функции (см. Рис. 7).
Рис. 7. Графики функций и
Если необходимо построить график функций , то из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика меньше в 2 раза, чем у . Графически это означает, что график функции расширяется по сравнению с графиком функции (см. Рис. 8).
Рис. 8. Графики функций и
Чтобы построить график функции , где и , нужно ординаты точек заданного графика умножить на . Такое преобразование называется растяжением от оси с коэффициентом , если , и сжатием к оси, если (см.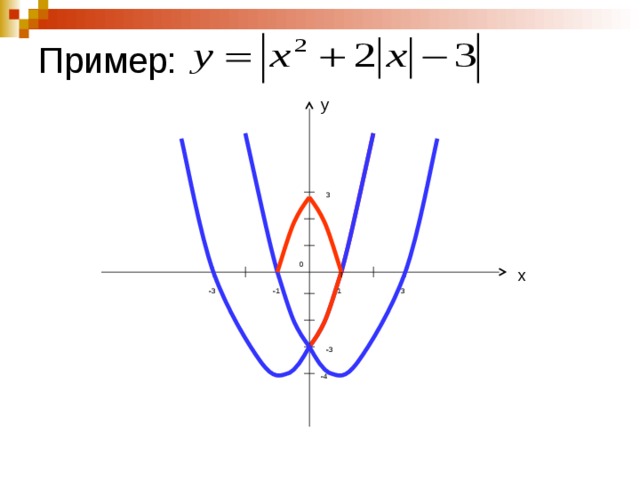 Рис. 9, 10).
Рис. 9, 10).
Рис. 9. Растяжение от оси
Рис. 10. Сжатие к оси
Параллельный перенос вдоль оси Ox
Предположим, что у нас есть функция , необходимо построить график функции . Вычислим значения некоторых точек для графиков этих функций.
Из таблиц видно, что одинаковым значениям функции соответствуют значения аргумента, отличающиеся на 2 единицы. Это означает, что график данной функции переместился на 2 единицы относительно оси ординат влево (см. Рис. 11), так как для получения одинаковых значений функций приходится брать значения аргумента на 2 меньше:
, при
при
Следовательно, если необходимо было построить график функции , то сдвиг на 3 единицы относительно оси ординат был бы вправо (по сравнению с графиком функции ) (см.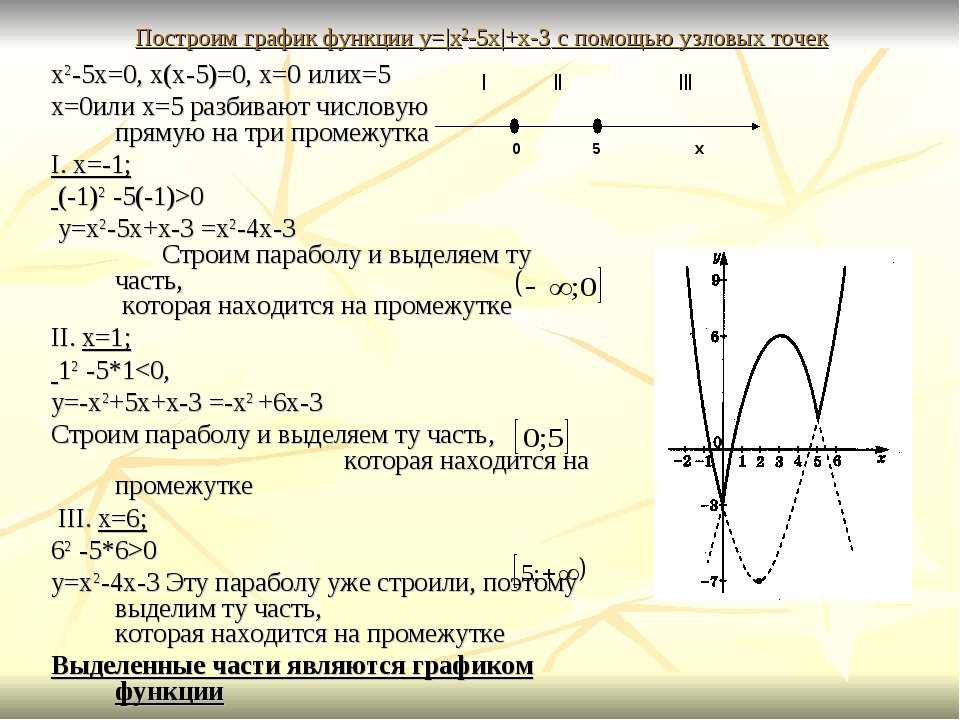 Рис. 11).
Рис. 11).
Рис. 11. Графики функций , и
График получается из графика функции параллельным переносом последнего на единиц влево, если , и на единиц вправо, если (см. Рис. 12, 13).
Рис. 12. Параллельный перенос влево при
Рис. 13. Параллельный перенос вправо при
Обратите внимание на то, что по этому принципу из графика не построить график , ведь мы добавили 1 не ко всем вхождениям в это выражение.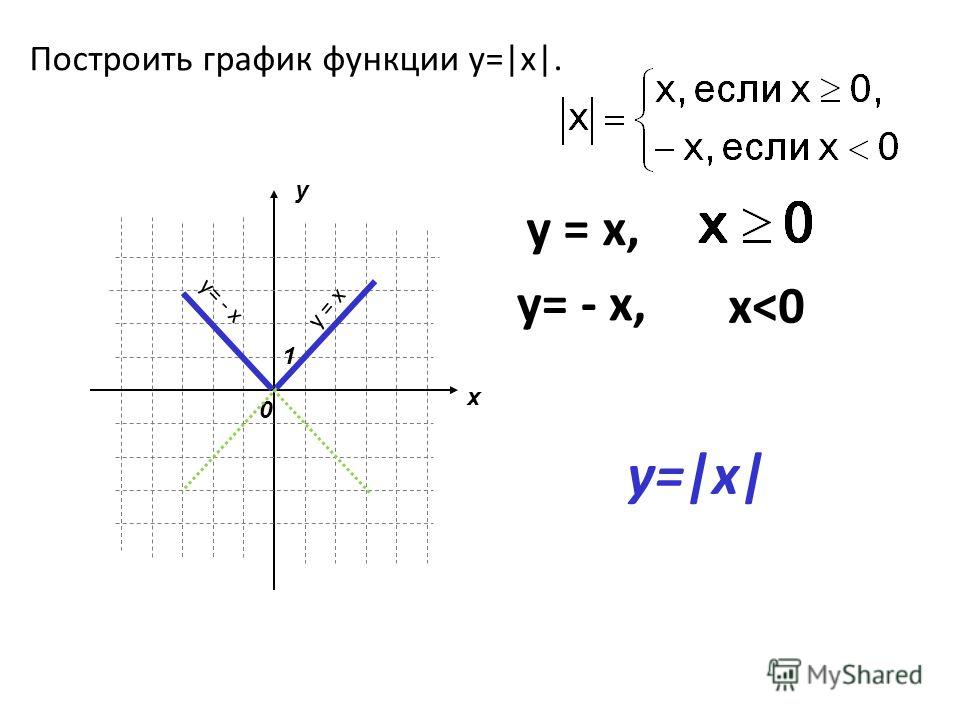 А вот график построить можно, сдвинув исходный график на 1 влево (см. Рис. 14).
А вот график построить можно, сдвинув исходный график на 1 влево (см. Рис. 14).
Рис. 14. Графики функции и
Растяжение от оси Oy и сжатие к оси Oy
График функции , где и , получается из графика функции сжатием с коэффициентом к оси (если указанное «сжатие» фактически является растяжением с коэффициентом ) (см. Рис. 15, 16).
Рис. 15. Сжатие к оси
Рис.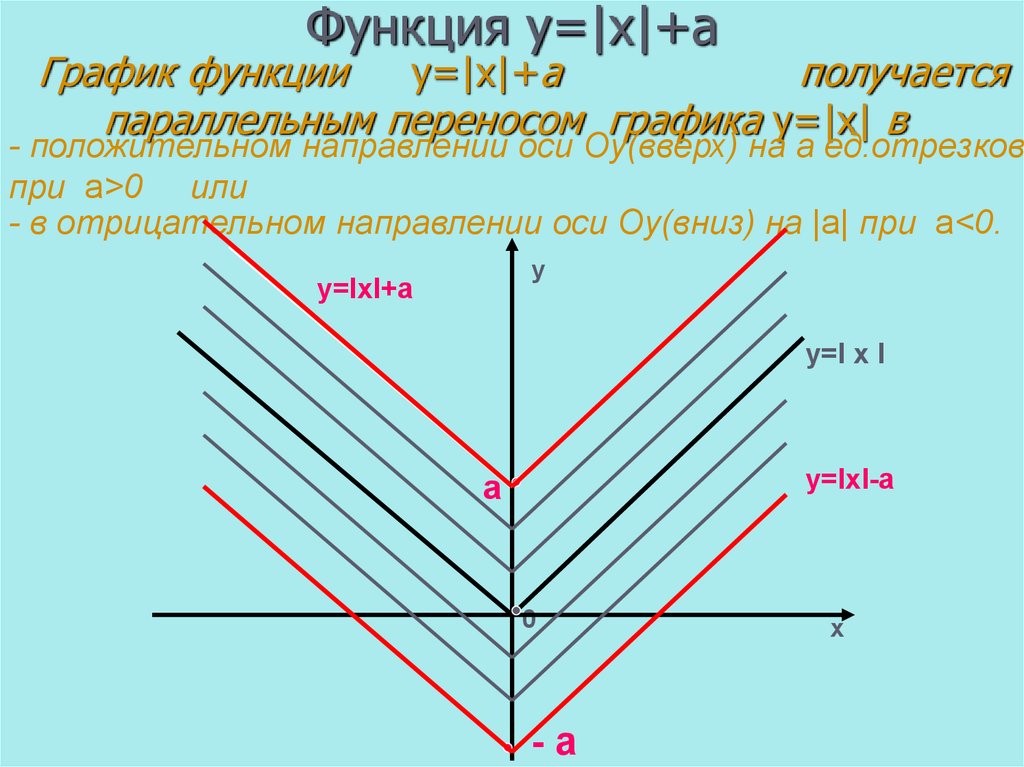 16. Растяжение от оси
16. Растяжение от оси
Подобное преобразование мы уже рассматривали в случае построения графика функции .
Преобразование симметрии относительно оси Oy
Ранее мы рассматривали преобразование симметрии относительно оси Ox, то есть функция умножалась на (-1). Рассмотрим случай, когда на (-1) умножается только аргумент.
В этом случае график симметрично отображается относительно оси ординат, так как значения функций будут одинаковы при противоположных значениях аргумента:
для функции :
при
при
для функции :
при
при
График получается из графика функции преобразованием симметрии относительно оси (см.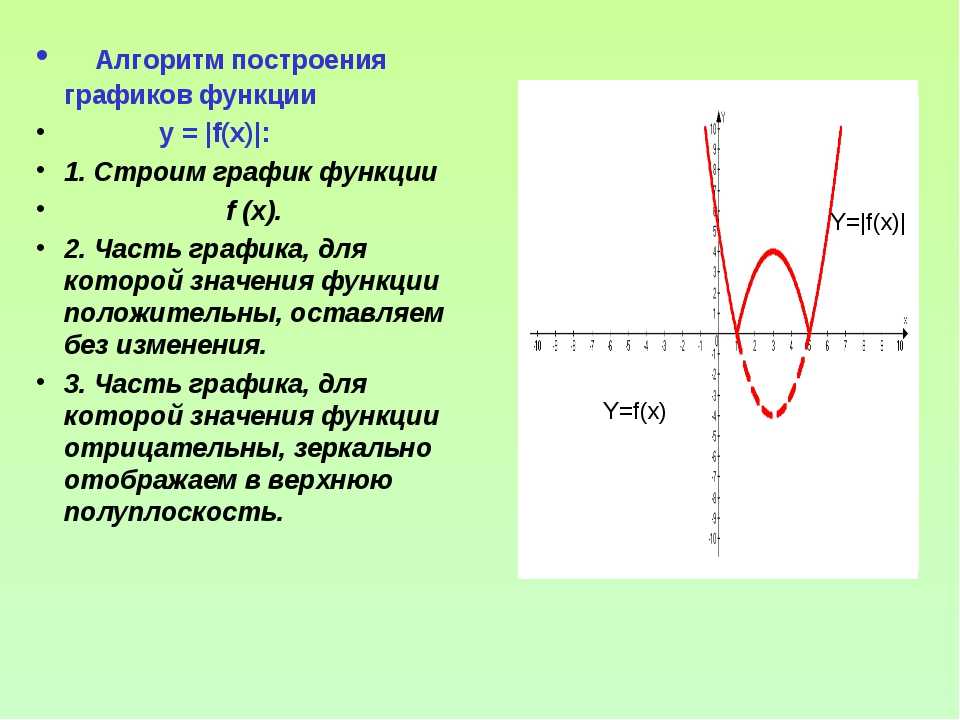 Рис. 17).
Рис. 17).
Рис. 17. Преобразование симметрии относительно оси Oy
Построение графиков и
Пусть дан график , построим график . Для начала раскроем модуль по определению:
Следовательно, те точки, в которых значения функции положительны или равны 0, остаются на месте, а все точки, в которых значения отрицательны, – отражаются относительно оси (см. Рис. 18).
Рис.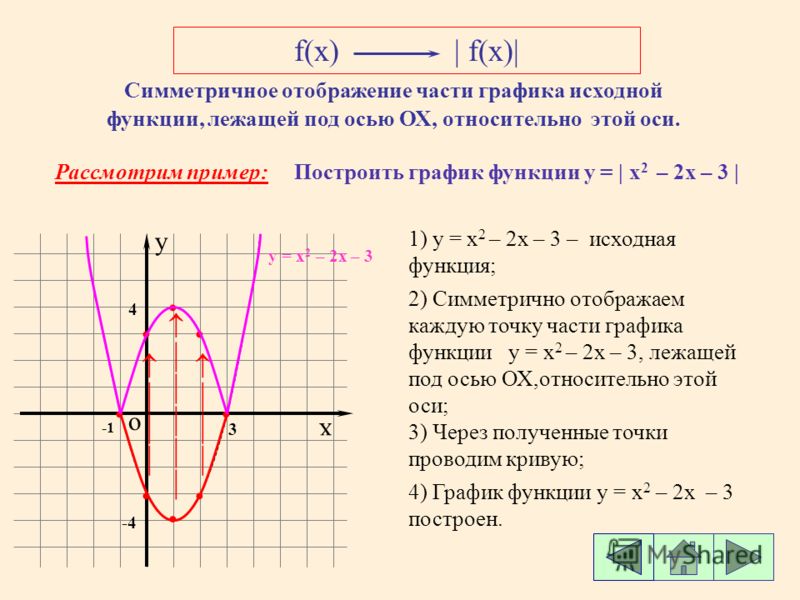 18. Графики функций и (красным цветом выделена общая часть этих графиков)
18. Графики функций и (красным цветом выделена общая часть этих графиков)
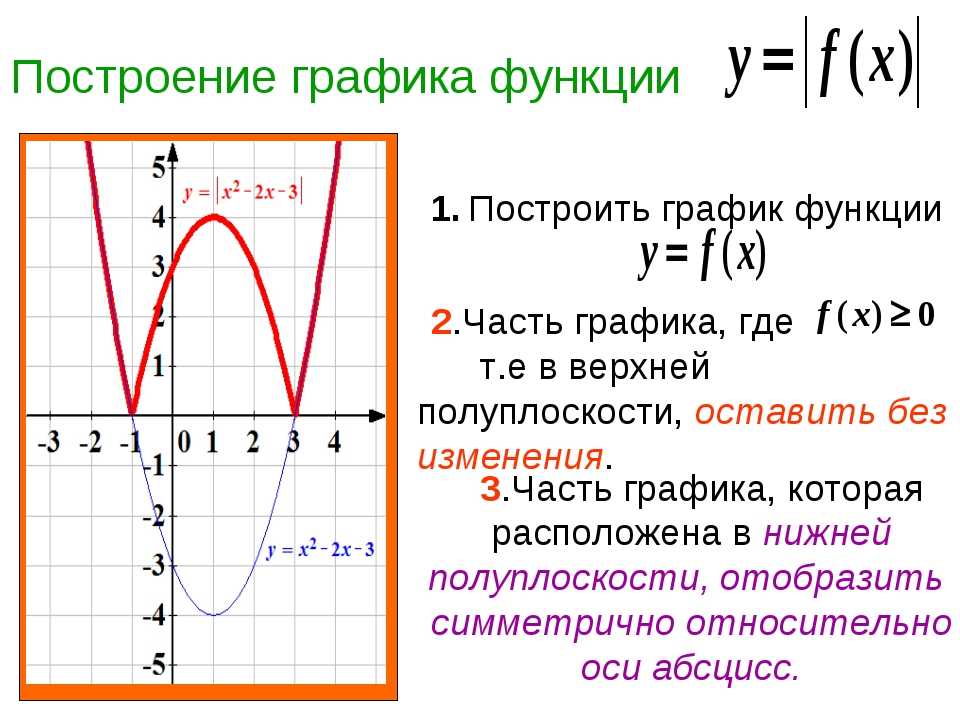
Для того чтобы построить график , нужно часть исходного графика, лежащую выше оси , оставить без изменения, а нижнюю отразить наверх относительно оси .
Пусть дан график , построим график . Для начала раскроем модуль по определению:
Следовательно, все точки с положительными или равными нулю абсциссами остаются без изменения, а все точки с отрицательными – заменяются точками с противоположными абсциссами (см. Рис. 19).
Рис. 19. Графики функций и (красным цветом выделена общая часть этих графиков)
19. Графики функций и (красным цветом выделена общая часть этих графиков)
Для того чтобы построить график , нужно часть исходного графика, соответствующую значениям , оставить без изменений и отразить ее относительно оси для значений .
Задача 1
Построить график функции .
Решение
Построим график заданной функции последовательно (см. Рис. 20):
1. Строим график .
2. График получается из графика параллельным переносом последнего на 2 единицы вправо.
График получается из графика параллельным переносом последнего на 2 единицы вправо.
3. График получается из графика функции параллельным переносом последнего вдоль оси ординат на 3 единицы вверх.
Рис. 20. Иллюстрация к задаче
Мы могли бы сделать операции в обратном порядке, то есть сначала поднять график на 3 единицы вверх, а потом получившийся график сдвинуть вправо на 2 единицы (см. Рис. 21).
Рис. 21. Иллюстрация к задаче
Обратите внимание, что не все графики функций можно строить в произвольном порядке. Например, для построения графика сначала нужно построить график , затем график (растяжение от оси ), а далее – график (параллельный перенос вдоль оси ординат) (см. Рис. 22). Если же сделать в другой последовательности, то есть построить , то далее на 2 придется умножить всё выражение.
Например, для построения графика сначала нужно построить график , затем график (растяжение от оси ), а далее – график (параллельный перенос вдоль оси ординат) (см. Рис. 22). Если же сделать в другой последовательности, то есть построить , то далее на 2 придется умножить всё выражение.
– ПРАВИЛЬНО
– НЕПРАВИЛЬНО
Рис. 22. Иллюстрация к задаче
Пример
Построить график .
Решение
1. Строим график (гипербола) (см. Рис. 23).
Строим график (гипербола) (см. Рис. 23).
2. Строим график (из аргумента вычитается 2, следовательно, сдвигаем график на 2 единицы вправо) (см. Рис. 23).
3. Строим график (домножение функции на (-1), следовательно, отражаем график относительно оси ) (см. Рис. 24).
4. Строим график (добавление 2 к функции, следовательно, сдвигаем график на 2 единицы вверх) (см. Рис. 24).
5. Строим график (модуль функции, следовательно, отражаем нижнюю часть графика относительно оси , а верхнюю оставляем без изменений) (см. Рис. 25).
Рис.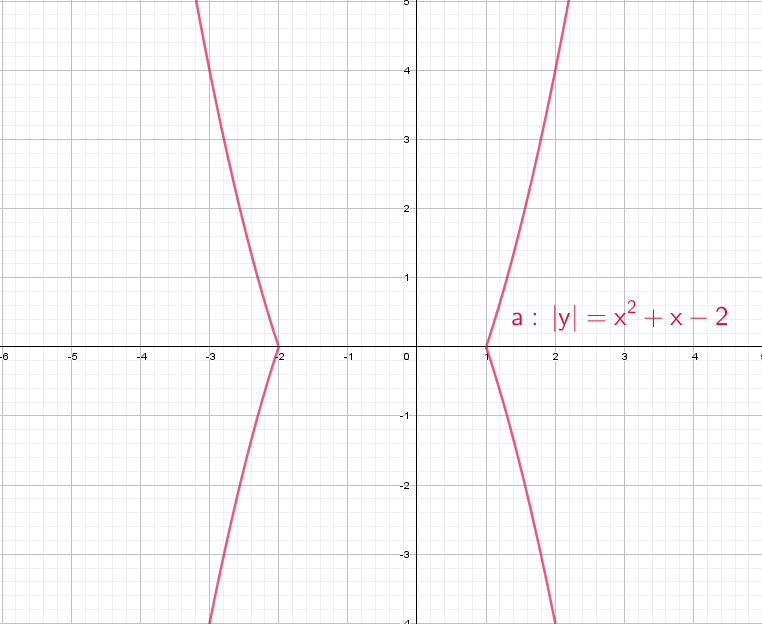 23. Иллюстрация к задаче
23. Иллюстрация к задаче
Рис. 24. Иллюстрация к задаче
Рис. 25. Иллюстрация к задаче (искомый график)
Список литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений. – 4-е изд. – М.: Мнемозина, 2002. – 192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. – 4-е изд.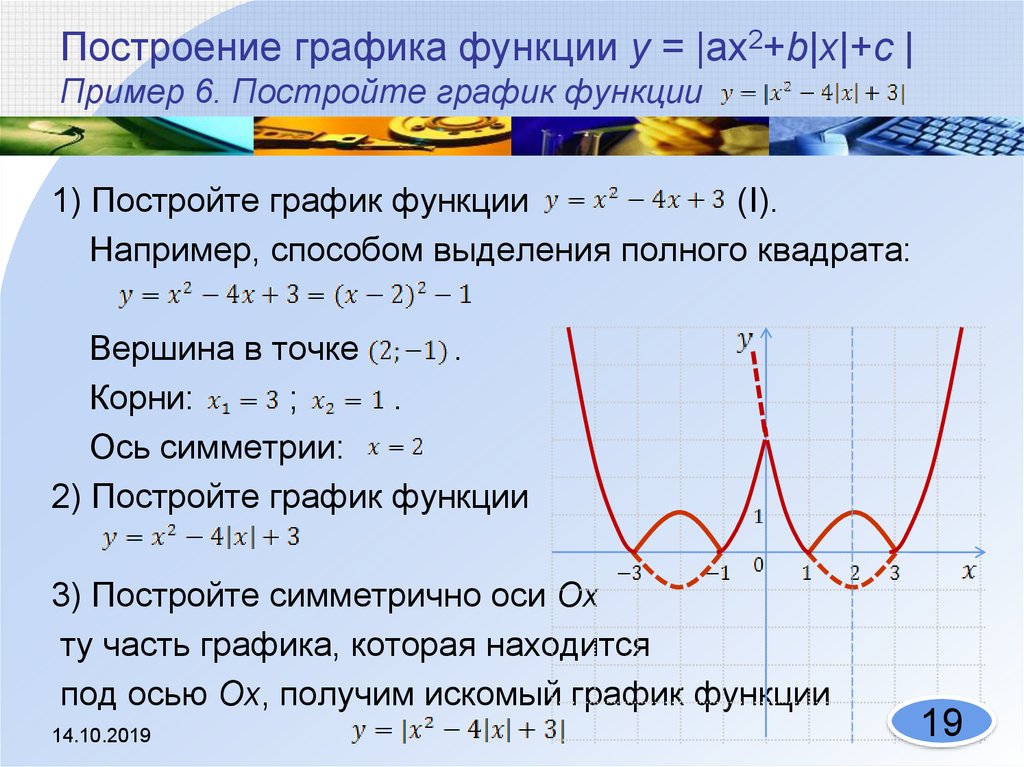 – М.: Мнемозина, 2002. – 143 с.: ил.
– М.: Мнемозина, 2002. – 143 с.: ил.
3. Макарычев Ю.Н. Алгебра. 9 класс : учеб.для учащихся общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов. – 7-е изд., испр. и доп. – М.: Мнемозина, 2008.
5. Виленкин Н.Я., Сурвилло Г.С. и др. Алгебра 9 кл. С углубленным изучением математики. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт учебного центра «Резольвента» (Источник)
2. Интернет-сайт «Инфоурок» (Источник)
3. Интернет-сайт YouTube (Источник)
Интернет-сайт YouTube (Источник)
Домашнее задание
1. Упражнения 64, 66, 68 (б, г), 69 (в, ж), 70 (и) (стр. 65-69) Виленкин Н.Я., Сурвилло Г.С. и др. Алгебра 9 кл. (Источник).
2. Даны графики функций: а) ; б) ; в)
Какое уравнение будет иметь функция, график которой образуется из данных графиков функций: 1. при параллельном переносе вверх на 3 единицы; 2. при растяжении в 3 раза; 3. при параллельном переносе вправо на 3 единицы?
3. Постройте график функции .
Построение графиков онлайн.
 Построение графиков онлайн Построить график y sin 2x
Построение графиков онлайн Построить график y sin 2x«Построение графика функции с модулем» — Y = lnx. Закрепили знания на ранее изученных функциях. Построение графиков функций. Вопрос классу. Y = x2 – 2x – 3. Проектная деятельность. Урок обобщения и систематизации знаний. График функции. Актуализация знаний о графиках функций. Обобщение. Попробуйте самостоятельно построить графики. Y = f(x).
««Графики функций» 9 класс» — Цели урока. Большему значению аргумента соответствует большее значение функции. Нули функции. Определение. Заполните пропуски. Установите соответствие между функцией и вершиной. Тренажер. Выберите уравнение, с помощью которого задана линейная функция. Установите соответствие. Выберите уравнение. Обратная пропорциональность.
«Графики функций с модулями» — Найдём вершину функции. Кубическая функция. Отрицательная сторона. Графики функций. Квадратичная функция. Сложная функция. Функция с модулем. Графики функций надо обязательно уметь строить. Подготовка к ЕГЭ. Графики функций с модулями. Парабола. График функции.
Графики функций с модулями. Парабола. График функции.
«Уравнение касательной к графику функции» — Производная в точке. Правила дифференцирования. График функции. Алгоритм нахождения уравнения. Ответьте на вопросы. Геометрический смысл производной. Номера из учебника. Уравнение касательной к графику функции. Определение. Касательная к графику функции. Основные формулы дифференцирования. Провести касательную.
«Построение графиков функций» — Построение графика функции y = sinx. Линия тангенсов. Алгебра. Тема: Построение графиков функций. График функции y = sinx. Выполнила: Филиппова Наталья Васильевна учитель математики Белоярская средняя общеобразовательная школа №1. Построить график функции y=sin(x) +cos(x).
«График обратной пропорциональности» — Применение гиперболы. Гипербола. Монотонность функции. Чётность, нечётность. Функция «Обратная пропорциональность». График. Построение графика обратной пропорциональности. Гипербола и космические спутники. Однополостной гиперболоид.
Всего в теме 25 презентаций
Как построить график функции y=sin x? Для начала рассмотрим график синуса на промежутке .
Единичный отрезок берём длиной 2 клеточки тетради. На оси Oy отмечаем единицу.
Для удобства число π/2 округляем до 1,5 (а не до 1,6, как требуется по правилам округления). В этом случае отрезку длиной π/2 соответствуют 3 клеточки.
На оси Ox отмечаем не единичные отрезки, а отрезки длиной π/2 (через каждые 3 клеточки). Соответственно, отрезку длиной π соответствует 6 клеточек, отрезку длиной π/6 — 1 клеточка.
При таком выборе единичного отрезка график, изображённый на листе тетради в клеточку, максимально соответствует графику функции y=sin x.
Составим таблицу значений синуса на промежутке :
Полученные точки отметим на координатной плоскости:
Так как y=sin x — нечётная функция, график синуса симметричен относительно начала отсчёта — точки O(0;0).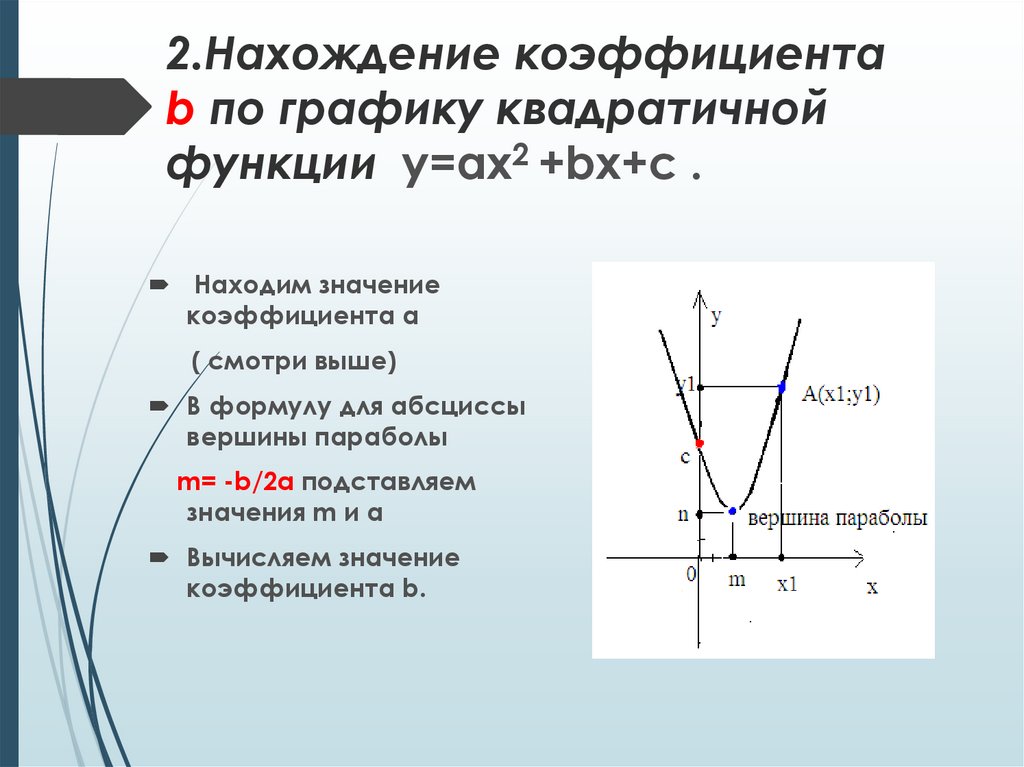
С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
- Свойства функции Y=sin(X).
- График функции.
- Как строить график и его масштаб.
- Примеры.
Свойства синуса. Y=sin(X)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы помните их?
Давайте познакомимся поближе с функцией Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.
3) Функция Y=sin(X) возрастает на отрезке и убывает на отрезке [π/2; π].
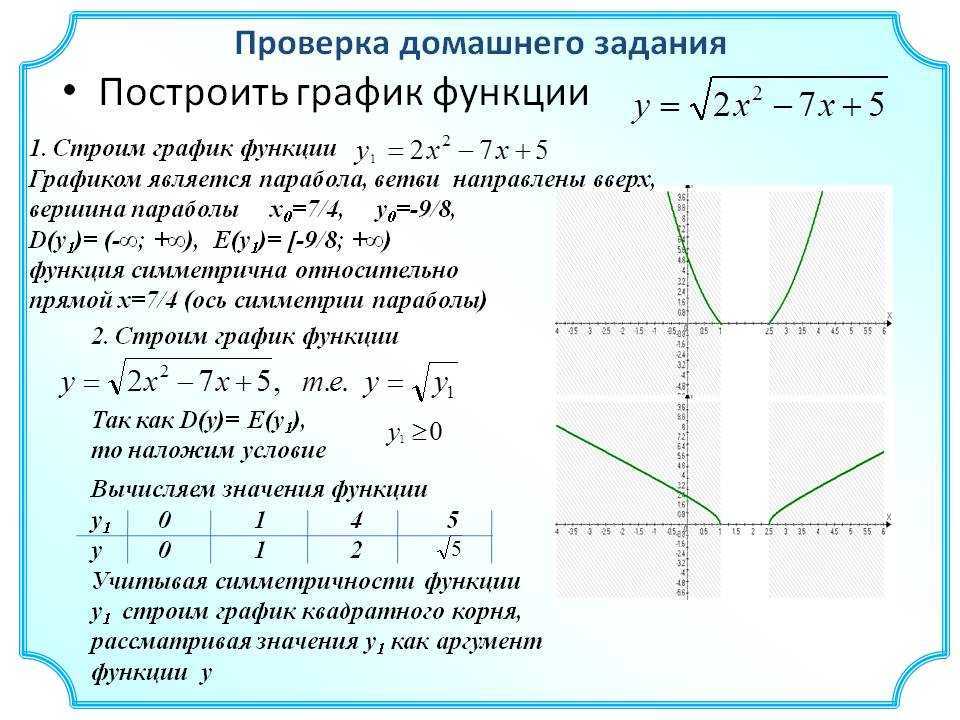 Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.
Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk). Наибольшее значение функции равно 1 (при х = π/2+ πk).
Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X). Будем строить наш график последовательно, применяя наши свойства. Начнем строить график на отрезке .
Особое внимание стоит обратить на масштаб. На оси ординат удобнее принять единичный отрезок равный 2 клеточкам, а на оси абсцисс — единичный отрезок (две клеточки) принять равным π/3 (смотрите рисунок).
Построение графика функции синус х, y=sin(x)
Посчитаем значения функции на нашем отрезке:
Построим график по нашим точкам, с учетом третьего свойства.
Таблица преобразований для формул привидения
Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:
Мы знаем, что sin(x+ 2π) = sin(x).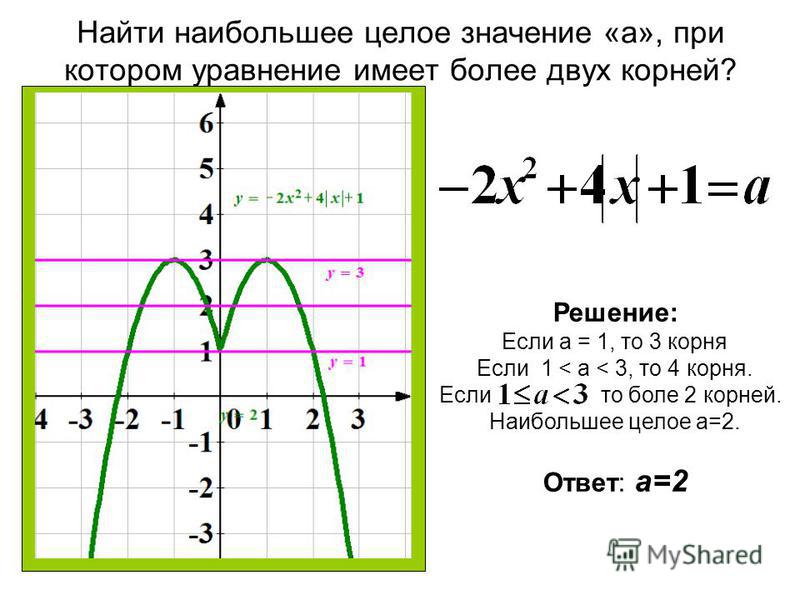 Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
График функции Y=sin(X) называют — синусоидой.
Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
8) Область значений: отрезок [- 1; 1]. Это также хорошо видно из графика функции.
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.
Примеры задач с синусом
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см. рисунок).
рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π
2. Построить график функции y=sin(π/6+x)-1
Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.
Задачи на синус для самостоятельного решения
- Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
- Построить график функции y=sin(π/3+x)-2
- Построить график функции y=sin(-2π/3+x)+1
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]
Топ-5 лучших библиотек Python для построения графиков и построения графиков
В этой статье рассказывается о некоторых из лучших библиотек Python для построения графиков и построения графиков! Прежде чем мы начнем со списка лучших библиотек, давайте кратко рассмотрим, зачем нужна визуализация данных и что
Зачем нужна визуализация данных?
В эпоху стремительного развития анализа данных часто удобнее просматривать результаты нашего анализа и делать выводы, чем просматривать текстовые данные или файлы csv для понимания результатов.
Следовательно, визуализация данных — это простой способ найти ответы на сложные вопросы. Это также позволяет пользователям выражать результаты лучше, чем таблицы.
Визуализация данныхТоп-5 лучших библиотек Python для построения графиков и построения графиков
Вот краткий список нескольких библиотек Python для построения графиков и построения графиков, которые мы обсудим:
- Matplotlib: Легко строит графики во всех приложениях, используя свой API.
- Seaborn: Универсальная библиотека на основе matplotlib, позволяющая сравнивать несколько переменных.
- ggplot: Создает визуализацию для предметной области
- Боке: Предпочтительные библиотеки для потоковой передачи и данных в реальном времени.
- Plotly: Позволяет создавать очень интерактивные графики с помощью JS.
1. Matplotlib
Matplotlib Matplotlib — это библиотека для построения графиков для Python. Он предоставляет объектно-ориентированный API, который позволяет нам строить графики в самом приложении. Это бесплатно и с открытым исходным кодом. Поддерживает десятки типов вывода объявлений.
Он предоставляет объектно-ориентированный API, который позволяет нам строить графики в самом приложении. Это бесплатно и с открытым исходным кодом. Поддерживает десятки типов вывода объявлений.
Matplotlib позволяет использовать панды в качестве обертки для своего API. Эта библиотека имеет лучшее время работы и занимает мало места в памяти.
Преимущества использования Matplotlib
- Понимание корреляции между переменными
- Сообщает о подгонке данных модели библиотека, доступная в python, на основе matplotlib. У Seaborn есть API, основанный на наборах данных, которые позволяют сравнивать несколько переменных.
Он поддерживает многосюжетные сетки, которые, в свою очередь, упрощают построение сложной визуализации. Он имеет одномерные и двумерные визуализации, доступные для сравнения между подмножествами данных.
Он использует различные цветовые палитры для отображения различных узоров. Он также автоматически оценивает модели линейной регрессии.

Seaborn против Matplotlib
Matplotlib пытается сделать простые вещи простыми, а сложные возможными, Seaborn также пытается определить четко определенный набор сложных вещей. На самом деле matplotlib хорош, но Seaborn лучше. Matplotlib оставляет менее привлекательные графики, но у Seaborn есть высокоуровневые интерфейсы и настраиваемые темы для решения этой проблемы.
При работе с пандами matplotlib плохо работает с фреймами данных. В то время как морские функции работают с фреймами данных.
3. ggplot
GgplotПервоначально реализованная в R, ggplot — одна из универсальных библиотек для построения графиков в Python. Это предметно-ориентированный язык для создания предметно-ориентированных визуализаций, особенно для анализа данных.
Ggplot позволяет построить график простым способом, используя всего 2 строки кода. Однако тот же код, написанный с использованием matplotlib, очень сложен и включает много строк кода. Следовательно, ggplot упрощает кодирование графика.
 Это чрезвычайно ценная библиотека Python.
Это чрезвычайно ценная библиотека Python.Для достижения всех возможностей ggplot необходимо использовать pandas.
4. Bokeh
BokehBokeh, библиотека, похожая на ggplot, основана на грамматике графики. Тем не менее, это библиотека, родная для Python, и она не была импортирована из R. Создает интерактивные веб-графики, которые можно выводить в различных форматах, таких как HTML-документы и объекты JSON.
Bokeh — одна из наиболее предпочтительных библиотек для потоковой передачи и передачи данных в реальном времени.
Боке доступно пользователям на трех уровнях, а именно — высокий уровень, средний уровень и низкий уровень. Пользователи высокого уровня могут легко и быстро создавать гистограммы и гистограммы. Пользователи среднего уровня могут использовать инфраструктуру matplotlib для создания точек для точечных диаграмм.
5. Plotly
PlotlyPlotly — это онлайн-платформа визуализации с поддержкой библиотеки. Здесь мы можем создавать интерактивные графики так же, как боке, но с дополнительными графиками, такими как контурные графики, трехмерные диаграммы и дендрограммы.
 Plotly также распознает события наведения мыши и щелчка курсором, что делает Plotly уникальной библиотекой с графикой и JavaScript.
Plotly также распознает события наведения мыши и щелчка курсором, что делает Plotly уникальной библиотекой с графикой и JavaScript.Bokeh и Plotly — похожие библиотеки, однако с Plotly вам придется преобразовывать данные в словари. Тем не менее, plotly проще, когда дело доходит до обработки фреймов данных с помощью Pandas.
Подводя итог…
Использование Python для построения графиков выгодно и невыгодно по той простой причине, что Python предлагает широкий выбор опций. Выбор лучшей библиотеки полностью зависит от типа задачи, которую вы пытаетесь выполнить. Обратите внимание, что ни одна библиотека не превосходит другую, и использование каждой библиотеки зависит от потребностей пользователя.
Matplotlib, тем не менее, служит ядром всех этих библиотек и позволяет программистам накладывать на него инструменты. Seaborn, используя matplotlib, создает сложные и интерактивные визуализации. Боке, с другой стороны, помогает создать собственный сервер для визуализации.
 Используйте эти библиотеки и дайте нам знать, что вы думаете, в разделе комментариев ниже.
Используйте эти библиотеки и дайте нам знать, что вы думаете, в разделе комментариев ниже.5 библиотек Python для создания интерактивных графиков
По словам эксперта по визуализации данных Энди Кирка, существует два типа визуализации данных: исследовательская и объяснительная. Цель пояснительных визуализаций — рассказывать истории — они тщательно сконструированы для выявления основных выводов.
Исследовательские визуализации, с другой стороны, «создают интерфейс в наборе данных или предмете… они облегчают пользователю изучение данных, позволяя ему находить собственные идеи: результаты, которые они считают важными или интересными».
Чаще всего исследовательские визуализации интерактивны. Хотя существует множество библиотек для построения графиков Python, лишь немногие из них могут создавать интерактивные диаграммы, которые можно встраивать в сеть и распространять. Сегодня мы делимся пятью нашими любимыми.
Сообщите нам в комментариях, какие библиотеки вам нравятся.
 Мы используем запросы клиентов для определения приоритетности библиотек для поддержки в ноутбуках Mode Python.
Мы используем запросы клиентов для определения приоритетности библиотек для поддержки в ноутбуках Mode Python.Библиотеки Python для создания интерактивных графиков:
- mpld3
- пигал
- Боке
- HoloViews
- Сюжет
mpld3
Пример пользовательского плагина (Джейк Вандерплас)
mpld3 объединяет основную библиотеку Python для построения графиков matplotlib и популярную библиотеку построения графиков JavaScript D3 для создания визуализаций, удобных для браузера. Вы можете создать график в matplotlib, добавить интерактивные функции с помощью плагинов, использующих как Python, так и JavaScript, а затем отобразить его с помощью D3.
mpld3 включает встроенные плагины для масштабирования, панорамирования и добавления всплывающих подсказок (информация, которая появляется при наведении указателя мыши на точку данных). Однако реальная мощь mpld3 заключается в его хорошо документированном API, позволяющем создавать собственные плагины.
 Если вы знакомы с D3 и JavaScript, вы можете создавать бесконечное количество графиков.
Если вы знакомы с D3 и JavaScript, вы можете создавать бесконечное количество графиков.Когда ваш график будет готов к публикации, добавьте в конце дополнительную строку кода, чтобы преобразовать ваш график в строку HTML и JavaScript, которую можно встроить в любую веб-страницу.
mpld3 лучше всего работает с наборами данных малого и среднего размера; графики с тысячами точек данных будут тормозить в браузере.
, созданный: Jake Vanderplas
Где узнать больше: http://mpld3.github.io/Pygal
Basic Dot Plot (Florian Mounier)
PYGGAL IS AREGAL IS AREGAL IS AREGAL IS AREGAL IS AREGAL IS AREGAL IS AREGAL IS AREGAL IS AREGAL IS AREGAL IS AREGAL IS AREGAL IS AREGAL. для создания красивых готовых диаграмм с очень небольшим количеством строк кода. Каждый тип диаграммы упакован в метод (например,
pygal.Histogram()создает гистограмму,pygal.Box()создает коробчатую диаграмму), и существует множество красочных стилей по умолчанию. Если вам нужен больший контроль, вы можете настроить почти каждый элемент графика, включая размер, заголовки, метки и визуализацию.
Если вам нужен больший контроль, вы можете настроить почти каждый элемент графика, включая размер, заголовки, метки и визуализацию.Графики отображают всплывающие подсказки по умолчанию, но в настоящее время нет возможности увеличивать и уменьшать масштаб или перемещаться по графикам.
Вы можете вывести диаграммы в формате SVG и добавить их на веб-страницу с помощью тега внедрения или путем вставки кода непосредственно в HTML. Как и mpld3, pygal подходит для небольших наборов данных.
Создатель: Florian Mounier
Где узнать больше: http://www.pygal.org/en/latest/index.htmlBokeh
9 Пример кросс-фильтров (Bokeh)
Боке вдохновлен концепциями, изложенными в Грамматика графики . Вы можете накладывать компоненты друг на друга, чтобы создать готовый график — например, вы можете начать с осей, а затем добавить точки, линии, метки и т. д.
Графики можно выводить в виде объектов JSON, документов HTML или интерактивных веб-приложения.
 Bokeh позволяет пользователям манипулировать данными в браузере с помощью ползунков и раскрывающихся меню для фильтрации. Как и в mpld3, вы можете масштабировать и панорамировать для навигации по графикам, но вы также можете сфокусироваться на наборе точек данных с помощью рамки или выбора лассо.
Bokeh позволяет пользователям манипулировать данными в браузере с помощью ползунков и раскрывающихся меню для фильтрации. Как и в mpld3, вы можете масштабировать и панорамировать для навигации по графикам, но вы также можете сфокусироваться на наборе точек данных с помощью рамки или выбора лассо.Создано: Anaconda
Где узнать больше: https://docs.bokeh.org/en/latest/Holoviews
Карта с использованием Bokeh Backend (IOAM)
. на самом деле не библиотека для построения графиков. Вместо этого он позволяет создавать структуры данных, которые способствуют визуализации. Переместив данные в объект-контейнер HoloView, например GridMatrix для многовариантного анализа или макет для отображения компонентов рядом друг с другом, вы можете просматривать данные визуально. Графика выполняется отдельно в бэкэндах matplotlib или Bokeh, поэтому вы можете сосредоточиться на данных, а не на написании кода для построения графика.

Основная интерактивная функция, предлагаемая HoloViews, — это ползунки, поэтому люди могут играть с переменной, чтобы увидеть ее эффект. При использовании бэкэнда Bokeh вы можете комбинировать компонент ползунка с инструментами Bokeh для изучения графиков, такими как масштабирование и панорамирование.
HoloViews интегрируется с Seaborn и пандами, открывая возможности панд DataFrames и статистических диаграмм Seaborn.
Создатели: Жан-Люк Стивенс, Филипп Рюдигер и Джеймс А. Беднар
Где узнать больше: http://holoviews.org/Plotly
Пример ползунка диапазона (Plotly)
От скромной гистограммы до сложных трехмерных сетевых графиков Plotly предлагает широкий выбор типов диаграмм публикационного качества.
Plotly — это веб-служба по умолчанию, но вы можете использовать библиотеку в автономном режиме в Python и загружать графики на бесплатный общедоступный или платный частный сервер Plotly.
 Оттуда вы можете вставлять свои графики на веб-страницу.
Оттуда вы можете вставлять свои графики на веб-страницу.Все графики Plotly содержат всплывающие подсказки, и вы можете создавать настраиваемые элементы управления (такие как ползунки и фильтры) поверх диаграммы, как только она будет встроена с помощью API JavaScript Plotly.
Еще один способ работать в Plotly и делиться графиками — в режиме. Вы можете получить данные с помощью SQL, использовать автономную библиотеку Plotly в блокноте Python, чтобы отобразить результаты вашего запроса, а затем добавить интерактивную диаграмму в отчет. Отчет находится в Интернете по общедоступному URL-адресу и может быть встроен в другие страницы, например, в эту диаграмму, показывающую, как размеры наборов Lego изменились с 1950 года: узнать больше: https://plotly.com/python/
Попробуйте Plotly в режиме.
Интерактивные графики могут помочь вам раскрыть новые идеи в ваших данных. Попробуйте перечисленные здесь, чтобы лучше рассказывать истории об идеях, которые вы находите в режиме.

Нет опыта программирования? Без проблем. Изучите Python, используя данные из реального мира, с помощью нашего бесплатного учебного пособия и начните строить интерактивные графики в режиме уже сегодня.
7 самых популярных способов построения графиков данных в Python
«Как мне создавать графики в Python?» раньше был простой ответ: Matplotlib был единственным способом. В настоящее время Python является языком науки о данных, и выбор гораздо шире. Что следует использовать?
Это руководство поможет вам принять решение. Он покажет вам, как использовать каждую из четырех самых популярных библиотек для построения графиков Python — Matplotlib , Seaborn , Plotly и Bokeh , а также пару отличных перспективных библиотек, которые стоит рассмотреть: Altair . , с его выразительным API, и Pygal , с его прекрасным выводом SVG. Я также рассмотрю очень удобный API для построения графиков, предоставляемый pandas .

Для каждой библиотеки я включил фрагменты исходного кода, а также полный веб-пример с использованием Anvil, нашей платформы для создания веб-приложений только с Python. Давайте взглянем.
Пример графика
Каждая библиотека использует свой подход к отображению данных. Чтобы сравнить их, я сделаю один и тот же график с каждой библиотекой и покажу вам исходный код. Для моего примера данных я выбрал эту сгруппированную гистограмму результатов выборов в Великобритании с 1966 года:
Я собрал набор данных об истории выборов в Великобритании из Википедии: количество мест в парламенте Великобритании, полученных Консервативной, Лейбористской и Либеральной партиями (в широком смысле) на каждых выборах с 19с 66 до 2019 года плюс количество мест, выигранных «другими». Вы можете скачать его в виде CSV-файла.
Matplotlib
Matplotlib — старейшая библиотека Python для построения графиков, и она до сих пор остается самой популярной. Он был создан в 2003 году как часть SciPy Stack, библиотеки научных вычислений с открытым исходным кодом, похожей на Matlab.

Matplotlib дает вам точный контроль над вашими графиками — например, вы можете определить отдельную x-позицию каждого столбца в вашей гистограмме. Вот код для построения графика (вы можете запустить его здесь):
import matplotlib.pyplot as plt
import numpy as np
from voices import wide as df# Инициализировать фигуру. subplots() без аргументов дает один график.
fig, ax = plt.subplots()# Небольшая подготовка данных. Примечание: расчет «уклонения» столбцов вручную
ax.bar(x - 3*width/2, df['консервативный'], width, label='Conservative', color='#0343df')
ax.bar(x - width/2, df['labour'], width, label='Labour', color='#e50000')
ax.bar(x + width/2, df['liberal'] , width, label='Liberal', color='#ffff14')
ax.bar(x + 3*width/2, df['others'], width, label='Others', color='#929591' )# Настройка некоторых свойств отображения
ax.
ax.set_title('Результаты выборов в Великобритании')
ax.set_xticks(x) # Это гарантирует, что у нас будет один тик в год, иначе мы получим меньше
ax.set_xticklabels(years.astype(str).values, rotate='vertical')
ax.legend()# Попросите Matplotlib показать график
plt.show()А вот результаты выборов, нанесенные на график в Matplotlib:
Seaborn
Seaborn — это уровень абстракции поверх Matplotlib; он дает вам действительно аккуратный интерфейс, позволяющий очень легко создавать широкий спектр полезных типов графиков.
Но мощность не идет на компромисс! Seaborn предоставляет аварийные люки для доступа к базовым объектам Matplotlib, так что вы по-прежнему имеете полный контроль.
Код Seaborn проще, чем необработанный Matplotlib (можно запустить здесь):
import seaborn as sns
# Здесь создается фактический сюжет
ax = sns. barplot(data=df, x="year", y="seats", hue="party", pause=['blue', 'red', 'желтый', 'серый'], насыщенность=0,6)
barplot(data=df, x="year", y="seats", hue="party", pause=['blue', 'red', 'желтый', 'серый'], насыщенность=0,6) # Настройка некоторых свойств отображения
ax.set_title('Результаты выборов в Великобритании')
ax.grid(color='#cccccc')
ax.set_ylabel('Места')
ax.set_xlabel(None)
ax.set_xticklabels(df["year"] .unique().astype(str), rotate='vertical')# Попросите Matplotlib показать это
plt.show()И создаст эту диаграмму:
Plotly
Plotly — это экосистема построения графиков, включающая библиотеку построения графиков Python. Он имеет три разных интерфейса:
- Объектно-ориентированный интерфейс
- Императивный интерфейс, который позволяет указать график с использованием структур данных, подобных JSON
- Интерфейс высокого уровня, похожий на Seaborn, под названием Plotly Express .
Графики Plotly предназначены для встраивания в веб-приложения.
 По своей сути Plotly — это библиотека JavaScript! Он использует D3 и stack.gl для рисования графиков.
По своей сути Plotly — это библиотека JavaScript! Он использует D3 и stack.gl для рисования графиков.Вы можете создавать библиотеки Plotly на других языках, передавая JSON в библиотеку JavaScript. Официальные библиотеки Python и R делают именно это. В Anvil мы портировали Python Plotly API для работы в веб-браузере.
Вот исходный код Plotly (вы можете запустить его здесь):
import plotly.graph_objects as go
from voices import wide as df# Получить удобный список значений x
years = df['year ']
x = list(range(len(years)))# Укажите графики
bar_plots = [
go.Bar(x=x, y=df['консервативный'], name='консервативный', маркер =go.bar.Marker(color='#0343df')),
go.Bar(x=x, y=df['labour'], name='Labour', marker=go.bar.Marker(color= '#e50000')),
go.Bar(x=x, y=df['либерал'], name='либерал', marker=go.bar.Marker(color='#ffff14')),
go. Bar(x=x, y=df['others'], name='Others', marker=go.bar.Marker(color='#929591')),
Bar(x=x, y=df['others'], name='Others', marker=go.bar.Marker(color='#929591')),
]# Настройка некоторых свойств отображения
layout = go.Layout(
title =go.layout.Title(text="Результаты выборов", x=0,5),
yaxis_title="Места",
xaxis_tickmode="array",
xaxis_tickvals=list(range(27)),
xaxis_ticktext=tuple(df ['год'].значения),
)# Создание графика с несколькими столбиками
Bokeh
Bokeh (произносится как «BOE-kay») специализируется на построении интерактивных сюжетов, поэтому этот стандартный пример не демонстрирует его в лучшем виде. Как и Plotly, графики Bokeh предназначены для встраивания в веб-приложения; он выводит свои графики в виде файлов HTML.
Вот код в Bokeh (который вы можете запустить здесь)
из bokeh.io import show, output_file
из bokeh.models import ColumnDataSource, FactorRange, HoverTool
из bokeh. plotting factor_cmap
plotting factor_cmap
from voices import long as df# Укажите файл для записи графика
output_file("elections.html")# Кортежи групп (год, партия)
x = [(str(r[1]) ['year']), r[1]['party']) для r в df.iterrows()]
y = df['seats']# Bokeh оборачивает ваши данные в свои собственные объекты для поддержки интерактивности
source = ColumnDataSource(data=dict(x=x, y=y))# Создать карту цветов
cmap = {
'консерватор': '#0343df',
'лейборист': '#e50000',
'liberal': '#ffff14',
'ore': '#929591',
}
fill_color = '#929591',
}
fill_color = фактор. ', палитра=список(cmap.values()), факторы=список(cmap.keys()), начало=1, конец=2)# Создайте график
p = цифра(x_range=FactorRange(*x), width=1200, title="Результаты выборов")
p.vbar(x='x', top='y', width=0,9, source=source, fill_color=fill_color, line_color=fill_color)# Настройка некоторых свойств отображения major_label_orientation = 1
p. xgrid.grid_line_color = None
xgrid.grid_line_color = None И сюжет:
Altair
Altair основан на декларативном языке построения графиков (или "грамматике визуализации") под названием Vega. Это означает, что это хорошо продуманный API, который хорошо масштабируется для сложных графиков, спасая вас от потери в аду вложенных циклов.
Как и в случае с боке, Altair выводит свои графики в виде файлов HTML. Вот код (который вы можете запустить здесь):
import altair as alt
from voices import long as df# Настройка цветовой карты
CMAP = {
'Conservative': '#0343DF',
'лейборист': '#E50000',
'Либерал': '#ffff14',
'Другое лет в строки
df['year'] = df['year'].astype(str)# Здесь мы делаем график
chart = alt.Chart(df).mark_bar().encode(
x= alt.X('партия', title=Нет),
y='места',
column=alt.Column('год', sort=list(df['год']), title=Нет),
color=alt. Color('party', scale=alt.Scale(domain=list(cmap.keys()), range=list(cmap.values())))
Color('party', scale=alt.Scale(domain=list(cmap.keys()), range=list(cmap.values())))
)# Сохранить как HTML файл.
chart.save('altair-elections.html')Итоговая диаграмма:
Pygal
Pygal фокусируется на внешнем виде. По умолчанию он создает графики SVG, поэтому вы можете увеличивать их бесконечно или распечатывать без пикселизации. Графики Pygal также имеют некоторые встроенные хорошие интерактивные функции, что делает Pygal еще одним недооцененным кандидатом, если вы хотите встроить графики в веб-приложение.
Исходный код выглядит следующим образом (вы можете запустить его здесь):
import pygal
from pygal.style import Style
from voices import wide as df# Определить стиль
custom_style 4 = Style( 9 ('#0343df', '#e50000', '#ffff14', '#929591')
font_family='Roboto, Helvetica, Arial, sans-serif',
background='transparent',
label_font_0size=1 ) label_font_0size=1 )# Настройте гистограмму, готовую для данных
c = pygal. bar (
bar (
title = "Результаты выборов в Великобритании",
Style = custom_style,
y_title = 'seats',
width = 1200,
x_label_rotation = 270,
)# Добавить. plot
c.add('Консерватор', df['консервативный'])
c.add('Труд', df['труд'])
c.add('Либерал', df['либерал'])
c.add('Others', df['others'])# Определение X-меток
c.x_labels = df['year']# Запишите это в файл SVG
c.render_to_file('pygal.svg')И диаграмму:
Pandas
Pandas — чрезвычайно популярная библиотека данных для Python. Он позволяет масштабировать все виды манипуляций с данными, а также имеет удобный API для построения графиков. Поскольку он работает непосредственно с фреймами данных, пример pandas является наиболее кратким фрагментом кода в этой статье — даже короче, чем код Seaborn!
API-интерфейс pandas является оболочкой для Matplotlib, поэтому вы также можете использовать базовый API-интерфейс Matplotlib для детального управления вашими графиками.


 Это чрезвычайно ценная библиотека Python.
Это чрезвычайно ценная библиотека Python. Используйте эти библиотеки и дайте нам знать, что вы думаете, в разделе комментариев ниже.
Используйте эти библиотеки и дайте нам знать, что вы думаете, в разделе комментариев ниже. Мы используем запросы клиентов для определения приоритетности библиотек для поддержки в ноутбуках Mode Python.
Мы используем запросы клиентов для определения приоритетности библиотек для поддержки в ноутбуках Mode Python.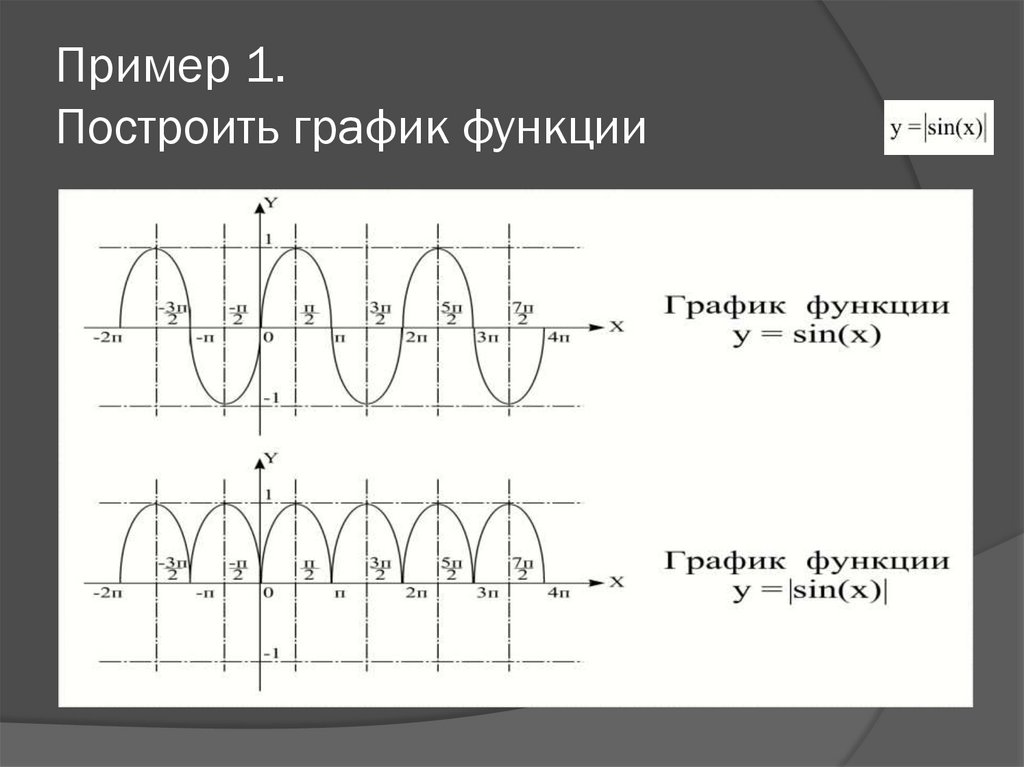 Если вы знакомы с D3 и JavaScript, вы можете создавать бесконечное количество графиков.
Если вы знакомы с D3 и JavaScript, вы можете создавать бесконечное количество графиков.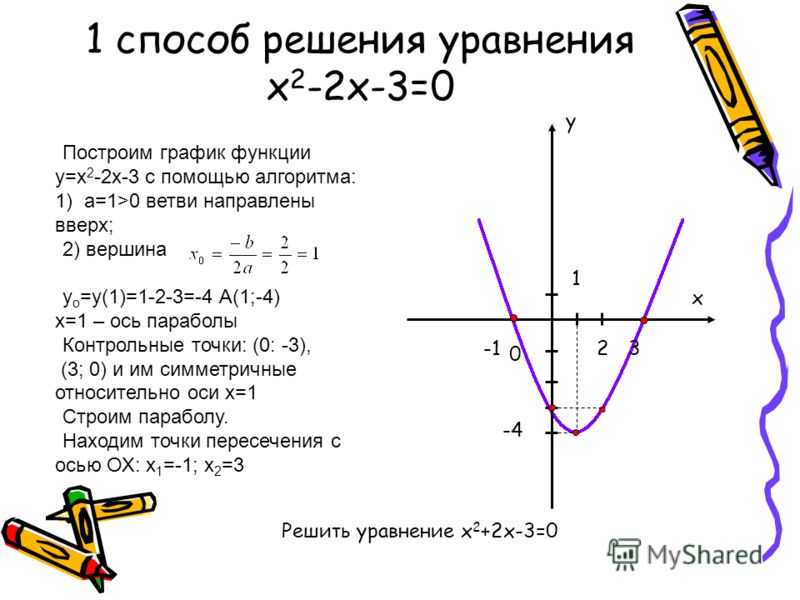 Если вам нужен больший контроль, вы можете настроить почти каждый элемент графика, включая размер, заголовки, метки и визуализацию.
Если вам нужен больший контроль, вы можете настроить почти каждый элемент графика, включая размер, заголовки, метки и визуализацию.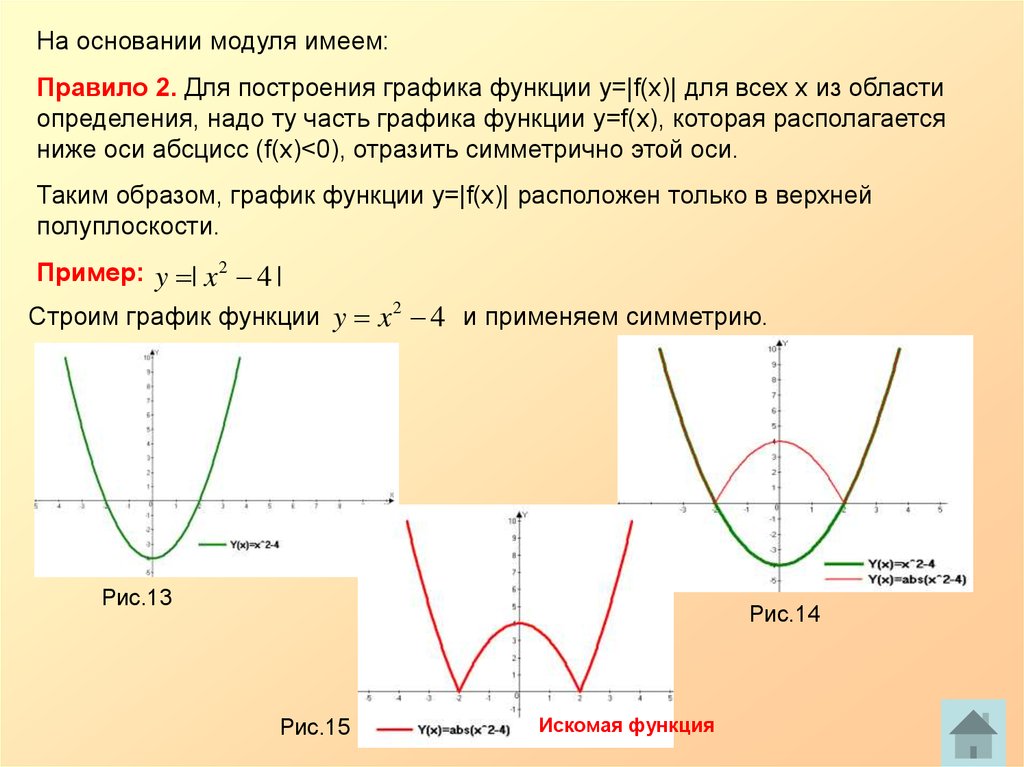 Bokeh позволяет пользователям манипулировать данными в браузере с помощью ползунков и раскрывающихся меню для фильтрации. Как и в mpld3, вы можете масштабировать и панорамировать для навигации по графикам, но вы также можете сфокусироваться на наборе точек данных с помощью рамки или выбора лассо.
Bokeh позволяет пользователям манипулировать данными в браузере с помощью ползунков и раскрывающихся меню для фильтрации. Как и в mpld3, вы можете масштабировать и панорамировать для навигации по графикам, но вы также можете сфокусироваться на наборе точек данных с помощью рамки или выбора лассо.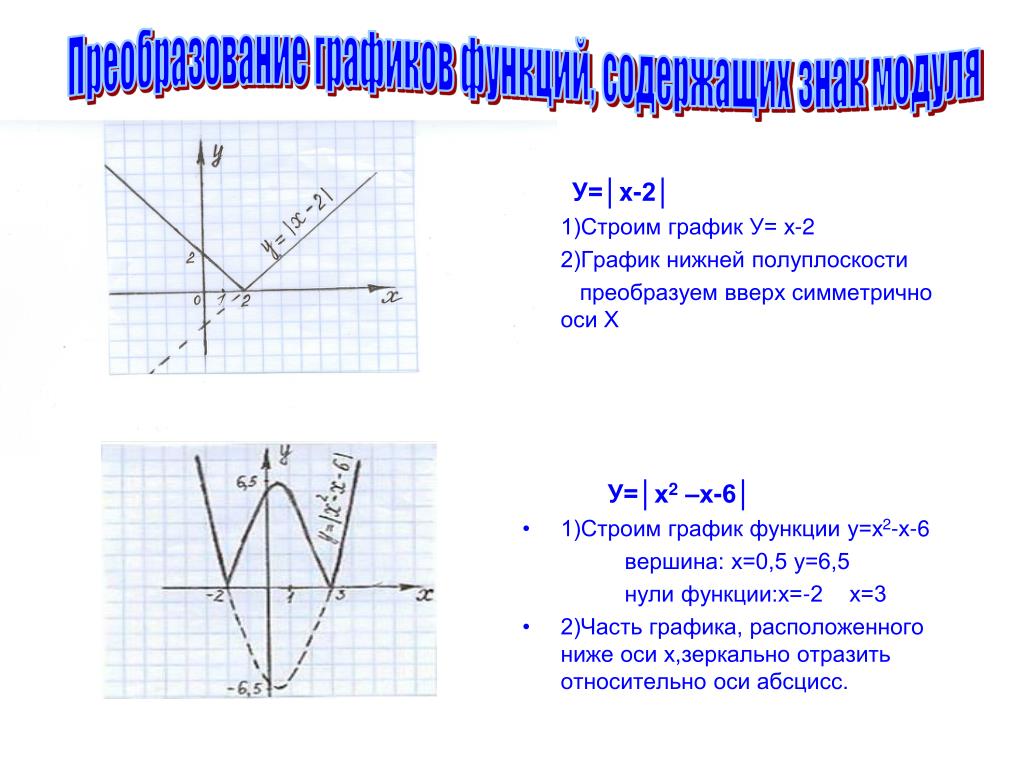
 Оттуда вы можете вставлять свои графики на веб-страницу.
Оттуда вы можете вставлять свои графики на веб-страницу.


 barplot(data=df, x="year", y="seats", hue="party", pause=['blue', 'red', 'желтый', 'серый'], насыщенность=0,6)
barplot(data=df, x="year", y="seats", hue="party", pause=['blue', 'red', 'желтый', 'серый'], насыщенность=0,6)  По своей сути Plotly — это библиотека JavaScript! Он использует D3 и stack.gl для рисования графиков.
По своей сути Plotly — это библиотека JavaScript! Он использует D3 и stack.gl для рисования графиков. Bar(x=x, y=df['others'], name='Others', marker=go.bar.Marker(color='#929591')),
Bar(x=x, y=df['others'], name='Others', marker=go.bar.Marker(color='#929591')),  plotting factor_cmap
plotting factor_cmap  xgrid.grid_line_color = None
xgrid.grid_line_color = None  Color('party', scale=alt.Scale(domain=list(cmap.keys()), range=list(cmap.values())))
Color('party', scale=alt.Scale(domain=list(cmap.keys()), range=list(cmap.values())))  bar (
bar (