Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа
| Справочник по математике | Элементы математического анализа | Производная функции |
| Схема исследования поведения функций, применяемая для построения графиков функций |
| Примеры построения графиков функций |
Схема исследования поведения функций, применяемая для построения графиков функций
Для построения графика функции y = f (x) желательно сначала провести исследование поведения функции y = f (x) по следующей схеме.
Найти область определения D ( f ).

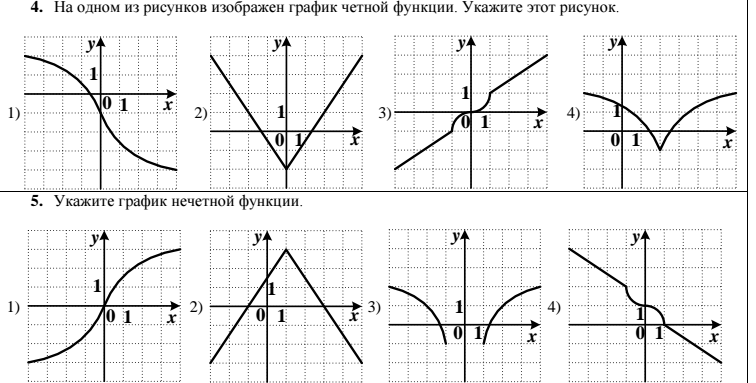
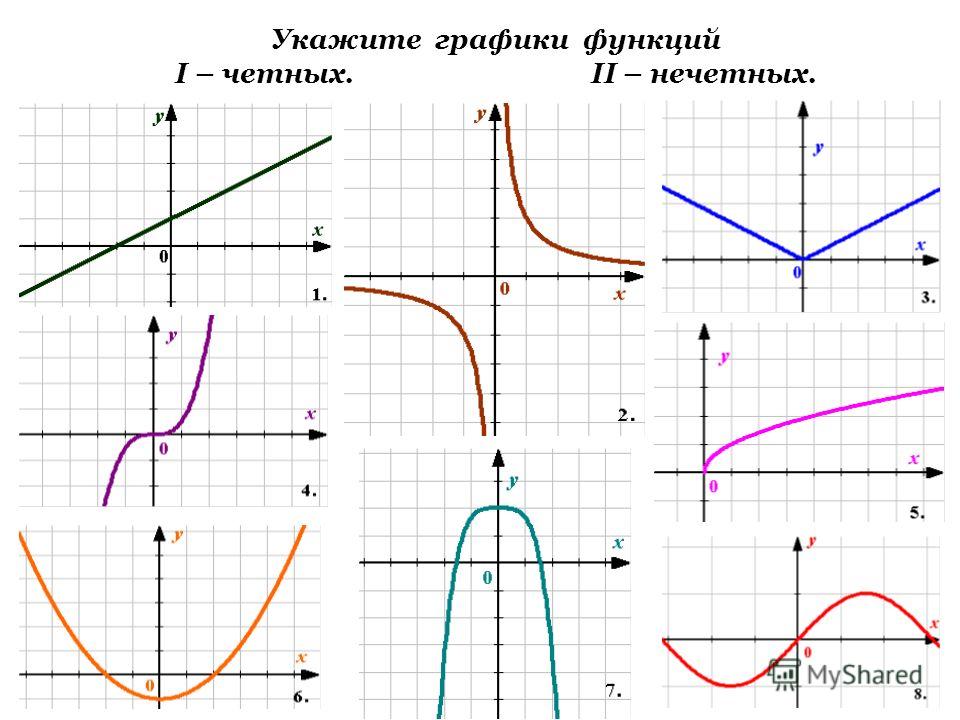
Выяснить, является ли функция y = f (x) четной или нечетной.
Выяснить, является ли функция y = f (x) периодической.
Найти асимптоты графика функции.
Вычислить производную функции f ‘ (x) .
Найти критические точки функции y = f (x) .
Найти интервалы возрастания и убывания функции y = f (x) .
Найти экстремумы функции y = f (x) .
Найти точки пересечения графика функции y = f (x) с осями координат.
Если не удается точно найти нули функции, то есть точки, в которых график функции пересекает ось абсцисс Ox, то нужно попытаться найти интервалы, на которых нули функции располагаются.
 Часто эти интервалы удается найти, зная точки максимума и минимума функции.
Часто эти интервалы удается найти, зная точки максимума и минимума функции.Вычислить вторую производную функции f » (x) .
Найти интервалы, на которых функция y = f (x) выпукла вверх, а также интервалы, на которых функция y = f (x) выпукла вниз.
Найти точки перегиба графика функции y = f (x) .
Замечание. Желательно рисовать схему поведения функции параллельно с проведением исследования свойств функции по описанному выше плану.
Примеры построения графиков функций
Пример 1. Построить график функции
| y = x3 + 8x2 + 16x + 128 | (1) |
Решение. Областью определения функции (1) является вся числовая прямая.
Областью определения функции (1) является вся числовая прямая.
Функция (1) не является ни четной, ни нечетной.
Функция (1) не является периодической.
Вертикальных асимптот у графика функции (1) нет, так как для любого числа x0
Проверим, есть ли у графика функции (1) наклонные асимптоты. Поскольку
то делаем вывод, что наклонных асимптот у графика функции (1) нет.
Теперь вычислим производную функции (1):
y’ (x) = 3x2 + 16x + 16 .
Поскольку y’ (x) существует для всех , то все критические точки функции являются ее стационарными точками, то есть точками, в которых
y’ (x) = 0 ./Tablitsy%20s%20formulami/Grafiki%20elementarnyh%20funkciy.jpg)
Найдем стационарные точки функции (1), интервалы, на которых y’ (x) сохраняет знак, а также экстремумы функции. Для этого решим квадратное уравнение
3x2 + 16x + 16 = 0.
Изобразим на рисунке 1 диаграмму знаков производной y’ (x)
Рис.1
На интервалах и производная y’ (x) положительна, значит, функция (1) возрастает. На интервале производная y’ (x) отрицательна, значит, функция (1) убывает. Схематически поведение функции (1) изображено на рисунке 2.
Рис.2
При переходе через точку x = – 4 производная функции y’ (x) меняет знак с «+» на «–» . Следовательно, точка x = – 4 является точкой максимума функции (1). При переходе через точку производная функции y’ (x) меняет знак с «–» на «+» . Следовательно, точка является точкой минимума функции (1).
Следовательно, точка является точкой минимума функции (1).
Найдем значения функции (1) в стационарных точках:
y (–4) = 256 ,
Теперь вычислим вторую производную функции (1):
y» (x) = (y’ (x))‘ = (3x2 + 16x + 16)‘ = 6x + 16 .
y» (x) = (y’ (x))‘ =
= (3x2 + 16x + 16)‘ =
= 6x + 16 .
Вторая производная y» (x) обращается в нуль при . Изобразим на рисунке 3 диаграмму знаков второй производной y» (x)
Рис.3
При переходе через точку вторая производная функции y» (x) меняет знак с «–» на «+» . Следовательно, – точка перегиба графика функции (1). При функция (1) выпукла вверх, при функция (1) выпукла вниз.
При функция (1) выпукла вверх, при функция (1) выпукла вниз.
Дополним схему поведения функции, представленную на рисунке 2, новыми данными о направлении выпуклости функции (рис. 4).
Рис.4
Для того, чтобы найти точки пересечения функции (1) с осью Ox , решим уравнение
x3 + 8x2 + 16x + 128 = 0 ,
x2 (x + 8) + 16 (x + 8) = 0 ,
(x + 8) (x2 + 16) = 0 .
Таким образом, точка (– 8; 0) является единственной точкой пересечения графика функции (1) с осью Ox . Точкой пересечения графика функции (1) с осью Oy будет точка (0; 128) .
На схеме поведения функции, представленной на рисунке 4, добавим информацию о знаках функции (1) (рис. 5).
Рис. 5
5
Принимая во внимание результаты исследования поведения функции (1) (большая часть данных компактно представлена на рисунке 5), мы можем построить график функции (1) (рис.6):
Рис.6
Пример 2. Построить график функции
| (2) |
Решение. Областью определения функции (2) является вся числовая прямая, за исключением точки x = 0 , то есть .
Функция (2) не является ни четной, ни нечетной.
Функция (2) не является периодической.
Прямая x = 0 является вертикальной асимптотой графика функции (2), так как
Для того, чтобы выяснить, имеются ли у графика функции (2) наклонные асимптоты, представим правую часть формулы (2) в другом виде:
| (3) |
Из формулы (3) получаем равенство
откуда вытекает, что прямая
y = x + 3
является наклонной асимптотой графика функции (2), как при , так и при .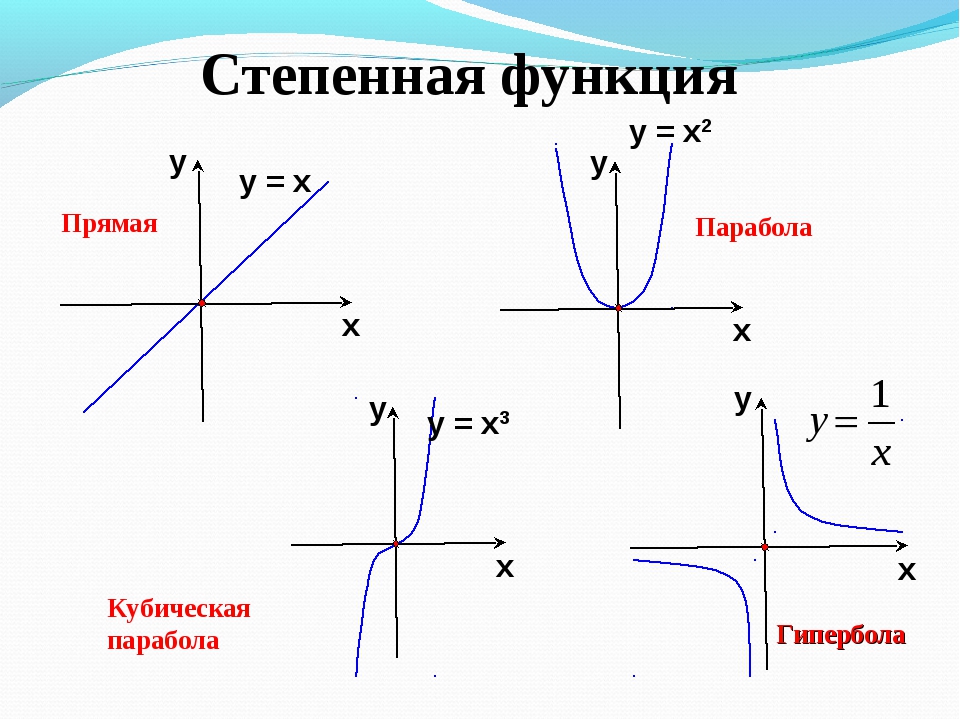
Теперь вычислим производную функции (2). Проще всего это сделать, воспользовавшись формулой (3):
| (4) |
Для того, чтобы найти стационарные точки функции (2), преобразуем правую часть формулы (4):
Следовательно,
| (5) |
и стационарными точками функции (2) являются точки x = – 1 и x = 2 .
Изобразим на рисунке 7 диаграмму знаков производной y’ (x)
Рис.7
На интервалах , и производная y’ (x) положительна, значит, функция (2) возрастает на этих интервалах. На интервале (0, 2) производная y’ (x) отрицательна, значит, функция (2) убывает на этом интервале. Схематически поведение функции (2) изображено на рисунке 8.
Рис.8
При переходе через точку x = – 1 производная функции y’ (x) знак не меняет, значит, в этой точке экстремума нет. При переходе через точку x = 2 производная функции y’ (x) меняет знак с «–» на «+» . Следовательно, точка x = 2 является точкой минимума функции (2).
Найдем значения функции (1) в стационарных точках:
y (–1) = 0 ,
Теперь перейдем к вычислению второй производной функции (2). Проще всего это сделать, воспользовавшись формулой (4):
Вторая производная y» (x) обращается в нуль при x = – 1 . Изобразим на рисунке 9 диаграмму знаков второй производной y» (x)
Рис.9
При переходе через точку x = – 1 вторая производная функции y» (x) меняет знак с «–» на «+» .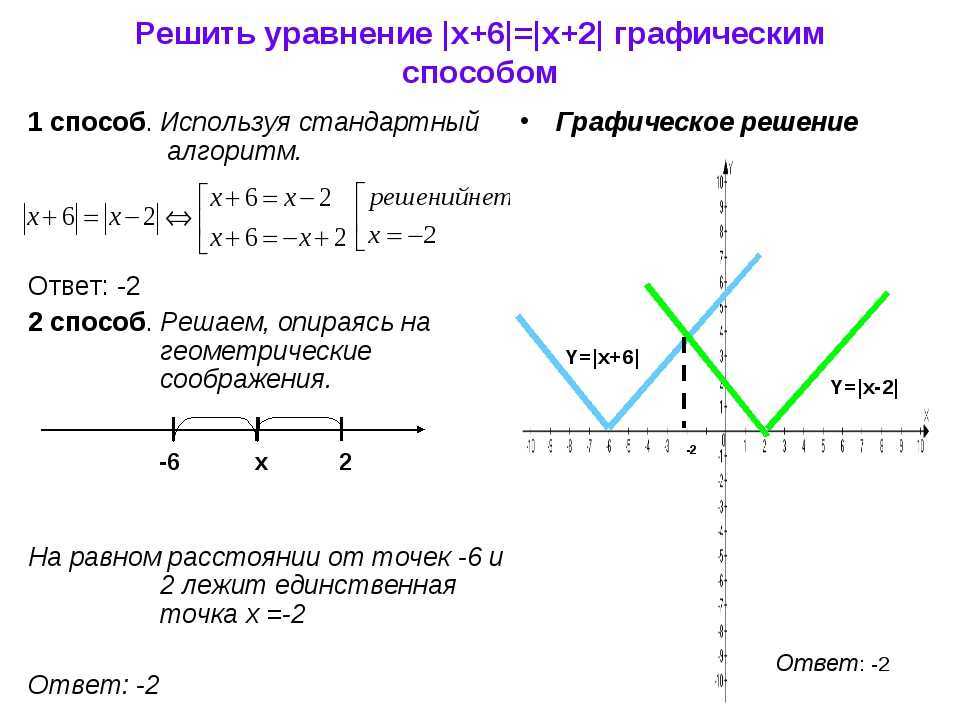 Следовательно, x = – 1 – точка перегиба графика функции (2). При x < – 1 функция (2) выпукла вверх, при x > – 1 функция (2) выпукла вниз.
Следовательно, x = – 1 – точка перегиба графика функции (2). При x < – 1 функция (2) выпукла вверх, при x > – 1 функция (2) выпукла вниз.
Дополним схему поведения функции, представленную на рисунке 8, данными о направлении выпуклости функции (рис. 10).
Рис.10
Найдем точки пересечения функции (2) с осями координат: точка (– 1; 0) является единственной точкой пересечения графика функции (2) с осью Ox , а точек пересечения графика функции (2) с осью Oy нет, поскольку x = 0 не входит в область определения функции (2).
На схеме поведения функции, представленной на рисунке 10, добавим информацию о знаках функции (2) (рис. 11).
Рис.11
Принимая во внимание результаты исследования поведения функции (2) (большая часть данных компактно представлена на схеме рисунка 11), мы можем построить график функции (2) (рис. 12):
12):
Рис.12
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Преобразование графиков функций — подготовка к ЕГЭ по Математике
Анна Малкова
В этой статье мы расскажем об основных преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.
Очень жаль, что эта тема — полезная и очень интересная — выпадает из школьной программы. На нее постоянно не хватает времени. Из-за этого многим старшеклассникам не даются задачи с параметрами — которые на самом деле похожи на конструктор, где вы собираете решение из знакомых элементов. Хотя бы для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.
Но конечно, не только для того, чтобы сдать ЕГЭ. Первая лекция на первом курсе технического или экономического вуза посвящена функциям и графикам.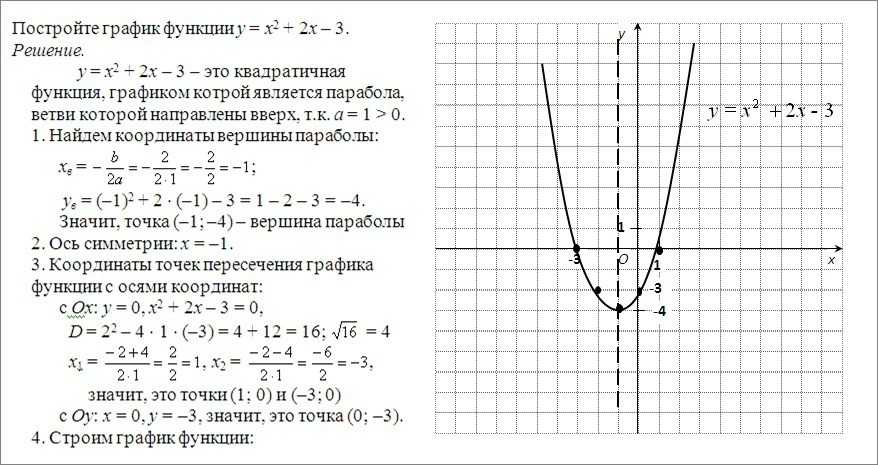 Первые зачеты в курсе матанализа связаны с функциями и графиками.
Первые зачеты в курсе матанализа связаны с функциями и графиками.
Начнем со сдвигов графиков по Х и по Y.
1. Сдвиг по горизонтали.
Пусть функция задана формулой и Тогда график функции сдвинут относительно исходной на а вправо. График функции сдвинут относительно исходной на а влево.
2. Сдвиг по вертикали.
Пусть функция задана формулой и С — некоторое положительное число. Тогда график функции сдвинут относительно исходного на С вверх. График функции сдвинут относительно исходного на С вниз.
Теперь растяжение графика. Или сжатие.
3. Растяжение (сжатие) по горизонтали.
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в k раз по горизонтали, если , и сжат относительно исходного в k раз по горизонтали, если
4. Растяжение (сжатие) по вертикали.
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в М раз по вертикали, если , и сжат относительно исходного в М раз по вертикали, если
И отражение по горизонтали.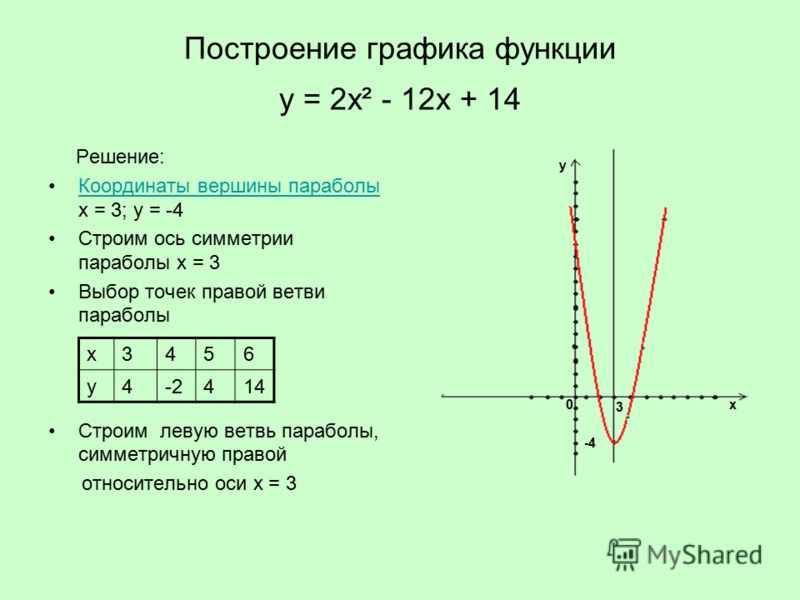
5. Отражение по горизонтали.
График функции симметричен графику функции относительно оси Y.
6. Отражение по вертикали.
График функции симметричен графику функции относительно оси Х.
Друзья, не возникло ли у вас ощущения, что вы все это где-то видели? Да, наверняка видели, если когда-либо редактировали изображения в графическом редакторе на компьютере. Изображение можно сдвинуть (по горизонтали или вертикали). Растянуть (по горизонтали или вертикали). Отразить. И все это мы делаем с графиками функций.
И еще два интересных преобразования. Здесь в формулах присутствует знак модуля. Если не помните, что такое модуль, — срочно повторите эту тему.
7. Графики функций и
На рисунке изображен график функции Она специально взята такая — несимметричная относительно нуля.
Построим график функции
Конечно же, мы пользуемся определением модуля.
Это мы и видим на графике.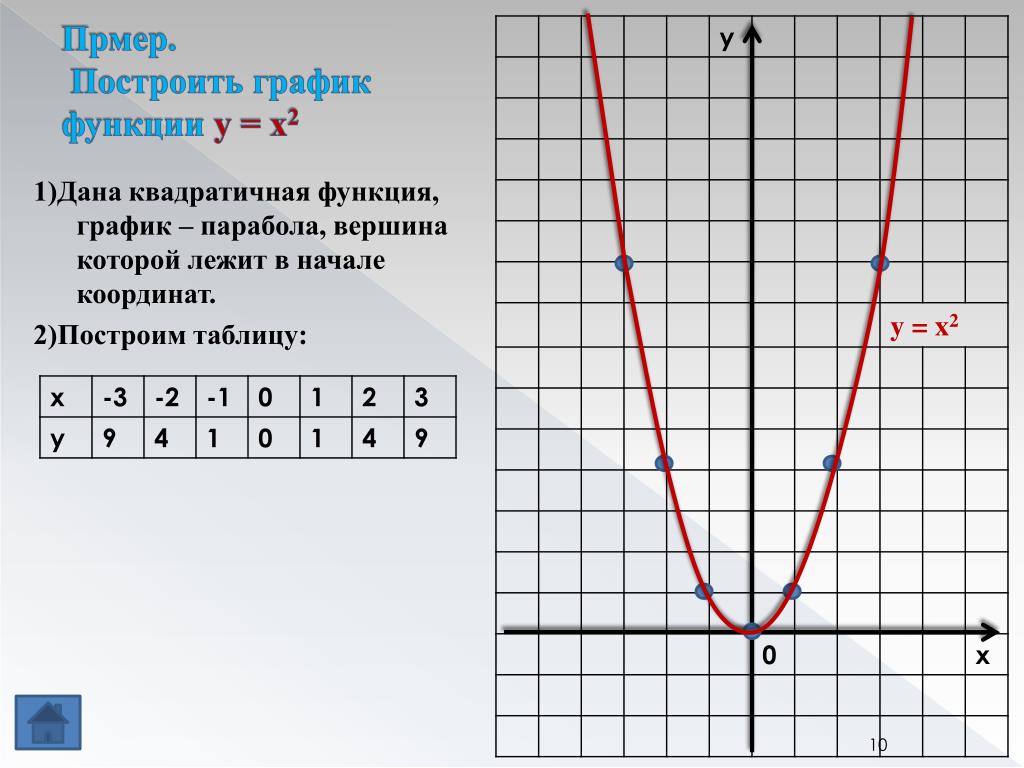 Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.
Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.
Теперь график функции Вы уже догадались, что будет. Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.
Как определить по формуле функции, будет график преобразован по горизонтали (по Х) или по вертикали (по Y)? Разница очевидна. Если сначала мы что-либо делаем с аргументом х (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по Х. Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, — преобразование по Y.
Вот самые простые задачи на преобразование графиков.
1.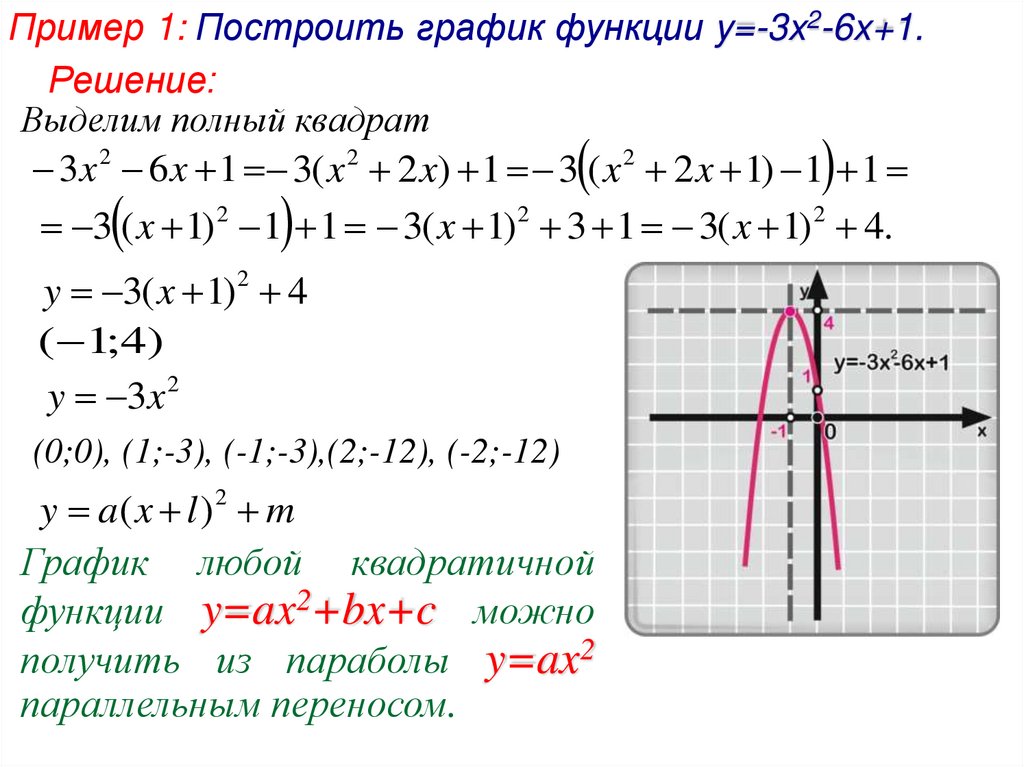 Построим график функции
Построим график функции
Это квадратичная парабола, сдвинутая на 3 влево по x и на 1 вниз по y.
Вершина в точке
2. Построим график функции
Выделим полный квадрат в формуле.
График — квадратичная парабола, сдвинутая на 2 вправо по x и на 5 вниз по y.
Обратите внимание: график функции пересекает ось y в точке На нашем графике это точка
Продолжение — в статье «Построение графиков функций».
Спасибо за то, что пользуйтесь нашими публикациями. Информация на странице «Преобразование графиков функций» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
07. 04.2023
04.2023
Объяснение родительских функций и родительских графиков — Mashup Math
Изучение родительских функций и родительских графов даст вам лучшее представление о поведении множества других функций, с которыми вы часто сталкиваетесь в алгебре и не только. Ваше концептуальное понимание родительских функций и их графиков является ключом к разработке преобразований уравнений и графиков.
Следующее бесплатное руководство по Родительские функции и их графики объяснит, что такое родительские функции, как выглядят их графики и почему понимание их поведения так важно в математике. В этом посте мы рассмотрим родительские функции следующих часто встречающихся функций:
Родительская функция абсолютного значения
Линейная родительская функция
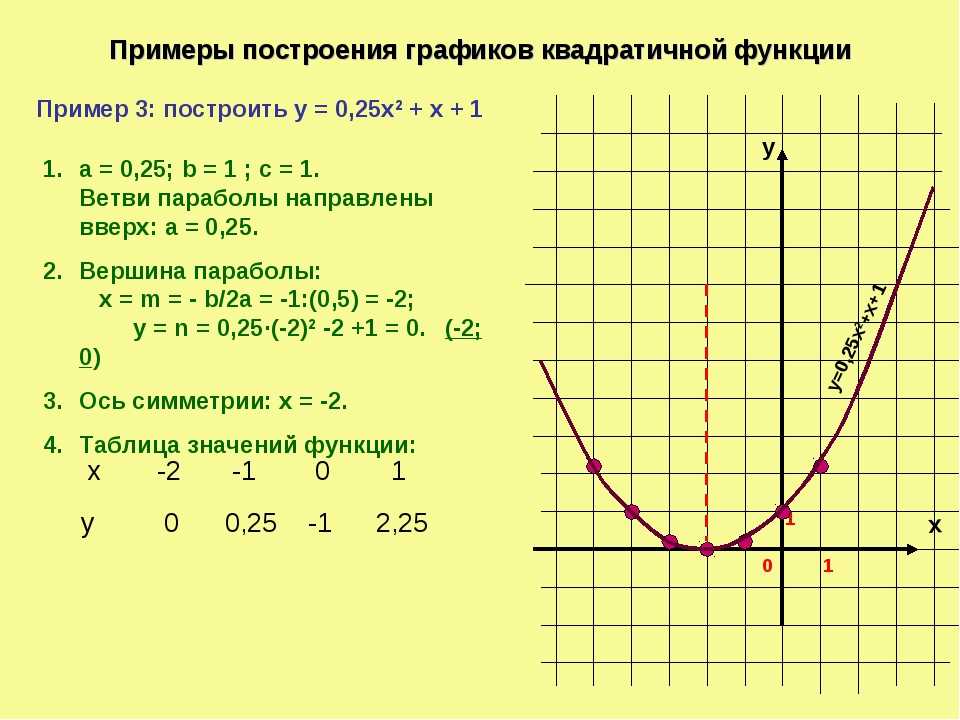
Квадратичная родительская функция
90 Par 0016Экспоненциальная родительская функция
Обратная родительская функция
Родительская функция квадратного корня определить функцию, связанную с графиком с легкостью!
Прежде чем вы узнаете о родительских функциях и графиках родительских функций, давайте кратко рассмотрим некоторые ключевые словарные термины и определения, относящиеся к родительским функциям.
 Что такое родительская функция? Что такое родительский граф?
Что такое родительская функция? Что такое родительский граф?В математике родительская функция — это функция из семейства функций, которая находится в простейшей форме — это означает, что она вообще не преобразовывалась.
Родительский график — это график родительской функции на координатной плоскости.
Хотя на первый взгляд эти определения могут показаться запутанными, на самом деле концепции довольно просты, если смотреть на них визуально.
Например, рассмотрим линейные функции y=x и y=x+3.
В этом случае семейство функций представляет собой линейную функцию (любую функцию вида y=mx+b), которая представляет линию координатной плоскости.
Таким образом, в данном случае y=x — это линейная родительская функция, а y=x+3 — просто преобразованная версия родительской функции (поскольку она была смещена на три единицы вверх по сравнению с положением исходной родительской функции на графике) .

Опять же, обратите внимание, что функция y=x является линейная родительская функция (линия y=x на координатной плоскости является родительским графиком ) и что функция y=x+3 является преобразованной версией родительской функции (она была смещена на 3 единицы вверх).
Все родительские функции…Если вы понимаете линейную родительскую функцию и то, что она представляет, то вы можете понять все родительские функции.
Анимированный GIF справа дополнительно демонстрирует, что такое линейная родительская функция и как она связана со всеми другими линейными функциями.
Главный вывод сейчас состоит в том, что каждое семейство функций (линейных, квадратичных, кубических, квадратного корня и т. д.) имеет родительскую функцию, из которой все остальные функции в этом семействе могут быть получены простым преобразованием базовой родительской функции.

Что такое родительская функция и что такое графики родительской функции?
Определение: Родительская функция — это основная функция, из которой выводится семейство подобных функций. Выполняя различные операции, такие как сложение, вычитание, умножение и т. д. над родительской функцией, вы получаете функцию, принадлежащую тому же семейству.
Графики родительской функции — это графики соответствующей родительской функции. Любой график может быть графически представлен путем перевода, отражения, увеличения или применения их комбинации к графу его родительской функции.
Теперь подробнее о родительских функциях и родительских графах следующих типов уравнений:
1. Линейное
2. Квадратичное
3. Кубическое
4. Кубическое
4.
Экспоненциальное
6.
 Квадратный корень
Квадратный корень7. Абсолютное значение
*Обратите внимание, что в этом руководстве y= и f(x)= взаимозаменяемы и означают одно и то же.
Линейные функции — один из самых простых типов функций, которые вам предстоит изучить. Общая форма линейной функции с одной переменной такова: f(x) = mx + b, где m и b — константы, а a — ненулевые.
Некоторые примеры линейных функций, производных от линейной родительской функции:
f(x) = 2x +5
f(x) = -3x +8
f(x) = 5x + 10
Родительская функция = линейная, xy = линейная что является простейшей формой, из которой могут быть получены члены семейства линейных функций.
Линейная родительская функция: f(x) = x
График родительской функции линейных функций представляет собой прямую линию с наклоном 1 и проходит через начало координат.
 2 + c*x +d, где 92 — 6x, может показаться, что функция резко отличается от родительской функции, но визуально график родительской функции и график кубической функции ниже не сильно отличаются друг от друга (см. графики ниже для справки)
2 + c*x +d, где 92 — 6x, может показаться, что функция резко отличается от родительской функции, но визуально график родительской функции и график кубической функции ниже не сильно отличаются друг от друга (см. графики ниже для справки)Примеры Кубические функции:
Как и визуальное сходство, функции также демонстрируют поведенческое сходство со своими родительскими функциями, поэтому важно знать о них.
Обратите внимание, что в родительском экспоненциальном графике график стремится к y = 0, когда x стремится к отрицательной бесконечности. Это горизонтальная асимптота функции. Вы столкнетесь с горизонтальными асимптотами для функций, родительская функция которых экспоненциальна.
Далее посмотрим, как выглядят примеры графиков экспоненциальных функций. Посмотрите, сможете ли вы определить их горизонтальные асимптоты.

Примеры экспоненциальных функций:
Обратные функции, также известные как обратные функции, имеют переменную (x) в знаменателе функции.
Обратная родительская функция: f(x) = 1/x.
Некоторые примеры функций, подпадающих под семейство обратных функций, производных от обратной родительской функции, включают: 10)
f(x) = 2/(2x+3)
Родительская обратная функция имеет вертикальную асимптоту на оси y (x = 0), что видно по поведению графика при стремлении x к 0.
Следовательно, наличие вертикальных асимптот на графике может указывать на то, что исходная функция является обратной. Узнаете ли вы вертикальные асимптоты на графиках приведенных ниже примеров обратных функций?
Примеры обратных функций:
Родительской функцией функций квадратного корня является f(x) = sqrt(x).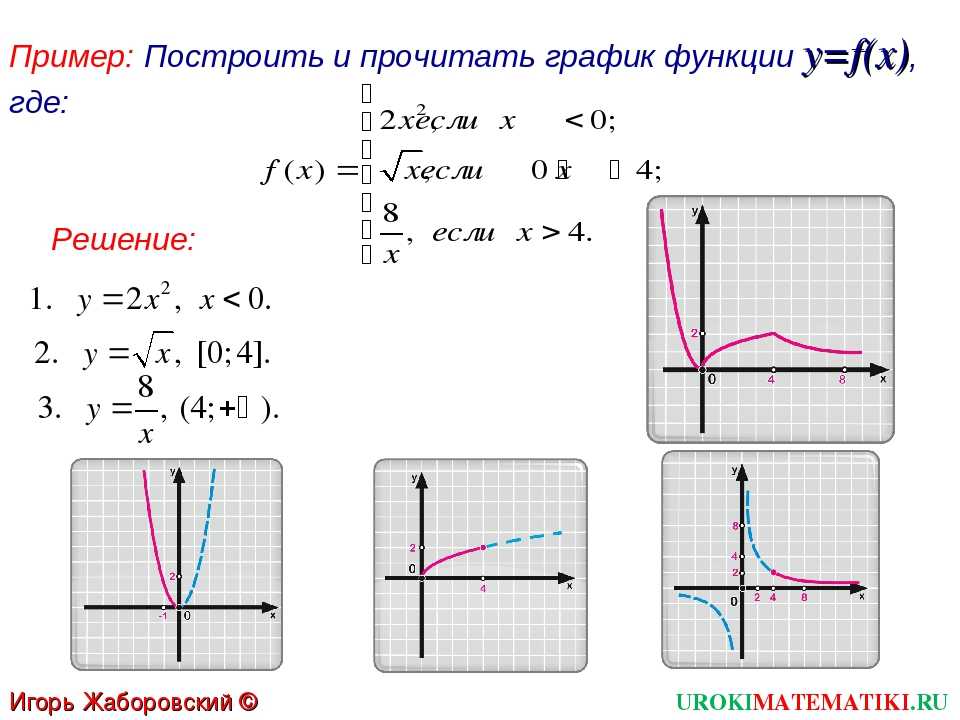
Ниже приведены примеры функций квадратного корня, полученных из родительской функции квадратного корня:
f(x) = sqrt(x+1)
f(x) = sqrt(3x -9)
f(x) = sqrt(-x)
Родительская функция квадратного корня имеет диапазон выше 0 и область (возможные значения x) всех положительных действительных значений. Поэтому родительский граф f(x) = sqrt(x) выглядит так, как показано ниже:
Графики примеров функции квадратного корня также имеют ограниченные домены.
Примеры функций извлечения квадратного корня:
*Примечание: Из типов родительских функций, обсуждаемых в этом блоге, только функции, производные от квадратного корня и обратные родительские функции, наследуют ограничения домена. Вы можете использовать этот шаблон, чтобы четко отличать функции от других.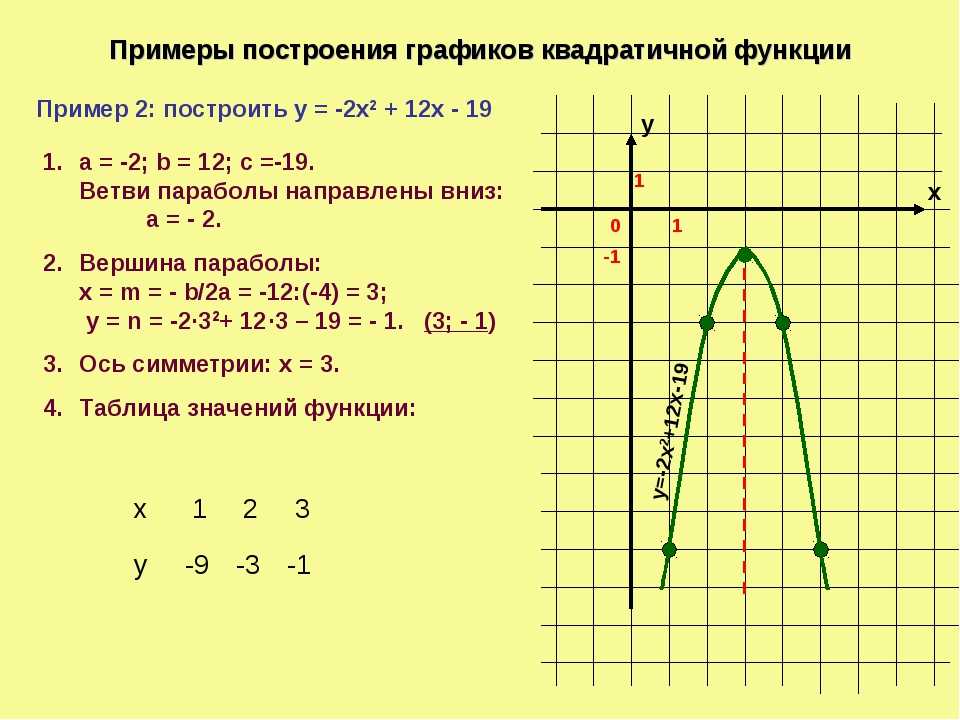
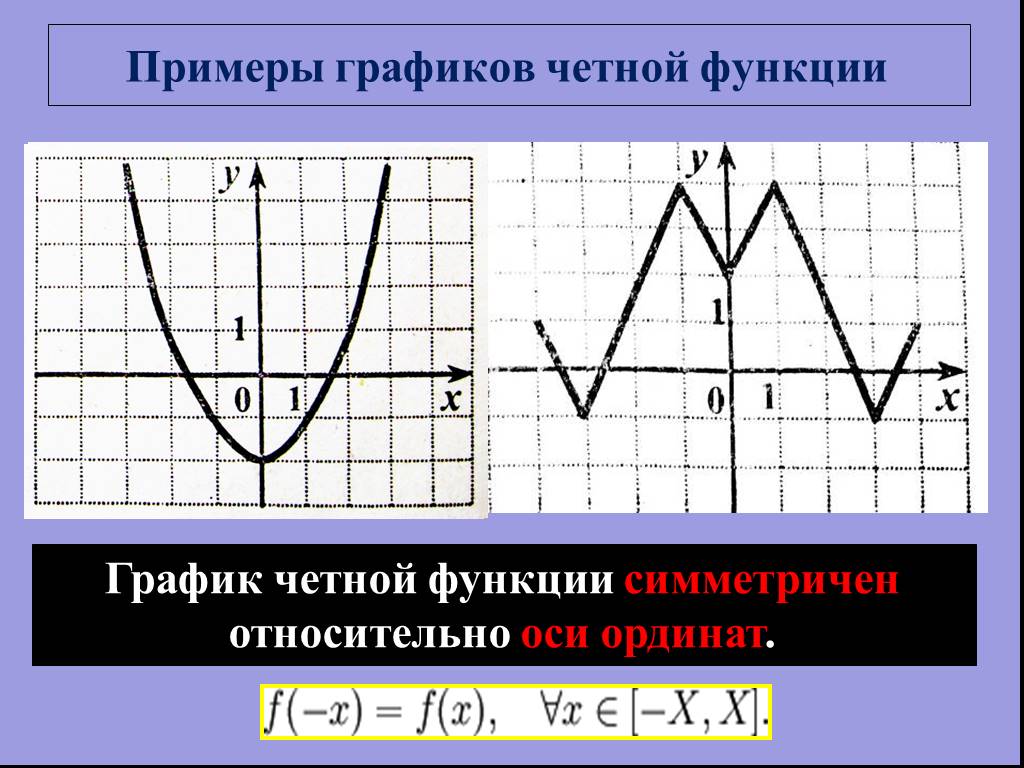
Последняя родительская функция, описанная в этом руководстве, — родительская функция абсолютного значения f(x) = | х |.
Ниже приведены примеры функций абсолютного значения, полученных из родительской функции абсолютного значения:
Родительская функция абсолютного значения определяется своей V-образной формой с острой и заостренной вершиной. Внимательно изучите приведенные ниже примеры функции абсолютного значения, чтобы увидеть их связь с родительской функцией.
Примеры функций абсолютного значения:
Заключение: родительские функции и родительские графы Существует бесконечно много функций, но все они могут быть классифицированы как производные от конкретной родительской функции. Функции, как правило, наследуют поведение и характеристики, такие как ограничения предметной области, диапазон, асимптоты и т. д., от своих соответствующих родительских функций. Следовательно, понимание шаблонов родительских функций и их графиков облегчит нам работу со сложными функциями.
д., от своих соответствующих родительских функций. Следовательно, понимание шаблонов родительских функций и их графиков облегчит нам работу со сложными функциями.
Нужна дополнительная помощь?
Посмотрите наш анимационный видео-урок о родительских функциях и их преобразованиях:
Комментарий
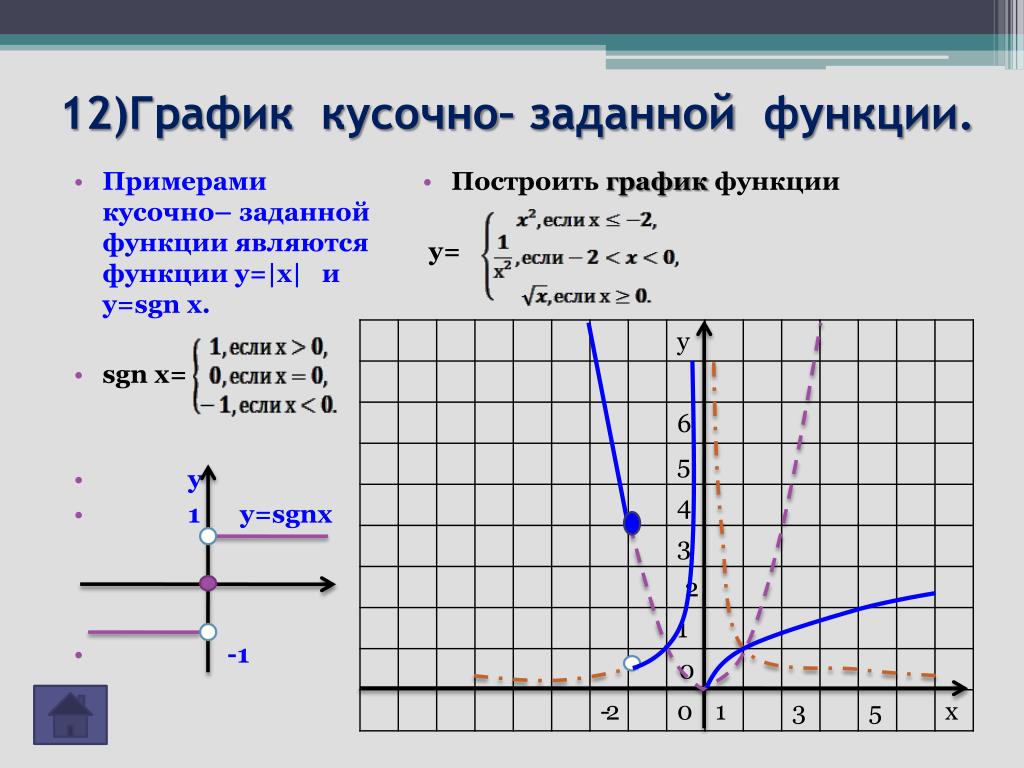
4. График функции
График функции представляет собой набор всех точек, координаты которых ( x , y ) удовлетворяют функции `y = f(x)`. Это означает, что на каждые x -значение соответствует y -значению, которое получается при подстановке в выражение для `f(x)`.
Поскольку нет ограничений на возможное количество точек для графика функции, мы сначала будем следовать этой процедуре:
- Выберите несколько значений x (не менее 5)
- Получите соответствующие значения функции и занесите их в таблицу
- Нанесите эти точки на график, соединив их плавной кривой
Тем не менее, вам рекомендуется изучить общие формы некоторых общих кривых (таких как прямая линия,
парабола, тригонометрические и экспоненциальные кривые, с которыми вы столкнетесь в последующих главах).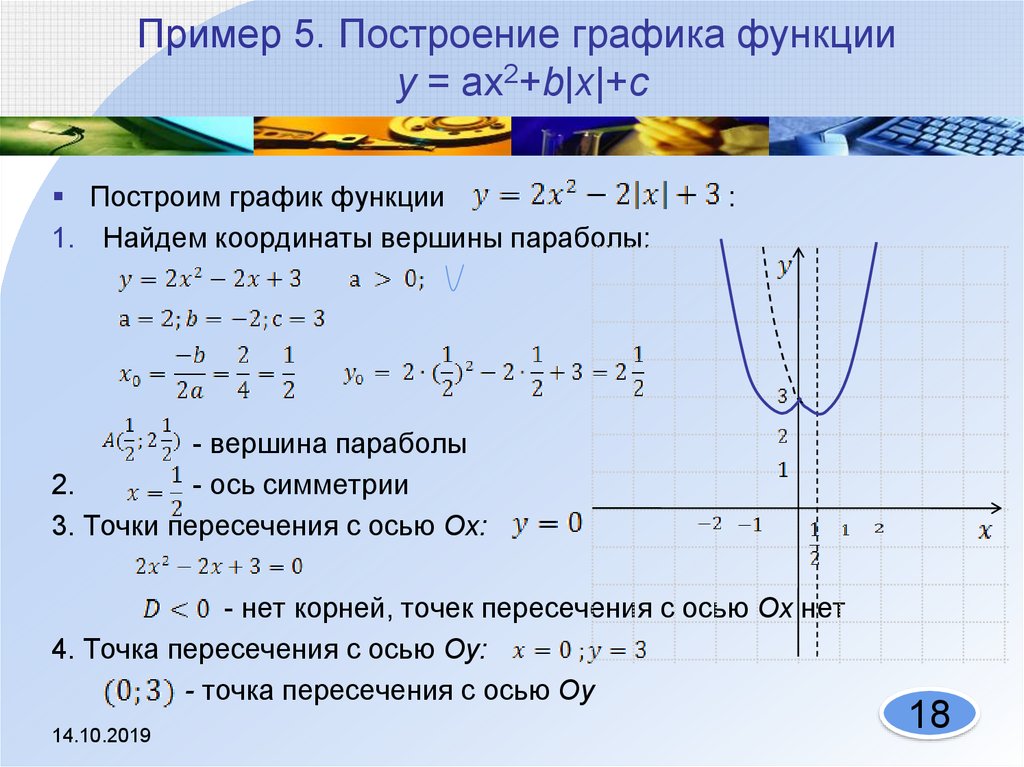 Это намного проще, чем рисовать точки, и полезнее на потом!
Это намного проще, чем рисовать точки, и полезнее на потом!
Пример 1
Нужна миллиметровка?
Значок миллиметровкиСкачать миллиметровку
Человек ростом `2 м« бросает мяч прямо вверх, и его высота в момент времени t (в s ) определяется как ч = 2 + 9 т — 4,9 т 2 м.
График функции.
Ответ
Мы начинаем с `t = 0`, так как отрицательные значения времени здесь нет практического смысла.
Мы выбираем значения с интервалом `0,5` секунды (если бы мы использовали интервалы `t = 1\ «s», мы бы не увидели достаточно деталей на графике).
| т | 0 | 0,5 | 1 | 1,5 | 2 |
| ч | 2 | 5,3 | 6,1 | 4,5 | 0,4 |
График снаряда (парабола).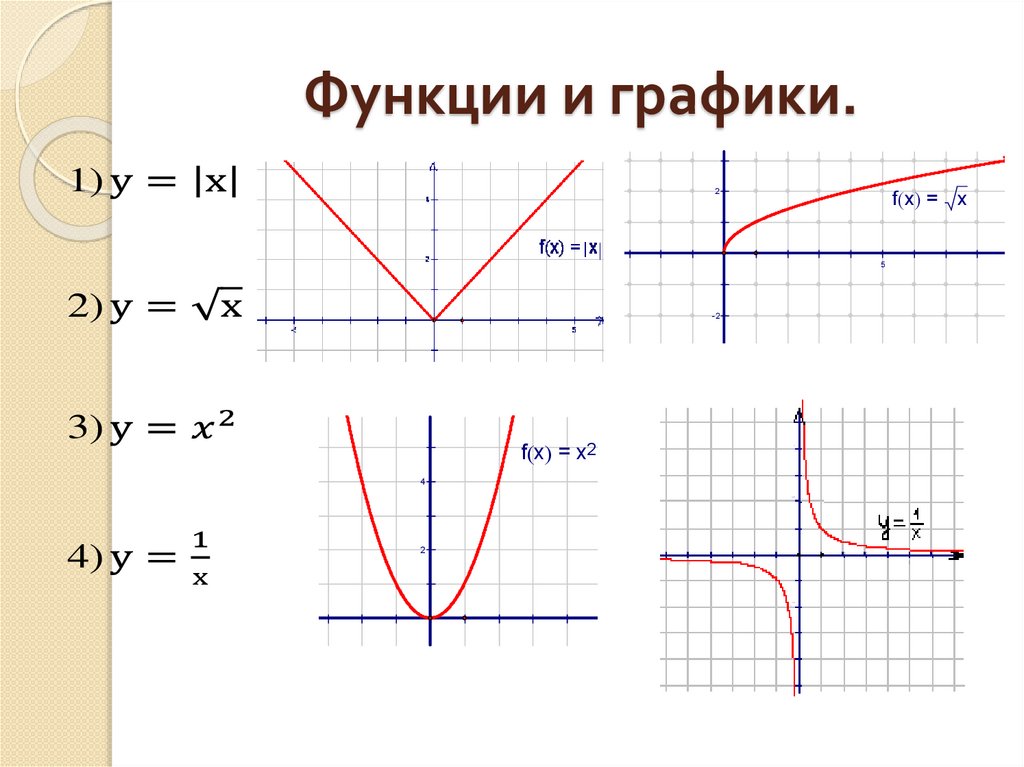
Эта форма называется параболой и является в приложениях математики.
ПРИМЕЧАНИЕ:
(1) Этот график представляет собой высоту в зависимости от времени. Мяч пошел прямо вверх, а не вперед. (На нашем графике может создаться впечатление, что мяч двигался в x — направление, а также вверх, но это было не так.)
(2) Мы могли бы написать функцию в этом примере с h ( t ), а не просто h . Следующие 2 уравнения означают одно и то же.
ч = 2 + 9 т − 4,9 т 2
ч ( т ) = 2 + 9 т − 4.9 т 2
Пример 2
Скорость (в м/с) мяча в примере 1 в момент времени t (в s ) дано по
v = 9 − 9,8 т
Нарисуйте график v — t . Что скорость в момент удара мяча о землю?
Ответ
Это прямая линия, так как она представлена в виде
y = m x + c
Подробнее о прямой линии.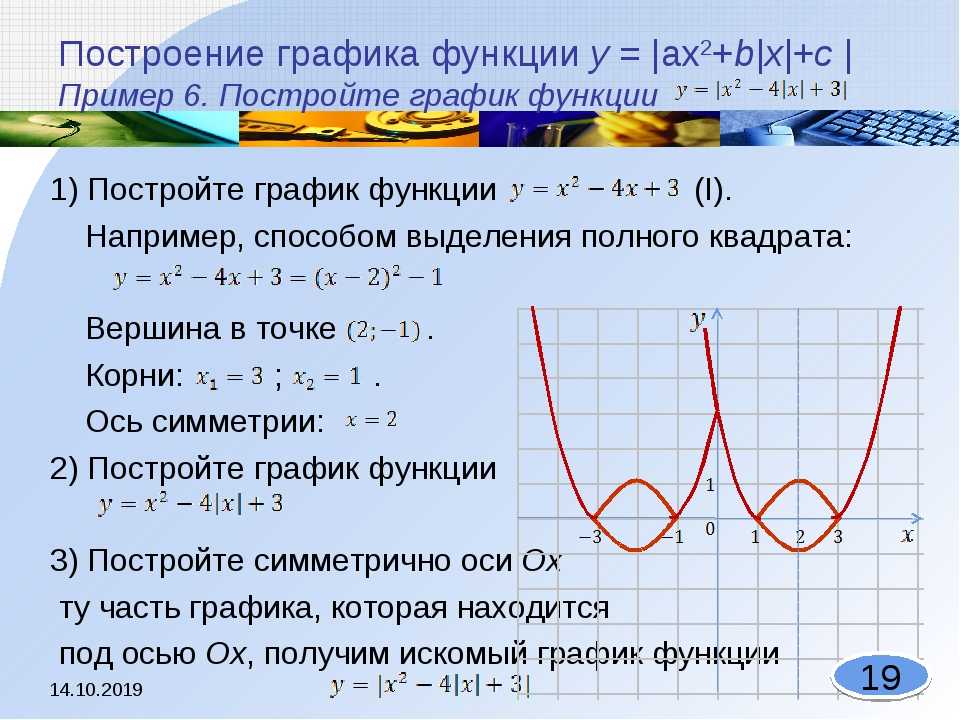
Поскольку мы узнали, что это прямая линия, нам нужно только построить 2 точки и присоединяйтесь к ним. Но мы находим 3 точки, просто чтобы убедиться, что у нас правильная линия.
| т | 0 | 1 | 2 |
| против | 9 | -0,8 | -10,6 |
График `v` против `t` — прямая линия.
Наш график начинается с `t = 0` (поскольку отрицательные значения времени в этом примере не имеют значения).
В течение первых `0,918\ «с»` мяч движется вверх (положительная скорость, т.е. синяя линия выше т -ось), но тормозит.
После этого мяч падает на землю и становится быстрее (участок, где синяя линия находится ниже оси t ).
Мяч упал на землю примерно через `t = 2,04\ «с»` (мы можем
см. это из примера 1). Скорость , когда
удар мяча о землю на графике, который мы только что нарисовали, составляет около `-11\
«м/с»`. На этом график останавливается.
На этом график останавливается.
Наш график предполагает, что мяч приземляется на песок и не отскакивает.
Обычно, как мы сделали здесь, мы берем скорость от до направление должно быть положительным.
Пример 3
Постройте график функции y = x − x 2 .
Ответ
(a) Определите значения y- для типичного набора значений x и запишите их в таблицу.
| х | −2 | −1 | 0 | 1 | 92`, парабола.
| х | `-4` | `-3` | `-2` | `-1` | `1` | `2` | `3` | `4` |
| г | `3/4` | `2/3` | `1/2` | `0` | `2` | `3/2` | `4/3` | `5/4` |
(c) Мы знаем, что около `x = 0` произойдет что-то странное (поскольку граф там не определен). Итак, мы проверяем, что происходит в некоторых типичных точках между `x = -1` и `x =
1`:
Итак, мы проверяем, что происходит в некоторых типичных точках между `x = -1` и `x =
1`:
, когда `x = −0,5,` `y = 1 + 1/(−0,5) = 1 − 2 = −1`
, когда `x = 0,5,\ y = 1 + 1/(0,5) = 1 + 2 = 3`
(d) По мере приближения значения x к `0` точки приближаются к и -ось, хотя они ее не трогают. Ось и называется асимптотой кривой.
(Чтобы убедиться в этом, нарисуйте точки, где «x = 0,4», «x = 0,3», «x = 0,2», «x = 0,1» и даже «x = 0,01».)
12345-1-2 -3-4-512345-1-2-3-4xyОткрыть изображение на новой страницеГрафик `y=1+1/x`, гипербола. Это прерывистая функция.
На этой кривой есть еще одна асимптота: `y = 1`, которая отмечена пунктирной линией. Обратите внимание, что кривая не проходит через это значение.
Пример 5
График функции `y=sqrt(x+1)`
Ответ
(a) Примечание: y не определяется для значений x меньше
чем `-1`. (Попробуйте что-нибудь в своем калькуляторе, например, `x = −4`. )
)
(b) Мы определяем некоторые x -значения и соответствующие y -значения и запишите их в таблицу:
| x | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| у | 0 | 1 | 1,4 | 1,7 | 2 | 2,2 | 2,4 |
(c) Нарисуем наш график следующим образом.
123456-1123-1xyОткрыть изображение на новой странице 92`График зависимости мощности от сопротивления.
Ответ
(a) Отрицательные значения для R не имеют физического значение, поэтому P не отображается для отрицательных значений Р.
(б) Составьте таблицу значений:
| Р | 0 | 1 | 2 | 3 | 4 | 5 | |||||||
| П | 0 92`.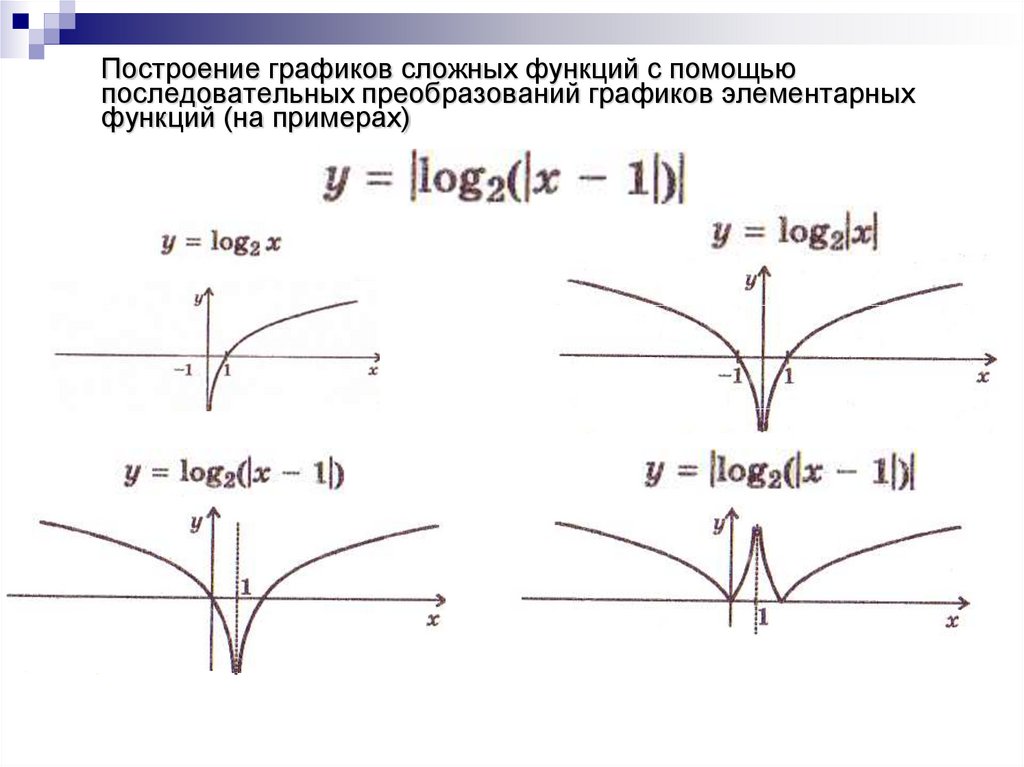 Обратите внимание, что оси помечены R (сопротивление) и P (мощность). (d) Выводы: (i) Максимальная мощность 50 «Вт» достигается, когда сопротивление R = 0,5 «Вт» `0,5\ «Ш»` График заданных функций Q1. y = х 3 − х 2 Ответ (a) Нет ограничений на значения, которые x можно взять в этом примере, так как это общий вопрос, не имеющий практического значения. (b) Составьте таблицу значений:
Так как `y = 0`, когда `x = 0` и `x = 1`, мы исследуем, что происходит между этими 2 x -значения: Когда `x = 1/2, y = -1/8.` Вот наш график: 12-11234-1-2xyОткрыть изображение на новой странице График y = x 3 − x 2 , куб. Q2. `y=sqrt(x)` Ответ Мы можем извлечь квадратный корень только из положительного числа, поэтому `x ≥ 0`. Квадратный корень числа может быть только положительным, поэтому `y ≥ 0`. Этот график на самом деле представляет собой половину параболы с горизонтальной осью. 123412xyОткрыть изображение на новой страницеГрафик `y=sqrt(x)`, полупарабола. Конический бак для воды Q3. ( Заявка ) Вода вытекает из бака в форме перевернутого конуса (т.е. вода вытекает через острый конец конуса и самую широкую часть конус вверху). Объем воды уменьшается на постоянная ставка. Начертите эскизный график высоты воды в конусе против времени. Ответ Нам нужно смоделировать высоту в момент времени t на основе того, что мы знаем о конусах. Мы также должны предположить несколько вещей. (Мы упрощаем себе жизнь по мере продвижения вперед. Нам разрешено это делать, поскольку нам просто нужно придумать базовый график высоты воды в момент времени t ). |


 Часто эти интервалы удается найти, зная точки максимума и минимума функции.
Часто эти интервалы удается найти, зная точки максимума и минимума функции.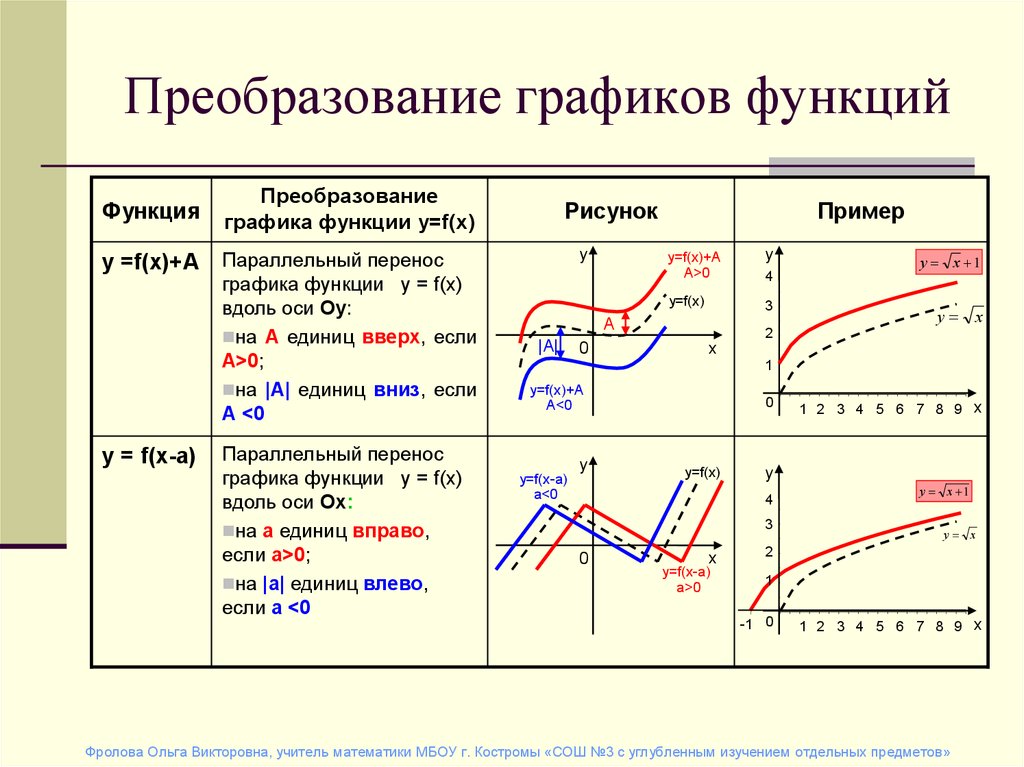
 Квадратный корень
Квадратный корень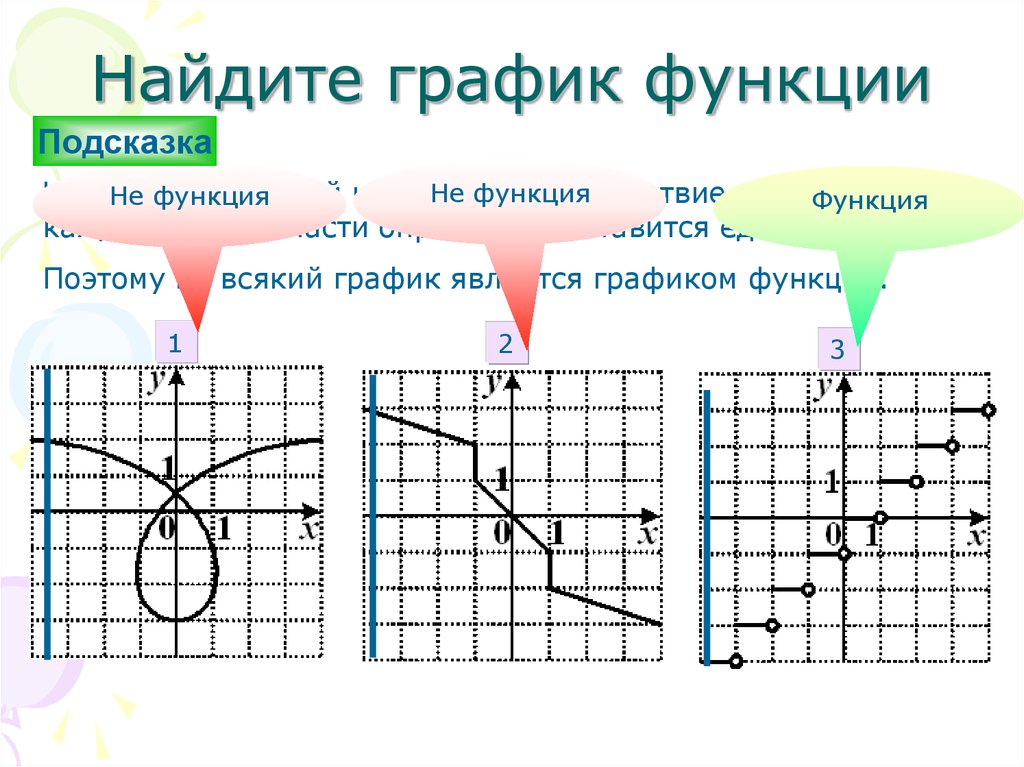 2 + c*x +d, где 92 — 6x, может показаться, что функция резко отличается от родительской функции, но визуально график родительской функции и график кубической функции ниже не сильно отличаются друг от друга (см. графики ниже для справки)
2 + c*x +d, где 92 — 6x, может показаться, что функция резко отличается от родительской функции, но визуально график родительской функции и график кубической функции ниже не сильно отличаются друг от друга (см. графики ниже для справки)