Алгебра. Учебник для 6-8 классов
Алгебра. Учебник для 6-8 классов
ОглавлениеГЛАВА ПЕРВАЯ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ. § 2. Алгебраические выражения. § 3. Допустимые значения букв. § 4. Порядок действий. § 5. Основные законы сложения и умножения. § 6. Краткие исторические сведения. ГЛАВА ВТОРАЯ. РАЦИОНАЛЬНЫЕ ЧИСЛА. § 7. Положительные и отрицательные числа. § 8. Числовая ось. § 9. Противоположные числа. § 10. Абсолютная величина числа. § 11. Сравнение рациональных чисел. § 12. Сложение рациональных чисел. § 13. Сложение нескольких чисел. § 14. Законы сложения. § 15. Вычитание рациональных чисел. § 16. Алгебраическая сумма. § 17. Умножение. § 18. Умножение нескольких чисел. § 19. Законы умножения. § 20. Деление. § 21. Свойства деления. § 22. Возведение в степень. § 23. Порядок выполнения действий. § 24. Уравнения. § 25. Решение задач с помощью уравнений. § 26. Графики. § 27. Краткие исторические сведения. (Из истории отрицательных чисел.) ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ.  § 28. Одночлен и многочлен. § 29. Тождества и тождественные преобразования. § 30. Коэффициент. § 31. Расположенные многочлены. § 32. Приведение подобных членов. § 33. Сложение одночленов и многочленов. § 34. Противоположные многочлены. § 35. Вычитание одночленов и многочленов § 36. Умножение одночленов. § 37. Умножение многочлена на одночлен. § 38. Умножение многочленов. § 39. Умножение расположенных многочленов. § 40. Возведение одночленов в степень. § 41. Формулы сокращённого умножения. § 42. Общие замечания о делении целых алгебраических выражений. § 43. Деление одночленов. § 44. Деление многочлена на одночлен § 45. Примеры решения уравнений. ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ. § 47. Равносильные уравнения. § 49. Уравнения, содержащие неизвестное в обеих частях. § 50. Уравнение первой степени с одним неизвестным. § 51. Общие указания к решению уравнений.  § 52. Решение задач с помощью уравнений. § 53. Краткие исторические сведения. (Из истории уравнений.) ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ. § 54. Понятие о разложении на множители. § 55. Вынесение за скобки общего множителя. § 56. Способ группировки. § 57. Применение формул сокращённого умножения. § 58. Применение нескольких способов. § 59. Деление многочленов при помощи разложения на множители. ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ. § 60. Понятие об алгебраической дроби. § 61. Основное свойство дроби и сокращение дробей. § 62. Перемена знака у членов дроби. § 63. Целая отрицательная и нулевая степени числа. § 64. Приведение дробей к общему знаменателю. § 65. Сложение дробей. § 66. Вычитание дробей. § 67. Умножение дробей. § 68. Деление дробей. § 69. Возведение дроби в натуральную степень. § 70. Дробные уравнения. § 71. Примеры решения уравнений с буквенными коэффициентами. ГЛАВА СЕДЬМАЯ.  КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ.§ 72. Координаты точки на плоскости. § 73. Прямо пропорциональная зависимость. § 74. График прямо пропорциональной зависимости. § 75. Линейная зависимость. § 76. Обратно пропорциональная зависимость. ГЛАВА ВОСЬМАЯ. СИСТЕМА УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ. § 77. Уравнение первой степени с двумя неизвестными. § 78. Система двух уравнений первой степени с двумя неизвестными. § 79. Равносильные системы. § 80. Решение систем уравнений. § 81. Графическое решение системы двух уравнений. § 83. Уравнение с тремя неизвестными. § 84. Система трёх уравнений с тремя неизвестными. ГЛАВА ДЕВЯТАЯ. СЧЁТНАЯ (ЛОГАРИФМИЧЕСКАЯ) ЛИНЕЙКА. § 85. Равномерные и неравномерные шкалы. § 86. Устройство счётной (логарифмической) линейки. § 87. Основная шкала. § 88. Умножение и деление с помощью счётной линейки. ГЛАВА ДЕСЯТАЯ. КВАДРАТНЫЙ КОРЕНЬ. § 89. Построение графика зависимости y = x^2 § 90. 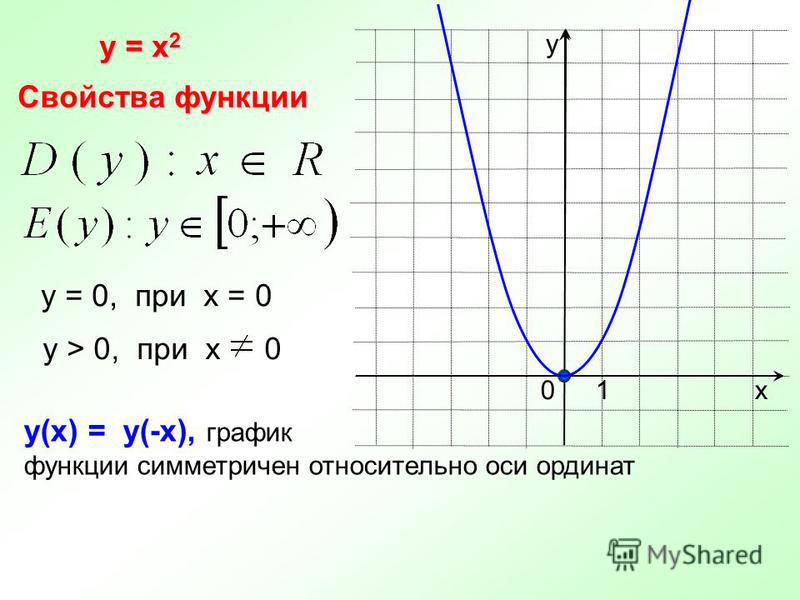 (1/3)§ 130. Примеры графического решения уравнений и систем уравнений. |
График функции y 0.5 x 2. Как построить график функции. Построение графика линейной функции
«Преобразование функций» — Качелями. Сдвиг по оси y вверх. Включи полную громкость – увеличишь a (амплитуду) колебаний воздуха. Сдвиг по оси x влево. Задачи урока. 3 балла. Музыкой. Постройте график функции и определите D(f), E(f) и T: Сжатие по оси x. Сдвиг по оси y вниз. Добавь красного цвета в палитру – уменьшишь k (частоту) электромагнитных колебаний.
«Функции нескольких переменных» — Производные высших порядков. Функцию двух переменных можно изобразить графически. Дифференциальное и интегральное исчисления. Внутренние и граничные точки. Определение предела функции 2-х переменных. Курс математического анализа. Берман. Предел функции 2-х переменных. График функции. Теорема. Ограниченная область.
«Понятие функции» — Способы построение графиков квадратичной функции.
Изучение разных способов задания функции – важный методический прием. Особенности изучения квадратичной функции. Генетическая трактовка понятия «функция». Функции и графики в школьном курсе математики. Представление о линейной функции выделяется при построении графика некоторой линейной функции.
«Тема Функция» — Анализ. Нужно выяснить не то, что ученик не знает, а то, что он знает. Заложение основ для успешной сдачи ЕГЭ и поступление в ВУЗы. Синтез. Если ученики работают по-разному, то и учитель должен с ними работать по-разному. Аналогия. Обобщение. Распределение заданий ЕГЭ по основным блокам содержания школьного курса математики.
«Преобразование графиков функций» — Повторить виды преобразований графиков. Сопоставить каждому графику функцию. Симметрия. Цель урока: Построение графиков сложных функций. Рассмотрим примеры преобразований, объясним каждый вид преобразования. Преобразование графиков функций. Растяжение. Закрепить построение графиков функций с использованием преобразований графиков элементарных функций.
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.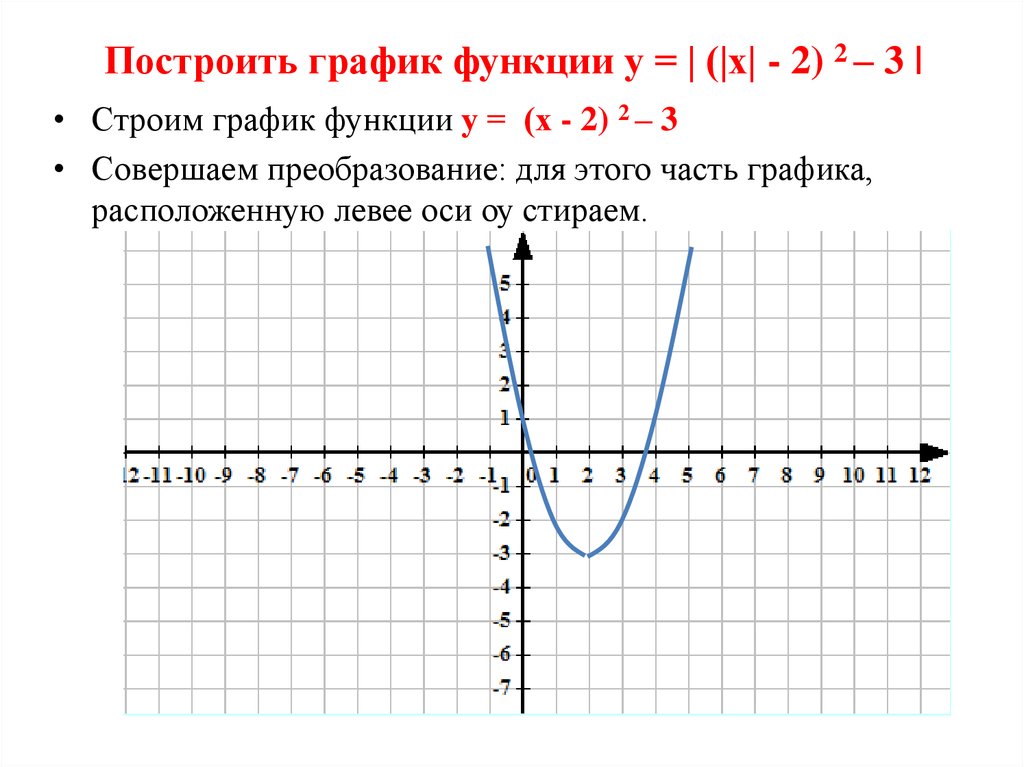
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке , потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U; график f(х) = х + 2 – это прямая, параллельная прямой f(х) = х, но сдвинутая на две единицы вверх и поэтому проходящая через точку с координатами (0,2) (потому что постоянная равна 2).
Построение графика сложной функции
Найдите нули функции. Нули функции – это значения переменной «х», при которых у = 0, то есть это точки пересечения графика с осью Х. Имейте в виду, что нули имеют не все функции, но это первый шаг процесса построения графика любой функции. Чтобы найти нули функции, приравняйте ее к нулю.
{2}}}}
), приравняйте знаменатель к нулю и найдите «х». В полученных значения переменной «х» функция не определена (в нашем примере проведите пунктирные линии через х = 2 и х = -2), потому что на 0 делить нельзя. Но асимптоты существуют не только в случаях, когда функция содержит дробное выражение. Поэтому рекомендуется пользоваться здравым смыслом:
График квадратичных функций (примеры и графики) — Math Novice
Некоторые квадратичные графики восходящие, некоторые нисходящие, некоторые пересекаются с осью X, другие нет. Каковы атрибуты этих графиков? Как мы можем использовать их при построении графика функции?
Атрибуты квадратичного графа
Основными характеристиками квадратичного графа являются точки пересечения x и y, вершина и ее ориентация. Они необходимы для построения графика квадратичной функции. Коэффициенты квадратичной функции управляют этими атрибутами. В следующей таблице перечислены эти черты и их отношение к коэффициентам.
| Graph trait | Coefficients controlling the trait |
|---|---|
| Upward | A > 0 |
| Downward | A < 0 |
| Vertex | x v = − B /(2a), y = f (x V ) |
| Оси симметрии | x =-b/(2a) |
| y retercept | Значение C |
| n-in x-in x-in x-in x-in x-in x-in x-in x-in x-in x-in x-in x-in x-inte | D < 0 |
| One x-intercept | D = 0 |
| Two x-intercepts | D > 0 |
| Graph Width | Magnitude of A |
Where A, B, C — коэффициенты квадратичной функции в стандартной форме:
f(x) = Ax 2 + Bx + C и
D = B 2 − 4AC
понимать эти атрибуты.
Восходящий/нисходящий график
Коэффициент А определяет форму квадратичного графика и его ориентацию.
В сторону увеличения или уменьшения в зависимости от знака коэффициента A .
Пример
y = x 2 + 2x + 2
A (=1) положительный, график вверх . Вершина — самая нижняя точка ( минимальное значение ).
y = − x 2 + 3x − 2
A (=-1) отрицательно, график вниз . Вершина — самая высокая точка ( максимальное значение ).
По оси абсцисс по мере удаления от начала координат (либо к – ∞ , либо к + ∞ ):
- Значение x 2 увеличивается быстрее, чем все остальные члены вместе взятые
- 2 x 2 всегда положительно, поэтому знак члена Ax 2 определяется как A
- Если A положительное , Ax 2 переходит к +∞ (в любом направлении оси x). Поэтому график восходящий
- Если A отрицательное , то Ax 2 идет к -∞ (в любом направлении оси x).
Следовательно, график направлен вниз
Следовательно, график направлен вниз Вершина квадратичной функции
Вершина является поворотной точкой на графике. В квадратичном графе есть только одна вершина. Он симметричен относительно вертикальной линии, проходящей через вершину. Эта линия является его осью симметрии .
Для вершины верно:
- Это самая высокая (или максимальная) точка, когда A < 0 (нисходящий график)
- Это самая низкая (или минимальная) точка, когда A > 0 (восходящий график)
- x-координата = − B/(2A )
- y-координата =f(2A−B)=4A4AC−B2
- Через нее проходит ось симметрии
Пример
Найти вершину квадратичной функции y = x 2 + 2x + 1 , Используя приведенную выше формулу, вы можете вычислить значения x и y вершины как:
- x = − B/(2A) = − 2/2 = − 1
- y = f(x) = f( − 1) = 1 − 2 + 1 = 0
Ось симметрии проходит через x = -1 и параллелен оси Y.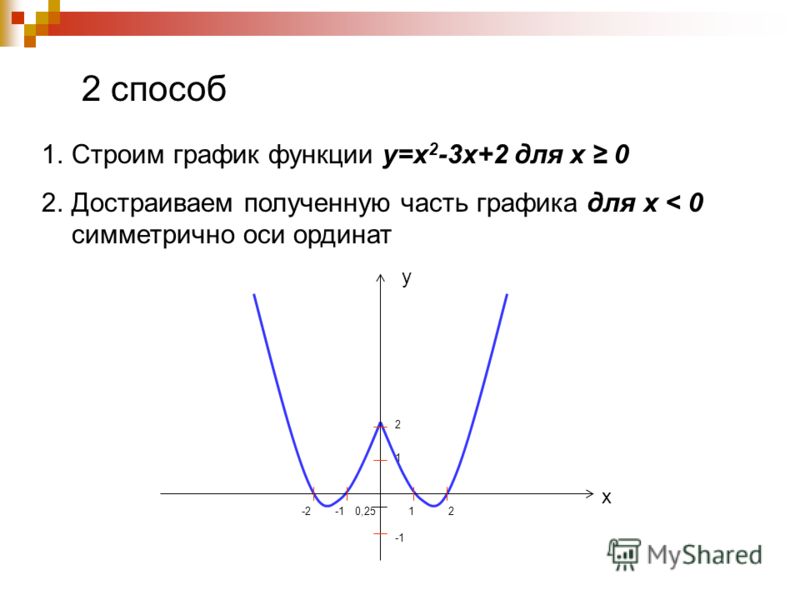
Точка пересечения по оси y
Точка пересечения с осью Y — это точка пересечения графика с осью Y. Значение x равно нулю на оси y. Поэтому его координату y легко вычислить:
y = f(0) = A.0 2 + B.0 + C = C
Следовательно, точка пересечения с осью y всегда равна (0, C).
Значение C увеличивает (или уменьшает, если C отрицательно) значение функции.
Если C положителен, график смещается вверх, а если C отрицателен, то вниз.
Пример
Графики ниже показывают этот сдвиг с использованием следующих функций: x2−x+1 y-пересечение = ( 0 , 1 )
Сравнение y-значений y-пересечения
Разница значений y g(x) и f(x) равна 2 ( = 1 – (-1) ). Точно так же разница в y-значениях h(x) и g(x) равна 1 (= 2 – 1). Графики сдвинуты по вертикали (на разность соответствующих значений C). ось Y , значение функции равно соответствующему значению C .
Так как C является точкой пересечения с осью y, то даже графики разных квадратичных функций с одинаковым значением C будут совпадать на оси y.
Точка пересечения x
Точка пересечения графика с осью x. Вы бы заметили выше, что не все графики пересекают ось x. Если да, то у него есть корень (или корни). X-пересечение является корнем.
Существование корней зависит от знака дискриминанта D.
- D = B 2 − 4AC
- Если D > 0, то имеются две точки пересечения х
- Если D = 0, график только касается ось х и, следовательно, только одна точка пересечения с осью х
- Если D < 0, график будет выше или ниже оси абсцисс.
x 1 = ( − B + √D)/(2A)
x 2 = ( − B − √D)/(2A)
, где D = B 2 − 4AC
Пример: нет точки пересечения x
Когда дискриминант отрицателен, график не касается x- ось.
Х-перехвата нет. Вы можете увидеть это для функции ниже:
- f(x) = x 2 + 2x + 2
- Дискриминант функции f(x) = B 2 — 4AC = — 4
- x-пересечение: нет
Пример: одна точка пересечения по оси x
Если дискриминант равен нулю, график будет касаться оси x в одной точке, поэтому имеется только одна точка пересечения по оси x.
- График x 2 + 2x + 1
- Дискриминант = 0
- x-отрезок: ( − 1, 0)
функция имеет положительный дискриминант. График пересекает ось x в двух точках. Он имеет два x-перехвата.
- График −x2+27x−23
- Дискриминант = 25/4( > 0)
- x-отрезки: (0.5, 0) и (3, 0)
Ширина графика
Ширина графика является сравнительным признаком. Между любыми двумя квадратичными графами тот, у которого A больше, будет уже.
Член x 2 растет быстрее, чем все остальные члены вместе взятые.
Коэффициент А оказывает мультипликативное влияние на рост x 2 . Его влияние зависит от |A| (величина А). Таким образом, функция с наибольшим значением |A| растет (или падает для A < 0 ) быстрее всего. Его график самый узкий.
Пример
Например, если у нас есть следующие две функции:
- f(x) = 2x 2 + 1 |A| = 2
- g(x) = − 5x 2 + 1 |A| = 5
Как |-5| > |2|, g(x) имеет более узкий график.
Пример
Приведенные ниже графики соответствуют следующим функциям: x2+1
|А| является наибольшим для функции g(x). Поэтому его график самый узкий и растет быстрее всего. Значение |А| для f(x) и h(x) одинаковы. Графики обеих функций имеют одинаковую ширину.
График квадратичной функции в стандартной форме
Используя вышеприведенные признаки, мы можем быстро построить график квадратичной функции. Мы будем использовать следующие шаги:
- Определить, направлен ли график вверх или вниз
- Найти его вершину
- Вычислить точки пересечения x и y
- Наконец, используя ось симметрии, найти несколько зеркально отраженных точек и построить график .
Давайте посмотрим на пример.
Пример
График функции f(x) = x 2 − 3x + 2
Коэффициенты функции f(x): A = 1, B = -3, C = 2
Вверх/вниз
Поскольку коэффициент A > 0, мы имеем восходящий график.
Вершина
Найдем вершину по формуле: 2 − 3(1,5) + 2
= 4,25 − 4,5 = − 0,25
Координаты вершины (1,5, -0,25)
y-пересечение
Координаты отрезка y: (0, C) = (0, 2)
отрезка x
Найдем координаты отрезка x. Сначала мы должны вычислить дискриминант:
D = B 2 − 4AC
D = ( − 3) 2 − 4(1)(2) = 9 − 8 = 1
Поскольку дискриминант D > 0 , есть два x-перехвата (корня). Используя следующую формулу для корней квадратичной функции, мы вычисляем точки пересечения по оси x.
x1=2(1)3+1x2=2(1)3−1
x 1 = (3 + 1)/2x 2 = (3 − 1)/2
x 1 = 4/2 = 2x 2 = 2/2 = 1
2 x
-перехваты: ( 2, 0 ) и ( 1, 0 ).Использование симметрии
Мы вычисляем еще несколько точек, чтобы сделать наш график точным. Мы используем те, которые находятся на равном горизонтальном расстоянии от оси, чтобы уменьшить наше усилие вдвое.
| x | y = f(x) |
|---|---|
| -1,0 | f(-1,0) = 6,0 |
| -0.5 | f(-0.5) = 3.75 |
| 0.0 | f(0) = 2.0 |
| 0.5 | f(0.5) = 0.75 |
| 2.5 | f( 2.5) = 0.75 |
| 3.0 | f(3.0) = 2.0 |
| 3.5 | f(3.5) = 3.75 |
| 4.0 | f(4.0) = 6.0 |
We now вершина графика ( 1.5 , -0.25 ), точка пересечения по оси Y ( 0, 2 ), точка пересечения по оси X ( 1, 0 ) и ( 2 , 0 ) вместе с точками выше.
Подробнее
Нахождение корней квадратичных (уравнение с примерами, графики) ➤
Факторинг квадратичного в 4 простых шагах (+ Вопросы) ➤
Факторов Кубических полиномов (+ вопросы) ➤
. Факторические полиномы (+ вопросы) ➤
.
Идентифицирующие характеристики квадратичных функций
Подобно линейным и экспоненциальным функциям, квадратичные функции представляют собой уникальный тип функций, обладающих определенными общими качествами. Анализируя эти функции с точки зрения их характеристики позволяют узнать важную информацию.
Квадратичная функция — это функция от 2. Это означает, что наивысший показатель степени равен 2. Простейшая квадратичная функция — это y=x2, а график любой квадратичной функции — это .
Присущая форма порождает несколько общих характеристик.
Парабола открывает либо вверх , либо вниз . Это называется его направлением.
Поскольку парабола открывается либо вверх, либо вниз, всегда есть одна точка, которая является или функции. Эта точка называется .
В вершине функция меняется с , или наоборот.
Все параболы симметричны, то есть существует линия, которая делит график на два зеркальных отображения. Для квадратичных функций эта линия всегда направлена к оси y и называется осью симметрии.
Ось симметрии всегда пересекает вершину параболы и записывается как , где h может быть любым .
В зависимости от правила парабола может пересекать ось x в 0, 1 или 2 точках. Поскольку значение функции в точке всегда равно 0, эти точки называются нулями или иногда корнями.
Поскольку все графики квадратичных функций бесконечно простираются влево и вправо, каждый из них имеет точку вдоль оси Y в любом месте.
Для квадратичной функцииу=х2-4х,
создайте таблицу значений, чтобы отобразить ее. Затем определите его направление, вершину, нули и ось симметрии.Показать решение expand_more
Для начала мы воспользуемся правилом функции для создания таблицы значений. Затем, чтобы построить график функции, мы нанесем точки из таблицы. Начнем с х=0.
у=х2-4х
у=02-4(0)
у=0
Таким образом, точка (0,0) лежит на параболе. Мы можем выполнить те же вычисления для других значений x, близких к x=0.
| х | х2-4х | г. |
|---|---|---|
| -2 | (-2)2−4(-2) | 12 |
| -1 | (-1)2−4(-1) | 5 |
| 0 | 02−4(0) | 0 |
| 1 | 12−4(1) | -3 |
| 2 | 22−4(2) | -4 |
Наносим эти точки на координатную плоскость.
Мы можем начать видеть левую часть параболы. Давайте добавим в таблицу еще несколько значений x, чтобы определить более полную форму.
| х | х2-4х | г. |
|---|---|---|
| 3 | 32−4(3) | -3 |
| 4 | 42−4(4) | 0 |
| 5 | 52−4(5) | 5 |
Мы также добавим эти точки в систему координат.
Глядя на точки, мы теперь видим обе стороны параболы. Мы можем соединить точки плавной кривой.
График можно использовать для описания желаемых характеристик параболы.
ось направления симметриивершинынулей:вверх:x=2:(2,-4):(0,0) и (4,0)
На координатной плоскости изображены три квадратичные функции.
Для каждого графика сопоставьте его с соответствующими характеристиками.направление:вершина:вершина:ось симметрии:Y-пересечение:ноль:вверх,внизминимум,максимум(-2,2),(0,-6),(2,-4)x=-2,x= 2,x=0y=-6,y=-2, y=0,y=4x=0, x=4,x=-6
Показать решение expand_more
Вместо того, чтобы рассматривать каждую функцию отдельно, мы рассмотрим характеристики по отдельности и суммируем наши выводы в таблице в конце.
Во-первых, давайте рассмотрим направление . Мы видим, что А и С открываются вверх, а В открывается вниз. Направление параболы определяет, является ли вершина минимумом или максимумом.
Вершина для каждого графа находится в минимуме или максимуме функции. Для A вершина лежит в (2,-4). Точно так же вершина B лежит в точке (-2,2), а вершина C находится в точке (0,-6).
Ось симметрии — это вертикальная линия, пересекающая вершину. Следовательно, ось симметрии для графика А равна х=2, для В это х=-2, а для С это х=0.
Находятся там, где параболы пересекают ось Y. A имеет y-пересечение y=0, B имеет y=-2 и C имеет y=-6. Один из вариантов, y=4, не совпадает ни с одним графом.
Нули находятся там, где параболы пересекают ось x. Затем функция A имеет нули x=4 и x=0, которые являются двумя из нулей, указанных в подсказке. Ни функция B, ни функция C не имеют нуля при x=-6.
Подведем итог тому, что мы узнали о характеристиках трех квадратичных функций.