Геометрический способ решения уравнений и неравенств с модулем, 9-й класс
Геометрический способ решения уравнений и неравенств с модулем, 9-й класс- Ковалькова Виктория Михайловна
Разделы: Математика
Класс: 9
Цель: рассмотреть геометрическое определение модуля. Уметь применять его для решения уравнений и неравенств с модулем, развивать умение исследовать уравнения с параметрами.
Ход урока
1. Организационная часть (Цель занятия)
2. Актуализация знаний
- Алгебраическое определение модуля
|a| =
- Вычислите модули чисел:

- Решите уравнения
|x| = 4 |x| = -4 |x| = 0 - Решите неравенства
|x| > 5 |x| - Запишите к каждому чертежу соответствующее уравнение или неравенство
3. Изучение нового материала
- Найдите расстояние между двумя точками координатной прямой
А) А(-1) и В(3)
Б) Р(0,0001) и Q(132)
В) М(-2) и N(-87) - Формула расстояния между двумя точками координатной прямой
с координатами х и а:
ρ(x,a) = |x — a|
Геометрическое истолкование выражения |x-a|- это расстояние между двумя точками координатной прямой.
- Отметить на координатной прямой точки, для которых
|x| = 1 |x| ≥ 3 |x| > 2 1 < |x| < 4 |x| = 0 |x| = -1
- Каков смысл выражений?
Изобразите множества, задаваемые этими предложениями на координатной прямой.
 Иными словами переведем
аналитические модели на геометрический язык.
Иными словами переведем
аналитические модели на геометрический язык. - Решим неравенство |х-2| <3
Переведем аналитическую модель на геометрический язык: нужно найти на координатной прямой такие точки х, которые удовлетворяют условию ρ (х,2) < 3. Другими словами удалены от точки с координатой 2 на расстояние меньше 3.
Это все точки, принадлежащие интервалу (-1;5)
Ответ: (-1;5)
- Как решить уравнение?
|х-5|+|х+1|=8
Выражение |х-5| можно истолковать, как расстояние между точками с координатами х и 5.
Выражение |х+1| можно истолковать, как расстояние между точками с координатами х и -1.
Тогда уравнение означает, что нужно найти такую точку Х(х), сумма расстояний от которой до точек с координатами 5 и -1 равна 8.
Расстояние между точками с координатами 5 и -1 равно 6 < 8, следовательно, точка с координатой х находиться вне отрезка [-1;5] и таких точек две.

Ответ: х=-2, х=6
Что произойдет, если вместо 8 взять число 1, 6, 100,…? Сколько будет тогда корней уравнения?
При равенстве суммы модулей 1 – нет решений, так как 1
При равенстве суммы модулей 6 – множество решений, так как все точки отрезка [-2;6] удовлетворяют условию уравнения.
При равенстве суммы модулей 100, или любому числу больше 6, уравнение имеет два решения.
Вывод:
- Если сумма модулей больше расстояния между двумя точками, то уравнение имеет два решения.
- Если сумма модулей равна расстоянию между двумя точками, то уравнение имеет множество решений, которых принадлежат отрезку между точками.
- Если расстояние между двумя точками меньше суммы модулей, то решений нет.
4. Закрепление полученных знаний
- Решите неравенство: |х-5|
Ответ: (3;7) - Решите неравенство: |х+3| ≥ 4
Ответ: x ≤ -7, x ≥ 1 - Решите уравнение: |х-1| +|х+2|=5
Ответ: x=2, x=-3
- Изобразите на координатной плоскости решения
неравенств:
1.
 |х-1|+|х+2|=5
|х-1|+|х+2|=52. | х-1|+|х+2|<5
-
Самостоятельно исследуйте, сколько решений может иметь уравнение в зависимости от значений а:
|х+3| +|х-1|=
Ответ:
а) Если, а=4, то уравнение имеет множество решений – отрезок [-3;1] б) Если а>4, то уравнение имеет 2 корня
в) Если а
5. Домашнее задание
1. Исследовать уравнение: |х+3| -|х-1|=а
2. Решить № 13, № 16 (а,б)
6. Итог занятия:
- Геометрический смысл модуля
- Как применить геометрический смысл модуля для решения неравенств
- Как применить геометрический смысл модуля для решения уравнений
Литература
1. Мордкович А.Г. Алгебра ,9 класс, в двух частях,6 издание, Москва, Мнеиозина,2004
2. «Метод координат», учебное пособие для учащихся, ОЛ ВЗМШ, Москва ,2002
Предварительное исчисление по алгебре
— Пожалуйста, помогите, как работать с неравенством (x-1)/(x-5)
$\begingroup$
Я готовлюсь к выпускным экзаменам колледжа и не могу решить неравенство (x-1)/(x-5)<0, используя метод, которому нас научил профессор, который я должен использовать на экзамене.
Это еще одно неравенство с использованием указанного метода:
Я заметил, что неравенство, которое я разместил, имеет другой символ, чем на картинке, но первое — единственный пример такого типа, который профессор дал нам с символом меньше.
Вот как я пытался это решить:
Я ценю любую вашу помощь. Заранее спасибо.
- алгебра-предварительное исчисление
- неравенство
$\endgroup$
2
$\begingroup$
Если $\dfrac{x-1}{x-5}<0$, это означает, что $x-1$ и $x-5$ имеют противоположный знак.
Итак, $x-1<0$ и $x-5>0$
или $x-1>0$ и $x-5<0$.
Что из этого возможно?
$\endgroup$
3
$\begingroup$
Помните, что если $\frac ab < 0$, то $a$ и $b$ являются "разными знаками".
Итак, если $\frac {x-1}{x-5} < 0$, то либо
1) $x — 1 > 0$ и $x -5 < 0$
ИЛИ
2) $x -1 < 0$ и $x-5 > 0$.
В случае 1) имеем $x — 1> 0$, поэтому $x > 1$ и $x-5 < 0$, поэтому $x < 5$. Таким образом, $x$ находится между $1$ и $5$ или $1 < x < 5$
В случае 2) имеем $x-1 < 0$ и $x< 1$ и $x-5> 0$, поэтому $x > 5$. Таким образом, $x$ одновременно меньше $1$ и больше $5$. Это невозможно.
Итак, случай 1: это истинный случай и $1 < x < 5$.
…..
Альтернативно. $1 < 5$ всегда и поэтому $-5 < -1$ всегда и $x-5
Итак, когда мы знаем, что $x-1$ и $x-5$ являются «разными знаками», мы знаем, что $x-5$ должно быть отрицательным (потому что оно меньше) и $x-1$ должен быть положительным, потому что он больше.
Итак, $x -5 < 0 < x-1$
$\endgroup$
$\begingroup$
Нарисуйте линию чисел.
Частное $\frac{x-1}{x-5} <0$, когда:
(1) $x-1 <0$ И $x-5 >0$
(2) $x- 1 >0$ И $x-5<0$
Определите отрезок, где $x-1>0$ и $x-1<0$ на линии.
Определите сегмент, где $x-5>0$ и $x-5<0$ на линии.
Условие (1) выше показано в виде среднего отрезка: $x \in (1,5)$.
Условие (2) выше выполняется для сегментов (A) и (B). Однако $x$ не может одновременно находиться в отрезках (A) и (B), это невозможно.
Итак, $x \in (1,5)$ — ваш ответ.
Всегда тестируйте несколько значений для проверки.
$\endgroup$
$\begingroup$
Сначала начертите числовую прямую и поместите любые значения $x$, при которых левое точно равно правому. Это означает, что $(x-1)(x-5)=0$ и решениями этого уравнения являются $5$ и $1$.
Итак, отметьте $5$ и $1$ в числовой строке.
Обратите внимание, что ваша функция не может двигаться выше или ниже оси $x$ (изменить знак) где-либо еще, поскольку она должна пройти через ноль, и единственные места, где ваша функция равна нулю, это $5$ и $1$.
Итак, выберите любое значение в каждом сегменте, образованном числовой линией и ее пересечением (это означает, что один сегмент от отрицательной бесконечности до $1$, другой от $1$ до $5$ и последний от $5$ до бесконечности в качестве вашей функции не изменит свой знак на этих интервалах, так как в этих областях нет нулей).
Теперь выберите любое число в каждом разделе, чтобы увидеть, удовлетворяет ли ваш сегмент общему неравенству:
Для $(-\infty,1)$ выберите $-3$ и убедитесь, что это делает нашу функцию равной положительному значению, которое не что мы хотим.
Перейдите к разделу $(1,5)$ и подключите $3$. Это дает нам $-4$, что удовлетворяет нашему неравенству, что означает, что вся область находится ниже оси $x$, поэтому мы можем включить эту область.
Последний раздел равен $(5,\infty)$, и давайте подставим $7$, что дает положительное значение при подключении и не удовлетворяет общему неравенству.
Теперь обратите внимание, что значения, которые делают нашу функцию равной нулю, не должны быть включены в ответ, поскольку мы хотим, чтобы он был ниже нуля и равен нулю.
Таким образом, $(1,5)$ — это наш диапазон значений, который ему удовлетворяет.
$\endgroup$
1
Зарегистрируйтесь или войдите
Зарегистрироваться через Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Решение рациональных неравенств
Решение рациональных неравенствДополнительно
Показать рекламу
Скрыть рекламу
О рекламе
Рациональное
Рациональное выражение выглядит так:
Неравенства
Иногда нам нужно решать рациональные неравенства, подобные этим:
Символ | Слова | Пример |
|---|---|---|
| | | |
> | больше | (х+1)/(3−х) > 2 |
< | меньше | х/(х+7) < −3 |
≥ | больше или равно | (x−1)/(5−x) ≥ 0 |
≤ | меньше или равно | (3−2x)/(x−1) ≤ 2 |
| | | |
Решение
Решение неравенств очень похоже на решение уравнений. .. вы делаете почти то же самое.
.. вы делаете почти то же самое.
| Когда мы решим неравенства мы пытаемся найти интервал(ы) , такие как отмеченные «<0" или ">0″ |
Вот шаги:
- найти «достопримечательности»:
- точки «=0» (корни) и
- «вертикальные асимптоты» (где функция не определена)
- между «достопримечательностями», функция либо больше нуля (>0) или меньше нуля (<0)
- затем выберите тестовое значение, чтобы узнать, какое оно (>0 или <0)
Вот пример:
Пример:
3x−10 x−4 > 2Сначала , упростим!
Но нельзя умножать на (x−4)
Поскольку «x−4» может быть как положительным, так и отрицательным.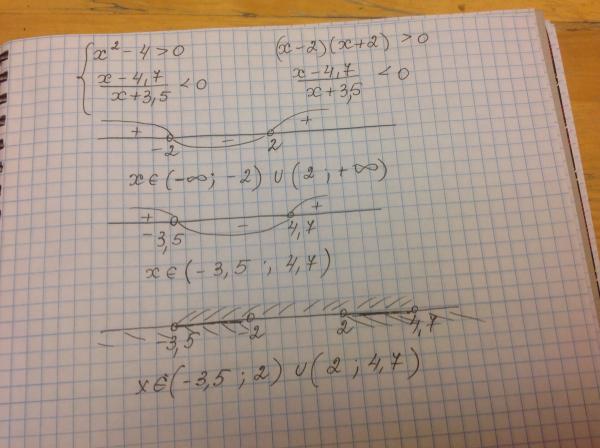


 Иными словами переведем
аналитические модели на геометрический язык.
Иными словами переведем
аналитические модели на геометрический язык.
 |х-1|+|х+2|=5
|х-1|+|х+2|=5