8.2.5. Разложение квадратного трехчлена на линейные множители.
Главная » 8 класс. Алгебра. » 8.2.5. Разложение квадратного трехчлена на линейные множители
Квадратный трехчлен ax2+bx+c можно разложить на линейные множители по формуле:
ax2+bx+c=a (x-x1)(x-x2), где x1, x2 — корни квадратного уравнения ax2+bx+c=0.
Разложить квадратный трехчлен на линейные множители:
Пример 1). 2x2-7x-15.
Решение. Найдем корни квадратного уравнения: 2x2-7x-15=0.
a=2; b=-7; c=-15. Это общий случай для полного квадратного уравнения. Находим дискриминант D.
D=b2-4ac=(-7)2-4∙2∙(-15)=49+120=169=132>0; 2 действительных корня.
Применим формулу: ax2+bx+c=a (x-x1)(x-x2).
2x2-7x-15=2 (х+1,5)(х-5)=(2х+3)(х-5). Мы представили данный трехчлен 2x2-7x-15 в виде произведения двучленов 2х+3 и х-5.
Ответ: 2x2-7x-15=(2х+3)(х-5).
Пример 2). 3x2+2x-8.
Решение. Найдем корни квадратного уравнения:
3x2+2x-8=0.
a=3; b=2; c=-8. Это частный случай для полного квадратного уравнения с четным вторым коэффициентом (b=2). Находим дискриминант D1.
Применим формулу: ax2+bx+c=a (x-x1)(x-x2).
Мы представили трехчлен 3x2+2x-8 в виде произведения двучленов х+2 и 3х-4.
Ответ: 3x2+2x-8=(х+2)(3х-4).
Пример 3). 5x2-3x-2.
Решение. Найдем корни квадратного уравнения:
5x2-3x-2=0.
a=5; b=-3; c=-2. Это частный случай для полного квадратного уравнения с выполненным условием: a+b+c=0 (5-3-2=0). В таких случаях первый корень всегда равен единице, а второй корень равен частному от деления свободного члена на первый коэффициент:
Применим формулу: ax2+bx+c=a (x-x1)(x-x2).
5x2-3x-2=5 (х-1)(х+0,4)=(х-1)(5х+2). Мы представили трехчлен 5x2-3x-2 в виде произведения двучленов х-1 и 5х+2.
Ответ: 5x2-3x-2=(х-1)(5х+2).
Пример 4). 6x2+x-5.
Решение. Найдем корни квадратного уравнения:
6x2+x-5=0.
a=6; b=1; c=-5. Это частный случай для полного квадратного уравнения с выполненным условием: a-b+c=0 (6-1-5=0). В таких случаях первый корень всегда равен минус единице, а второй корень равен минус частному от деления свободного члена на первый коэффициент:
Применим формулу: ax2+bx+c=a (x-x1)(x-x2).
Мы представили трехчлен 6x2+x-5 в виде произведения двучленов х+1 и 6х-5.
Ответ: 6x2+x-5=(х+1)(6х-5).
Пример 5). x2-13x+12.
Решение. Найдем корни приведенного квадратного уравнения:
x2-13x+12=0.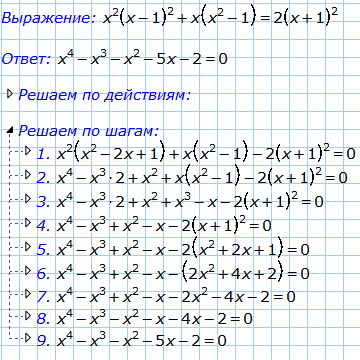
Проверим, можно ли применить теорему Виета. Для этого найдем дискриминант и убедимся, что он является полным квадратом целого числа.
a=1; b=-13; c=12. Находим дискриминант D.
D=b2-4ac=132-4∙1∙12=169-48=121=112.
Применим теорему Виета: сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, а произведение корней должно быть равно свободному члену:
x1+x2=13; x1∙x2=12. Очевидно, что x1=1; x2=12.
Применим формулу: ax2+bx+c=a (x-x1)(x-x2).
x2-13x+12=(х-1)(х-12).
Ответ: x2-13x+12=(х-1)(х-12).
Пример 6). x2-4x-6.
Решение. Найдем корни приведенного квадратного уравнения:
x2-4x-6=0.
a=1; b=-4; c=-6. Второй коэффициент — четное число. Находим дискриминант D1.
Дискриминант не является полным квадратом целого числа, поэтому, теорема Виета нам не поможет, и мы найдем корни по формулам для четного второго коэффициента:
Применим формулу: ax2+bx+c=a (x-x1)(x-x2) и запишем ответ:
Друзья, для того, чтобы разложить квадратные трехчлены на множители, мы решали каждое квадратное уравнение рациональным способом. Все эти способы мы рассмотрели ранее в теме: «Решение полных квадратных уравнений».
Алгебра 8 Мордкович (упр. 34.1
Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2021). § 34. Комбинаторные и вероятностные задачи к главе 4. ОТВЕТЫ на упражнения 34.1 — 34.7. ГЛАВА 4. КВАДРАТНЫЕ УРАВНЕНИЯ. Нажмите на спойлер, чтобы посмотреть ответ на задание.
которые имеют хотя бы один корень?
Смотреть ответы на № 34.1
Задание № 34.2. Для составления квадратного уравнения с заранее заданными корнями х1 и х2 поступают так. Сначала составляют произведение (х – х1)(х – х2). Затем раскрывают скобки и приводят подобные члены. Полученный квадратный трёхчлен приравнивают нулю. Сколько различных квадратных уравнений можно составить таким образом, выбирая:
а) корень х1 из чисел 1, 2, а корень х2 из чисел 5, 6;
б) корень х1 из чисел 1, 2, 3, а корень х2 из чисел 4, 5, 6;
г) оба корня из чисел 2, 3, 4, если корни должны быть различными?
Смотреть ответы на № 34.2
Задание № 34.3. Заполните таблицу значений дискриминанта для уравнений вида ах2 + bх + с = 0:
Какова процентная частота уравнений:
а) не имеющих корней;
б) имеющих единственный корень;
в) имеющих хотя бы один корень?
Смотреть ответы на № 34.
3
Задание № 34.4. a) Откройте задачник на с. 161. В каждом из заданий 28.6–28.10 определите количество корней квадратного уравнения. Результаты поочерёдно внесите во вторую строку таблицы и подведите в ней же числовой итог.
| Кол-во уравнений, имеющих 2 корня | Кол-во уравнений, имеющих 1 корень | Кол-во уравнений, не имеющих корней |
б) Каков объём проведённого измерения?
в) Какова процентная частота уравнений, не имеющих корней?
Смотреть ответы на № 34.4
Задание № 34.5. Уравнение относительно переменной х имеет вид ах + b/x + с = 0, где коэффициенты а, b – натуральные числа от 1 до 5 (совпадения допустимы), а коэффициент с равен 6 или 7.
а) Изобразите схематично дерево вариантов составления уравнений такого вида.
б) Сколько различных уравнений такого вида можно составить?
в) Сколько среди них уравнений, у которых а = b?
г) Сколько среди них уравнений, у которых с = 2а?
Смотреть ответы на № 34.
5
Задание № 34.6. Вот что прочёл богатырь на камне у распутья: «Налево, прямо или направо пойдёшь – к таким же распутьям придёшь, а от каждого из них опять к таким же распутьям придёшь, но потом всё равно в тридевятое царство попадёшь».
б) Сколько имеется путей, по которым придётся один раз поворачивать влево и два раза – вправо?
в) Сколько имеется путей, по которым придётся один раз поворачивать вправо и два раза – влево?
г) Сколько имеется путей, по которым придётся поворачивать ровно два раза?
Смотреть ответы на № 34.6
Задание № 34.7. Х–файл расположен в директории «Мои документы», где–то в папках А, В, С или D первого уровня. Папка А содержит «подпапки» АА, АВ, АС второго уровня. Папки В и D также содержат по три «подпапки»: BA, ВВ, ВС и DA, DB, DC соответственно, а в папке С содержатся «подпапки» СА, СВ, СС, CD, СЕ второго уровня. Каждая из папок второго уровня содержит по 7 папок третьего уровня, кроме папки ВС, в которой 8 папок третьего уровня.
а) Изобразите схематично соответствующее дерево вариантов прохождения путей до файла,
б) Сколькими путями можно из папки А дойти до файла?
в) Сколькими путями можно из папки «Мои документы» дойти до файла?
г) Какова вероятность того., что нужный файл окажется в папке С?
Смотреть ответы на № 34.7
Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2021). ГЛАВА 4. КВАДРАТНЫЕ УРАВНЕНИЯ. § 34. Комбинаторные и вероятностные задачи к главе 4. ОТВЕТЫ на упражнения 34.1 — 34.7. Вернуться в ОГЛАВЛЕНИЕ.
Просмотров: 8 449
Пусть f(x)=|x-x1|+ |x-x2| где x1 » и » x2 — несовпадающие действительные числа точек, в которых f(x) минимальна, равна
Вопрос
Обновлено: 02.12.2020
ЦЕЛЬ RD SHARMA-MAXIMA AND MINIMA -Chapter Test
21 видеоРЕКЛАМА
Текст Решение
A
Более 3
Ответ
Правильный ответ A
Решение
График f(x) показан на рис.
1. Это видно из графика f( x), что она достигает минимальных значений в каждой точке [x1,x2]
Ответить
Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Похожие видео
Многочлен степени 2, который принимает значения y_0,y_1,y_2 в точках x_0,x_1,x_2 соответственно, задается как p(x) = ((x-x_1)(x-x_2))/ ((x_0-x_1)(x_0-x_2)) y_0 + ((x-x_0)(x-x_2))/((x_1-x_0)(x_1-x_2)) y_1 + ((x-x_0)(x- x_1))/((x_2-x_0)(x_2-x_1)) y_2 Многочлен степени 2, принимающий значения y_0, y_0, y_1 в точках x_0, x_(0+t), x_1 t!=0, равен
Если f — функция с действительным знаком, не тождественно равная нулю и удовлетворяющая f(x_1 + x_2)) + f(x_1 — x_2) = 2 f(x_1)f(x_2)для всех x_1,x_2 , тогда f(x) есть ( 1) Нечетная функция(2) Четная функция (3) Ни четная, ни нечетная(4) f(0) = 1/2
12371724
Если |f(x1)−f(x2)|≤(x1− x2)2,∀x1,x2∈R.
Найдите уравнение касательной к кривой y=f(x) в точке (1,2).
46805727
Найдите область определения f(x)=loge.1−x1+x. Далее покажите, что
f(x1)+f(x2)=f(x1+x21+x1x2),x1,x2∈(−1,1)
234800274
I : Если f(x) = ch x + sh x, то f(x1+x2+…+xa)=f(x1)⋅f(x2)⋆f(xn)
II : Если f (x) = ch x + sh x, тогда f(x1)+f(x2)+…+f(xn)=f(x1)⋅f(x2)⋆f(xn)
308712299
f( x)=loge(1−x1+x) দেখাও যে , f(x1)+f(x2)=f(x1+x21+x1x2),x1,x2∈(−1,1)
470820277
, если |f(x1)−f(x2)|≤ (x1−x2)2Найти уравнение касательной к кривой y=f(x) в точке (1,2).
642533754
Пусть x1,x2,x3 — точки, в которых f(x)=|1−|x−4∣∣,x∈R не дифференцируема, тогда f(x1)+f(x2)+f(x3 ) =
642697049
Текст Решение
Если f(x)>0″ तथा «f(x)>0,AA x in R Если любые два действительных числа x_1» तथा «x_2(x_1 ne x_2) for
3 90951 0 642
Найдите область определения f(x)=loge(1−x1+x). Далее покажем, что f(x1)+f(x2)=f(x1+x21+x1x2),x1,x2∈(−1,1 )
643969456
Количество таких линий на кривой y=sinx равно 9.0003644011782
Если |f(x2)−f(x1)|≤(x2−x1)2∀x1,x2∈R, то уравнение касательной к кривой y = f(x) в точке (1 ,2) равно
644176000
. )=x1(−x) и ‘a’ — действительное число. Если x0=a, x1=f(x0),x2=f(x1),x3=f(x2) и так далее. Если x2009=1, то значение обратной величины ‘a’ равно
644220641
Text Solution
Многочлен степени 2, который принимает значения y0,y1,y2 в точках x0,x1,x2 соответственно, задается p (x)=(x−x1)(x−x2)(x0−x1)(x0−x2)y0+(x−x0)(x−x2)(x1−x0)(x1−x2)y1+(x−x0 )(x−x1)(x2−x0)(x2−x1)y2 Многочлен степени 2, принимающий значения y0,y0,y1 в точках x0,x0+t,x1 t≠0, определяется как
645252241
Формула раздела – Внутреннее и внешнее разделение | Координатная геометрия
Предположим, что точка делит отрезок на две части, которые могут быть равными или нет, с помощью формулы сечения мы можем найти эту точку, если заданы координаты отрезка, а также мы можем найти отношение, в котором точка делит данный отрезок, если заданы координаты этой точки.
Когда точка C делит отрезок AB в отношении m:n, мы используем формулу сечения, чтобы найти координаты этой точки. Формула раздела имеет 2 вида. Эти типы зависят от точки C, которая может находиться между точками или вне сегмента прямой.
Два типа:
- Формула внутреннего сечения
- Формула внешнего сечения
Формула внутреннего сечения
координаты отрезка, то мы можем использовать эту формулу. Его также называют внутренним отделом.
Если координаты A и B равны (x1, y1) и (x2, y2) соответственно, то формула внутреннего сечения задается как:
Вывод формулыПусть A (x1, y1) и B (x2, y2) — концы данного отрезка AB, а C(x, y) — точка, которая делит AB в отношение м : н.
Тогда AC / CB = m / n
Мы хотим найти координаты (x, y) точки C. , Q и R по оси X.
Глядя на приведенную выше диаграмму,
AM = PQ = OQ – OP = (x – x1)
CN = QR = OR – OQ = (x2 – x)
CM = CQ – MQ = (y – y1)
BN = BR – NR = (y2 – y)
Как видно, ∆AMC и ∆CNB подобны, а значит, их стороны пропорциональны по правилу конгруэнтности AA.
AC / CB = AM / CN = CM / BN
Теперь подставив значения в приведенное выше соотношение
=> m / n = [x – x1 / x2 -x] = [y – y1 / y2 – y]
=> m / n = [x – x1 / x2 -x] и m / n = [y – y1 / y2 – y]
Решение 1-го условия,
=> m(x2 – x) = n(x – x1)
=> (m + n)x = (mx2 + nx1)
=> x = (mx2 + nx1) ) / (m + n)
Решение 1-го условия,
=> m(y2 – y) = n(y – y1)
=> (m + n)y = (my2 + ny1)
= > y = (my2 + ny1) / (m + n)
Следовательно, координаты C (x, y) равны
{ (m × x 2 + n × x 1 ) / (m + n ) , (m × y 2 + n × y 1 ) / (m + n ) }
Формула внешнего сечения
Когда точка, делящая отрезок, делится снаружи в отношении m : n, лежит вне отрезка, т.е. когда мы продолжаем прямую, она совпадает с точка, то мы можем использовать эту формулу. Его также называют внешним отделом.
Если координаты A и B равны (x1,y1) и (x2,y2) соответственно, то формула внешнего сечения задается как
Вывод формулы
Для получения внутреннего сечения мы взяли отрезок и точку C(x, y) внутри линии, но в случае формулы внешнего сечения мы должны взять эту точку C(x, y) вне линии сегмент.
Пусть A(x1, y1) и B(x2, y2) — концы данного отрезка AB, а C(x, y) — точка, которая внешне делит AB в отношении m : n.
Мы хотим найти координаты (x, y) точки C. Для этого проведем перпендикуляры точек A, B, C, параллельные координате Y, соединяющиеся в точках P, Q и R по оси X.
По приведенной выше диаграмме
AM = PR = OR – OP = (x – x1)
BN = QR = OR – OQ = (x – x2)
аналогично,
CM = RC – MR = (y – y1)
CN = CR – NR = (y – y2)
Как видно, треугольник AMC и треугольник BNC подобны, а значит, их стороны пропорциональны по правилу конгруэнтности AA
AC / BC = AM / BN = CM / CN
Теперь подставив значения в приведенное выше соотношение
=> m / n = [x – x1 / x – x2] = [y – y1 / y – y2]
=> m / n = [x – x1 / x – x2] и m / n = [y – y1 / y – y2]
Решение 1-го условия,
=> m(x – x2) = n (x – x1)
=> (m – n)x = (mx2 – nx1)
=> x = (mx2 – nx1) / (m – n)
Решение 2-го условия,
=> m (y – y2) = n(y – y1)
=> (m – n)y = (my2 – ny1)
=> y = (my2 – ny1) / (m – n)
Следовательно, координаты C (x, y) равны
{ (m × x 2 – n × x 1 ) / (m – n) , (m × y 2 – n × y 1 ) / (m – n ) }
Задачи по формуле сечения
Задача 1: Найдите координаты точки C (x, y), где она делит отрезок, соединяющий (4, – 1) и (4, 3) в соотношении 3 : 1 внутри ?Решение:
Даны координаты A (4, -3) и B (8, 5)
Пусть C (x, y) — точка, которая делит отрезок в отношении 3 : 1 т.
е. m : n = 3 : 1
Теперь, используя формулу C(x, y) = {(m × x2 + n × x1) / (m + n), (m × y2 + n × y1) / (m + n)} как C делится внутри.
=> C(x, y) = {(3*4 + 1*4 ) / (3+1), (3 * 3 + 1 *(-1)) / (3+1)}
= > C(x, y) = {16/4, 8/4}
=> C(x, y) = {4, 2}
Следовательно, координаты равны (4, 2).
е. m : n = 3 : 1 Задача 2: Если точка P(k, 7) делит отрезок, соединяющий A(8, 9) и B(1, 2), в отношении m : n, то найти значения m и n.
Решение:
Не упоминается, что точка делит отрезок внутри или снаружи. Итак, в то время мы будем рассматривать внутренний раздел по умолчанию.
Даны координаты A (8, 9) и B (1, 2)
Пусть заданная точка P (k, 7) делит отрезок в отношении m : 1
Теперь используем сечение формула, находящая только координату x,
=> k = (m × x2 + n × x1) / (m + n )
=> k = (m × 1 + 1 × 8) / (m +1)
=> k = (m + 8) / (m + 1)
=> km + k = m + 8 … ….
Снова используем формулу сечения для координаты y.
=> 7 = (m × y2 + n × y1) / (m + n)
=> 7 = (m × 2 + 1 × 9) / (m + 1)
=> 7 = (2m + 9) / (m +1)
=> 7m + 7 = 2m +9
=> 5m = 2
=> m = 5 / 2
Таким образом, искомое соотношение равно 5 : 2
Следовательно, значение m равно 5, а значение n равно 2
(1)Задача 3: A (4, 5) и B (7, -1) — две заданные точки, причем точка C делит отрезок AB внешним образом в отношении 4 : 3. Найдите координаты точки C
Решение:
= (my2 – ny1) / (m – n )Даны координаты A (4, 5) и B (7, -1)
Пусть C (x, y) — точка, которая делит отрезок снаружи в отношении 4 : 3 т.е. m : n = 4 : 3
Теперь, используя формулу C(x, y) = { (m × x2 – n × x1) / (m – n) , (m × y2 – n × у1) / (м – п ) } , так как C делится внутри.
значение x = (mx2 – nx1) / (m – n)
=> (4 * 7 – 3 * 4) / (4 – 3)
значение г
=> (4 * (-1) – 3 * 5) / (4 – 3)
=> -19
Следовательно, координаты (16, -19).
Задача 4: Прямая 2x+y−4=0 делит отрезок, соединяющий точки A(2,−2) и B(3,7). Найдите отношение отрезка, на который делится прямая?
Решение:
Даны координаты A (2, -2) и B (3, 7).
Прямая с уравнением 2x + y – 4 = 0 делит отрезок в точке C (x, y)
Предположим, что данная прямая пересекает отрезок в отношении 1 : n.
По формуле сечения,
=> x = (m * x2 + n * x1) / (m + n)=> x = (3 + 2n) / (1 + n) ………..1
Аналогично,
=> y = (m * y2 + n * y1) / (m + n)
=> y = (7 – 2n) / (1 + n) ……….2
Теперь подставим уравнения 1 и 2 в данное уравнение прямой.
=> 2x + y – 4 = 0 > 6 + 4n + 7 — 2n — 4(1 + n) = 0
=> 13 + 2n — 4 — 4n = 0
=>9 — 2n = 0
0 2 0 9 0 / 2 => 9 n => 9 n => 9 Следовательно, отношение, в котором прямая делится, равно 9.
