Калькулятор распределения хи-квадрат — MathCracker.com
Решатели Статистика
Инструкции: Используйте этот калькулятор для вычисления вероятностей распределения хи-квадрат. Введите количество степеней свободы \(df\) и укажите событие, вероятность которого вы хотите вычислить, в форме ниже:
Числитель Степени свободы \((df)\) =
Two-Tailed:
Left-Tailed:
\( \chi^2 \le\)
Right-Tailed:
\( \chi^2 \ge \)
Подробнее о распределении хи-квадрат
Распределение хи-квадрат — одно из самых фундаментальных распределений в статистике, наряду с нормальным распределением и распределением F.
Технически распределение хи-квадрат получается путем суммирования квадрата переменных, которые являются независимыми и нормально распределенными.
Распределение хи-квадрат — одно из важнейших непрерывных распределений в статистике. Вы можете использовать другие калькуляторы вероятностей для непрерывных распределений, такие как наш
калькулятор нормальной вероятности
,
Калькулятор F-распределения
или наш
калькулятор равномерной вероятности
, среди многих других.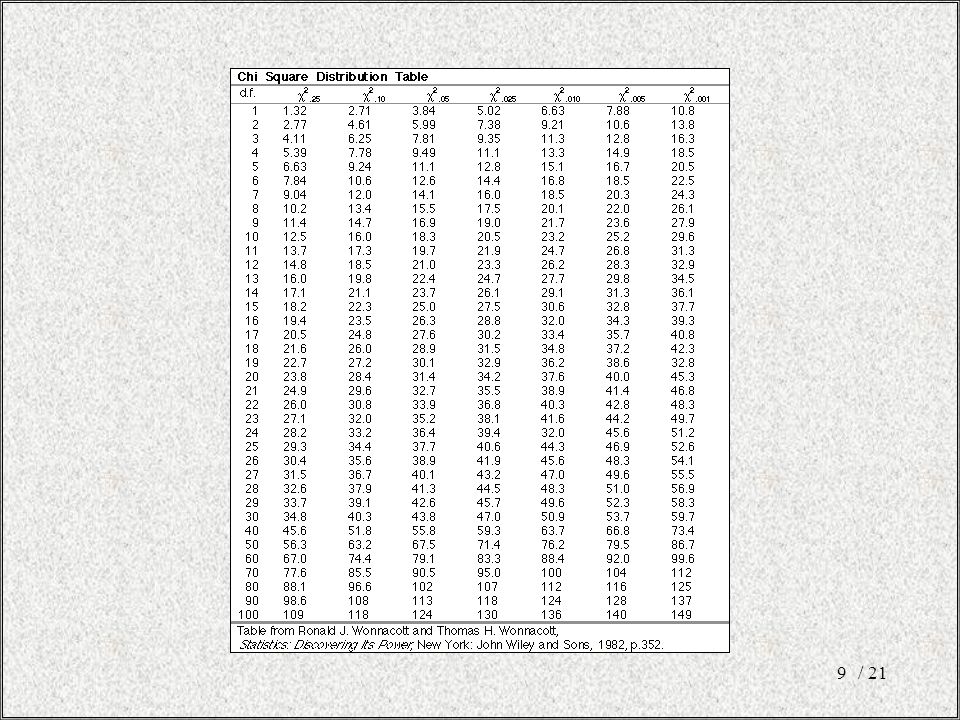
Базовый пакет статистики Распределение хи-квадрат Калькулятор вероятностей Распределение вероятностей Калькулятор статистики Статистический решатель
Когда использовать критерий хи-квадрат (с примерами)
В статистике есть два разных типа тестов хи-квадрат:
1.
Хи-квадрат критерия согласия — используется для определения того, следует ли категориальная переменная гипотетическому распределению.
2.Критерий независимости хи-квадрат — используется для определения наличия значимой связи между двумя категориальными переменными.
Обратите внимание, что оба эти теста подходят для использования только при работе с категориальными переменными.Это переменные, которые принимают имена или метки и могут вписываться в категории. Примеры включают:
- Цвет глаз (например, «голубой», «зеленый», «карий»)
- Пол (например, «мужской», «женский»)
- Семейное положение (например, «замужем», «холост», «разведен»)
В этом руководстве объясняется, когда использовать каждый тест, а также несколько примеров каждого из них.
Хи-квадратный тест на соответствиеВы должны использовать критерий согласия хи-квадрат всякий раз, когда хотите знать, следует ли какая-либо категориальная переменная некоторому гипотетическому распределению.
Вот несколько примеров, когда вы можете использовать этот тест:
Пример 1: подсчет клиентов
Владелец магазина хочет знать, одинаковое ли количество людей заходит в магазин каждый день недели, поэтому он подсчитывает количество людей, которые заходят каждый день в течение случайной недели.
Он может использовать критерий согласия Хи-квадрат соответствия, чтобы определить, соответствует ли распределение покупателей теоретическому распределению, согласно которому равное количество покупателей заходит в магазин каждый будний день.
Пример 2. Проверка правильности выпавшего кубика
Предположим, исследователь хотел бы знать, является ли игральная кость справедливой. Она решает бросить его 50 раз и записать, сколько раз он выпадет на каждое число.
Она может использовать критерий согласия Хи-квадрат соответствия, чтобы определить, соответствует ли распределение значений теоретическому распределению, согласно которому каждое значение встречается одинаковое количество раз.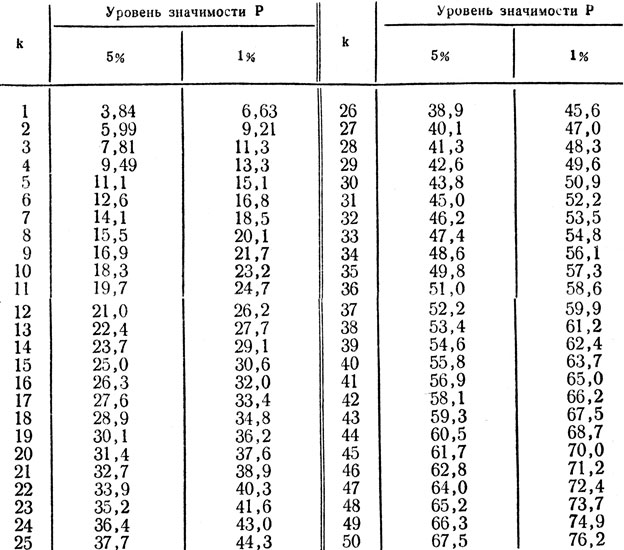
Пример 3: подсчет M&M’s
Предположим, мы хотим узнать, является ли процент M&M’s, который находится в упаковке, следующим: 20% желтых, 30% синих, 30% красных, 20% других. Чтобы проверить это, мы открываем случайный пакет M&M’s и подсчитываем, сколько выпадает каждого цвета.
Мы можем использовать критерий согласия Хи-квадрат соответствия, чтобы определить, равно ли распределение цветов заданному нами распределению.
Пошаговый пример теста на соответствие хи-квадрату см. в этом примере в Excel.
Хи-квадрат тест независимостиВы должны использовать критерий независимости хи-квадрат, когда хотите определить, существует ли значительная связь между двумя категориальными переменными.
Вот несколько примеров, когда вы можете использовать этот тест:
Пример 1: предпочтения при голосовании и пол
Исследователи хотят знать, связан ли пол с предпочтениями политических партий в определенном городе, поэтому они опрашивают 500 избирателей и записывают их пол и предпочтения политических партий.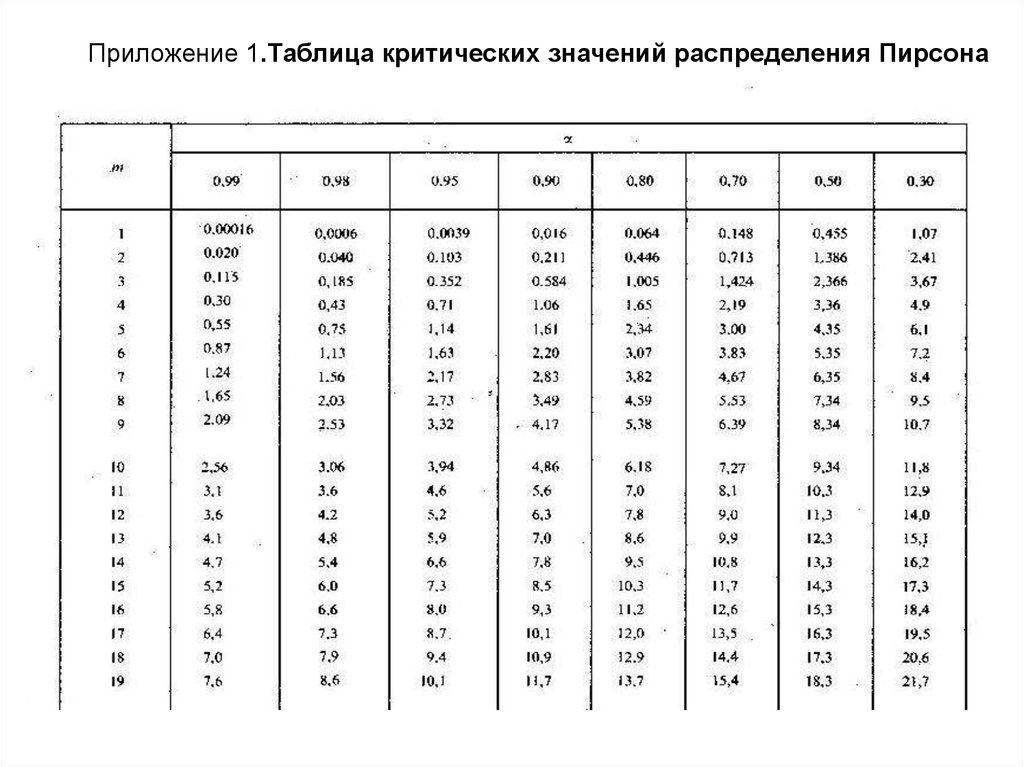
Они могут выполнить критерий независимости хи-квадрат, чтобы определить, существует ли статистически значимая связь между предпочтениями при голосовании и полом.
Пример 2: любимый цвет и любимый вид спорта
Исследователи хотят знать, связан ли любимый цвет человека с его любимым видом спорта, поэтому они опрашивают 100 человек и спрашивают их об их предпочтениях в отношении обоих видов спорта.
Они могут выполнить тест независимости хи-квадрат, чтобы определить, существует ли статистически значимая связь между любимым цветом и любимым видом спорта.
Пример 3: Уровень образования и семейное положение
Исследователи хотят знать, связаны ли уровень образования и семейное положение, поэтому они собирают данные об этих двух переменных на простой случайной выборке из 2000 человек.
Они могут выполнить критерий независимости Хи-квадрат, чтобы определить, существует ли статистически значимая связь между уровнем образования и семейным положением.
Пошаговый пример теста независимости хи-квадрат см. в этом примере в Excel.
Дополнительные ресурсыСледующие калькуляторы позволяют выполнять оба типа тестов хи-квадрат бесплатно онлайн:
Хи-квадрат Калькулятор критерия согласия
Калькулятор критерия хи-квадрат независимости
Интерактивные тесты хи-квадрат
Интерактивный инструмент для расчета критерия хи-квадрат согласия и независимости
Расчет теста хи-квадрат: интерактивный инструмент расчета критерия хи-квадрат согласия и независимости
Кристофер J. Preacher ( Университет Вандербильта )
Как цитировать эту страницу
Эту веб-утилиту можно цитировать в стиле APA следующим образом:
Preacher, K. J. (2001, апрель). Расчет теста хи-квадрат: интерактивный инструмент для расчета теста хи-квадрат на соответствие и независимость [Компьютерное программное обеспечение]. Доступно на http://quantpsy.org.
Назначение этой страницы
Эта веб-страница предназначена для предоставления краткого введения в тесты хи-квадрат независимости и согласия.
Эти тесты используются для обнаружения групповых различий с использованием данных о частоте (количестве). Эта страница также предоставляет интерактивный инструмент, позволяющий исследователям проводить тесты хи-квадрат для своих собственных исследований. В любом вводном тексте по прикладной статистике должно быть хорошее описание этих тестов хи-квадрат, но ниже следует краткое введение.
О тесте независимости хи-квадрат
Часто исследователь хочет увидеть, варьируется ли частота случаев, обладающих некоторым качеством, между уровнями данного фактора или между комбинациями уровней двух или более факторов. В таких ситуациях подходящим тестом является критерий согласия хи-квадрат или критерий независимости хи-квадрат для k групп .
Как это делается
Для проведения теста хи-квадрат исследователь вводит наблюдаемые частоты, соответствующие комбинациям уровней релевантных факторов (здесь они называются «состояние» и «группа», но это обозначения для удобства).
Затем вычисляются суммы элементов в строках и столбцах (назовем эти маргинальный номер ). Критерий независимости хи-квадрат используется для проверки нулевой гипотезы о том, что частота внутри ячеек соответствует ожидаемой, учитывая эти предельные значения N. Критерий согласия хи-квадрат используется для проверки гипотезы о том, что общая выборка N равномерно распределена между всеми уровнями соответствующего фактора.
Ожидаемое значение в каждой ячейке, если нулевое условие истинно (т. е. если факторы не оказывают существенного влияния на наблюдаемые частоты в генеральной совокупности), является просто произведением суммы строки и суммы столбца, деленной на общую выборку N для проверки независимости и N, деленное на количество уровней одного фактора для проверки согласия. Если O ij — наблюдаемая частота, а E ij — ожидаемая частота для ячейки, соответствующей условию i th и группе j th 6 0:0:0047
Если имеется только один интересующий фактор с уровнями ( k > 1), будет работать та же формула с i или j , установленной на 1.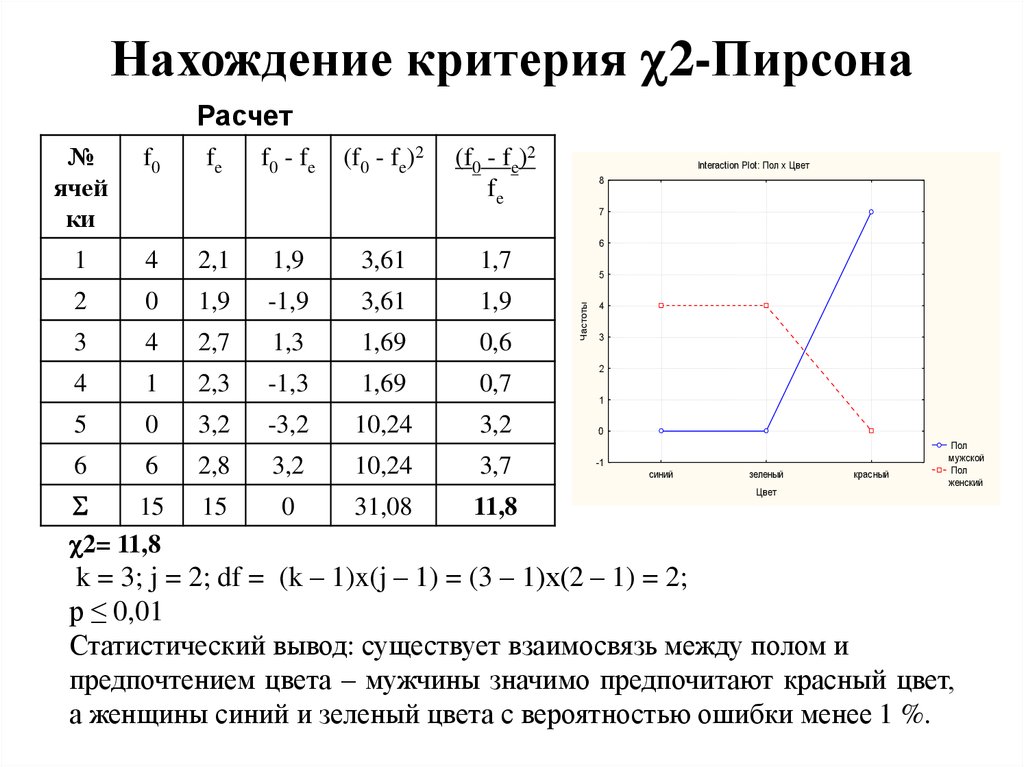
Представленный здесь тест можно использовать только для проверки 1- или 2-мерные массивы. Возможны массивы более высокой размерности, они основаны на том же принципе и даже используют ту же формулу, хотя они включают множественные вложенные суммирования.
Как пользоваться этой страницей
Введите наблюдаемые частоты в белые ячейки. Я понимаю, что не так уж много дизайнов включают ровно 10 условий и 10 групп — если ваш дизайн меньше, то выберите некоторое подмножество строк и столбцов, в которое нужно ввести ваши данные. Например, если ваш дизайн (2 x 3), вы можете ввести свои данные в 6 ячеек в верхней левой части таблицы данных, определенных первыми двумя условиями и первыми тремя группами. Вы можете выбрать любое подмножество строк и столбцов для своих данных. Вы также можете оставить ячейки, соответствующие наблюдаемым частотам, нулевыми. Допускаются нецелочисленные наблюдаемые частоты, хотя трудно представить, как их можно получить в реальных исследованиях.
Если вы выполняете тест на соответствие, вы можете ввести свои данные в любой отдельный столбец или строку.
Однако наблюдаемые нулевые частоты должны быть явно включены (т. е. вам нужно фактически ввести «0» в эти ячейки, в противном случае предполагается, что эти ячейки не являются частью вашего проекта). После того, как вы ввели свои данные, нажмите кнопку Calculate и ожидайте увидеть результат в бежевых ячейках (они должны быть белыми, если вы используете старые версии Netscape). Не паникуйте, если вы видите научное обозначение для вашего p -значение — это просто означает, что p действительно мало.
Этот инструмент также дает хи-квадрат, включающий поправку Йейтса на непрерывность . Эта коррекция часто используется для повышения точности выборочного распределения хи-квадрат при нулевых условиях. Вероятно, его следует использовать только для тестов 1-df (т. е. тестов на соответствие или тестов независимости с таблицами непредвиденных обстоятельств 2×2), поэтому используйте его на свой страх и риск для тестов с df>1.
Предупреждения
Использование тестов хи-квадрат неуместно , если какая-либо ожидаемая частота ниже 1 или если ожидаемая частота меньше 5 более чем в 20% ваших клеток.
Ячейка состояния в нижней части таблицы сообщит вам, есть ли проблема. В случае 2 x 2 критерия независимости хи-квадрат ожидаемые частоты менее 5 обычно считаются приемлемыми, если используется поправка Йейтса.
«Пользовательские» ожидаемые частоты
При использовании критерия согласия хи-квадрат иногда бывает полезно указать свои собственные ожидаемые частоты. Если для этого есть теоретическая причина, следующая таблица позволит вам ввести свои собственные E ij . Допускаются нецелые ожидаемые частоты. Используйте столько ячеек в этой таблице, сколько необходимо, убедившись, что (1) предельная сумма одинакова как для наблюдаемых, так и для ожидаемых частот, (2) нет ожидаемых частот меньше 1 и (3) не более 20% ожидаемых частот меньше 5. Если частота введена в ячейку Наблюдаемая, то частота также должна быть введена в соответствующую ячейку Ожидаемая (и наоборот).
Благодарности
Исходная версия опубликована в апреле 2001 г. Я благодарю Нэнси Бриггс и Ребекку Уайт за помощь в написании сценариев, а также Дерека Рукера, Джеффри Леонарделли и Тома Найгрена за тестирование ранних версий этой страницы.
Бесплатные сценарии JavaScript, предоставленные The JavaScript Source и John C. Pezzullo.
Калькулятор хи-квадрата — критерий хи-квадрата независимости, однородности или согласия
Используйте этот калькулятор хи-квадрата, чтобы легко проверить таблицы непредвиденных обстоятельств категориальных переменных на независимость или для теста согласия. Можно использовать как Калькулятор критерия согласия хи-квадрат , как Калькулятор критерия независимости хи-квадрат или как критерий однородности. Поддерживает неограниченное количество строк и столбцов (групп и категорий): 2×2, 3×3, 4×4, 5×5, 2×3, 2×4 и произвольные таблицы непредвиденных обстоятельств N x M. Выходы Χ 2 и p-значение.
Быстрая навигация:
- Использование калькулятора хи-квадрат
- В качестве критерия хи-квадрат независимости или однородности
- В качестве критерия согласия хи-квадрат
- Критерий независимости хи-квадрат
- Критерий однородности хи-квадрат
- Критерий согласия хи-квадрат Сравнение трех типов хи-квадрата -Тесты квадрата
- Другие тесты
Вышеупомянутый простой в использовании инструмент может работать в двух основных режимах: как тест на согласие и как тест на независимость/однородность.
Эти режимы применяются к различным ситуациям, подробно описанным ниже. Режим работы можно выбрать с помощью переключателя под полем ввода данных в интерфейсе калькулятора хи-квадрат.
Как критерий независимости или однородности хи-квадрат
Скопируйте/вставьте данные из файла электронной таблицы в поле ввода данных калькулятора или введите их вручную, используя пробел ( ) в качестве разделителя столбцов и новую строку в качестве строки разделитель. Данные во всех ячейках следует вводить в виде счетчиков (целые числа, целые числа). Например, если у вас есть эти данные в Excel:
, просто скопируйте и вставьте числовые ячейки в поле ввода калькулятора выше. Щелкните здесь, чтобы увидеть, как работает этот пример. Если известно, что данные выборки независимы, результат можно рассматривать как тест на однородность. Если данные основаны на двух категориальных переменных, измеренных в одной и той же совокупности, результат можно интерпретировать как тест на независимость между переменными.
В качестве критерия согласия хи-квадрат
Калькулятор критерия хи-квадрат можно использовать в качестве калькулятора согласия, введя наблюдаемые значения (числа) в первый столбец и ожидаемые частоты для каждый результат во втором столбце. Ожидаемые частоты должны суммироваться до ~1. Например, если мы проверяем, является ли игральная кость честной, у нас будет ожидаемая частота 0,1666 (6) для каждого числа. Примерный набор данных может выглядеть так:
| Номер | Количество показов | Ожидаемая частота |
|---|---|---|
| 1 | 168 | 0,1666 |
| 2 | 170 | 0,1666 |
| 3 | 160 | 0,1666 |
| 4 | 163 | 0,1666 |
| 5 | 173 | 0,1666 |
| 6 | 166 | 0,1666 |
| Итого | 1000 | 1 |
Щелкните здесь, чтобы загрузить примеры данных в калькулятор и выполнить тест на соответствие.
Убедитесь, что выбран соответствующий тип теста «Хи-квадрат критерия согласия».
Что такое «тест хи-квадрат»?Критерий хи-квадрат — это любой статистический тест, в котором выборочное распределение параметра является Χ 2 -распределенным в соответствии с нулевой гипотезой и, таким образом, относится к целому ряду различных видов тестов, основанных на этом распределении. В своей первоначальной версии он был разработан Карлом Пирсоном в 1900 году как тест на соответствие: проверка того, соответствует ли конкретный набор наблюдаемых данных частотному распределению из семейства распределений Пирсона (критерий хи-квадрат Пирсона). Пирсон в 1904 расширил свое приложение до проверки независимости между строками и столбцами таблицы непредвиденных обстоятельств категориальных переменных [1] . В дальнейшем она была расширена Р. Фишером в 1922-24 гг.
Статистическая модель , стоящая за тестами, требует, чтобы переменные были результатом простой случайной выборки и, таким образом, были независимыми и одинаково распределенными (ID) (при нулевой гипотезе).
Следовательно, тест можно использовать как тест на независимость или тест на однородность (идентичность распределений). В некоторых ограниченных ситуациях он также может функционировать как тест на разницу в дисперсиях. Это, однако, также означает, что если кто-то хочет протестировать данные, отличные от IID, следует выбрать другой тест.
Как и большинство статистических тестов, он плохо работает при очень малом размере выборки, в частности потому, что допущение Χ 2 может не соответствовать имеющимся данным. Для простой таблицы непредвиденных обстоятельств 2 на 2 требуется, чтобы каждая ячейка имела значение больше 5. Для больших таблиц не более 20% всех ячеек должны иметь значения меньше 5. Наш калькулятор хи-квадрат проверит некоторые из этих условий. и выдавать предупреждения, где это уместно.
Хи-квадрат Формула Формула одинакова независимо от того, проводите ли вы тест на соответствие, тест на независимость или на однородность .
Однако, несмотря на то, что формула всех трех тестов одинакова, все три имеют разные нулевые гипотезы и интерпретации (см. Ниже). Формула хи-квадрат выглядит просто:
, где n — количество ячеек в таблице, а O i и E i — наблюдаемые и ожидаемые значения каждой ячейки. В результате Χ 2 Кумулятивная статистическая функция распределения вычисляется из распределения хи-квадрат с (r — 1) · (c — 1) степенями свободы (r — количество строк, c — количество столбцов).
Типы тестов хи-квадратЗдесь мы рассмотрим три применения критерия хи-квадрат: как критерий независимости, как критерий однородности (идентичное распределение) и как критерий согласия.
Тест независимости хи-квадрат
Этот тест также иногда называют «тест ассоциации» , и он определяет, являются ли две категориальные переменные для одного образца независимыми или связанными друг с другом.
Например, в ходе опроса респондентов могут попросить указать уровень их образования, рост и состояние, чтобы определить, существует ли зависимость одной переменной от других. Таким образом, нулевая гипотеза H 0 будет следующей: переменные образование, рост и богатство независимы . Альтернативная гипотеза H 1 тогда: «некоторые переменные образование, рост и чистое состояние зависят друг от друга». Обратите внимание, что в случае наличия более двух переменных значение null будет отклонено, даже если некоторые переменные не зависят друг от друга: достаточно одной зависимости в таблице, чтобы потенциально сделать значение null недействительным.
При использовании калькулятора в качестве теста на независимость получение небольшого значения p следует интерпретировать как свидетельство того, что две (или более) группы не являются независимыми. Обратите внимание, что если имеется более двух переменных, вы не можете сказать, какие из них независимы, а какие нет: это могут быть все они или только некоторые из них.
Тест однородности хи-квадрат
Этот тест относится к проверке того, имеют ли две или более переменные одно и то же распределение вероятностей , и также поддерживается этим онлайн-калькулятором хи-квадрат. Тест на однородность используется для определения того, различаются ли две или более независимых выборки в своих распределениях по одной интересующей переменной: сравнение двух или более групп по категориальному результату. Например, можно сравнить образовательные уровни групп людей из разных городов страны, чтобы определить, одинаковы ли пропорции между группами или есть статистически значимая разница. Нулевая гипотеза H 0 заключается в том, что пропорции между группами одинаковы, а альтернатива H 1 заключается в том, что они различны.
Обратите внимание, что, наблюдая низкое значение p, можно только сказать, что по крайней мере одна пропорция отличается по крайней мере от одной другой пропорции, но мы не можем сказать, какая.
Необходимо использовать дополнительные процедуры, такие как Шеффе, Холм или Данн-Бонферрони, чтобы выбрать подходящее критическое значение для дальнейших тестов для выявления попарно значимых различий.
Когда это технически возможно, рандомизация часто используется для получения независимых выборок.
Критерий согласия хи-квадрат
Критерий согласия можно использовать для оценки того, насколько хорошо определенное частотное распределение соответствует ожидаемому (или известному) распределению . Нулевая гипотеза H 0 состоит в том, что данные следуют заданному распределению, в то время как альтернатива H 1 состоит в том, что они не следуют этому распределению. Отказ от нулевого значения означает, что выборка отличается от генеральной совокупности по интересующей нас переменной.
Например, если мы знаем, что игра в кости должна выдавать каждое число с частотой 1/6, то мы можем бросить кости 1000 раз, записать, сколько раз мы наблюдали данное число, а затем сравнить его с идеальным распределением костей.
чтобы убедиться, что это справедливо. Если мы получаем 168 единиц, 170 двоек, 160 троек, 163 четверки, 173 пятерки и 166 шестерок, есть ли у нас доказательства того, что кости подстроены? Загрузите пример данных в калькулятор, чтобы выполнить расчет.
Другим примером являются обследования населения, когда требуется репрезентативное обследование по определенному демографическому параметру или географическому региону. Зная возрастное распределение всего населения из недавней переписи или регистров рождений и смертей, вы можете сравнить частоты в своей выборке с частотами всего населения. При достаточно большой выборке тест будет достаточно чувствительным, чтобы выявить любое существенное несоответствие между вашей выборкой и совокупностью, которую вы пытаетесь представить.
Сравнение трех типов тестов хи-квадрат
Эта таблица дает краткий обзор различий между тремя основными вариантами использования теста Χ 2 и должна быть полезна всем, кто использует наш калькулятор X 2 для любых целей.
.
| Атрибут | Проверка независимости | Проверка однородности | Проверка качества прилегания |
|---|---|---|---|
| Тип отбора проб | Одиночный зависимый образец | 2 или более независимых образца | Образец из популяции |
| Нулевая гипотеза | Переменные независимы | Пропорции между группами одинаковы | Распределение выборки совпадает с распределением населения |
| Нуль отклонен | Сделать вывод, что пропорции разные | Сделайте вывод, что распределение выборки отличается от распределения населения |
Другие тесты
При определенных условиях тест X 2 можно использовать в качестве теста на различие дисперсий. Когда оба предельных распределения фиксированы, критерий хи-квадрат также можно использовать в качестве теста несвязанной классификации.