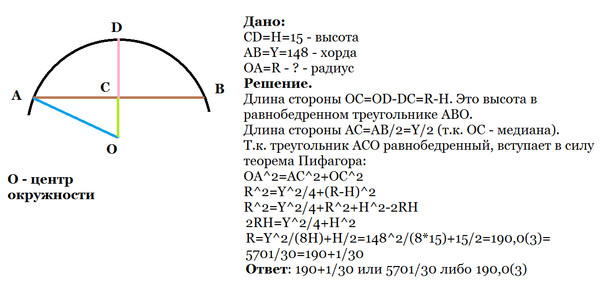
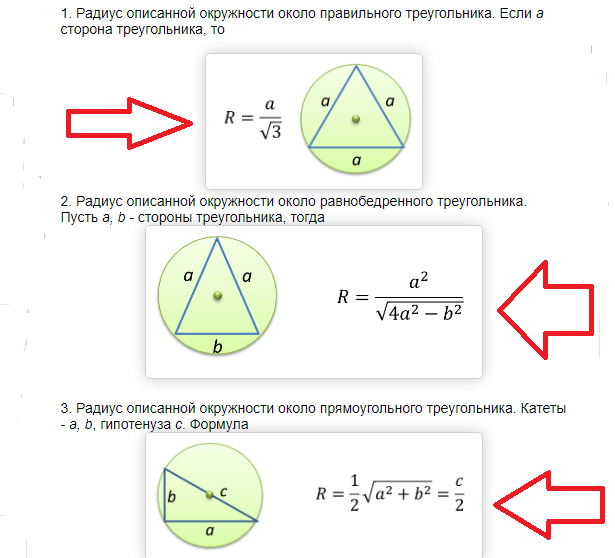
Длина хорды окружности
В элементарной геометрии хордой называют отрезок прямой линии, который соединяет две точки, лежащие на некоторой кривой (окружности, эллипсе, параболе). Хорда, которая проходит через центр окружности, называется ее диаметром.
Определение длины хорды окружности
Длина хорды окружности может быть определена по формуле:
L = 2r × sin ( α / 2 )
L – хорда
r – радиус окружности
O – центр окружности
α – центральный угол
Следует заметить, что такую величину, как длина хорды, инженерам, конструкторам различных машин и механизмов, а также архитекторам приходится вычислять не так уж и редко. Чаще всего этот параметр необходим для того, чтобы правильно сконструировать и разметить весьма распространенные в технике фланцевые соединения.
Основные их элементы, фланцы, представляют собой плоские кольца, на которых на одинаковом друг от друга расстоянии располагаются отверстия, куда устанавливаются резьбовые шпильки или болты.
Фланцы используются для соединения между собой участков различных трубопроводов и валов, причем применяются они в большинстве случаев попарно. Для того чтобы определить, в каких именно местах при изготовлении этих деталей следует просверлить отверстия, необходимо знать, какова длина хорды окружности, проходящей через их центры. При этом имеется в виду та хорда, которая располагается между центрами соседних отверстий. Зная этот параметр, можно не только составить правильный чертеж, по которому в дальнейшем будут производиться фланцы, но и впоследствии проконтролировать точность их изготовления. С большой точностью определить такой параметр, как длина хорды, требуется и тогда, когда разрабатываются детали машин и механизмов, имеющих форму криволинейных скоб: именно он определяет расстояние между конечными точками этих изделий.
Важную роль длина хорды играет и в баллистике – науке, изучающей движение тел, брошенных в пространстве. Дело в том, что перемещаются они по эллиптической траектории, и для того чтобы определить такой параметр, как, скажем, расстояние по прямой, которое при тех или иных условиях преодолеет пуля или баллистическая ракета, требуется вычислить именно длину хорды.
При этом специалистами используются достаточно сложные математические методы и формулы, учитывающие большое количество различных параметров, и для того, чтобы определить такую, казалось бы, простую величину, как длина хорды, в баллистике широко применяется современная высокопроизводительная вычислительная техника.
Что касается хорд в архитектуре, то их чаше всего можно встретить там, где используются различные сводчатые и арочные конструкции. Например, для того, чтобы точно рассчитать ширину дверного проема, верхняя часть которого выполнена в виде арки, требуется вычислить именно такой параметр, как длина хорды. При проектировании строений, которые увенчаны куполами (например, христианские храмы), архитекторам также в обязательном порядке нужно пользоваться формулами расчета хорд для того, чтобы правильно определить параметры снования этих конструкций (например, требуемые их диаметры).
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Окружность и круг |
| Отрезки и прямые, связанные с окружностью |
| Свойства хорд и дуг окружности |
| Теоремы о длинах хорд, касательных и секущих |
| Доказательства теорем о длинах хорд, касательных и секущих |
| Теорема о бабочке |
Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства |
| Окружность | Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности | |
| Круг | Конечная часть плоскости, ограниченная окружностью | |
| Радиус | Отрезок, соединяющий центр окружности с любой точкой окружности | |
| Хорда | Отрезок, соединяющий две любые точки окружности | |
| Диаметр | Хорда, проходящая через центр окружности. Диаметр является самой длинной хордой окружности | |
| Касательная | Прямая, имеющая с окружностью только одну общую точку. Касательная перпендикулярна к радиусу окружности, проведённому в точку касания | |
| Секущая | Прямая, пересекающая окружность в двух точках |
| Окружность |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности |
| Круг |
Конечная часть плоскости, ограниченная окружностью |
| Радиус |
Отрезок, соединяющий центр окружности с любой точкой окружности |
| Хорда |
Отрезок, соединяющий две любые точки окружности |
| Диаметр |
Хорда, проходящая через центр окружности. Диаметр является самой длинной хордой окружности |
| Касательная |
Прямая, имеющая с окружностью только одну общую точку. Касательная перпендикулярна к радиусу окружности, проведённому в точку касания |
| Секущая |
Прямая, пересекающая окружность в двух точках |
Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. | |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. | |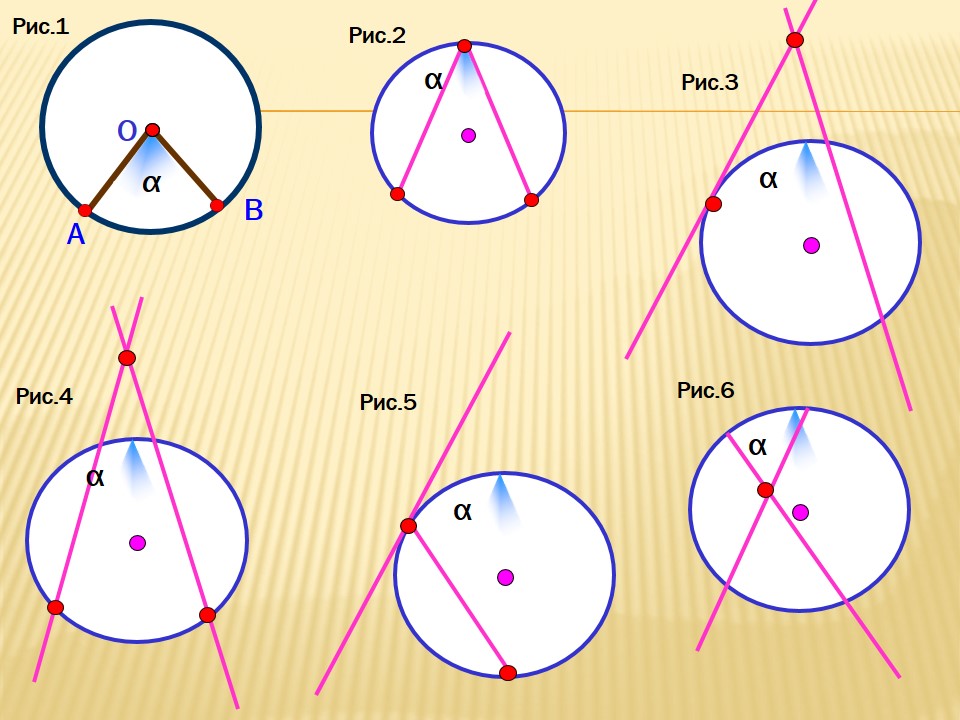
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины | Большая из двух хорд расположена ближе к центру окружности. | |
| Равные дуги | У равных дуг равны и хорды. | |
| Параллельные хорды | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды |
Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. |
| Равные хорды |
Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности |
Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. |
| Две хорды разной длины |
Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |
У равных дуг равны и хорды. |
| Параллельные хорды |
Дуги, заключённые между параллельными хордами, равны. |
Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема |
| Пересекающиеся хорды | Произведения длин отрезков, на которые разбита каждая из хорд, равны: Посмотреть доказательство | |
| Касательные, проведённые к окружности из одной точки | Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Посмотреть доказательство | |
| Касательная и секущая, проведённые к окружности из одной точки | Справедливо равенство Посмотреть доказательство | |
| Секущие, проведённые из одной точки вне круга | Справедливо равенство: Посмотреть доказательство |
| Пересекающиеся хорды | |
Произведения длин отрезков, на которые разбита каждая из хорд, равны: Посмотреть доказательство | |
| Касательные, проведённые к окружности из одной точки | |
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Посмотреть доказательство | |
| Касательная и секущая, проведённые к окружности из одной точки | |
Справедливо равенство Посмотреть доказательство | |
| Секущие, проведённые из одной точки вне круга | |
Справедливо равенство: Посмотреть доказательство | |
| Пересекающиеся хорды |
Произведения длин отрезков, на которые разбита каждая из хорд, равны: Посмотреть доказательство |
| Касательные, проведённые к окружности из одной точки |
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. AB = AC Посмотреть доказательство |
| Касательная и секущая, проведённые к окружности из одной точки |
Справедливо равенство Посмотреть доказательство |
| Секущие, проведённые из одной точки вне круга |
Справедливо равенство: Посмотреть доказательство |
Доказательства теорем о длинах хорд, касательных и секущих
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Рис. 1
Тогда справедливо равенство
Доказательство. Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A, лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Рис. 2
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство. Заметим, что угол ABC образован касательной AB и хордой BC, проходящей через точку касания B. Поэтому величина угла ABC равна половине угловой величины дуги BC. Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC. Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A, лежащей вне круга, к окружности проведены секущие AD и AF (рис.
3).
Рис. 3
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство. Проведём из точки A касательную AB к окружности (рис. 4).
Рис. 4
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Теорема о бабочке
Теорема о бабочке. Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Рис. 5
Доказательство. Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным.
Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B. Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG, получим
| (1) |
Воспользовавшись теоремой синусов, применённой к треугольнику AKG, получим
| (2) |
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Поэтому
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL, получим равенство
откуда вытекает равенство
x = y ,
что и завершает доказательство теоремы о бабочке.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Хорда формулы длины окружности, теоремы и свойства
Хорда окружности — это отрезок, соединяющий две точки на окружности окружности. Окружность — это двумерная фигура, в которой набор всех точек находится на равном расстоянии от фиксированной точки на плоскости. Неподвижная точка называется центром окружности. Диаметр круга — это линия, которая пересекает 2 точки на краю круга и проходит через центр, а расстояние, окружающее круг, называется окружностью. Таким образом, мы можем понять, что диаметр — это самая длинная хорда окружности, проходящая через центр окружности.
Что такое хорда окружности?Хорда окружности может быть определена как отрезок, соединяющий любые две точки на окружности окружности. Рассмотрим диаграмму ниже, где «O» — это центр, а AB и CD — хорда окружности. Здесь OE обозначает радиус окружности. AB является как диаметром, так и хордой на диаграмме.
Это означает, что диаметр окружности является самой длинной хордой.
Хорды, находящиеся на равном расстоянии от центра окружности, признаются равными хордами. Однако хорды, которые не находятся на одинаковом расстоянии от центра окружности, считаются неравными хордами.
Существуют 2 основные формулы для определения длины хорды окружности:
- Формула длины хорды окружности по перпендикулярному расстоянию от центра
- Формула длины хорды окружности с применением тригонометрии
Формула длины хорды окружности по расстоянию от центра по перпендикуляру: 92\right)}\)
Вот доказательство того, как найти длину хорды окружности по перпендикулярному расстоянию от центра.
На приведенной выше диаграмме r — это радиус окружности, а d — расстояние по перпендикуляру от хорды до центра окружности. Образуется треугольник, где r будет гипотенузой треугольника.
Как известно, биссектриса, проведенная из хорды к центру окружности, делит хорду пополам.
\(По\ теореме Пифагора\) 92\right)}=2\times\sqrt{\left(81−36\right)}=2\times\sqrt{45}\)
\(Хорда\длина\=13,416\)
Узнать о площади окружности и симметрии в окружности
Как найти хорду длины окружности с помощью тригонометрииРассмотрим приведенный выше рисунок, где r обозначает радиус окружности, а c — угол, стягиваемый в центре.
\(Хорда\ длина=2r\sin\left(\frac{c}{2}\right)\)
Примечание: Стягивающий угол
Рассмотрим круг выше с CD в качестве хорды. Пусть P и Q — любые точки на окружности, кроме хорды, как показано на рисунке. Можно видеть, что концы хорды CD соединены с точкой P, тогда ∠CPD определяется как угол, образуемый хордой CD в положении P. Точно так же угол ∠CQD представляет собой угол, образуемый хордой CD на Q а угол ∠COD — это угол, образуемый хордой CD в центре O.
Пример: 9{\circ}\ \)
\(радиус\ круга\,\ r=24\ см\)
\(Тогда\ По\ формуле,\)
\(Хорда\ длина=2r \sin\left(\frac{c}{2}\right)\)
\(=2\times24\times Sine\left(\frac{80}{2}\right)\)
\(= 2\times24\times Sine\ 40\)
\(=48\times Sine\ 40\)
\(=30,853\)
Узнайте о частях окружности и концентрических окружностях
Теоремы о хорде окружностиХорда окружности Теорема 1: Аккорды, равные по размеру, образуют равные углы в центре окружности. Это также известно как теорема о равных хордах и равных углах.
Хорда окружности Теорема 2: Эта теорема утверждает, что если углы, образуемые хордами окружности, равны по размеру, то длины хорд равны. Это также известно как теорема о равных углах и равных хордах или теорема, обратная теореме 1.
Хорда окружности Теорема 3: Перпендикуляр, проведенный из центра окружности к хорде, делит ее пополам на равные половины.
Хорда окружности Теорема 4 : Прямая, проходящая через центр окружности и делящая хорду, перпендикулярна хорде. Проще говоря, любая линия из центра, которая делит хорду пополам, перпендикулярна хорде. Это обратная теорема 3.
Хорда окружности Теорема 5: Равные хорды окружности находятся на равном расстоянии от центра окружности.
Хорда окружности Теорема 6: Эта теорема является обратной теореме 5. Она утверждает, что хорды на равном расстоянии от центра окружности равны по размеру.
Хорда окружности Теорема 7: Мера углов, опирающихся на любую точку окружности из одной и той же дуги, эквивалентна половине угла, опирающегося в центре на ту же дугу. Другими словами, угол, образуемый дугой в центре окружности, в два раза больше угла, образуемого дугой в любом другом заданном месте на окружности.
Хорда окружности Теорема 8: Углы, образуемые на одном и том же отрезке окружности, всегда равны по размеру.
Хорда окружности Теорема 9: Если отрезок, соединяющий любую пару точек, образует одинаковые углы в двух других точках, лежащих на соответствующей стороне, то они называются конциклическими. Это говорит о том, что все они покоятся в одном круге.
Хорда окружности Теорема 10: Если есть 3 точки, не лежащие на одной прямой, то через них может проходить только одна окружность.
Узнать о секущей окружности
Связь между радиусом и хордой окружностиРадиус круга определяется как любой отрезок, соединяющий центр круга с любым местом на круге. Однако хорда окружности — это отрезок, соединяющий любые две точки на окружности окружности. Диаметр в два раза больше радиуса и также является хордой, проходящей через центр окружности.
Узнайте о разнице между кругом и сферой
Свойства хорды круга- Радиус круга работает как биссектриса хорды.
- Длина хорды увеличивается по мере уменьшения перпендикулярного расстояния от центра окружности до хорды и наоборот.
- Диаметр — это самая длинная хорда окружности, при этом длина перпендикуляра от центра к хорде равна нулю.
- Два радиуса, соединяющие концы хорды с центром окружности, образуют равнобедренный треугольник.
- Две хорды равны по длине, если они находятся на одинаковом расстоянии от центра окружности. 9{\circ}\).
Пример 2: В данной окружности \(O\) является центром, а \(AB\), являющейся хордой окружности, равна \(16\) см. Найдите длину \(AD\), если \(OM\) — радиус окружности.
Решение: Мы знаем, что радиус окружности всегда перпендикулярен хорде окружности и действует как серединный перпендикуляр.
Следовательно, \(AD = \frac{1}{2}\times AB = \frac{16}{2} = 8\).
Следовательно, \(AD = 8 см\). 9{2} = 25 – 16 = 9\).
Таким образом, \(AM = \sqrt{9} = 3\).
Так как \(OM\) является серединным перпендикуляром к \(AB\), то \(AM = MB\).
Следовательно, хорда \(AB = 2 \times 3 = 6\) дюймов.
Пример 4: Хорда окружности равна ее радиусу. Найдите угол, образуемый этой хордой в точке большого отрезка.
Решение: Пусть \(O\) будет центром, а \(AB\) будет хордой окружности.
Итак, \(OA\) и \(OB\) — радиусы. 9{\circ}\).
Мы надеемся, что приведенная выше статья об аккорде окружности поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы о хорде окружностиВ.1 Что такое хорда окружности?
Ответ 1 Хорда окружности может быть определена как отрезок, соединяющий любые две точки на окружности окружности.
В.2 Как найти хорду окружности?
Ответ 2 Любой отрезок, концы которого лежат на окружности, называется хордой этой окружности.
Q.3 Является ли диаметр самой длинной хордой?
Ответ 3 Хорда, проходящая через центр окружности, называется диаметром, а диаметр также является самой длинной хордой этой конкретной окружности.
Q.4 Как найти радиус окружности с длиной хорды?
Ответ 4 Радиус окружности можно определить, если длина хорды определяется длиной хорды с использованием перпендикулярного расстояния или длины хорды формулы окружности с применением формулы тригонометрии, как описано в статье.
Q.5 В чем разница между хордой и радиусом в окружности?
Ответ 5 Радиус круга определяется как любой отрезок, соединяющий центр круга с любым местом на круге. Однако хорда окружности — это отрезок, соединяющий любые две точки на окружности окружности.
Скачать публикацию в формате PDF| Линейный график: Изучите определение, части, типы, шаги для чтения, используя примеры! |
| Уравнение окружности: вывод стандартного уравнения окружности |
| Примечания по анализу финансовых отчетов: значение, важность, методы и типы для бухгалтерского учета! |
| Правило Крамера: изучайте значения формул на примерах! |
| Центроид треугольника с определением, формулой, выводом, свойствами и примерами |
Длина хорды при разделении на равные сегменты
Калькулятор длины хорды
радиус (м, фут.
.)
№. отрезки
Длину — L — хорды при делении окружности на равное количество отрезков можно рассчитать по таблице ниже. Длина хорды — L — в таблице указана для «единичного круга» с радиусом = 1 .
Чтобы вычислить фактическую длину хорды, умножьте длину «единичного круга» — L — на радиус фактического круга.
Пример — Длина хорды
Окружность с радиусом 3 м разделена на 24 сегмента . Из таблицы ниже: длина — L — одной хорды в «единичном круге» с 24 сегментами составляет 0,2611 единиц .
Длина хорды окружности радиусом 3 м может быть рассчитано как
0,2611 (3 м) = 0,7833 м
Суммированная длина всех хордов в круге может быть рассчитана как
(0,7833 м) 24
= 6,26533334).
= 18.7959 m
The circumference of the circle can be calculated as
C = 2 π r
= 2 π (3 m)
= 18.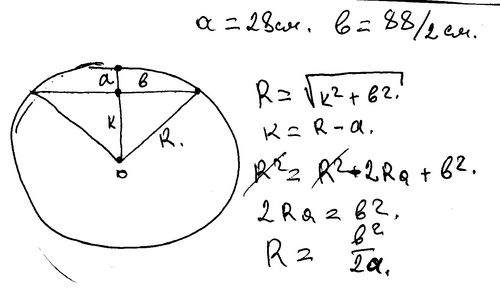
8496 m
| Number of Segments — n — | Center Angle — θ — | Length of Single Chord — L — | Summarized Lengths of Chords | ||||||
|---|---|---|---|---|---|---|---|---|---|
| degrees | radians | ||||||||
| 2 | 180.0000 | 3.1416 | 2.0000 | 4.0000 | |||||
| 4 | 90.0000 | 1.5708 | 1.4142 | 5.6569 | |||||
| 6 | 60.0000 | 1.0472 | 1.0000 | 6.0000 | |||||
| 8 | 45.0000 | 0.7854 | 0.7654 | 6.1229 | |||||
| 10 | 36.0000 | 0,6283 | 0,6180 | 6.1803 | |||||
| 12 | 30,0000 | 0,5236 | 353530303540,5236 | 353530303035540,5236 | 43530303035035..0353 6.2117 | ||||
| 14 | 25.7143 | 0.4488 | 0.4450 | 6.2306 | |||||
| 16 | 22.5000 | 0.3927 | 0.3902 | 6.2429 | |||||
| 18 | 20.0000 | 0.3491 | 0.3473 | 6.2513 | |||||
| 20 | 18.0000 | 0.3142 | 0.3129 | 6.2574 | |||||
| 22 | 16.3636 | 0.2856 | 0.2846 | 6.2619 | |||||
| 24 | 15.0000 | 0.2618 | 0.2611 | 6.2653 | |||||
| 26 | 13.8462 | 0.2417 | 0.2411 | 6.2679 | |||||
| 28 | 12,8571 | 0,2244 | 0,2239 | 6,2700 | |||||
| 30 | 0.2091 | 6.2717 | |||||||
| 32 | 11. 2500 | 0.1963 | 0.1960 | 6.2731 | |||||
| 34 | 10.5882 | 0.1848 | 0.1845 | 6.2742 | |||||
| 36 | 10.0000 | 0,1745 | 0,1743 | 6.2752 | |||||
| 38 | 9,4737 | 0,1653 | 03554 | 03503554 | 9354455455455545545545545554455545555455455455455455455455455455555545555353553ще0354 | ||||
| 40 | 9.0000 | 0.1571 | 0.1569 | 6.2767 | |||||
| 42 | 8.5714 | 0.1496 | 0.1495 | 6.2773 | |||||
| 44 | 8.1818 | 0.1428 | 0.1427 | 6.2778 | |||||
| 46 | 7.8261 | 0.1366 | 0.1365 | 6.2783 | |||||
| 48 | 7.5000 | 0.1309 | 0.1308 | 6. 2787 | |||||
| 50 | 7.2000 | 0.1257 | 0.1256 | 6.2791 | |||||
| 52 | 6.9231 | 0.1208 | 0.1208 | 6.2794 | |||||
| 54 | 6,6667 | 0,1164 | 0,1163 | 6,2796 | |||||
| 56 | 6,4286 | 0,1123535353535353535353535353535353535353535353535353535353535353535353535353535353535686.0354 | 6.2799 | ||||||
| 58 | 6.2069 | 0.1083 | 0.1083 | 6.2801 | |||||
| 60 | 6.0000 | 0.1047 | 0.1047 | 6.2803 | |||||
| 62 | 5.8065 | 0.1013 | 0.1013 | 6.2805 | |||||
| 64 | 5.6250 | 0.0982 | 0.0981 | 6.2807 | |||||
| 66 | 5.4545 | 0.0952 | 0. 0952 | 6.2808 | |||||
| 68 | 5.2941 | 0.0924 | 0.0924 | 6.2810 | |||||
| 70 | 5.1429 | 0.0898 | 0.0897 | 6.2811 | |||||
| 72 | 5,0000 | 0,0873 | 0,0872 | 6,2812 | |||||
| 74 | . 4,86464999995555555555353535535535355355355355355353553553553555555555555555555555555555555555555555559н | 0.0849 | 6.2813 | ||||||
| 76 | 4.7368 | 0.0827 | 0.0826 | 6.2814 | |||||
| 78 | 4.6154 | 0.0806 | 0.0805 | 6.2815 | |||||
| 80 | 4.5000 | 0.0785 | 0.0785 | 6.2816 | |||||
| 82 | 4.3902 | 0.0766 | 0.0766 | 6.2816 | |||||
| 84 | 4. 2857 | 0.0748 | 0.0748 | 6.2817 | |||||
| 86 | 4.1860 | 0.0731 | 0.0730 | 6.2818 | |||||
| 88 | 4.0909 | 0.0714 | 0.0714 | 6.2819 | |||||
| 90 | 4.0000 | 0.0698 | 0.0698 | 6.2819 | |||||
| 92 | 3.9130 | 0.0683 | 0.0683 | 6.2820 | |||||
| 94 | 3.8298 | 0.0668 | 0.0668 | 6.2820 | |||||
| 96 | 3.7500 | 0.0654 | 0.0654 | 6.2821 | |||||
| 98 | 3,6735 | 0,0641 | 0,0641 | 6,2821 | |||||
| 100 | 3,6000 | 0,06354 | 3,6000 | 0,06354 | 3,6000 | 0,06354 | .0354 | 6. 2822 | |
| 102 | 3.5294 | 0.0616 | 0.0616 | 6.2822 | |||||
| 104 | 3.4615 | 0.0604 | 0.0604 | 6.2822 | |||||
| 106 | 3.3962 | 0.0593 | 0.0593 | 6.2823 | |||||
| 108 | 3.3333 | 0.0582 | 0.0582 | 6.2823 | |||||
| 110 | 3.2727 | 0.0571 | 0.0571 | 6.2823 | |||||
| 112 | 3.2143 | 0.0561 | 0.0561 | 6.2824 | |||||
| 114 | 3.1579 | 0.0551 | 0.0551 | 6.2824 | |||||
| 116 | 3,1034 | 0,0542 | 0,0542 | 6,2824 | |||||
| 1184 34 40353 0.0532 | 0.0532 | 6.2824 | |||||||
| 120 | 3. 0000 | 0.0524 | 0.0524 | 6.2825 | |||||
| 122 | 2.9508 | 0.0515 | 0.0515 | 6.2825 | |||||
| 124 | 2.9032 | 0.0507 | 0.0507 | 6.2825 | |||||
| 126 | 2.8571 | 0.0499 | 0.0499 | 6.2825 | |||||
| 128 | 2.8125 | 0.0491 | 0.0491 | 6.2826 | |||||
| 130 | 2.7692 | 0.0483 | 0.0483 | 6.2826 | |||||
| 132 | 2.7273 | 0.0476 | 0.0476 | 6.2826 | |||||
| 134 | 2,6866 | 0,0469 | 0,0469 | 6.2826 | 2.6471 | 0.0462 | 0.0462 | 6.2826 | |
| 138 | 2. 6087 | 0.0455 | 0.0455 | 6.2826 | |||||
| 140 | 2.5714 | 0.0449 | 0.0449 | 6.2827 | |||||
| 142 | 2,5352 | 0,0442 | 0,0442 | 6,2827 | |||||
| 144 | 2,50000354 | 0.0436 | 6.2827 | ||||||
| 146 | 2.4658 | 0.0430 | 0.0430 | 6.2827 | |||||
| 148 | 2.4324 | 0.0425 | 0.0425 | 6.2827 | |||||
| 150 | 2.4000 | 0.0419 | 0.0419 | 6.2827 | |||||
| 152 | 2.3684 | 0.0413 | 0.0413 | 6.2827 | |||||
| 154 | 2.3377 | 0.0408 | 0.0408 | 6.2827 | |||||
| 156 | 2.3077 | 0.0403 | 0.0403 | 6. 2828 | |||||
| 158 | 2.2785 | 0.0398 | 0.0398 | 6,2828 | |||||
| 160 | 2,2500 | 0,0393 | 0,0393 | 6,2828 | 3 92 31903 53 2.22220.0388 | 0.0388 | 6.2828 | ||
| 164 | 2.1951 | 0.0383 | 0.0383 | 6.2828 | |||||
| 166 | 2.1687 | 0.0379 | 0.0378 | 6.2828 | |||||
| 168 | 2.1429 | 0.0374 | 0.0374 | 6.2828 | |||||
| 170 | 2.1176 | 0.0370 | 0.0370 | 6.2828 | |||||
| 172 | 2.0930 | 0.0365 | 0.0365 | 6.2828 | |||||
| 174 | 2.0690 | 0.0361 | 0.0361 | 6.2828 | |||||
| 176 | 2. | 0.0357 | 0.0357 | 6.2829 | |||||
| 178 | 2.0225 | 0.0353 | 0.0353 | 6.2829 | |||||
| 180 | 2.0000 | 0.0349 | 0.0349 | 6.2829 | |||||
| 182 | 1.9780 | 0.0345 | 0.0345 | 6.2829 | |||||
| 184 | 1.9565 | 0.0341 | 0.0341 | 6.2829 | |||||
| 186 | 1,9355 | 0,0338 | 0,0338 | 6,2829 | |||||
| 0.0334 | 0.0334 | 6.2829 | |||||||
| 190 | 1.8947 | 0.0331 | 0.0331 | 6.2829 | |||||
| 192 | 1.8750 | 0.0327 | 0.0327 | 6.2829 | |||||
| 194 | 1.8557 | 0.0324 | 0. 0324 | 6.2829 | |||||
| 196 | 1.8367 | 0.0321 | 0.0321 | 6.2829 | |||||
| 198 | 1.8182 | 0.0317 | 0.0317 | 6.2829 | |||||
| 200 | 1.8000 | 0.0314 | 0.0314 | 6.2829 | |||||
| 202 | 1.7822 | 0.0311 | 0.0311 | 6.2829 | |||||
| 204 | 1.7647 | 0.0308 | 0.0308 | 6.2829 | |||||
| 206 | 1.7476 | 0.0305 | 0.0305 | 6.2829 | |||||
| 208 | 1.7308 | 0.0302 | 0.0302 | 6.2829 | |||||
| 210 | 1.7143 | 0.0299 | 0.0299 | 6.2830 | |||||
| 212 | 1,6981 | 0,0296 | 0,0296 | 6,2830 | |||||
| 692 | 40353 0. 0294 | 0.0294 | 6.2830 | ||||||
| 216 | 1.6667 | 0.0291 | 0.0291 | 6.2830 | |||||
| 218 | 1.6514 | 0.0288 | 0.0288 | 6.2830 | |||||
| 220 | 1.6364 | 0.0286 | 0.0286 | 6.2830 | |||||
| 222 | 1.6216 | 0.0283 | 0.0283 | 6.2830 | |||||
| 224 | 1.6071 | 0.0280 | 0.0280 | 6.2830 | |||||
| 226 | 1.5929 | 0.0278 | 0.0278 | 6.2830 | |||||
| 228 | 1.5789 | 0.0276 | 0.0276 | 6.2830 | |||||
| 230 | 1,5652 | 0,0273 | 0,0273 | 6.2830 | 1. 5517 | 0.0271 | 0.0271 | 6.2830 | |
| 234 | 1.5385 | 0.0269 | 0.0269 | 6.2830 | |||||
| 236 | 1.5254 | 0.0266 | 0.0266 | 6.2830 | |||||
| 238 | 1,5126 | 0,0264 | 0,0264 | 6,2830 | |||||
| 240 | 2 | 1,500003540.0262 | 6.2830 | ||||||
| 242 | 1.4876 | 0.0260 | 0.0260 | 6.2830 | |||||
| 244 | 1.4754 | 0.0258 | 0.0258 | 6.2830 | |||||
| 246 | 1.4634 | 0.0255 | 0.0255 | 6.2830 | |||||
| 248 | 1.4516 | 0.0253 | 0.0253 | 6.2830 | |||||
| 250 | 1.4400 | 0.0251 | 0. 0251 | 6.2830 | |||||
| 252 | 1.4286 | 0.0249 | 0.0249 | 6.2830 | |||||
| 254 | 1.4173 | 0.0247 | 0.0247 | 6,2830 | |||||
| 256 | 1,4063 | 0,0245 | 0,0245 | 6,2830 | 3 5 30.0244 | 0.0244 | 6.2830 | ||
| 260 | 1.3846 | 0.0242 | 0.0242 | 6.2830 | |||||
| 262 | 1.3740 | 0.0240 | 0.0240 | 6.2830 | |||||
| 264 | 1,3636 | 0,0238 | 0,0238 | 6,2830 | |||||
| 266 | 1,3534 | 9353 0,0356666666666666666666666666666666666666666666666666666666636363636тели1,3534 | 266 | .0353 0.02366.2830 | |||||
| 268 | 1. 3433 | 0.0234 | 0.0234 | 6.2830 | |||||
| 270 | 1.3333 | 0.0233 | 0.0233 | 6.2830 | |||||
| 272 | 1.3235 | 0.0231 | 0.0231 | 6.2830 | |||||
| 1.3139 | 0.0229 | 0.0229 | 6.2830 | ||||||
| 276 | 1.3043 | 0.0228 | 0.0228 | 6.2830 | |||||
| 278 | 1.2950 | 0.0226 | 0.0226 | 6.2831 | |||||
| 280 | 1.2857 | 0.0224 | 0.0224 | 6.2831 | |||||
| 282 | 1.2766 | 0.0223 | 0.0223 | 6.2831 | |||||
| 284 | 1.2676 | 0.0221 | 0.0221 | 6.2831 | |||||
| 286 | 1.2587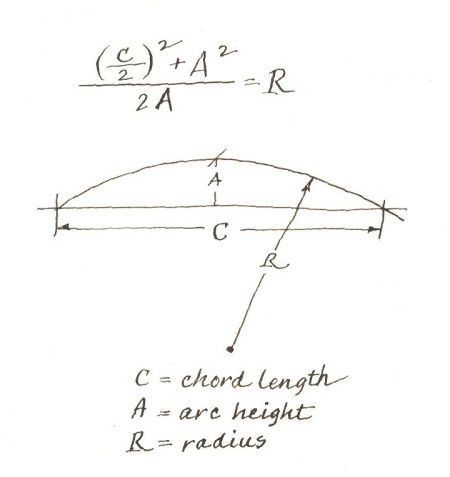 | 0. 0220 | 0.0220 | 6.2831 | |||||
| 288 | 1.2500 | 0.0218 | 0.0218 | 6.2831 | |||||
| 290 | 1.2414 | 0.0217 | 0.0217 | 6.2831 | |||||
| 292 | 1.2329 | 0.0215 | 0.0215 | 6.2831 | |||||
| 294 | 1.2245 | 0.0214 | 0.0214 | 6.2831 | |||||
| 296 | 1.2162 | 0.0212 | 0.0212 | 6.2831 | |||||
| 298 | 1.2081 | 0.0211 | 0,0211 | 6.2831 | |||||
| 300 | 1,2000 | 0,0209 | 0,0209 | 6.2831 | 1.1921 | 0.0208 | 0.0208 | 6.2831 | |
| 304 | 1. 1842 | 0.0207 | 0.0207 | 6.2831 | |||||
| 306 | 1.1765 | 0.0205 | 0.0205 | 6.2831 | |||||
| 308 | 1,1688 | 0,0204 | 0,0204 | 6,2831 | |||||
| 3104 140353 0.0203 | 0.0203 | 6.2831 | |||||||
| 312 | 1.1538 | 0.0201 | 0.0201 | 6.2831 | |||||
| 314 | 1.1465 | 0.0200 | 0.0200 | 6.2831 | |||||
| 316 | 1.1392 | 0.0199 | 0.0199 | 6.2831 | |||||
| 318 | 1.1321 | 0.0198 | 0.0198 | 6.2831 | |||||
| 320 | 1.1250 | 0.0196 | 0.0196 | 6.2831 | |||||
| 322 | 1.1180 | 0.0195 | 0.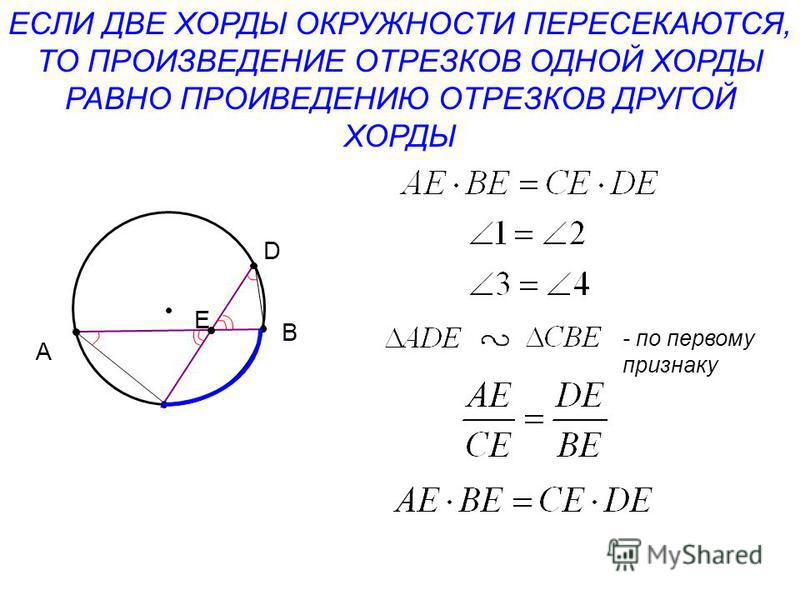 0195 | 6.2831 | |||||
| 324 | 1.1111 | 0.0194 | 0.0194 | 6.2831 | |||||
| 326 | 1,1043 | 0,0193 | 0,0193 | 6.2831 | 1.0976 | 0.0192 | 0.0192 | 6.2831 | |
| 330 | 1.0909 | 0.0190 | 0.0190 | 6.2831 | |||||
| 332 | 1.0843 | 0.0189 | 0.0189 | 6.2831 | |||||
| 334 | 1,0778 | 0,0188 | 0,0188 | 6,2831 | |||||
| 336 | 70.0187 | 6.2831 | |||||||
| 338 | 1.0651 | 0.0186 | 0.0186 | 6.2831 | |||||
| 340 | 1.0588 | 0.0185 | 0.0185 | 6. | |||||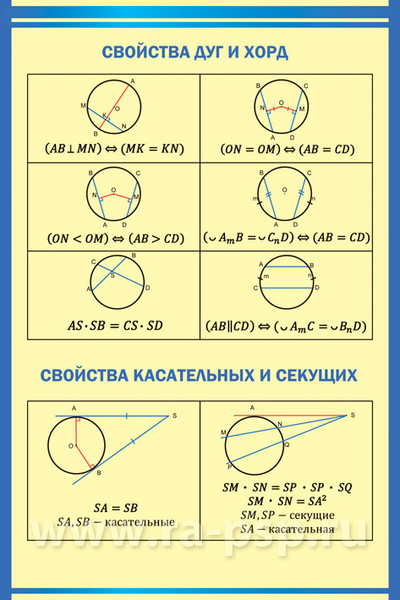
