Игрек равен косинус икс: Свойства функции y = cosx и её график — урок. Алгебра, 10 класс.

y = 1/cos(x)

Графики функций, Построение графиков Работа проверена: Slavikk85 Время решения: 13 мин Сложность: 4.0

Дано

$$f{left (x right )} = frac{1}{cos{left (x right )}}$$

График функции

Область определения функции

Точки, в которых функция точно неопределена:
$$x_{1} = 1.5707963267949$$
$$x_{2} = 4.71238898038469$$

Точки пересечения с осью координат X

График функции пересекает ось X при f = 0
значит надо решить уравнение:
$$frac{1}{cos{left (x right )}} = 0$$
Решаем это уравнение
Решения не найдено,
может быть, что график не пересекает ось X

Точки пересечения с осью координат Y

График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в 1/cos(x).
$$frac{1}{cos{left (0 right )}}$$
Результат:
$$f{left (0 right )} = 1$$
Точка:

(0, 1)

Экстремумы функции

Для того, чтобы найти экстремумы, нужно решить уравнение
$$frac{d}{d x} f{left (x right )} = 0$$
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$frac{d}{d x} f{left (x right )} = $$
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = 0$$
$$x_{2} = pi$$
Зн. {2}} f{left (x right )} = $$
Решаем это уравнение
Решения не найдены,
возможно перегибов у функции нет

Вертикальные асимптоты

Есть:
$$x_{1} = 1.5707963267949$$
$$x_{2} = 4.71238898038469$$

Горизонтальные асимптоты

Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo
$$lim_{x to -infty} frac{1}{cos{left (x right )}} = langle -infty, inftyrangle$$
Возьмём предел
значит,
уравнение горизонтальной асимптоты справа:

$$y = langle -infty, inftyrangle$$

Наклонные асимптоты

Наклонную асимптоту можно найти, подсчитав предел функции 1/cos(x), делённой на x при x->+oo и x ->-oo

True

Возьмём предел
значит,
уравнение наклонной асимптоты справа:
$$y = x lim_{x to infty}left(frac{1}{x cos{left (x right )}}right)$$

Чётность и нечётность функции

Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
$$frac{1}{cos{left (x right )}} = frac{1}{cos{left (x right )}}$$
– Да
$$frac{1}{cos{left (x right )}} = – frac{1}{cos{left (x right )}}$$
– Нет
значит, функция
является
чётной

   

Функция y=cos x и её свойства и график с примерами решения

Содержание:

Некоторые свойства функции 

Например, областью определения функции  является множество всех действительных чисел, множеством значений функции  является отрезок  наименьший положительный период функции  равен 

Определение:

Зависимость, при которой каждому действительному числу  соответствует значение  называется функцией 

Свойства функции y=cos x

Свойства функции  приведены в таблице.:

График функции y=cos x

График функции  изображен на рисунке 83. Этот график может быть получен путем преобразования (сдвига) графика функции 

Пример №1

Определите, какие из данных точек принадлежат графику функции 

Решение:

а) Подставим в формулу  значение аргумента  и найдем соответствующее значение функции Полученное значение функции равно ординате точки  значит, точка  принадлежит графику функции 

б)    При  — получим  Точка  принадлежит графику функции 

в)    При  получим  Точка  не принадлежит графику функции 

г)    При  получим  Точка  принадлежит графику функции 

Пример №2

Найдите область определения и множество значений функции 

Решение:

Областью определения функции является множество всех действительных чисел, т.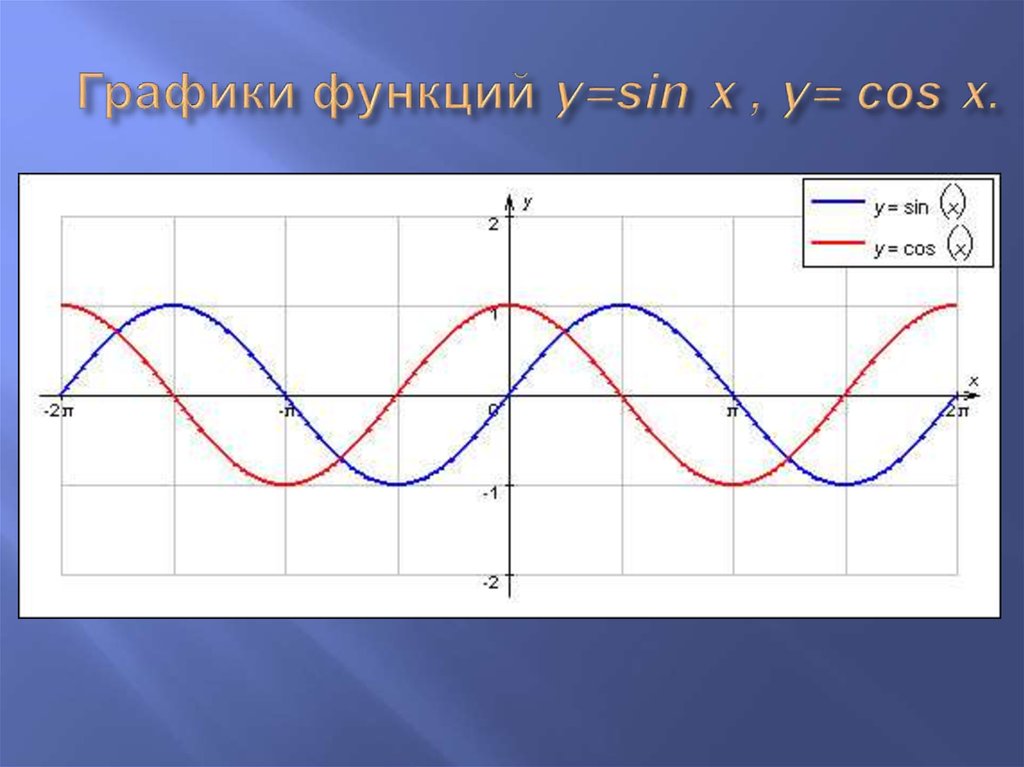 е. 

Множеством значений функции  является отрезок  значит,  Тогда по свойству неравенств  Таким образом, 

Пример №3

Найдите наименьшее значение функции 

Решение:

Так как  значит,  тогда  Наименьшее значение функции  равно -6.

Пример №4

Используя свойство периодичности функции  найдите значение выражения:

Решение:

Так как число  является наименьшим положительным периодом функции  Тогда:

• Заказать решение задач по высшей математике

Пример №5

Используя свойство четности функции  найдите значение выражения:

Решение:

Так как функция  четная, то 

Тогда:

Пример №6

Исследуйте функцию на четность (нечетность):

Решение:

а)  — область определения симметрична относительно нуля;

 значит, функция является четной.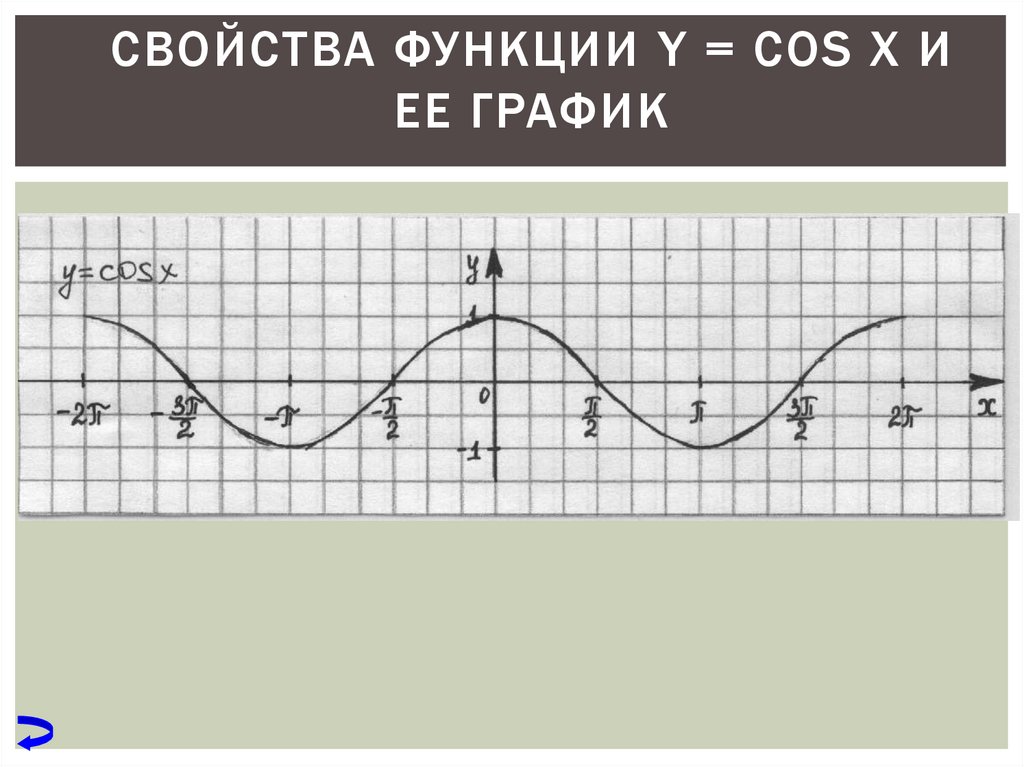

  —  область определения симметрична относительно нуля;

 значит, функция является нечетной.

Пример №7

Найдите нули функции:

Решение:

а) Пусть  Нулями функции  являются числа  Тогда  значит,  Таким образом, числа  являются нулями функции 

б)    Пусть  Нулями функции  являются числа  Тогда  значит, 

Таким образом, числа  являются нулями функции  

Пример №8

Определите знак произведения 

Решение:

Так как   т. е. углы

4,5 радиана и 2 радиана принадлежат промежутку  на котором функция  принимает отрицательные значения, значит, 

Угол 7 радиан принадлежит промежутку, на котором функция  принимает положительные значения, т. е.  Значит, 

Пример №9

Что больше: 

Решение:

Так как функция  убывает на промежутке  то из того, что  следует, что 

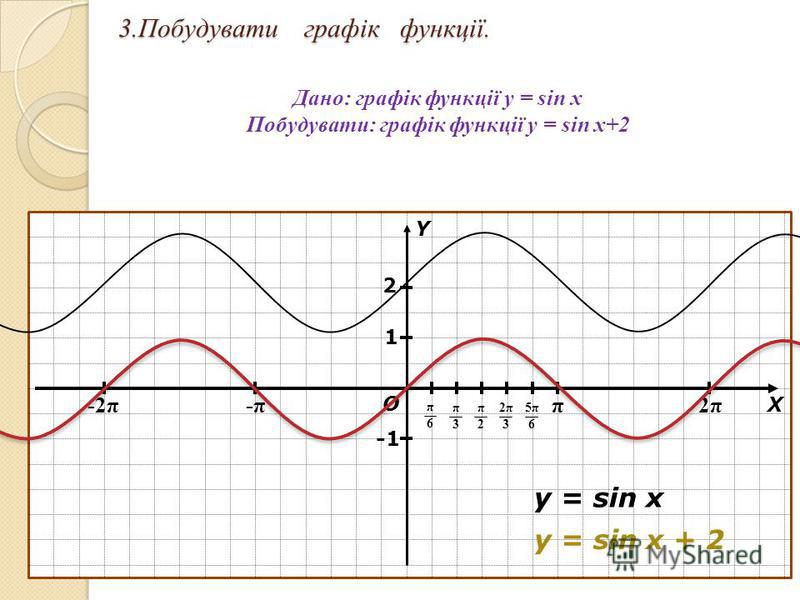
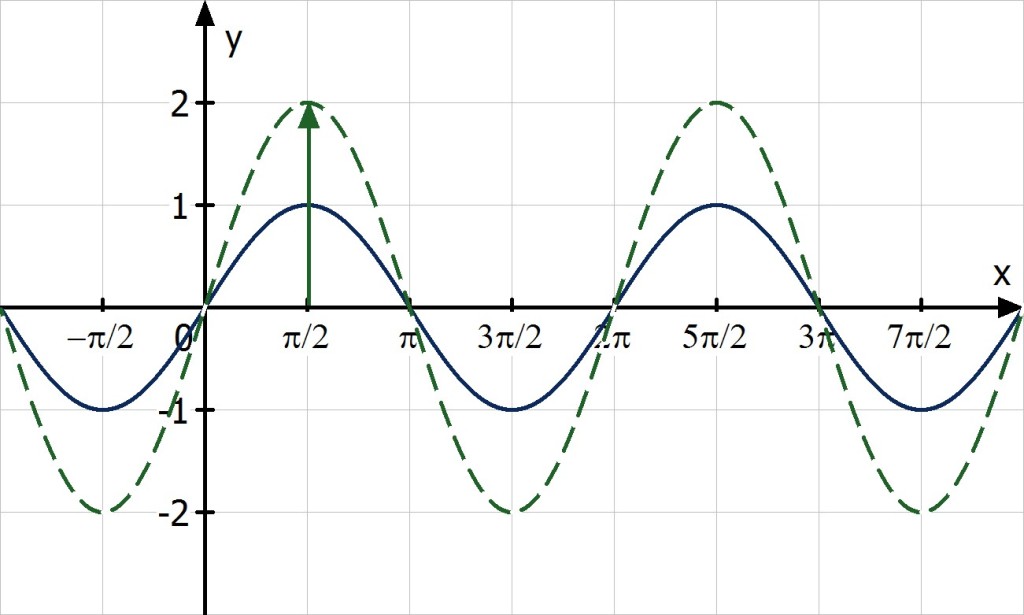
Пример №10

Постройте график функции:

Решение:

а) График функции  получаем из графика функции  сдвигом его вдоль оси абсцисс на  влево (рис. 86).

б)    График функции  получаем из графика функции  сдвигом его вдоль оси ординат на 2 единицы вниз (рис. 87).

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

график зависимости y, равной cos bx|найдите уравнение косинуса по данному графику графика.

Период — это расстояние, которое требуется, чтобы кривая косинуса снова начала повторяться.
Как известно, период косинуса равен 2π. Таким образом, отношение между периодом (2π) и «b» определяется как
Период = $ \frac{2π}{b}$
По мере увеличения значения ‘b’ период уменьшается.

Шаги для построения графика зависимости y от cos bx

Шаг 1: Получите значения a и b.
Шаг 2: Нарисуйте график зависимости y = cos x и отметьте точки, в которых он пересекает ось X.
Шаг 3: Разделите x-координаты точек, где y = cos x пересекает ось X, на b, а также отметьте максимальное и минимальное значения y = a cos bx как «a» и «-a» на оси Y .
Например: 1) y = 3 sin 2x
Здесь амплитуда = a = 3
Период =$ \frac{2π}{b}$
b= 2
⇒ Период =$ \frac{2π}{2}$
Таким образом, кривая косинуса пересекает ось x в точке (π/4,0), (3π/4,0),(5π/4,0),…
График будет иметь вид

2) y = 2 cos 2x
Здесь амплитуда = a = 2
Период =$ \frac{2π }{b}$
b= 2
⇒ Период =$ \frac{2π}{2} = π $
Таким образом, кривая косинуса пересекает ось x в точках (π/4,0), (3π/4,0 ),(5π/4,0),. ..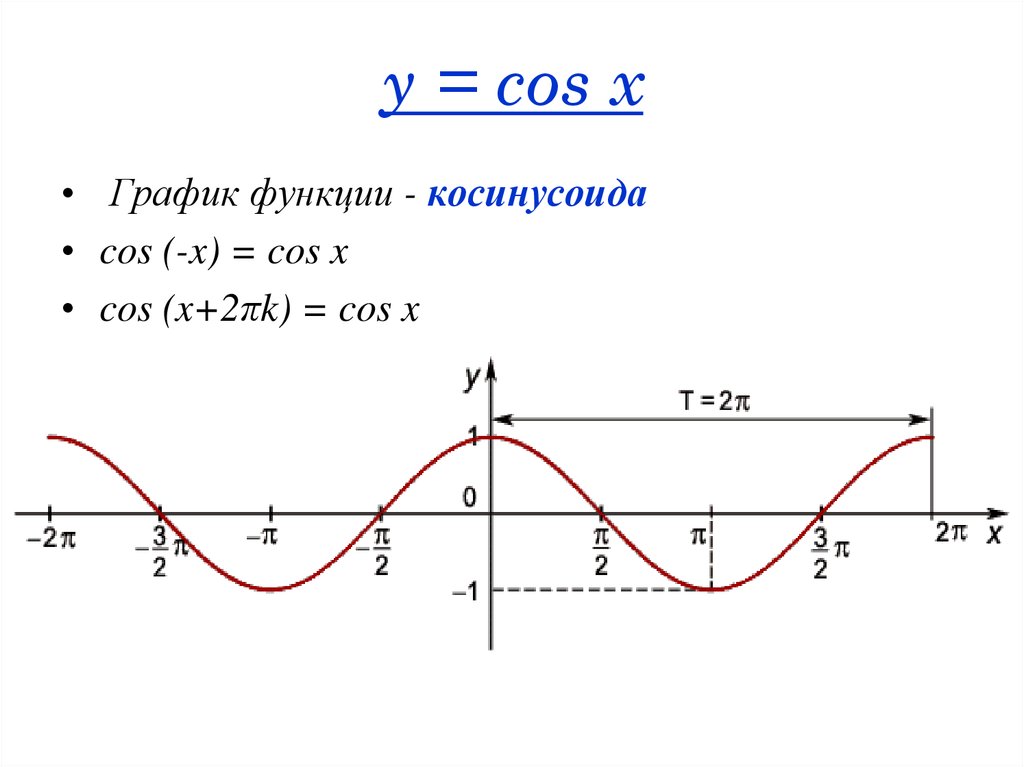

3) По данному графику найдите уравнение.

Из приведенного выше графика видно, что график представляет собой убывающую кривую, то есть косинусоидальную кривую.
Таким образом, уравнение будет иметь вид y = a cos bx
Здесь амплитуда = a = 1
Чтобы найти период,
один период косинуса равен 2π/3, поэтому
Период =$ \frac{2π}{b}$ = $ \frac{2π}{3}$
Таким образом, b = $ \frac{2π.3}{2π}$
b = 3
Таким образом, уравнение приведенного выше графика имеет вид y = 1 cos(3x).

Потренируйтесь на графике y равной cos bx

1) Укажите амплитуду и период для y = 4 cos 2x и нарисуйте уравнение для интервала $-π\leq x \leq 2π $
2) Сравните амплитуды y = 1/2 cos x и y = 2 cos x с амплитудой y = cos x и начертить график каждого в той же системе координат для $ 0 \leq x \leq 2π $

Математика 11 класса

От графика y равно cos bx до дома

Мы в ask-math считаем, что учебные материалы должны быть бесплатными для всех.