Индикатор EMA — экспоненциальная скользящая средняя
Любая скользящая средняя (Moving Average — МА) сглаживает движения цены и представляет собой трендоследящий индикатор. МА не могут предсказать будущих движений. Они выполняют единственную функцию — показать текущую ситуацию с некоторой задержкой.
Рис. 1. Общий вид индикатора ЕМА (10).
Скользящие средние не могут заглядывать в будущее, поскольку в формулу для их расчета подставляются прошлые цены. Однако, несмотря на такое ограничение, скользящие средние сглаживают цены и отфильтровывают шум. К тому же многие индикаторы берут за основу одну или несколько скользящих средних, например, полосы Боллинджера, MACD.
Типы скользящих средних
Вам уже известна простая МА и как она строится — Simple Moving Average. Однако существует множество других типов скользящих. Простой поиск индикаторов по запросу «moving average» на платформе MTBankFX обнаружит это многообразие.
Рис. 2. Поиск индикаторов по фильтру «moving average».
Все они выполняют следующие задачи: сгладить ценовые движения и показать текущее положение тренда.
Давайте рассмотрим вторую по популярности скользящую — экспоненциальную.
Экспоненциальная МА — построение индикатора
Для построения простой скользящей с периодом 10 — SMA (10) — потребуется взять десять последних цен закрытия, суммировать их и разделить на их количество (10). Из этой формулы следует, что каждая цена закрытия имеет в формуле расчета одинаковый вес.
Чтобы придать больший вес самым свежим ценам закрытия, а старые немного понизить в «ранге», была создана экспоненциальная скользящая средняя. Вес самых свежих цен закрытия будет зависеть от периода скользящей.
Построение индикатора происходит в три этапа:
- Получить значение простого скользящего — SMA. Экспоненциальная МА должна откуда-то начинаться, поэтому сперва мы получаем SMA.
Формула: Сумма последних 10-ти цен закрытия, деленная на 10 - Вычислить «вес» значений в ЕМА.
Формула: 2 / (Период скользящей + 1) = 2 / (10+1) = 0.1818 = 18.18% - Вычислить саму ЕМА.
Формула: (Цена закрытия — ЕМАвчера) * вес + ЕМАвчера
Проверим, как это работает, на конкретном примере.
Пример вычисления ЕМА
Мы возьмем уже готовый график с нанесенной ЕМА и проверим, верны ли наши вычисления.
Первый шаг с вычислением простой скользящей SMA мы пропустим, т.к. история котировок уходит очень далеко влево.
На втором шаге получим «вес» значений в ЕМА. Поскольку на графике используется 10-периодная ЕМА, то возьмем результат из вычислений выше = 0.1818.
Третий шаг: взять текущую цену закрытия (123.718), вчерашнюю ЕМА (121.763) и подставить в формулу.
Рис. 3. Получить цену закрытия «последнего» бара.
Рис. 4. Получить «вчерашнюю» ЕМА.
Получив необходимые значения, переходим к расчетам:
ЕМАсегодня = (Цена закрытиясегодня — ЕМАвчера) * вес + ЕМАвчера
ЕМАсегодня = (123.718 — 121.763) * 0.1818 + 121.
763
ЕМАсегодня = 122.118
Проверим это прямо на графике.
Рис. 5. Искомая ЕМА.
Расчеты оказались верны.
Какой тип скользящей использовать?
Оценив, сколько типов скользящих существует, каждый трейдер может задаться вопросом: «Какую из них выбрать?».
Если задуматься о назначении скользящих (фильтровать цены, убирать шум, показывать тренд) и об их ограничениях (запаздывание), то вывод один: не стоит слишком серьезно и долго заниматься поиском той самой скользящей, ведь в каждой из них запрограммировано некое отставание от текущей ситуации.
В этом можно убедиться, попробовав несколько типов скользящих на одном графике.
Рис. 6. Сравнение простой и экспоненциальной скользящих средних с периодом 10.
Опытные трейдеры рекомендуют воздерживаться от слишком сложных типов скользящих, поскольку трейдер, принимающий торговое решение, должен понимать, как именно его индикатор получил то или иное значение.
Еще больше новостей – в нашем Telegram-канале
Подписаться на канал
Поделитесь своей новостью или «денежной» историей через @myfinby_bot
Оцените статью:
Помогите с решением следующего. Необходимо научиться вычислять вероятность события по выражению, Один из примеров: Исходные данные: Неясно каким образом из выражения: где — функция-индикатор, причем Было получено выражение: где — ступенчатая единичная функция, [А.И. Перегуда, Р.Е. Твердохлебов Обобщение математической модели АТК «Объект Привожу необходимую информацию по рассматриваемой задаче: С каждым событием можно связать случайную величину [Севастьянов Б.А. Курс теории вероятности и математической статистики. – М.: Если случайная величина имеет функцию распределения Свойства математического ожидания: 2. Постоянный множитель выносится за знак математического ожидания: . 3. Математическое ожидание суммы любых случайных величин (как угодно связанных) равно сумме их математических ожиданий: . 4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: [Гнеденко Б. Более простой пример с использованием аналогичных методов: Допустим и — независимые непрерывные случайные переменные, имеющие плотности распределения и , соответственно. где [M.Ross Introduction to Probability Models Ninth Edition. Sheldon Тем не менее мне все равно не удалось понять как решаются такие задачи. Как от выражения вида Перейти к выражению, построенному на функциях распределения? |
Ядерная энергетика, № 2 , 2006]
В., Беляев Ю.К., Соловьев А.Д. Математические методы в теории Функция индикатора | Случайная величина индикатора
Марко Табога, доктор философии
Индикаторная функция события представляет собой случайную величину, которая занимает:
Индикаторные функции также называют индикаторными случайными величинами.
Содержание
Что нужно запомнить0003
Properties
Powers
Expected value
Variance
Intersections
Indicators of zero-probability events
Very similar concepts
Solved упражнения
упражнение 1
упражнение 2
упражнение 3
Что нужно помнить
Чтобы понять следующее определение, нужно помнить, что случайная переменная это функция :
Если
является одним из возможных исходов, то
это значение, принимаемое
когда понял
результат
.
Также помните, что событие является подмножеством выборочного пространства .
Определение
Вот определение.
Определение Позволять быть образцом пространства и быть событием. Функция индикатора из , обозначается , случайная величина, определяемая как
Иногда мы также используем обозначениегде греческая буква чи.
Пример
Мы подбрасываем кубик, и лицом вверх может выпасть одно из шести чисел от 1 до 6.
Пример пространства это
Определите событие описал предложением «Четное число появляется лицевой стороной вверх».
Случайная величина, которая принимает значение 1, когда лицевой стороной вверх выпадает четное число. значение 0 в противном случае является индикатором события .
Индивидуальное определение этого показателя
Показатели дискретные переменные
Из вышеприведенного определения легко видеть, что является дискретным случайным переменная с поддерживать и вероятностная масса функция
Свойства
Индикаторные функции обладают следующими свойствами.
Пауэрс
-й сила равно :
Доказательство
Это следствие того факта, что может быть или , и
Ожидаемое значение
Ожидаемая стоимость равно
Доказательство
Доказательство следующее:
Разница
Дисперсия равно
Proof
Благодаря обычному формула дисперсии и степени свойство выше, мы получить
Перекрестки
Если и два события, то
Доказательство
Если , затем и если , то и
Индикаторы событий с нулевой вероятностью
Позволять быть событием с нулевой вероятностью и интегрируемая случайная переменная. Тогда
Доказательство
Хотя строгое доказательство этого факта
за рамками этого вводного изложения, это свойство должно быть
интуитивный. Случайная величина
равен нулю для всех точек выборки
,
кроме, пожалуй, очков
.
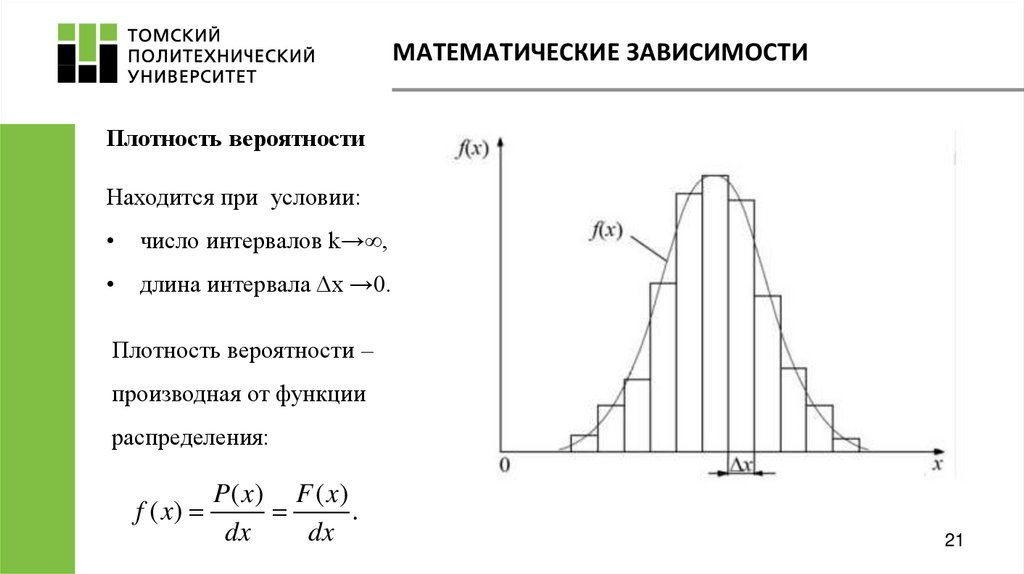Ожидаемое значение представляет собой средневзвешенное значение значений
может приниматься, где каждое значение взвешивается по соответствующей вероятности.
ненулевые значения
могут быть взвешены с нулевой вероятностью, поэтому
должен быть равен нулю.
Очень похожие концепции
В теории вероятностей и статистике есть два важных понятия, которые почти идентичны индикаторной переменной:
Бернулли распределение;
-
фиктивная переменная.
Решенные упражнения
Ниже вы можете найти несколько упражнений с поясненными решениями.
Упражнение 1
Рассмотрим случайную величину и еще одна случайная величина определяется как функция .
Выражать используя индикаторные функции событий и .
Раствор
Обозначим через
в
индикатор события
и обозначим через
в
индикатор события
.
Мы можем написать
как
Упражнение 2
Позволять быть положительной случайной величиной, то есть случайной величиной, которая может принимать только положительные значения.
Позволять быть константой.
Докажи это где является индикатором события .
Решение
Прежде всего обратите внимание, что сумма индикаторов и всегда равно :Как следствие, мы можем написать сейчас, Обратите внимание, что является положительной случайной величиной и что ожидаемое значение положительного случайного переменная положительный: Таким образом,
Упражнение 3
Позволять быть событием и обозначим его индикаторную функцию через .
Позволять быть дополнением и обозначим его индикаторную функцию через .
Можете ли вы выразить как функция ?
Решение
Сумма двух показателей всегда равно :Поэтому
Как цитировать
Пожалуйста, цитируйте как:
Табога, Марко (2021).
«Индикаторная функция», Лекции по теории вероятностей и математической статистике. Прямая публикация Kindle. Онлайн приложение. https://www.statlect.com/fundamentals-of-probability/indicator-functions.
Функция индикатора | Случайная величина индикатора
Марко Табога, доктор философии
Индикаторная функция события представляет собой случайную величину, которая занимает:
Индикаторные функции также называют индикаторными случайными величинами.
Table of contents
Things to remember
Definition
Example
Indicators are discrete variables
Properties
Powers
Expected value
Дисперсия
Перекрестки
Индикаторы событий с нулевой вероятностью
Решенные упражнения
Упражнение 1
Упражнение 2
.
Чтобы понять следующее определение, нужно помнить, что
случайная переменная
это функция :Если является одним из возможных исходов, то это значение, принимаемое когда понял результат .
Также помните, что событие является подмножеством выборочного пространства .
Определение
Вот определение.
Определение Позволять быть образцом пространства и быть событием. Функция индикатора из , обозначается , случайная величина, определяемая как
Иногда мы также используем обозначениегде греческая буква чи.
Пример
Мы подбрасываем кубик, и лицом вверх может выпасть одно из шести чисел от 1 до 6.
Пример пространства это
Определите событие описал предложением «Четное число появляется лицевой стороной вверх».
Случайная величина, которая принимает значение 1, когда лицевой стороной вверх выпадает четное число. значение 0 в противном случае является индикатором события .
Индивидуальное определение этого показателя
Показатели являются дискретными переменными
Из вышеприведенного определения легко видеть, что является дискретным случайным переменная с поддерживать и вероятностная масса функция
Свойства
Индикаторные функции обладают следующими свойствами.
Пауэрс
-й сила равно :
Доказательство
Это следствие того факта, что может быть или , и
Ожидаемое значение
Ожидаемая стоимость равно
Доказательство
Доказательство следующее:
Разница
Дисперсия равно
Proof
Благодаря обычному формула дисперсии и степени свойство выше, мы получить
Перекрестки
Если и два события, затем
Доказательство
Если , затем и если , то и
Индикаторы событий с нулевой вероятностью
Позволять быть событием с нулевой вероятностью и интегрируемая случайная переменная.
ТогдаДоказательство
Хотя строгое доказательство этого факта за рамками этого вводного изложения, это свойство должно быть интуитивный. Случайная величина равен нулю для всех точек выборки , кроме, пожалуй, очков . Ожидаемое значение представляет собой средневзвешенное значение значений может приниматься, где каждое значение взвешивается по соответствующей вероятности. ненулевые значения могут быть взвешены с нулевой вероятностью, поэтому должен быть равен нулю.
Очень похожие концепции
В теории вероятностей и статистике есть два важных понятия, которые почти идентичны индикаторной переменной:
Бернулли распределение;
фиктивная переменная.
Решенные упражнения
Ниже вы можете найти несколько упражнений с поясненными решениями.
Упражнение 1
Рассмотрим случайную величину и еще одна случайная величина определяется как функция .
Выражать используя индикаторные функции событий и .
Раствор
Обозначим через в индикатор события и обозначим через в индикатор события . Мы можем написать как
Упражнение 2
Позволять быть положительной случайной величиной, то есть случайной величиной, которая может принимать только положительные значения.
Позволять быть константой.
Докажи это где является индикатором события .
Решение
Прежде всего обратите внимание, что сумма индикаторов и всегда равно :Как следствие, мы можем написать сейчас, Обратите внимание, что является положительной случайной величиной и что ожидаемое значение положительного случайного переменная положительный: Таким образом,
Упражнение 3
Позволять быть событием и обозначим его индикаторную функцию через .
Чтобы понять следующее определение, нужно помнить, что
случайная переменная
это функция :
Тогда
