Инъекция, сюръекция, биекция : Чулан (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
| Millerrussia |
| ||
07/02/14 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| Millerrussia |
| ||
07/02/14 |
| ||
| |||
| provincialka |
| |||
18/01/13 Казань |
| |||
| ||||
| Millerrussia |
| ||
07/02/14 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| bot |
| |||
21/12/05 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 7 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
1.
 10.2 Функции и отображения
10.2 Функции и отображенияПонятие функции является одним из основных в математике. В математическом анализе под функцией чаще всего понимается «числовая» функция, отображающая одно числовое множество в другое. Здесь мы будем рассматривать, прежде всего, функцию, отображающую одно конечное множество объектов в другое конечное множество.
Определение. Пусть А и В конечные множества.
Функцией называется функциональное соответствие.
Если функция устанавливает соответствие между множествами А и В, то говорят, что функция имеет тип АВ.
Обозначается : АВ.
Таким образом, функция – специальный тип отношения из А в В.
Каждому элементу а из области
определения функция
ставит в соответствие элемент b из области значений. Это обозначается
(а) = b.
Элемент а – аргумент функции, элемент b – значение функции на а.
Отображением А в В называется всюду определённая функция : АВ.
Образом отображения А в В называется множество (А) всех значений (а), которое оно принимает при всевозможных аА. Образ является подмножеством множества В.
Отображением А на В называется всюду определённое и при этом сюръективное функциональное соответствие
: АВ.
К специальным отображениям часто относятся понятия оператора и функционала.
Оператор – отображение одного множества на другое, каждое из которых наделено некоторой структурой.
Функционал – отображение произвольного
множества Х в множество комплексных
или действительных чисел.
Отображением типа АА часто называют преобразованием множества А.
Функции и g равны, если:
Таким образом, функции могут быть строго одинаковыми только тогда, когда их области определения и значений совпадают (A1=A, и B1=B) .
Если fA =A, то функция называется тотальной, а если – частичной.
Таблица 1.
Соответствие | Обязательное свойство | ||
функцио- нальное | всюду определённое | сюръек- тивное | |
Функция | + | – | – |
Отображение А в В | + | + | – |
Отображение А на В | + | + | + |
Функция называется функцией n аргументов или n—местной функцией.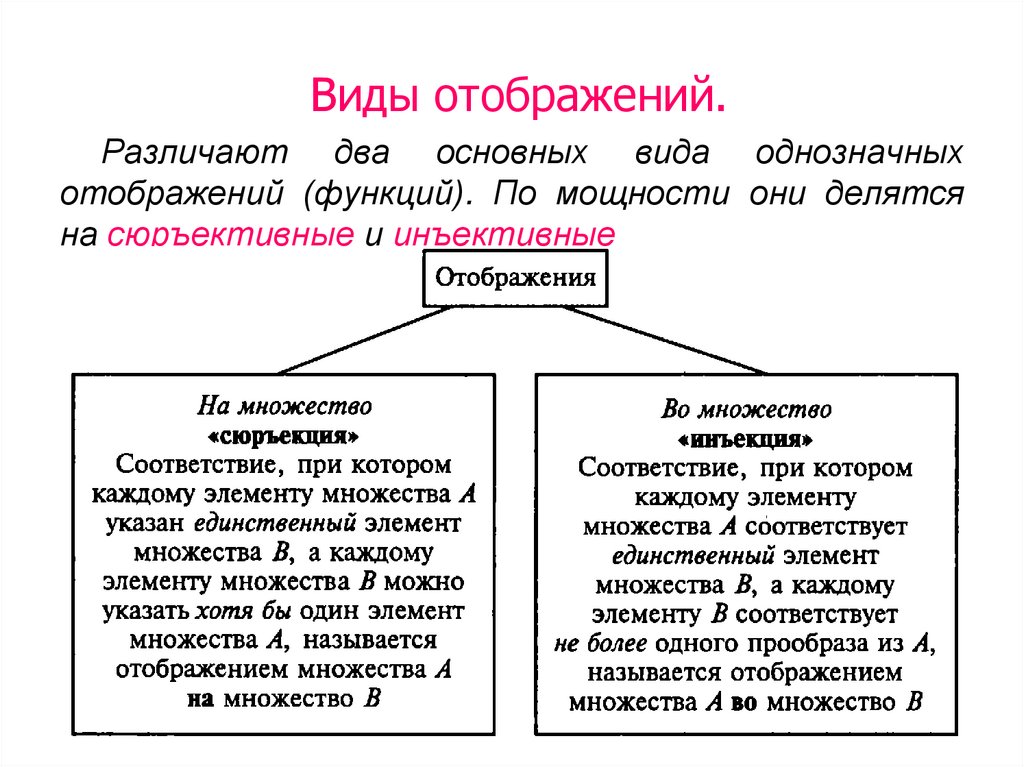 В этом случае принято считать,
что функция имеет n аргументов: ,
где .
В этом случае принято считать,
что функция имеет n аргументов: ,
где .
Пусть дано соответствие . Тогда соответствие называется обратным к G (обозначается G -1), если Н таково, что (b, a)H тогда и только тогда, когда
(а, b)G.
Если соответствие, обратное к функции : АВ, является функциональным, то оно называется функцией, обратной
к (обозначается f-1).
Для функции : АВ обратная функция существует только тогда, когда является взаимно однозначным соответствием между своими областями определения и значений.
Пусть : АВ.
1, Функция называется инъективной, или инъекцией, если
из в А следует, что в В, т. е., если и .
Иными словами, инъекция переводит
различные элементы области А в
различные элементы области В.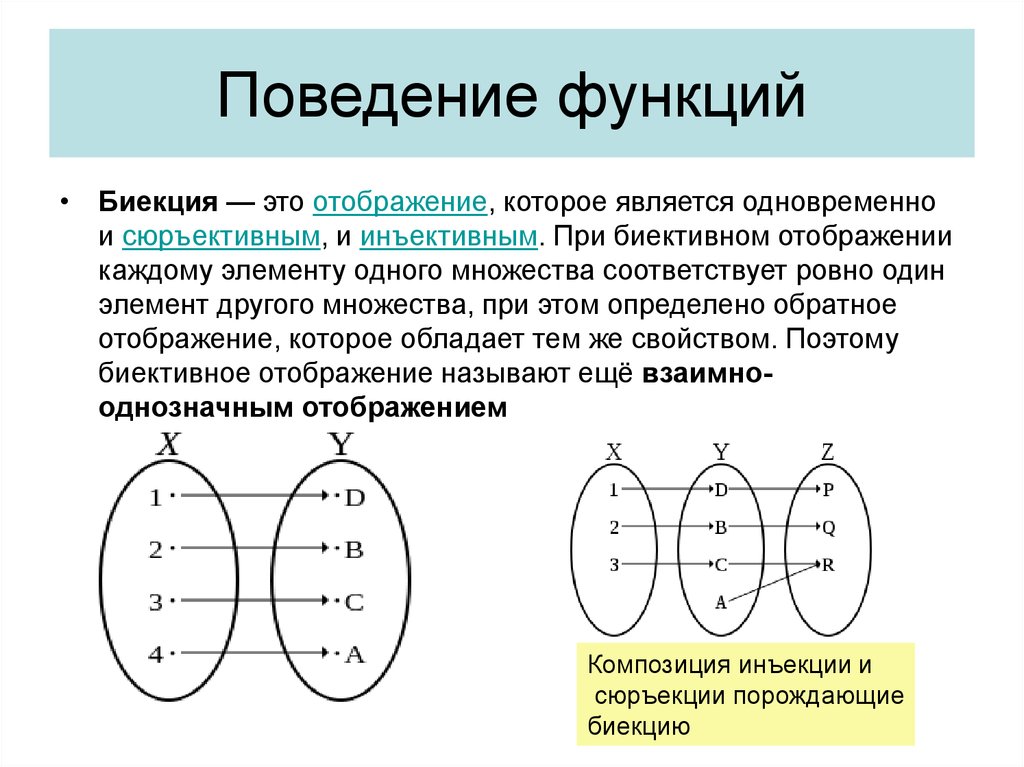 Её
часто называют взаимно однозначным отображением А в В.
Её
часто называют взаимно однозначным отображением А в В.
По другому: функция : АВ называется инъективной, или инъекцией, если каждый элемент bB имеет хотя бы один прообраз аА либо вообще не имеет прообраза. Можно видеть, что условие для любого bB или |A||B| определяет инъекцию.
Пример 1. Пусть A={1, 2, 3}; . Функция : АВ инъективна, если .
2. Функция называется сюръективной, или сюръекцией, если её образ совпадает со всей областью В, т. е. для каждого bB существует хотя бы один элемент аА такой, что (а)=b. Сюръекции часто обозначаются так и называется отображением А на (все) В.
Т. е. .
Иначе: функция : АВ называется сюръективной или сюръекцией,
если любой элемент bB есть образ по крайней мере одного аА. Условие для любого bB или |x||y|
характеризует сюръекцию.
Условие для любого bB или |x||y|
характеризует сюръекцию.
Пример 2. Пусть A={1, 2, 3,4}; . Функция : АВ сюръективна, если . Та же функция Ψ:{1, 2, 3} с условием
(1)= (3)=y1 ; (2)= (4)=y3 не является сюръективной.
2. Функция называется биективной, или биекцией, если она является одновременно инъекцией и сюръекцией. Иными словами, биективное отображение взаимно однозначно и является отображением на ( ).
Для биективной функции для любого bB или |x|=|y|.
Пример 3: Пусть A={1, 2, 3}; .
Функция : АВ биективна, если
Биективная функция определяет взаимно
однозначноесоответствие между
множествами А и В.
Схематически различные виды отношений изображены на рис.8.
Р ис.8.
Если между множествами А и В можно установить взаимно однозначное соответствие, то А называется эквивалентным множеству В. Установление взаимно однозначного соответствия между множествами играет важную роль. Так, определение числа элементов конечного множества Х, т. е. установление равенства |x|=n при некотором n, фактически сводится к отыскиванию некоторого взаимно однозначного соответствия между множествами Х и N={1, 2, 3, …, n}. Множества, равномощные N, называются счётными.
Множества равномощны, если между их элементами можно установить взаимно однозначное соответствие, т. е. эквивалентные множества являются равномощными.
Пример 4. Биекцией между множеством натуральных чисел N={0, 1, 2, …} и множеством целых чисел
Z{0, ±1, ±2, …} является функция : NZ, для которой
Таким образом, обратная функция существует для биекции
П
ример
5. На рис.9 графически показаны функции
:
На рис.9 графически показаны функции
:
fi:[0, 1][0, 1], i{1, 2, 3, 4}.
Функция f1 сюръективна, но не инъективна;
Функция f2 инъективна, но не сюръективна;
Функция f3 биективна, а функция f4 не инъективна и не сюръективна
Пример 2. Рассмотрим три функции
fi:: RR, i=1, 2, 3:
1. функция f1(x)= ex инъективна, но не сюръективна;
2. функция f2(x)= xsinx сюръективна, но не инъективна;
3. функция f3(x)= 2x-1 биективна.
Пример 6. Среди функций из Z
в Z отображение биективно; отображение инъективно, но не сюръективно, а
отображение не инъективно и не сюръективно (почему?).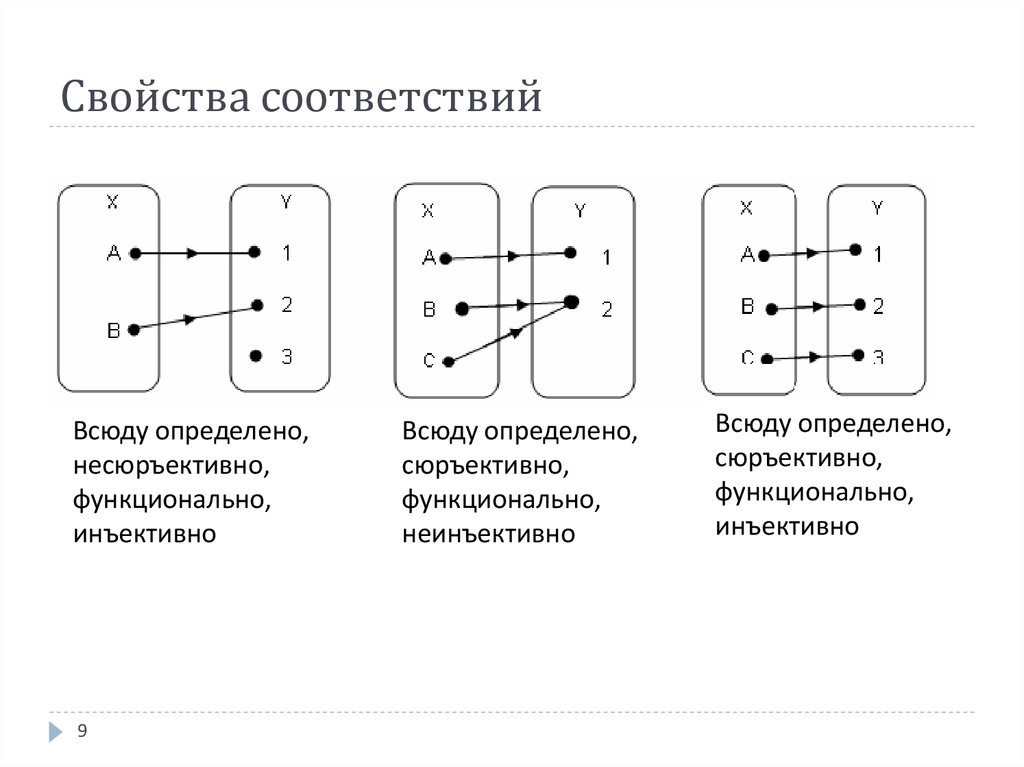
Биекция, инъекция и сюръекция | Brilliant Math & Science Wiki
Патрик Корн, Анант Джаядев, Кристофер Уильямс, и
способствовал
Содержимое
- Определение функции
- инъективный
- Сюръективный
- Биективный
Функция \(f \colon X\to Y\) — это правило, по которому каждому элементу \( x\in X,\) соответствует элемент \( f(x) \in Y.\) Элемент \ (f(x)\) иногда называют образом \(x,\), а подмножество \(Y\), состоящее из образов элементов из \(X\), называют образом \(f. \) то есть
\) то есть
\[\text{image}(f) = \{ y \in Y : y = f(x) \text{ для некоторого } x \in X\}.\]
Пусть \(f \colon X \to Y\) — функция. Тогда \(f\) является инъективным , если различные элементы \(X\) отображаются в различные элементы \(Y.\)
То есть, если \(x_1\) и \(x_2\) находятся в \(X\) так, что \(x_1 \ne x_2\), то \(f(x_1) \ne f(x_2)\).
Это равносильно тому, что если \(f(x_1) = f(x_2)\), то \(x_1 = x_2\).
Синоним слова «инъективный» — «один к одному».
Функция \( f\colon {\mathbb Z} \to {\mathbb Z}\), определяемая выражением \( f(n) = 2n\), является инъективной: если \( 2x_1=2x_2,\) обе части делятся на \ ( 2 \) дает \(x_1=x_2.\)
Функция \( f\colon {\mathbb Z} \to {\mathbb Z}\), определяемая выражением \( f(n) = \big\lfloor \frac n2 \big\rfloor\), не является инъективной; например, \(f(2) = f(3) = 1\), но \( 2 \ne 3.\)
Функция \( f\colon \{ \text{Немецкие футболисты, одетые для финала ЧМ-2014}\} \to {\mathbb N} \), определяемая выражением \(f(A) = \text{номер футболки } А\) инъективен; никаким двум игрокам не разрешалось носить один и тот же номер.
Существование инъективной функции дает информацию об относительных размерах ее области определения и диапазона:
Если \( X \) и \( Y \) конечные множества и \( f\colon X\to Y \) инъективны, то \( |X| \le |Y|.\)
\[х\] \[г\] \[г\] Ничего из вышеперечисленного
9{-1} (1). \)
Пусть \(f \colon X\to Y\) будет функцией. Тогда \(f\) является сюръективным , если каждый элемент \(Y\) является образом хотя бы одного элемента \(X.\). То есть \( \text{image}(f) = Y. \)
Символически,
\[\для всех y \in Y, \существует x \in X \text{ такое, что } f(x) = y.\]
Синоним слова «сюръективный» — «на».
Функция \( f\colon {\mathbb Z} \to {\mathbb Z}\), определяемая выражением \(f(n) = 2n\), не является сюръективной: не существует целого числа \(n\) такого, что \( f(n)=3,\), так как \( 2n=3\) не имеет решений в \( \mathbb Z.
\) Таким образом, \( 3\) не находится в образе \( f.\)
Функция \( f\colon {\mathbb Z} \to {\mathbb Z}\), определяемая выражением \( f(n) = \big\lfloor \frac n2 \big\rfloor\), является сюръективной. Для любого целого числа \( m,\) обратите внимание, что \( f(2m) = \big\lfloor \frac{2m}2 \big\rfloor = m,\), поэтому \( m \) находится в образе \( f.\) Таким образом, образ \(f\) равен \(\mathbb Z.\)
Функция \(f \colon \{\text{сенаторов США}\} \to \{\text{штаты США}\}\), определяемая выражением \(f(A) = \text{состояние, которое} A \ text{представляет}\) сюръективен; в каждом штате есть хотя бы один сенатор.
Существование сюръективной функции дает информацию об относительных размерах ее области определения и диапазона:
Если \(X\) и \(Y\) конечные множества и \(f\colon X\to Y\) сюръективно, то \( |X| \ge |Y|.\)
Пусть \( E = \{1, 2, 3, 4\} \) и \(F = \{1, 2\}.\) Тогда каково число онто-функций из \( E \) в \( F?\)
Функция биективна для двух множеств, если каждому элементу одного множества соответствует только один элемент второго множества, а каждому элементу второго множества соответствует только один элемент первого множества.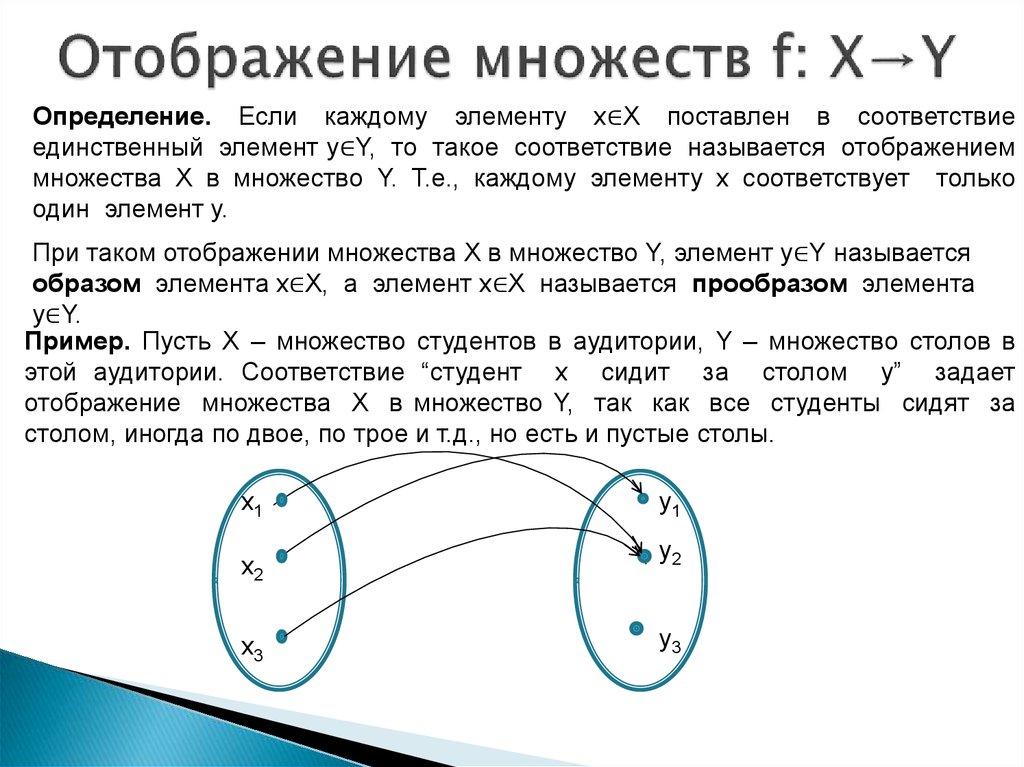 Это означает, что все элементы спарены и спарены один раз.
Это означает, что все элементы спарены и спарены один раз.
Пусть \(f \colon X \to Y \) будет функцией. Тогда \(f\) биективно , если оно инъективно и сюръективно; то есть каждый элемент \( y \in Y\) является образом ровно одного элемента \( x \in X.\)
Функция \( f \ двоеточие {\ mathbb R} \to {\ mathbb R} \), определяемая выражением \( f (x) = 2x \), является биекцией.
Функция \( f \colon {\mathbb Z} \to {\mathbb Z} \), определяемая выражением \( f(n) = \begin{cases} n+1 &\text{if } n \text{, нечетное} \\ n-1&\text{если } n \text{ четное}\end{cases}\) является биекцией. 9\text{th} \text{ месяц}\) является биекцией.
Обратите внимание, что приведенные выше обсуждения подразумевают следующий факт (примеры см. Вики биективных функций):
Если \(X\) и \(Y\) конечные множества и \(f\двоеточие X\к Y\) взаимно однозначно, то \( |X| = |Y|.\)
Следующая альтернативная характеристика биекций часто полезна в доказательствах:
Предположим, что \( X \) непусто.
Тогда \( f \colon X \to Y \) является биекцией тогда и только тогда, когда существует функция \( g\colon Y \to X \) такая, что \( g \circ f \) является тождеством на \( X \) и \( f\circ g\) является тождеством на \( Y;\), то есть \(g\big(f(x)\big)=x\) и \( f\big(g (y)\big)=y \) для всех \(x\in X, y \in Y.\). Когда это происходит, функция \( g \) называется 92.\) Почему бы и нет?\(\большой)\)
Процитировать как: Биекция, инъекция и сюръекция. Brilliant.org . Извлекаются из https://brilliant.org/wiki/bijection-injection-and-surjection/
Инъективный, Сюръективный и Биективный
«Инъективный, Сюръективный и Биективный» говорит нам о том, как ведет себя функция.
Функция — это способ сопоставления элементов набора «A» — набора «B»:
Давайте посмотрим на это более внимательно:
A Общая функция указывает от каждого члена «A» к члену «B».
Это никогда не имеет одного «А», указывающего на несколько «В», поэтому один ко многим не подходит в функции (так что-то вроде «f (x) = 7 или 9″ не допускается)
Но более одного «А» может указывать на один и тот же «В» ( «многие к одному» допустимо )
Инъективный означает, что у нас не будет двух или более «А», указывающих на одну и ту же «В».
Таким образом, «многие к одному» НЕ подходит для (что подходит для общей функции).
Так как это тоже функция один-ко-многим не подходит
Но у нас может быть «В» без соответствующего «А»
Инъективный также называется » Один-к-одному »
Surjective означает, что у каждого «B» есть по крайней мере одно , соответствующее «A» (возможно, более одного).
Не будет пропущена буква «В».
Bijective означает одновременно и Injective, и Surjective.
Думайте об этом как об «идеальном сочетании» между наборами: у каждого есть партнер, и никто не остается в стороне.
Таким образом, существует идеальное » однозначное соответствие » между членами наборов.
(но не путайте это с термином «один к одному», используемым для обозначения инъективного).
Биективные функции имеют обратную !
Если каждое «А» идет к уникальному «Б», и каждому «Б» соответствует «А», то мы можем двигаться вперед и назад, не сбиваясь с пути.
Дополнительные сведения см. в разделе Обратные функции.
На графике
Итак, давайте рассмотрим несколько примеров, чтобы понять, что происходит.
Когда A и B являются подмножествами действительных чисел, мы можем изобразить взаимосвязь.
Пусть у нас есть A по оси x и B по оси y, и посмотрите на наш первый пример:
Это не функция , потому что у нас есть A со многими Б . Это все равно, что сказать f(x) = 2 или 4
. Это не проходит «Тест вертикальной линии» и, следовательно, не является функцией. Но это все еще действительные отношения, так что не сердитесь на это.
Но это все еще действительные отношения, так что не сердитесь на это.
Теперь общая функция может быть такой:
A Общая функция
МОЖЕТ (возможно) иметь B со многими A . Например, синус, косинус и т.д. Совершенно допустимые функции.
Но Инъективная функция » является более строгим и выглядит так:
«Инъективный» (один к одному)
На самом деле мы можем провести «Тест горизонтальной линии»:
Чтобы быть Инъективным , Горизонтальная линия никогда не должна пересекают кривую в 2 или более точках. тест вертикальной линии это функция
Формальные определения
Хорошо, ждите более подробной информации обо всем этом:
Инъективная
Функция f является инъективной тогда и только тогда, когда , х = у .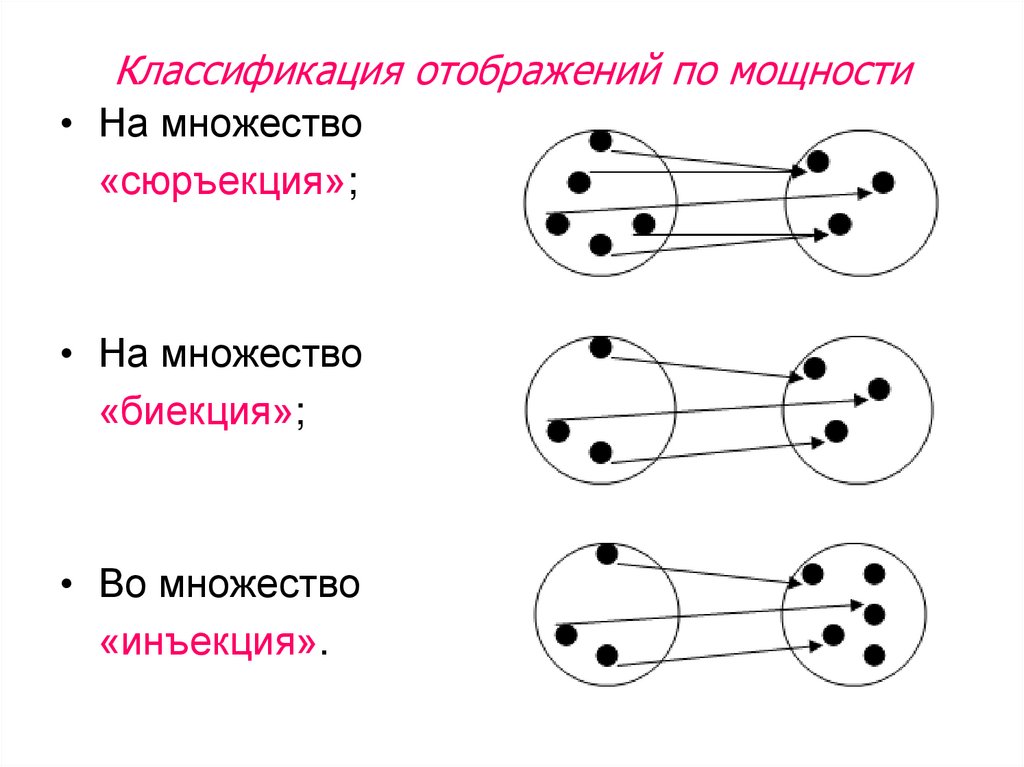
Пример: f ( x ) = x+5 из множества действительных чисел to является инъективной функцией.
Верно ли, что всякий раз, когда f(x) = f(y) , x = y ?
Представьте, что x=3, тогда:
- f(x) = 8
Теперь я говорю, что f(y) = 8, каково значение y? Их может быть только 3, поэтому x=y
Пример: f ( x ) = x 2 из множества действительных чисел в не является инъективной функцией из-за такого рода вещей:
- f ( 2 ) = 4 и
- ф ( -2 ) = 4
Это противоречит определению f(x) = f(y) , x = y , потому что f(2) = f(-2), но 2 ≠ -2
Другими словами, есть два значения A , которые указывают на одно B .
НО если бы мы сделали его из набора натуральных числа к, то это инъективно, потому что:
- f ( 2 ) = 4
- f(-2) отсутствует, потому что -2 не является натуральным номер
Так что домен и кодовый домен каждого набора важны!
Surjective (также называется «на»)
A Function F (от Set A до B ) — IF IF IF IF IF IF IF IF 9013IER IF 9013IVE и 9013VE IF 9013IVE. y в B , существует хотя бы один x в A такой, что f x 3 ) = y , другими словами f сюръективно
если и только если f(A) = B .
y в B , существует хотя бы один x в A такой, что f x 3 ) = y , другими словами f сюръективно
если и только если f(A) = B .
Проще говоря: в каждом B есть A.
Пример: Функция f ( x ) = 2x чисел к множеству неотрицательных четных чисел является сюръективной функцией.
НО ф ( х ) = 2х из набора натуральных числа не являются сюръективными , потому что, например, ни один член in не может быть сопоставлен с 3 с помощью этой функции.
Биективное
Функция f (от множества A до B ) является биективной , если для каждого 6 y 9013 0137 , ровно один x в A Такой, что F ( x ) = Y
IS 92 F IS .

 ;
; А так — снесуть.
А так — снесуть.
 ;
;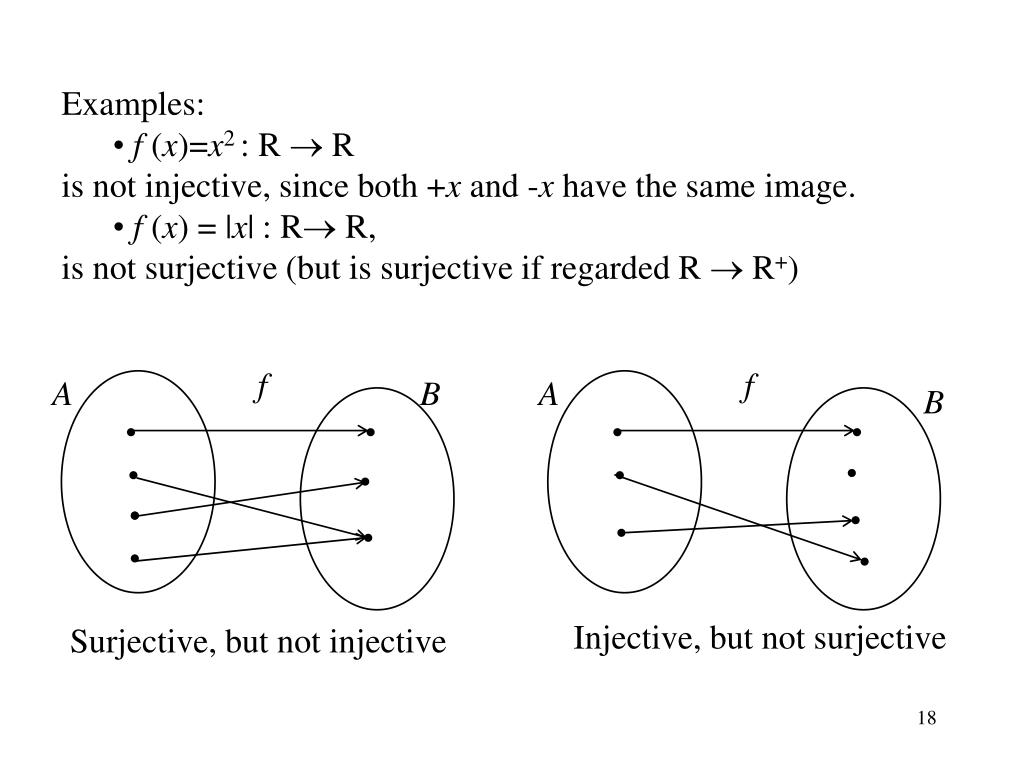 ;
;
 От этого многое зависит — ответ на любой из трёх вопросов может быть положительным или отрицательным.
От этого многое зависит — ответ на любой из трёх вопросов может быть положительным или отрицательным.
 \) Таким образом, \( 3\) не находится в образе \( f.\)
\) Таким образом, \( 3\) не находится в образе \( f.\)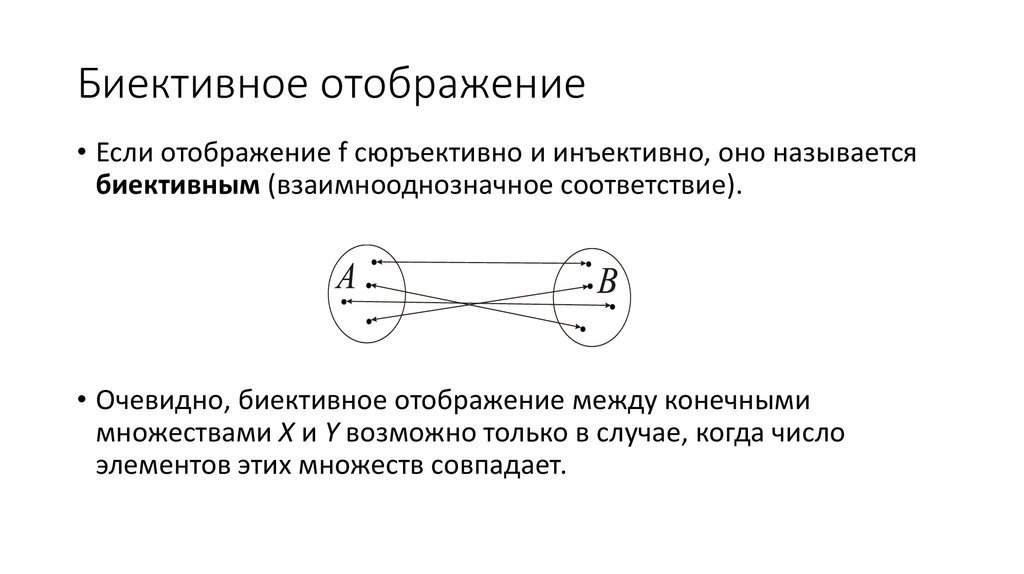 Тогда \( f \colon X \to Y \) является биекцией тогда и только тогда, когда существует функция \( g\colon Y \to X \) такая, что \( g \circ f \) является тождеством на \( X \) и \( f\circ g\) является тождеством на \( Y;\), то есть \(g\big(f(x)\big)=x\) и \( f\big(g (y)\big)=y \) для всех \(x\in X, y \in Y.\). Когда это происходит, функция \( g \) называется 92.\) Почему бы и нет?\(\большой)\)
Тогда \( f \colon X \to Y \) является биекцией тогда и только тогда, когда существует функция \( g\colon Y \to X \) такая, что \( g \circ f \) является тождеством на \( X \) и \( f\circ g\) является тождеством на \( Y;\), то есть \(g\big(f(x)\big)=x\) и \( f\big(g (y)\big)=y \) для всех \(x\in X, y \in Y.\). Когда это происходит, функция \( g \) называется 92.\) Почему бы и нет?\(\большой)\)